Analysis of Tourists' Route Selection in Scenic Areas Based on Game
Theory Model
Ruimin Ma
1
and Lifei Yao
2
1
School of Management, Guangzhou University, Guangzhou, China
2
School of Geography and Tourism, Guangdong University of Finance & Economics, Guangzhou, China
Keywords: Route Choice Behaviour, Evolutionary Game Model, Guidance Information, Numerical Simulation.
Abstract: This paper focuses on analysing the game behaviour of tourists within the scenic area sightseeing system. It
examines how tourists' decision-making in choosing routes is influenced by their perception of crowds and
guidance information. A game pay-off matrix is constructed, taking into account the impact of guidance
information, to understand the decision-making process and optimal choices under different strategies.
Additionally, a replication dynamic equation is established to study the evolution of route choice behaviour
over time. Numerical simulations are conducted to assess the effects of guidance information on tourists' route
choices. The findings indicate that the uniqueness of the Evolutionarily Stable Strategy (ESS) depends on the
magnitude of payoffs loss resulting from congestion, as conveyed through the guidance information.
1 INTRODUCTION
In China, tourist congestion during holiday travel is a
common issue, often resulting in stranded tourists
unable to exit the scenic areas. To alleviate this
problem and enhance the overall tourism experience,
the concept of "smart" has garnered the attention of
scenic area managers. They have introduced various
advanced information technologies such as GPS
positioning, RFID, and Mobile Network
Technologies (4G), as well as handheld navigation
terminals and tourism apps for visitors. These
advanced information technologies facilitate the
collection of spatio-temporal data on tourists, which
in turn supports scenic area managers in designing
effective visitor management and control measures,
and enables them to provide timely and accurate
guidance information. Conversely, for the tourists,
this means they can now access information released
by the scenic area managers, enabling them to
proactively identify congested areas in advance.
Armed with this knowledge, tourists can plan their
visits more effectively, avoiding crowded spots and
optimizing their overall experience and satisfaction.
The impact of guidance information on tourist
flow within the scenic area can be understood as the
macroscopic manifestation of game behaviors
between tourists and other tourists, as well as between
tourists and scenic area managers. From the tourists'
perspective, they aim to enhance their travel
experience by following the guidance information
and switching to alternative routes. On the other hand,
there may be other tourists who choose to continue
with the original route for sightseeing, disregarding
the guidance information. This creates a game-like
dynamic where individual tourists seek to maximize
their own experience. From the viewpoint of scenic
area managers, their objective is to optimize the
fraction of tourists who choose alternative routes
based on the re-evaluation of the utility of remaining
scenic spots along the original route using the
guidance information. By achieving an optimal
balance, the managers aim to improve the overall
tourist experience (assuming that fewer visitors on a
certain tour route would result in a better experience).
Additionally, this approach helps reduce tourist
congestion along the original route.
The remainder of this study is organized as
follows. In Section 2, we present a literature review.
The evolutionary game model to deal with the tourist
route choice behavior is established in Section 3.
Numerical experiment is done in Section 4. Finally,
we summarize the findings in Section 5.
2 LITERATURE REVIEW
In recent years, there has been significant research
conducted on the scientific management of scenic
344
Ma, R. and Yao, L.
Analysis of Tourists’ Route Selection in Scenic Areas Based on Game Theory Model.
DOI: 10.5220/0012283300003807
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (ANIT 2023), pages 344-349
ISBN: 978-989-758-677-4
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

areas, particularly in tourist volume forecasting.
Several prediction methods have been proposed by
scholars. Chen et al. proposed a hybrid approach that
combines Support Vector Regression (SVR) with
adaptive genetic algorithm (AGA) and seasonal index
adjustment to forecast holiday daily tourist flow (R.
Chen, 2015). Assaf et al. introduced a comprehensive
approach based on a Bayesian global vector
autoregressive (BGVAR) model for tourism demand
analysis (A.G. Assaf, 2019). Yang et al. used web
search query volume to predict visitor numbers for a
popular tourist destination in China, comparing the
predictive power of Google and Baidu search data (X.
Yang, 2015). Li et al. proposed a model named PCA-
ADE-BPNN for forecasting tourist volume based on
Baidu index (S. Li, 2018). Sun et al. developed a
forecasting framework using machine learning and
internet search indexes to forecast tourist arrivals in
popular destinations in China, comparing the
performance of Google and Baidu search results (S.
Sun, 2019). Researchers have also focused on tourist
shunt schemes, which aim to direct visitors along
specific travel routes. Zheng et al. proposed shunt
strategies based on different behavior characteristics
and applied them to Jiuzhaigou as a case study (W.
Zheng, 2013). Kamruzzaman and Karmakar
presented a dynamic content distribution scheme for
sharing contents in tourist attractions, taking practical
issues into consideration (J. Kamruzzaman, 2019).
Furthermore, in the post-modern tourism era, tourist
route recommendation has become a hot topic.
Various methods have been developed based on the
popularity of attractions and available time for
tourists (F. M.Hsu-W. Zheng). However, tourists'
route preferences often change during their tour,
leading to errors in practical application. Moreover,
existing methods do not consider the influence of
guidance information. Therefore, this paper aims to
discuss the route choice behavior of different tourist
groups in scenic areas using evolutionary game
theory.
3 MODEL AND ANALYSIS
A. Hypothesis
In order to analyze the problem of tourist route choice
behavior under guidance information, this paper
makes the following assumptions:
H1: Game participants are tourist groups in scenic
area system, which meet the characteristics of
bounded rationality.
H2: Tourists in the system show heterogeneity
and adjust their tour plans based on their perception
of crowding. Some tourists, who are sensitive to
crowded areas, may choose to visit less crowded spots
first by taking a detour. In this paper, we categorize
tourists into two groups based on their perception of
crowding: Group G
1
, consisting of tourists with low
crowding perception or sensitivity to travel distance,
and Group G
2
, consisting of tourists with high
crowding perception or less sensitivity to travel
distance.
H3: All visitors in the system will visit each scenic
spot in turn, as shown in Figure.1, the strategy set of
game players is S ={S
1
:Route 1; S
2
:Route 2 }, where
S
1
represents tourists first visit the scenic spot A
1
and
then visit A
2
, S
1
represents tourists first visit the scenic
spot A
2
and then visit A
1
. S
1
is the planned tour route
before the tour, which conforms to the predilection of
tourist route choice. S
2
is an alternative route, which
need to take a longer distance.
A
1
A
2
O
A
1
A
1
A
2
A
2
D
Route 1
Route 2
O
D
Information
DM
DM
Figure 1. Analysis on the evolution of tourist routing
behavior.
B. Evolutionary Game Model
1) Payoffs Matrix and Variables
Based on the above analysis and model assumptions,
the costs and benefits of tourist groups in different
strategies can be obtained. Let V
ij
be the payoffs of
tourist group G
i
selecting the strategy S
j
. In this paper
i =1,2 and j=1, 2. Table 1 shows the payoffs matrix of
the tourist group route choice with guidance
information.
Table 1: Payoffs matrix tourist group G
1
and G
2.
Tourist group G
1
Tourist group G
2
S
1
S
2
S
1
V
11
-R, V
11
-R
V
11
+R
1
, V
22
-D
1
S
2
V
12
-D
2
, V
21
+R
2
V
12
-D
3
, V
22
-D
4
In Fig. 1, upon receiving the induced message of
congestion on route 1, tourists in G
1
will reconsider
their travel routes at point DM, considering the
behavior of other tourists and payoffs of different
route choices to maximize their benefits. If G
1
adopts
strategy S
1
(traveling on the original route), with no
changes from other tourists, G
1
will experience more
serious congestion (payoff loss denoted as V
11
-R). If
G
1
adopts strategy S
2
(traveling on the alternative
route), there will be temporary path replacement
effects and detour losses (payoff loss denoted as V
12
-
Analysis of Tourists’ Route Selection in Scenic Areas Based on Game Theory Model
345

D
2
). If G
2
adopts strategy S
1
after receiving the
information, G
1
's payoff varies depending on whether
G
1
chooses strategy S1 or S
2
. Choosing S
1
leads to
congestion reduction and benefits for G
1
(V
11
+ R
1
).
Choosing S
2
results in congestion on the alternative
route due to the shift in tourists and detour losses (V
12
-
D
3
). For G
2
, their payoffs depend on G
2
's strategy
decisions: V
21
-R and V
21
+R
2
for strategy S
1
, V
22
-D
1
and V
22
-D
4
for strategy S
2
. Due to G
1
's low crowding
perception and sensitivity to travel distance, detours
result in more payoff loss for G
1
(D
3
> D
4
). When the
two groups choose different strategies, congestion on
route 1 is eased. Tourists on route 1 benefit without
the need for detours, while those on route 2 incur
losses from detour costs.
For the group selecting S
1
, G
1
's benefits exceed
G
2
's (R
1
> R
2
). For the group selecting S
2
, G
1
's loss is
smaller than G
2
's due to travel distance sensitivity (D
2
> D
1
). The losses incurred by detouring (D
3
) are
greater than intensified congestion ((D
2
), and the
same applies to D
4
and D
1
. In summary, the relations
are: D
3
> D
2
> D
4
> D
1
and R
1
> R
2
.
2) Replicator Dynamic Equation and Equilibrium
Points
In this paper, we refer to the replication dynamic
mechanism to address the strategies selecting
problem of the tourist group G
1
and G
2
with the
influence of guidance information. The idea is that the
next stage the growth rate of population in some
strategy and select the strategy in the current
population and the proportion of the profits were
positively correlated, evolve over time, high yield of
population proportion will increase, low income
population proportion will be reduced, until dying.
Let the fraction of G
1
choosing S
1
be x, then the
fraction of G
2
choosing S
2
be 1-x. Let the fraction of
G
2
choosing S
1
be y, then the fraction of G
2
choosing
S
2
be 1-y.
The payoffs of G
1
choosing S
1
are:
11 1 11 1
( ) ( )
x
U R R y V R    
(1)
The payoffs of G
1
choosing S
2
are:
1
12 3 2 12 3
( ) ( )
x
U D D y V D

   
(2)
Then, the average expected payoffs of different
strategies of G
1
is:
1 2 3 1 1 3 3 2 1 3
( ) ( ) ( ) ( )U D D R R xy R D x D D y V D         
(3)
The payoffs of G
2
choosing S
1
are:
21 2 21 2
( ) ( )
y
U R R x V R    
(4)
The payoffs of G
2
choosing S
2
are:
1
22 4 1 22 4
( ) ( )
y
U D D x V D

   
(5)
Similarly, the average expected payoffs of
different strategies of G
2
is:
2 1 4 2 2 4 4 2 2 4
( ) ( ) ( ) ( )U D D R R xy R D y D D x V D         
(6)
The replicated dynamic equation of G
1
choosing
route 1 is as follows:
11 1 3 1 2 1 3
( ) ( ) ( 1)[( ) ( )]
dx
V x x U U x x D R R D y R D
dt
         
(7)
The replicated dynamic equation of G
2
choosing
route 1 is as follows:
21 2 4 2 1 2 4
( ) ( ) ( 1)[( ) ( )]
dy
V y y U U y y D R R D x R D
dt
         
(8)
When y=(R
1
+D
3
)/(D
3
+R+R
1
-D
2
), at this time
V(x)≡0, that means if the initial fraction of G
2
choosing route 1 satisfies the above equation, the
system must be stable, no matter whatever the
strategies are chosen by the tourists in G
1
, the payoffs
they get are the most satisfactory.
When 0<y<(R
1
+D
3
)/(D
3
+R+R
1
-D
2
), at the
moment, V’(0)>0 and V’(1)<0, the evolutionary
stable strategies of the dynamic system (abbreviated
as ESS) is x
*
=1. That means if the initial fraction of
G
2
choosing route 1 satisfies the above equation, the
payoffs of G
1
choosing route 1are larger than the
payoffs of G
1
choosing route 2, so that, as time goes
on, all the tourists in G
1
in the dynamic system will
choose route 1.
When (R
1
+D
3
)/(D
3
+R+R
1
-D
2
)<y<1, at the time,
V’(0)<0 and V’(1)>0, the ESS of dynamic system is
x
*
=0. That means if the initial fraction of G
2
choosing
route 1 satisfies the above equation, the payoffs of G
1
choosing route 2 are larger than the payoffs of G
1
choosing route 1, so that, as time goes on, all the
tourists in G
1
in the dynamic system will choose route
2.
3) Equilibrium Point Stability Analysis
According to Friedman's evolutionary game
theory, the equilibrium points of the dynamic system
may include (0,0), (0,1), (1,0), (1,1), and (x
0
, y
0
). The
equilibrium points can be determined by analyzing
the local stability of the Jacobian matrix. Specifically,
in this paper, the Jacobian matrix of the path selection
game system is examined:
3 1 2 1 3 3 1 2
4 2 1 4 2 1 2 4
(2 1)[( ) ( )] ( 1)( )
( 1)( ) (2 1)[( ) ( )]
x D R R D y R D x x D R R D
y y D R R D y D R R D x R D
         



         

J
The determinant of Jacobian matrix
det J
is:
3 1 2 1 3 4 2 1 2 4
3 1 2 4 2 1
det (2 1)[( ) ( )](2 1)[( ) ( )]
( 1)( ) ( 1)( )
x D R R D y R D y D R R D x R D
x x D R R D y y D R R D
            
        
J
The trajectory of Jacobian matrix
trJ
is:
3 1 2 1 3 4 2 1 2 4
(2 1)[( ) ( )]+(2 1)[( ) ( )]tr x D R R D y R D y D R R D x R D            J
In this paper, we will pay more attention on how
the guidance information has an effect on the
evolution process of tourists' route choice, so we will
not give more discussion about the point (x
0
, y
0
). This
paper analyzes how the value of
R
influences the
dynamic evolution process of tourists’ route choice
behavior. The discussion of R is mainly divided into
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
346

the following four situations, the stability analysis
about different values of R is shown in Table 2.
Table 2. The evolutionary stability state under various
cases.
R=0
0<R<D
1
(x, y)
(0, 0)
(0, 1)
(1, 0)
(1, 1)
(0, 0)
(0, 1)
(1, 0)
(1, 1)
det J
+
-
-
+
+
-
-
+
trJ
+
Uncertai
n
-
-
+
-
-
State
Unstable
Saddle
point
Unstabl
e
ESS
Unstabl
e
Saddl
e
point
Unstable
ESS
D
1
<R<D
2
R>D
2
(x, y)
(0, 0)
(0, 1)
(1, 0)
(1, 1)
(0, 0)
(0, 1)
(1, 0)
(1, 1)
det J
+
-
+
-
+
+
+
+
trJ
+
Uncertai
n
-
+
-
-
+
State
Unstable
Saddle
point
ESS
Saddl
e
point
Unstabl
e
ESS
ESS
Unsta
ble
When R=0, tourists cannot obtain information
about tourist congestion in the subsequent tour route
during the tour. Therefore, they will follow the pre-
planned route without any route choice during the
tour. The evolutionary trajectory will ultimately
stabilize at the ESS (1,1), where all tourists choose
route 1. This is because without real-time guidance
information, tourists lack awareness of the congestion
status on route 2 and choosing route 2 would result in
detouring and loss of payoffs. Hence, tourists prefer
to choose route 1 based on finding the most
satisfactory travel route.
When 0<R<D
1
, the scenic area provides guidance
information indicating congestion on route 1, but the
payoffs loss caused by congestion is less than the
payoffs loss of detouring to route 2. The evolutionary
trajectory will also stabilize at the ESS (1,1), with all
tourists continuing to choose route 1. Despite the
release of real-time guidance information, the
congestion's impact on payoffs is not significant
enough to outweigh the detouring losses, resulting in
no change in tourists' route choice.
When D
1
<R<D
2
， the scenic area provides
guidance information indicating congestion on route
1, and the congestion's impact on payoffs is larger
than the detouring losses to route 2 but smaller than
detouring losses to route 1. The evolutionary
trajectory will stabilize at the ESS (1,0), with tourists
in Group G1 (low crowding perception) continuing to
choose route 1 and tourists in Group G2 (high
crowding perception) choosing route 2. In this case,
Group G1 is less sensitive to the payoffs loss caused
by increasing tourist volume and prefers to tour with
higher tourist density. However, Group G2, being
more sensitive to crowding, chooses the alternative
route (route 2) to avoid congested areas and mitigate
payoffs loss.
When R>D
2
, the scenic area provides guidance
information indicating congestion on route 1, and the
congestion's impact on payoffs is larger than the
detouring losses to route 2. The evolutionary
trajectory will stabilize at the ESS (0,1) and (1,0),
with tourists either in Group G1 touring route 1 and
tourists in Group G2 touring route 2, or vice versa. In
this case, both groups bear the payoffs loss caused by
congestion. When one group chooses the alternative
route to alleviate congestion, the other group avoids
the loss caused by congestion on the original route.
The stable convergence of the system in this situation
is uncertain, as it depends on the specifics of the
payoffs matrix and initial parameter values.
4 NUMBERICAL SIMULATION
The MATLAB 2016a software is applied to simulate
the dynamic evolutionary trajectories of the
evolutionary system, for the purpose of verifying the
accuracy of model consequences and making
dynamic evolution trend more explicitly and vividly.
The initial values of each parameter are listed as
follows: D
1
=4, D
2
=8, D
3
=10, D
4
=6, R
1
=5, R
2
=6.
(a)
(b)
Figure 2. (a) and (b) Dynamic evolutionary paths (R=0).
In Fig. 2(a), higher initial fractions of G2 choosing
route 1 result in faster convergence to the ESS, while
lower initial fractions of G1 choosing route 1 lead to
faster convergence in Fig. 2(b).
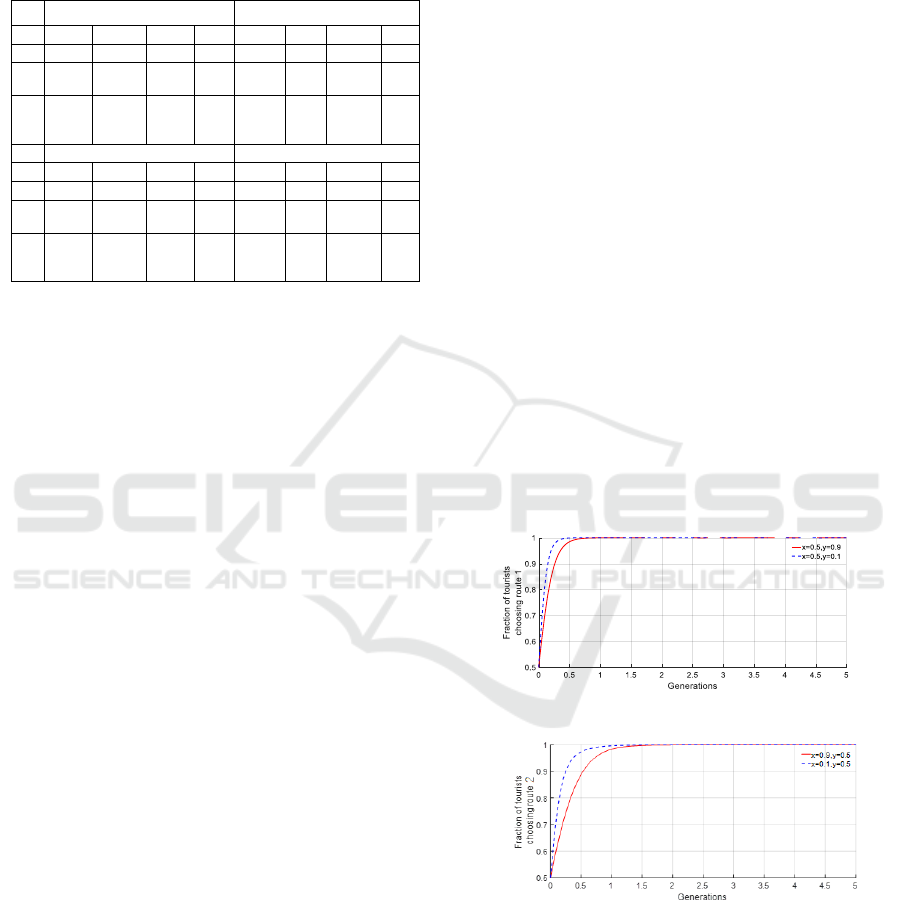
In Fig. 3(a), higher initial fractions of G2 choosing
route 1 result in faster convergence to the ESS.
Analysis of Tourists’ Route Selection in Scenic Areas Based on Game Theory Model
347

Initially, some tourists in G2 try to tour on route 2 but
eventually realize that the payoffs of choosing route
1 are larger. This realization takes a relatively long
time for G2 to converge to the ESS. In Fig. 3(b), lower
initial fractions of G1 choosing route 1 lead to faster
convergence to the ESS. This is because G1, with
high crowding perception, experiences larger payoffs
for detouring compared to touring route 1 when the
fraction choosing route 1 is high. As time progresses,
the payoffs for G1 choosing route 2 decline gradually,
leading G1 to evolve towards route 1 and ultimately
stabilize on route 1.
(a)
(b)
Figure 3. (a) and (b) Dynamic evolutionary paths (0<R<
D
1
, R=2).
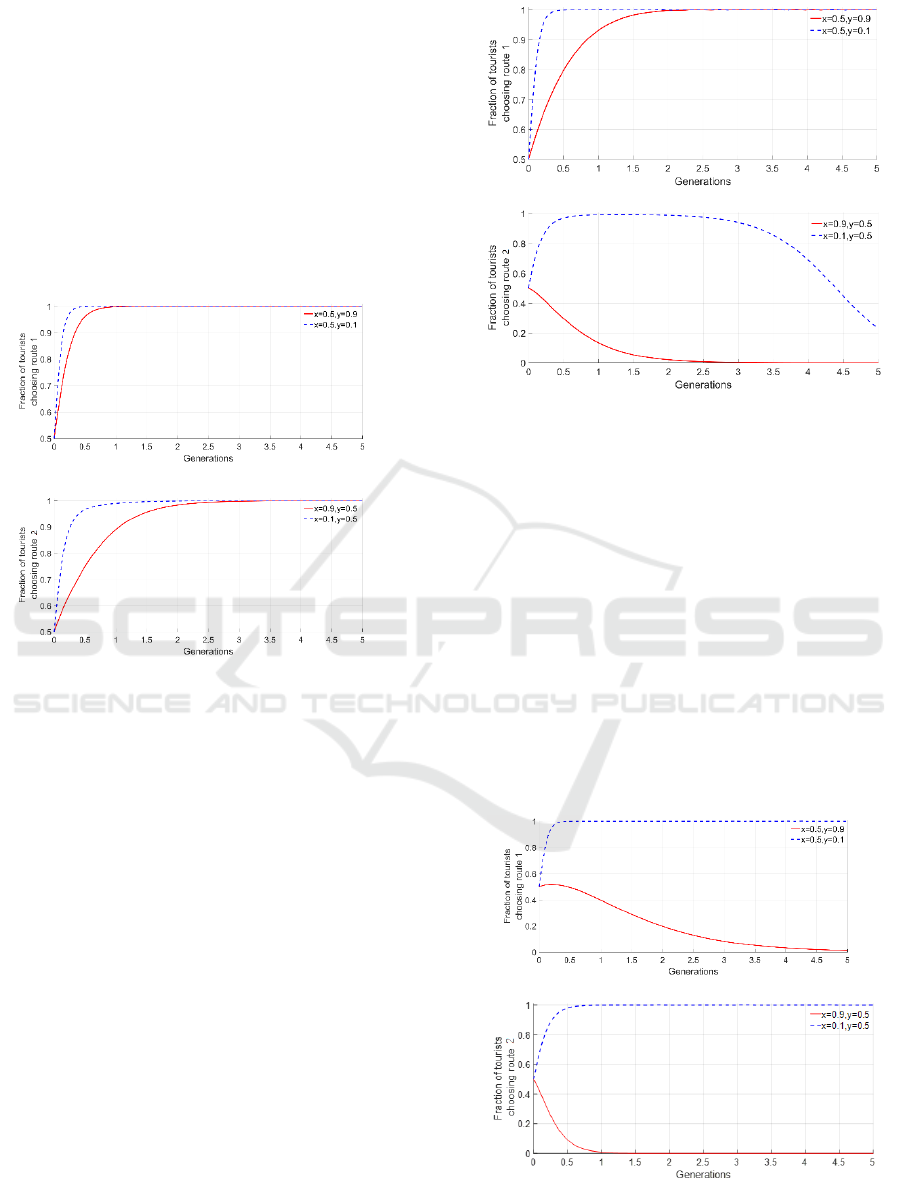
In Fig. 4(a), lower initial fractions of G2 choosing
route 1 lead to faster convergence to the ESS. When
most tourists initially choose route 2, the higher
payoffs for G2 choosing route 1 result in all tourists
in G2 ultimately traveling on route 1, leading to a
quick convergence to the stable state. Fig.4(b)
illustrates that for initial fractions of (0.1,0.5) and
(0.9,0.5), the trajectory towards the stable state varies
greatly. Initially, G1 experiences a rapid increase in
the fraction choosing route 1 due to higher payoffs.
However, over time, the payoffs for G1 choosing
route 1 decrease relative to choosing route 2, leading
to a gradual increase in the fraction choosing route 2.
Ultimately, all tourists in G1 choose route 2,
converging to the stable state. When R=6, regardless
of the initial x value, all tourists in G1 will eventually
choose route 2.
(a)
(b)
Figure 4. (a) and (b) Dynamic evolutionary paths
(D
1
<R<D
2
, R=6).
In Fig. 4(a), for G1 with initial strategy fractions
of (0.5,0.1) and (0.5,0.9), different evolutionary
stable states are observed. When y=0.1, G
1
tends to
ESS (1,0) due to higher payoffs on route 1. When
y=0.9, despite low crowding perception, G
1
prefers
route 2 due to larger congestion payoffs, leading to
ESS (0,1). In Fig.4(b), for G
2
with initial strategy
fractions of (0.1,0.5) and (0.9,0.5), different
evolutionary stable states emerge. When x=0.1, G
2
tends to ESS (1,0) due to lower initial fraction on
route 1. When x=0.9, higher crowded perception in
G
2
makes congestion payoffs larger, resulting in a
preference for route 2 and ESS (0,1) for G
1
.
(a)
(b)
Figure 4. (a) and (b) Dynamic evolutionary paths (R>D
2
,
R=9).
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
348

5 CONCLUSIONS
This paper applies evolutionary game theory to study
the route choice behavior of tourist groups with
different perceptions of crowding within a scenic
area. The influence of guidance information on route
choice is analyzed, considering various strategies of
information supply. A game model is constructed to
examine the evolutionary stable states of tourist route
choices under the impact of guidance information.
Dynamic equations are used to analyze the long-term
stability evolution trend of the scenic tours system.
Numerical experiments are conducted to simulate the
effects of different guidance information strategies on
the system's evolution. The main conclusions are as
follows: (1) Without guidance information, all
tourists choose the original route (unique ESS). (2)
With guidance information, the uniqueness of ESS
depends on the size of payoffs loss caused by
congestion revealed in the information: (a) When the
payoffs loss from congestion is small, all tourists still
choose the original route (little effect from guidance
information); (b) When the payoffs loss from
congestion falls between the detouring payoffs loss of
two tourist groups, tourists with low crowding
perception choose the original route and those with
high crowding perception choose alternative routes
(successful guidance information to ease congestion);
(c) When the payoffs loss from congestion exceeds
the detouring payoffs loss of both groups, the ESS for
route choice becomes non-unique, with each group
choosing different routes to avoid congestion.
ACKNOWLEDGMENTS
This work was supported by Humanities and social
sciences fund of the Ministry of Education
(No.19YJC630119).
REFERENCES
R. Chen, C.Y. Liang, W.C. Hong, D.X. Gu, Forecasting
holiday daily tourist flow based on seasonal support
vector regression with adaptive genetic algorithm(J).
Appl. Soft Comput., 2015, 26: 435-443.
https://doi.org/10.1016/j.asoc.2014.10.022
A. G. Assaf, G. Li, H. Song, M. G. Tsionas, Modeling and
forecasting regional tourism demand using the Bayesian
global vector autoregressive (BGVAR) model (J). J.
Travel Res, 2019, 58(3): 383-397,
https://doi.org/10.1177/0047287518759226
X. Yang, B. Pan, J. A. Evans, B. Lv. Forecasting Chinese
tourist volume with search engine data (J). Tourism
Manage., 2015, 46, 386-397.
https://doi.org/10.1016/j.tourman.2014.07.019
S. Li, T. Chen, L. Wang, C. Ming, Effective tourist volume
forecasting supported by PCA and improved BPNN
using Baidu index (J). Tourism Manage., 2018, 68: 116-
126. https://doi.org/10.1016/j.tourman.2018.03.006
S. Sun, Y. Wei, K. L. Tsui, S. Wang, Forecasting tourist
arrivals with machine learning and internet search index
(J). Tourism Manage., 2019, 70:1-10.
https://doi.org/10.1016/j.tourman.2018.07.010
W. Zheng, P. Ren, P. Ge, Q. An, M. Jin, Tourist
management based on behaviour characteristics during
peak travel period - a case study of Jiuzhaigou (J). Int.
J. Environ. Pollut., 2013, 51(3-4):222-237.
https://doi.org/10.1504/IJEP.2013.054031
J. Kamruzzaman, G.Karmakar, A dynamic content
distribution scheme for decentralized sharing in tourist
hotspots (J). J.Netw. Comput. Appl., 2019, 129, 9-24.
https://doi.org/10.1016/j.jnca.2018.12.011
F. M. Hsu, Y. T. Lin, T. K. Ho, Design and implementation
of an intelligent recommendation system for tourist
attractions: The integration of EBM model, Bayesian
network and Google Maps (J). Expert Syst. Appl., 2012,
39(3): 3257-3264.
https://doi.org/10.1016/j.eswa.2011.09.013
J. Ruiz-Meza, J. R. Montoya-Torres, Tourist trip design
with heterogeneous preferences, transport mode
selection and environmental considerations. Ann. Oper.
Res., 2021, 305(1-2): 227-249.
https://doi.org/10.1007/s10479-021-04209-7
I. Y.Choi, Y. U.Ryu, J. K. Kim, A recommender system
based on personal constraints for smart tourism city(J).
Asia Pac. J. Tourism Res., 2021, 26(4): 440-453.
https://doi.org/10.1080/10941665.2019.1592765
Z. Liao, W. Zheng, Using a heuristic algorithm to design a
personalized day tour route in a time-dependent
stochastic environment (J). Tourism Manage., 2018,
68:284-300.
https://doi.org/10.1016/j.tourman.2018.03.012
W. Zheng, H. Ji, C. Lin, W. Wang, B. Yu, Using a heuristic
approach to design personalized urban tourism
itineraries with hotel selection (J). Tourism Manage.,
2020, 76:103956.
https://doi.org/10.1016/j.tourman.2019.103956
Analysis of Tourists’ Route Selection in Scenic Areas Based on Game Theory Model
349