Analysis and Improvement of Oscilloscope Jitter Measurement Floor

Based on Simulation Experiments

Jiangmiao Zhu, Yufen Sun, Kaige Man, Yidi Wang and Yifan Wang

Beijing University of Technology, Beijing, China

Keywords: Oscilloscope, Clock Jitter, Inherent Noise, Jitter Measurement Floor, Simulation Experiment.

Abstract: Oscilloscopes are crucial universal instruments in the fields of electronic information and communication,

capable of making time-domain measurements of signals and systems. Due to imperfect hardware,

oscilloscopes exhibit a certain jitter. This paper refers to the jitter originating from the oscilloscope itself is

called the oscilloscope jitter measurement floor. During the process of measuring signal jitter using an

oscilloscope, the jitter measurement floor inevitably affects the measurement results, introducing errors. This

paper primarily investigates factors influencing the oscilloscope jitter measurement floor, including the

oscilloscope’s sampling clock jitter, inherent noise, and input signal frequency，etc.. Simultaneously, the

impact of these factors on oscilloscope measurement results is assessed, and experimental verification is

conducted using an oscilloscope simulation platform. Finally, methods for reducing the oscilloscope jitter

measurement floor are proposed.

1 INTRODUCTION

The definition of jitter varies slightly across different

fields, leading to inconsistencies in the definitions

provided by international organizations and

institutions such as the International Electrotechnical

Commission (IEC), Institute of Electrical and

Electronics Engineers (IEEE), and American

National Standards Institute (ANSI), etc.(Std, I.-

Peterich, D.),. This paper adopts the latest standard

for defining jitter as provided by IEEE in 2020, i.e.,

jitter is the deviation between the actual time of a set

of events and their ideal values (Std, I., Zhu

Jiangmiao).

Jitter is a measure of short-term uncertainty in the

time domain of a signal and is assessed using phase

noise in the frequency domain to measure the short-

term instability of the signal. Oscilloscopes are

indispensable for time-domain measurement and

analysis of signals. However, due to the presence of

oscilloscope jitter measurement floor, the measured

jitter results inevitably contain errors other than the

signal jitter. If the signal jitter is significantly greater

than the oscilloscope jitter measurement floor, then

these errors can be neglected. However, if the above

requirement is not met, the oscilloscope jitter

measurement floor will cause significant errors,

thereby affecting the accuracy of the measurement

results. Therefore, it is of great importance to identify

the factors contributing to the oscilloscope jitter

measurement floor, understand how these factors

affect the measurement results, and minimize their

impact in order to study oscilloscope measurement.

Oscilloscopes can be categorized as analog

oscilloscopes and digital oscilloscopes. With

technological advancements, analog oscilloscopes

have been gradually replaced by digital oscilloscopes,

and digital oscilloscopes can further be classified into

sampling oscilloscopes and real-time oscilloscopes.

Sampling oscilloscopes are also known as

communication signal analyzers. However, whether it

is a sampling oscilloscope or real-time oscilloscope,

the components such as analog-to-digital converter

(ADC), attenuators and amplifiers in the analog front-

end, are vital for their operation.

The primary sources contributing to the

oscilloscope jitter measurement floor are the

sampling clock jitter in the ADC, oscilloscope's

analog front-end and digital processing. On the basis

of clarifying how the above factors affect the

oscilloscope jitter measurement floor is crucial for

effectively reducing their impact on the measurement

results.

Zhu, J., Sun, Y., Man, K., Wang, Y. and Wang, Y.

Analysis and Improvement of Oscilloscope Jitter Measurement Floor Based on Simulation Experiments.

DOI: 10.5220/0012284700003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 391-396

ISBN: 978-989-758-677-4

391

2 SAMPLING PRINCIPLE OF

SAMPLING OSCILLOSCOPE

An oscilloscope is an electronic instrument that

converts electrical signals, primarily voltage, into

visible traces on a display screen. In other words, an

oscilloscope can convert electrical signals into optical

signals and dynamically plot the electrical signals in

a two-dimensional form over time. The voltage is

plotted on the vertical axis of the oscilloscope display

screen, while the time is plotted on the horizontal axis.

The plotted voltage and time are ultimately displayed

as a graph of the input signal, often referred to as a

"waveform". As the characteristics of the input signal

change, the displayed waveform on the oscilloscope

screen is continuously updated.

The bandwidth range of a sampling oscilloscope

is much wider than that of a real-time oscilloscope,

meaning it can measure signals with a broader

bandwidth range. Due to the high frequency of the

input signal, the oscilloscope does not directly display

the measured signal. Instead, it uses a frequency-

conversion method to sample the signal at different

positions in the waveform of the measured signal,

using a time much shorter than the period of the

measured signal. The sampling is performed

sequentially in a stepped order for each waveform of

the signal (Wang Shibiao).

PRBS

1 2 3

Re-arm time

15bit

Trigger point

Sampling point

Sequential delay

Reconstructed

waveform

Pattern

trigger

Fig. 1. Schematic diagram of sampling principle of

sampling oscilloscope-

Taking PRBS code as an example, Fig 1 illustrates

the sampling principle of a sampling oscilloscope. A

trigger point is provided by a pattern trigger from the

clock signal, and sampling is performed after the

trigger. After each pattern trigger, new sampling is

carried out at sampling points slightly away from the

pattern trigger point and repeated. Then, the sampled

oscilloscope reconstructs the waveform. This paper

focuses on studying the jitter of sampling

oscilloscopes, and the oscilloscopes mentioned

following the paper refer to digital sampling

oscilloscopes unless otherwise specified.

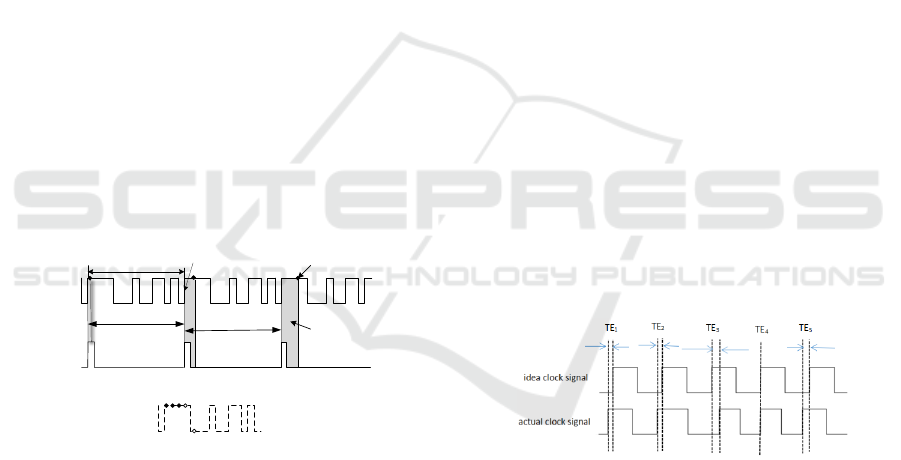
3 SAMPLE CLOCK JITTER

The sampling clock is an essential part of ADC. The

sampling oscilloscope through the ADC to sample the

input signal, and then converting each sample point

of the analog signal into a digital value. The sampling

clock controls when the ADC performs the sampling.

In other words, the frequency of the sampling clock

determines the time interval of the oscilloscope.

However, the clock signal generated by the sampling

clock itself exhibits a certain jitter, which is referred

to as clock jitter. Clock jitter is an inherent

characteristic that cannot be completely eliminated (S.

Huang) and is one of the main sources of the

oscilloscope jitter measurement floor.

Clock jitter can be classified into random jitter and

deterministic jitter. Random jitter is caused by

thermal noise, flicker noise, and shot noise, which are

related to the electronic and hole characteristics of

electronic and semiconductor devices. The sources of

deterministic jitter are switching power supply noise,

crosstalk, and electromagnetic interference, etc.,

which are related to circuit design (LI Liping, Zhang

Changjun).

Clock jitter can be represented in various ways

(Zhu Jiangmiao), such as Period jitter (PEJ), Cycle to

Cycle jitter (C2C), and Timing Error (TE). In this

paper, TE is used to represent clock jitter, which

refers to the deviation between the actual edge of the

clock and the ideal edge. Fig 2 gives the schematic

diagram of TE.

Fig. 2. Schematic diagram of TE in clock jitter.

Due to the high sampling clock frequencies of

modern high-bandwidth oscilloscopes, which can

reach up to 160G/s or higher, the time interval

between samples is very small. Therefore, ensuring

that each actual sample point falls at the ideal position

is challenging. In other words, the existence of clock

jitter causes the sampled amplitude of the signal to not

correspond exactly to its actual sampling time,

thereby affecting the measurement results of the

oscilloscope. Since clock jitter includes both

deterministic jitter and random jitter, averaging

multiple waveforms can effectively remove the

random jitter in clock jitter, reducing the magnitude

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

392

of clock jitter. Fig 3 illustrates the impact of clock

jitter on the measurement results through simulation

experiments. In the figure 3, a represents the input

signal measured by the oscilloscope without

waveform averaging, and b represents the input signal

measured by the oscilloscope with waveform

averaging.

Fig. 3. Schematic diagram of measurement results with and

without clock jitter.

Therefore, to ensure that the deviation between

the actual sampling time and the ideal sampling time

of each sampling point instant, i.e. TE, as small as

possible, is a critical task to improve the measurement

accuracy of the oscilloscope. However, regardless of

technological advancements, the jitter value will

never be zero due to the inherent characteristics of the

hardware equipment.

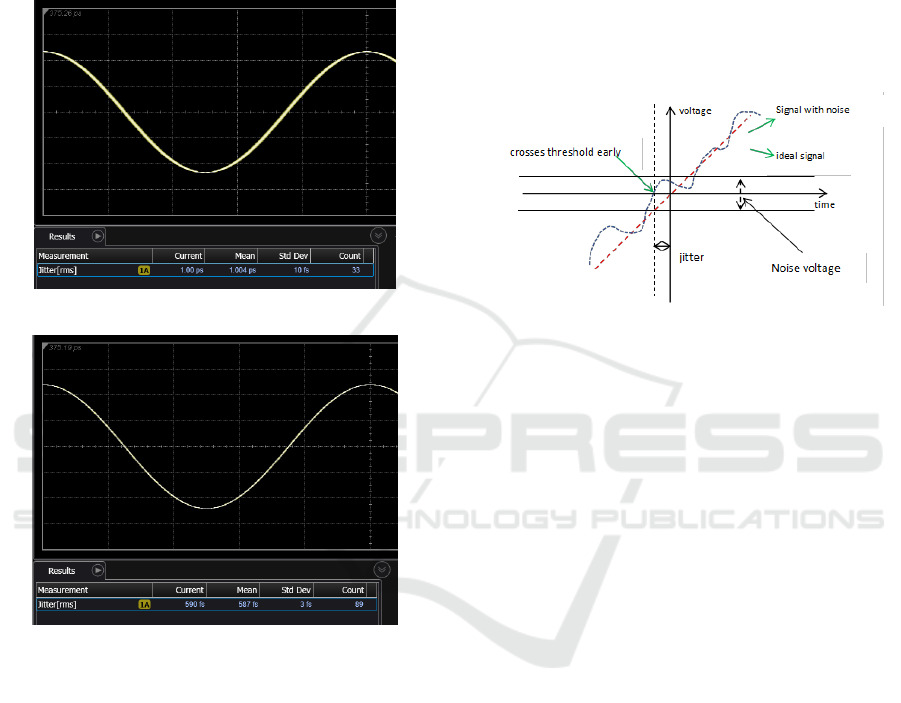
4 INHERENT NOISE

The noise in the analog front-end and digital

processing of an oscilloscope is also one of the

sources of jitter measurement floor, which is referred

to as inherent noise in this article. In addition to

introducing amplitude measurement errors, the

inherent noise of an oscilloscope can also cause

changes in the threshold crossing time of the signal,

resulting in jitter (M. Shimanouchi, 2001).The

schematic diagram illustrating the specific impact of

inherent noise on jitter measurement floor is shown in

Figure 4. Next, we will separately discuss the noise in

the digital processing of the oscilloscope and the

noise generated by the analog front-end.

Figure 4: Schematic diagram showing the impact of noise

on jitter measurement floor.

4.1 Quantization Noise

Quantization error in the digital processing of an

oscilloscope is also known as quantization noise,

which is introduced by the oscilloscope's analog-to-

digital converter (ADC) and is mainly related to the

resolution and performance of the ADC.

According to the principles of sampling and

quantization in a sampling oscilloscope, the

resolution of the ADC chip directly determines the

vertical sampling accuracy of the oscilloscope. For

example, if the ADC conversion chip is 8-bit, the

vertical signal can be divided into 256 segments and

then quantized. Assuming the input signal amplitude

is 1V, the quantization accuracy is 1V/256, which

means the ADC can only distinguish voltage signals

greater than 1/256V. if the ADC conversion chip is

10-bit, the vertical signal can be divided into 1024

segments, and keep the input signal amplitude still at

1V, the quantization accuracy becomes 1V/1024,

meaning the ADC can distinguish voltage signals

greater than 1/1024V. It can be seen that the higher

the number of bits of the ADC chip in the oscilloscope,

the higher the vertical resolution and the smaller the

quantization noise of the oscilloscope. However, for

the same oscilloscope, the number of quantization

bits is generally constant, and therefore its

quantization noise is also fixed.

Analysis and Improvement of Oscilloscope Jitter Measurement Floor Based on Simulation Experiments

393

4.2 Noise Generated by the Analog

Front-End of the Oscilloscope

The noise generated by the analog front-end of the

oscilloscope is mainly caused by the attenuator and

the preamplifier. The analog-to-digital converter

(ADC) cannot distinguish between signal and noise

during sampling, so when the signal is amplified, the

noise will also be amplified. The amplification factor

of the attenuator and preamplifier is not fixed,

resulting in the variability of this noise.

The attenuator and preamplifier of the

oscilloscope can be used to control and adjust the

vertical sensitivity of the oscilloscope, which is an

important component in the front-end circuit of the

oscilloscope, allowing users to select different

sensitivity ranges for the signal to accommodate input

signals with different amplitudes. Therefore, the

vertical sensitivity setting of the oscilloscope and the

amplitude of the input signal can affect the noise

generated by the analog front-end of the oscilloscope

and then affect the jitter measurement floor. To verify

this conclusion, this article uses simulation

experiments to verify the influence of vertical

sensitivity setting and input signal amplitude on the

jitter measurement floor.

1) Influence of Vertical Sensitivity on jitter

measurement floor

Figure 5: Relationship between vertical sensitivity and jitter

rms.

First, a sinusoidal signal with a jitter value of 400

fs is inputted into the simulation software. In the case

of other parameters remain unchanged, the vertical

sensitivity is adjusted and the number of measuring

result (jitter rms) at different vertical sensitivities are

recorded. To avoid experimental variability, multiple

signals with different frequencies are tested, and

multiple sets of data are recorded and plotted. As

shown in Figure 5, regardless of the change in signal

frequency, the oscilloscope's jitter measurement

results decrease as the vertical sensitivity increases. It

should be noted that a higher numerical value of the

vertical sensitivity indicates lower sensitivity. As the

vertical sensitivity decreases, the oscilloscope

measurement results increase. However, the input

signal jitter remains unchanged, indicating that the

jitter measurement floor of the oscilloscope is

increasing, and the trend is consistent with the change

in the measured results in Figure 5.

When the vertical sensitivity decreases, the noise

increases, resulting in an increase in the jitter

measurement floor of the oscilloscope. Therefore,

when using an oscilloscope to measure a signal, it is

advisable to fill the waveform on the oscilloscope

screen as much as possible to reduce the jitter

measurement floor.

2) Influence of Input Signal Amplitude on jitter

measurement floor

To investigate the influence of input signal

amplitude on the jitter measurement floor of the

oscilloscope, the vertical sensitivity of the

oscilloscope is kept constant while changing the input

signal amplitude. Experimental data is recorded and

plotted. As shown in Figure 6, it can be observed that

under the condition of constant vertical sensitivity,

the smaller the signal amplitude, the larger the jitter

measurement result of the oscilloscope. Similarly, the

input signal jitter remains unchanged. This indicates

that the jitter measurement floor increases. This is

because the smaller the signal amplitude, the larger

the amplification factor, and the more severe the

effect of noise. However, this does not mean that a

larger signal amplitude is always better, as once the

signal amplitude exceeds the measurement range of

the oscilloscope, the measurement result will be

invalid.

Figure 6: Relationship between the amplitude of input

signal and jitter rms.

In conclusion, the inherent noise of an

oscilloscope mainly consists of the two factors

mentioned above. The quantization noise is fixed for

a given oscilloscope, while the impact of oscilloscope

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

394

analog front-end noise on jitter is related to the

vertical sensitivity and input signal amplitude of the

oscilloscope. A higher vertical sensitivity setting of

the oscilloscope results in a smaller noise, and vice

versa. Within the measurement range of the

oscilloscope, a larger input signal amplitude leads to

a smaller noise. Therefore, when measuring the input

signal, the vertical sensitivity of the oscilloscope can

be adjusted to make the vertical sensitivity as large as

possible when the signal is displayed completely on

the oscilloscope.

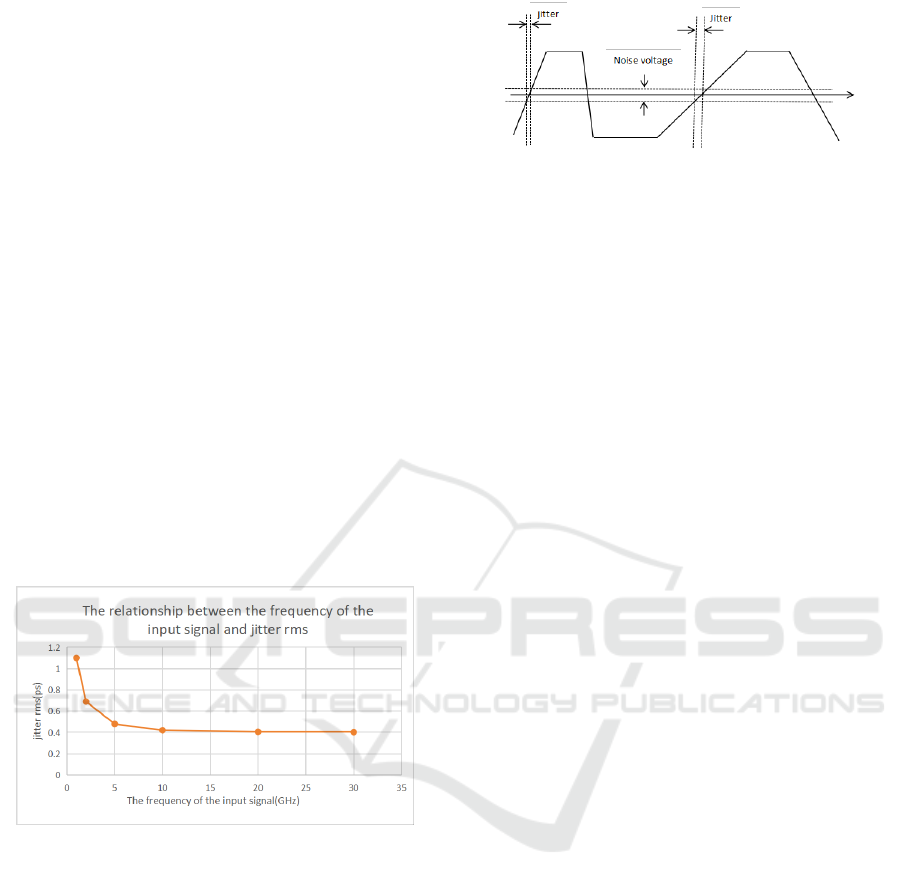
5 INPUT SIGNAL FREQUENCY

In addition to the factors mentioned above, the

frequency of the input signal during actual

measurement will also have an impact on jitter. By

keeping the input signal jitter and vertical sensitivity

constant, the frequency of the input signal is changed,

and the measurement results are recorded. Figure 7

shows the relationship between input signal

frequency and measurement results of oscilloscope in

the simulation experiment.

Figure 7: Relationship between the frequency of input

signal and jitter rms.

According to Figure 7, it can be observed that as

the input signal frequency increases, the jitter

measurement results (jitter rms) of the oscilloscope

decrease. This is because the higher the frequency of

the input signal, the faster the signal conversion rate,

and the less the impact of noise superimposed on the

time axis. The specific impact is illustrated in Figure

8. In other words, the influence of inherent noise on

the measurement results decreases with higher input

signal frequency. This also demonstrates the effect of

the oscilloscope's inherent noise on the jitter

measurement floor.

Figure 8: Schematic diagram of the impact of signal slope

on jitter measurement floor.

6 CONCLUSION

Based on the theoretical analysis and simulation

studies, we can conclude that the jitter measurement

floor of an oscilloscope is affected by the

oscilloscope's sampling clock jitter, inherent noise,

and input signal frequency. The sampling clock jitter

is beyond the control of users, thus the oscilloscope

manufacturers require continuous optimization of its

circuit design and hardware equipment to minimize

its jitter value. The quantization noise in the inherent

noise of an oscilloscope is related to the resolution of

the ADC conversion chip. Higher resolution leads to

smaller quantization errors, which is also the reason

why many oscilloscope manufacturers have been

continuously improving the ADC resolution in recent

years.

It can be verified by experiments that the analog

front-end noise in the inherent noise, under the

condition of constant input signal, is closely related

to the vertical sensitivity setting of the oscilloscope

and the input signal frequency. In many cases, the

impact of analog front-end noise on jitter

measurement floor is much greater than other factors.

Therefore, selecting the appropriate vertical

sensitivity during the measurement process is one of

the important means to reduce the oscilloscope jitter

measurement floor. After reducing the jitter

measurement floor, its contribution to the

oscilloscope measurement results will

correspondingly decrease.

ACKNOWLEDGMENT

This work is supported by Key Special Project

“Broadband Sampling Oscilloscope” on National

Key Research and Development Program of

“Fundamental Research Conditions and

Development of Major Scientific Instruments”. No.

2022YFF0707104.

Analysis and Improvement of Oscilloscope Jitter Measurement Floor Based on Simulation Experiments

395

REFERENCES

Std, I., IEEE Standard for Terminology and Test Methods

for Analog-to-Digital Converters(S). IEEE, 2011.

M Komárek, and J Roztočil. Selecting Sinewave Test

Frequencies for Dynamic ADC Tests (J).

Instrumentation for the ICT. 2010, 528-532.

Peterich, D., Ham, B., Van, S., Edward, D. & Grivna, L.

Fibre Channel- Methodologies for Jitter and Signal

Quality Specification(S). 2003.

Std, I., IEEE Standard for Transitions, Pulses, and Related

Waveforms(S). IEEE, 2011.

Zhu Jiangmiao, Sun Yufen, Chen Junyu. Measurements and

Calculation Methods of Jitter in Broadband Sampling

Oscilloscope(C). 16th International Conference on

Electronic Measurement & Instruments. 2023, 81-85.

Wang Shibiao. Research of Key Techniques for Time

Domain Calibration of Broadband Sampling

Oscilloscope (D). Beijing University of Technology,

2019.

J. Towfic, S. -K. Ting, A. H. Sayed. Sampling clock jitter

estimation and compensation in ADC circuits(C).

Proceedings of 2010 IEEE International Symposium on

Circuits and Systems, 2010, 829-832.

J. Elbornsson, F. Gustafsson, J.-E. Eklund. Blind adaptive

equalization of mismatch errors in a time-interleaved

A/D converter system (J). IEEE Transactions on

Circuits and Systems I. Vol. 51, no. 1, Jan. 2004, 151–

158.

C. Fu, H. Wang. Adaptive optimization in A/D converter

system(C), 6th IEEE International Conference on

Industrial Informatics. July 2008, 627–630.

S. Huang, B. Levy. Blind calibration of timing offsets for

fourchannel time-interleaved ADCs (J). IEEE

Transactions on Circuits and Systems I. Vol. 54, no. 4,

April 2007, 863–876.

LI Liping. Jitter Analysis in High-speed Serial

Interconnection (D). Xidian University, 2010.

Zhang Changjun. Basic series of signal integrity Analysis -

- Clock jitter Measurement and Analysis (J). Foreign

Electronic Measurement Technology, 2010, 7-11.

Johnnie Hancock Agilent Technologies. Regonize the

Noise and its Influence on Oscilloscope Measurement

(J). Electronics Quality. 2005, 17-20.

M. Shimanouchi. An approach to consistent jitter modeling

for various jitter aspects and measurement methods(C).

Proceedings International Test Conference 2001, 848-

857.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

396