Analysis and Research on the Age Structure of Population Based on

Multiple Regression Model

Yiwen Zhai

, Jie Shen

, Yun Wu

and Tianhong Zhou

Wuhan Business University, Wuhan, China

Wuhan Polytechnic, Wuhan, China

Keywords: Grey Prediction, Multiple Linear Regression, Grey System Modeling.

Abstract: People's desire to have children has not been strengthened under the three-child policy, and the most important

thing is to look at the relevant supporting measures after childbearing. Based on the data of the population

age structure of our country, this paper establishes a grey prediction model to predict the population status of

China in the next 10 years after the opening of the three-child policy. At the same time, by using the index

data of the main factors affecting the newborn population, a multiple regression model is established, and it

is concluded that the three-child policy will indeed have an impact on the future population. The problem of

population aging in China is still serious in the future, and the "double reduction" policy will have an impact

on the new population.

1 INTRODUCTION

The three-child policy is a family planning policy that

China has implemented in response to its population

ageing. That is, in order to further optimize the

fertility policy, implement the policy that a couple can

have three children and supporting measures. How to

carry out the supporting measures after giving birth is

one of the most concerned problems for people of

childbearing age. In view of the realistic background,

this paper establishes a prediction and regression

model to predict the age structure of China's

population in the next ten years, analyzes the factors

that will affect the newborn population, and judges

whether the double reduction will have an impact on

the newborn population.

2 LITERATURE REVIEW

Since the reform and opening up, China's fertility

policy has experienced the "one-child policy" to

control population growth, the gradual "two-child

policy" to alleviate the labor shortage and the aging

of the population, and the "three-child policy" to

optimize the fertility policy to promote the long-term

balanced development of the population (Zhang Jun,

2021). the three-child policy is the implementation of

the policy that a couple can have three children and

supporting measures in order to further optimize the

fertility policy (Wang Jun et al., 2021). the

liberalization of the three-child policy can have a

positive impact on population structure and

population growth, and the magnitude of the impact

depends on how strong the supporting measures are,

how wide the scope is, and how scientific and targeted

they are (TAM Ho-chun, 2021).

In terms of national conditions, the fertility

problem is the biggest in the country. Population is

the main body of social life, the basis of social

survival, but also the motive force of social

development, and fertility is the source and root of

population (Mu Guangzong, 2021). There are many

factors that affect the reproductive desire and

behavior of women of childbearing age, and different

individuals, families or social characteristics of

women of childbearing age are affected differently.

Identity is reflected in such factors as the ideal

number of children, age, income and so on will affect

fertility and fertility behavior at the same time; The

difference is mainly manifested in the level of

education, occupation, marital status and other factors

have a positive or negative impact on fertility desire

and fertility behavior (Pei Deyu, 2022).

Lebenstein's cost-utility theory, which states that

a family makes a birth decision by weighing the costs

and benefits of having a child, that is, the costs and

benefits of having children affect the willingness and

behavior to have children. Easterling's fertility-

Zhai, Y., Shen, J., Wu, Y. and Zhou, T.

Analysis and Research on the Age Structure of Population Based on Multiple Regression Model.

DOI: 10.5220/0012286500003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 493-499

ISBN: 978-989-758-677-4

493

determined supply-demand theory states that income

and employment that affect people's economic

conditions affect fertility rates, and are also different

and constantly changing (Pei Deyu, 2022).

The high cost of raising, economic pressure,

conditions do not allow, and other factors are

currently our families do not want to give birth to

important reasons. To solve this problem, the

implementation of the three-child policy and

supporting economic and social policies have been

put on the agenda.

3 DATA SOURCE AND DATA

DESCRIPTION

A. Data Sources

Given the availability and accuracy of the data, the

sample was selected for the period 2012-2021-2021.

The data involved in this paper are all from the

National Bureau of Statistics.

B. Data Description

Regarding our country's population structure, our

country generally divides the population according to

the age the following three stages: 0-14 years old, 15-

64 years old, 65 years old and above (Chen Guolin et

al., 2020).

There are many factors that affect the new-born

population. The birth of each child brings not only

economic pressure, but also life pressure to a family

(Zhang Yuhan, 2011), here we consult the relevant

literature to establish four factors that affect the new-

born population: the level of education expenditure,

residents' consumption level, per capita income, per

capita medical level, using the data of four factors in

the past 10 years.

4 GREY PREDICTION MODEL

OF POPULATION AGE

STRUCTURE

4.1 Data Collection

Because our country generally divides the population

into three stages according to the age: 0-14 years old,

15-64 years old and over 65 years old, we found the

data of population age structure in the past ten years

in the National Bureau of Statistics (Beijing: China

Statistics Press, 2021)

as follows.

Table 1. Population age structure data.

Year 0-14 years old 15-64 years old Over 65

2012 22427 100718 12777

2013 22423 101041 13262

2014 22712 101032 13902

2015 22824 100978 14524

2016 23252 100943 15037

2017 23522 100528 15961

2018 23751 100065 16724

2019 23689 99552 17767

2020 25277 96871 19064

2021 26302 94902 20056

4.2 Draw a Time Series Diagram

According to this data, the time series of three age

groups can be drawn by MATLAB as follows:

Figure 1. Time series diagram.

According to Figure 1, the original data is non-

negative data column, and the period is 10, so we can

use GM (1,1) model to solve this problem (He

Mingfang, 2012).

4.3 Test of Quasi-Exponential Law

The theory of grey system modeling is based on the

quasi-exponential law of data. In the GM (1,1) model,

the order ratio of sequence x

(1)

(Leung Chin, 2017).

(1)

Defined

as the smoothness

ratio of the original sequence x

(0)

, the following figure

can be drawn according to MATLAB:

2012 2013 2014 2015 2016 2017 2018 2019 2020 2021

Year

0-14 years old

15-64years old

65 years of age and older

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

494

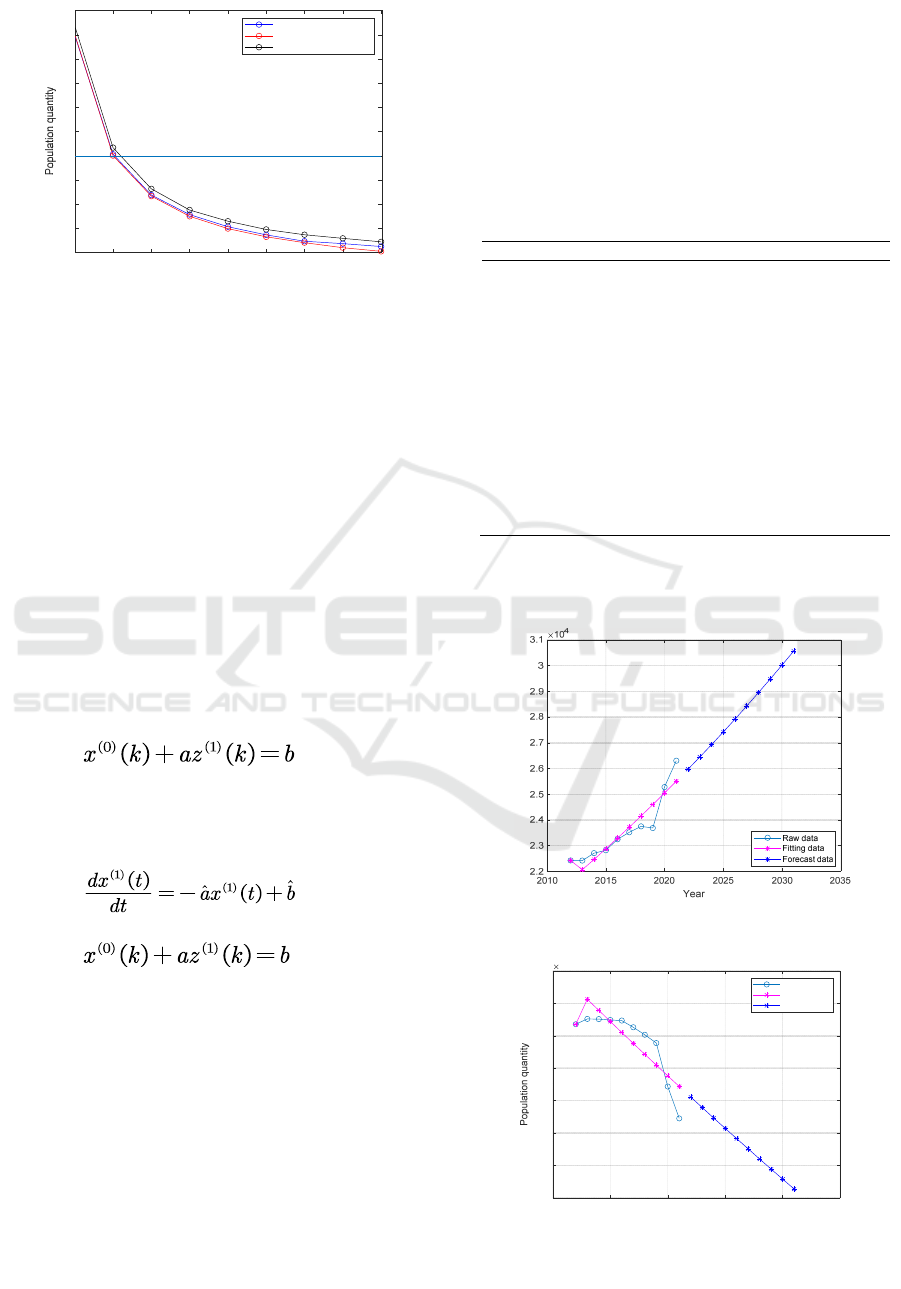
Figure 2. Smoothness diagram.

As can be seen from figure 2, except for the first

two periods, the smoothness of all the data in the three

age groups is less than 0.5. Generally, the first two

periods may not meet the requirements, and it is

enough to focus on the number of subsequent periods.

At the same time, accurate values can be obtained

through MATLAB. The proportion of data with a

smoothness ratio less than 0.5 is 77.7778%. Except

for the first two periods, the proportion of data with

smoothness ratio less than 0.5 is 100%, and the

proportion is higher, so the data of this question can

pass the test and make grey prediction.

4.4 Make Grey Prediction

The following equations are the basic form of the GM

(1,1) Model ( k=2，3，…，n) (Zhang Yaozhen, 2019).

(2)

Where b denotes grey action volume. - a denotes

coefficient of development. The following

differential equations are referred to as albino

equations for the GM (1,1) model:

(3)

(4)

is called the gray differential equation.

Because the number of periods of this question

is 10, the last three periods are taken as the

experimental group, and the first is the training group,

and the data of the training group are used to train

three kinds of GM models respectively, and the

trained models are used to predict the data of the third

phase of the experimental group. Using the real data

of the third period of the experimental group and the

predicted data of the third period, through MATLAB,

we can calculate that the sum of squares of the

prediction errors of the traditional GM (1Mague 1),

the new information GM (1Power1) and the

metabolic GM (1Magee 1) are 4558869.8592,

4556750.9468 and 4200780.9789, respectively.

Among them, the sum of squares of the metabolic

GM (1 ~ 1) model is the smallest. So, we should

choose it for prediction.

Using MATLAB to predict the three age groups,

the predicted data are shown in Table 2 below.

Table 2. Predicted data tables.

Year 0-14 years old 15-64 years old Over 65

2022 25969.15 96220.25 20957.35

2023 26443.31 95571.53 22092.92

2024 26926.12 94927.19 23290.01

2025 27417.75 94287.19 24551.96

2026 27918.35 93651.5 25882.3

2027 28428.1 93020.1 27284.72

2028 28947.15 92392.96 28763.12

2029 29475.68 91770.05 30321.64

2030 30013.85 91151.33 31964.6

2031 30561.86 90536.79 33696.58

A time series diagram of the predicted and original

data can be drawn as follows:

Figure 3. Time sequence chart of 0-14 age group.

Figure 4. Time sequence chart of 15-64 age group.

2014 2015 2016 2017 2018 2019 2020 2021

Year

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0-14 years old

15-64 years old

65 years of age and older

Population quantity

2010 2015 2020 2025 2030 2035

Yea

9.2

9.4

9.6

9.8

10.2

10.4

Raw data

Fitting data

Forecast data

Analysis and Research on the Age Structure of Population Based on Multiple Regression Model

495

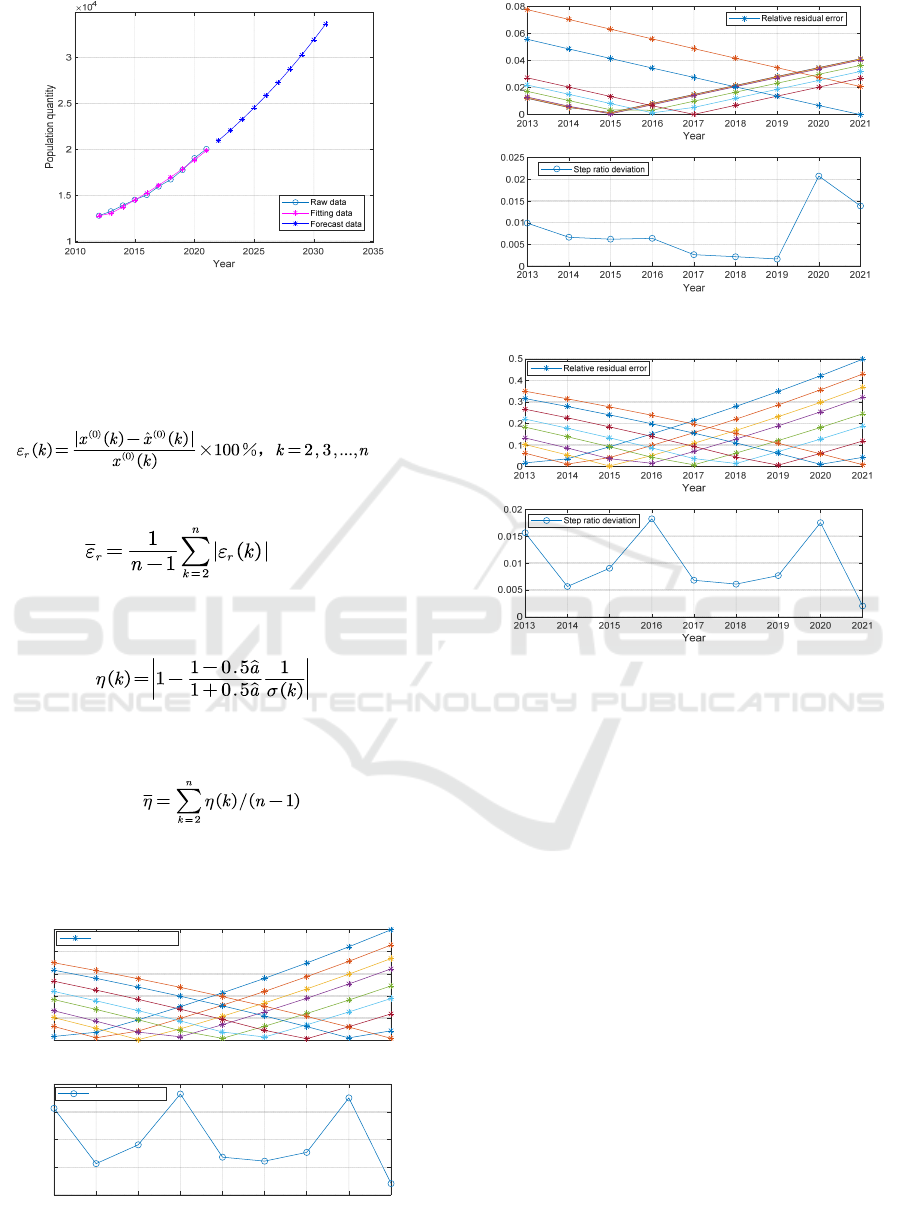
Figure 5. Time sequence chart of over 65 age group.

4.5 Evaluation of Grey Prediction

Model

Relative residuals (Liu Pengfei, 2021).

(5)

Mean relative residuals

(6)

Step ratio deviation

((7)

Average order ratio deviation

(8)

The figure below can be obtained through

MATLAB.

Figure 6. Test chart of 0-14 years old.

Figure 7. Test chart of 15-64 years old

Figure 8. Test chart of the age group over 65 years old.

As can be seen from figure 6-8, the relative

residual of most data is less than 0.1 and the order

deviation is less than 0.1. The model fits the data of

0-14 years old, 15-64 years old and over 65 years old

well, and the average relative residual is 0.054875,

0.021947444 and 0.157455556 respectively. The

order ratio deviations are 0.015618, 0.0078004 and

0.009866 respectively, which shows that the

prediction result of the model is ideal.

5 REGRESSION MODEL OF

INFLUENCING FACTORS ON

NEWBORN POPULATION

UNDER “DOUBLE

REDUCTION”

5.1 The Definition of "Double

Reduction" and the Influencing

Factors of Newborn Population

"Double reduction" means to lighten the homework

2013 2014 2015 2016 2017 2018 2019 2020 2021

Year

0.1

0.2

0.3

0.4

0.5

Relative residual error

2013 2014 2015 2016 2017 2018 2019 2020 2021

Year

0.005

0.01

0.015

0.02

Step ratio deviation

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

496

burden of students, and to lighten the burden of out-

of-school training. The measures to reduce the

homework burden include quantifying the homework

time of each grade, reducing the total amount and

length of homework, requiring teachers to improve

the quality of homework design, and strictly

forbidden to assign homework to parents or in

disguised form (Wang Yanjun, 2022).

There are many factors that affect the new-born

population. We have identified four factors that affect

the new-born population by reviewing relevant

literature: the level of education expenditure, the level

of household consumption, the level of per capita

income, and the level of per capita medical care. The

data of four factors in the past 10 years were used for

the study.

5.2 Establish the Regression Model of

Newborn Population

Mathematical models for multiple linear regression

were (Isheng et al., 2016):

(9)

Among them, there are

explanatory variables,

is a random error, is also a random variable. If you

find the conditional expectation under a given

condition, there are

(10)

Formula (10) is a multivariate linear regression

equation with unknown parameter

，，…，

.Because the parameter estimation is based on the

sample data, the parameter after the parameter

estimation is only the estimated value

，，…，

of the true value ，，…， of the

parameter, so there are estimated multiple linear

regression equations:

(11)

In formula (11), the explanatory variable

the birth rate, and the explained variables

represent the level of

education expenditure, residents' consumption level,

per capita income level and per capita medical level

respectively. In order to explore the causal

relationship and influence degree between variables,

it is necessary to test the economic significance of the

parameter estimation results of the regression model

and the statistical test of the regression equation,

including the significance test of the regression

equation, the significance test of the regression

coefficient, the residual analysis and so on (Ma cedar,

2022).

5.3 Goodness of Fit Test

Ordinary least squares estimation is a kind of

common statistical fitting criterion, which can

estimate every parameter in the model (Tam wai-wah,

2020) for multivariate linear regression equations

(12)

The least square estimation is to find the

estimated value

，，…， of the parameter

，，…， to minimize the sum of squares

of the deviation.

(13)

OLS regression analysis was performed using

the regress function in Stata, assuming the original

hypothesis: .

The joint significance test of the four

explanatory variables is obtained, so the original

hypothesis is rejected at 95% confidence level, that is,

the joint significance test is passed.

According to the following formula

(14)

The following conclusions can be drawn:

(15)

5.4 Test for Heteroscedasticity

According to the significance test of the regression

coefficients obtained, the significance of all

explanatory variables is insufficient, so White text is

performed on the data (Wei Yanhua, 2022) results are

shown in table 3 below:

Table 3. White test results.

Source Chi2 df p

Heteroskedasticity 10 9 0.3505

Skewness 3.31 4 0.5068

Kurtosis 0.58 1 0.4466

Total 13.89 14 0.4577

Among them, White tests the original hypothesis:

there is no heteroscedasticity.

Analysis and Research on the Age Structure of Population Based on Multiple Regression Model

497

is obtained by using Stata, so at 95% confidence level,

the original hypothesis is accepted, so there is no

heteroscedasticity.

5.5 Test for Multicollinearity

Using the variance expansion factor to test the

multiple collinearities, the larger the

, the

greater the correlation between the

variable and

other variables. If

> 10, it is considered that the

regression equation has serious multicollinearity.

The results are shown in table 4 below:

Table 4. VIF test results.

Variable VIF 1/VIF

Per capita consumption 2313.48 0.000432

Per capita income 1586.87 0.00063

Medical expenses 189.18 0.005286

Education spending 183.07 0.005462

Mean VIF 1068.15

As can be seen from table 4,

multicollinearity

therefore exists and needs to be addressed for

multicollinearity.

We used backward stepwise regression to solve

the multicollinearity problem, with results shown in

table 5 below:

Table 5. Backward stepwise regression to address

multicollinearity.

Birth rate Coef. Std. Err. t P > t [95% conf. Interval ]

Per capita

consumption

-0.002 0.004 -0.500 0.640 -0.011 0.008

Education

spending

0.008 0.009 0.930 0.394 -0.015 0.032

Medical

expenses

-0.005 0.009 -0.540 0.613 -0.029 0.019

Per capita

income

0.001 0.002 0.310 0.770 -0.004 0.006

_cons 20.201 5.932 3.410 0.019 4.952 35.449

6 CONCLUSION

6.1 Results of Projections on the Age

Structure of the Future Population

Considering the age structure of our country, the

population situation in the next 10 years after the

opening of the three-child policy is forecasted. First

of all，the three-child policy began to be implemented

on May 31, 2021, so it can be seen that the population

in 2021 has received the impact of the three-child

policy, so using 2021 data to predict future data can

be regarded as the prediction results under the

influence of the three-child policy. Therefore,

considering the age structure of China, the population

situation in the next 10 years after the opening of the

three-child policy is predicted as follows: the

population of the 0-14 age group showed an

increasing trend after the implementation of the three-

child policy, but the growth rate declined after a few

years of implementation. The population of 15-64

years old shows a downward trend, the population

over 65 years old is showing a growth trend, the

growth rate of the three-child policy is slow at the

beginning of the implementation, and then it slowly

picks up, the problem of population aging in China is

still difficult to solve.

6.2 The Impact of the "Double

Reduction" Policy on the Newborn

Population

According to the STATA calculation, the regression

coefficient

is 20.2, - 0.001, 0.008, -0.005 and

0.001 respectively, and the regression equation is

(16)

According to the regression equation to predict

the new-born population, we can analyze, we can get

the regression equation growth trend, thus we can get

“Double reduction” policy implementation will have

an impact on the new-born population.

ACKNOWLEDGMENTS

This work was financially supported by the Industry-

University Research Innovation Funding of Chinese

University [grant number 2020HYA06007], the

Knowledge Innovation Program of Wuhan-Shuguang

Project [grant number 2022010801020429].

REFERENCES

Zhang Jun. A study on the fiscal and tax policies to promote

the long-term balanced development of population in

the context of the “Three-child policy”—— from the

perspective of fertility, parenting and education [J]. Tax

Economics, 2021, 26(05): 89-94.

Wang Jun, Li Xiangmei. China's three-child policy: low

fertility, difficulties and solutions [J]. Youth Exploration,

2021, No. 234(04): 50-61.

TAM Ho-chun. Can the three-child policy change the

population [J]. Finance, 2021, No. 401(07): 32-33.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

498

Mu Guangzong. The three-child policy and the

optimization of China's population and fertility:

background, prospects and vision [J]. Journal of

Yangzhou University (Humanities and social sciences),

2021, 25(04): 65-77.

Pei Deyu. Fertility desire and behavior of women of

childbearing age under the “Three-child” policy [D].

Hebei Normal University, 2022.

Chen Guolin, Xu Yan, Ye Zhiqun. Future population change

in China based on data revisions [J]. Jiangxi science,

2020, 38(04): 450-454.

Zhang Yuhan. Analysis of the quality of birth population

and its influencing factors in six counties of three

provinces in China [D]. Peking Union Medical College,

2011.

National Bureau of Statistics of the People's Republic of

China. China statistical yearbook [M]. Beijing: China

Statistics Press, 2021.

He Mingfang. Population prediction model based on grey

system theory [D]. South China University of

Technology, 2012.

Leung Chin. Grey prediction model-based prediction of the

ageing population [D]. Harbin Institute of Technology,

2017.

Zhang Yaozhen. Empirical analysis of Henan population

based on Arima model and GM (1,1) Model [D].

Guangxi Normal University, 2019.

Liu Pengfei. Principal component analysis and grey

prediction based comprehensive level measure of new

urbanization [D]. University of South China, 2021.

Wang Yanjun. A cross-case study on the implementation

effect of the “Double reduction” policy for primary

school students in Lanzhou [D]. Lanzhou University,

2022.

Isheng, Xue Qiuzhi. Green supply chain management and

Green Innovation: an empirical study based on Chinese

manufacturing enterprises [J]. Scientific research

management, 2016, 37(06): 103-110.

Ma cedar. Chinese population projections based on Leslie

model and screening for influencing factors [D]. Beijing

Jiaotong University, 2022.

Tam wai-wah. Logistics demand forecast in Jiangxi

province based on multiple regression and neural

network [D]. Jiangxi University of Finance and

Economics, 2020.

Wei Yanhua, Ma Liping, Wang Bingshen. Trend of

population change and regional differences in China

based on functional data [J]. Statistics and policymaking,

2022, 38(08): 82-86.

Analysis and Research on the Age Structure of Population Based on Multiple Regression Model

499