Application K-Nearest Neighbor Method with Particle Swarm

Optimization for Classiﬁcation of Heart Disease

Irmawati Carolina

, Baginda Oloan Lubis

, Adi Supriyatna

and Rachman Komarudin

Universitas Bina Sarana Informatika, Jakarta, Indonesia

Universitas Nusa Mandiri, Jakarta, Indonesia

Keywords:

K-Nearest Neighbor Method, Particle Swarm Optimization, Classiﬁcation of Heart Disease.

Abstract:

Heart disease is a condition in which there is dysfunction in the work of the heart. Diseases of the heart are

of many types such as cardiovascular, coronary heart disease and heart attack. Cardiac groaning is one of the

deadliest diseases in the world with mortality reaching 12.90% of all heart diseases. This lack of access to ﬁnd

information about heart disease leads to an increase in mortality rates in each case. Therefore, a classiﬁca-

tion system is needed that can provide information about heart attack disease and can check the classiﬁcation

early about heart attack disease experienced by a person. The application of the K Nearest Neighbor algo-

rithm model and the K Nearest Neighbor (K-NN) algorithm based on Particle Swarm Optimization (PSO) was

carried out to ﬁnd out which model provided the best results in detecting chronic kidney disease. The selec-

tion of both models is considered because the K Nearest Neighbor algorithm is one of the best data mining

algorithms, but it tends to have weaknesses in overlapping data, classes and many attributes. Therefore, the

Particle Swarm Optimization (PSO) optimization technique. From the results of the study, it was obtained that

the PSO-based K-NN algorithm model was able to select attributes so that it could increase a better accuracy

value with a result of 9 2.98% with an AUS value of 0.961 compared to the individual model of the K-NN

algorithm which produced an accuracy value of 92.32% and an AUC value of 0.956%.

1 INTRODUCTION

The circulatory system is one of the most important

systems in the human body. This system has two

main functions, namely to circulate oxygen and nutri-

ents to all organs of the human body and transport the

rest of the metabolic products. One of the important

organs in the human circulatory system is the heart

(Wibisono and Fahrurozi, 2019). If the heart is dis-

turbed, blood circulation in the body can be disrupted

so that maintaining heart health is very important to

avoid various types of heart disease(Pradana et al.,

2022). Heart disease is a condition in which there is

dysfunction in the work of the heart (Sepharni et al.,

2022). Diseases of the heart are of many types such

as cardiovascular, coronary heart disease and heart at-

tack (Utomo and Mesran, 2020). Cardiacgroaning is

one of the deadliest diseases in the world with mor-

tality reaching 12.90% of all heart diseases (Pradana

et al., 2022). This lack of access to ﬁnd information

about heart disease leads to an increase in mortality

rates in each case. Therefore, a classiﬁcation system

is needed that can provide information about heart

attack disease and can check the classiﬁcation early

about heart attack disease experienced by a person.

Some studies that discuss the classiﬁcation of heart

disease include comparative research of classiﬁcation

algorithms in classifying coronary heart disease data

(Wibisono and Fahrurozi, 2019) comparing 4 alo-

gorhythms, namely Naive Bayes, K-Nearest Neigh-

bor, Decision Tree, and Random Forest. The results

showed that Naive Bayes got an accuracy score of

80.33%, K-Nearest Neigbor 69.67%, Decision Tree

80.33% and Random Forest 86.66%.

Classiﬁcation performance of the K-Nearest

Neighbor algorithm and cross-validation in heart dis-

ease (Azis et al., 2020). dataset1 (50:50 dataset)

obtained the best performance values at 82% accu-

racy, 82% precision, 82% recall and 82% f-measure,

at K=13. Dataset2 (20:80 dataset) obtained the best

performance values at 87% accuracy, 87% precision,

97% recall, and 92% f-measure, at K=3. Dataset3

(80:20 dataset) obtained the best performance values

at 91% accuracy, 92% precision, 60% recall and 72%

f-measure, at K=5. Performance is found in the 80:20

ratio with an accuracy of 91% considering that it is

Carolina, I., Lubis, B., Supriyatna, A. and Komarudin, R.

Application K-Nearest Neighbor Method with Particle Swarm Optimization for Classiﬁcation of Heart Disease.

DOI: 10.5220/0012446200003848

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Advanced Information Scientiﬁc Development (ICAISD 2023), pages 181-186

ISBN: 978-989-758-678-1

181

good to balance the precision and recall values and

the absence of outlier values on the boxplot.

Optimization of SVM and K-NN algorithms based

on Particle Swarm Optimization on the sentiment

analysis of the hashtag phenomenon #2019gantipres-

iden (Saepudin et al., 2022) the calculation results of

the SVM method have an Accuracy of 88.00% and

an AUC of 0.964 while the SVM + PSO Method pro-

duces an Accuracy of 92.75% and an AUC of 0.973.

Testing has also been compared using PSO-based k-

NN and k-NN methods. The calculation results ob-

tained from testing data using the k-NN method re-

sulted in Accuracy of 88.50% and AUC of 0.948.

Meanwhile, the PSO-based k-NN method resulted

in an Accuracy value which actually decreased by

75.25% and an AUC of 0.768.

Comparison of optimization of C4.5 and Na

ıve

Bayes data classiﬁcation algorithms based on Parti-

cle Swarm Optimization Credit Risk Determination

(Rifai and Aulianita, 2018). Based on the test results,

the accuracy value of the C4.5 algorithm is 85.40%

and the accuracy value of the Na

ıve Bayes algorithm

is 85.09%. From the two algorithms, a combination

was then carried out with Particle Swarm Optimiza-

tion optimization, with the results of the C4.5 + PSO

algorithm having the highest value based on the ac-

curacy value of 87.61%, AUC of 0.860 and precision

of 88.96% while the highest recall value was obtained

by the Na

ıve Bayes + PSO algorithm of 96.75%. The

classiﬁcation results of each algorithm in this study

will be compared to get the best performance evalua-

tion in breast cancer detection. Thus, one of the op-

timization data techniques is needed that aims to im-

prove the performance of the conventional data min-

ing classiﬁcation method that has been chosen. One

optimization algorithm that is quite popular is Parti-

cle Swarm Optimization (PSO). Particle Swarm Opti-

mization (PSO) has solved many algorithm optimiza-

tion problems (Yoga and Prihandoko, 2018).

2 RESEARCH METHODOLOGY

2.1 Dataset Acquisition

The dataset used in this study is the data uploaded by

Ronan Azarias on the kaggle.com page entitled heart

desease dataset. The dataset amounts to 500 data. The

attributes contained in the data include:

a. Age: patient’s age (years)

b. Sex: patient’s sex (M: Male, F: Female)

c. ChestPainType: chest pain type (TA: Typical

Angina, ATA: Atypical Angina, NAP: Non-

Anginal Pain, ASY: Asymptomatic)

d. RestingBP: resting blood pressure (mm Hg)

e. Cholesterol: serum cholesterol (mm/dl)

f. FastingBS: fasting blood glucose (1: if FastingBS

¿ 120 mg/dl, 0: otherwise)

g. RestingECG: Resting ECG results (Normal: nor-

mal, ST: with ST-T wave abnormality, LVH: show-

ing probable or deﬁnite left ventricular hypertro-

phy by Estes criteria)

h. MaxHR: maximum heart rate reached (Numeric

value between 60 and 202)

i. ExerciseAngina: exercise-induced angina (Y: Yes,

N: No)

j. Oldpeak: old peak = ST (Numerical value mea-

sured in depression)

k. ST Slope: the slope of the peak exercise ST seg-

ment (Up: upsloping, Flat: ﬂat, Down: downslop-

ing) In addition, there is the response variable,

which in this case is a binary variable:

l. HeartDisease: output class (1: heart disease, 0:

normal)

2.2 Pre-Processing

Data cleaning is a step that is done before entering

the data mining process [9]. Data cleaning contains

several activities whose main purpose is to introduce

and improve the data to be studied. The need for

improvements to the data to be studied is due to the

fact that raw data tends not to be ready for mining.

A frequent case is the presence of missing values in

the data. Missing values in datasets come from data

whose attributes have no informational value. This in-

formation is not obtained possible due to the process

that occurs when merging data. Handling of miss-

ing value in this study was carried out by reducing

data objects (under sampling). As a result of the data

cleaning carried out, there were 456 records from the

initial number of 500 records.

2.3 K-Nearest Neighbor

K-Nearest Neighbor is also called lazy learner be-

cause it is learning-based. K-Nearest Neighbor delays

the process of modeling training data until it is needed

to classify samples of test data. The sample train data

is described by numeric attributes on the n-dimension

and stored in n-dimensional space. When a sample of

test data (label of unknown class) is given, K-Nearest

Neighbor searches for the training k sample closest to

ICAISD 2023 - International Conference on Advanced Information Scientiﬁc Development

182

the test data sample (Hidayatul and S, 2018). ”Prox-

imity” is usually deﬁned in terms of metric distance.

In this study, distance measurements will be carried

out using euclidean distance. The euclidean distance

formula is represented in equation 1 (Lestari, 0 09).

d(x

) =

∑

(r=1)

− x

)

(1)

Description:

d(x

) = Euclidean distance n = Data dimensions

= Test/testing data x

= Training data r = Variable

Data

The K-NN algorithm is basically done with the

following steps.

a. Determining the value of K

b. Calculate the distance between the test data and the

numerical training data

c. Sorting distances from smallest to largest

d. Retrieves as much data as the nearest K

e. Choosing a major class

2.4 Particle Swarm Optimization

Particle swarm optimization was formulated by Ed-

wardan Kennedy in 1995. The thought process be-

hind this algorithm is inspired by the social behavior

of animals, such as birds in groups or a group of ﬁsh.

The position of each particle can be considered as a

candidate solution for an optimization problem. Each

particle is assigned a ﬁtness function designed accord-

ing to the corresponding problem (Fakhruddin et al.,

2020). This algorithm is about changes in behavior

or social nature consisting of the actions of each in-

dividual and the magnitude of the inﬂuence of each

other individual into one group. Each particle in the

PSO is also related to a velocity. Particles tend to

have the property to move to a better search area af-

ter going through the tracing process (Yunus, 2018).

Particle Swarm Optimization (PSO) is a very simple

optimization technique for implementing and modify-

ing multiple parameters. PSO is widely used to solve

the problem of weight optimization and feature selec-

tion (feature selection). The PSO has the advantage of

achieving a centering pattern and the ability to solve

complex optimization problems in a wide variety of

domains (Fakhruddin et al., 2020). Brieﬂy, the PSO

process starts from the initialization of the population

to the termination of computing, such as the following

algorithm:

a. Initialization of population (random position and

speed) in hyperspace

b. Fitness evaluation of individual particles

c. Speed modiﬁcation based on previous best (previ-

ous best:pbest) and best global or local (global or

neighborhood best; gbest or lbest)

d. Stop based on multiple conditions

e. Re-do step 2

To ﬁnd the optimal solution, each article will

move towards the best position before (pbest) and the

best position globally (gbest). The formula for calcu-

lating the displacement of the position and speed of

the particle is:

(t) = V

(t − 1) + c



pbest i

− X

(t)



Gbest i

− X

(t)]–X

(t)

(2)

(t) = V

(t − 1) +V

(t) (3)

Where:

(t) : particle velocity i current iteration t X

(t) :

the position of the particle i at iteration t C

and C

Learning Rates for Individual Ability (Cognitive) and

Inﬂuence Social (Group) r − 1 and r

: random num-

bers that are distributeduniformally in intervals 0 and

1 X

Pbest i

: best position of particle i X

gbest i

: global

best position

2.5 K-Fold Cross Validation Testing

The validation model used in this study is 10 fold

cross validation. 10 fold cross validation is used to

measure model performance. Each dataset is ran-

domly divided into 10 parts of the same size. For 10

times, 9 parts are used to train the model (data train-

ing) and 1 part is used to test (data testing) the others.

each time a test is carried out. The measurement on

classiﬁcation performance evaluation aims to ﬁnd out

how accurate the classiﬁcation model is in the class

prediction of a row of data (Yoga and Prihandoko,

2018).

2.6 Confusion Matrix

Confusion Matrix is a tool used to evaluate classiﬁ-

cation models used to estimate true and false objects.

The predicted results will be compared with the orig-

inal class of the data. Confusin Matrix evaluates the

performance of a model based on the predictive ac-

curacy capabilities of a model (Khoerunnisa et al.,

2016). Confusion matrix is a method used to mea-

sure the performance of a classiﬁcation model based

on the calculation of testing objects, where the pre-

dicted result data exists between two classes, namely

producing a positive class and a negative class.

Application K-Nearest Neighbor Method with Particle Swarm Optimization for Classiﬁcation of Heart Disease

183

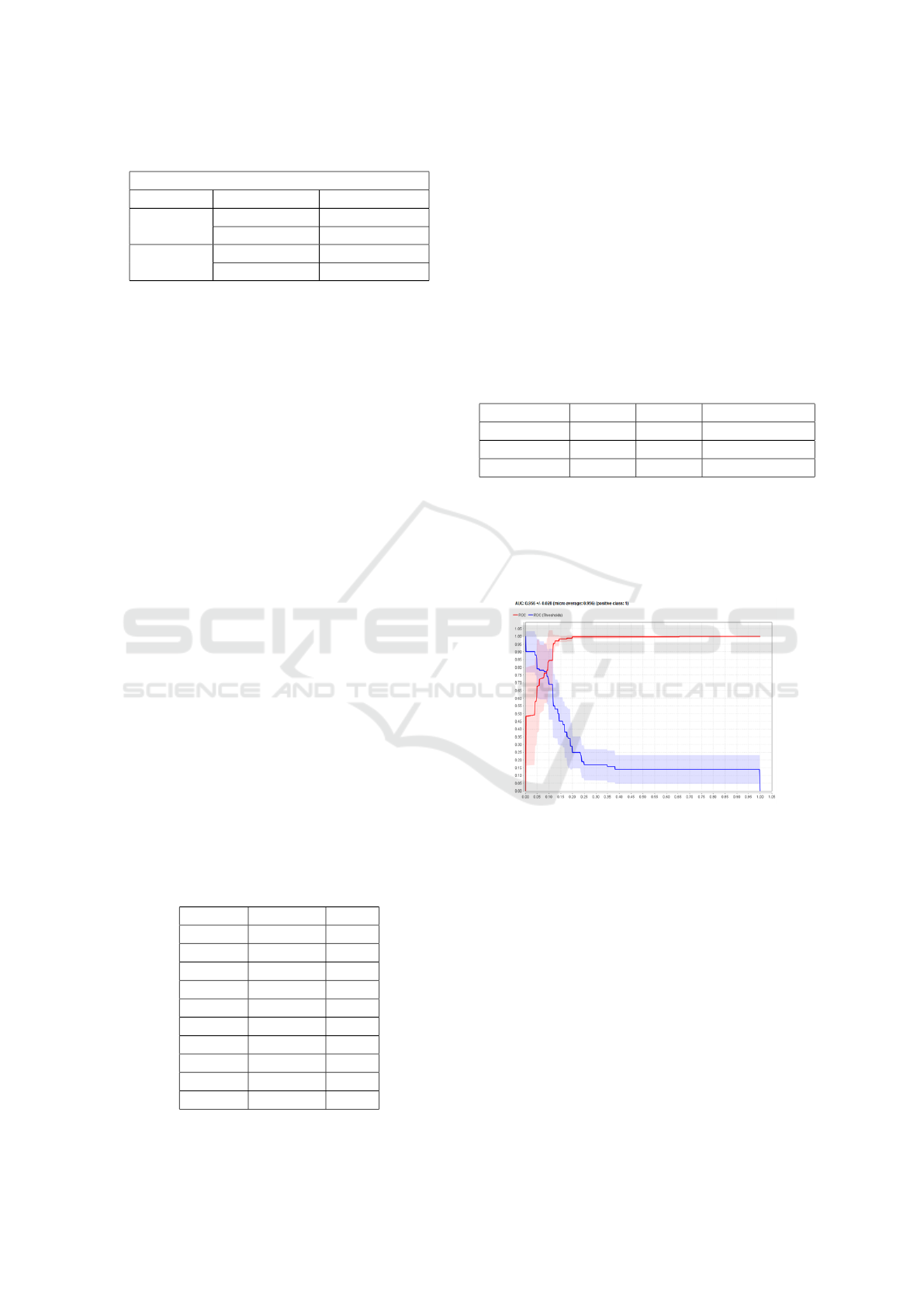
Table 1: Confusion Matrix.

Predicted Class

Class=Yes Class=No

Class=Yes

A B

True Positive False Negative

Class= No

C D

False negative True Negativ

For the evaluation process with a confusion ma-

trix, the precision, recall, and accuracy values ob-

tained from the following formula will be obtained

(Kurniawan and Rosadi, 2017).

Precision = T P/(T P + F p)

Recall = T P/(T P + FN)

Accuracy = (T P + T N)/(TP + T N + FP + FN)

(4)

Where:

T P: Number of positive cases classiﬁed as positive

FP: Number of negative cases classiﬁed as positive

T N: Number of negative cases classiﬁed as negative

FN: Number of positive cases classiﬁed as negative

3 RESULTS AND DISCUSSION

3.1 Calculation Results from the

K-Nearest Neighbor (K-NN)

Algorithm

The value of k used represents the number of closest

neighbors involved in determining the prediction of

the class label on the test data. To estimate the best

value of k, it can be done using cross-validation tech-

niques (Cross Validation).

Table 2: K-Nearest Neighbor Algorithm Training Value De-

termination Experiment.

K Value Accuracy AUC

1 88.82% 0.500

2 87.50% 0.886

3 91.01% 0.913

4 91.01% 0.937

5 91.67% 0.921

6 92.32% 0.952

7 92.32% 0.950

8 92.32% 0.952

9 92.32% 0.955

10 92.32% 0.956

The test results showed that the application of the

k-Nearest Neighbor method in table 11 with the de-

termination of the value of k = 10 resulted in Ac-

curacy = 92.32% and AUC = 0.956 was the highest

value. From the dataset used in the modeling, a total

of 456 tuples were obtained with details of the data

True Positive (TP) = 184, False Negative (FN) = 12,

False Positive (FP) = 23 and True Negative (TN) =

237. Based on the details of the data, accuracy, sen-

sitvity, speciﬁty, Positive Predictive Value (PPV) and

Negative Predictive Value (NPV) values can be ob-

tained which are presented in the table 3.

Table 3: Confusion Matrix Algorithm K-NN.

True 0 True 1 Class precision

Pred. 0 184 12 93.88%

Pred. 1 23 237 91.15%

Class recall 88.89% 98.18%

Testing of this model was also carried out by look-

ing at the ROC graph expressed in AUC values of

0.956 which showed that the test accuracy of individ-

ual models of the K-Nearest Neighbor algorithm was

included in the Excellent Classiﬁcation level.

Figure 1: K-NN algorithm AUC Results.

3.2 Calculation Results of the K-Neares

Neighbor (K-NN) Algorithm Based

on Particle Swarm Optimization

(PSO)

The test results using the PSO-based k-NN method

can be seen in table 4.

The calculation results from Table 4 above show

that by entering the value of k = 6 and Population

Size = 5 produced Accuracy = 92.98% and AUC =

0.961 is the highest value among other k values, in

this PSO-based K-NN accuracy it turns out that there

is an increase in accuracy results of 0.66% from the

accuracy results of the k-NN method without PSO-

ICAISD 2023 - International Conference on Advanced Information Scientiﬁc Development

184

Table 4: PSO-Based K-NN Algorithm Training Value De-

termination Experiment.

size K value Accuracy AUC

5 1 89.91% 0.500

5 2 88.38% 0.889

5 3 92.11% 0.893

5 4 92.11% 0.927

5 5 92.76% 0.928

5 6 92.98% 0.961

5 7 92.76% 0.947

5 8 92.54% 0.943

5 9 92.76% 0.953

5 10 92.78% 0.958

based optimization.

From the dataset used in the modeling, a total of

456 tuples were obtained with details of the data True

Positive (TP) = 184, False Negative (FN) = 10, False

Positive (FP) = 23 and True Negative (TN) = 239.

Based on the details of the data, accuracy, sensitvity,

speciﬁty, Positive Predictive Value (PPV) and Nega-

tive Predictive Value (NPV) values can be obtained

which are presented in Table 5.

Table 5: Confusion Matrix of PSO-Based K-NN Algo-

rithms.

True 0 True 1 Class precision

Pred. 0 184 10 94.85%

Pred. 1 23 239 91.22%

Class recall 88.89% 95.98%

Testing of this model was also carried out by look-

ing at the ROC graph expressed in AUC values of

0.928 which showed that the test accuracy of individ-

ual models of the K-Nearest Neighbor algorithm was

included in the Excellent Classiﬁcation level.

Figure 2: AUC results of the PSO-based K-NN algorithm.

The indicators in the PSO attribute selection based

on Optimize Weight (Evolutionary) are population,

max number of generations, and tournament size

which can affect maximum accuracy results. The

population used in this study was 5 populations. In the

PSO indicator adjustment, the max number of genera-

tions value contains 30 and the tournament size value

is 0.25. The values of c1 and c2 are 0 each because the

particles are in the ﬁrst round. Based on the process

model that has been successfully carried out, the fol-

lowing attribute weighting selection data is obtained:

Table 6: PSO Optimization Weight Indicators.

Attribute Weight

Age 0.240

Sex 0.501

ChestPainType 1

RestingBP 0

Cholesterol 0.095

FastingBS 0.076

RestingECG 0.013

MaxHR 0.229

ExerciseAngina 1

Oldpeak 0

ST Slope 0.166

Table 7: Comparative Results of Accuracy and AUC of

PSO-based K-NN and K-NN algorithms.

Algorithm Accuracy AUC

K-NN 92.32% 0.956

K-NN + PSO 92.98% 0.961

4 CONCLUSIONS

Based on tests that have been carried out on heart

disease data taken from kaggle. Testing using the

k-Nearest Neighbor (k-NN), and k-Nearest Neighbor

methods based on Particle Swarm Optimization (k-

NN+PSOmaking calculations of the K-NN method

has an Accuracy of 92.32% and an AUC of 0.956

while the K-NN+PSO Method produces an Accuracy

of 92.98% and an AUC of 0.961. The application of

Particle Swarm Optimization (PSO) has been shown

to improve the accuracy of the K-NN algorithm on the

classiﬁcation of heart disease data to identify between

p positive or negative heart disease. The application

of PSO optimization to the k-NN algorithm increased

by 0.66%. It can be concluded that in this study the

application of optimization using PSO can optimize

the accuracy value, especially in the k-NN algorithm.

Future suggestions for further research can improve

the level of accuracy can be done by combining sev-

eral algorithms and can also add several other opti-

mization algorithms.

Application K-Nearest Neighbor Method with Particle Swarm Optimization for Classiﬁcation of Heart Disease

185

REFERENCES

Azis, H., Purnawansyah, P., Fattah, F., and Putri, I. (2020).

Performance of k-nn classiﬁcation and cross valida-

tion in data on patients with heart disease. Ilk. J. Ilm,

12(2):81–86,.

Fakhruddin, H., Toar, H., Purwanto, E., Oktavianto, H.,

Apriyanto, R., and Aditya, A. (2020). Particle swarm

optimization (pso) based 3-phase induction motor

speed control. Elkomika J. Tek. Electriﬁed energy.

Tech. Telecommun. Tech. Electron, 8(3):477,.

Hidayatul, S. and S, Y. A. (2018). Selection of informa-

tion gain features for heart disease classiﬁcation using

a combination of k-nearest neighbor and na

ıve bayes

methods. J. Pengemb. Technol. Inf. and ComputAry

Science, 2(9):2546–2554,. Available:.

Khoerunnisa, A., Irawan, B., and Rumani, M. (2016). Anal-

ysis and implementation of the c.45 algorithm com-

parison with na

ıve bayes for product offering predic-

tion. E-Proceeding Eng, 3(3):5029–5035,.

Kurniawan, M. Y. and Rosadi, M. E. (2017). Decision

tree optimization using particle swarm optimization

on out-of-school student data. J. Teknol. Inf. Univ.

Hull Mangkurat, 2(1):7–14,.

Lestari, M. (2010-09). Application of the nearest neighbor

(k-nn) classiﬁcation algorithm to detect heart disease.

Fakt. Exacta, 7:366–371,.

Pradana, D., Alghifari, M., Juna, M., and Palaguna, D.

(2022). Classiﬁcation of heart disease using artiﬁ-

cial neural network method. Indones. J. Data Sci,

3(2):55–60,.

Rifai, A. and Aulianita, R. (2018). Comparison of c4.5

classiﬁcation algorithms and na

ıve bayes based on

particle swarm optimization for credit risk determi-

nation. J. Speed-Sentra Penelit. Eng. and Education,

10(2):49–55,.

Saepudin, A., Aryanti, R., Fitriani, E., and Dahlia (2022).

Sentiment analysis of vtuber development using

smote-based vector machine support method. J. Tek.

Compute. AMIK BSI, 8(2):174–180,.

Sepharni, C., Hendrawan, A., and Rozikin, I. E. (2022).

Classiﬁcation of heart disease by using. STRING (Ris.

and Inov. Units of Writing. Technol, 7(, vol. 7, no.

2):177–126,.

Utomo, D. and Mesran, M. (2020). Comparative analysis

of data mining classiﬁcation methods and attribute re-

duction in heart disease data sets. J. Information Me-

dia. Budidarma, 4(2):437,.

Wibisono, A. and Fahrurozi, A. (2019). Comparison

of classiﬁcation algorithms in classifying coronary

heart disease data. J. Ilm. Technol. and Engineering,

24(3):161–170,.

Yoga, T. and Prihandoko (2018). Application of particle

swarm optimization (pso) based optimization of na

ıve

bayes and k-nearest neighbor algorithms as a compar-

ison to ﬁnd the best performance in detecting breast

cancer. J. Bangkit Indones, 7(2):1,. Available:.

Yunus, W. (2018). Particle-based swarm optimization-

based k-nearest neighbor algorithm for chronic kid-

ney disease prediction. J. Tek. Electro CosPhi,

2(2):51–55,.

ICAISD 2023 - International Conference on Advanced Information Scientiﬁc Development

186