Forecasting Cost-Push Inflation with LASSO over Ridge Regression

Sree Roshan Nair and N. Deepa

Saveetha University, Chennai, Tamilnadu, India

Keywords: Consumer Price Index, Cost-Push Inflation, Economy, Forecasting, Machine Learning, Novel Least Absolute

Shrinkage and Selection Operator, Prediction, Ridge Regression.

Abstract: This study undertook an experimental analysis to forecast Cost-push Inflation using the Novel LASSO

regression algorithm, contrasting it with the Ridge algorithm. Moreover, future Consumer Price Index (CPI)

values were determined. To achieve maximum accuracy in predicting Cost-Push Inflation, the performance

of the Novel LASSO algorithm (N=21) was evaluated against the Support vector regression algorithm (N=21).

Sample sizes were determined utilising G-power, considering a pretest power of 0.80 and an alpha of 0.05.

Notably, the mean accuracy value for the Novel LASSO algorithm stood at 81.95%, surpassing the Support

vector regression algorithm's 75.57%. Statistical analysis highlighted a significant difference between the two

methods (p=0.001, p<0.05), emphasising the superior accuracy of the Novel LASSO approach.

1 INTRODUCTION

The primary purpose of software is to obtain the

desired output by pairing input with a chosen

algorithm. In contrast, ML creates an algorithmic

model by combining data and output (Choi et al.

2016). It's a computer science branch where

computers are allowed to learn, rather than being

explicitly programmed. Machine learning plays a role

in our daily lives, for instance in detecting potential

fraudulent activities, predicting traffic, and

forecasting gambling outcomes (Devillers, Vidrascu,

and Lamel 2005). Sudden inflationary shifts can

impact a country's economy, thus controlling

inflation is paramount to avoid upheaval. Annually,

governments predict CPIs using various constraints to

maintain stability. The Consumer Price Index (CPI)

serves as a barometer for a country's inflation rate.

Relying solely on annual CPI predictions might be

problematic due to their potential influence on the

global economy (Shapiro and Wilcox 1996).

Therefore, leveraging historical data to forecast the

future is essential to prevent significant disruptions.

Inflation denotes the rate of price increase or decrease

for products over time, crucial for assessing a

country's cost of living—a primary consideration for

migrants. Cost-push inflation, a result of increased

raw material and wage costs, drives up product and

service prices, impacting the economy. CPI

measurements can capture these inflation types. This

study focuses on Cost-push inflation since predicting

it could help avert significant disasters (Diewert and

Erwin Diewert 2001). Resolving this issue entails

inputting data into an algorithm to produce an output

(Klutse, Sági, and Kiss 2022). In the domain of

inflation prediction via supervised machine learning

algorithms, various papers are accessible on

platforms like Google Scholar, IEEE, Springerlink,

and ScienceDirect. To be precise, 6000 articles on

Google Scholar, 90 on Springerlink, 3500 on

ScienceDirect, and 125 on IEEE. In the near future,

supervised machine learning algorithms might be

instrumental in predicting the Consumer Price Indices

of different countries. A pivotal reference for this

study explored numerous methods for accurately

predicting inflation and poverty rates using machine

learning models (Bryan and Cecchetti 1993). The

challenge in this research was the multifactorial

environment of inflation data prediction. This study

achieved an impressive 93.75% accuracy. Another

noteworthy article, cited 63 times, discusses

forecasting inflation and unemployment using the

Ridge regression algorithm (Sermpinis et al. 2014).

The current system for predicting Cost-push

inflation employs machine learning algorithms like

Ridge regression, linear, and Support vector

regression algorithms. However, these have

shortcomings. Due to frequently fluctuating data

points, achieving accuracy is challenging. These three

algorithms typically exhibit a larger margin of error

compared to the Novel LASSO (Plakandaras et al.

2017). Algorithmic accuracy varies due to data point

Nair, S. and Deepa, N.

Forecasting Cost-Push Inﬂation with LASSO over Ridge Regression.

DOI: 10.5220/0012559200003739

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Artiﬁcial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 64-70

ISBN: 978-989-758-661-3

similarities. Notably, the Novel LASSO outperforms

existing systems in terms of accuracy. The ultimate

aim of this research is to refine CPI forecasts using

the Novel LASSO regression.

2 MATERIALS AND METHODS

The solution-seeking analysis for this issue was

conducted at the Machine Learning Lab, SSE,

SIMATS. This lab is equipped with top-tier systems

to facilitate the above study and ensure precise

results. This review involved two collections, each

with a sample size of 21. These figures were

determined using a G-Power value of 80%, an alpha

of 0.05, a beta of 0.2, and a 95% confidence interval

(Kane, Phar, and BCPS).

The research utilised a dataset in CSV (Comma

Separated Values) format, encompassing the

consumer price index data of 270 countries over 64

years. This dataset was sourced from Kaggle (Rathore

2022). It details the CPIs of numerous countries for

specific years, offering insights into their economic

structures. Moreover, it's instrumental for forecasting

the future CPIs of any given country.

For the analytical process, Google Colab was

employed, a platform analogous to the Jupyter

Notebook environment but with the distinction of

operating entirely in the cloud. This online tool allows

for the creation, implementation, and sharing of

Python-based code, ideal for machine learning

applications. Essential Python libraries, such as

Numpy, Pandas, and Matplotlib, were utilised to

implement machine learning methods and visualise

inflation forecasts.

2.1 Novel Least Absolute Shrinkage

and Selection Operator Algorithm

Novel LASSO employs the principle of shrinkage and

falls under sample preparation group 1. In this context,

shrinkage refers to the reduction of data points towards

their average value. The method uses regularization to

enhance the interpretation of the model (Kapetanios

and Zikes 2018). Among the different regression

algorithm models, the Novel LASSO stands out for its

aptitude in subset variable selection, delivering

forecasts with greater accuracy. It operates using the

L1 regularization technique, which adds a penalty

proportional to the absolute magnitude of coefficients

(Campos, McMain, and Pedemonte 2022). Given that

CPI values are continuous but distinct, the Novel

LASSO regression is especially suited for inflation

prediction. This approach draws potential error values

towards a central reference, typically the mean. The

formula for L-1 regression is depicted in Equation 1,

while Table 1 provides a detailed breakdown of the

Novel Least Absolute Shrinkage and Selection

Operator algorithm's procedure.

L-1 Regression formula:

W = (RSS or Least Squares) + 𝜆 ∗ (Aggregate of

absolute values of coefficients) (1)

where,

1. RSS stands for Residual sum of squares

2. Lambda represents the aggregate of shrinkage

in the Novel LASSO regression equation.

2.2 Ridge Regression Algorithm

In this context, the data values are continuous,

lending an edge to the Ridge regression algorithm,

which places it in sample preparation group 2. The

Ridge regression algorithm is adept at addressing data

points afflicted by multicollinearity, by fine-tuning

the model. In contrast to the proposed regression

algorithm, Ridge regression employs the L-2

regularization technique. The associated formula for

this technique is as follows:

= argmin

𝞫

min 𝚺

- 𝞫’ x

)

+ 𝛌 𝚺

k=1

𝞫

(2)

The tuning parameter, denoted as 𝛌, governs the

relative influence of the two terms in ridge regression.

This approach is akin to linear regression, wherein a

modest bias is incorporated to facilitate more

sustainable long-term predictions. Ridge regression

determines an outcome by identifying the optimal line

or boundary. This boundary delineates the n-

dimensional space into classes, allowing for the

addition or determination of a data point based on

historical data points (Pavlov and New Economic

School 2020). The L-2 regularization's computational

formula is represented by Equation 2. The steps for

executing the Ridge regression algorithm are detailed

in Table 2.

2.3 Statistical Analysis

The analysis for this investigation was conducted

using IBM SPSS version 2.3. Within SPSS, a dataset

comprising 21 sample sizes, each with Consumer

Price Indexes (CPIs), was prepared for both the Novel

LASSO and Ridge regression algorithms. The dataset

covered attributes such as 270 countries spanning 64

years. Herein, the Consumer Price Index is the

dependent variable, whilst the independent variables

encompass factors like wage increases, taxation

Forecasting Cost-Push Inﬂation with LASSO over Ridge Regression

measures, demand-supply dynamics, economic

margins, and governmental regulations.

3 RESULTS

Table 1 outlines the procedure for the Novel LASSO

Algorithm. The process begins by initialising the

standard libraries, followed by training the model

using the dataset of Consumer Price Indexes.

Table 2 details the steps involved in the Ridge

Regression Algorithm. Similar to the Novel LASSO,

it commences with the initialisation of the standard

libraries and then proceeds to train the model using

the dataset of Consumer Price Indexes.

Table 3 offers a comparative analysis of the

accuracy between raw data from both the Novel

LASSO regression algorithm and the Ridge

Regression Algorithm.

Table 4 provides group statistical values for both

algorithms. These statistics include the mean,

standard deviation, and standard error mean. The

dataset is further analysed using an independent

sample T-test, with confidence set at 95%.

Table 5 showcases the results from the independent

t-sample test for the two algorithms. The table

furnishes details on the mean of loss, as well as a

comparative accuracy analysis between the two

algorithms. Both the T-test for equality of means and

the Levene’s test for equality of variance are presented.

Importantly, the table highlights a statistically

significant difference between the Novel LASSO

algorithm and the Ridge Regression algorithm, as

evidenced by a p-value of 0.001 (p<0.05).

Table 1: Proposed algorithm is the Novel LASSO regression algorithm procedure. Afterwards the Novel LASSO algorithm

takes the subsets of the problem to get the unique solution in order to predict future Consumer Price Index of Cost-Push

Inflation.

Input: Consumer Price Index Dataset

Output: Accurate prediction of CPI’s

1. Required packages are imported

2. Kaggle is used to download dataset.

3. First the rows and columns were preprocessed. After that, the missing variables were handled in order to

make it error free.

4. Training of Novel LASSO model for getting the accuracy values.

5. Model has been tested with the dataset.

6. Accuracy of Novel LASSO is calculated.

7. Estimation of accuracy from the loss value.

Table 2: Represents the procedure of the Ridge Regression Algorithm. First initialization of the standard libraries is done and

the model is trained with the dataset of Consumer price indexes. Testing and training are two sets of the models for the dataset

and these are assigned to different functions to calculate the accuracy.

Input: Consumer Price Index Dataset

Output: Accurate prediction of CPI’s

1. Required packages are imported.

2. Kaggle is used to download dataset.

3. All the rows and columns were preprocessed after which missing variables were handled.

4. Training of Ridge regression model.

5. Model has been tested with the data set.

6. Accuracy of Ridge regression is calculated.

7. Estimation of accuracy from loss value.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

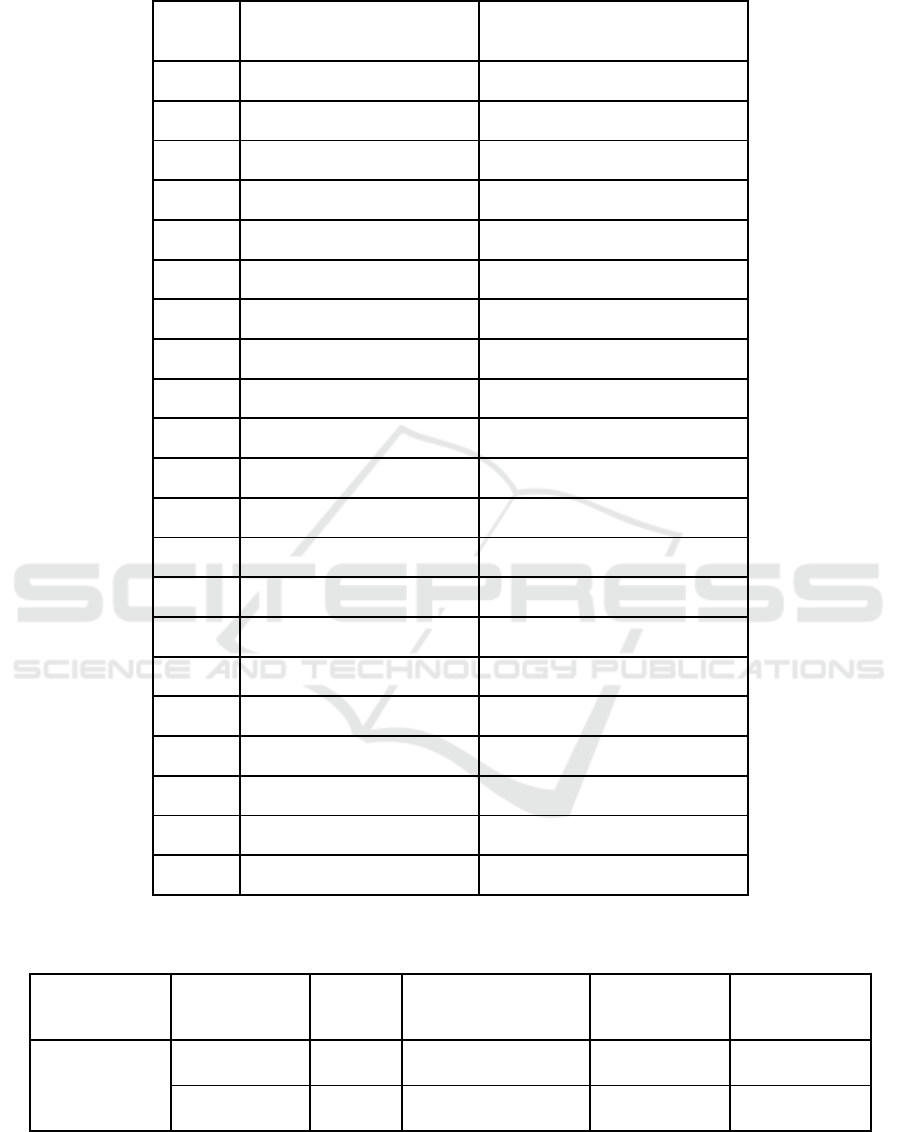
Table 3: Depicts the raw data table of accuracy between Novel LASSO regression algorithm and Ridge Regression Algorithm.

S.No

Novel LASSO Algorithm

Accuracy (%)

Ridge Regression Accuracy (%)

Table 4: Lists the group statistics values for the two algorithms along with the mean, standard deviation, and standard error

mean. The dataset is subjected to an independent sample T-test with a 95% confidence level.

Group

Mean

Std

deviation

Std.Error Mean

Accuracy

Novel LASSO

81.95

6.895

1.505

RIDGE

67.86

7.914

1.727

Forecasting Cost-Push Inﬂation with LASSO over Ridge Regression

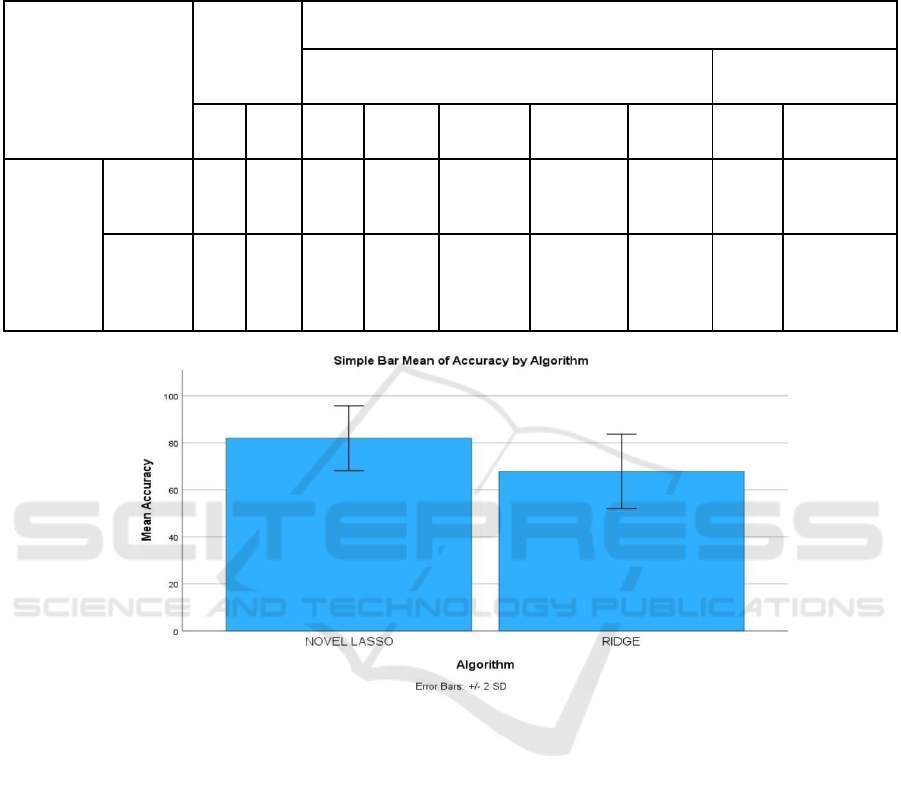
Table 5: Depicts an independent t-sample test for algorithms. Mean of loss and comparative accuracy analysis between the

two algorithms are provided. T test for equality of means and Levene’s test for equality of precision are provided. It shows

that there is a statistical significance difference between the Novel LASSO algorithm and Ridge Regression algorithm with

p=0.001 (p<0.05).

Levene’s test

for equality

of precision

T test for equality of means

95% confidence

intervals of difference

Sig.

Sig. (2-

tailed)

Mean

Difference

Std. Error

difference

Lower

Upper

Accuracy

Equal

variances

assumed

.634

.431

6.154

.001

14.095

2.291

9.466

18.725

Equal

variances

not

assumed

6.154

39.264

.001

14.095

2.291

9.463

18.727

Figure 1: Comparison of Novel LASSO regression (81.95) and Ridge regression (67.86) with respect to mean accuracy. The

accuracy value of the Novel LASSO algorithm is better than the Ridge regression algorithm and the standard deviation of

LASSO is better than Ridge. X-axis: Novel LASSO vs Ridge regression algorithm. Y-axis: Mean accuracy of data +/- 2 SD.

Figure 1 visually compares the mean accuracy and

mean loss of the Novel LASSO Algorithm and Ridge

Regression Algorithm.

4 DISCUSSION

The results from the Sample T-Test analysis allow for

an effortless determination of the significance value.

With a significance value of 0.611, which is greater

than 0.05, there is no significant difference between

the groups for the selected dataset, as highlighted in

Table 5. The accuracy of the Ridge regression stands

at 67.86%, lower than that of the Novel LASSO

regression, which is 81.95% (p > 0.05).

This paper's ultimate aim is to accurately forecast

the Cost-push inflation rate from the provided dataset.

By utilising the Consumer Price Index (CPI),

predictions for a specific year are made by averaging

data points to their mean (Stewart and Reed 2000).

Future CPIs can also be calculated, considering both

independent and dependent variables (Fixler 2009). A

failure to address Cost-push inflation can result in

severe economic repercussions (Huang and Mintz

1990). This could adversely affect countless

individuals, especially in countries with a lower cost

of living. A spike in the prices of daily essential raw

materials, such as gold, steel, and petrol, can lead to

public unrest (Seelig 1974), with demands for pay

raises potentially resulting in company closures or

layoffs.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

According to a study by Pavlov in 2020 (Pavlov

and New Economic School 2020), the accuracy rate

for Ridge regression is approximately 74.956%. In

contrast, the Novel LASSO delivers more accurate

values with an accuracy rate of 81.95%. With a

comprehensive database spanning 60 years and

covering 268 countries with recorded CPIs, accurate

prediction becomes more feasible. The proposed

model boasts superior accuracy coupled with a lower

processing rate, attributable to the use of extensive

databases. For improved speed and accuracy, smaller

databases are favoured (Ho 1982). Despite the wealth

of data, many researchers have argued that various

predictive models are not designed for accurately

forecasting a country's CPI for a particular year.

Ridge regression's drawbacks include its time-

consuming nature and its less intuitive user interface,

especially when compared to the Novel Least

Absolute Shrinkage and Selection Operator. This

implies that implementing the Ridge regression

algorithm is cumbersome, time-intensive, and

generally inferior to the Novel LASSO regression

algorithm. Looking forward, the Novel LASSO

regression algorithm is poised to be the go-to tool for

running ML models, aiming to forecast inflation rates

and predict economic stability.

5 CONCLUSION

The intricate dynamics of inflation prediction,

especially in the context of the Cost-push inflation

rate, represent a vital area of study in economic

research. The stakes are high: accurate prediction

methodologies can inform policy decisions,

streamline financial forecasting, and foster economic

stability. Our exploration into this domain yielded

several key observations that shaped the findings and

contributed to our understanding of the topic.

● Database Depth: The expansive database

spanning over 60 years and covering 268

countries provided a robust foundation for

analysis. Such a comprehensive data set

ensures that the algorithms can train and test

on varied and representative data, enhancing

the generalisability of the results.

● Impact of Raw Materials: The volatility in the

prices of essential raw materials, such as gold

and petrol, underscores the importance of

accurate inflation prediction. These

fluctuations have a ripple effect on the

economy, affecting wage demands, consumer

prices, and corporate profitability.

● Economic Implications: A misstep in

predicting Cost-push inflation can lead to

adverse economic repercussions. Failing to

account for inflationary pressures can imperil

economic health, affecting trade balances,

purchasing power, and even leading to

recessions.

● Algorithmic Advantages: The Novel LASSO

algorithm's inherent design, which focuses on

both feature selection and regularisation, lends

it an edge over other algorithms. Its ability to

reduce model complexity while retaining

significant variables makes it particularly

effective for complex economic predictions.

● Usability Concerns: Beyond mere accuracy,

the ease of use and processing time of an

algorithm play a significant role in its real-

world application. As observed, Ridge

regression, despite its merits, is more time-

consuming and less user-friendly compared to

Novel LASSO.

● Future Scope: The continual evolution of

machine learning models hints at the

possibility of even more refined and accurate

prediction models in the future. Keeping

abreast of these developments will be crucial

for maintaining the edge in economic

forecasting.

In light of the above points, the outcome of the

present study of Cost-push inflation prediction is

encouraging. With the Ridge regression algorithm

delivering a mean accuracy of 67.86% and the Novel

LASSO algorithm presenting a commendable mean

accuracy of 81.95%, the latter clearly stands out.

Hence, it is concluded that the Novel LASSO

Algorithm exhibits superior accuracy when

juxtaposed with the Ridge regression algorithm. This

distinction, coupled with the aforementioned insights,

paves the way for more informed decisions in

economic modelling and forecasting.

REFERENCES

Bryan, Michael F., and Stephen G. Cecchetti. 1993. “The

Consumer Price Index as a Measure of Inflation.”

w4505. National Bureau of Economic Research.

https://doi.org/10.3386/w4505.

Campos, Chris, Michael McMain, and Mathieu Pedemonte.

2022. “Understanding Which Prices Affect Inflation

Expectations.” Economic Commentary (Federal

Reserve Bank of Cleveland).

https://doi.org/10.26509/frbc-ec-202206.

Choi, Sun, Young Jin Kim, Simon Briceno, and Dimitri

Mavris. 2016. “Prediction of Weather-Induced Airline

Forecasting Cost-Push Inﬂation with LASSO over Ridge Regression

Delays Based on Machine Learning Algorithms.” 2016

IEEE/AIAA 35th Digital Avionics Systems Conference

(DASC). https://doi.org/10.1109/dasc.2016.7777956.

Devillers, Laurence, Laurence Vidrascu, and Lori Lamel.

2005. “Challenges in Real-Life Emotion Annotation

and Machine Learning Based Detection.” Neural

Networks: The Official Journal of the International

Neural Network Society 18 (4): 407–22.

Diewert, W. Erwin, and W. Erwin Diewert. 2001. “The

Consumer Price Index and Index Number Purpose.”

Journal of Economic and Social Measurement.

https://doi.org/10.3233/jem-2003-0183.

Fixler, Dennis. 2009. “Incorporating Financial Services in

A Consumer Price Index.” Price Index Concepts and

Measurement.

https://doi.org/10.7208/chicago/9780226148571.003.0

007.

G. Ramkumar, R. Thandaiah Prabu, Ngangbam Phalguni

Singh, U. Maheswaran, Experimental analysis of brain

tumor detection system using Machine learning

approach, Materials Today: Proceedings, 2021, ISSN

2214-7853,

https://doi.org/10.1016/j.matpr.2021.01.246.

ho, Yan-Ki. 1982. “A Trivariate Stochastic Model For

Examining The Cause Of Inflation In A Small Open

Economy: Hong Kong.” The Developing Economies.

https://doi.org/10.1111/j.1746-1049.1982.tb00831.x.

Huang, Chi, and Alex Mintz. 1990. “Ridge Regression

Analysis of the Defence‐growth Tradeoff in the United

States.” Defence Economics.

https://doi.org/10.1080/10430719008404676.Kane,

Sean P., Phar, and BCPS. n.d. “Sample Size

Calculator.” Accessed April 18, 2023.

https://clincalc.com/stats/samplesize.aspx.

Kapetanios, George, and Filip Zikes. 2018. “Time-Varying

Lasso.” Economics Letters.

https://doi.org/10.1016/j.econlet.2018.04.029.

Klutse, Senanu Kwasi, Judit Sági, and Gábor Dávid Kiss.

2022. “Exchange Rate Crisis among Inflation Targeting

Countries in Sub-Saharan Africa.” Risks.

https://doi.org/10.3390/risks10050094.

Kumar M, M., Sivakumar, V. L., Devi V, S.,

Nagabhooshanam, N., & Thanappan, S. (2022).

Investigation on Durability Behavior of Fiber

Reinforced Concrete with Steel Slag/Bacteria beneath

Diverse Exposure Conditions. Advances in Materials

Science and Engineering, 2022.

Pavlov, Evgeny, and New Economic School. 2020.

“Forecasting Inflation in Russia Using Neural

Networks.” Russian Journal of Money and Finance.

https://doi.org/10.31477/rjmf.202001.57.

Plakandaras, Vasilios, Periklis Gogas, Theophilos

Papadimitriou, and Rangan Gupta. 2017. “The

Informational Content of the Term Spread in

Forecasting the US Inflation Rate: A Nonlinear

Approach.” Journal of Forecasting.

https://doi.org/10.1002/for.2417.

Rathore, Bhupesh Singh. 2022. “World Inflation Dataset

1960-2021.”

https://www.kaggle.com/bhupeshsinghrathore/world-

inflation-dataset-19602021.

S. G and R. G, "Automated Breast Cancer Classification

based on Modified Deep learning Convolutional Neural

Network following Dual Segmentation," 2022 3rd

International Conference on Electronics and

Sustainable Communication Systems (ICESC),

Coimbatore, India, 2022, pp. 1562-1569, doi:

10.1109/ICESC54411.2022.9885299.

Seelig, Steven A. 1974. “Rising Interest Rates And Cost

Push Inflation.” The Journal of Finance.

https://doi.org/10.1111/j.1540-6261.1974.tb03085.x.

Sermpinis, Georgios, Charalampos Stasinakis,

Konstantinos Theofilatos, and Andreas

Karathanasopoulos. 2014. “Inflation and

Unemployment Forecasting with Genetic Support

Vector Regression.” Journal of Forecasting.

https://doi.org/10.1002/for.2296.

Shapiro, Matthew, and David Wilcox. 1996.

“Mismeasurement in the Consumer Price Index: An

Evaluation.” https://doi.org/10.3386/w5590.

Stewart, Kenneth J., and Stephen B. Reed. 2000. “Data

Update Consumer Price Index Research Series Using

Current Methods (CPI-U-RS), 1978-1998.” Industrial

Relations. https://doi.org/10.1111/0019-8676.00158.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics