Comparative Analysis of K-Nearest Neighbours Algorithm and Naive

Bayes Algorithm for Prediction of Storm Warning

Challa Rohini

and S. Magesh Kumar

Department of Computer Science and Engineering, Saveetha School of Engineering, Saveetha Institute of Medical and

Technical Sciences, Saveetha University, Chennai, Tamil Nadu, 602105, India

Keywords: Novel K-Nearest Neighbours Algorithm, Machine Learning, Naive Bayes Algorithm, Pandemic, Poverty,

Storm Warning.

Abstract: The primary aim of this research was to enhance the accuracy of storm warnings by employing the novel K-

Nearest Neighbours algorithm and comparing it to the Naive Bayes method. This investigation divided

participants into two groups: the Novel K-Nearest Neighbours and the Naive Bayes Algorithm, each

comprising ten representatives. The mean accuracy was determined using the ClinCalc software tool in a

supervised learning setting, considering an alpha value of 0.05, a G-Power of 0.8, and a 95% confidence

interval. The K-Nearest Neighbours algorithm showcased a notable accuracy rate of 68.20%, outstripping the

57.31% accuracy of the Naive Bayes. The difference between the two was statistically significant (p=0.000).

In conclusion, the K-Nearest Neighbours approach substantially surpassed the Naive Bayes.

1 INTRODUCTION

Storms, intense atmospheric disturbances

characterised by strong winds, rain, thunder, and

lightning, can have dire implications. As highlighted

by Benvenuto et al. (2020), these disturbances can not

only disrupt day-to-day activities but also lead to

pervasive poverty. During rainy periods amidst

pandemics, the US National Weather Services issue

storm warnings, particularly for maritime regions

(Fogarty et al. 2021). These warnings play a pivotal

role in safeguarding both lives and wealth (Chen

2019; G. Ramkumar et al. 2022). Despite the wealth

of research on storm warnings, there is still room for

improvement in accuracy. Interestingly, the concept

has even permeated popular culture, as seen in the 9th

book of the Clues Series by Linda Sue Park. Notably,

severe weather conditions, including storms, thunder,

tsunamis, and earthquakes, have profound

socioeconomic impacts, often causing poverty. Such

conditions are frequently monitored by institutions

like the National Weather Service (Lagerquist et al.

2020; Padma, S. et al. 2022).

Recent studies underscore the significance of storm

warnings. For instance, among the multitude of

articles, some are catalogued in IEEE Digital Xplore,

Science Direct, Google Scholar, and SpringerLink.

Research Scholar, Research Guide, Corresponding Author

Various machine learning methodologies have been

adopted to enhance storm prediction accuracy, from

supervised techniques reporting an F1 score of 79%

(Werbach 2020) to Random Forest algorithms with

62% accuracy (Liu et al. 2022) and even SVMs hitting

80% (McGovern et al. 2019). Beyond immediate

dangers, storm warnings serve as a crucial tool to

protect socio-economic structures, especially given the

potential for significant losses leading to poverty.

However, a conspicuous research gap persists.

Despite extensive literature, the precision of storm

warnings still demands hefty data, especially from

national agencies like the National Weather Service.

This results in time-consuming training processes for

prediction models. Thus, this study aspires to refine

the accuracy of storm warnings using the K-Nearest

Neighbour’s Algorithm, compared against Naive

Bayes, all while requiring less data, thereby

expediting the warning process and potentially saving

countless lives and assets.

2 MATERIALS AND METHODS

The proposed study was undertaken at the Artificial

Intelligence Lab of Saveetha School of Engineering.

The research encompassed two distinct groups:

Rohini, C. and Kumar, S.

Comparative Analysis of K-Nearest Neighbours Algorithm and Naive Bayes Algorithm for Prediction of Storm Warning.

DOI: 10.5220/0012569500003739

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Artiﬁcial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 103-108

ISBN: 978-989-758-661-3

103

Group 1 employed the K-Nearest Neighbours

technique, while Group 2 harnessed the Naive Bayes

method. Both approaches were evaluated

intermittently on a cohort of 20 participants.

Statistical computations were informed by G-power

values of 0.8, an alpha level of 0.05, beta set at 0.2,

and were executed with a confidence threshold of

95%. Additionally, an 80% pretest power was

adopted as per Chang, Hsu, and Chang (2019).

The research utilised the 'Storm Warning' dataset,

tailored for sensors that detect adverse meteorological

conditions that may potentially usher in pandemics.

This dataset, procured from Kaggle.com

(Muthukumar 2017), boasts 19 attributes, notably

including summary, humidity, and wind speed. Each

group was allocated ten samples, culminating in ten

apiece for both test and training data. After

segmenting the dataset, the respective methodologies

were implemented to ascertain the accuracy metrics,

leveraging the delineated training and test sets.

K-Nearest Neighbours Classifier

The k-nearest neighbours (KNN or k-NN) is a

supervised learning algorithm that operates on the

principle of proximity to make inferences about a data

point's potential classification. Predominantly used

for classification, the foundation of KNN lies in the

notion that data points with similar characteristics are

proximal to each other, though it's also suitable for

regression tasks.

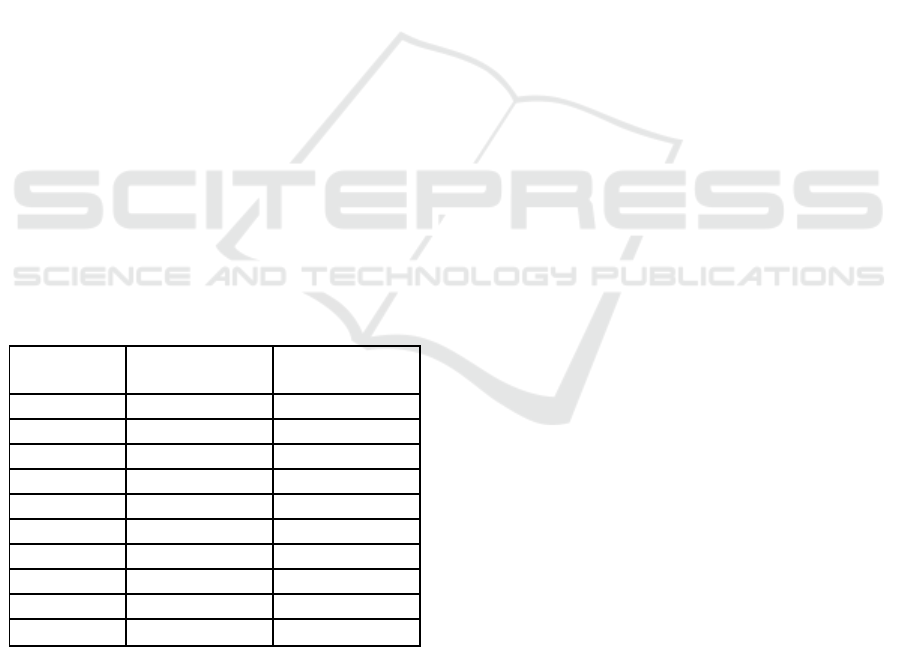
Table 1: Accuracy of K Nearest Neighbours and Naive

Bayes classifiers.

S.NO

KNN

Algorithm

72.6

62.6

69.45

60.34

71.34

58.90

68.23

61.48

72.56

62.0

69.88

63.5

70.34

61.89

71.56

56.45

72.0

62.10

66.45

60.34

The value 'k' in the k-NN algorithm denotes the

count of neighbouring points considered to classify a

given point. For instance, with k=1, a data instance is

categorised based on its closest single neighbour.

Proper selection of 'k' is essential to balance between

overfitting and underfitting. Larger 'k' values may

induce notable bias and reduced variance, while

smaller 'k' values tend to have elevated variance but

diminished bias. The nature of the data, especially its

noise level or presence of outliers, will significantly

impact the optimal 'k' choice. Typically, an odd 'k'

value is favoured to mitigate potential classification

ties.

Fig. 1 graphically depicts the structure of a KNN

model with two input variables leading to a singular

output. The crux of this model is using proximity as a

tool for classification or prediction.

Procedure for Novel K-Nearest Neighbours

Algorithm

1. Insert the necessary packages and the dataset.

2. Specify what X and Y are.

3. Establish training and testing sets for the data.

4. X train, X test, Y test, and Train Test Split (X, Y,

Random State=50, Test Size=0.3)

5. Model_ KNN & K Neighbour’s (n neighbours = 5,

p = 2)

6. Fit Model KNN (trains x and y)

7. Simulation knn.predict(x test) is used.

8. Simulation KNN.Score(x test, y test)

9. Display the Accuracy.

Naive Bayes Classifier

The Naive Bayes algorithm is a supervised learning

method rooted in the Bayes theorem, primarily

tailored for classification tasks. Widely adopted in

text classification, it uses substantial training data.

Despite its simplicity, the Naive Bayes Classifier is

efficient and effective, facilitating the creation of

robust machine learning models. As a probabilistic

classifier, it predicates its decisions on the likelihood

of an event's occurrence. Common applications of

Naive Bayes include spam filtering, sentiment

analysis, and categorising articles.

Naive Bayes employs a probabilistic framework

and, while simple, frequently delivers impressively

accurate results. For example, it underpins many

email applications' spam filters. In this piece, I'll

expound on the reasoning behind Naive Bayes and

illustrate its application in a Python-based spam filter.

The ultimate goal is to enhance accuracy, potentially

aiding in poverty reduction.

This solution operates on a 64-bit system, using

Jupyter and Python via the Anaconda platform,

bolstered by 8GB of RAM and an Intel i7 10th Gen

processor. In the context of storm warning prediction,

temperature and humidity serve as the independent

variables, with optimal accuracy values being the

dependent variable. The dependent variables react to

any shifts in the independent variables.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

104

Procedure for Naive Bayes Algorithm

1. Insert the necessary packages and the dataset.

2. Specify what X and Y are.

3. Establish training and testing sets for the data.

4. X train, X test, Y test, and Train Test Split (X, Y,

Random State=50, Test Size=0.3)

5. GaussianNB()

6. (x train, y train) gnb.fit

7. Model gnb.predict(x test), Y predicted _nb,

8. Model NB.Score(x test, y test);

9. Display the Accuracy.

Statistical Analysis

For the statistical analysis in this research, IBM SPSS

version 26 was employed. In the study, the

independent variables were temperature and wind,

while the increased accuracy values served as the

dependent variable. A separate t-test analysis was

conducted as part of the study, as referenced by Jha,

Bloch, and Lamond (2012).

3 RESULTS

In this study, the Novel K-Nearest Neighbours

technique and the Naive Bayes method were applied

to a sample size of 20 participants, using Google

Collab for computation. The results, presented in

Table 1, revealed that the K-Nearest Neighbours

technique is seemingly more accurate when

compared to the Naive Bayes method. This was

further substantiated by an independent sample T-test

(showcased in Table 3), indicating a statistically

significant difference between the two methods with

a 2-tailed p-value of 0.000 (p < 0.05).

The mean accuracy discrepancy between the two

methods is 10.886. Delving into the details, Table 2

reveals that, from an analytical assessment of 10

samples, the K-Nearest Neighbours approach has a

standard deviation of 4.251 and a mean error of 0.850.

In contrast, the Naive Bayes method presented a

standard deviation of 4.245 and a mean error of 0.849.

The accuracy percentages indicate that K-Nearest

Neighbours (68.20%) outperforms Naive Bayes

(57.31%). This superior performance is further

illustrated in Figure 2, a bar graph that highlights the

slightly lower standard deviation for K-Nearest

Neighbours compared to Naive Bayes. In this figure,

the X-axis represents the comparison between the K-

Nearest Neighbour Algorithm and the Naive Bayes

Algorithm Classifier, while the Y-axis depicts the

mean detection accuracy, encompassed within a

range of +/- 2SD.

Table 2: Group statistics of Accuracy for K Nearest Neighbours and Naive Bayes classifiers.

Algorithm

Mean

Std. Deviation

Std. Error Mean

Accuracy

KNN

68.20

4.251

.850

57.31

4.245

.849

Table 3: Independent sample T-Test for K Nearest Neighbours and Naive Bayes Classifiers. There is a statistically significant

difference between the Novel K-Nearest Neighbours algorithm and Naive Bayes with a 2-tailed value p= 0.000 (p < 0.05).

Levene’s Test for

Equality of

Variances

T-Test for Equality of Mean

95 % Confidence

Interval of

Difference

Sig.

Sig. (2-

tailed)

Mean

Differenc

Std.

Error

Differenc

Lower

Upper

Equal

variances

assumed

0.136

0.714

9.060

48.000

.000

10.886

1.201

8.470

13.302

Equal

variances

assumed

9.060

48.000

.000

10.886

1.201

8.470

13.302

Comparative Analysis of K-Nearest Neighbours Algorithm and Naive Bayes Algorithm for Prediction of Storm Warning

105

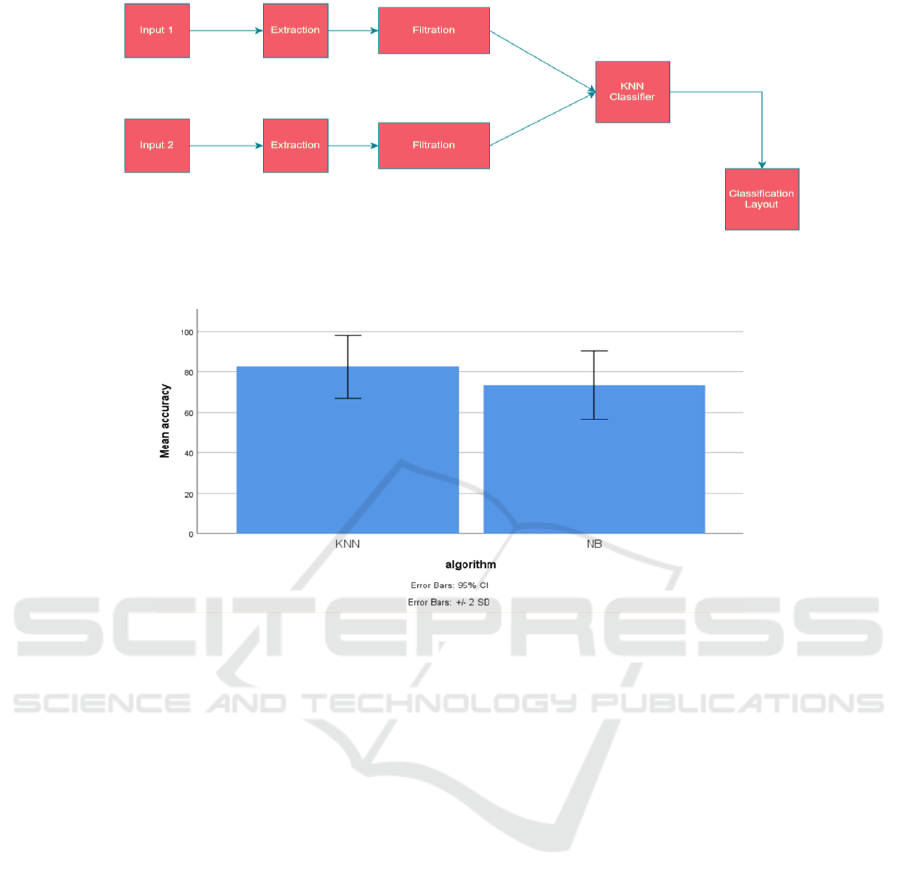
Figure 1: Architecture of KNN with 2 inputs and 1 output. It has been done using High-level Synthesis and solves both

classification and regression problems.

Figure 2: In comparing the K-Nearest Neighbour's Algorithm with the Naive Bayes Classifier, the former outperforms the

latter in storm warning accuracy. The X-Axis contrasts the two algorithms, while the Y-Axis displays the mean detection

accuracy within +/- 2SD.

4 DISCUSSION

In the presented study, the accuracy of predicting

Storm Warnings was evaluated using two

classification methods: the K-Nearest Neighbours

Classifier, which achieved 68.20% accuracy, and the

Naive Bayes Classifier, recording 57.31% accuracy.

The KNN Classifier outperformed Naive Bayes in

terms of Storm Warning prediction. With a

significance value of 0.000 (p < 0.05), it's evident that

the results for the two classifiers are statistically

distinct.

Various machine learning techniques, integrated

with the Previstorm system, were employed to

mitigate catastrophic events (Jha, Bloch, and Lamond

2012). The Decision tree method recorded a 93%

success rate, KNN achieved a proficiency of 95%,

and Naive Bayes secured 92% in categorising storm

warning predictions. A significant contribution in this

area was made by Whan and Schmeits (2018),

highlighting a commendable 90% accuracy using K-

Nearest Neighbours (Han, Sun, and Zhang 2020).

Content analysis reveals a broad application of

machine learning techniques for forecasting the

precision of Storm Warnings (Benvenuto et al. 2020).

With a primary focus on categorisation, K-Nearest

Neighbours demonstrated superior accuracy relative

to previous research findings.

Environmental factors like a swift shift in

temperature can trigger significant meteorological

disruptions. Due to inherent variability and

unpredictability, there's a threshold to accurate long-

term weather forecasting. Such unpredictabilities can

result in substantial financial loss and escalate

poverty, especially during pandemic situations. To

combat such challenges in the future, refining the

accuracy of Storm Warnings is crucial.

5 CONCLUSION

In recent years, the unpredictable nature of weather

patterns has highlighted the importance of accurate

Storm Warning predictions. The ability to predict

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

106

storms with precision not only has implications for

safeguarding assets and human lives but also plays a

pivotal role in strategizing for potential disaster

management. The present experimentation aimed to

enhance the accuracy of Storm Warning prediction, a

quest of vital importance in meteorology and

climatology.

Given the complexity and unpredictable nature of

weather systems, machine learning techniques have

emerged as promising tools for accurate prediction.

This research article delves into the efficacy of two

such algorithms: the Novel K-Nearest Neighbour's

method and the Naive Bayes. The contrast between

the two is instrumental in understanding their

respective strengths and potential areas of

application. The results obtained were enlightening.

The Novel K-Nearest Neighbour's method

demonstrated an impressive accuracy rate of 68.20%,

whereas the Naive Bayes method lagged slightly

behind, recording an accuracy of 57.31%.

Drawing from these findings, here are six key

points to consider:

• Methodology Matters: The distinction in

accuracy between the two algorithms

underscores the importance of selecting the

appropriate method for specific prediction

tasks.

• Data Sensitivity: K-Nearest Neighbour's

method, by its inherent design, is sensitive to

the locality of data points, which could be

beneficial for weather predictions.

• Probabilistic Predictions: The Naive Bayes

method, being probabilistic in nature, can

offer insights into the likelihood of various

outcomes, allowing for a risk-based analysis.

• Computational Efficiency: While accuracy is

paramount, the computational efficiency of

algorithms can also play a significant role,

especially when real-time predictions are

needed.

• Scope for Ensemble Methods: Given that

different algorithms have unique strengths,

there's potential in exploring ensemble

methods that combine the predictions of

multiple algorithms to achieve higher

accuracy.

• Continuous Evolution: As with all machine

learning methods, continuous training with

fresh data can refine and enhance the

prediction accuracy over time.

In conclusion, this research article provides

valuable insights into the domain of Storm Warning

prediction, underscoring the significance of

algorithmic selection and the potential benefits of

continuous data integration and analysis.

REFERENCES

Benvenuto, F., C. Campi, A. M. Massone, and M. Piana.

2020. “Machine Learning as a Flaring Storm Warning

Machine: Was a Warning Machine for the 2017

September Solar Flaring Storm Possible?”

Astrophysical Journal Letters 904 (1): L7.

Bringi, V. N., and V. Chandrasekar. 2001. Polarimetric

Doppler Weather Radar: Principles and Applications.

Cambridge University Press.

Chang, Fi-John, Kuolin Hsu, and Li-Chiu Chang. 2019.

Flood Forecasting Using Machine Learning Methods.

MDPI.

Chen, Shien-Tsung. 2019. “Probabilistic Forecasting of

Coastal Wave Height during Typhoon Warning Period

Using Machine Learning Methods.” Journal of

Hydroinformatics 21 (2): 343–58.

Fogarty, Eloise S., David L. Swain, Greg M. Cronin, Luis

E. Moraes, Derek W. Bailey, and Mark Trotter. 2021.

“Developing a Simulated Online Model That Integrates

GNSS, Accelerometer and Weather Data to Detect

Parturition Events in Grazing Sheep: A Machine

Learning Approach.” Animals : An Open Access

Journal from MDPI 11 (2).

https://doi.org/10.3390/ani11020303.

G. Ramkumar, G. Anitha, P. Nirmala, S. Ramesh and M.

Tamilselvi, "An Effective Copyright Management

Principle using Intelligent Wavelet Transformation

based Water marking Scheme," 2022 International

Conference on Advances in Computing,

Communication and Applied Informatics (ACCAI),

Chennai, India, 2022, pp. 1-7, doi:

10.1109/ACCAI53970.2022.9752516.

Han, Lei, Juanzhen Sun, and Wei Zhang. 2020.

“Convolutional Neural Network for Convective Storm

Nowcasting Using 3-D Doppler Weather Radar Data.”

IEEE Transactions on Geoscience and Remote

Sensing: A Publication of the IEEE Geoscience and

Remote Sensing Society 58 (2): 1487–95.

Huntingford, Chris, Elizabeth S. Jeffers, Michael B.

Bonsall, Hannah M. Christensen, Thomas Lees, and

Hui Yang. 2019. “Machine Learning and Artificial

Intelligence to Aid Climate Change Research and

Preparedness.” Environmental Research Letters: ERL

[Web Site] 14 (12): 124007.

Jha, Abhas K., Robin Bloch, and Jessica Lamond. 2012.

Cities and Flooding: A Guide to Integrated Urban

Flood Risk Management for the 21st Century. World

Bank Publications.

Lagerquist, Ryan, Amy McGovern, Cameron R. Homeyer,

David John Gagne II, and Travis Smith. 2020. “Deep

Learning on Three-Dimensional Multiscale Data for

Next-Hour Tornado Prediction.” Monthly Weather

Review 148 (7): 2837–61.

Comparative Analysis of K-Nearest Neighbours Algorithm and Naive Bayes Algorithm for Prediction of Storm Warning

107

Liu, Peng, Zhe Zhang, Mohd Anul Haq, and Yizhe Zhan.

2022. Big Earth Data Intelligence for Environmental

Modeling. Frontiers Media SA.

McGovern, Amy, Christopher D. Karstens, Travis Smith,

and Ryan Lagerquist. 2019. “Quasi-Operational

Testing of Real-Time Storm-Longevity Prediction via

Machine Learning.” Weather and Forecasting 34 (5):

1437–51.

Muthukumar, J. 2017. “Weather Dataset.”

https://www.kaggle.com/muthuj7/weather-dataset.

Padma, S., Vidhya Lakshmi, S., Prakash, R., Srividhya, S.,

Sivakumar, A. A., Divyah, N., ... & Saavedra Flores, E.

I. (2022). Simulation of land use/land cover dynamics

using Google Earth data and QGIS: a case study on

outer ring road, Southern India. Sustainability, 14(24),

16373

Werbach, Kevin. 2020. After the Digital Tornado:

Networks, Algorithms, Humanity. Cambridge

University Press.

Whan, Kirien, and Maurice Schmeits. 2018. “Comparing

Area Probability Forecasts of (Extreme) Local

Precipitation Using Parametric and Machine Learning

Statistical Postprocessing Methods.” Monthly Weather

Review 146 (11): 3651–73.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

108