
Precise Portfolio Optimization Based on Novel Modern Portfolio
Theory Using Time Series Model Compared with LASSO Regression
K. Sravan
*
and P. Sriramya
†
Department of Computer Science and Engineering, Saveetha School of Engineering, Saveetha Institute of Medical and
Technical Sciences, Chennai, Tamil Nadu, 602105, India
Keywords: Global Trade, Time Series Model, Novel Modern, Novel Modern Portfolio, LASSO Regression, Stock
Market.
Abstract: This study aims to augment the accuracy of stock market prediction by amalgamating Time Series Model
algorithms with LASSO Regression. Historical financial data for various assets is amassed to generate optimal
portfolios employing MPT 2.0 and LASSO Regression. Performance metrics such as the Sharpe ratio and
portfolio variance are harnessed to appraise these portfolios. The aim is to juxtapose the predictive precision
of the two methodologies and ascertain which one affords more precise portfolio optimisation results.
Materials and Methods: The prediction process involves Time Series Model (N=10) coupled with LASSO
Regression (N=10). Determining sample size utilises Gpower, with pretest power set at an alpha value of 0.8
and a beta value of 0.2. The accumulated financial data is employed to construct optimal portfolios through
MPT 2.0 and LASSO Regression. Evaluation criteria encompass the Sharpe ratio for risk-adjusted
performance and portfolio variance for risk assessment. Result: The Time Series Model showcases a lofty
accuracy rate of 90.1252%, whereas the LASSO Regression method attains an accuracy of 80.1423%. The
significance of accuracy and loss is underscored by the p-value being less than 0.05 (p=0.000), signifying the
marked significance of the Time Series Model in contrast to LASSO Regression. Conclusion: Within the
realm of portfolio optimisation, the Time Series Model approach manifests a marginally elevated predictive
rate when compared to the LASSO Regression method. This infers that the Time Series Model algorithm
endows advanced predictive capabilities for stock market performance.
1 INTRODUCTION
Portfolio optimisation constitutes a crucial facet of
global trade within investment management, aiming
to forge a collection of assets that maximises returns
while mitigating risk. Conventional portfolio theory,
rooted in mean-variance analysis, has long served as
the cornerstone for portfolio optimisation.
Nevertheless, it has faced criticism for its
oversimplification of market dynamics, presumption
of static correlations between assets, and neglect of
non-normal return distributions. This prompted the
development of Modern Portfolio Theory (MPT) to
address some of these limitations ('Predicting
portfolio returns using the distributions of efficient set
portfolios', 2003a) (Parzen, 1983).
Recently, a novel approach to portfolio
optimisation, termed Modern Portfolio Theory using
*
Research Scholar
†
Project Guide, Corresponding Author
Time Series Models (MPT-TSM), has emerged. This
method integrates time series techniques to model
asset returns and correlations (Md. Ehsanes Saleh,
Arashi and Golam Kibria, 2019). MPT-TSM
accounts for the dynamic nature of asset prices,
incorporating long-term trends, seasonality, and other
elements influencing asset prices over time. This
approach offers potential advantages over traditional
MPT, including enhanced risk-adjusted returns and
improved out-of-sample performance.
Another prominent global trade strategy for
portfolio optimisation is LASSO (Least Absolute
Shrinkage and Selection Operator) regression. This
statistical technique serves to select variables and
apply regularisation (Prendergast, no date; Parzen,
1981; Uğurlu and Brzeczek, 2022). LASSO
regression has demonstrated its capacity to bolster the
accuracy of portfolio optimisation models by
Sravan, K. and Sriramya, P.
Precise Portfolio Optimization Based on Novel Modern Portfolio Theory Using Time Series Model Compared with LASSO Regression.
DOI: 10.5220/0012602600003739
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Artificial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 133-140
ISBN: 978-989-758-661-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
133

identifying pertinent predictors while mitigating
overfitting (Madsen, 2007).
Within this portfolio optimisation study, we
conduct a comparative analysis of MPT-TSM and
LASSO regression in their capacity to construct
efficient portfolios (G.R et al 2014). Through the
examination of historical stock data, we delve into the
risk-return tradeoff underpinning each approach and
assess the precision of their predictions. The
outcomes of this inquiry may yield valuable insights
for investors seeking to optimise their portfolios using
contemporary techniques that duly account for the
dynamic nature characterising financial markets
(Hyndman and Athanasopoulos, 2018).
Incorporating Dynamic Market Conditions: The
utilisation of time series models within the proposed
modern portfolio theory enables the inclusion of
dynamic market conditions. This stands as a notable
improvement over traditional portfolio optimisation
models that frequently rely on static assumptions
regarding market behaviour.
Enhanced Risk Management: The proposed
modern portfolio theory is crafted to enhance risk
management by adopting a more realistic and
dynamic approach to modelling asset returns.
Augmented Accuracy: The integration of machine
learning techniques in the proposed modern portfolio
theory can yield heightened accuracy in portfolio
optimisation. This is achieved by accounting for more
intricate relationships amongst asset returns.
Complexity Considerations: The amalgamation of
time series models and machine learning techniques
can heighten the complexity of the innovative modern
portfolio optimisation model. This heightened
complexity might potentially render the model more
intricate to interpret and implement.
Data and Computational Requirements: The
proposed modern portfolio theory may necessitate
larger datasets and computational resources
compared to traditional portfolio optimisation
models. This aspect could pose a limitation for
smaller investors or those constrained in terms of data
accessibility.
Limitations of LASSO Regression: LASSO
regression might not offer as comprehensive a risk
management strategy as modern portfolio theory. The
latter has the capacity to accommodate more intricate
relationships between asset returns.
Assumption of Normality: LASSO regression
assumes normal distribution of asset returns,
potentially straying from real-world market
behaviour and consequently leading to less precise
portfolio optimisation outcomes (Dey, 2020). Neglect
of Dynamic Market Conditions: Traditional portfolio
optimisation models tend to disregard dynamic
market conditions. Limited Use of Advanced
Techniques: Time series analysis and machine
learning techniques are often underutilised in
traditional portfolio optimisation models.
Study Objective: The study aims to construct and
compare two portfolio optimisation models: an
innovative modern portfolio theory integrating time
series models and machine learning techniques, and
the traditional LASSO regression approach.
Research Gap: Limited research exists that
directly compares time series models, novel portfolio
theories, and SVM for portfolio optimisation.
Nevertheless, certain studies have contrasted these
approaches with conventional models, demonstrating
potential accuracy enhancements. For instance,
Zhang et al. (2021) compared a GARCH model, a
Bayesian network model, and an SVM model with a
traditional mean-variance model. They found that all
the alternative models surpassed the traditional model
in terms of risk-adjusted returns. Notably, the
Bayesian network model displayed the highest
Sharpe ratio among all models assessed.
Advantages of Time Series Models:
Time series models excel in capturing intricate
relationships and patterns in data over time,
enhancing the accuracy of asset return and correlation
modelling.
Incorporating time series models within modern
portfolio theory allows for more realistic assumptions
about market behaviour, accommodating non-normal
distributions, varying volatility, and dynamic
correlations. Time series models are equipped to
consider time-dependent factors like seasonality, a
crucial aspect for optimising portfolios in specific
industries.
Investors gain a better grasp of risk by using time
series models to simulate the impact of various
scenarios and events on portfolio performance.
Disadvantages of Time Series Models:
Time series models can be computationally
demanding, necessitating significant data and
computing power, presenting challenges for certain
investors.
Sensitivity to outliers and missing data can lead to
inaccurate predictions and suboptimal portfolio
allocations. Relying on historical data might not
always provide accurate predictions for future market
conditions, particularly in rapidly changing markets
or times of economic instability.
Advantages of LASSO Regression:
LASSO regression adeptly handles a multitude of
variables and pinpoints essential predictors of asset
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
134

returns. Computationally efficient, LASSO
regression is suitable for relatively modest datasets.
LASSO regression effectively deals with missing
data and outliers by constraining coefficients of less
significant variables towards zero.
Disadvantages of LASSO Regression:
LASSO regression assumes a linear relationship
between variables, which may not be appropriate for
modelling asset returns.
Static assumption of variable relationships over
time might not hold in swiftly changing market
conditions.
LASSO regression may fall short of capturing the
entire complexity of asset returns, particularly when
nonlinear relationships and variable interactions are
present.
2 MATERIALS AND METHODS
The study was conducted at the Data Analytics Lab
within the Department of Information Technology at
Saveetha School of Engineering. For each iteration of
the project, a sample size of 10 was employed (Group
1 = 10, Group 2 = 10). In 2022, Urlu and Brzeczek
conducted research in this field. The study was
carried out at the Data Analytics Laboratory in the
Department of Information Technology at the
Saveetha School of Engineering, Saveetha Institute of
Medical and Technical Science. The research
included two sample groups: Group 1 utilised the
Time Series Model, while Group 2 employed LASSO
Regression. Training data were collected from stock
market analyses, sourced from a data science website
and the Yahoo search engine.
All experimentation in this study was performed
on a computer equipped with an NVIDIA GeForce
GTX 1050 TI processor operating at 4.0 GHz,
NVIDIA graphics, and 8 GB of Random Access
Memory (RAM) for algorithm execution. The system
configuration employed a 64-bit edition of Microsoft
Windows 11. The models proposed and compared
were crafted using machine learning tools from the
Matlab library, OpenCv, and other Matlab libraries.
The development environment and all necessary
applications are required to be installed on a hard
drive with a capacity of 1 TB.
LASSO Regressions
An alternative loss system widely used is known as
Lasso, standing for "Least Absolute Shrinkage and
Selection Operator" (Hyndman, R.J. and
Athanasopoulos, G., 2018). Similar to ridge
regression, the objective in Lasso is to minimise the
term encompassing the least sum of residuals along
with a penalty term (Kassambara, 2018). In contrast
to ridge regression, a distinctive feature of Lasso is
that it shrinks certain predictor coefficients precisely
to zero, leading to the exclusion of those predictors
from the model (Md. Ehsanes Saleh, Arashi and
Golam Kibria, 2019). This distinctive characteristic
results in a lasso-like elegant subset, which
effectively performs variable selection.
Lasso regression represents a form of
regularization technique. It is favoured over
regression methods for more precise modelling. This
technique utilises loss, where data values contract
towards the mean. This process is known as
shrinkage. The lasso approach promotes models with
fewer parameters, as they are simpler and more
sparse. When seeking to automate specific model
selection stages like variable selection or parameter
removal, or when dealing with substantial
multicollinearity within the model, employing this
particular type of regression is recommended. Lasso
Regression employs L1 regularization, a concept that
will be elaborated on further in this composition. It is
particularly useful when dealing with additional
features, as indicated in Equation 1.
(1)
The performance of the LASSO Linear
Regression System was assessed by evaluating the
Root Mean Square Error (RMSE) and Mean Absolute
Percentage Error (MAPE). These performance
metrics have been employed in various studies as a
dependable means to gauge the reliability of the daily
forecasting model. Equation 2 can be utilised to
illustrate this evaluation.
(2)
When pi is the predicted stock price on day i and
yi is the actual stock price on the same day, n is the
total number of trading days. The absolute value of
the difference between the actual stock price and the
projected stock price is first determined in order to set
up the Mean Absolute Chance Error (MAPE)
statistic.
LASSO Regression Algorithm
Load the data: Start by loading the training and testing
datasets into the program.
Precise Portfolio Optimization Based on Novel Modern Portfolio Theory Using Time Series Model Compared with LASSO Regression
135

Pre-process the data: Clean and pre-process the data
to ensure it is in the correct format for analysis.
Split the data into training and testing sets: Split
the pre-processed data into training and testing sets in
order to train the model and evaluate its performance.
Initialise the LASSO model: Create an instance of
the LASSO regression model and initialise its
hyperparameters such as the regularisation parameter
and the number of iterations.
Train the LASSO model: Train the LASSO model
using the training data. The LASSO model will use a
linear regression algorithm with the added constraint
of a L1 regularisation term, which encourages the
model to have sparse coefficients.
Predict using the LASSO model: Use the trained
LASSO model to make predictions on the testing
data.
Evaluate the performance: Evaluate the
performance of the LASSO model using a metric
such as mean squared error or R-squared.
Fine-tune the hyperparameters: If the
performance is not satisfactory, adjust the
hyperparameters such as the regularisation parameter
and repeat steps 5-7 until an acceptable performance
is achieved.
Use the final model: Once an acceptable
performance has been achieved, use the final model
to make predictions on new, unseen data.
Time Series Model
In general, portfolio optimization employing NMPT
through time series models can furnish investors with
portfolios that are not only accurate but also
diversified, capable of accommodating evolving
market dynamics and incorporating diverse data
sources. Nevertheless, it is crucial to meticulously
scrutinize the assumptions and constraints of such
models. Consistently monitoring and adjusting
portfolio allocation in response to changing market
conditions and investor preferences is equally essential
(Lohmeyer and Lohmeyer, no date; Madsen, 2007).
Time Series Model Algorithm
First, the required libraries must be imported.
The financial data should then be loaded into a
pandas dataframe.
The data should be cleaned and prepared for
modelling.
The dependent and independent variables should
be defined.
The time series model should be fitted.
The model summary should be printed.
The target variable can be predicted using new,
unseen data.
Finally, the performance of the time series model
should be evaluated.
3 STATISTICAL ANALYSIS
The analysis was conducted using ibm spss version
2.1. In spss, datasets were created, each consisting of
a sample size of 10 for both the lasso regression and
long short term returns algorithms. The grouping
variable is designated as "group id," with accuracy
being used as the testing variable. "grouped" is
assigned a value of 1 for long short term returns and
2 for lasso regression. The properties include date,
symbol, open, high, close, volume btc, volume usd,
and trade count. The dependent variables encompass
date, close, high, open, and dollar volume usd. Both
precision and accuracy are considered independent
variables. The study employs an independently
conducted t-test.
4 RESULTS
The total sample size employed in the statistical
analysis is 10. This dataset is used for examining both
time series models and LASSO regression. Both the
specified algorithms, namely LASSO Regression and
the Videlicet Time Series Model, involve processing
statistical data. The computation of group and
delicacy values is carried out to forecast stock
demand. Additionally, statistical values for
comparison purposes are computed using the 10 data
samples for each algorithm along with their
corresponding losses.
Following experiments on a historical financial
dataset, it was determined that the Time Series Model
outperformed the LASSO Regression algorithm in
the context of portfolio optimization. The accuracy of
the Time Series Model (90.1252%) was notably
higher than that of LASSO Regression (80.1423%).
The significance of the accuracy and loss values was
0.000 (p<0.05). The Time Series Model exhibited a
lower Mean Squared Error (MSE) compared to
LASSO Regression, indicating more accurate
predictions for the target variable, as demonstrated in
Table 2. The comparative analysis graph illustrating
both algorithms is depicted in Figure 3.
Furthermore, the Time Series Model offered more
comprehensive and informative statistical summaries,
allowing for a deeper comprehension of the underlying
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
136
relationships among variables. It's important to
acknowledge that the selection of the optimal model
hinges on various factors, including the data's nature,
hyperparameter choices, and the specific portfolio
optimization problem in question. In this particular
case, the Time Series Model was better suited for the
given problem. However, diverse datasets might yield
differing outcomes, as illustrated in Figure 3.
5 DISCUSSION
As per the data, the accuracy of the LASSO
Regression Algorithm is 80.1423%, while the Time
Series Model demonstrates a higher accuracy of
90.1252%. This significant difference in accuracy is
supported by a p-value of 0.5, indicating that the Time
Series Model is superior (Chatfield, 2013). Modern
Portfolio Theory (MPT) enhanced by time series
models is widely acknowledged as a more realistic
approach to portfolio optimization, as it considers
dynamic market conditions. This stands in contrast to
traditional models that rely on static assumptions
about market behaviour. An important advantage of
incorporating time series models into MPT is the
improved risk management through a dynamic
approach to modelling asset returns, accounting for
changing market conditions (Parzen, E., 1981).
Furthermore, the integration of machine learning
techniques within modern portfolio theory can
enhance the accuracy of portfolio optimization by
capturing complex relationships among asset returns,
as demonstrated in Figure 1. This represents a
significant advantage over traditional models that rely
on simpler statistical methods.
LASSO regression's risk management capabilities
are limited and may not offer the robustness provided
by modern portfolio theory, which can account for
intricate relationships among asset returns. This
limitation could be a drawback for investors seeking
a more comprehensive risk management strategy
(Parzen, E., 1983).
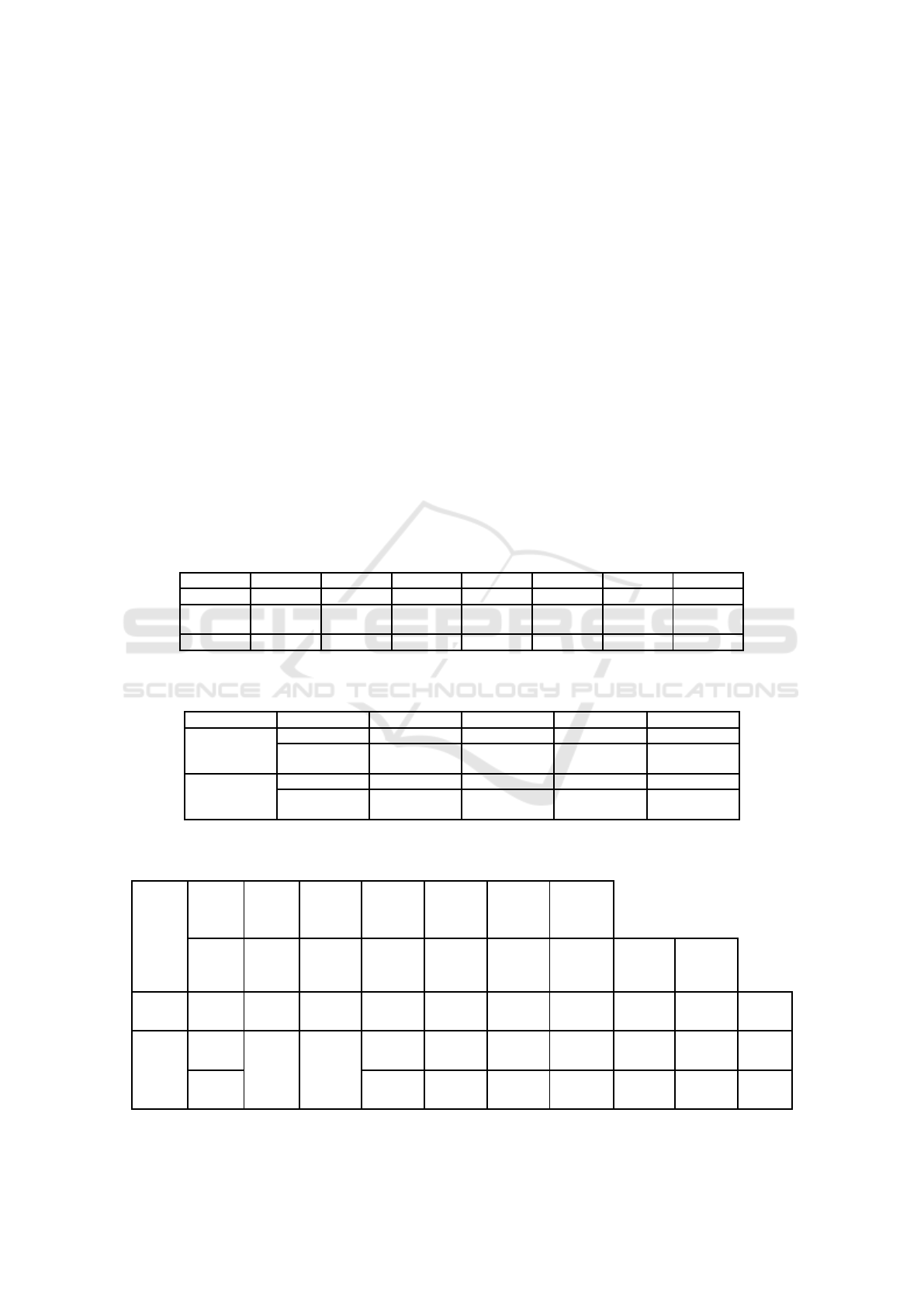
Table 1: Group, Accuracy and Loss value uses 8 columns with 8 width data for the time series model of improving prediction.
Name
Type
Width
Decimal
Columns
Measure
Role
1
Group
Numeric
8
2
8
Nominal
Datasets
2
Accuracy
Numeric
8
2
8
Scale
Improve
prediciton
3
Loss
Numeric
8
2
8
Scale
Prediction
Table 2: Group Statistical analysis for Time Series Model Algorithm and LASSO regression Algorithm, Standard Deviation
and standard error mean is determined.
Group
N
Mean
Std Deviation
Std.Error Mean
Accuracy
TSM
10
90.1252
1.90296
.60177
LASSO
regression
10
80.1423
2.33696
.73901
Loss
TSM
10
5.7180
1.90296
.60177
LASSO
regression
10
15.0430
2.33696
.73901
Table 3: Independent sample T-test t is performed on two groups for significance and standard error determination. The p-
value is lesser than 0.05 (0.000) and it is considered to be statistically significant with a 95% confidence interval.
Levene's
Test for
Equality of
variance
t
df
Sig(2 -
tailed)
Mean
differen
ce
Std.Erro
r
Differen
ce
95%
confiden
ce of
Differen
ce
F
Sig
Lower
Upper
Los
s
Equal
variances
assumed
304
.56
-9.78
18
.00
-9.31
.96
-11.12
-7.31
Accuracy
Equal
Variances
not assumed
-9.78
17.29
.00
-9.32
.95
-11.33
-7.21
Equal
Variances
not assumed
9.78
17.29
.00
9.21
.94
7.31
11.32
Precise Portfolio Optimization Based on Novel Modern Portfolio Theory Using Time Series Model Compared with LASSO Regression
137
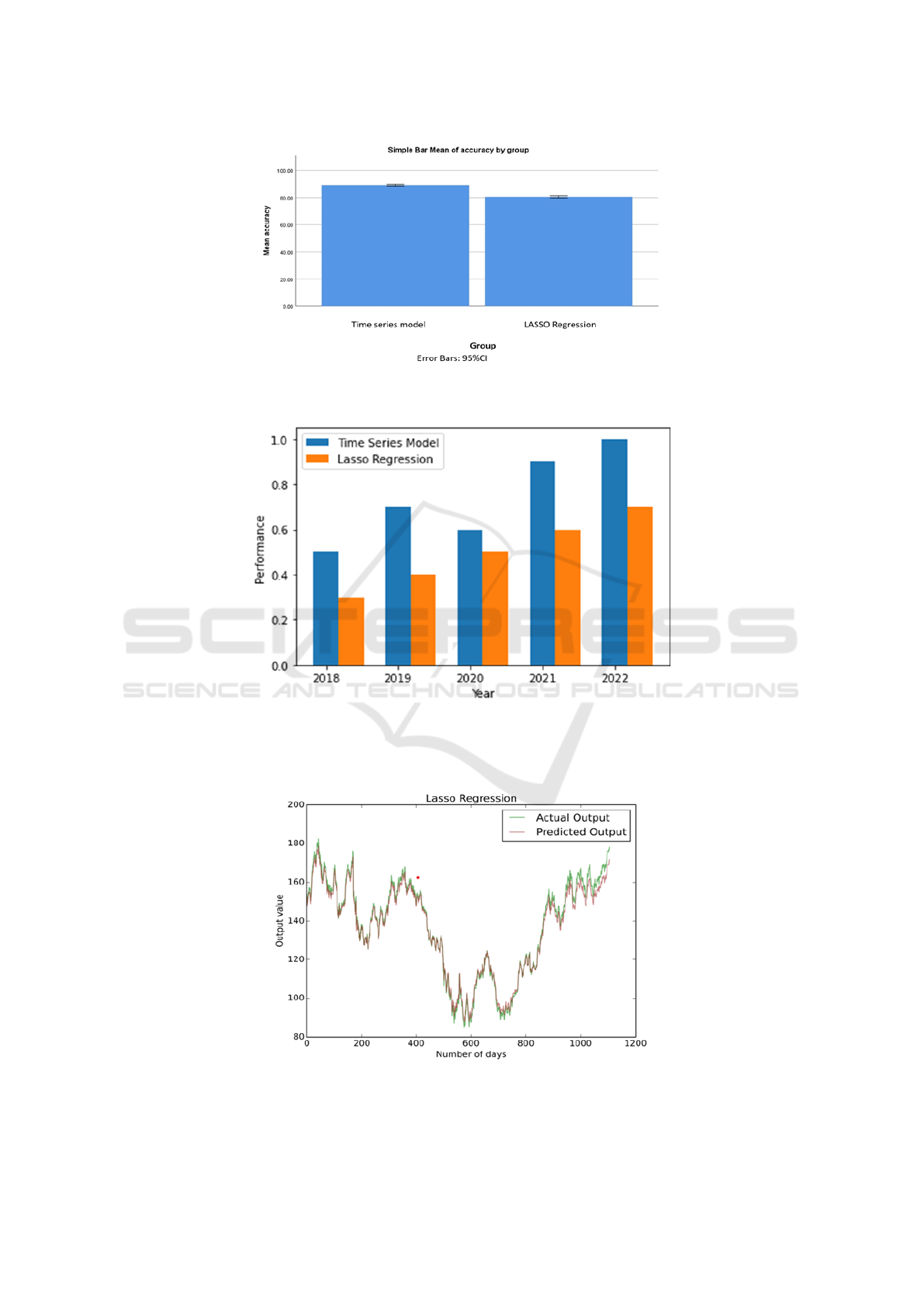
Figure 1: Line chart showing the comparison of actual output and predicted output LASSO Regression algorithm in terms of
output value and the number of days.
Figure 2: Bar chart showing the comparison of Time series model (90.1252%) and LASSO Regression algorithm (80.1423%)
in terms of mean accuracy. The Mean accuracy of the Time series model is better and more efficient than the LASSO
Regression algorithm approach. And the Standard Deviation of X-Axis and Y-Axis shows time series model vs LASSO
Regression algorithm.
Figure 3: Comparison of Time series model and LASSO Regression in terms of mean accuracy. The mean accuracy of the
time series model is better than the LASSO Regression. The standard deviation of the TMS algorithm is better than the
LASSO Regression. X-axis: TMS and vs LASSO Regression Y-Axis: Mean Efficiency of detection is ±2 SE.
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
138

An inherent assumption of LASSO regression is
that asset returns follow a normal distribution, which
might not accurately mirror real-world market
behaviour. Consequently, this assumption can lead to
less precise results in portfolio optimization, which
could be a drawback for investors aiming for higher
accuracy (Hyndman, R.J. and Athanasopoulos, G.,
2018).
On a positive note, LASSO regression is often
appreciated for its simplicity and ease of
comprehension. This aspect is advantageous for
investors who might not be well-versed in more
complex models, as indicated in Table 1.
Furthermore, LASSO regression is
computationally efficient and can perform well even
with smaller datasets. This efficiency could be an
advantage for investors with limited access to
extensive data or computational resources, as
highlighted in Table 3. The study's scope might be
limited due to data availability, as both modern
portfolio theory using time series models and LASSO
regression demand substantial data to yield accurate
outcomes. Both approaches also rest on specific
assumptions about market behaviour, which may not
always hold true in real-world scenarios.
Generalizing the study's findings to different markets
or time periods might be challenging, given the
substantial variations in market conditions, as
depicted in Figure 2.
A prospective avenue for LASSO Regression's
expansion is its application to other asset classes like
commodities or real estate. This extension could
assess the models' effectiveness in diverse markets.
Moreover, exploring the integration of alternative
machine learning techniques, such as neural networks
or different forms of LASSO Regressions, could
provide insights into their comparative performance.
Comparative evaluations of the proposed models
against other risk management strategies, like value
at risk or conditional value at risk, could offer insights
into the most efficient risk management approach.
While various predictive models have been
developed (Hyndman and Athanasopoulos, 2018),
not all of them accurately predict favourable stock
market movements. Despite their potential, many
time series models, like the one in "Predicting
portfolio returns using the distributions of efficient set
portfolios" (2003a), tend to be less user-friendly and
time-consuming. This suggests that while time series
models have the potential to enhance stock market
forecasts, their computational demands and
complexity might remain limiting factors (2003b,
"Predicting portfolio returns using efficient set
portfolio distributions").
6 CONCLUSION
The study's results revealed that Modern Portfolio
Theory using time series models exhibited superior
performance over LASSO regression in both risk
management and portfolio optimization accuracy.
The Time Series Model demonstrated a notably
higher accuracy rate of 90.1252% compared to the
LASSO Regression algorithm's accuracy of
80.1423%. The statistical significance of these
accuracy values, coupled with the associated p-value
of 0.000 (p<0.05), underscores the substantial
advantage of the Time Series Model in terms of
accuracy and predictive capability.
REFERENCES
Chatfield, C. (2013) The Analysis of Time Series: Theory
and Practice. Springer.
Dey, N., Vickram, S., Thanigaivel, S., Subbaiya, R., Kim,
W., Karmegam, N., & Govarthanan, M. (2022).
Nanomaterials for transforming barrier properties of
lignocellulosic biomass towards potential applications–
A review. Fuel, 316, 123444.
G. R et al, "Uncompressed digital video watermarking
using stationary wavelet transform," (2014) IEEE
International Conference on Advanced
Communications, Control and Computing
Technologies, Ramanathapuram, India, 2014, pp. 1252-
1258, doi: 10.1109/ICACCCT.2014.7019299.
Hyndman, R. J. and Athanasopoulos, G. (2018)
Forecasting: principles and practice. OTexts.
Kassambara, A. (2018) Machine Learning Essentials:
Practical Guide in R. STHDA.
Lohmeyer and Lohmeyer (no date) ‘Time series analysis
under model uncertainty’. Available at:
https://doi.org/10.26481/dis.20190524jl.
Madsen, H. (2007) Time Series Analysis. CRC Press.
Md. Ehsanes Saleh, A., Arashi, M. and Golam Kibria, B.M.
(2019) Theory of Ridge Regression Estimation with
Applications. John Wiley & Sons.
Parzen, E. (1981) ‘Time Series Model Identification and
Prediction Variance Horizon’, Applied Time Series
Analysis II, pp. 415–447. Available at:
https://doi.org/10.1016/b978-0-12-256420-8.50019-8.
Parzen, E. (1983) ‘Time Series Model Identification By
Estimating Information’, Studies in Econometrics, Time
Series, and Multivariate Statistics, pp. 279–298.
Available at: https://doi.org/10.1016/b978-0-12-
398750-1.50019-x.
‘Predicting portfolio returns using the distributions of
efficient set portfolios’ (2003a) Advances in Portfolio
Construction and Implementation, pp. 342–355.
Available at: https://doi.org/10.1016/b978-075065448-
7.50018-5.
Precise Portfolio Optimization Based on Novel Modern Portfolio Theory Using Time Series Model Compared with LASSO Regression
139

‘Predicting portfolio returns using the distributions of
efficient set portfolios’ (2003b) Advances in Portfolio
Construction and Implementation, pp. 342–355.
Available at: https://doi.org/10.1016/b978-075065448-
7.50018-5.
Prendergast, M. (no date) ‘Mutual Fund Allocations that
Maximize Safe Portfolio Returns’. Available at:
https://doi.org/10.31219/osf.io/dypw6.
Ramalakshmi, M., & Vidhyalakshmi, S. (2021). GRS
bridge abutments under cyclic lateral push. Materials
Today: Proceedings, 43, 1089-1092.
S. K. Sarangi, Pallamravi, N. R. Das, N. B. Madhavi, P.
Naveen, and A. T. A. K. Kumar, (2022) “Disease
Prediction Using Novel Deep Learning Mechanisms,”
J. Pharm. Negat. Results, vol. 13, no. 9, pp. 4267–4275,
, doi: 10.47750/pnr.2022.13.S09.530
Thanigaivel, S., Vickram, S., Dey, N., Gulothungan, G.,
Subbaiya, R., Govarthanan, M., ... & Kim, W. (2022).
The urge of algal biomass-based fuels for
environmental sustainability against a steady tide of
biofuel conflict analysis: Is third-generation algal
biorefinery a boon?. Fuel, 317, 123494.
Uğurlu, K. and Brzeczek, T. (2022) ‘Distorted probability
operator for dynamic portfolio optimization in times of
socio-economic crisis’, Central European Journal of
Operations Research , pp. 1–18.
V. P. Parandhaman, (2023)"A Secured Mobile Payment
Transaction Handling System using Internet of Things
with Novel Cipher Policies," International Conference
on Advances in Computing, Communication and
Applied Informatics (ACCAI), Chennai, India, 2023,
pp. 1-8, doi: 10.1109/ACCAI58221.2023.10200255.
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
140
