Fast Encryption Scheme with Logic Gate and Linguistic Algorithm
Ashish Kumar Soni, Rajendra Gupta and Ankur Khare
Department of Computer Science, Rabindranath Tagore University, Raisen, 464993, Madhya Pradesh, India
Keywords: Linguistic Algorithm, Cryptography, Keys Distribution Method.
Abstract: User data is not safe in the world because hackers are doing their best and advanced approaches to get user-
sensitive data. There are available different keys for unlocking security systems. The keys are produced by
generating different situations and the relation of keys to the encryption scheme is independent or not
independently decided by the selection of the encryption scheme. Higher security is demanding a more
protectable scheme of encryption for protecting user data. A fast Encryption Scheme is achieving a quick
response in milliseconds which is not given time for hackers. The key exchange scheme help to make
authentication between end users by the linguistic algorithm with a discrete distribution scheme to find an
unreadable bit of end-user data. The presented scheme proofing the fast security scheme and explored
different kinds of attacks also proves to make a strong and fast conversion scheme in a secure environment.
1 INTRODUCTION
The development of the protection of user data is the
most essential part of research in the world. It
generates a race to make more strong protection of
data. All the transmission media is not safe in the
world for authenticated access. The dynamic keys
exchange scheme is presented by many researchers.
It is making sure the authentic process used the
Diffie-Hellman key exchange scheme in (Pan et al.,
2022). Find the best approach for MANETs Networks
media by multiplicative key exchange scheme in
(Manjula, et al., 2021).
The key exchange scheme can help to generate the
security of sensitive medical information of patients
and process for generating encryption keys (Ermatita,
et al., 2020). A brief study explored the Diffie-
Hellman key exchange scheme to make sure authentic
steps in unsafe media (Mishra, et al., 2019). The
Diffie-Hellman scheme is implemented for reliable
key exchange in transmission media (Aryan, et al.,
2017). The MITM attack is proven by the
authentication scheme in (Knezevic et al., 2020;
Pavicic, (2021)).
The encryption scheme is based on many different
patterns that are based on linear or non-linear
schemes in cryptanalysis. The non-linear confusion-
based encryption scheme is explored in (Munir, et al.,
2021). The S-box scheme in the cryptography of
substitution is improved with the Latin square scheme
and S-box application defined in different
applications in (Hua, et al., 2021).
2 PROPOSED SCHEME
The proposed scheme is preceded by an encryption
and decryption scheme. It is pointing below:
Encryption Scheme:
1. Take data M and get length L = L + 1. And get
the ASCII value and store as D
n
.
2. Generate keys exchange scheme Diffie-
Hellman
3. Choose private key XPDa where XPDa<q.
4. And find a public key by the scheme YDa =
(∝ ) XPDa mod q.
5. Check authentication by generating a K value
with the help of a shared public key. K value
is calculated by K = (YDb)
XPDa
mod q;
6. If authentication is successful then generate a
function Dc(n) by the formula Dc(n) = (Dc
n
+
D
n
× R
n
) mod 251; If n==1 then Dc(n) =
(Dc
n
+ D
n
) and hide by the formula DcE(n) =
(Dc(n) + R
n
) mod 251;
7. Convert Dc (n) by formula DcE(n) = (Dc (n)
+ R
n
) mod 251;
Soni, A., Gupta, R. and Khare, A.
Fast Encryption Scheme with Logic Gate and Linguistic Algorithm.
DOI: 10.5220/0012603400003739
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Artificial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 611-614
ISBN: 978-989-758-661-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
611

8. Generated keys by method Rk
n
=C
n
×Rk
n
(Rk
n
-
1); If (Rk
n
>255) then Rk
n
=Rk
n
mod 251; The
Rk
n
keys are calculated of 7 key values.
9. Generate encryption scheme by two steps
logic gates:
a. AD
n
=Rk
n
XOR Dc (n).
b. BD
n
=AD
n
XOR D
n
.
c. The Encrypted value DEnc = DB
n
.
Where, private key = XP
Da,
public key Y
Da
, C
n
=
(1,2,3,….n); R
n
= Random Number by discrete
Distribution scheme, D
n
= ASCII values.
Decryption Scheme:
1. Take encrypted data D2n = ASCII (DEnc) and
get length L = L.
2. Generate keys exchange scheme Diffie-
Hellman
3. Choose private key XPDb where XPDb<q.
And find a public key by the scheme YDb =
(∝ ) XPDb mod q.
4. Check authentication by generating a K value
with the help of a shared public key. K value
is calculated by K=K=(YDa )XPDb mod q.
5. Convert DcE(n) by formula Dc(n) = (DcE (n)-
Rn) mod 251;
6. Generated keys by method Rk
n
= C
n
×Rk
n
(Rk
n
-
1); If (Rk
n
>255) then Rk
n
=Rk
n
mod 251; The
Rk
n
keys are calculated of 7 key value.
7. Generate decryption scheme by two steps
logic gates:
a. AD1
n
=Rk
n
XOR Dc (n).
b. BD1
n
=AD1
n
XOR D2
n
.
c. The Decrypted value Data = BD1
n
.
Where, private key XP
Db
, public key Y
Db
, C
n
=
(1,2,3,….n); R
n
= Random Number by discrete
Distribution, D2
n
= ASCII values.
3 CRYPTANALYSIS OF ATTACKS
The proposed scheme security can be verified by
cryptanalysis of attack. The scheme is stepped by
breaking the code of the method and generating the
possible keys and user data as well. All the results are
presented in tabular form as expected examples.
3.1 Cipher Text Only Attack
Given Parameters (q=7, L = 7, R
n
= 12, C
n
=5).
Keys = (158, 244, 141, 41, 202, 153, 47).
Given: Encryption steps DE1, DE2:- Enc
1
= E
K1
(D1), Enc
2
= E
K2
(D
2
)………, Enc
i
= E
Kq
(D
i
) where q=1:7, DE
Kq
= DE1, DE2 (K
q
)
Deduce: - Either D
1
, D
2
….D
i
;
RK
1
, RK
2
, RK
3
, RK
4
, RK
5
, RK
6
, RK
7
;
In Table 1, if any value is repeated one or more times
in the information, then the converted data is
generating a difference for the same value U. The
converted data of value U first value is unlike from U
finding as N time value in the data.
3.2 Known Plain Text Attack
Given Parameters (q=7, L = 7, R
n
=12, C
n
= 5).
Keys = (158, 244, 141, 41, 202, 153, 47).
Given: Encryption steps DE1, DE2:-Enc
1
= E
K1
(D
1
), Enc
2
= E
K2
(D
2
)… Enc
i
= E
Kq
(D
i
) where q=1:7,
DE
Kq
= DE1, DE2 (K
q
)
Deduce: - Either RK
1
, RK
2
, RK
3
, RK
4
, RK
5
, RK
6
,
RK
7
;
Table 1: Cipher Text Only Attack.
D
1
=U then Enc
1
=E
K1
( D
1
)=E
158
U =ª
D
2
=UU then Enc
2
=E
K1,2
(D
2
)=E
158,244
UU =ç•
D
3
=UUU then Enc
3
=E
K1,2,3
(D
3
)=E
158,244,141
UUU =÷•ä
D
4
=UUUU then Enc
4
=E
K1,2,3,4
(D
4
)=E
158,244,141,41
UUUU =•í•0
D
5
=UUUUU then Enc
5
=E
K1,2,3,4,5
(D
5
)=E
158,244,141,41,202
UUUUU =•ý• Ã
D
6
=UUUUUU then Enc
6
=E
K1,2,3,4,5,6
(D
6
)=E
158,244,141,41,202,153
UUUUUU=§Í´ó
D
7
=UUUUUUU then Enc
7
=E
K1,2,3,4,5,6,7
(D
7
)=E
158,244,141,41,202,153,47
UUUUUUU=·Ý¤ ã°
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
612

Table 2: Known Plain Text Attack.
D
1
=W then Enc
1
=E
K1
( D
1
)=E
158
W=ª
D
2
=WW then Enc
2
=E
K1,2
(D
2
)=E
158,244
WW=•ÿ
D
3
=WWW then Enc
3
=E
K1,2,3
(D
3
)=E
158,244,141
WWW=M'^
D
4
=WWWW then Enc
4
=E
K1,2,3,4
(D
4
)=E
158,244,141,41
WWWW=evÒ
D
5
=WWWW then Enc
5
=E
K1,2,3,4,5
(D
5
)=E
158,244,141,41,202
WWWWW=•w•ªI
D
6
=WWWWW then Enc
6
=E
K1,2,3,4,5,6
(D
6
)=E
158,244,141,41,202,153
WWWWWW=È¢Û•Ï
D
7
=WWWWWW then Enc
7
=E
K1,2,3,4,5,6,7
(D
7
)=E
158,244,141,41,202,153,47
WWWWWWW=à•óW´çQ
In Table 2, it is explored known plain text attacks with
given 7 examples. It is hard to calculate the keys or
the scheme that is used for encrypting data for
decryption. The converted data of text W got as the
first value isn’t the same as the value W got as the N
time value in the data.
3.3 Chosen Cipher Text Attack
Given Parameters (q=7, L=7, R
n
= 12, C
n
= 5).
Keys = (158, 244, 141, 41, 202, 153, 47).
Given: Encryption steps DE1, DE2:-Enc
1
, D
1
=
Dec
K1
(Enc
1
), Enc
2
, D
2
= Dec
K2
(Enc
2
),………, Enc
q
,
D
q
= Dec
Kq
(Enc
q
),where q=1:7, Dec
Kq
= Dec1,
Dec2(K
q
).
Deduce: - Either RK
1
, RK
2
, RK
3
, RK
4
, RK
5
, RK
6
,
RK
7
;
Example: Enc
1
= •å then Encrypted Text D
1
=
Dec
K1, 2
(Enc
1
) = Dec
158, 244
(•å) =WU
Enc
2
= •ç then Encrypted Text D
2
= Dec
K1, 2
(Enc
2
) = Dec
158, 244
(•ç) = UW
The random keys are calculated by the 3
dissimilar parameters L, Rn, and Cn which are very
sensitive and different from each other, so it is very
hard to deduce the random keys by awarding the
encrypted data and decrypted original data.
4 COMPARATIVE ANALYSIS OF
THE PROPOSED SCHEME
The experimental analysis is generated in changed
test patterns of the proposed scheme and compared
the experimental result with existing popular
schemes. All the experimental analysis is presented in
related parameters and environment using Intel®
Core(TM) i3-6006U CPU @ 2.GHz, 4 GB Random
Access Memory, 64-bit operating system, x64-based
processor and programming platform used in
MATLAB.
4.1 Analysis of Execution Running
Time
The comparative table is shown comparative results
between the proposed scheme, Advanced Encryption
Standard & RSA method plain data
“PETCYXNVDKYUIWS*” with decimal values
“80, 69, 84, 67, 89, 88, 78, 86, 68, 75, 89, 85, 73, 87,
83, 42”. The algorithm running time is concerned
with key generation, encryption process, and all the
related terms of the proposed scheme and existing
method.
The experimental result is presented in Table 3
between the proposed scheme, Advanced Encryption
Standard, and RSA algorithm. The experimental
result displayed fast encryption running time and
algorithm running time in comparison to existing
methods AES and RSA.
Table 3: Compared Execution Running Time.
Algorithm
Encryption
Time in
secon
d
Algorithm
Runtime in
secon
d
1 AES 0.059130 0.097861
2 RSA 0.089786 0.181050
3 Proposed-Scheme 0.007437 0.034629
4.2 Algorithm Process Time
All the process times are added in algorithm process
time like key generation process and encryption
running time also. This processing time is achieved at
the time of the process of the scheme. The proposed
scheme is compared with the RSA scheme with 10
dissimilar sizes of data files and the file size is taken
from 0.51 kb to 10.70 kb.
Fast Encryption Scheme with Logic Gate and Linguistic Algorithm
613

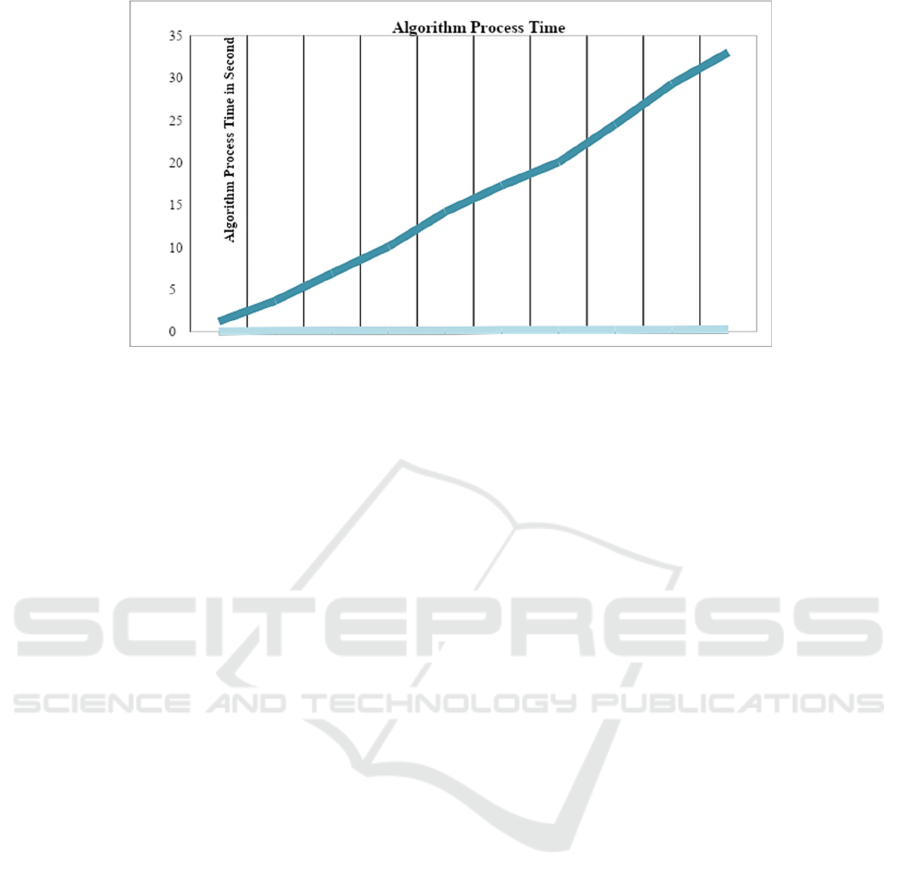
Figure 1: Analysis for the Process Time.
A linear graph is shown in Fig 1 with ten different
sizes of data files and results compared between RSA
and the proposed scheme. The linear results are
shown as the best result of the proposed scheme
which achieved a fast process time with all the key
points in comparison RSA method.
5 CONCLUSION
User data is the first essential point in the whole
world. The proposed scheme is preceding quick
response for hiding user data. The logic gate bit-XOR
is making too fast an encryption process in
milliseconds. The MITM attack is prevented in this
proposed scheme by the key distribution scheme and
data is converted into an unreadable form by the
suggested linguistic scheme for generating a secure
and fast transmission. Cryptanalysis attacks are
proofing for the protection of different kinds of
attacks which is representing the best result of attacks.
The fast access time is presented with encryption time
and algorithm running time in different sizes of data.
A comparative result is to generate a more secure and
fast access time after adding the proposed scheme.
Future work will be enhanced the scheme and
improve the result of security and privacy key points
by modern data hiding schemes.
REFERENCES
Pan, J., Qian C. and Rigerud, M. (2022). Signed (Group)
Diffie-Hellman Key Exchange with Tight Security.
Journal of Cryptography. 35(4):1 42.
https://doi.org/10.1007/s00145-022-09438-y
Manjula, T. and Anand, B. (2021). A Secured
Multiplicative Diffie Hellman Key Exchange Routing
Approach for Mobile Ad Hoc Network. Journal of
Ambient Intelligence and Humanized Computing.
12(3):1 11. https://doi.org/10.1007/s12652-019-01612-
8
Ermatita, Prastyo Y. B., I. Pradnyana. W. W. and Adrezo,
M. (2020). Diffie-Hellman Algorithm for Securing
Medical Record Data Encryption keys. International
Conference on Informatics, Multimedia, Cyber and
Information System (ICIMCIS). IEEE. 1 5. doi:
10.1109/ICIMCIS51567.2020.9354297.
Mishra, M. R. and Kar J. (2019). A Study on Diffie-
Hellman Key Exchange Protocols. International
Journal of Pure and Applied Mathematics. 1 12. doi:
10.12732/ijpam.v114i2.2
Aryan, Kumar C. and Vincent D. R. P. M. (2017). Enhanced
Diffie-Hellman Algorithm for Reliable Key Exchange.
ICSET IOP Conf. Series: Materials Science and
Engineering. 1 8. doi:10.1088/1757-899X/263/4/
042015
Knezevic, M., Tomovic, S. and Mihaljevic, M. J. (2020).
Man-In-The-Middle Attack against Certain
Authentication Protocols Revisited: Insights into the
Approach and Performances Re-Evaluation.
Electronics. 9(8):1 23. doi:10.3390/electronics9081296.
Pavicic, M. (2021). How Secure Are Two- Way Ping-Pong
and LM05 QKD Protocols under a Man-in-the-Middle
Attack?. Entropy. 23(2):1 10. https://doi.org/10.3390/
e23020163
Munir, N., Khan, M., Shah, T., Alanazi, A. S. and Hussain,
I. (2021). Cryptanalysis of Nonlinear Confusion
Component Based Encryption Algorithm. Integration.
79:1 7. https://doi.org/10.1016/j.vlsi.2021.03.004
Hua, Z., Li, J., Chen, Y. and Yi, S. (2021). Design and
Application of an S-Box Using Complete Latin Square.
Nonlinear Dynamics. 104:1 19. https://doi.org/10.1007/
s11071-021-06308-3
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
614