Job Block Scheduling in a Two-Stage, No-Idle Flow Shop with Job
Weighting to Reduce Total Machine Rental Costs
Shakuntla Singla
1,*
, Harshleen Kaur
1,†
, Deepak Gupta
2,‡
and Jatinder Kaur
3,*
1
Department of Mathematics and Humanities, MMEC, MM (DU), Mullana, Ambala, India
2
Department of Mathematics and Humanities, M.M. Engineering College, MMEC, MM (DU), Mullana, Ambala, India
3
Department of Mathematics, Guru Nanak Girls College (of Affiliation) Yamunanagar, Haryana, India
Keywords: Scheduling, No Idle, Job Block, Weights of Jobs, Flow Shop.
Abstract: The handling interval of the jobs is connected with likelihoods and the two of the jobs have stood together as
a block in the current paper's study of a flow shop scheduling model in two stages under no idle restriction.
Weight of Jobs is also introduced due to its practicality and significance value in the actual world scenarios.
The objective of the study is to present a heuristic algorithm that, when used, provides an ideal or nearly
optimal schedule to reduce the amount of downtime and lower rental prices. The effectiveness of the proposed
approach is demonstrated through a numerical sample. This work can also be extended by considering various
parameters like breakdown effect, fuzzy trapezoidal numbers, set up time etc.
1 INTRODUCTION
Scheduling is an indispensable process that focuses
on the challenges of allocating resources to carry out
a series of operations with the objective to identify the
optimum solution in light of the need to optimize a
function. Scheduling problems arise daily in several
production units. The well-known flow shop
scheduling problem conforms evaluating the best
sequence for two or more jobs to be performed on two
or more pre-ordered machines to optimize some
measure of effectiveness. The critical constraint in an
industrialized flow shop scenario is the no-idle time
on machines or the inability to halt a machine after it
has been started. As a result, there can be no
downtime for the machines as they must run
continually.
In the past five decades, there has been considerable
attention paid to solve the problem of scheduling.
However, (Johnson 1954) prepared the first
triumphant mathematical model that successfully
acquired an optimal solution for the two and three
stage flow shop scheduling problem. The efficacy of
Johnson’s model garners significant attention from
numerous researchers, who are inclined to explore
*
Associate Professor
†
Research Scholar
‡
Professor
this avenue. Further, in a scheduling paradigm, the
weight of each job indicates its position among other
jobs in terms of importance. The weight of each job
increases with how significant it is for processing in
relation to other jobs. From the groundbreaking
research conducted by Johnson in 1954, the available
scholarly literature pertaining to scheduling models
exhibits a notable absence of any discussions
regarding the concept of job weightage prior to the
year 1980. The first investigation of the m-machine
no-idle condition in a flow shop was conducted by
(Adiri and Pohoryles 1982). An approach to reduce
rental cost for the no idle two-stage flow shop
scheduling problem that takes job weighting into
account was provided by (Gupta et al. 2021). The
comparative analysis of the subsystem failed
simultaneously was discussed by (Shakuntla et al.
2011). (Shakuntla et al 2011) discussed the behavior
analysis of polytube using supplementary variable
procedure. PSO was used by (Kumari et al. 2021) to
research limited situations. Using a heuristic
approach, (Rajbala et al. 2022) investigated the
redundancy allocation problem in the cylinder
manufacturing plant.
Singla, S., Kaur, H., Gupta, D. and Kaur, J.
Job Block Scheduling in a Two-Stage, No-Idle Flow Shop with Job Weighting to Reduce Total Machine Rental Costs.
DOI: 10.5220/0012609800003739
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Artificial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 185-188
ISBN: 978-989-758-661-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
185

2 PRACTICAL SITUATION
Numerous practical and empirical scenarios are
prevalent in our routine engagement within
manufacturing and fabrication environments,
wherein diverse tasks necessitate processing on a
range of distinct machinery. The cotton industry,
leather manufacturing unit, textile factory, etc., are
possible practical examples of the weightage of jobs.
Different varieties of cotton, shoes, jackets, and fabric
of varying sizes or qualities are manufactured with
varying degrees of importance in various production
facilities. Due to a lack of finances in his early
profession, one needs to rent the machines. For
example, to start a pathology laboratory, much
expensive equipment like a microscope, water bath,
lab incubator, glucometer, blood cell counter, organ
bath, haematology analyzer, urine analyzer,
centrifuge, coagulometer, autoclave, tissue
diagnostics, etc., one does not buy these machines but
instead take on rent. Medical equipment rentals are
quick and reasonably priced, which is the better
option. Renting enables saving capital investments,
helping choose the right equipment for the job and
access the latest technology.
Assumptions
Two machines, J and K, process the jobs
independently of one another in the following order:
JK with no allowance of any inter-machine transfer.
There is no way for two machines to process on the
same job at the same time.
Calculating utilization time does not take machine
breakdown or setup times into account.
Rental Policy (P)
The machines will be rented out as needed and
returned as soon as they are no longer needed. i.e., the
first machine will be rented when processing jobs
begins, and the second machine will be rented when
the first work is finished on the first machine.
3 NOTATIONS
I: Jobs sequence 1,2,…, n
S
1
: Optimal sequence using Johnson’s technique
J: 1
st
machine
K: 2
nd
machine
P
i
: Probability allied with j
i
Q
i
: Probability allied with k
i
W
i
: Weightage of job i
u
1
(s
1
): Utilization time required for machine M1 in
sequence s
1
u
2
(s
1
): Utilization time required for machine M
2
in
sequence s
1
4 PROBLEM FORMULATION
Assume that two machines J and K are to process
certain jobs i (1, 2… n). Finally, let Wi be the ith job's
weightage. The matrix-formatted mathematical
representation of the model may be expressed as in
Table 1. Our objective is to identify the sequence of
job {s
1
} which helps to keep machines’ rental costs
down.
Table 1: Matrix-Formatted Mathematical Formulation.
Job Machine J Machine K Weight
I j
i
p
i
k
i
q
i
W
i
1
j
1
p
1
k
1
q
1
W
1
2
j
2
p
2
k
2
q
2
W
2
3
j
3
p
3
k
3
q
3
W
3
n
j
n
p
n
k
n
q
n
W
n
5 ALGORITHM
Step 1: Calculate the expected processing times,
named as J
i
& K
i
, for the machines J & 𝑲 respectively:
𝐽

 𝑗

× 𝑝

(1)
𝐾

= 𝑘

× 𝑞

(2)
Step 2: If min (𝐽

, 𝐾

) = 𝐽

,
then
𝐽


=






(3)
and 𝐾

′ =




If min (𝑱
𝒊
, 𝑲
𝒊
) = 𝑲
𝒊
,
then
𝐽


=




(4)
And 𝐾

′ =






Step 3: Consider jobs k and m are working in a job
block ‘α’ with fix order of jobs in which priority is
given to job k over m. The concept of a job block can
be considered as being equivalent to a single job,
denoted as α, where α is defined as (l, m).:
𝐽


=
𝐽


+
𝐽


−𝑚𝑖𝑛 (
𝐽


, 𝐾


)
𝐾


= 𝐾


+ 𝐾


−
(
𝐽


, 𝐾


)
Step 4: Replace jobs 𝒍 and 𝒎 with a single job α to
transform the given problem into a new one.
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
186

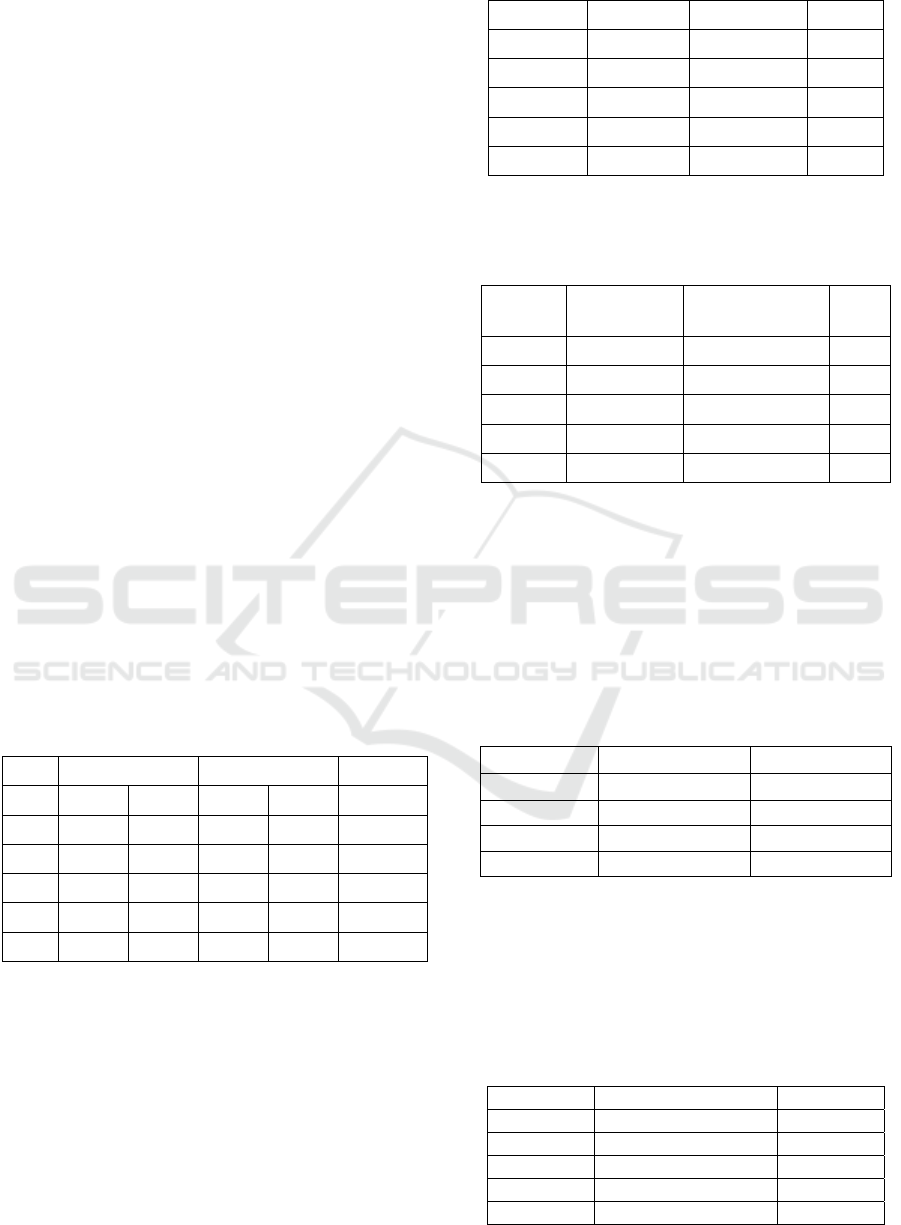
Step 5: Get the optimum sequence s
1
while reducing
the overall elapsed time by utilizing Johnson's
method (Johnson, 1954).
Step 6: For schedule s
1
, create a flow in- out table and
determine total elapsed time 𝑻
𝒊𝟐
.
Step 7: Calculate
𝑙

= 𝑇

−


𝑘

(
7
)
Step 8: Construct flow in-flow out table for the
machines using the most recent time 𝒍
𝟐
for machine
K to begin processing.
Step 9: Calculate utilization time u
1
(s
1
) and u
2
(s
1
) of
machines J and K
by
𝑢

(𝑠

)=


𝑗

(
8
)
𝑢

(𝑠

)=𝑇

−𝑙

Step 10: Finally, calculate
r(s
1
) = u
1
(s
1
) ∗ c
1
+ u
2
(s
1
) ∗ c
2
(9)
Numerical Illustration
Consider Five Jobs and Two Machines With No-Idle
Flow Shop Scheduling Problems In Which
Processing Times Associated With Probabilities And
Job Weightage, Are Given In table 2. Machines J And
K Have Rental Costs Per Unit Time of Four and Six
Units, Respectively. Our Goal Is To Acquire The Best
Possible Job Sequencing at The Lowest Feasible
Amount By Considering Jobs 2,4 In A Block (2,4)
That The Machines May Be Rented Out For.
Table 2: Data Set for the Indicated Problem.
Jobs Machine J
Machine K Weight
I j
i
p
i
k
i
q
i
W
i
1 16 0.2 26 0.2 2
2 26 0.2 18 0.1 3
3 14 0.3 24 0.2 1
4 7 0.2 3 0.3 5
5 16 0.1 6 0.2 4
Solution: Table 3 presents, in accordance with
Step
1, the expected processing times for machines J
and K are as follow:
Table 3: Expected Process Time on Machines.
I
𝐽

𝐾

W
i
1 3.2 5.4 2
2 5.4 1.8 3
3 4.2 4.8 1
4 1.4 0.9 5
5 1.6 1.0 4
The weighted flow shop times J
i
' & K
i
′ are
displayed in table 4 according to Step 2.
Table 4: The Weighted Flow Shop Times.
Jobs I Machine J
IN-OUT
Machine K
IN-OUT
Wi
5 0-1.6 6.7-7.7 4
1 1.6-4.8 7.7-13.1 2
2 4.8-10.2 13.1-14.9 3
4 10.2-11.6 14.9-15.8 5
3 11.6-15.8 15.8-20.6 1
Designating it by α, as per step 3. Equation (5)(6)is
used to calculate how long a single job α will take to
process on the two machines:
𝐽


= 𝐽


+ 𝐽


−𝑚𝑖𝑛 (𝐽


, 𝐾


)=1.8
𝐾


= 𝐾


+ 𝐾


−
(
𝐽


, 𝐾


)
= 2.5
Table 5 Presents, in accordance with Step-4, the two
processing times J
i
′and K
i
′.
Table 5: Portable Process Times for An Equivalent Job.
I J
i
2 K
i
2
1 0.6 2.7
α 1.8 2.5
3 3.2 4.8
5 0.4 1.25
As per Step 5; Adopting Johnson's method, the order
of the optimum sequence with minimum elapsed time
is
s
1
= 5– 1 – α – 3 = 5 – 1 – 2 – 4 – 3.
For schedule s
1
, according to Step 6, a flow in- flow
out table 6 is depicted below:
Table 6: Flow In-Out Table for Schedule S
1
Jobs Machine J Machine K
5 0-1.6 1.6-2.6
1 1.6-4.8 4.8-10.2
2 4.8-10.2 10.2-12.0
4 10.2-11.6 12.0-12.9
3 11.6-15.8 15.8-20.6
Job Block Scheduling in a Two-Stage, No-Idle Flow Shop with Job Weighting to Reduce Total Machine Rental Costs
187

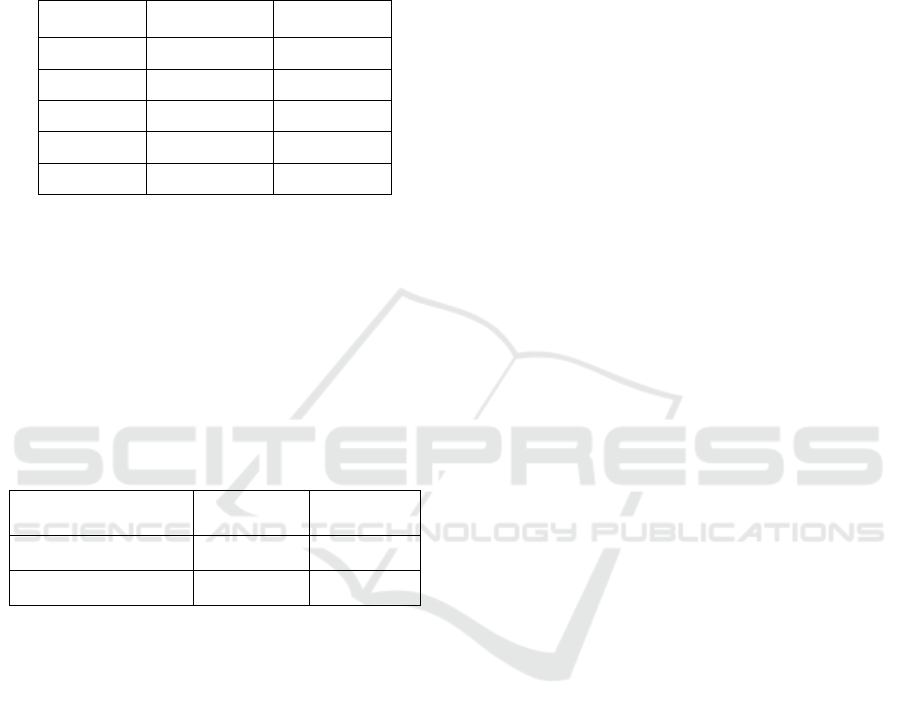
Total elapsed time =20.6
As per Step-7; 𝑙

= 20.6 – 13.9 = 6.7
As per Step 8, Create the IN-OUT table as indicated
in table 7to solve the updated scheduling problem
Table 7: Flow In-Out Table for Route J→ K With Zero Idle
Time.
Jobs I J
i
′ K
i
′
1 0.6 2.7
2 1.8 1.6
3 3.2 4.8
4 0.28 1.18
5 0.4 1.25
As per Step-9; u
1
(s
1
) = 15.8; u
2
(s
1
) = 20.6 - 6.7 =1 3.9
As per Step-10; r(s
1
) = u
1
(s
1
) ∗ c
1
+ u
2
(s
1
) ∗ c
2
=
15.8 * 4 + 13.9 * 6 = 146.6 units
Hence the above calculated results obtained for
machine route J →K of the opmal sequence s
1
={5,
1, 2, 4, 3} are described in table 8
Hence from the above table 8, we conclude that
the proposed heuristic algorithm created for machine
route J →K provides the minimum utilization time
and rental cost for optimum solution s
1
.
Table 8: Comparative Analysis of Results.
Machine Route
J → 𝐾
Utilization
Time of K
Rental
Costs
Proposed Algorithm
13.9 units 146.6 units
Johnson Algorithm
19.0 units units
6 CONCLUSION
The proposed heuristic algorithm in this paper
provides an efficient solution to no-idle two stage
flow shop scheduling problem considering various
factors such as processing time, job weightage and
job block criteria by simultaneously optimizing the
rental cost and utilization time. This work can also be
extended by considering various parameters like
breakdown effect, fuzzy trapezoidal numbers, set up
time etc.
REFERENCES
Johnson, S. M. (1954). Optimal two‐and three‐stage
production schedules with setup times included. Naval
Research Logistics (NRL), 1(1), 61–68.
Gupta, D., Goel, R. and Kaur, H. (2021). Optimizing rental
cost with no idle constraints in two machines with
weightage,” Mater Today Proc, Feb. 2021, doi:
10.1016/j.matpr.2021.01.09.
Shakuntla, Lal, and Bhatia S., (2011). Reliability analysis
of polytube tube industry using supplementary variable
Technique. Applied Mathematics and Computation,
3981-3992.
Adiri, D. I. and Pohoryles (1982). Flow shop no-idle or no-
wait scheduling to minimize the sum of completion
times,” Nav. Res. Logist., 29( 3), 495–504.
Kumari, S., Khurana, P., Singla, S., Kumar, A. (2021).
Solution of constrained problems using particle swarm
optimization, International Journal of System
Assurance Engineering and Management, 1-8.
Rajbala, Kumar, A. and Khurana, P. (2022). Redundancy
allocation problem: Jayfe cylinder Manufacturing
Plant. International Journal of Engineering, Science &
Mathematic, 11(1), 1-7.
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
188