Sum Divisor Cordial Labelling of Sunflower Graphs

A. Anto Cathrin Aanisha

1,2,*

and R. Manoharan

Sathyabama Institute of Science and Technology, Chennai, India

School of Education, DMI, St. John The Baptist University, Mangochi, Malawi

Department of Mathematics, Sathyabama Institute of Science and Technology, Chennai, India

Keywords: Sum Divisor Cordial Labeling, Sunflower Graph.

Abstract: Consider the simple graph G with vertex set W, let g: W→ {1, 2 . . . |W|} be a bijective function of G. The

function f is known as SDC labeling if the distinction between the number of lines categorized with 0 and the

number of lines categorized with 1 is less than or equal to one such that a line xy is categorized 1 if 2 divides

sum of f(x) and f(y), and categorized 0 otherwise for every line. A graph that is having SDC labeling is

referred to as an SDC graph. This paper shows that the sunflower graph is an SDC graph for all n≥ 3.

1 INTRODUCTION

Graph theory is the study of relationships between

objects. Graph theory is an ancient subject with

numerous exciting modern applications. Graph

theory is an important part of many different fields.

(Chakraborty et al., 2018) demonstrated the use of

graphs in social networks, whose complexity is

increasing as social media advances. Graph theory is

related to chemistry. Most theoretical chemists used

mathematics to crunch numerical data until recently,

but graph theory has influenced a shift toward non-

numerical techniques. Labeling is one of the topics in

graph theory. It has many applications in pure,

applied mathematics and natural science. Some of the

fields where graph labeling applies include coding

theory, x-ray, crystallography, astronomy, network

theory, etc. (Prasanna, 2014) demonstrated how graph

labeling applies in network security, the numerical

network portion of an IP address, the channel

assignment process, and social media. (Kumar &

Kumar vats, 2020) explained how graph labeling

applies in crystallography. Graph theory principles

are also used in several computer science areas such

as database management systems, software

architecture, algorithm design, multiprocessing, data

structure, and so on. (Vinutha, 2017) has discussed

how graph coloring and labeling applies in computer

science. Graph coloring is used in GSM networks,

aircraft scheduling etc. Also graph labeling is applied

in many areas in computer science. For example,

signal interference from different radio station is

avoided by assigning channel to each station through

the use of radio labeling.

There are many labeling in graph theory. They are

prime labeling, magic labeling, graceful labeling,

edge labeling, radio labeling and many others. In

graph theory, one of the labeling is sum divisor

cordial labeling. Sum divisor cordial graphs have

thrilling features which are captivating to discover as

it isn't every graph that allow sum divisor cordial

labeling (Lourdusamy St Xavier & Patrick St Xavier,

2016).

Graph labeling involves assigning integers to

nodes(vertices) or lines(edges) or both, according to

certain rules. Labeling is referred to as vertex labeling

if the domain of the function is the set of nodes.

Labeling is known as edge labeling if the domain of

the function is the set of lines. Total labeling is

labeling where labels are assigned to both vertices

and edges of the graph. For more information about

this, we can refer (Gallian, 2018). (Thomas et al.,

2022) have proved that integer cordial labeling admits

on some graphs like olive tree, jewel graph, and

crown graph. (Mitra & Bhoumik, 2022) have proved

that a few graphs are tribonacci cordial graphs.

(Abhirami et al., 2018) have mentioned even sum

cordial labeling that admits a few graphs like the

crown graph, comb graph, and many others. The topic

of divisor cordial labeling became started out the way

of (Varatharajan et al., 2011). (U. Prajapati & Prerak,

2020) have proved that friendship-related graphs are

divisor cordial graphs. Also (Barasara & Thakkar,

2022) have proved that ladder-related graphs are sum

Aanisha, A. and Manoharan, R.

Sum Divisor Cordial Labelling of Sunﬂower Graphs.

DOI: 10.5220/0012614800003739

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Artiﬁcial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 305-308

ISBN: 978-989-758-661-3

305

divisor cordial graphs. Recently (Sharma &

Parthiban, 2022) have proved that the Lilly graph is a

divisor cordial graph. (Kanani & Bosmia, 2016) have

proved that the flower graph Fln satisfies the axioms

of the cube divisor cordial graph for all n. The idea of

sum divisor cordial labeling was initiated with the aid

of (Lourdusamy St Xavier & Patrick St Xavier,

2016). Currently (Adalja, 2022) has proved that a few

bistar-related graphs are sum divisor cordial graphs.

Also (Lourdusamy & Patrick, 2022) have proved that

the axiom of sum divisor cordial labeling has been

satisfied for all transformed tree. (U. M. Prajapati &

Patel, 2016) have shown that an edge product cordial

labeling admits in the sunflower graph for n≥3. The

graph used here is simple and finite.

2 DEFINITIONS

Consider the simple graph G with vertex set W, let g:

W→ {1, 2 . . . |W|} be a bijective function of G. The

function f is known as DC labeling if the distinction

between the number of lines categorized with 0 and

the number of lines categorized with 1 is less than or

equal to one such that a line xy is categorized 1 if f(x)

is a divisor of f(y) or f(y) is a divisor of f(x), and

categorized 0 otherwise for every line. A graph that is

having DC labeling is referred to as an DC graph.

Consider the simple graph G with vertex set W,

let g: W→ {1, 2 . . . |W|} be a bijective function of G.

The function f is known as SDC labeling if the

distinction between the number of lines categorized

with 0 and the number of lines categorized with 1 is

less than or equal to one such that a line xy is

categorized 1 if 2 divides sum of f(x) and f(y), and

categorized 0 otherwise for every line. A graph that is

having SDC labeling is referred to as an SDC graph.

A wheel graph is a graph which is formed by cycle

and a vertex at the center which connects to all

vertices of the cycle. Let W

be a wheel with x

the center vertex and x

, x

, . . . x

as the nodes of its

cycle. The sunflower graph G is formed by adding

new vertices y

, y

. . . y

such that y

is connected to

, xi

(mod n) (Ponraj et al., 2015).

2.1 Theorem

The graph SF

is an SDC graph for all n≥3.

Proof:

Let G = SF

Let W(SF

) = {x

, x

, y

: 1≤ j≤ n } and E(G)={x

: 1 ≤ j ≤n; x

: 1≤ j ≤n; y

j+1

: 1≤ j≤ n-1; y

j+1

: 1≤ j≤

n-1; x

; y

Then the order and size of the graph G are 2n+1

and 4n respectively.

Define g: W(G)→ {1, 2, 3 . . . 2n+1} by:

g(x

)= 1

g(x

)= 2j+1, 1≤ j≤ n;

g(y

)= 2j, 1≤ j≤ n;

Then the induced edge labels are

)= 1, 1≤ j≤ n;

)= 0, 1≤ j≤ n;

j+1

)= 0, 1≤ j≤ n-1;

j+1

)= 1, 1≤ j≤ n-1;

)= 0;

)= 1;

We notice that, e

(0)= 2n and e

(1)= 2n.

Thus |e

(0)-e

(1)|= |2n-2n|= 0≤ 1

Hence, the sunflower graph SF

is an SDC graph

for all n≥3.

2.2 Example

The sunflower graph SF

, in which n=3 is shown in

figure 1.

Figure 1.

From figure 1, |e

(0)-e

(1)|= |6-6|= 0≤ 1.

So, we conclude that the sunflower graph SF

where n= 3 is having SDC labeling.

Hence the sunflower graph SF

, in which n=3 is

an SDC graph.

2.3 Example

The sunflower graph SF

, in which n=4 is shown in

figure 2.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

306

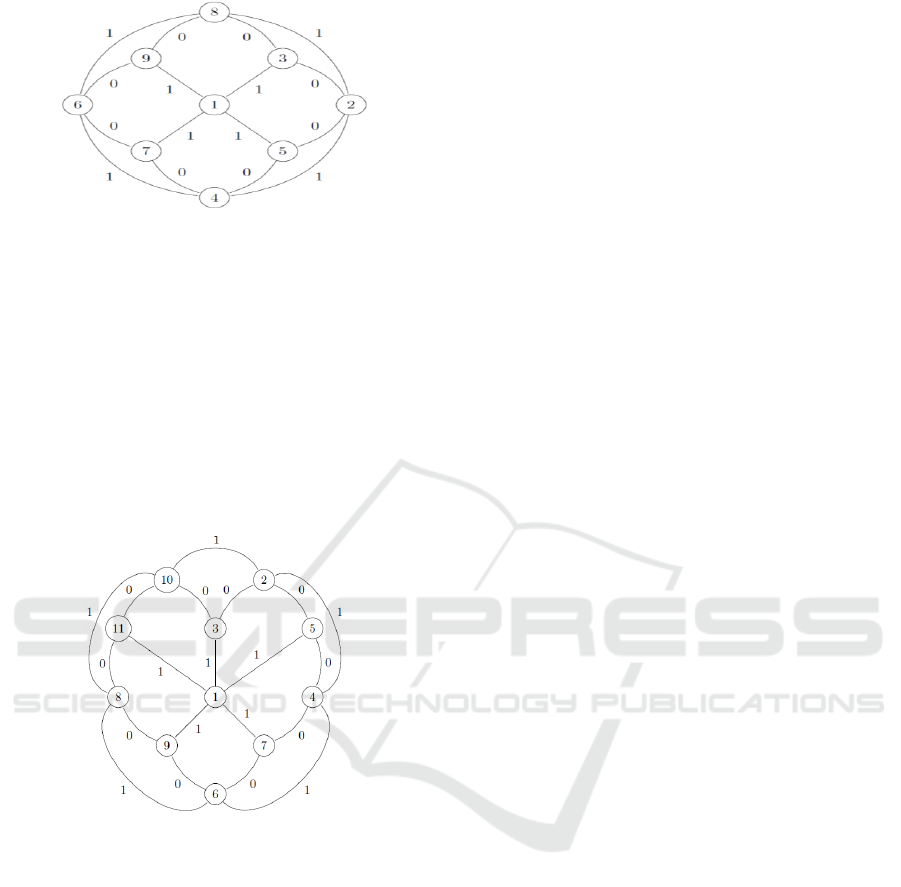
Figure 2.

From figure 2, |e

(0)-e

(1)|= |8-8|= 0≤ 1.

So, we conclude that the sunflower graph SF

where n= 4 is having SDC labeling.

Hence the sunflower graph SF

, in which n=4 is

an SDC graph.

2.4 Example

The sunflower graph SF

, in which n=5 is shown in

figure 3.

Figure 3.

From figure 3, |e

(0)-e

(1)|= |10-10|= 0≤ 1.

So, we conclude that the sunflower graph SF

where n= 5 is having SDC labeling.

Hence the sunflower graph SF

, in which n=5 is

an SDC graph.

3 CONCLUSION

In this paper, we have shown that the sunflower graph

is an SDC graph for all n≥ 3.

REFERENCES

Abhirami, S., Vikramaprasad, R., & Dhavaseelan, R.

(2018). Even sum cordial labeling for some new graphs.

International Journal of Mechanical Engineering and

Technology, 9(2), 214–220.

Adalja, D. G. (2022). Sum Divisor Cordial Labeling in the

Context of Graphs Operations on Bistar. Turkish World

Mathematical Society Journal of Applied and

Engineering Mathematics, 12(2), 588–599.

Barasara, C. M., & Thakkar, Y. B. (2022). Divisor cordial

labeling for ladders and total graph of some graphs.

21(7), 3577–3594.

Chakraborty, A., Dutta, T., Mondal, S., & Nath, A. (2018).

Application of Graph Theory in Social Media.

International Journal of Computer Sciences and

Engineering, 6(10), 722–729.

https://doi.org/10.26438/ijcse/v6i10.722729

Gallian, J. A. (2018). A dynamic survey of graph labeling.

Electronic Journal of Combinatorics,

1(DynamicSurveys).

Kanani, K. K., & Bosmia, M. I. (2016). Cube Divisor

Cordial Labeling of some Standard Graphs.

International Journal of Mathematics and Soft

Computing, 6(1), 163.

https://doi.org/10.26708/ijmsc.2016.1.6.14

Kumar, A., & Kumar vats, A. (2020). WITHDRAWN:

Application of graph labeling in crystallography.

Materials Today: Proceedings, October 2020.

https://doi.org/10.1016/j.matpr.2020.09.371

Lourdusamy, A., & Patrick, F. (2022). Several Results on

Sum Divisor Cordial Graph. Jordan Journal of

Mathematics and Statistics, 15(3 B), 643–660.

https://doi.org/10.47013/15.3.16

Lourdusamy St Xavier, A., & Patrick St Xavier, F. (2016).

Sum divisor cordial graphs. In Proyecciones Journal of

Mathematics (Vol. 35, Issue 1).

Mitra, S., & Bhoumik, S. (2022). Tribonacci Cordial

Labeling of Graphs. Journal of Applied Mathematics

and Physics, 10(04), 1394–1402.

https://doi.org/10.4236/jamp.2022.104098

Ponraj, R., Narayanan, S. S., & Kala, R. (2015). A note on

difference cordial graphs. 4(1), 189–197.

Prajapati, U. M., & Patel, N. B. (2016). Edge Product

Cordial Labeling of Some Cycle Related Graphs. Open

Journal of Discrete Mathematics, 06(04), 268–278.

https://doi.org/10.4236/ojdm.2016.64023

Prajapati, U., & Prerak, P. (2020). Divisor cordial labeling

in the Context of Friendship Graph. Journal of Xidian

University, 14(5). https://doi.org/10.37896/jxu14.5/018

Prasanna, N. L. (2014). Applications of Graph Labeling in

Communication Networks. Oriental Journal Computer

Science and Technology, 7(1).

Sharma, V., & Parthiban, A. (2022). On Recent Advances

in Divisor Cordial Labeling of Graphs. Mathematics

and Statistics, 10(1), 140–144.

https://doi.org/10.13189/ms.2022.100111

Thomas, A., Mathew, L., Surya, S. S., Thomas, A., &

Mathew, L. (2022). On integer cordial labeling of some

Sum Divisor Cordial Labelling of Sunﬂower Graphs

307

families of graphs. 42, 105–114.

https://doi.org/10.23755/rm.v39i0.709.

Vaidya, S. K., & Shah, N. H. (2013). Prime cordial labeling

of some wheel related graphs. Malaya Journal of

Matematik, 4(1)(1), 148–156.

Varatharajan, R., Navanaeethakrishnan, S., & Nagarajan,

K. (2011). Divisor cordial graphs. Int. J. Math. Comb.,

2011(4), 15–25.

Vinutha, M. S. (2017). Applications of Graph Coloring and

Labeling in Computer Science. International Journal

on Future Revolution in Computer Science and

Communication Engineering, 8(August 2017), 14–16.

AI4IoT 2023 - First International Conference on Artiﬁcial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry

and Consumer Electronics

308