
Time Fractional Radon Diffusion Equation and Crank Nicholson
Finite Difference Algorithm
S. V. Lathkar
1,*
and R. N. Ingle
2
1
Dept of Mathematics, NES Science College Nanded, SRTMU Nanded, Maharashtra, India
2
Dept of Mathematics, Bahirji smarak Maha Vidyalaya Vasmat, SRTMU Nanded, Maharashtra, India
Keywords: Fractional, Diffusion, Crank Nicholson Method, Stability, Convergence.
Abstract: The motivation behind this paper is to study the spread of radioactive active substance Radon in the air
medium. The Radon diffusion equation in air medium has been solved by applying finite difference scheme.
Basic Time fractional Radon diffusion equation has been solved using Crank Nicholson method of finite
difference scheme. The numerical solution is discussed for its stability and convergence. The stability of
obtained solution is significantly validated for the accuracy and consistency of the solution using
Mathematica. The Crank Nicholson Finite Difference Scheme is found to be the best suitable scheme after
observing the estimates and errors of radon concentration and its graphical representation. The solution to the
Radon diffusion equation is observed to be categorically stable and convergent.
1 INTRODUCTION
The detail study of Radon Diffusion equation in
various mediums serves the motive of study of
propagation of Radon gas and its ill effect in our
surroundings and its natural growth which is harmful
for living beings. Hence the sole purpose of this paper
is to detect the Radon concentration in the air
medium, by solving the Radon Diffusion Equation by
using FDM.
The hypothesis of this research paper hence are:
1. To study the estimates of Radon
concentration through air medium
2. To solve the Time Fractional Radon
Diffusion equation
3. To apply the Crank Nicholson Finite
Difference Scheme to solve the TFRDE
4. To understand the stability of the solution
obtained by the FDM.
5. To observe the convergence of solution
obtained by computational method
6. To validate the solution by graphical
representation of solution using
Mathematica.
*
Research Scholar
Crank Nicholson Finite Difference Scheme has
been used to solve the time fractional diffusion
equation here. The computations have been supported
from the numerical data for different parameters from
the (Millar, 1993). The structure of this paper has
section wise development. Section one includes
overview; section II contains the Crank Nicholson
FDM and the solution to TFRDE. The section III
discusses stability criteria of solution. Section IV
includes convergence of the solution. Section V
includes conclusion and discussions.
2 CRANK NICHOLSON FINITE
DIFFERENCE ALGORITHM
The finite difference algorithms try to solve
Fractional Partial Differential Equations by akin to
the equation over the provided boundary conditions
by converting it to a scheme of algebraic equations.
The algebraic equations are solved to obtain the
numerical solutions to fractional partial differential
equation. The finite difference schemes like Implicit,
Explicit and Crank Nicholson are associated but vary
in stability, exactness and performance speed. The
modelling of a fractional partial differential equation
322
Lathkara, S. and Ingle, R.
Time Fractional Radon Diffusion Equation and Crank Nicholson Finite Difference Algorithm.
DOI: 10.5220/0012615600003739
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Artificial Intelligence for Internet of Things: Accelerating Innovation in Industry and Consumer Electronics (AI4IoT 2023), pages 322-328
ISBN: 978-989-758-661-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

problem, involves three major attributes: 1. Actual
partial differential equation. 2. The space-time
domains applicable to the fractional partial
differential equation, and 3. The auxiliary boundary
values and initial value conditions.
Crank Nicolson algorithm is a finite difference
algorithm applied to solve diffusion differential
equations. This algorithm is implicit in time,
unconditionally stable and has higher order of
accuracy when used for regular heat equations
without any nonlinear expression coming into the
equation.
Figure 1.
3 RADON DIFFUSION
EQUATION
The radon concentration through air medium is the
outcome of the second order Radon diffusion
equation which is the prime interest in this paper.
Crank Nicholson finite difference algorithm has been
used for solving TFRDE.
α
α
λ
λ
We consider the following equation which is time
fractional diffusion equation,
α
α
λ
., (1)
IC:
(2)
. (3)
3.1 Application of Crank Nicholson
Finite Difference Algorithm by
Discretization
To covert the time fractional derivative in discrete
form, we use
.
Let v (
be the exact solution of TFRDE from
(1) - (3) at the mesh point (
Let
be the
numerical approximation of the point
The time fractional derivative is approximated in
Caputo sense is given by,
Substitute
we get
=
Where,
but
so we have;
We implement central difference second order
scheme in space for every interior grid point
So the numerical approximation equation thus
obtained by using the central difference and time
fractional approximation the Crank Nicholson type
numerical approximation to equation (1-3), expressed
as follows:
v
Time Fractional Radon Diffusion Equation and Crank Nicholson Finite Difference Algorithm
323
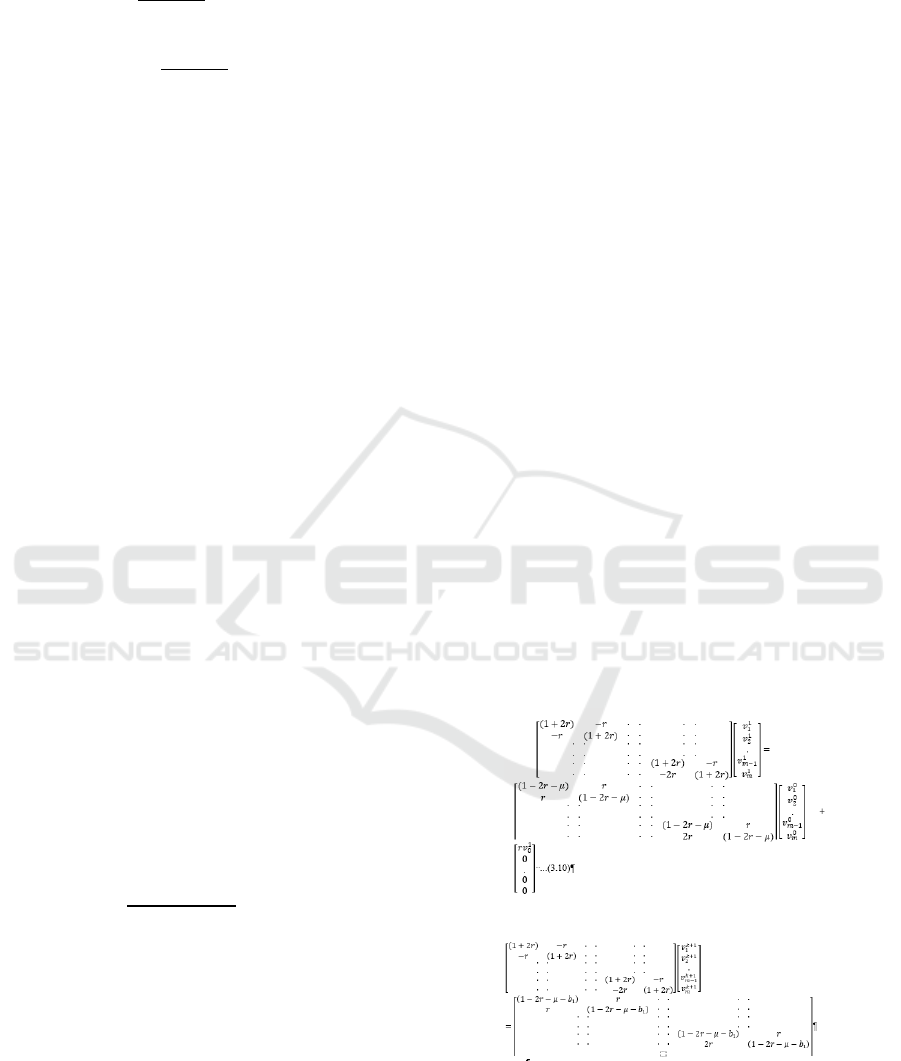
D
.
Let
(4)
Further,
where,
;
Now we convert the initial condition and
boundary conditions in discritized format:
;
The boundary conditions
and
the
discritization scheme implements as:
(From 4)
(6)
For
With initial condition
......... (8)
And boundary condition
The problem (6) to (9) is the complete discretized
form of (1) to (3)
So, the equation can be expressed in to matrix
form at
Can be represented in matrix form as;
+
... (10)
Now for ;
The matrix representation is given by,
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
324
+
….. (11)
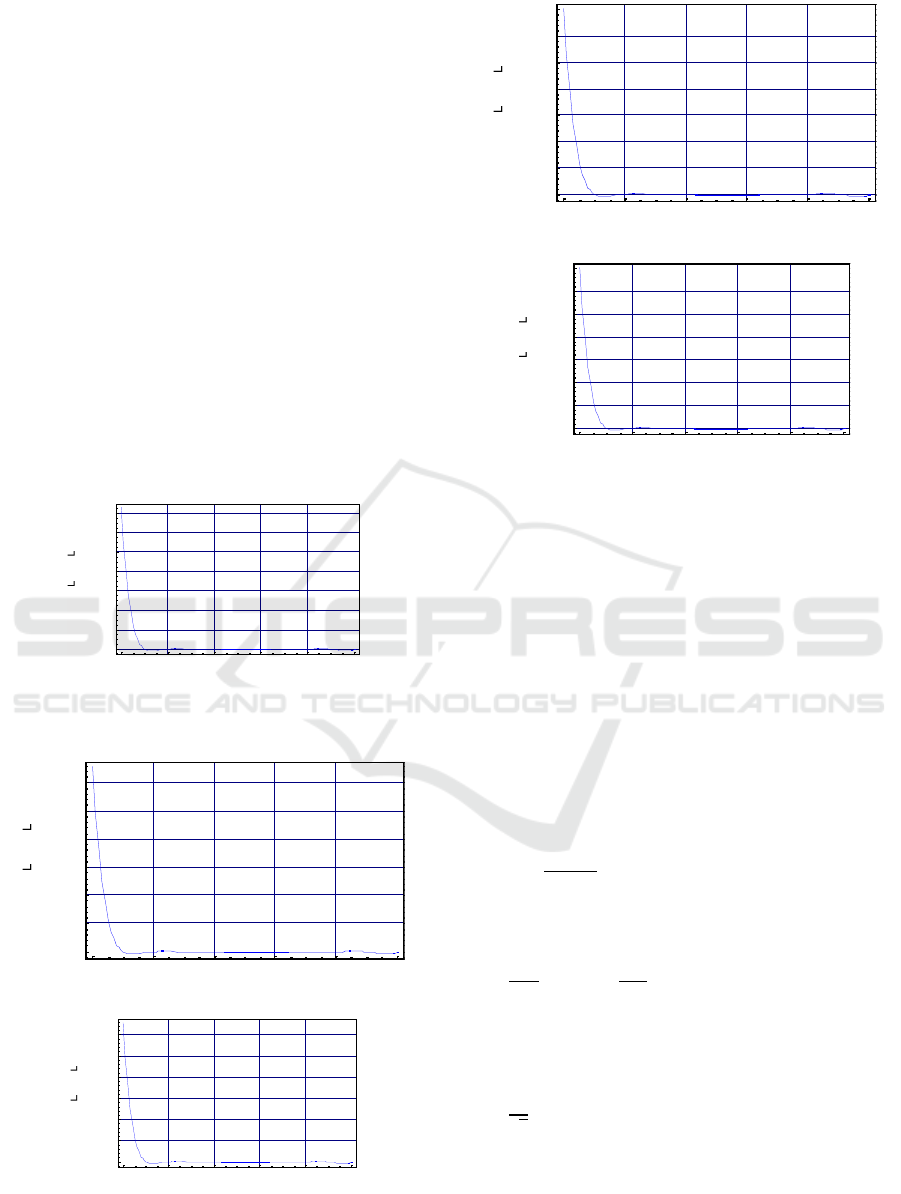
Figure 2: Radon concentration at 0.9 fractional order
derivative.
Figure 3: Radon Concentration at 0.8 fractional order
derivative.
Figure 4: Radon Concentration at 0.7 fractional order
derivative.
4 THE INVESTIGATION OF
RADON DIFFUSION IN AIR BY
CRANK NICHOLSON FINITE
DIFFERENCE METHOD
The secondary data for different parameters included
in the Radon diffusion in air medium has been
referred from “Numerical and Analytical Assessment
of Radon, Diffusion in Various Media and Potential
of Charcoal “, as Radon Detector by (Sasaki,2006),
• The diffusion coefficient of radon in air.
.
• The radon concentration in ambient air
• The radon absorption coefficient
• The length of cylinder for measurement
• The volume of cylinder for measurement
• Radius of cylinder used for measurement is,
.
• The experiment for measurement of Radon
diffusion was conducted for 72 hours duration,
for saturation of radon activity in air.
0 0.2 0.4 0.6 0.8 1
X
0
2000
4000
6000
8000
10000
12000
14000
u x, t
0 0.2 0.4 0.6 0.8 1
X
0
2500
5000
7500
10000
12500
15000
u x, t
0 0.2 0.4 0.6 0.8 1
X
0
2500
5000
7500
10000
12500
15000
u x, t
0 0.2 0.4 0.6 0.8 1
X
0
2500
5000
7500
10000
12500
15000
17500
u x, t
0 0.2 0.4 0.6 0.8 1
X
0
2500
5000
7500
10000
12500
15000
17500
u x, t
Time Fractional Radon Diffusion Equation and Crank Nicholson Finite Difference Algorithm
325

•
.
is the decay
coefficient of Radon.
•
•
•
Let the fractional order derivative
and
• For
• For
• For
• The estimates are used to solve the system of
equations obtained in matrix form finding the
relation between the radon concentration as
function of distance x and time t. Similarly
solving it for fractional order derivative
we see the solution interpreted
graphically by using ‘Mathematica’.
5 STABILITY
Lemma 5.1: If
, represents equations of
matrix A then the following results are true.
And
,
For
Lemma 5.2: The solution obtained for the time
fractional radon diffusion equation is unconditionally
stable for air medium.
Proof: The stability of the solution obtained for time
fractional radon diffusion equation mentioned above,
we prove the relation
from
(3.10)
By Principle of induction, we extend this statement
for ;
From (11)
+
These conditions affirm us about the
unconditional stability of Crank Nicholson finite
difference scheme to the Radon diffusion equation.
6 CONVERGENCE
The convergence of the approximate solution
obtained by Crank Nicholson finite difference
scheme of approximation towards the exact solution
is observed here (Savovic, 2008). Let
be the
exact solution of the time fractional diffusion
equation in (1) to (3) and
be the approximate
solution for (6) to (9) at some point (
) obtained
by Crank Nicholson finite difference scheme
i =1, 2, 3.... m-1;
k =1, 2, 3……n.
Let
.
From the discretised scheme
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
326

Lemma 6.1: The fractional order Crank Nicholson
finite difference scheme for the TFRDE
converges to
the relation between the
two solutions satisfies the relation
These conditions affirm us about the
unconditional convergence of Crank Nicholson finite
difference scheme to the Radon diffusion equation.
7 DISCUSSION AND
CONCLUSION
The time fractional radon diffusion equation (1) - (3)
has been solved by discretising the equation in time
fractional form. The Crank Nicholson finite
difference scheme has been used for approximation.
The numerical solution is obtained using time
fractional radon diffusion equation in air medium
with initial and boundary conditions. The solution has
been validated by using ‘Mathematica’ software. We
believe the one- boundary conditions 0< x <1, 0< α ≤
1, t > 0 initial condition: dimensional time fractional
diffusion equation subjected to initial and
, a
At α = 0.9,0.8 ,0.7. The
numerical solutions are analysed at t = 0.05 by taking
into consideration the terms τ = 0.005, h = 0.1.
Convergent numerical solution is obtained for the
diffusion equation under analysis. The Radon
movement and transportation through a cylinder of
air is calculated as the concentration at various levels.
The study of the fractional order Crank Nicholson
finite difference scheme for time fractional radon
diffusion equation is best fit, which gives
unconditionally stable and convergent solution.
REFERENCES
Ayoe Hoff, (1997). Radon Transport in Fractured Soil:
Laboratory Experiments and Modelling, (1997), ISBN
87-550-2315-0; ISSN 0106-2840.
Bigu J., (1986). Nuclear Instruments and Methods in
Physics Research, A251, pp. 366-373.
Dongfang Li, (2016) A linear finite difference scheme for
generalized time fractional Burgers equation,
http://dx.doi.org/10.1016/j.apm.2016.01.043 S0307-
904X (16)30039-7/© Elsevier
Dosimetry, (1985), The Numerical Solution of the
Diffusion Equation Describing the Flow of Radon
Through Cracks in a Concrete Slab, Radiation
Protection, Volume 11, Issue 4, Pages 229–236
Dosimetry, (2003), Radon transport through concrete and
determination of its diffusion coefficient, Radiation
Protection, 104(1):65-70 ·
Huynh Nguyen Phong, Thuab Nguyen Van, Thanga Le
Cong Haoab, (2020), The effects of some soil
characteristics on radon emanation and diffusion,
Journal of Environmental Radioactivity, Volume 216,
106189.
K. C. Takale, V. R. Nikam and A. S. Shinde, (2013), Finite
Difference Scheme for Space Fractional Diffusion
Equation with Mixed Boundary Conditions, American
Jr. of Mathematics and Sciences, Vol. 2.
K. S. Miller and B. Ross, (1993), An Introduction to the
Fractional Calculus and Fractional Differential
Equations, John Wiley, New York.
S. Shen, F. Liu, (2005), Error Analysis of an explicit Finite
Difference Approximation for the Space Fractional
Diffusion equation with insulated ends, ANZIAM J.46
(E), pp. C871 - C887
S. V. Lathkar, R. N. Ingle;( 2019), Adomian
Decomposition Method for solving Non Linear Three
variable, Parabolic Fractional Partial Differential
Equation, IJRAR, Volume 6, Issue 1 www.ijrar.org (E-
ISSN 2348-1269, P- ISSN 2349-5138)
S. V. Lathkar, R. N. Ingle;(2021) Computational and
analytical measurement of radon concentration in air
medium using implicit finite difference scheme for time
fractional radon diffusion equation, Malaya Journal of
Matematik, Vol. 9, No. 1, 1000-1005,
https://doi.org/10.26637/MJM0901/0176
S. V. Lathkar., R. N, Ingle;( 2021) Comparative Analysis
of Radon Concentration in Air and Charcoal Medium
through Time Fractional Radon Diffusion Equation,
Science, Technology and Development, ISSN: 0950-
0707, Volume X Issue XII DECEMBER ISSN: 0950-
0707 Page No : 104-112.
Time Fractional Radon Diffusion Equation and Crank Nicholson Finite Difference Algorithm
327

Sasaki, T., Gunji, Y., Okuda, T., (2006), Investigation of
soil radon diffusion coefficient measurements and
methodology.RAE-50344-001-1, URS Corporation,
Salt Lake.
Savovic,S., Djordjevich, A., (2008), numerical solution of
the diffusion equation describing the flow of radon
through concrete SEQ CHAPTER, Applied Radiation
and Isotopes Volume 66, Issue 4, April 2008, Pages
552-555
Schery, S.D., Whittlestone, S., (1989), Description of radon
at the earth’s surface. J.Geophys.Res.94(D15),18297–
18303.
Tomozo SASAKI, Yasuyoshi GUNJI & Takao IIDA
(2007) Transient-Diffusion Measurements of Radon:
Practical Interpretation of Measured Data, Journal of
Nuclear Science and Technology, 44:7, 1032-1037.
V.C. Rogers, et al, Radon Flux Measurement and
Computational Methodologies, 1984
Y. Lin, C. Xu, (2007), ‖Finite difference/spectral
approximations for the time-fractional diffusion
equation, ‖ J. Compute. Phys. 225 , pp.1533-1552.
AI4IoT 2023 - First International Conference on Artificial Intelligence for Internet of things (AI4IOT): Accelerating Innovation in Industry
and Consumer Electronics
328
