Butterfly and Moth Image Recognition Based on Residual

Neural Network

Fengwei Liu

Glasgow College, University of Electronic Science and Technology, Chengdu, China

Keywords: Butterflies or Moths Image Recognition, ResNet, Convolutional Neural Network, Adam.

Abstract: Image recognition is presently a central area of study within the machine learning domain. Convolutional

neural networks (CNN) are a special type of artificial network model commonly used for image processing

and recognition. The design inspiration for this deep learning model comes from human visual recognition

systems, whose core idea is to use convolution operations to extract features from images. Then the network

utilizes a series of different functional hidden layers to ultimately recognize and classify the input image

data. This article constructs a deep CNN model utilizing the ResNet50 for image recognition and

classification on a dataset containing butterfly and moth images, and analyzes the classification results.

After 10 epochs, the CNN model demonstrated a 94.3% accuracy rate when applied to the test dataset.

According to research findings, the model exhibits commendable accuracy on the dataset. Nevertheless,

owing to the limited number of training epochs, the performance on the test set fell short of optimal

outcomes. Therefore, augmenting the number of epochs can be a viable approach to enhance the model's

classification accuracy for the dataset.

INTRODUCTION

Over the past few years, image recognition and

classification have emerged as pivotal areas of

investigation within the realm of computer vision.

Image classification, a cornerstone in computer

vision, involves categorizing images into distinct

classes based on their semantic attributes. It serves as

the cornerstone for various advanced visual tasks,

including but not limited to object detection, image

segmentation, and object tracking. Image

classification and recognition have extensive

applications in many fields, such as face recognition,

autonomous driving, intelligent video analysis, and

image recognition in the medical field (Chauhan et

al, 2018). CNN include input layers, convolutional

layers, pooling layers, Dense layers, etc., which

process raw pixel values or pixel values that have

undergone simple preprocessing (such as centering

and scaling), and are often used for image

recognition and classification. Traditional network

structures such as AlexNet and VGGNet have the

problem of insufficient network structure depth,

which means that when the network structure is

deeper, the classification performance of the model

does not meet expectations. In the ILSVRC 2015

classification task, Kaiming, Xiangyu, Shaoqing

introduced a novel deep CNN framework, which is

commonly referred to as the ResNet architecture (He

et al, 2016). A 152 layer network structure was

established on the ImageNet dataset and compared

with traditional network structures such as VGGNet

and GoogLeNet. The results showed that the

established residual neural network had higher

accuracy while maintaining lower network

complexity, indicating a lower risk of overfitting.

This article implements a method for recognizing

and classifying butterfly or moth images in datasets

based on ResNet network architecture. Expanding

the application of CNN in image recognition and

classification can enhance the precision and

efficiency of butterfly classification, benefiting

biologists in their assessments. This article uses a 50

layer residual neural network for image feature

extraction and recognition, while the Dense layer

achieves the final classification of the

image. Moreover, a dropout layer was added to the

model to randomly shut down neurons in the dense

layer, this aids in further diminishing the potential

for overfitting in the model. Employing Adam

optimization functions within the network

architecture enhances the model's learning

efficiency.

Liu, F.

Butterﬂy and Moth Image Recognition Based on Residual Neural Network.

DOI: 10.5220/0012798500003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 211-217

ISBN: 978-989-758-705-4

211

The following content was written in the

subsequent part of this article: Part 2 summarizes the

relevant work in the field of deep learning, which is

a literature review. The third part introduces the

established deep CNN model and provides a detailed

description of its internal architecture and the

optimization function Adam of the model. In the

fourth section, we elucidate the model's

classification outcomes on the dataset and conduct a

comprehensive performance assessment. Section 5

summarizes the main work of this article and

proposes the shortcomings of the research.

RELATED WORKS

With the development of machine learning, related

algorithms are facing new opportunities and

challenges in computer vision. In image

recognition, the classification performance of deep

learning algorithms for images is becoming

increasingly accurate. The following is a list of

relevant developments:

R. Chauhan, K.K. Ghanshala, R.C. Joshi, et al.

developed two distinct CNN architectures for both

the MNIST and CIFAR-10 datasets, exclusively

relying on CPU-based computation (Chauhan et al,

2018). CNN performed well on the MNIST dataset,

achieving an accuracy of 99.6% after 10

epochs. On the CIFAR-10 dataset, due to

insufficient training epoch size, the accuracy is only

80.17%. Furthermore, a suggestion is put forth to

augment the training epoch as a means to further

enhance the model's accuracy.

Deep learning in medicine helps to effectively

diagnose epidemics. Boukaye, Bernard, Fana et al.

used efficient CNN to effectively recognize and

classify pathogen images of cholera and malaria in

microscopic images, ultimately achieving an

accuracy of 94% (Traore et al, 2018). And it is

proposed that integrating pathogen image

recognition methods from this microscope into a

medical microscope can help diagnose and prevent

crises caused by epidemics. HYU, SOYOUN,

KYUNGYONG et al. based on ResNet deep CNN

and recognition of chest X-ray images, can

effectively diagnose cardiac hypertrophy (Yoo et al,

2021). The accuracy of model recognition is close to

80%. In addition, this work evaluated and compared

the classification results obtained by four types of

optimization functions SGD, Adam, AdaGrad, and

RMSProp in neural networks. According to this

work, when SGD is used as the optimizer in neural

networks, the model performs best in diagnosing

cardiac hypertrophy.

Weather recognition stands as a pivotal

application in the field of computer vision. Bin,

Xuelong, Xiaoqiang et al. assigned multiple weather

condition labels to each weather image in two

datasets, and completed the multi label classification

task based on a special CNN-RNN network model

(Zhao et al, 2018). In this model, CNN is extended

to a channel attention model. This model not only

effectively identifies weather, but also explores the

interrelationships within different weather conditions.

This study has markedly enhanced the model's

precision when contrasted with the conventional

approach of treating weather recognition as a

single-label classification task. Furthermore, we

conducted a comparative analysis involving AlexNet,

multi-label versions of VGGNet, ML-KNN,

ML-ARAM, and various other network models

using two distinct weather recognition datasets.

Finally, it was found that the CNN-RNN performed

best in multi label classification tasks on this dataset.

CLASSIFIER MODEL

3.1 CNN Model

CNN typically consist of several layers. They

include input layers, convolutional layers, pooling

layers, and dense layers (commonly referred to as

fully connected layers) and so on (Gu et al, 2018).

Convolutional layers are adept at extracting

pivotal features from the input image data. Within

neural networks, these layers necessitate multiple

convolutional kernels for computation. Each element

within these kernels corresponds to the network's

weight coefficients and bias vectors, taking

inspiration from the feedforward neural networks

found in biological organisms. The location on the

output feature map of the convolutional layer, in

relation to the pre-convolution input region, defines

the portion where the features of the CNN perceive

the input image. This region's size is contingent

upon the dimensions of the convolutional kernel

employed in the correlation operations of the

convolutional layer, commonly referred to as the

"receptive field. " (Gu et al, 2018).

Pooling layer is used for downsampling

convolutional layers, thereby reducing the number of

data points. Two prevalent pooling techniques are

frequently employed: average pooling and max

pooling.

Dense layer is used to classify the extracted

features mentioned above (similar to the fully

DAML 2023 - International Conference on Data Analysis and Machine Learning

212

connected layer in general neural networks) (Gu et

al, 2018). Before entering the dense layer, the 3D

data is elongated into a one-dimensional vector (i.e.

the data is flattened). A dense layer, also known as a

fully connected layer, signifies that each node within

it is intricately linked to every node in the preceding

layer. This layer's purpose is to amalgamate and

synthesize the features that have been extracted from

the preceding layers.

3.2 Residual Neural Network

Residual neural network is a classic deep CNN

model. The ResNet50 network structure

usedindicates that this CNN has 50 layers.

The table 1 lists a basic network structure

configuration of ResNet. Table 1 illustrates the

network architecture of ResNet50, a deep CNN that

serves as the primary model in this study (He et al,

2016).

Table 1: Basic ResNet50 Structure Configurations.

Conv la

er out

ut size 50-la

ers number

Sta

e1:Conv

1 112x112 7x7,64,stride2

Stage2:Conv_2

56x56

3x3

max_pool,stride2













)256(1x1

)64(3x3

)64(1x1

，

Stage3:Conv_3 28x28













)512(1x1

)128(3x3

)128(1x1

，

Stage4:Conv_4 14x14













)1024(1x1

)256(3x3

256,1x1

，

）（

Stage

5:Conv_5

7x7













)2048(1x1

)512(3x3

)512(1x1

，

The internal architecture of the entire network model

established based on ResNet50 in this article is

described in detail in Table 2.

Table 2: Network Structure.

Layer Size/Shape

ResNet50 2048

Flatten 2048

Dense_1 512

Dropout 512

Dense_2 100

ResNet with different depths has the following

characteristics: At the initial stage, they all

underwent the same process of convolutional layer

conv1 and maximum pooling (max-pool).

ResNet neural networks of different depths are

all composed of stacked basic residual blocks, and

the basic residual module of the 50 layer ResNet is

labeled as Bottleneck, which includes three

convolutions. The residual blocks stacked by ResNet

in stage 2 are identical and there is no downsampling.

The first residual block stacked in stages 3 to 5 in

the ResNet model is different from the remaining

residual blocks. Each stage (3-5 stages)

downsampling the feature image size, and

downsampling is sent at the first residual block in

each stage, while the remaining residual blocks are

not downsampling (with the same size).

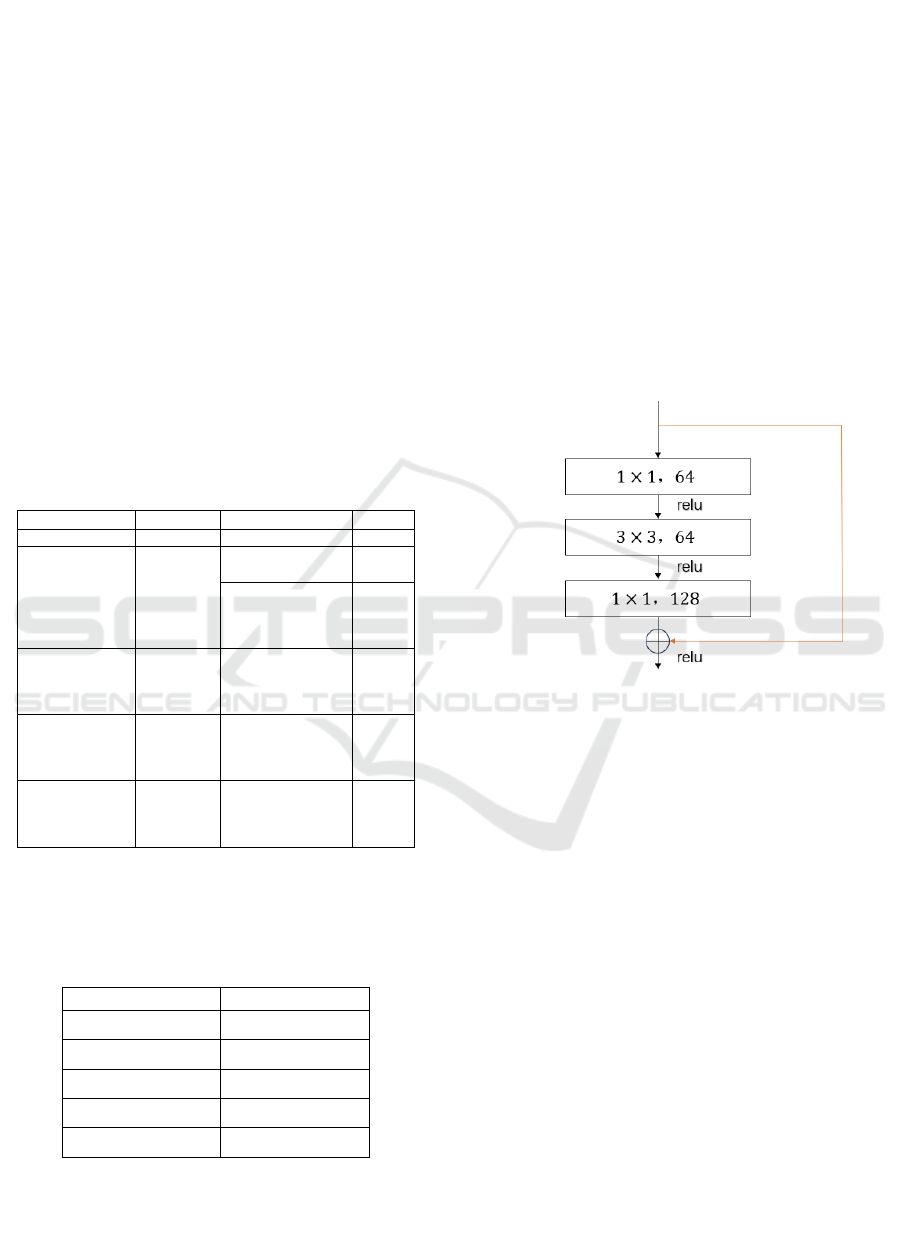
The residual block model in the ResNet network

model is shown in Fig.1:

Figure 1: The residual block model (Picture credit:

Original).

The Fig.1 shows a block proposed for deep networks,

called the "bottomleneck" block, with the main

purpose of dimensionality reduction. Firstly, a 1x1

convolution is used to reduce the 256 dimensional

channel to 64 channels, and finally, a 1x1

convolution of 256 channels is used to recover, such

as ResNet-50.

3.3 Dropout to Reduce Overfitting

While learning different features from the dataset,

neural networks also learn noise from the dataset.

This results in good performance of the network on

the training set, but poor performance on new data

(test set), which is known as overfitting. To solve the

overfitting problem, we add a dropout layer to the

network structure. In this article, a dropout layer is

added to the ResNet network structure to prevent

overfitting from occurring (Srivastava et al, 2014).

In neural networks, dropout refers to the random

deletion of some nodes in the input layer and hidden

layer with probability p, and all forward and

Butterﬂy and Moth Image Recognition Based on Residual Neural Network

213

backward connections to the deleted nodes will be

temporarily deleted, thereby creating a new network

architecture. The probability parameter of keeping

hidden nodes in the network is set to 0.5. Within

each training batch, a substantial reduction in

overfitting can be achieved by introducing a random

node dropout mechanism in specific hidden layers.

This strategy effectively mitigates interdependencies

among feature detectors, where individual detectors

are less reliant on the output of other detectors for

their function.

3.4 Adam Optimizer

The Adam optimizer, as referenced in, represents a

modification of the gradient descent algorithm

utilized for weight updates within neural networks

(Zhang, 2018). It integrates principles from both the

Stochastic Gradient Descent Algorithm (SGD) and

the Adaptive Learning Rate Algorithm, offering the

advantage of expedited convergence and reduced

training duration (Mehta, 2019). The Adam

optimizer calculates the independent adaptive

learning rate for each parameter without the need for

manual adjustment of the learning rate, making it

widely used in practice.

Neural network optimization in deep learning.

The Adam optimizer is a dynamic optimization

algorithm capable of fine-tuning the learning rate by

leveraging past gradient information. This approach

amalgamates concepts from two distinct

optimization algorithms, RMSProp and Momentum,

and normalizes parameter updates to ensure that

each parameter update has a similar magnitude,

thereby improving training effectiveness (Zou et al,

2019). The Adam optimizer excels in numerous

practical applications, particularly when employed

to train deep neural networks on extensive datasets

(Mehta, 2019).

The main function of the Adam optimizer is to

update neural network parameters based on gradient

information, thereby minimizing the loss function.

Specifically, its main functions include:

The Adam optimizer possesses the ability to

dynamically fine-tune the learning rate by drawing

insights from historical gradient information (Zhang,

2018). This adaptive learning rate mechanism allows

for the application of a larger learning rate during

the initial training phases, facilitating rapid

convergence. As the training progresses into its later

stages, a smaller learning rate is employed to refine

the search for the minimum of the loss function,

enhancing accuracy.

The Adam optimizer can adjust momentum

parameters to balance the impact of the previous

gradient and the current gradient on parameter

updates, thereby avoiding premature trapping in

local minima.

The Adam optimizer normalizes the updates of

parameters, so that each parameter update has a

similar magnitude, thereby improving the training

effect.

The Adam optimizer combines the idea of L2

regularization to regularize parameters during

updates, thereby preventing neural networks from

overfitting training data.

Overall, the Adam optimizer can quickly and

accurately minimize the loss function, improving the

training effectiveness and generalization ability of

deep neural networks.

RESULTS

4.1 Dataset

The dataset used in this article is used to identify the

species of butterflies and moths. The dataset

contains a total of 100 category labels for butterflies

or moths, and each image has a size of 224×224

pixels (50176 pixels) as input to the neural network.

The training set consists of 12594 images, divided

into 100 sub directories, each corresponding to a

species. The test dataset comprises 500 images,

organized into 100 subdirectories, each containing 5

test images per category. Additionally, within the

same dataset, there are 5 validation images per

category, yielding the same overall count of 500

images. Fig.2 visually presents a selection of images

from this dataset.

Figure 2: Some samples of datasets (Picture credit:

Original).

DAML 2023 - International Conference on Data Analysis and Machine Learning

214

4.2 The Loss Function

The loss function is a non negative function that

quantifies the dissimilarity between the predicted

outcome, denoted as f(x), produced by a neural

network, and the ground truth value, Y. Smaller

values of the loss function correspond to improved

predictive performance, indicating better model

results.

In this research, the employed loss function is the

softmax loss function, and its mathematical

representation is as follows:

LYf





=-

log

∑

j=1

(1)

i=1

From a standard form, the softmax loss function

should be classified as logarithmic loss. In

supervised learning, due to its widespread use, it

forms a separate category. The softmax loss function

can be seen as a natural extension of the logistic

regression model, especially applicable in the

context of multi-class classification tasks. It

frequently finds application as the preferred loss

function in CNN models. At its core, the softmax

loss function serves the purpose of mapping an

arbitrary real vector 'x' of dimension 'k' to another

real vector of the same dimension 'k'. This mapping

operation ensures that each element in the resulting

output vector falls within the range of (0,1), that is,

the softmax loss function outputs the prediction

probability of each category. The softmax loss

function, renowned for its capacity to facilitate

inter-class separability, finds extensive application in

a spectrum of tasks including classification,

segmentation, face recognition, automatic image

annotation, and face verification. Notably, it excels

in optimizing inter-class distances, yet its

performance in optimizing intra-class distances is

comparatively less pronounced.

The softmax loss function is renowned for its

ability to facilitate inter-class separability and is

frequently employed in tackling feature separation

challenges within the realms of multi-classification

and image annotation tasks. In CNN-based

classification scenarios, the softmax loss function is

typically designated as the primary loss function.

Nevertheless, the features derived from the softmax

loss function often lack the requisite level of

distinctiveness. As a remedy, it is common practice

to complement it with contrast loss or center loss

techniques to augment discriminative capabilities.

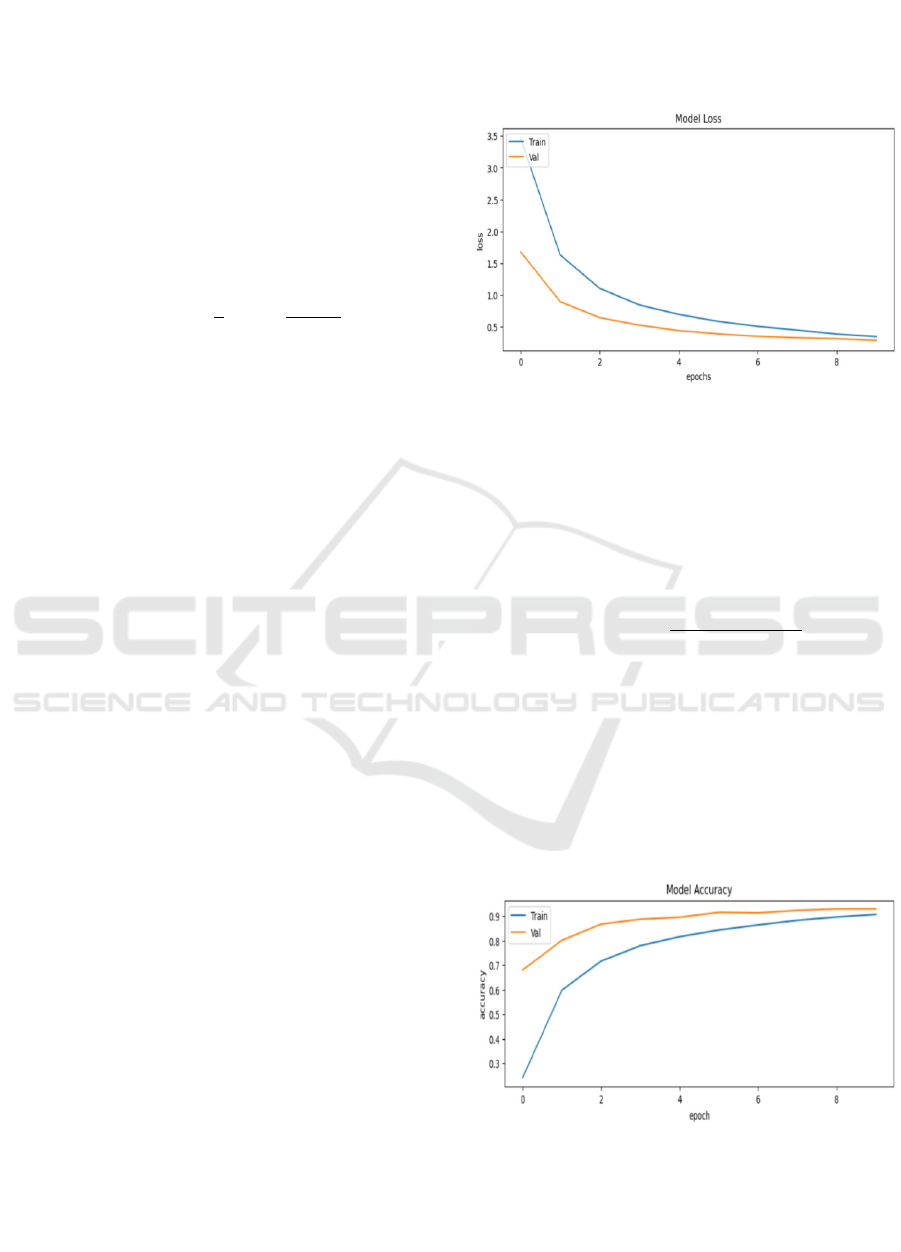
The graphical representation in Fig.3 illustrates

the outcomes of the loss function within this

research. With the prolonged duration of training,

there is a consistent reduction in the model's loss

function for both the training and validation datasets.

This decline signifies an enhancement in the model's

classification performance over time.

Figure 3: Loss function of the model (Picture credit:

Original).

4.3 Accuracy

The precision of a neural network pertains to the

ratio of accurately predicted samples to the total

number of samples in the testing dataset. This is

mathematically expressed as:

Accuracy=

TP+TN

TP+TN+FP+FN

2

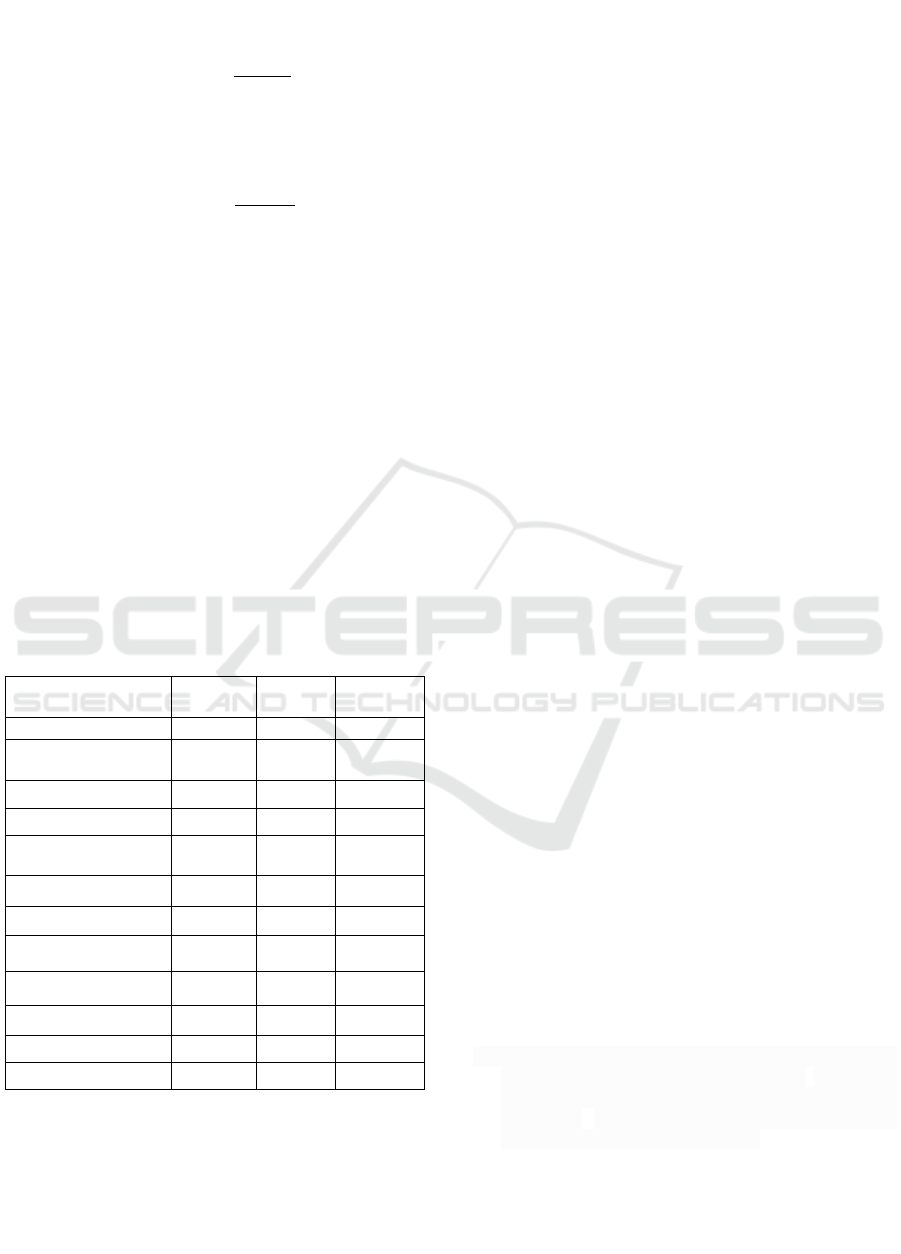
The accuracy of this article is shown in Fig.4. As

the training cycle increases, the model's performance

steadily enhances on both the training and validation

datasets, signifying a continuous improvement in the

network's efficacy. The accuracy of neural networks

represents the degree of prediction accuracy in the

results of the positive sample. Ultimately, the

network model's accuracy on the test set culminated

at 94.3%.

Figure 4: Accuracy of the model(Picture credit: Original).

4.4 Performance Measurement Results

Precision pertains to the likelihood of being a

Butterﬂy and Moth Image Recognition Based on Residual Neural Network

215

positive sample within the set of all predicted

positive samples and is represented as

Precision=

TP+FP

3

Recall, denoted as the likelihood of being

classified as a positive sample among the true

positive instances, is mathematically articulated as

Recall=

TP+FN

4

F1-score, also known as BalancedScore,

represents the harmonic mean between accuracy and

recall. The F1 score, a statistical metric ranging from

0 to 1, serves as a measure to assess the accuracy of

outcomes produced by a binary model. The F1 score

provides a comprehensive evaluation of the

classification accuracy achieved by neural network

models, considering both the precision of

classification results and the recall rate of dataset

samples. A heightened F1 score indicates enhanced

resilience in the constructed network architecture.

Table 3 presents the classification outcomes of

the model developed in this study for a set of 100

distinct butterfly and moth species. Specifically, the

table showcases the model's classification results for

the top 10 butterfly and moth categories, listed

alphabetically.

Table 3: Classification Results on the Test Set.

Category Precision Recall F1-score

ADONIS 0.65 1.00 0.79

AFRICAN GIANT SW

ALLOWTAIL

1.00 1.00 1.00

AN 88 1.00 1.00 0.90

APPOLLO 1.00 1.00 1.00

ARCIGERA FLOWER

MOTH

0.80 1.00 0.91

ATALA 1.00 1.00 1.00

ATLAS MOTH 1.00 1.00 1.00

BANDED ORANGE

HELICONIAN

1.00 1.00 1.00

BANDED PEACOCK 1.00 1.00 1.00

Accuracy / / 0.94

Macro average 0.95 0.94 0.94

Weighted average 0.95 0.90 0.90

In table 3, CNN's classification performance in t

he ADONIS, AMERICAN SNOOT, AN 88, AR

CIGERA FLOWER MOTH categories is not acc

urate enough, and there are no errors in the clas

sification results of the other butterfly or moth c

ategories.

CONCLUSIONS

This article presents a novel approach to image

recognition and classification based on ResNet

network structure. This method is used to distinguish

100 species of butterflies or moths in the dataset.

After 10 training epochs, the CNN architecture

demonstrated an impressive 94.3% classification

accuracy on the test set, underscoring its proficiency

in accurately classifying butterfly or moth datasets.

Because of the limited training epochs executed on

the CPU, the model's performance in terms of

classification accuracy on the test set fell short of

optimal outcomes. Therefore, augmenting the

epochs can be contemplated as a means to enhance

the model's classification accuracy on the given

dataset. Before inputting data, denoising the image

data using corresponding preprocessing algorithms

can help convolutional layers extract image features

more effectively.

REFERENCES

R. Chauhan, K. K. Ghanshala, and R. C. Joshi,

"Convolutional neural Network (CNN) for image

detection and recognition," 2018 First International

Conference on Secure Cyber Computing and

Communication (ICSCCC), 2018, pp. 278-282.

K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual

learning for image recognition," Proceedings of the

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), 2016, pp. 770-778.

B.B. Traore, B. Kamsu-Foguem, and F. Tangara, "Deep

convolution neural network for image recognition,"

Ecological Informatics, vol. 48, pp. 257-268, 2018.

H. Yoo, S. Han, and K. Chung, "Diagnosis support model

of cardiomegaly based on CNN using ResNet and

explainable feature map," in IEEE Access, vol. 9, pp.

55802-55813, 2021, doi: 10.1109/ACCESS.

2021.3068597.

Zhao, X. Li, X. Lu, and Z. Wang, "A CNN–RNN

architecture for multi-label weather recognition,"

Neurocomputing, vol. 322, pp. 47-57, 2018.

J. Gu et al., "Recent advances in convolutional neural

networks," Pattern Recognition, vol. 77, pp. 354-377,

2018.

N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, I.

Salakhutdinov, and R. Salakhutdinov, "Dropout: a

simple way to prevent neural networks from

overfitting," The journal of machine learning research,

vol. 15, no. 1, pp. 1929-1958, 2014.

Z. Zhang, "Improved adam optimizer for deep neural

networks," 2018 IEEE/ACM 26th international

symposium on quality of service (IWQoS), 2018, pp.

1-2.

DAML 2023 - International Conference on Data Analysis and Machine Learning

216

S. Mehta, C. Paunwala, and B. Vaidya, "CNN based traffic

sign classification using adam optimizer," in 2019

international conference on intelligent computing and

control systems (ICCS), 2019, pp. 1293-1298.

F. Zou, L. Shen, Z. Jie, and W. Liu, "A sufficient condition

for convergences of adam and rmsprop," Proceedings

of the IEEE/CVF Conference on computer vision and

pattern recognition(CVPR), 2019, pp. 11127-11135.

Butterﬂy and Moth Image Recognition Based on Residual Neural Network

217