The Analysis of Hidden Units in LSTM Model for Accurate Stock

Price Prediction

Menghao Deng

The Faculty of Science, The University of Hong Kong, Hong Kong, China

Keywords: Stock Market Prediction, Long Short-Term Memory, Hidden Units, Deep Learning.

Abstract: Stock market forecasting has always been difficult due to its complicated and volatile character. Deep learning

approaches have demonstrated promising results in a variety of domains, including stock market prediction,

in recent years. This research introduces Long Short-Term Memory (LSTM) for forecast of stock market and

examines the impact of model's hidden units. The LSTM model is developed on historical stock market data

to find intricate patterns and linkages. Technical indicators and sentiment analysis can also be used as potential

input variables to improve the model's predictive capacity. The suggested model is tested against a large

dataset of stock market values and compared to established algorithms of deep learning. The purpose of this

research is to investigate the role and implementation of hidden units in LSTM networks. These hidden units

learn long-term dependencies and recall them in a way that many other forms of Recurrent Neural Networks

(RNN) do not. Investigations in paper show that changing the number of hidden units has an effect on

prediction results. The findings of this work add to the expanding corpus of research on using deep learning

techniques for stock market forecasting and analysis, with potential implications in financial decision-making

and risk management.

1 INTRODUCTION

The stock market is a financial market characterized

by complexity and volatility, making stock market

prediction a challenging task. Traditional prediction

methods often struggle to capture the intricate patterns

and dependencies within stock market data. Deep

learning algorithms, on the other hand, have

demonstrated encouraging results in time series

forecasting in recent years. It opens up new avenues

for stock market forecasting. The purpose of this

research is to present a novel approach for stock

market forecasting and analysis that is based on Long

Short-Term Memory (LSTM) model. This study

successfully capture the complex patterns and

dependencies present in the data by training an LSTM

model using historical stock market data. The Author

hopes to give relevant references and direction for

future research and practical applications in the field

of stock market prediction and analysis through this

work, ultimately providing more trustworthy decision

support for investors and financial institutions. Many

researches in Speech recognition and Image and

Video Processing are also based on LSTM. Sequence

to Sequence Learning with Neural Networks, which

introduced the use of LSTM for machine translation

(Sutskever et al 2014). Show and Tell: A Neural

Image Caption Generator, used LSTM for generating

captions for images (Vinyals et al 2015). DeepSpeech:

Scaling up end-to-end speech recognition, which

employed LSTM for speech recognition tasks

(Hannun et al 2014). The original LSTM architecture

included memory cells, input gates, forget gates, and

output gates. It enabled the network to selectively

recall or forget information over extended time

intervals, allowing it to capture long-term

dependencies in sequential data. Over the years,

researchers have proposed various modifications and

improvements to the original LSTM architecture

(Gers et al 2000). Some notable variants include Gated

Recurrent Unit (GRU), which simplified the LSTM

architecture, and Peephole LSTM, which introduced

peephole connections to the gates (Rui et al 2016).

Natural Language Processing (NLP) tasks such as

sentiment analysis, text synthesis, sentiment modeling,

and machine translation have all made extensive use

of LSTM. The capacity of LSTM to capture long-term

dependencies allows it to understand and generate

cohesive word sequences. LSTM has also been used

successfully for time series forecasting jobs such as

stock market forecasting, weather forecasting, and

demand forecasting. Because of its power to capture

temporal patterns, it is well suited for modeling and

predicting sequential data.

Deng, M.

The Analysis of Hidden Units in LSTM Model for Accurate Stock Price Prediction.

DOI: 10.5220/0012799100003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 411-416

ISBN: 978-989-758-705-4

411

The objective of this study is to introduce LSTM

to build a stock price prediction model and analyze the

amount of LSTM hidden units to determine the

optimal model for improving the capability of the

stock price forecasting model. To be more specific,

this study explores how different quantities of LSTM

hidden units affect the accuracy and performance of

stock market predictions. By systematically adjusting

the amount of hidden units in the applied LSTM

model, the author can observe the variations in

prediction results and identify the configuration that

yields the best outcomes. The practical significance of

this research lies in utilizing deep learning models,

particularly LSTM models, to analyze and predict

time series data such as stock prices, weather data, etc.

This provides valuable insights and predictions for

decision-making in fields such as finance and

meteorology. he unique aspect of the paper could be

its focus on the influence of the number of hidden

units in LSTM models on the accuracy of stock price

predictions. This is a crucial aspect, as the number of

hidden units is a key hyperparameter that determines

the complexity and capacity of the model. Given the

intricate factors influencing stock prices, a more

complex model might be necessary to encapsulate

these variables. However, an overly complex model

might overfit the training data, leading to subpar

performance on unseen data. Conversely, a model

with an insufficient number of hidden units could

underfit the data, unable to capture the necessary

patterns for accurate prediction.

In this context, the authors' exploration of the

selection of an appropriate number of hidden units and

the impact of varying numbers of hidden units on

prediction accuracy could provide valuable insights.

This differentiates the paper from other research

papers that might not specifically investigate the

influence of the number of hidden units on prediction

accuracy or might not utilize LSTM models for stock

price prediction.

2 METHODOLOGY

2.1 Dataset Description and

Preprocessing

In this study, the author employs the AAPL database

collected from Yahoo Finance (Dataset 2023). The

AAPL database is a compilation of historical market

data for Apple Inc.'s shares. With data spanning from

2016 to 2023, this database offers a wide range of

financial indicators, including Apple's stock's trading

volume, lowest price, highest price, closing price, and

opening price. The following parameters are included

in the AAPL database: Date: The trading session's date.

The opening price, which is the value of the day's first

deal. High: The price attained during the trading

session. Low: The price attained during the trading

session. Close: The closing price, which is the price of

the day's final trade. Adj Close: The adjusted closing

price, which takes stock splits and dividends into

account. Volume: The total number of shares

exchanged during the trading session is referred to as

volume.

2.2 Proposed Approach

The major goal of this study is to analyze and

investigate the data within the AAPL database. By

utilizing LSTM models, the goal is to predict stock

market trends to a certain degree of accuracy.

Furthermore, through comparative analysis, the study

aims to enhance the LSTM model's performance by

adjusting crucial parameters like units. Specifically,

first, the ‘Sequential’ model is used to create an

instance of a sequential model so that the author can

add layers sequentially to build a complete neural

network model. Second, by adding an LSTM layer,

which has units of 125 to the sequential model, the

model is enabled by the author to recognize temporal

dependencies and patterns in the input data. LSTM

layers are particularly effective in capturing long-term

dependencies and are commonly used in time series

analysis and sequence prediction tasks. Third, the

author applies additional non-linear changes to the

input by introducing a fully connected layer to the

sequential model, allowing the model to learn more

complicated representations and patterns. Fully

connected layers are commonly used in neural

networks to perform tasks such as classification or

regression. Then, by compiling the model with the

optimizer and loss function, respectively using

Adaptive Moment Estimation (Adam) model and

Mean Square Error (MSE) lose function, the author

defines how the model will be trained and how the

model's performance will be evaluated. The optimizer

determines how the model's weights will be updated,

and the loss function quantifies the error between

those true values and predicted values, which the

optimizer will minimize during training. The author

last gives a summary function of the LSTM model,

including the layers, output shapes, and the number of

parameters in each layer.

2.2.1 LSTM

LSTM is an advanced type of Recurrent Neural

Network (RNN) that has garnered significant

attention in various fields, including the realm of

DAML 2023 - International Conference on Data Analysis and Machine Learning

412

stock market prediction (Vinyals et al 2015). What

sets LSTM apart is its unique capability to capture

and understand long-term dependencies and patterns

within sequential data. When it comes to predicting

stock market trends, LSTM demonstrates great

potential. It excels at analyzing historical stock prices,

trading volumes, and other pertinent factors over

time. By taking into account the sequential nature of

stock market data, LSTM can effectively uncover

intricate relationships and dependencies that may

exist, such as trends, seasonality, and irregular

patterns. The strength of LSTM lies in its ability to

learn from historical stock market data and utilize that

knowledge to make predictions based on the learned

patterns. This makes it well-suited for forecasting

future stock prices and market trends. By training the

LSTM model on a substantial dataset of historical

stock market information, it can potentially uncover

hidden patterns and trends that may elude human

analysts (Dataset 2023). Besides, LSTM models

possess the remarkable capability to adapt and update

their predictions as new data becomes available. This

flexibility allows them to continuously learn and

adjust their forecasts, making them highly suitable for

the dynamic and ever-changing nature of the stock

market (Karim et al 2017). Furthermore, LSTM

models have the ability to adapt to changing market

conditions. This is because of their inherent capability

to learn and forget information as required, enabling

them to dynamically adjust to new data and forget

irrelevant past data. This feature is especially

beneficial in the volatile and ever-changing landscape

of the stock market, where patterns and trends can

shift rapidly. Instead of relying solely on intuition or

traditional analysis methods, investors can leverage

the predictive power of LSTM models to analyze vast

amounts of historical stock data and identify potential

future trends. This empowers investors to make well-

informed investment decisions, potentially leading to

better investment outcomes. It can provide them a

competitive edge in the stock market by enabling

them to anticipate market movements and act

accordingly. Therefore, the use of LSTM models in

stock market prediction can revolutionize the way

investors strategize their investment plans, making

the process more efficient and effective. The process

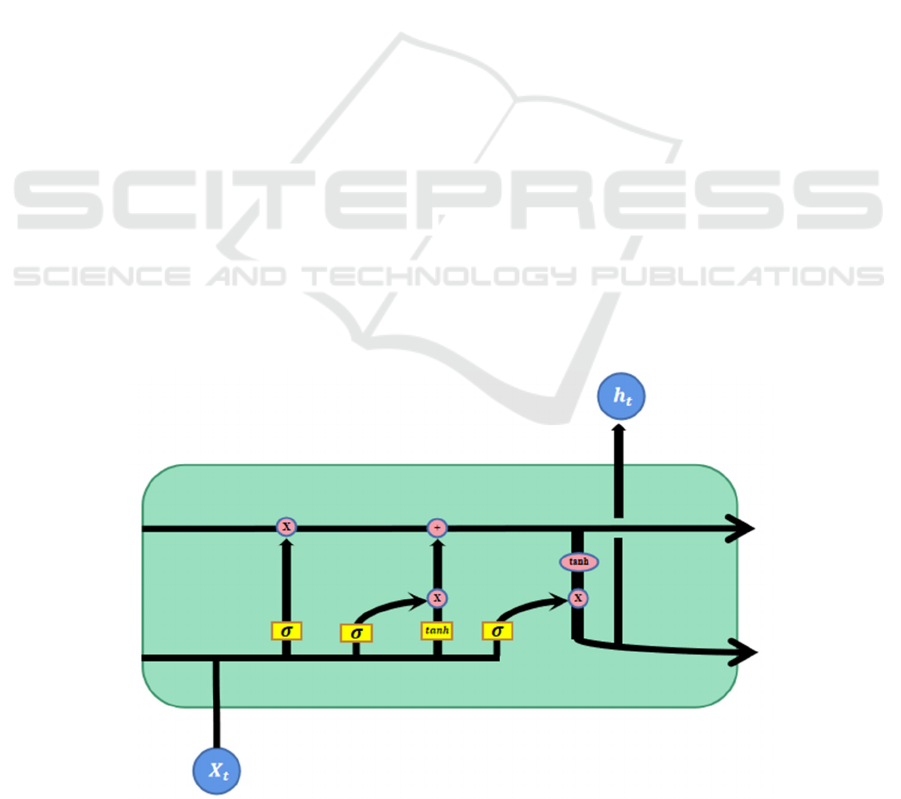
of LSTM is shown in the Fig. 1.

2.2.2 Hidden Units

The author's main goal in this study is to investigate

the effect of updating concealed units. The hidden

units in an LSTM model play a crucial role. They are

the LSTM's main components, assisting the model in

learning patterns and contextual information in input

sequences, allowing it to recall and anticipate long-

term dependencies. An LSTM's hidden units perform

two vital tasks. Long-term dependency memory:

LSTM stores and propagates information via memory

cells, while hidden units control the flow of

information to determine whether to recall or forget

specific information. This method enables LSTM to

manage long-term dependencies successfully, which

is critical for tasks like language modeling and

Figure 1: LSTM model (Picture credit: Original).

The Analysis of Hidden Units in LSTM Model for Accurate Stock Price Prediction

413

machine translation. Information flow control: The

hidden units in LSTM are outfitted with gate units

that manage the flow of information. Gate units are

classified into three types: input gates, output gates,

and forget gates. These gates mentioned above

determine whether or not to allow information to flow

based on the input and previous states, thus

controlling the update and output of the memory cells

(Karim et al 2017).

Changing the number of hidden units in an LSTM

model has an effect. By increasing the number of

hidden units, the model's capacity and learning ability

can be improved, allowing it to capture complicated

patterns and long-term connections. Increasing the

number of hidden units, on the other hand, increases

model complexity and computational costs, and may

result in overfitting (Hochreiter and Schmidhuber

1996). Reducing the amount of hidden units may

reduce the model's capacity and learning capabilities,

making complex patterns and long-term connections

impossible to capture. However, reducing the number

of hidden units can decrease model complexity and

computational costs, helping to avoid overfitting and

improving generalization. In this study, the author

gives a comparison of using 125 units and 60 units.

The selection of this number is based on past habits of

LSTM research, as well as a desire to study the impact

of approximately doubling the number of hidden units

on various parameters. This approach provides a

balance between maintaining computational

efficiency and exploring the effects of increased

model complexity on prediction accuracy. The result

of the comparison is shown in section 3.

2.2.3 Loss Function

This study uses MSE and its square root pattern Root

Mean Squared Error (RMSE) in this report. MSE is a

popular loss function used in machine learning to

evaluate how well a model is predicting continuous

values.It works well with LSTM models, especially

when used to analyze sequential data like time series

data or natural language. MSE is a good choice for

these models because it is continuous, differentiable,

robust to outliers, and has a statistical interpretation

that aligns with many real-world regression problems

(Kim et al 2018 & Le et al 2019). Here is the

algorithm of MSE, as follows:

𝑀𝑆𝐸 





∑

𝑌



 𝑌













(1)

where n represents the total number of the samples,

𝑌



represents the real value, and 𝑌





represents the

estimated value.

3 RESULTS AND DISCUSSION

After conducting an in-depth study and predictive

analysis, the author has obtained the predicted stock

prices for the period from 2021 to August 31, 2023,

based on the comprehensive AAPL database spanning

from 2016 to 2020. This study showcases the results

and fitting degree when using 125 units, followed by

a demonstration of the results when reducing the units

to 60. Finally, this study conducts a comparative

analysis of the two, providing insights into whether

more or fewer units are more suitable for stock price

prediction analysis. These results can help readers

gain a deeper understanding of the optimal number of

units for stock price prediction analysis.

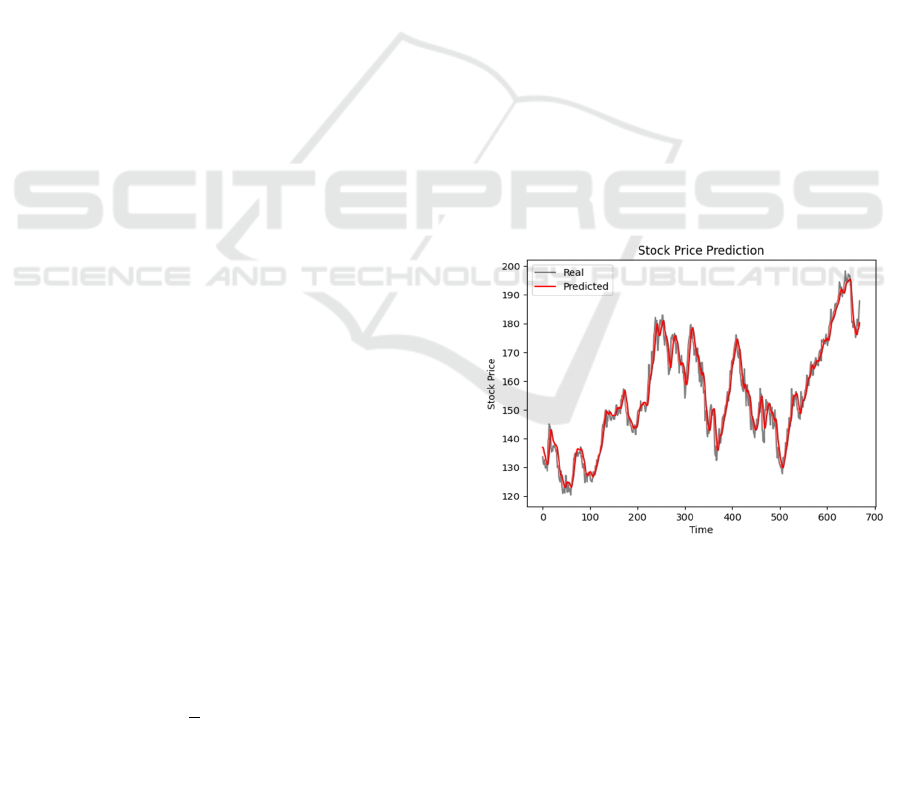
3.1 Results by Applying 125 Units

A relatively large number of hidden neurons can

increase the capacity and expressive power of the

model, enabling it to better capture complex patterns

and correlations in time series data. This can help

improve the accuracy and fitting degree of the

predictions, especially for complex stock price

prediction tasks. As shown in Fig. 2, it gives a result

which is highly similar to the real situation, with the

root mean squared error is 3.81. In this situation, the

total number of the parameter is 66,676.

Figure 2: The Prediction of Stock Price with hidden units of

125 (Picture credit: Original).

3.2 Results by Applying 60 Units

By turning the hidden units to 60, a relatively low

number, the author gets the following result shown in

Fig. 3. When the number of LSTM hidden neurons is

small, there are advantages such as high

computational efficiency and prevention of overfitting

(Hochreiter and Schmidhuber 1996). However, there

are disadvantages including information loss, limited

DAML 2023 - International Conference on Data Analysis and Machine Learning

414

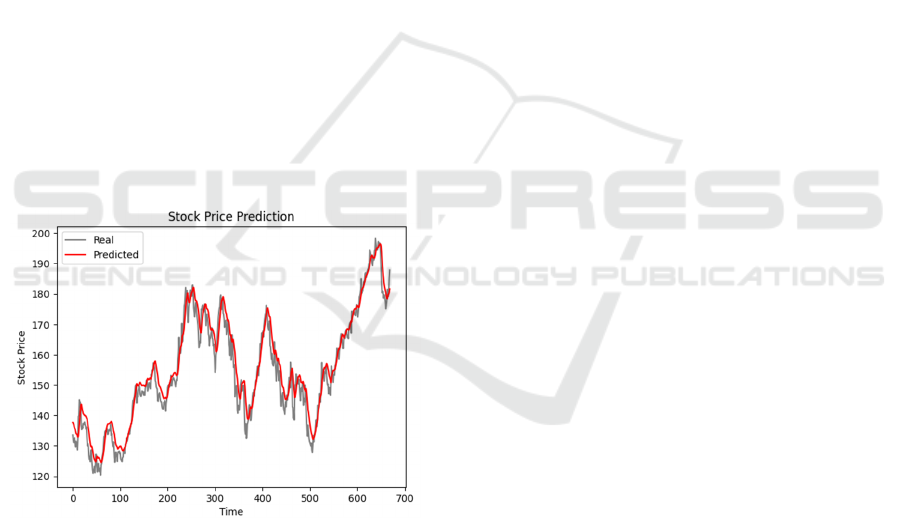
expression capacity, and decreased prediction

accuracy. Under this choice, the square root of mean

squared error is 4.20, and the total parameters are

16,431. This study finds that using a larger number of

hidden neurons compared to a smaller one leads to

more accurate stock price predictions, as reflected in a

small MSE value. his is at the expense of a substantial

increase in the total number of parameters, which goes

from 16,431 to 66,676, or more than four times the

initial figure. Additionally, training and learning time

also increase as a result. In the view of getting a better

estimation of stock market, more units might be better

due to the analysis above. The author compares

different results by applying different number of units.

And it comes to a summary that more units give better

prediction of certain stock markets. By varying the

number of hidden units, we can draw the conclusion

that the number of hidden units significantly

influences the total number of parameters, satisfying

an O(n^2) complexity. Simultaneously, it directly

alters the prediction results, thereby indicating that

this hyperparameter has a direct and significant impact

on the final stock price prediction to a certain extent.

In the real world, this finding has both practical and

learning implications, and it suggests that optimizing

the number of hidden neurons can lead to improved

performance in stock price prediction.

Figure 3: The Prediction of Stock Price with hidden units of

60 (Picture credit: Original).

4 CONCLUSION

This study emphasizes the significance of optimizing

the number of hidden neurons in LSTM models for

accurate stock price prediction. The findings

underscore the trade-off between model complexity

and computational efficiency, necessitating a careful

balance. While increasing the number of hidden

neurons improves prediction accuracy, it also leads to

longer training times and increased model complexity.

Nevertheless, this research offers valuable insights for

practitioners and researchers in the field, contributing

to the broader understanding of machine learning

applications in finance. Indeed, LSTM models have

shown great potential in stock price prediction, and

there may be even more untapped possibilities. By

further modifying and fine-tuning other parameters

and hyperparameters, it may be able to develop even

better prediction tools. The field of machine learning

is constantly evolving, and advancements in model

architecture, data preprocessing techniques, and

optimization algorithms can contribute to enhanced

performance. Therefore, continued research and

experimentation with LSTM models, along with other

deep learning techniques, hold promise for improving

the accuracy and reliability of stock price prediction.

In the context of stock price prediction, due to the

complexity of factors influencing stock prices, a more

complex model might be required to capture these

influences. However, a model that is too complex may

overfit the training data and perform poorly on unseen

data. Therefore, choosing an appropriate number of

hidden units is a crucial aspect.

The distinctiveness of the article lies in its focus on

the number of hidden units in LSTM models as an

independent research subject. This is unlike most

other studies on the use of LSTM for stock price

prediction or other forecasting tasks, where the

number of hidden units is usually not the main focus.

In this paper, the author delve into the impact of the

number of hidden units on the prediction accuracy,

underlining the significance of this parameter in

shaping the outcome of the forecast. By doing so, they

not only highlight the importance of carefully tuning

this parameter for stock price prediction but also

indicate its potential influence on other applications of

LSTM models. This research could provide a

benchmark for future studies in this direction,

emphasizing the need for a more nuanced

understanding and manipulation of the number of

hidden units in LSTM models. This unique focus sets

this paper apart from other research in the field.

Overall, this study serves as a reference for future

research and highlights the importance of considering

model capacity and computational resources in stock

price prediction.

REFERENCES

Sutskever, Ilya, O. Vinyals, V. Quoc, “Sequence to

sequence learning with neural networks,” Advances in

The Analysis of Hidden Units in LSTM Model for Accurate Stock Price Prediction

415

neural information processing systems, vol.2014, pp.

Vinyals, Oriol, et al, “Show and tell: A neural image caption

generator,” Proceedings of the IEEE conference on

computer vision and pattern recognition., vol. 2015, pp.

3156-3164

Hannun, Awni, et al, “Deep speech: Scaling up end-to-end

speech recognition,” arXiv, 2014, unpublished.

Gers, A. Felix, S. Jürgen, “Learning to forget: Continual

prediction with LSTM,” Neural computation, vol.

2000, pp. 2451-2471.

F. Rui, Z. Zhang, L. Li, “Using LSTM and GRU neural

network methods for traffic flow prediction,” 2016 31st

Youth academic annual conference of Chinese

association of Automation (YAC), 2016. pp. 324-328

Dataset, "Apple Inc. (AAPL)," Yahoo Finance, Last

accessed 24 August 2023, https://finance.yahoo.

com/quote/AAPL/history?p=AAPL

Karim, Fazle, et al, “LSTM fully convolutional networks

for time series classification,” IEEE access, vol. 6,

2017, pp. 1662-1669

Hochreiter, J. Schmidhuber, “LSTM can solve hard long

time lag problems,” Advances in neural information

processing systems, vol. 1996, pp. 9

Kim, H. Young, C. Won, “Forecasting the volatility of

stock price index: A hybrid model integrating LSTM

with multiple GARCH-type models,” Expert Systems

with Applications, vol. 103, 2018, pp. 25-37

X. Le, et al, “Application of long short-term memory

(LSTM) neural network for flood forecasting,” Water,

vol. 2019, pp. 1387

DAML 2023 - International Conference on Data Analysis and Machine Learning

416