A Comparison of Machine Learning Algorithms for National

Basketball Association (NBA) Most Valuable Player (MVP)

Vote Share Prediction

Zhicheng Cheng

College of Arts and Sciencs, Washington University in Saint Louis, Saint Louis, MO, U.S.A.

Keywords: Machine Learning Models, Regression Analysis, National Basketball Association, Most Valuable Player

Prediction, Sports Outcome Prediction.

Abstract: In an era of burgeoning sports betting, the quest to predict the Most Valuable Player (MVP) in a regular

National Basketball Association (NBA) season has become a novel way for people to be involved in the

world’s most popular basketball league. This paper adopts various Machine Learning Regression Models to

help predict the MVP win share of an arbitrary player in an arbitrary NBA season. More specifically, every

single NBA player’s statistics and MVP win share in the past 40 years are collected, preprocessed, and used

to train and test the machine learning models. After comparing each model’s R-squared value and MAPE, it

is concluded that the Extreme Gradient Boosting Regression Model is the best model in predicting the MVP

win share of an arbitrary player in an arbitrary season, with a R-squared value of 0.6399 and a MAPE of

22.90%. This means that 63.99% of the variation in the dependent variable (i.e., the actual MVP win share)

can be explained by the independent variables (the statistics), and that the prediction of the dependent variable

(i.e., the actual MVP win share) is only off by 22.90%.

1 INTRODUCTION

In the ever-evolving world of professional sports, few

spectacles can rival the frenzy that surrounds the

National Basketball Association (NBA). In recent

years, the best basketball league has catapulted itself

into the global spotlight, captivating the hearts and

minds of fans worldwide. As the league's popularity

continues to soar, an intriguing phenomenon has

emerged - the surge in betting activities that have

transformed the way people engage with the game

(Thabta et al 2019).

Each season, sports betting companies such as

BetMGM, Caesars Sportsbook, FanDuel, and

DraftKings, offer odds on various players’ likelihood

of winning the MVP title. Such behaviors have

tremendously raised spectators’ interest in predicting

the winner of the reward – as the prediction is no

longer confined to the casual conversation after family

dinner, but also a financial activity that can help them

earn windfalls.

In this research, different machine learning

algorithms are applied to a dataset that contains the

statistics and MVP win share of all the players in NBA

history. The most fitting model is then generated to

predict the MVP win share of an arbitrary player in an

arbitrary (including future) season, given that player’s

statistics such as points, rebounds, assists, etc.

Hopefully, this paper can bring new insights into

audiences’ prediction of MVP players under various

scenarios, especially betting.

2 BIBLIOGRAPHIC REVIEW

Many scholars have applied machine learning

algorithms to predict the MVP of the National

Basketball Association in various ways. In Dai et al.’s

research, different neural network models are trained

and tested on the dataset containing the NBA players’

performance from 1997 to 2016 and the winner of the

MVP award in each season. The model that has the

best performance successfully predicts the MVP

winner of the 2016-2017 season (Chen et al 2019).

Similarly, in Hu et al.’s publication, a BP neural

network model is trained on the dataset containing the

NBA players’ performance in the past ten years and

the winner of the MVP in each year. The final model

262

Cheng, Z.

A Comparison of Machine Learning Algorithms for National Basketball Association (NBA) Most Valuable Player (MVP) Vote Share Prediction.

DOI: 10.5220/0012800800003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 262-267

ISBN: 978-989-758-705-4

successfully predicts the MVP winner of the 2019-

2020 season, which is unknown at the time the paper

is published (Hu et al 2019). Chapman’s paper also

uses various machine learning models to predict the

MVP of the NBA regular season, and he finds that the

LightBGM Model paired with Overlapping

techniques produces the best training and testing

results, successfully predicting the MVP 80.65% of

the time (Chapman 2023). Li’s work uses four

machine learning models to predict the MVP of the

NBA regular season, and the model with the best

performance yields an accuracy of 67 percent (Li

2021). Chen’s investigation, on the other hand, uses

data mining to build different statistical models to

predict the 2017 NBA MVP (Chen 2017). Despite not

having a definite answer as the season has not ended

during his publication, his model concludes that team

record should be the dominant factor in deciding the

MVP. Last but not least, Jordan Malik’s study adopts

different machine learning models such as Artificial

Neural Networks, K-Nearest Neighbors, and Linear

Regression Models (LRM), as well as seven other

underlying models to predict the MVP of the NBA

regular season. Surprisingly, the combination of two

of the underlying models with an LRM framework

provides the most robust prediction and is thus

selected for future validation (McCorey 2021).

Past scholars have largely viewed the winning of

MVP as a discrete and binary variable - that is,

whether a player has won the MVP or not. Such

comprehension results in their usage of machine

learning models to classify all players into two

categories - one is winning and the other is not, and

the result they provide will be the player that falls into

the category of winning.

In this research, the MVP win share of an NBA

player is viewed as a continuous variable, with

regression models being used to predict the MVP win

share of an arbitrary player. In addition to predicting

who the MVP will be like the previous scholars do,

this research also provides information to audiences

on how likely an arbitrary player is going to win the

MVP.

3 METHODS

3.1 Data and Software Tool

In this research, the “1982 - 2022 NBA Player

Statistics with MVP Votes” dataset (later referred to

as the Dataset) is collected from the Kaggle Open

Datasets, which is published by Robert Sunderhaft

and originated from the Basketball Reference Website

(Robert 2023). The Dataset contains 17,698 entries,

with the same players playing in multiple seasons

being considered multiple times (for instance, a player

playing in both 21-22 season and 22-23 season

appears twice in the Dataset). Each entry in the

Dataset is accompanied by 55 attributes. Among them,

the award_share (MVP Voting Win Share

Percentage) is recognized as the dependent or

response variable, the season and the name are

disregarded as they are irrelevant to the prediction of

an arbitrary player’s MVP win share in future seasons,

and the rest 52 attributes are recognized as the

explanatory variables or features.

In this research, machine learning algorithms are

the primary tools used to predict the MVP win share

of an arbitrary player in future seasons, and all the data

pre-processing, machine learning algorithms, and

analysis of prediction results are implemented with

Python programming language in Jupyer Notebook.

3.2 Data Preprocessing

Preprocessing helps clean, transform, and integrate

data. These processes not only simplify the

construction of machine learning models but also

contribute to the attainment of heightened model

accuracy. The preprocessing techniques used in this

research include filling missing values, hot encoding

categorical variables, feature selection, and data

normalization.

Missing entries are first identified using Jupyter

Notebook and Python. Notice that all the attributes

that contain empty entries are of the type of

percentage. It is observed that the primary reason for

these empty percentages is that the divisor, or the total,

for calculating the percentage is 0 (for instance, the

three-point shot percentage becomes empty if a player

does not make any three-point shot). 0 is thus used to

replace these empty entries.

It is obvious that the two categorical variables in

the remaining Dataset are team_id and pos. On one

hand, each player’s team_id is the first three letters of

the team he has played for, and if a player has played

in multiple teams in one season, his team_id is valued

as “TOT”. In order to take this categorical variable

into account for the construction of a machine

learning, and thus mathematical, model, each new

string value for team_id is indexed along the column

(for instance, LAL is indexed with 1 and PHO is

indexed with 2 as they are the first two entries of the

column, and if another LAL appears, the index 1 is

given again). Similarly, each new string value for pos

on the court is also indexed along the column.

A Comparison of Machine Learning Algorithms for National Basketball Association (NBA) Most Valuable Player (MVP) Vote Share

Prediction

263

Excluding the irrelevant features season and name

and the hot-encoded features team_id and pos,

Pearson’s Correlation Method is used to identify the

other irrelevant features, and the method is

implemented with Jupyter Notebook and Python.

Pearson’s Correlation Method denotes that all

correlation coefficients between the explanatory and

response variables are in the range of -1 and 1, with a

value between -0.5 and 0.5 indicating an insignificant

correlation, and a value below -0.5 or above 0.5

indicating a notable correlation (Robert 2023). In this

research, 0.1 and -0.1 are used as the cut-offs for

dropping the irrelevant explanatory variable.

Feature Scaling is finally performed by

normalizing the remaining data to the range between

0 and 1, which essentially boosts the algorithms’

runtime.

3.3 Training and Testing Method for

the Dataset

After preprocessing, the Dataset is ready for the

machine learning algorithm to be trained and tested.

In this research, the 70% Train-test Splitting Method

is used to randomly split the 17,698 entries into a train

set with precisely 12,388 entries, and a test set with

precisely 5,310 entries. The train set is then used for

constructing the various machine learning algorithms,

and the test set is used for measuring the performance

of each of the algorithms.

3.4 Design of Regression Model

Comprehensive machine learning regression

techniques are applied to the Dataset, including Linear

Regression, Polynomial Regression (PR), Random

Forest Regression (RFR), Gradient Boosting

Regression (GBR), Extreme Gradient Boosting

(XGBoost), and Neural Network Regression (NNR).

In this research, three neural network models with

varying hidden layers are built to predict the MVP win

share of an arbitrary player in future seasons. More

specifically, the hidden layer of the neural network

models varies from 1, 2, to 3, and each model is

trained with 200, 400, and 800 epochs. Each of the

models also uses Rectified Linear Activation Function

(RELU) and linear function as the activation

functions, and Stochastic Gradient Descent (SGD) as

the optimizer. The details of each of the models are

explained in Table 1.

3.5 Measurement of Performance

After each of the machine learning regression models

is constructed based on the train set, the model

predicts the MVP win share of each of the players in

the test set, and the prediction is compared with the

actual value in the Dataset. Two parameters are then

used to measure how accurate each model predicts: the

Mean Absolute Percentage Error (MAPE) and the R-

squared value. More specifically, MAPE is calculated

by the formula 1

𝑀𝐴𝑃𝐸 =





∑



    

 

 (1)

where n represents the total number of entries in the

test set, and R-squared value is calculated by the

formula 2

𝑅



=1−

∑

(  )



∑

(      )



(2)

4 RESULT AND DISCUSSION

4.1 Results

The R-squared value of the Linear Regression Model

is 0.2898, and the MAPE is 0.6612. The R-squared

value of the Polynomial Regression Model is 0.5209,

and the MAPE is 56.21%.

Table 1: Neural Network Regression Model Parameters.

Number of hidden layers 1 2 3

Number of neurons in input layer 53 53 53

Number of neurons in each hidden layer 64 128, 64 256, 128, 64

Hidden layer activation function RELU RELU RELU

Output layer activation function Linear Linear Linear

Lost function SGD SGD SGD

Number of epochs 200, 400, 800 200, 400, 800 200, 400, 800

DAML 2023 - International Conference on Data Analysis and Machine Learning

264

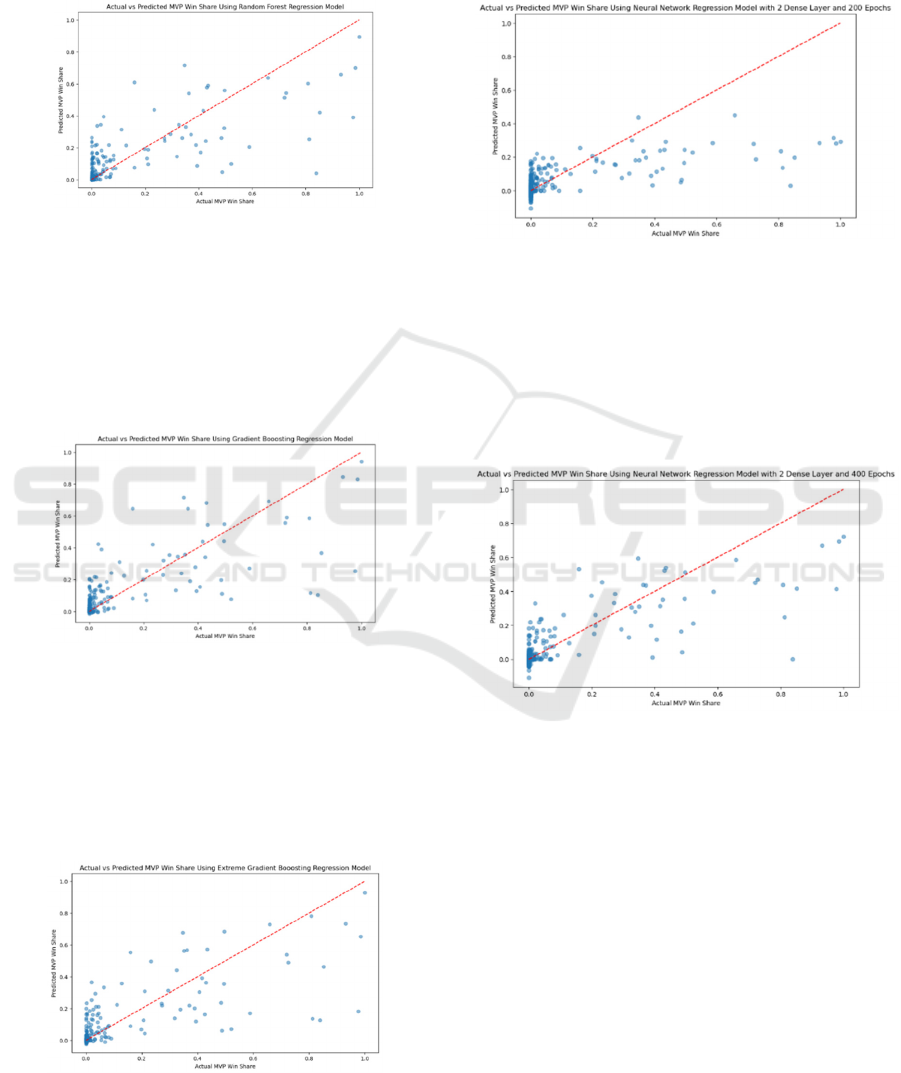
The R-squared value of the Random Forest

Regression Model is 0.6527, and the MAPE is

29.32%. The graph of predicted MVP win share vs.

actual MVP win share for the test set is presented in

Figure 1.

Figure 1: Actual vs. Predicted MVP Win Share Using

Random Forest Regression Model (Picture Credit:

Original).

The R-squared value of the Gradient Boosting

Regression Model is 0.6525, and the MAPE is

36.09%. The graph of predicted MVP win share vs.

actual MVP win share for the test set is presented in

Figure 2.

Figure 2: Actual vs. Predicted MVP Win Share Using

Gradient Boosting Regression Model (Picture Credit:

Original).

The R-squared value of the Extreme Gradient

Boosting Regression Model is 0.6399, and the MAPE

is 22.90%. The graph of predicted MVP win share vs.

actual MVP win share for the test set is presented in

Figure 3.

Figure 3: Actual vs. Predicted MVP Win Share Using

Extreme Gradient Boosting Model (Picture Credit: Original).

The R-squared value of the Neural Network

Regression Model with 2 Dense Layers and 200

Epochs is 0.4584, and the MAPE is 15.38%. The

graph of predicted MVP win share vs. actual MVP

win share for the test set is presented in Fig. 4.

Figure 4: Actual vs. Predicted MVP Win Share Using

Neural Network Regression Model with 2 dense layer and

200 epochs (Picture Credit: Original).

The R-squared value of the Neural Network

Regression Model with 2 Dense Layers and 400

Epochs is 0.6776, and the MAPE is 86.61%. %. The

graph of predicted MVP win share vs. actual MVP

win share for the test set is presented in Fig. 5.

Figure 5: Actual vs. Predicted MVP Win Share Using

Neural Network Regression Model with 2 dense layer and

400 epochs (Picture Credit: Original).

The R-squared value of the Neural Network

Regression Model with 2 Dense Layers and 800

Epochs is 0.2845, and the MAPE is 63.01%. The R-

squared value of the Neural Network Regression

Model with 3 Dense Layers and 200 Epochs is

0.5973, and the MAPE is 37.36%. The R-squared

value of the Neural Network Regression Model with

3 Dense Layers and 400 Epochs is 0.5987, and the

MAPE is 42.40%. The R-squared value of the Neural

Network Regression Model with 3 Dense Layers and

800 Epochs is 0.5774, and the MAPE is 60.16%. The

R-squared value of the Neural Network Regression

Model with 3 Dense Layers and 200 Epochs is

A Comparison of Machine Learning Algorithms for National Basketball Association (NBA) Most Valuable Player (MVP) Vote Share

Prediction

265

0.5787, and the MAPE is 42.85%. The R-squared

value of the Neural Network Regression Model with

3 Dense Layers and 400 Epochs is 0.5995, and the

MAPE is 95.24%. The R-squared value of the Neural

Network Regression Model with 3 Dense Layers and

800 Epochs is 0.5461, and the MAPE is 111.81%.

4.2 Discussion

It is observed that the Neural Network Regression

Model with 2 Dense Layers and 400 Epochs yields

the highest R-squared value of 0.6776, meaning that

67.76% of the variance in the dependent variable (i.e.,

the actual MVP win share) can be explained by the

independent variables. Such a high R-squared value

indicates that the model is a good fit for the Dataset.

However, the model also yields a MAPE of 86.61%,

meaning that the prediction of the dependent variable

(i.e., the actual MVP win share) is off by 86.61%.

Such a high MAPE also indicates that the prediction

result is far from being accurate (Akoglu 2018). One

typical reason for the simultaneous high R-squared

value and MAPE is that the model is overfitting,

meaning that the model fits the training data

exceptionally well but cannot be generalized to new,

unseen data (Dietterich 1995).

Similarly, the Neural Network Regression Model

with 2 Dense Layers and 200 Epochs yields the

lowest MAPE of 15.38%, meaning that the prediction

of the dependent variable (i.e., the actual MVP win

share) is only off by 15.38 %. Such a low MAPE

indicates that the prediction result is accurate.

However, the model yields an R-squared value of

0.4584, meaning that only 45.84% of the variance in

the dependent variable (i.e., the actual MVP win

share) can be explained by the independent variables.

Such an R-squared value also indicates that the model

is just a passable fit for the Dataset.

Therefore, upon providing the model with both a

good R-square value and a good MAPE, the Extreme

Gradient Boosting Regression Model is selected to be

the best model in predicting the MVP win share of an

arbitrary player in an arbitrary season. The R-squared

value of the Extreme Gradient Boosting Regression

Model is 0.6399, meaning that 63.99% of the variance

in the dependent variable (i.e., the actual MVP win

share) can be explained by the independent variables.

The model also yields a MAPE of 22.90%, meaning

that the prediction of the dependent variable (i.e., the

actual MVP win share) is only off by 22.90%.

5 CONCLUSION

In order to help audiences do a better job in predicting

the NBA regular season MVP under different

scenarios, this research applies different Machine

Learning Regression Models to predict the MVP win

share of an arbitrary player in an arbitrary NBA

season. More specifically, every single NBA player’s

statistics and MVP win share in the past 40 years are

collected, preprocessed, and used to train and test the

machine learning models. After comparing each

model’s R-squared value and MAPE, it is concluded

that the Extreme Gradient Boosting Regression

Model is the best model in predicting the MVP win

share of an arbitrary player in an arbitrary season,

with a R-squared value of 0.6399 and a MAPE of

22.90%.

While this research can certainly provide useful

information for future prediction of MVP, the final

result is not optimized due to the limited capability of

the facilities (i.e., computers). For instance, the tuning

of the hyperparameters of the neural network models

is not optimized, as only a few numbers of epochs and

dense layers are being tested. In future research

endeavors, it is conceivable to expand upon existing

machine learning models by incrementing the

hyperparameters such as the number of epochs and

dense layers. Researchers can also graph the

performance of these models with various

hyperparameters, thereby discovering the trends in

different models’ performance. It then becomes

feasible to pinpoint the optimal configuration that

maximizes the model's performance.

REFERENCES

F. Thabta, L.Zhang, N. Abdelhami., “NBA Game Result

Prediction Using Feature Analysis and Machine

Learning”, Annals of Data Science, vol. 6, no. 1, pp.

103-116, 2019.

Y. Chen, J. Dai, and C. Zhang, “A Neural Network Model

of the NBA Most Valued Player Selection Prediction”,

In Proceedings of the 2019 the International Conference

on Pattern Recognition and Artificial Intelligence

(PRAI '19), Association for Computing Machinery,

New York, NY, USA, pp. 16–20, 2019

J. Hu, H. Zhang, and J. Qiu, “Prediction of MVP Attribution

in NBA Regular Match Based on BP Neural Network

Model”, In Proceedings of the 2019 International

Conference on Artificial Intelligence and Advanced

Manufacturing (AIAM 2019), Article 43, pp. 1–5, 2019

A. L. Chapman, “The Application of Machine Learning to

Predict the NBA Regular Season MVP”, Doctoral

Dissertation, Utica University, 2023.

DAML 2023 - International Conference on Data Analysis and Machine Learning

266

X. Li, “National Basketball Association Most Valuable

Player prediction based on machine learning methods”,

Second IYSF Academic Symposium on Artificial

Intelligence and Computer Engineering. Vol. 12079.

SPIE, 2021.

M. Chen, “Predict NBA Regular Season MVP

Winner”, IEOM South American Conference

Proceedings. 2017.

J. McCorey, “Forecasting Most Valuable Players of the

National Basketball Association”, Doctoral

Dissertation. The University of North Carolina at

Charlotte, 2021.

S. Robert. "NBA Player Season Statistics with MVP Win

Share." Kaggle, Year of dataset publication,

https://www.kaggle.com/datasets/robertsunderhaft/nba

-player-season-statistics-with-mvp-win-share.

Accessed: Sept. 13, 2023. [Online]

H. Akoglu, “User's guide to correlation

coefficients”, Turkish journal of emergency

medicine vol. 18, no. 3, pp. 91-93, 2018

T. Dietterich, “Overfitting and undercomputing in machine

learning”, ACM computing surveys (CSUR) vol. 27 no.

3, pp. 326-327, 1995

A Comparison of Machine Learning Algorithms for National Basketball Association (NBA) Most Valuable Player (MVP) Vote Share

Prediction

267