Clinical Record Analysis of Heart Failure Identification of Key

Features and Disease Prediction

Xiaoqing Yao

Department of Statistics, University of Illinois Urbana-Champaign, Champaign, U.S.A.

Keywords: Heart Failure, Identification of Features, Disease Prediction, Machine Learning.

Abstract: In contemporary society, disease prediction has become an important healthcare domain. Various advanced

techniques have been utilized to enhance the accuracy and efficiency of disease prediction. This paper

employs machine learning techniques, specifically logistic regression and random forest models, to predict

mortality rates associated with heart failure using a clinical dataset. The findings highlight the importance of

key physiological measures in predicting outcomes, including age, ejection fraction, serum creatinine, serum

sodium, and time. Both models showed highly accurate predictive power, with logistic regression slightly

better than random forest on the Area Under the Curve (AUC) indicator. The study contributes to the existing

literature on heart failure risk prediction and underscores the transformative potential of machine learning for

improving patient outcomes via precise risk stratification and early intervention. This study plays an essential

role in understanding how machine learning technology can be used to investigate the key features and disease

prediction of heat failure based on the previous clinical record.

1 INTRODUCTION

The burgeoning prevalence of heart failure as a severe

cardiovascular disease has compelled healthcare

professionals to seek more accurate methods for

patient prognosis. In the United States, about 6.5

million people aged over 20 years have heart failure,

which accounts for around 8.5% of heart disease

deaths (Heart Failure Society of America).

Undeniably, focusing on the study of heart failure is

critical for devising personalized and effective

treatments. Fortunately, notable strides have been

made in this regard, particularly through the

integration of machine learning algorithms for

predictive modeling.

In recent years, machine learning has been widely

used in various areas regarding heart failure issues;

research to date has identified key variables

influencing heart failure outcomes. For instance,

Chicco and Jurman applied machine learning

techniques to pinpoint serum creatinine and ejection

fraction as vital risk factors, demonstrating that

focusing on these alone could enhance predictive

accuracy (Chicco and Jurman 2020). Meanwhile,

Wittenbecher et al. identified specific lipid

metabolites as potential biomarkers for heart failure

risk in a lipidomics study (Wittenbecher et al 2020).

Furthermore, machine learning algorithms, such as

those employed by Li et al., have been instrumental

in predicting mortality rates in ICU-admitted patients

with heart failure, using advanced techniques like

XGBoost and LASSO regression for feature selection

(Li et al 2021). Goals et al. developed a Deep Unified

Network (DUNs) -based machine learning model that

uses longitudinal electronic medical record data to

predict readmission risk in patients with heart failure

within 30 days of discharge (Golas et al 2018). By

using percussion techniques and effective data

mining techniques, Ishaq et al. successfully improved

the accuracy of predicting the survival of patients

with heart failure. Among many models, they found

that the Extra Tree Classifier (ETC) model excelled

at predicting survival of heart disease patients with an

astonishing accuracy of 0.92622 (Ishaq et al 2021).

Nagavelli, Samanta, and Chakraborty explore a

machine learn-based heart disease detection model,

using XGBoost to test different decision tree

classification algorithms aimed at improving the

accuracy of heart disease diagnosis and identifying

risk factors strongly associated with heart failure

(Nagavelli et al 2022). In addition, Rao et al.

developed an interpretable Transformer-based deep

learning model that uses electronic health records to

predict the onset of heart failure within 6 months,

Yao, X.

Clinical Record Analysis of Heart Failure Identiﬁcation of Key Features and Disease Prediction.

DOI: 10.5220/0012803900003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 297-304

ISBN: 978-989-758-705-4

297

revealing known and new heart failure risk factors

(Rao et al 2021). Clearly, professionals have noticed

the great function of machine learning and made

breakthroughs through its application in medical

analysis related to heart failure.

Several machine learning models, such as

Random Forest and Logistic Regression, have

demonstrated their efficacy across domains. For

example, Ishaq et al. utilized Random Forest along

with Synthetic Minority Over-sampling Technique

(SMOTE) to achieve high predictive accuracy (Ishaq

et al 2021), while Karthikeyan et al. and Joo et al.

successfully applied machine learning to COVID-19

mortality and cardiovascular disease prediction,

respectively (Karthikeyan et al 2020 & Joo et al

2020). Those indicate that machine learning could be

an effective approach to recognizing and predicting

medical symptoms and features.

Given the complexity of heart failure as a medical

condition and the promise of machine learning

algorithms in clinical prediction, our study aims to

contribute by developing a comprehensive predictive

model using 12 key clinical features. This approach is

intended to advance the current understanding and to

provide a more robust tool for clinical applications in

heart failure management.

The structure of this study is as follows: Chapter

2 delves into the meticulous selection and preparation

of clinical features for the predictive model through

data analysis. Chapter 3 presents our predictive

outcomes regarding the occurrence of heart failure

based on Logistic Regression and Random Forest

models. Finally, this paper will conclude and discuss

the study’s findings, implications, limitations, and

avenues for future research. Through this research

framework, this paper aims to fortify the arsenal of

predictive tools available for assessing the risk and

management of heart failure mortality.

2 ANALYSIS OF FACTORS

INFLUENCING HEART

FAILURE INCIDENCE

2.1 Data

This paper sourced patient medical records from the

UCI Machine Learning Repository to investigate the

key determinants of heart failure. Specifically, the

dataset encompasses the medical histories of 299

patients diagnosed with heart failure and is structured

to include 12 predictive variables along with a single

target variable labeled as DEATH EVENT. Each

record is thus a compilation of 13 distinct clinical

features. A detailed description of the variables can be

found in Table 1.

For a nuanced analysis, this study adopted

different statistical approaches for categorical and

continuous variables. For the categorical variables,

this paper focused on frequency distribution, detailing

the count and percentage of patients falling into each

category. That offers insights into the prevalence of

specific conditions, such as anemia or diabetes, among

the patient cohort.

As shown in Figure 1 and Figure 2, the cohort

manifests a blend of demographics and medical

conditions. Approximately 57% of the patients do not

exhibit anemia, while around 58% are free from

diabetes. High blood pressure is absent in about 65%

of the patients. The gender distribution leans toward

males, constituting approximately 65% of the dataset.

Non-smokers make up around 68% of the cohort.

As shown in Table 2, patients' ages range from 40

to 95 years, with an average age of about 61 years.

Creatinine Phosphokinase (CPK) levels vary widely

from 23 to 7861 mcg/L, with an average level close

to 582 mcg/L. The Ejection Fraction averages

Table 1: Variables Table.

Variable Name

Role

Description

Units

age

Feature

age of the patient

years

anaemia

Feature

decrease of red blood cells or hemoglobin

creatinine_phosphokinase

Feature

level of the CPK enzyme in the blood

mcg/L

diabetes

Feature

if the patient has diabetes

ejection_fraction

Feature

percentage of blood leaving the heart at

each contraction

high_blood_pressure

Feature

if the patient has hypertension

platelets

Feature

platelets in the blood

kiloplatelets/mL

serum_creatinine

Feature

level of serum creatinine in the blood

mg/dL

serum_sodium

Feature

level of serum sodium in the blood

mEq/L

sex

Feature

woman or man

smoking

Feature

if the patient smokes or not

time

Feature

follow-up period

days

death_event

Target

if the patient died during the follow-up

period

DAML 2023 - International Conference on Data Analysis and Machine Learning

298

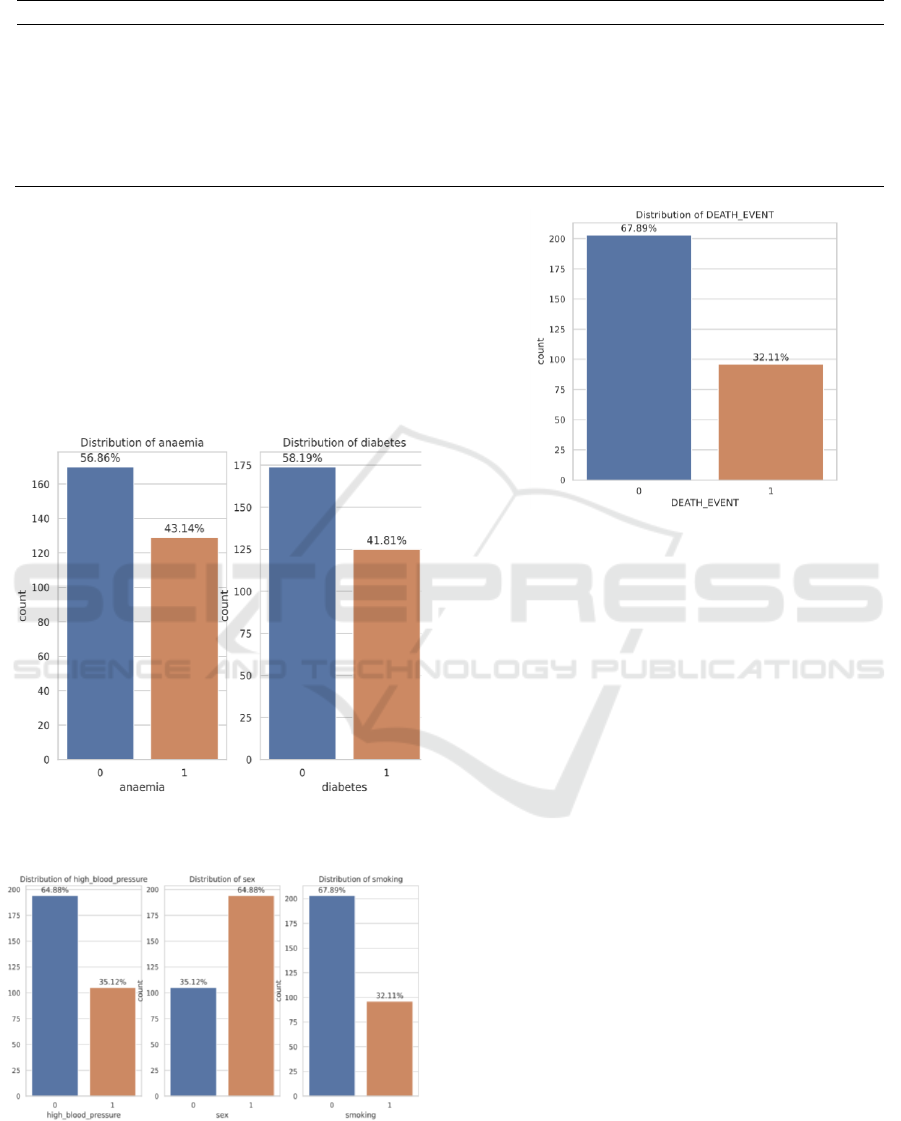
Table 2: Overview of Continuous Predictors.

Variable

Mean

Std Deviation

Min

Max

age

60.83

11.87

creatinine phosphokinase

581.84

968.66

116.5

582

7861

ejection fraction

38.08

11.82

platelets

263358

97640.55

25100

212500

303500

850000

serum creatinine

1.39

1.03

0.5

0.9

1.4

9.4

serum sodium

136.63

4.405

113

134

140

148

time

130.26

77.48

203

285

approximately 38%, ranging between 14% and 80%.

Platelet counts range from 25,100 to 850,000 kilo/mL,

with a mean of around 263,358 kilo/mL. Serum

creatinine and sodium levels display averages of

approximately 1.39 mg/dL and 137 mEq/L,

respectively. The follow-up period varies substantially

among the patients, averaging about 130 days. Most

notably, about 68% of the patients survived the

follow-up period, while approximately 32% did not.

Figure 1: Distribution of anaemia & Diabetes (Picture credit:

Original).

Figure 2: Distribution of high pressure & sex & smoking

(Picture credit: Original).

Figure 3: Frequency Distribution of Target Variables

(Picture credit: Original).

As can be seen from Figure 3, 32.11% of patients

died during the follow-up period, 67.89% of patients

did not die, and the ratio of deaths to non-deaths was

about 3:7. Therefore, this data is not an unbalanced

data set, and there is no need to balance the data.

Finally, the data has no missing values after

examination, so the analysis can continue.

2.2 Methodology and Model

Establishment

At present, there are 12 feature variables in this paper.

Considering that not all features extracted can play a

role in the final classification effect, and too many

redundant features will increase the training time of

the model, this paper will carry out feature selection

next. On the one hand, it is beneficial to improve the

accuracy of the classification algorithm. On the other

hand, it is also of great significance to explore the key

factors causing death by heart failure.

Binary variables: For the screening of Binary

variables, consider using information value (IV value)

to observe the strength of the correlation between the

feature variable and the target variable. It is generally

believed that when the IV value is greater than 0.02, it

is considered that there is a strong correlation between

the feature variable and the target variable. At the

Clinical Record Analysis of Heart Failure Identiﬁcation of Key Features and Disease Prediction

299

same time, in order to synthesize the results of

comparison, statistical inference is often used. To test

the Chi-square test of the independence of two

categorical variables, taking "anaemia" as an example,

the following hypothesis is established:

H_0: anaemia is independent of whether the

patient is death from heart failure

H_1: anaemia is not independent of whether the

patient is death from heart failure

Given the corresponding significance level α=

0.05, the chi-square value of the χ^2 test and the

corresponding P-value under the corresponding

significance level are observed, and the conclusion of

rejecting or retaining the original hypothesis H_0 is

given, and then the relationship between the two

qualitative variables is judged.

Continuous Variables: To accurately screen the

core quantitative variables that cause heart rate death,

this paper combined the advantages of different

feature selection methods and selected three methods,

point binomial correlation coefficient, generalized

cross-validation, and Boruta method based on random

forest, respectively, to screen quantitative variables

such as age. When variables are selected by two or

more methods, the selection variable is regarded as an

input quantitative variable.

In heart failure dataset, the Point-Biserial

Correlation Coefficient can be employed to assess the

relationship between binomial predictors like

'anaemia' or 'smoking' and continuous outcomes such

as 'age' or 'ejection fraction.' That specialized Pearson

correlation offers insights into how these different

types of variables interact. Then, subset selection will

be performed, and these subsets will be evaluated

using generalized cross-validation (GCV).

Specifically, this paper will traverse all possible

subsets of features, using a ridge regression model for

each subset and calculating its corresponding GCV

value. The number of feature subsets is 2^7=128

possible subsets. Furthermore, the Boruta algorithm

can be utilized to rigorously evaluate the importance

of each feature, including both continuous and

categorical variables, by comparing them with

randomly generated "shadow" features, enhancing the

robustness of our feature selection.

2.3 Analysis of Results

The feature selection process was conducted using

multiple methodologies to ensure robustness and

validity. As shown in Table 3, for continuous

variables, the Point-Biserial Correlation Coefficient,

Generalized Cross-Validation (GCV), and the Boruta

method based on Random Forest were employed. All

these methods consistently highlighted the importance

of age, ejection fraction, serum creatinine, serum

sodium, and time as significant predictors for the

occurrence of a death event. These features were

selected by at least two of the three methods used,

substantiating their relevance in the predictive model.

As shown in Table 4, for the categorical variables,

Chi-square tests and Information Value (IV) were

used for feature selection. The Chi-square tests did not

Table 3: Selection of Quantitative Variables.

Point Biserial

GCV

Boruta

Number of Methods

Final Selected

age

TRUE

FALSE

TRUE

creatinine phosphokinase

FALSE

ejection fraction

TRUE

FALSE

TRUE

platelets

FALSE

serum creatinine

TRUE

FALSE

TRUE

serum sodium

TRUE

FALSE

TRUE

time

TRUE

FALSE

TRUE

Table 4: Selection of Binary Variables.

Chi-square

(p-value < 0.05)

IV (IV >= 0.02)

Num Methods

Final Selected

anaemia

FALSE

TRUE

FALSE

diabetes

FALSE

High blood pressure

FALSE

TRUE

FALSE

sex

FALSE

smoking

FALSE

DAML 2023 - International Conference on Data Analysis and Machine Learning

300

find any of the categorical variables to be significantly

associated with the death event. Similarly, the

Information Value (IV) analysis identified all the

categorical variables (anaemia, diabetes, high blood

pressure, sex, and smoking) as weak predictors, with

IV values less than 0.02, except for anaemia and high

blood pressure. Based on these analyses, it can be

concluded that the categorical variables are relatively

weak predictors for the occurrence of a death event

compared to the selected continuous variables.

Based on the comprehensive analysis, the final set

of variables chosen for modeling includes the

following continuous variables: age, ejection fraction,

serum creatinine, serum sodium, and time. No

categorical variable was strong enough to be included

in the final model.

3 PREDICTION OF HEART

FAILURE INCIDENCE

3.1 Methodology and Model

Establishment

In the current study focused on predicting heart failure-

related death events, this paper employed two distinct

machine learning models—Logistic Regression and

Random Forest—to assess the predictability of

selected clinical features.

The Logistic Regression model was trained using

the default optimization algorithm and employed for

predicting the test set. Its key advantages lie in model

interpretability and computational efficiency. This

paper evaluated the model's performance using various

metrics, including accuracy, F1 score, precision, recall,

and AUC.

On the other hand, the Random Forest model is

more complex, involving an ensemble of multiple

decision trees. Through the use of grid search and 10-

fold cross-validation, this paper identified the optimal

combination of hyperparameters to achieve the best

predictive performance. The Random Forest model not

only allowed to capture potential nonlinear patterns in

the data but also provides additional insight into feature

importance, help people understand which variables

play a crucial role in predicting heart failure-related

death events.

The Logistic Regression model served as a

straightforward yet robust baseline for our predictions.

However, in order to capture potential nonlinear

relationships and interactions among the features, this

paper also employed a Random Forest model. The

Random Forest model underwent hyperparameter

tuning using grid search with 10-fold cross-validation

to identify the optimal parameter settings. The model

that demonstrated the best performance had

n_estimators=100, max depth=10, min samples

split=5, and min samples_leaf=1. These

hyperparameters indicate the complexity and depth of

decision trees within the Random Forest, tailored to

our specific dataset.

3.2 Analysis of Results

Both Logistic Regression and Random Forest models

were used to predict heart failure-related deaths. As

shown in Table 5, The logistic regression model, as a

linear algorithm, shows quite reasonable predictive

performance, especially in terms of Accuracy (78.3%)

and AUC (0.746).

On the other hand, the random forest model, as an

ensemble learning method, is inferior to the logistic

regression model in many aspects. In particular,

Random Forest fared slightly worse in terms of AUC

(0.703) and Accuracy (73.3%). However, it is

important to note that both models performed equally

in terms of Recall (0.52), meaning that the two models

were similar in their ability to identify positive (death

from heart failure).

As shown in Figure 4 and Figure 5, these

performance indicators further emphasize the

effectiveness of the feature set selected through

rigorous statistical testing (which mainly includes

continuous variables like age, ejection fraction, serum

sodium, serum creatinine and time). In both models,

none of the categorical variables behaved strongly

enough to be included in the final model. This

observation underscores the importance of these

physiological parameters in predicting mortality

associated with heart failure. As a result, this analysis

provides healthcare professionals with valuable

insights to identify key clinical features that

significantly impact patient outcomes.

Table 5: Metrics of Test Data.

Model

Accuracy

F1 Score

Precision

Recall

AUC

Logistic Regression

0.7833

0.666667

0.928571

0.52

0.745714

Random Forest

0.7333

0.619048

0.764706

0.52

0.702857

Clinical Record Analysis of Heart Failure Identiﬁcation of Key Features and Disease Prediction

301

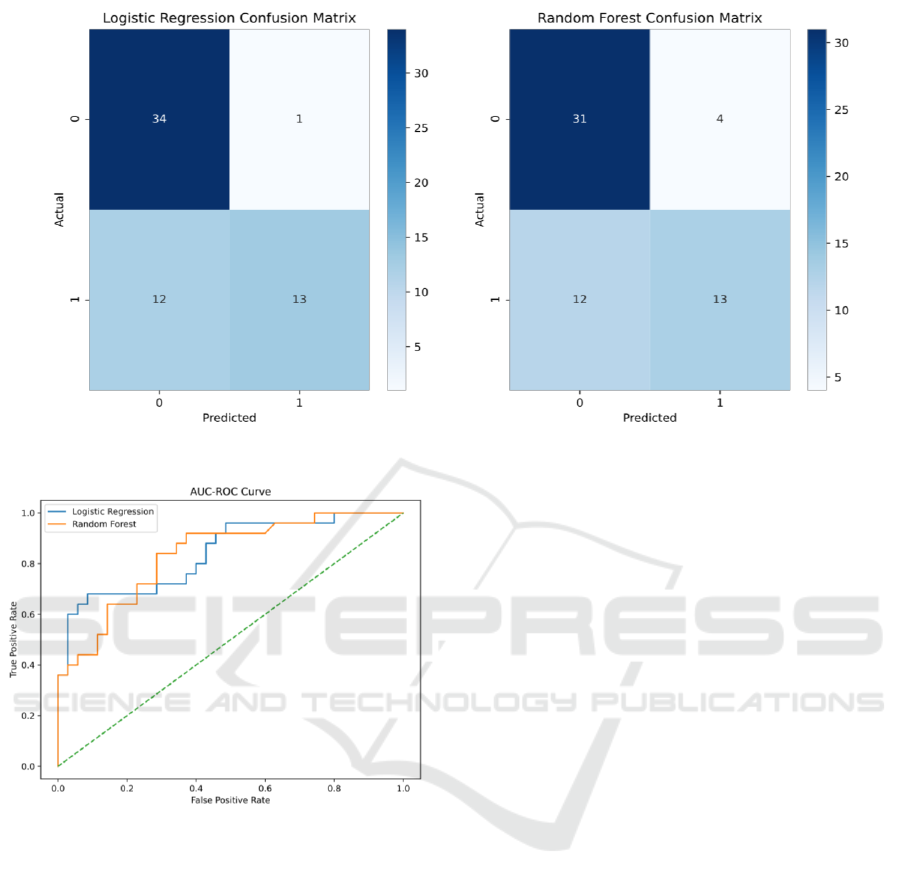
Figure 4: Confusion Matrix (Picture credit: Original).

Figure 5: ROC Curve (Picture credit: Original).

5 CONCLUSION

This study applied machine learning algorithms to

predict factors influencing mortality rates associated

with heart failure. Utilizing a clinical dataset, we

employed both logistic regression and random forest

modeling techniques to explore the predictive power

of specific indicators. This paper emphasizes the

critical roles of certain physiological variables,

including age, serum creatinine, serum sodium,

ejection fraction, and time. Both models exhibited

robust performance in terms of predictive accuracy;

however, the logistic regression model slightly

outperformed the random forest model in AUC

metrics. This enhanced performance suggests that

machine learning models may be more effective in

handling big data and nonlinear relationships, while

traditional logistic regression models appear superior

in capturing interdependencies between various

clinical features.

Not only does this study expand the existing body

of knowledge in the area of heart failure risk

prediction, but it also highlights the transformative

potential of machine learning in improving patient

outcomes through precise risk stratification and early

intervention. While this study provides a solid

foundation, it's crucial to acknowledge certain

limitations. The dataset used may not capture the full

spectrum of influencing variables, and the issue of

model interpretability remains a significant challenge,

which could hinder the seamless translation of our

research findings into actionable clinical decisions.

REFERENCES

Heart Failure Society of America. Heart failure facts &

information. https://hfsa.org/patient-hub/heart-failure-

facts-information

D. Chicco, and G. Jurman, Machine learning can predict

survival of patients with heart failure from serum

creatinine and ejection fraction alone. BMC Medical

Informatics and Decision Making, vol. 20, no. 1, pp. 16,

2020.

C. Wittenbecher, F. Eichelmann, E. Toledo, et al. Lipid

Profiles and Heart Failure Risk: Results from Two

Prospective Studies. Circulation Research, vol. 127, no.

12, pp. 1591-1601. 2020.

DAML 2023 - International Conference on Data Analysis and Machine Learning

302

F. Li, H. Xin, J.-D. Zhang et al. Prediction model of in-

hospital mortality in intensive care unit patients with

heart failure: machine learning-based, retrospective

analysis of the MIMIC-III database. BMJ Open, vol. 11,

no. 7, pp. 044779. 2021.

S. Golas, T. Shibahara, S. Agboola, et al. A machine

learning model to predict the risk of 30-day

readmissions in patients with heart failure: a

retrospective analysis of electronic medical records

data. BMC Medical Informatics and Decision Making,

vol. 18, no. 1, 2018.

A. Ishaq, S. Sadiq, M. Umer, et al. Improving the Prediction

of Heart Failure Patients’ Survival Using SMOTE and

Effective Data Mining Techniques. 2021, IEEE Access.

U. Nagavelli, D. Samanta and P. Chakraborty, Machine

Learning Technology-Based Heart Disease Detection

Models. Journal of Healthcare Engineering, 2022.

S. Rao, Y. Li, R. Ramakrishnan et al. An Explainable

Transformer-Based Deep Learning Model for the

Prediction of Incident Heart Failure. IEEE Journal of

Biomedical and Health Informatics. 2021.

A. Ishaq, S. Sadiq, M. Umer, et al. Improving the Prediction

of Heart Failure Patients’ Survival Using SMOTE and

Effective Data Mining Techniques. IEEE Access, vol.

9, pp. 3064084-3064095, 2021.

A. Karthikeyan, A. Garg, P. Vinod, U. Priyakumar,

Machine Learning Based Clinical Decision Support

System for Early COVID-19 Mortality Prediction.

Frontiers in Public Health, vol. 9, pp. 626697-626710.

2020.

G. Joo, Y. Song, H. Im, J. Park, Clinical Implication of

Machine Learning in Predicting the Occurrence of

Cardiovascular Disease Using Big Data. Nationwide

Cohort Data in Korea, vol. 8, pp. 148493-148503, 2020.

APPENDIX

Table 6: Test the Predicted Results of the Set.

True Label

Logistic Regression Prediction

Random Forest Prediction

281

265

164

278

109

173

195

184

154

147

108

140

155

104

247

275

280

116

213

236

239

Clinical Record Analysis of Heart Failure Identiﬁcation of Key Features and Disease Prediction

303

113

194

111

118

129

197

210

288

219

178

129

197

210

288

219

178

144

186

248

277

244

209

DAML 2023 - International Conference on Data Analysis and Machine Learning

304