
Effect Analysis of Loss Function for Image Super-Resolution Based
on Improved ESRGAN
Miao Pan
Software College, Zhejiang University, Ningbo, China
Keywords: ESRGAN, Loss, Evaluation, WGAN.
Abstract: The discipline of picture Super-Resolution (SR) has experienced an exceptional advancement with the
development of deep learning. The Generative Adversarial Network (GAN) has emerged as the most popular
deep learning technique for super-resolution. In order to create a super-resolution model, this study presents
Enhanced Super-Resolution GAN (ESRGAN). Loss types covered include Content Loss, Adversarial Loss,
and Total Variation Loss (TV Loss), with a focus on how the ESRGAN model affects picture super-resolution
when applying various loss functions. Then, many ESRGANs with various loss functions were compared and
assessed using common image evaluation indicators including Peak Signal-to-Noise Ratio (PSNR), Structure
Similarity Index Measure (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS). It is discovered
via the comparison of trials that changing the Wasserstein GAN (WGAN) adversarial loss from the ESRGAN
adversarial loss may significantly increase the stability of GAN network training. By modifying the loss
function, the enhanced ESRGAN suggested in this research may successfully enhance the super-resolution
impact of pictures.
1 INTRODUCTION
One of the fundamental computer vision problems,
Image Super-Resolution (SR), focuses on recovering
low-resolution pictures into high-resolution images
(Wang et al 2020). It has several uses in various
industries, including scene rendering, face
recognition, target tracking, and video surveillance.
Because there are several high-resolution versions of
a single low-resolution image, the issue of image
super-resolution is incredibly difficult.
There are three basic types of research
methodologies in the subject of SR. The first category
is built on interpolation techniques, which primarily
concentrate on filling in pixel values on faults that
remain null after zooming. Bilinear interpolation, for
instance, was discovered by Gribbon et al. The
second group consists of reconstruction-based
interpolation techniques, such as frequency-domain
and spatial-domain techniques, which often acquire
numerous frames of the same picture in exchange for
spatial resolution. Learning-based approaches, which
are mostly based on machine learning algorithms like
neural networks, make up the third group. To improve
image recovery, learn the a priori information from
low-resolution to high-resolution pictures. Examples
of this knowledge include sparse representation and
the neighborhood embedding approach. Convolution
Neural Networks (CNN), Residual Networks
(ResNet), and other models are gradually applied to
the field of SR with the rise of deep learning, giving
rise to algorithms such as Super-Resolution
Convolution Neural Networks (SRCNN), Efficient
Sub-Pixel Convolutional Neural Networks (ESPCN),
Very Deep Super Resolution (VDSR), and other deep
learning SR algorithms that significantly enhance the
quality of high-resolution images (Wang et al 2020).
However, experimental research has demonstrated
that these traditional deep learning algorithms have a
propensity to produce images that are deficient in
high-frequency information and details, and the
addition of a Generative Adversarial Network (GAN)
has once again enhanced the quality of images
produced by deep learning algorithms (Ledig et al
2017). The issue with Super-Resolution GAN
(SRGAN) was improved in four ways by Enhanced
Super-Resolution GAN (ESRGAN): The normalizing
layer is first taken off (Wang et al 2018). Second,
there is a thick link between these leftover bricks.
Third, to reduce perceptual loss, employ Visual
Geometry Group (VGG) characteristics before
activation. Introduce a novel approach for estimating
Pan, M.
Effect Analysis of Loss Function for Image Super-Resolution Based on Improved ESRGAN.
DOI: 10.5220/0012804500003885
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 149-153
ISBN: 978-989-758-705-4
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
149

the likelihood that the genuine picture is
comparatively more realistic than the fake image as
the fourth step in the discriminator output process. In
the field of SR, ESRGAN has recently gained
popularity. ESRGAN can produce images of
extremely high quality, however, its image-
generating details, model stability, and other aspects
are still flawed (Choi and Hanhoon 2023).
This study builds several loss functions, such as
Content Loss, Adversarial Loss, and Total Variation
Loss (TV Loss), to examine the impact of loss
function on the quality of GAN-generated pictures.
Peak Signal-to-Noise Ratio (PSNR), Structure
Similarity Index Measure (SSIM), and Learned
Perceptual Image Patch Similarity (LPIPS) are the
metrics used to evaluate the quality of images
generated. PSNR is simple to compute, comprehend,
and can serve as a general indicator of image quality.
A criterion for evaluating picture quality that follows
human intuition is proposed by SSIM. The impact of
various feature extraction networks on the outcomes
is unaffected by LPIPS. Different loss functions are
examined in comparative experiments to examine
their function and effect. According to experimental
findings, altering the adversarial loss can increase
training's stability. Increasing TV Loss and changing
the form of content loss will help improve the quality
of the picture.
2 METHODOLOGY
2.1 Dataset Description and
Preprocessing
The data set used in this article is div2k, which
contains 800 training data and 100 verification data
(Dataset). Randomly crop high-resolution images and
augment datasets with horizontal flips, random
rotations, and more. Finally, bicubic interpolation is
used to scale to obtain a 32×32 low-resolution image.
In the generation process, choose the resolution of
magnification 2, 3, and 4 times.
2.2 Proposed Approach
This paper explores the role and impact of different
losses from the perspective of the ESRGAN generator
and discriminator loss functions. First, this paper uses
image augmentation technology to expand the data set
to ensure that the ESRGAN model has basic effects.
Secondly, a basic ESRGAN model is constructed,
including adversarial loss and content loss. Finally,
different loss functions are designed, and the effects of
different models are studied by comparative
experiments. The process is shown in Figure 1.
Figure 1: The pipeline of the study (Picture credit:
Original).
2.2.1 ESRGAN
The ultimate objective of the SRGAN family of
super-resolution models is to train a generation
network using perceptual loss and assess its
performance using a discriminant network. On this
foundation, ESRGAN modifies the network structure
and loss function shape. Three benefits of ESRGAN:
First, the ESRGAN model can provide perceptions of
higher quality. In contrast to the conventional
discriminator, which calculates the likelihood that an
input picture x is genuine and organic, ESRGAN
learns to assess which images are more realistic than
others, instructing the generator to recreate textures
with greater detail. Third, by applying pre-activation
characteristics, which offer better supervision and
afterward restore more precise brightness and texture,
ESRGAN strengthens the perceptual loss.
2.2.2 Adversarial
In contrast to the discriminator in SRGAN, the
relative discriminator in ESRGAN is different. The
discriminator and the generator's particular
relativistic loss has the following form:
𝐿
−𝔼
lo g
𝐷
𝑥
, 𝑥
−
𝔼
lo g
1 −𝐷
𝑥
, 𝑥
1
𝐿
−𝔼
lo g
1 −𝐷
𝑥
, 𝑥
−𝔼
lo g
𝐷
𝑥
, 𝑥
2
𝐷
represents the interpolation between the
original value of the discriminator’s real image
judgment and the original value of the generated
image judgment. Considering the stability of
adversarial network training, this paper removes the
logarithmic function in the above formula. However,
in the course of the experiment, it is still prone to
DAML 2023 - International Conference on Data Analysis and Machine Learning
150

instability in the training of the adversarial network,
so this paper uses the adversarial loss in Wasserstein
GAN (WGAN) for comparison. This loss function
effectively avoids the situation that the gradient is zero
during the direction gradient transfer process, and
enhances the stability of network training. Its loss
function is as follows (Arjovsky and Léon 2017 &
Arjovsky et al 2017):
𝐿
=
1
𝑚
𝑓
𝑥
−
1
𝑚
𝑓
𝑔
𝑧
3
𝐿
=
𝑓
𝑔
𝑧
4
𝑤 stands for the discriminant network's parameters. 𝜃
stands for setting up network settings. The created
picture is represented by 𝑧. 𝑥 represents the real
image.
2.2.3 Total Variation Loss
In the process of SR, a little noise on the image may
have a great impact on the result, because many
algorithms will amplify the noise. To keep the image's
smoothness at this point, certain regularization
components must be included to the optimization
problem's model. A typical regularization problem is
TV Loss. By lowering the TV Loss, the disparity in
nearby pixel values in the image can be rectified
(Chan, et al 2005).
Loss
𝑧
=
,
𝑧
,
−𝑧
,
+ 𝑧
,
−𝑧
,
5
The created picture z's pixel value in Row i and
Column j is represented by
𝑧
,
. The square of the
difference between each pixel in the picture and the
following pixel in the horizontal direction, as well as
the square of the difference in the following pixel in
the vertical direction, are calculated using this
formula. Then open the root of β/2. Generally, the
default value of β is 2.
2.2.4 Total Variation Loss
Although directly tweaking MSE can result in greater
PSNR and SSIM, MSE as a loss-guided learning
cannot make the reconstructed picture capture precise
information when the up-scale factor is high. The
precise form looks like this:
𝐿𝑜𝑠𝑠
=
1
r
⋅W ⋅H
(I
,
−G
(I
)
,
)
(
6
)
G
means generating a network. Therefore, VGG
content loss is introduced in SRGAN, which has a
better ability to measure perceptual similarity than
MSE (Ledig, et al 2017 & Wang, et al 2018). The
specific form is as follows:
𝐿𝑜𝑠𝑠
=
1
W
,
H
,
,
,
(𝜙
,
G
(
I
)
,
−𝜙
,
(
I
)
,
)
(
7
)
𝜙 is based on the scoring function of the VGG
network. Because VGG is a loss for HR and SR
images as a whole. The same content loss can also be
adapted for other feature extraction networks. Since
this paper considers that the residual network can
preserve the details in the image feature extraction
process, the content loss of the Residual network is
used for comparison. The specific form is as follows:
𝐿𝑜𝑠𝑠
=
1
W
,
H
,
,
,
(𝜑
,
G
(
I
)
,
−𝜑
,
(
I
)
,
)
(
8
)
𝜑 is based on the scoring function of the Resnet.
2.3 Evaluation
The subjective and objective components of Image
Quality Assessment (IQA) can be separated based on
the approach. Using people's subjective perceptions,
one may evaluate the quality of a picture. Quantitative
values are provided through objective evaluations
using mathematical models. The primary PSNR,
SSIM, and LPIPS objective assessment metrics
chosen in this work.
Comparing the visual error between the created
picture and the real image is the most straightforward
technique to determine the quality of an image after it
has been generated. The PSNR ratio measures the
energy of the peak signal to the energy of the noise on
average. The Mean Square Error (MSE), given a clear
picture I
and a noisy image G
(I
) of size
m×n, is defined as:
𝑀𝑆𝐸=
1
𝑚𝑛
[I
,
−G
(I
)
,
]
(
9
)
PSNR is subsequently described as:
𝑃𝑆𝑁𝑅=10⋅𝑙𝑜𝑔
𝑀𝐴𝑋
𝑀𝑆𝐸
(
10
)
where 𝑀𝐴𝑋
is the image's highest pixel value. It is
255 if each pixel is represented by 8 bits of binary data.
A popular index for evaluating picture quality,
SSIM is a full-reference assessment approach. It is
predicated on the idea that when pictures are
examined, the human eye derives organized
Effect Analysis of Loss Function for Image Super-Resolution Based on Improved ESRGAN
151
information from them (Wang et al 2004). The
luminance, contrast, and structural comparisons
between samples x and y constitute the basis of the
SSIM formula.
𝑙
(
𝑥, 𝑦
)
=
2𝜇
𝜇
+ 𝑐
𝜇
+ 𝜇
+ 𝑐
(
11
)
𝑐
(
𝑥, 𝑦
)
=
2𝜎
𝜎
+ 𝑐
𝜎
+ 𝜎
+ 𝑐
(
12
)
𝑠
(
𝑥, 𝑦
)
=
𝜎
+ 𝑐
𝜎
𝜎
+ 𝑐
(
13
)
X's mean value is 𝜇
, while Y's mean value is 𝜇
.
𝜎
is X's variance, 𝜎
is Y's variance, and 𝜎
is X's
and Y's covariance. Two constants, c1 and c2, prevent
the denominator from being zero. The SSIM
expression is thus as follows:
𝑆𝑆𝐼𝑀
(
𝑥, 𝑦
)
= 𝑙(𝑥, 𝑦)
⋅𝑐(𝑥, 𝑦)
⋅𝑠(𝑥, 𝑦)
(14)
Set 𝛼, 𝛽, 𝛾 to 1, and then can get
𝑆𝑆𝐼𝑀
(
𝑥, 𝑦
)
=
2𝜇
𝜇
+ 𝑐
2𝜎
+ 𝑐
𝜇
+ 𝜇
+ 𝑐
𝜎
+ 𝜎
+ 𝑐
(
15
)
The difference between two photos is measured by
learning to recognize image patch similarities. This
metric emphasizes the perceptual similarity between
them and learns the inverse mapping of generated
pictures to ground truth (Zhang et al 2018). It also
requires the generator to learn to reconstruct the
inverse mapping of actual images from false ones. The
formula for the perceptual similarity measure is as
follows, given a noisy picture distortion block x_0 and
a Ground Truth image reference block x:
𝑑
(
𝑥, 𝑥
)
=
1
𝐻
𝑊
∣∣𝑤
⊙
(
𝑦
−𝑦
)
∣∣
,
(
16
)
The distance between the genuine x_0 picture and
the false image x is d. y ̂^l represents the output of
image x in layer l of the neural network. From L
layers, feature stacks are taken out and unit-
normalized in the channel dimension. Scale the
quantity of activation channels using the vector
𝑤
∈
ℝ
, then determine the L2 distance. Finally, sum
across channels and average over space.
2.4 Implementation Details
The resolution of the low-resolution image in this
paper is 32×32, and the high-resolution images of
64×64, 96×96, and 128×128 are obtained through
different magnifications of the generator. The
optimizer uses the Adam algorithm, and the specific
parameters are
𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔 = 0.0001, 𝑏𝑒𝑡𝑎𝑠 =
(0,0.9)
. The number of iteration rounds is 100,
𝑏𝑎𝑡𝑐ℎ𝑠𝑖𝑧𝑒 = 16. The hardware GPU resource is
the GPU T4×2 of the Kaggle platform. In the SSIM
evaluation index,
𝑐1 = 0.02, 𝑐2=0.06. In the
LPIPS evaluation index, the feature extraction
network uses Alex network (Alexnet).
3 RESULTS AND DISCUSSION
In this study, the three indicators PSNR, SSIM, and
LPIPS are compared and assessed. The greater the
PSNR and SSIM values, the lower the LPIPS value,
and the better the quality of the super-resolution of the
images.
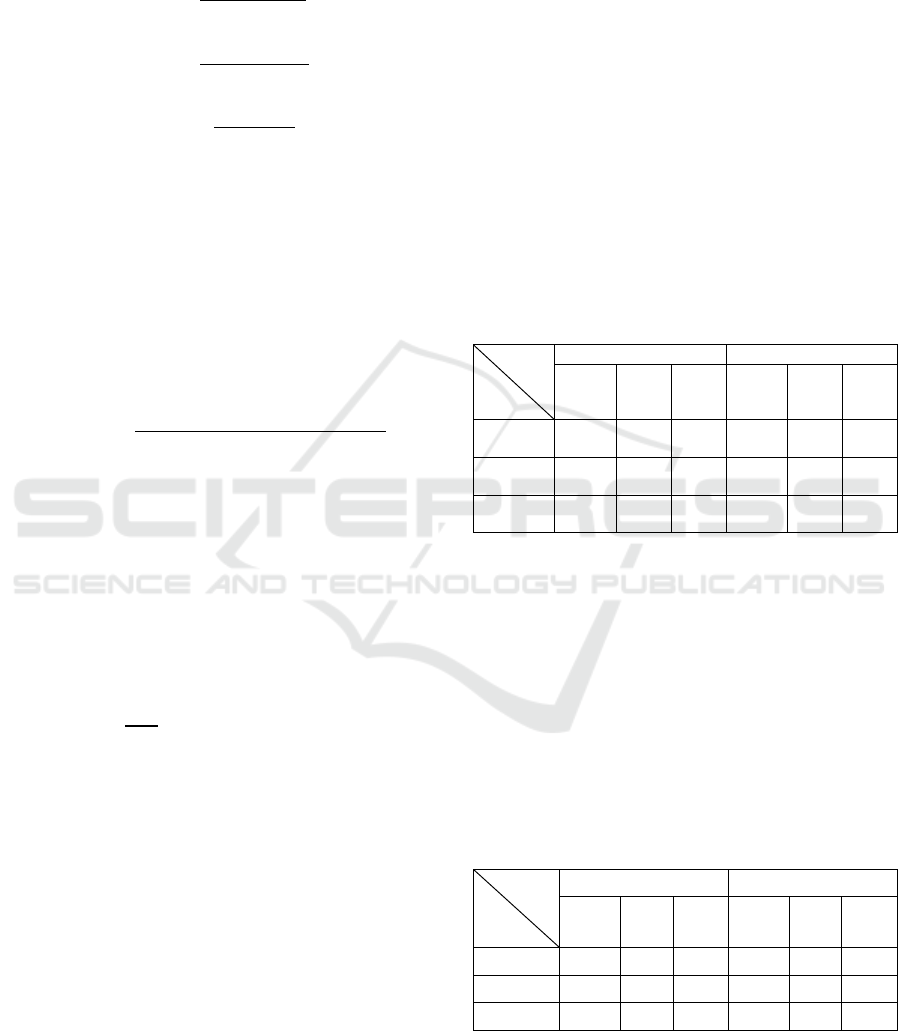
Table 1: Quality of SR Images Generated with Different
Adversarial Loss.
Content
loss
magnifyin
g powe
r
WGAN loss ESRGAN loss
PSNR SSIM LPIPS PSNR SSIM LPIPS
×2
73.862
0
0.9032 0.0460 75.283
2
0.9152 0.0338
×3
73.089
2
0.9097 0.1131 66.628
1
0.6519 0.3152
×4
69.412
5
0.8130 0.2633 58.996
7
0.0738 0.7005
Table 1 shows that the double-magnification
super-resolution job does benefit from ESRGAN loss,
but as the task difficulty rises, the super-resolution
impact becomes noticeably less effective than the
WGAN type of adversarial loss. It is clear that
ESRGAN's adversarial network training fails when
the super-resolution challenge is multiplied four
times. The model training is stable, even if the WGAN
form's super-resolution impact will diminish as the
task complexity rises.
Table 2: Quality of SR Images Generated with Different Tv
Loss.
Content
loss
magnifyin
g powe
r
Without TV Loss With TV Loss
PSNR SSIM LPIPS PSNR SSIM LPIPS
×2
73.8620 0.9032 0.0460 77.9831 0.9464 0.0320
×3
73.0892 0.9097 0.1131 73.3547 0.9013 0.1183
×4
69.4125 0.8130 0.2633 69.7261 0.7921 0.2579
According to Table 2, adding TV Loss to the loss
function can enhance the quality of the super-
resolution images, but as the job complexity rises, TV
DAML 2023 - International Conference on Data Analysis and Machine Learning
152

Loss' super-resolution effect diminishes. Even TV
Loss occurs when the super-resolution work is four
times enlarged. It is clear that training for adversarial
loss becomes increasingly crucial as task complexity
rises. The adversarial network may not have received
enough training if the TV Loss is raised at this point.
Table 3: Quality of SR Images Generated with Different
Content Loss.
Content
loss
magnifyin
g powe
r
Content loss with VGG Content loss with
ResNe
t
PSNR SSIM LPIPS PSNR SSIM LPIPS
×2
73.8620 0.9032 0.0460 77.2794 0.9347 0.0377
×3
73.0892 0.9097 0.1131 73.0973 0.9146 0.1136
×4
69.4125 0.8130 0.2633 72.0820 0.8824 0.1971
Table 3 shows that content loss adopts the Resnet
assessment format, which considerably raises the
standard of picture creation. This research argues that
Resnet-based loss is preferable than VGG-based loss
because Resnet makes it simple for the network to
remember certain shallow feature information and
combine it with deep feature information through skip
connections.
4 CONCLUSION
Although the adversarial loss in ESRGAN may
enhance the super-resolution impact of the images, it
is also simple to produce the issue of network training
collapse since the task's complexity rises. As a result,
the loss function of the model is improved by this
study. First off, the training is stable and the picture
super-resolution effect is better based on the
adversarial loss suggested by WGAN. Second, while
the addition of TV Loss can enhance the effects of
picture super-resolution, its impact diminishes with
increasing job complexity and can even make it more
difficult to train a GAN network. Third, the content
loss that results from employing the Resnet network
for feature extraction as opposed to the VGG can
further enhance the effects of picture super-resolution.
The impact of Resnet content loss on picture super-
resolution weakens as the task's complexity rises,
although it still has a favorable impact. The effect of
image super-resolution degrades as the task's zoom
factor increases. In order to accomplish the effect of
magnifying the resolution by 4 times, a cascade
approach will be used to increase the resolution by 2
times sequentially twice. The experimental findings
demonstrate that the suggested enhancement approach
can successfully increase model performance. The
results of this study will be used to deploy the model
in the field in the future.
REFERENCES
Z. H. Wang, J. Chen, and C. H. Steven, “Deep learning for
image super-resolution: A survey, ” IEEE
transactions on pattern analysis and machine
intelligence, vol. 43, 2020, pp. 3365-3387.
Gribbon, T. Kim, and G. D. Bailey, “A novel approach to
real-time bilinear interpolation,” Proceedings.
Second IEEE international workshop on electronic
design, test and applications, IEEE, 2004, pp. 126-
131.
C. Ledig, et al. “Photo-realistic single image super-
resolution using a generative adversarial network,”
Proceedings of the IEEE conference on computer
vision and pattern recognition. 2017, pp. 4681-4690.
X. T. Wang, et al. “Esrgan: Enhanced super-resolution
generative adversarial networks,” Proceedings of the
European conference on computer vision (ECCV)
workshops, 2018.
Y. Choi, and P. Hanhoon, “Improving ESRGAN with an
additional image quality loss,” Multimedia Tools and
Applications, vol. 82, 2023, pp. 3123-3137.
Dataset https://data.vision.ee.ethz.ch/cvl/DIV2K/
M. Arjovsky, and B. Léon, “Towards principled methods
for training generative adversarial networks,” arXiv
2017, unpublished.
M. Arjovsky, S. Chintala, and B. Léon, “Wasserstein
generative adversarial networks,” International
conference on machine learning. PMLR, 2017, pp.
214-223.
T. Chan, et al. “Recent developments in total variation
image restoration,” Mathematical Models of
Computer Vision, vol. 17, 2005, pp. 17-31.
Wang, Zhou, et al. “Image quality assessment: from error
visibility to structural similarity,” IEEE transactions
on image processing, vol. 13, 2004, pp. 600-612.
R. Zhang, et al. “The unreasonable effectiveness of deep
features as a perceptual metric,” Proceedings of the
IEEE conference on computer vision and pattern
recognition, 2018, pp. 586-595.
Effect Analysis of Loss Function for Image Super-Resolution Based on Improved ESRGAN
153
