Study for Urals Oil Price Based on ARIMA Model

Meixuan Lou

Meadowvale Secondary School, Ontario, Canada

Keywords: Oil Price Prediction, ARIMA Model, Short-Term Forecasting, Time Series Analysis.

Abstract: In time series forecasting, oil price forecasting is one of the most famous studies. That is because oil price

forecast is essential, for the price of oil is related to transportation cost, stock market, and consumer purchasing

power. Under the Russian-Ukrainian conflict and COVID-19 pandemic circumstances, the oil of Russia has

been influenced a lot. However, nowadays, there is research on the oil price combined with the Russia-Ukraine

conflict and the COVID-19 pandemic. In this paper, both the Autoregressive Integrated Moving Average

Model (ARIMA) (p, d, q) model and the auto_ARIMA model are used to analyze the time series. The short-

term estimate for the ural oil price is based on the ARIMA (0, 1, 1) model, which is clarified in detail. The

findings demonstrated that in the short-term prediction area, the ARIMA (0, 1, 1)model has a strong and

reliable potential. In addition, the price of Urals oil is expected to increase shortly. Besides this model can

also be used in different situations.

1 INTRODUCTION

Vehicles, ships, and airplanes without oil, will lead to

transportation paralysis, boilers, and heating furnaces

without oil, will lead to factory shutdown. For most

people in the world fuel oil is one of the necessities.

In addition to being people's everyday commodity, oil

is also a vital strategic resource. As a consequence, a

secure supply of oil is linked not only to the daily lives

of individuals but also to the country's economic

progress and stability in society. In general, the price

of oil has always been intertwined with international

political struggles, competing interests in the global

war effort, and even social ideologies, human rights,

and ethnoreligious conflicts and contradictions

(Marbuah 2017).

Russia has the largest land area in the world,

covering 12 climatic zones. One of the most important

oil-producing regions of Russia is the Siberian Plain

and Siberian Lowland. Here, petroleum resources

exist in the form of deep underground deposits of oil

and natural gas. In addition, Russia's climatic

conditions are favorable for oil production (Shaw and

Oldfield 2007). The short summers at high latitudes,

lead to additional time for photosynthesis and

promote the accumulation of biomass. This also

provides conditions for the formation of oil.

The Russian-Ukrainian conflict ensued after the

outbreak of the COVID-19 (Ibendahl 2022 &

Nerlinger and Utz 2022). In June 2022, the EU

imposed successive embargoes on Russian crude oil

exports by sea, and in December, together with the G7

and Australia, imposed price restrictions on Russian

crude oil exports by sea to third countries (Martinho

2022, Razek et al 2023 & Ha 2023).

The fluctuation of the oil will affect economic

decisions, and knowing roughly where oil price is

going in advance will help people make decisions. This

essay uses the ARIMA model to help investigate

whether the Russian oil industry will be affected in the

context of the Russo-Ukrainian conflict or not by

predicting the price of the Ural oil shortly which is

considered as using the Autoregressive Integrated

Moving Average Model (ARIMA) model to conduct a

short period prediction to help people make decisions.

2 THE ARIMA MODEL

ARIMA models have been confirmed to produce

accurate forecasts for the immediate future. It

routinely outperforms models with complex structural

in terms of prediction in a short period. The future

value of a variable in the ARIMA model is the result

of the linear combination of values in priority and

errors in the past.

The mathematical expressions of the Auto-

Regressive (AR), Moving Average (MA), and

Lou, M.

Study for Urals Oil Price Based on ARIMA Model.

DOI: 10.5220/0012808900003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 10-13

ISBN: 978-989-758-705-4

ARIMA models are the following:

11 2 2

ttt ptpt

AR Y c Y Y Y

φφ φ ξ

−− −

−+ + + + +

(1)

112 2

tttt qtq

MA Y

μθ θ θ

−− −

=+∈+∈ +∈ + + ∈

(2)

11 2 2

112 2

ttt ptpt

tt qtq

Yc Y Y Y

φφ φ

θθ θ

−− −

=+ + + + +∈

+∈+∈++ ∈



(3)

Box and Jenkins created the ARIMA model in

1970 (Ariyo et al 2014 & Contreras et al 2003). This

model is one of the most frequently employed

strategies in future projection.

The ARIMA model is one of the most commonly

utilized prediction models. And the core of ARIMA (p,

d, q) model is the combination of the variations in

procedure and the ARIMA (p, q) model, thus, the

ARMA (p, q) model becomes the ARIMA (p, d, q)

model shortly after d times of difference. The

methods' complete steps are as follows:

Step 1: to check for stationarity, locate the data set

and use the Augmented Dickey-Fuller test.

Step 2: if the p-value turns out to be smaller than

0.05, then the data set until the p-value is no longer

larger than 0.05.

Step 3: calculate the optimal value of parameters

p, d, and q using the ACF plot, PACF plot, and

auto_ARIMA model.

Step 4: forecast the price of oil.

3 METHOD

3.1 Find the Data Set

The oil is considered to be used as the data set for,

Russia is one of the countries that was affected greatly

by the Russia-Ukraine Conflict. The reference oil

brand used to price Russia's export mixed oil is Ural

oil. It's a mixed oil that consists of both light oil from

Western Siberia and a mixture of heavy sour oil from

the Urals and the Volga region. As a result, the prices

of oil from August 2017 to July 2023 are chosen from

Trading Economics to carry on research and forecast.

Ural oil data used in this paper includes 1559

observations. After collecting those data, the time

series is then cut by week to obtain the average price

for each week.

3.2 Stationary Test

To predict the oil’s future price, the ARIMA model

algorithm is considered to be used.

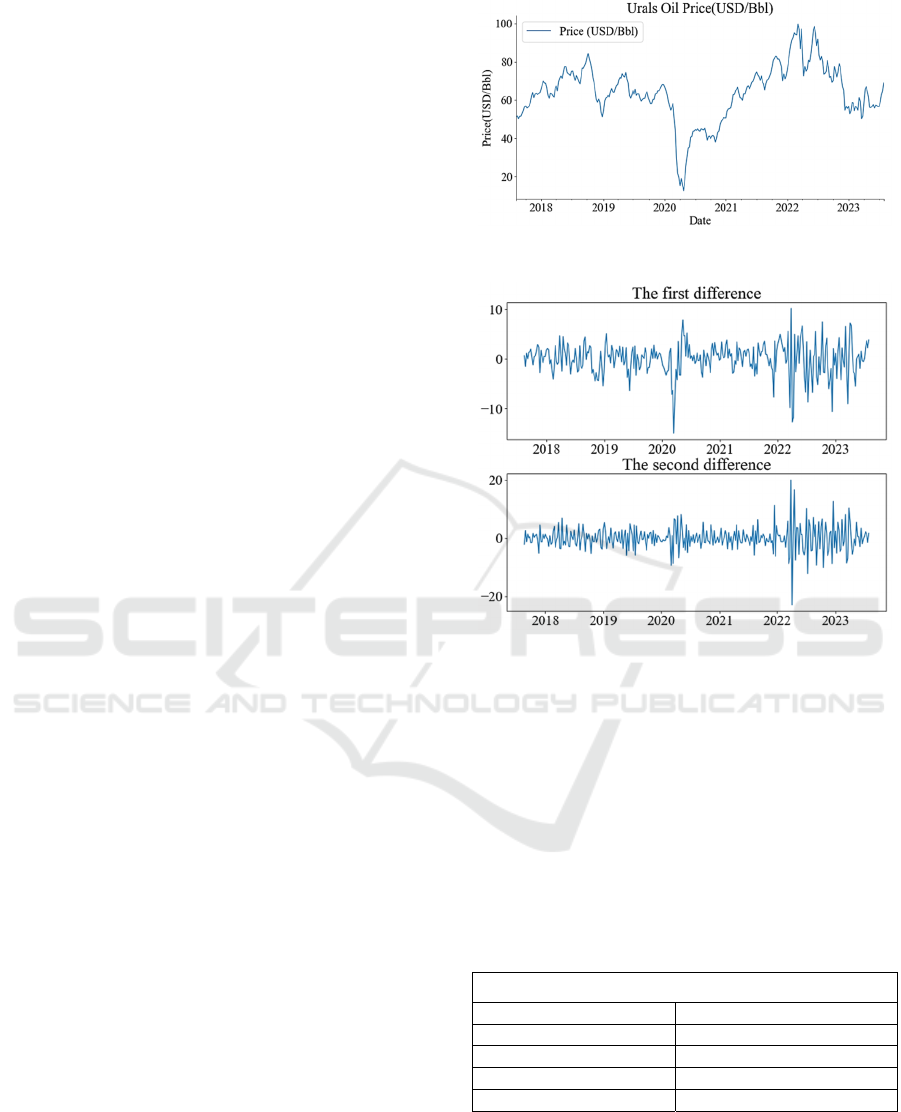
Figure 1 shows the data set of Urals oil weekly

average

price

the

opening

day

the

market

Figure 1: Urals oil price plot (Photo/Picture credit: Original).

Figure 2: First difference plot and second difference plot

(Photo/Picture credit: Original).

between August 2017 and July 2023. From the line

graph, it can be seen that the raw data is very unstable,

so the flowing step that needs to be introduced is to

differentiate the raw data set in order to get a smoother

data set.

Stationarity is one of the very important

components in the time series. Before the ARIMA

model forecasting model is used, the data set that is

being used needs to pass the ADF test.

Table 1: Adf Test Result of the Original Data Set.

ADF test result

ADF Test Statistic -1.979935560233871

P-value 0.29543935300876867

Critical Values

(

)

-3.4521175397304784

Critical Values (3%) -2.8711265007266666

Critical Values (5%) -2.571877823851692

Through the ADF test in Table I, the p-value =

0.29543935300876867 > 0.05, which means that the

data set is not stationary. So, the next step is to

transform this time series into a stationary series by

differencing it.

Study for Urals Oil Price Based on ARIMA Model

Table 3: Samples of the Actual Values, Predicted Values of ARIMA (0,1,1) and Their Difference Value.

Date Actual Values Predicted Values

2023/3/27 52.05 48.58

2023/4/3 64.65 52.4

2023/4/10 66.32 60.4

2023/4/17 65.79 66.92

2023/4/24 63.93 67.1

2023/5/1 62.2 63.89

2023/5/8 58.53 61.13

2023/5/15 56.46 55.08

2023/5/22 56.78 56.37

2023/5/29 57.37 56.75

2023/6/5 58.27 57.92

2023/6/12 57.37 55.37

2023/6/19 58.08 57.88

2023/6/26 55.74 56.9

2023/7/3 58.61 56.5

2023/7/10 61.53 56.8

2023/7/17 61.51 59.54

2023/7/24 67.41 63.47

2023/7/31 70.23 65.36

2023/8/7

69.67

Figure 2 shows a plot of the data after the first-

order difference and second-order difference which

shows that the data after the first-order difference is

much more smoother than the raw data set. To

determine whether the data after the first-order

difference is smooth enough. The result of the data

after the first difference is then tested for its p-value.

Table 2: Adf Test Result of the First Difference.

ADF test result

ADF Test Statistic -7.6390610799093315

P-value 1.917481762349957e-11

Critical Values

(

)

-3.4521175397304784

Critical Values (3%) -2.8711265007266666

Critical Values (5%) -2.571877823851692

Table 2 contains the values of the ADF test of the data

set after the first difference. Through the ADF test, the

𝑝𝑣𝑎𝑙𝑢𝑒  1.917481762349957𝑒11  0.05 ,

which signifies that the time series following this

treatment is deemed stationary. As a result, the value

of the parameter d can be calculated to be 1.

3.3 Determine the Values of

Parameters P and Q

The following step is to find the autocorrelation

coefficient and partial correlation coefficient which

are shown in the ACF plot of Figure 3 and the PACF

plot of Figure 4. When modeling ARIMA(p, d, q) for

time series, one of the most troublesome things is to

Figure 3: ACF plot (Photo/Picture credit: Original).

Figure 4: PACF plot (Photo/Picture credit: Original).

determine the hyperparameters p, d, and q. The

conventional practice is to use the stationarity test to

determine parameter d first, and then observe p and q

through ACF and PACF plots (Ahmed and Shabri

DAML 2023 - International Conference on Data Analysis and Machine Learning

2014). This combination of machine and manual

methods often takes a long time to develop and it's

error-prone.

A more convenient way is to call auto_ARIMA

directly. It turns out that when the values of the

parameters are (0, 1, 1), the AIC value equals

5014.207, which is the smallest value in all the test

models. When comparing the AIC of several models

for a given data set, the "best" model among all those

available for the data set is the one with the lowest

AIC score. Even if only subpar models are taken into

account, the AIC will still be able to choose the best

one. As a consequence, the ARIMA (0, 1, 1) is the best

algorithm for this collection of data (Mazerolle 2006

& Gasper and Mbwambo 2023).

3.4 The Comparison Between Actual

Values and Predicted Values

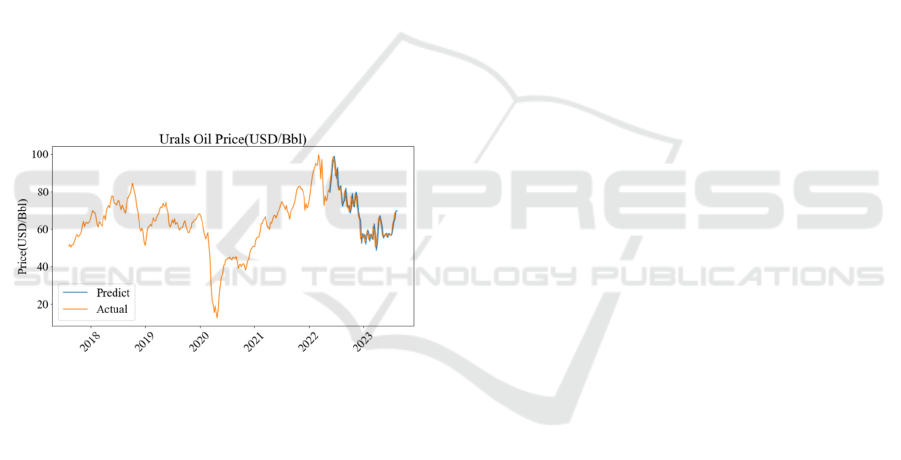
Figure 5 and Table III show the actual values of the

weekly data set and predicted values of the ARIMA

(0, 1, 1) model. As it is shown in the plot and table,

the Urals oil’s price will rise next week.

Figure 5: Plot of comparison with real and anticipated

values (Photo/Picture credit: Original).

4 CONCLUSIONS

The price of Urals oil is not stationary and it can be

affected by several factors, such as oil commodity and

financial attributes, supply and demand in the oil

market, the international economic situation,

fluctuations in the US dollar's exchange rate, and the

role of the law of value on the five major factors

affecting it. According to the study’s findings, the

Autoregressive Integrated Moving Average Model

(ARIMA) (0, 1, 1) is the best model used for the

future value prediction of the oil and it presented that

the average price in the next week will increase.

The study of oil price trends and the development

and application of forecasting models are both

important tools for financial strategy development

and important macroeconomic management tools.

However, at the same time, various models also have

certain limitations and risks, which need to be flexibly

selected in light of the specific market environment

and needs.

Besides, this model can also be used to conjecture

the price of another object in the future. The

seasonality of the data can also be taken into account

when constructing the model. BIC can be introduced

in addition to AIC to help provide a more

comprehensive view.

REFERENCES

G. Marbuah, Understanding crude oil import demand

behaviour in Africa: The Ghana case. Journal of

African Trade, vol.4, no.1-2, 2017, pp. 75-87.

D. J. Shaw, J. D. Oldfield, Landscape science: a Russian

geographical tradition. Annals of the association of

american geographers, vol.97, no.1, 2007, pp. 111-

126.

G. Ibendahl, The Russia-Ukraine conflict and the effect on

fertilizer. Department of Agricultural Economics,

Kansas State University: Manhattan, KS, USA. 2022.

M. Nerlinger, and S. Utz, The impact of the Russia-Ukraine

conflict on energy firms: A capital market perspective,

vol.50, 2022, pp.103243.

V. J. P. D Martinho, Impacts of the COVID-19 pandemic

and the Russia–Ukraine conflict on land use across

the world. Land, vol.11, no.10, 2022, pp.1614.

A. Razek, N. H. Galvani, V. et al. Can US Strategic

Petroleum Reserves Calm a Tight Market

Exacerbated by the Russia-Ukraine Conflict? 2023,

pp.4441644.

L. T. Ha, Dynamic interlinkages between the crude oil and

gold and stock during Russia-Ukraine War: evidence

from an extended TVP-VAR analysis. Environmental

Science and Pollution Research, vol.30, no.9, 2023,

pp. 23110-23123.

A. Ariyo, A. Adewumi, et al. Stock price prediction using

the ARIMA model. In 2014 UKSim-AMSS 16th

international conference on computer modelling and

simulation, IEEE. 2014, pp. 106-112.

Contreras, J., Espinola, R., et al. ARIMA models to predict

next-day electricity prices. IEEE transactions on

power systems, 2003, 18(3), pp. 1014-1020.

R. A. Ahmed, A. B. Shabri, Daily crude oil price forecasting

model using arima, generalized autoregressive

conditional heteroscedastic and support vector

machines. American Journal of Applied Sciences,

vol.11, no.3, 2014, pp. 425.

M. Mazerolle, Improving data analysis in herpetology:

using Akaike's Information Criterion (AIC) to assess

the strength of biological hypotheses. Amphibia-

Reptilia, vol.27, no.2, 2006, pp. 169-180.

L. Gasper, H. Mbwambo, Forecasting crude oil prices by

using ARIMA model: evidence from Tanzania. 2023.

Study for Urals Oil Price Based on ARIMA Model