Critical Illness Insurance Pricing and Markov Optimization Model:

Based on the Analysis of Severe Malignancies in China

Qijing Sun

Tianjin University of Finance and Economics, Institute of Statistics, Tianjin, China

Keywords: Critical Illness Insurance, Severe Malignant Neoplasms, Markov.

Abstract: With the development of the insurance market and the growth of public demand, more and more people

choose to buy critical illness insurance products to protect against related risks. With the introduction of many

new critical illness insurance products by insurance companies, the study of the pricing of critical illness

insurance-related products is of great significance. Based on the example of severe malignant tumors among

critical illnesses, this paper calculates the pricing of critical illness insurance for severe malignant tumors in

different age groups using traditional methods based on data from China. Subsequently, this paper explores

the optimization of critical illness insurance pricing with the Markov model. Finally, it summarizes the

conclusions and gives relevant suggestions on the pricing of critical illness insurance for severe malignant

tumors in terms of data, comprehensive coverage, and government supervision and control, so as to provide

a reference for the pricing and future development of standalone primary whole life critical illness insurance

products.

1 INTRODUCTION

In recent years, with the continuous advancement of

medical technology and increased attention to health,

critical illness insurance has become one of the

important risk management tools for people. Iranian

scholar Seyed Morteza Adyani argues that the

country's healthcare benefits are far from being

insufficient not enough at all to fully solve the financial

problems caused by high costs, and that the aid of

commercial health insurance is essential (Adyani and

Alizadeh 2018). CC Koay states in his article that

critical illness insurance is a means of protection by

which insurance companies provide payouts to insured

people and that when an insured person suffers from a

disease listed in the policy, such as cancer, the

insurance company will make a claim accordingly

(Koay 2003). Baione F and Levantesi did a study with

an Italian subject, who flexibly applied the pricing

model of medical insurance to critical illness

insurance, but he argued that the model is very

restricted and can only be applied under certain

conditions (Baione and Levantesi 2014).

However, because of the large differences in the

incidence and risk factors of critical illnesses, how to

rationalize pricing has become an important issue for

insurance companies. The traditional pricing method

of major disease insurance is mainly based on

statistical modeling and actuarial theory, but this

method has certain limitations when facing complex

risk factors. In order to predict the incidence and risk

level of major diseases more accurately, this paper will

consider introducing the method based on the Markov

model for pricing. Most of the basic definitions of the

Markov chain refer to BruceL. Jones's article

"Modeling Multi-State Processesus inga

MarkovAssumption" (Jone 1993). This article not only

provides a detailed definition of Markov chains but

also describes the use of pricing in long-term health

insurance practices by insurance companies. Ermanno

Pitacco's "Actuarial models for pricing disability

benefits: Toward saunify in gapproach" builds on

previous research by linking transfer probabilities and

transfer intensities of discrete Markov chains, and

initially constructs a three-state Markov model

(Pitacco 1995). Christiansen illustrates a framework

for actuarial modeling of Markov models as well as

Semi-Markov models for health insurance and

describes the need for randomization of transfer

intensities (Christiansen 2012). the need for

randomization. The multi-state Markov model was

initially used to measure the pricing of disability

income insurance, but has since been widely applied

Sun, Q.

Critical Illness Insurance Pricing and Markov Optimization Model: Based on the Analysis of Severe Malignancies in China.

DOI: 10.5220/0012819600003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 61-65

ISBN: 978-989-758-705-4

and extended to the pricing of other insurance products

including health insurance. The main objective of this

paper is to calculate the insurance pricing of severe

malignant tumors for different age groups in China

using the traditional pricing algorithm for critical

illness insurance. Further, this paper also explores how

to use the Markov chain for model optimization of

insurance pricing.

2 PRICING PROCESS AND

ACTUARIAL ASSUMPTIONS

2.1 The Basic Process of Pricing

Critical Illness Insurance

Maintaining the Integrity of the

Specifications

According to existing research findings, the pricing

process of critical illness insurance usually includes the

following steps: first, the insurance company will build

a Markov model based on information such as risk

factors, claims history, customer's age, gender,

occupation, etc., and use the model to predict the

customer's future risk level. Then, the insurer will

develop a pricing strategy based on the prediction

results. Specifically, the insurer will determine

premiums based on factors such as the customer's age,

gender, and occupation, while taking into account the

customer's historical risk factors and historical claims

history. It is important to note that actuarial

assumptions will vary as each insurance company is

different. However, usually, the Markov model takes

into account the influence of the customer's age,

gender, occupation, historical risk factors, and

historical claims record (Hailong 2023).

However, China's insurance industry has a limited

time to develop, so in the early stage, it mainly refers

to western empirical data, and can only be fit to China's

specific situation as much as possible when the

historical accumulated data is not complete. In this

paper, this paper use specific data from the "China Life

Insurance Industry Critical Illness Experience

Incidence Table (2020)" published by the China

Society of Actuaries to price critical illness insurance

based on the traditional insurance pricing model.

2.2 Actuarial Assumptions

The establishment of appropriate actuarial assumptions

is an important part of the pricing process of critical

illness insurance. Actuarial assumptions are reasonable

assumptions that are discussed and made in a certain

actuarial model about the influencing factors of pricing

(Yaling 2022). The purpose of actuarial assumptions is

to enable insurance companies to estimate risks more

accurately and thus develop more reasonable insurance

rates. The significance of actuarial assumptions is that

can help insurance companies to better manage risks

and improve the profitability and competitiveness of the

company.

2.2.1 Expected Incidence Assumptions

In insurance pricing, expected incidence is an

important assumption that can be used to predict

future levels of risk in order to set premiums

accordingly. The meaning of the expected incidence

assumption is that when insurance companies conduct

a risk assessment, they will predict the probability of

occurrence of a certain risk in the future based on

factors such as historical data and statistical modeling.

The purpose of expected incidence assumptions is to

help insurance companies better manage risks, and it

can also help consumers better choose insurance

products that suit their needs.

In terms of experience incidence of major

diseases, Table CI7 of the New Critical Illness Table,

which is a table of experience incidence of malignant

tumors - severe (2020 version definition), is selected.

After data cleaning, column xi is the prevalence rate

corresponding to each age under the New Critical

Illness Table, and column ki is the probability of death

of an individual with a critical illness at each age that

is not due to an accident. Probability.The incidence

rates of different age groups are shown in Table 1.

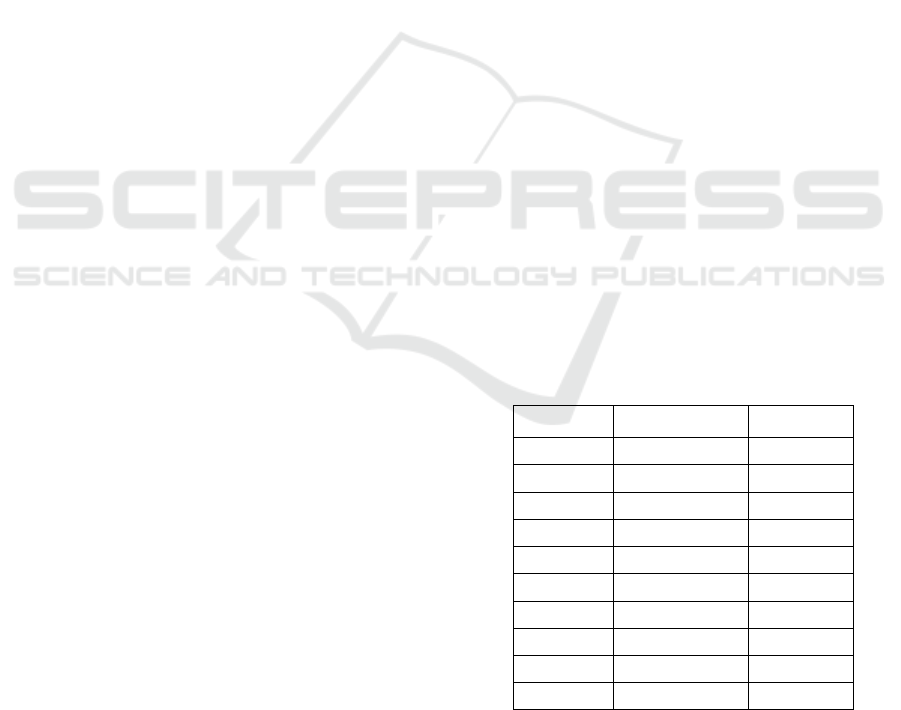
Table 1: Malignant Neoplasms - Severe (2020) Experience

Incidence Table Unit (%).

Age

0-10

0.151727273

0.188513636

11-20

0.16105

0.177435

21-30

0.3451

0.17205

31-40

1.09575

0.299565

41-50

2.87155

0.38123

51-60

5.8071

0.4476

61-70

110.1685

4.4838

71-80

17.0727

0.312105

81-90

21.9204

0.146565

91-100

25.93215

0.07823

2.2.2 Interest Rate Assumption

Plus, the interest rate assumption is an important

assumption that can be used to predict future changes

DAML 2023 - International Conference on Data Analysis and Machine Learning

in interest rates so that premiums can be set

accordingly. The purpose of the interest rate

assumption is to help insurance companies better

manage their risks, and it can also help consumers

better choose insurance products that suit their needs.

In this paper, with reference to the consistent

conservative attitude of insurance companies, and

comparing with the current insurance products

circulating in the market, the interest rate is assumed

to be

2.5%f =

2.2.3 Mortality Assumptions

Next, mortality assumptions in catastrophic insurance

pricing refer to the level of mortality assumed by the

insurer during the pricing process. The mortality (qx)

assumption is an important assumption that can be

used to predict future changes in mortality rates so that

premiums can be set accordingly. The purpose of

mortality assumptions is to help insurers better

manage risk and also to help consumers better choose

insurance products that are suitable for them.

Critical illness insurance belongs to a kind of

health insurance, so this paper adopts the non-pension

business one table in the experience life table of

China's life insurance industry.The relevant data of

different age groups and mortality in non-elderly care

businesses are shown in Table 2.

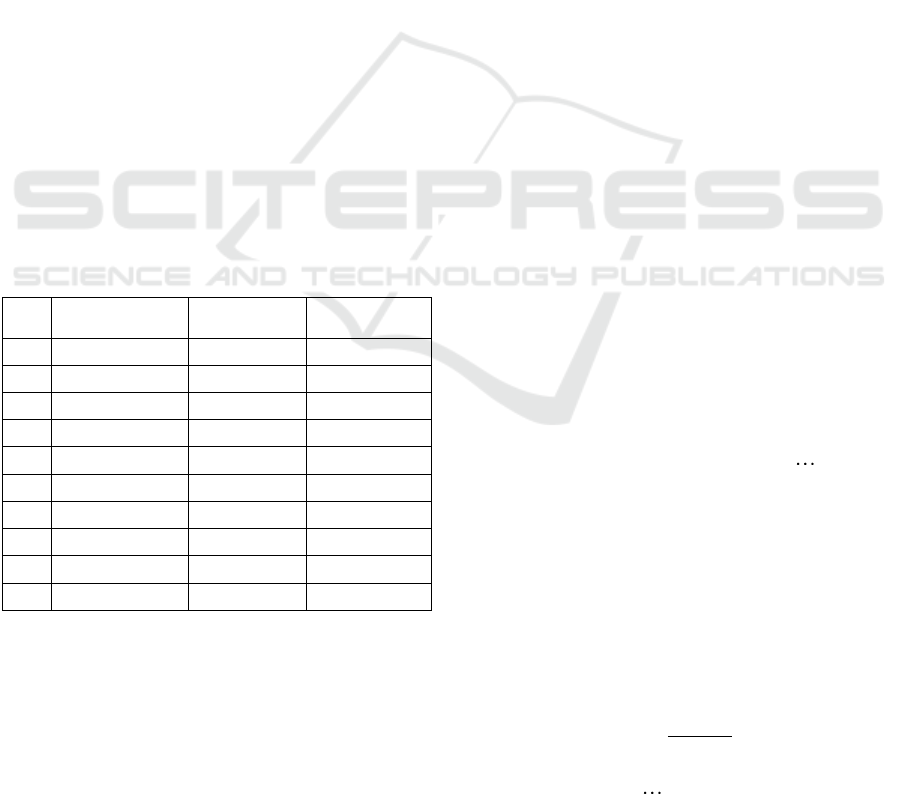
Table 2: Mortality, Real-Time Survival and Real-Time

Death Rates at Different Ages for Non-Pension Operations.

Age

（i）

Mortality

assumptions(qx)

Real-time

survival rate

Real-time

mortality rate

0-10

0.0308%

100.0000%

0.0308%

11-20

0.0314%

99.9692%

0.0314%

21-30

0.0472%

99.9378%

0.0472%

31-40

0.0842%

99.8906%

0.0842%

41-50

0.2061%

99.8065%

0.2061%

51-60

0.4862%

99.6004%

0.4862%

61-70

1.3277%

99.1142%

1.3277%

71-80

4.3794%

97.7865%

4.3794%

81-90

12.3894%

93.4072%

12.3894%

91-100

28.8295%

81.0177%

28.8295%

2.2.4 Internal Corporate Surcharge Rate

Assumptions

In the pricing of critical illness insurance, the internal

company surcharge rate assumption refers to the level

of the internal company surcharge rate assumed by the

insurance company in the pricing process. The China

Banking and Insurance Regulatory Commission

(CBIRC) issued the Circular on Actuarial

Requirements for General Life Insurance in early

2020 in order to enable insurance companies to

compete reasonably and fairly.According to the needs

of the article, the average level of

18%t =

surcharge

rate of the insurance industry in the Circular is

selected.

3 EMPIRICAL STUDY ON

PRICING OF CRITICAL

ILLNESS INSURANCE - AN

EXAMPLE OF SEVERE

MALIGNANT TUMOR

Because the Chinese insurance market is currently not

well equipped with data on the conditions of critical

illness patients of different ages, it is more difficult for

this paper to calculate the intensity of entering a

critical illness state without constant age, but this

paper can make reasonable assumptions by using the

critical illness table and the empirical mortality rate,

and explore as one of the commonly used types of

insurance in practice: the standalone primary type of

whole life critical illness insurance product.

A stand-alone primary type whole life critical

illness insurance policy is a type of critical illness

insurance that consists of two parts, death, and critical

illness liability, which are independent of each other,

each with a single sum assured. If the insured suffers

from a major illness, the insurance company pays the

major illness benefit, then the death benefit will be

zero, and if the insured does not suffer from a major

illness, then the death benefit will be paid.

In the case of such insurance products, the expected

incidence is affected and becomes

i i i x

M X X q=−

1, 2, 3, , 10i i i i= = = =

Corresponding to age groups of

0 10,11 20,21 30,... ,91 100− − − −

years old data

values. Under the above assumptions, the average price

for men and women for the different ages of annual

term critical illness insurance was calculated for the

critical illness experience incidence and normative

mortality rates of the new critical illness table. Where

the assumptions are that the unit sum assured is

100000Q =

30Y =

(1 )

, (1)

here,

1, 2, 3, , 10i i i i= = = =

corresponding to age

groups of

0 10,11 20,21 30,... ,91 100− − − −

. The

Critical Illness Insurance Pricing and Markov Optimization Model: Based on the Analysis of Severe Malignancies in China

premiums for severe malignant tumor diseases in

different age groups are shown in Table 3.

Table 3: Premiums corresponding to severe malignant

neoplasm diseases at different ages.

Age（i）

Premiums（Ii）

0-10

85.32889296

11-20

90.5712186

21-30

194.0466084

31-40

615.9023608

41-50

1612.079383

51-60

3250.93911

61-70

61153.15774

71-80

9183.744862

81-90

10803.66356

4 IMPROVED ALGORITHM FOR

PRICING CRITICAL ILLNESS

INSURANCE BASED ON

MARKOV MODELING

Markov model is a stochastic process model that can

describe the probability transfer relationship of a

system in different states. By building a Markov

model for major disease insurance, this paper can

obtain information such as correlation and transfer

probability between various diseases. This

information can help this paper to predict the

occurrence and risk level of major diseases more

accurately, thus providing a more scientific basis for

pricing (Pasaribu et al 2019).

Taking severe malignant tumors as an example,

the disease has high morbidity and mortality rates,

which impose a huge economic burden on individuals

and society. Therefore, research on pricing strategies

for severe malignant tumors is of great practical

importance. In this paper, this paper will take severe

malignant tumors as an example, and analyze the

degree of influence of different factors on the disease

and the law of transfer by constructing its Markov

model, so as to provide a reference for the

development of reasonable pricing strategies.

The application of the Markov model in the field

of insurance pricing is mainly to analyze the risk

factors of customers and predict their risk level, so as

to set reasonable premiums. The advantage of the

Markov model is that it can take into account the

historical risk factors of the customers, so as to more

accurately predict the future risk level. Also, the

Markov model can take into account a customer's

historical claims history to set more reasonable

premiums. However, Markov models also have some

limitations. First, the Markov model assumes that a

customer's risk factors are fixed, but in reality, a

customer's risk factors may change over time. Second,

the Markov model assumes that a customer's historical

claims record has no effect on premiums, but in

reality, the claims record may affect premiums

(Hailong 2023).

When pricing critical illness insurance, discrete

Markov chains are adopted for modeling, assuming

that the state space is {1,2,3, ... ,k}, then in the

stochastic process {x(t),x>0}, the state at moment t is

denoted by x(t), if it satisfies for all

,0st

and

( )  

, , 1,2,...,i j x u k

, both:

( ) ( ) ( ) ( )

 

( ) ( )

 

0| ,Pr X s t j X s i X u x u u s

Pr X s t j X s i

+ = = =  

= + = =

(2)

This paper then claims that this process satisfies a

discrete Markov chain and can be used as a pricing

model for critical illness insurance.

For the practical application of the Markov model,

the following assumptions need to be made according

to 2023 Zhao Hailong's study:

1) Taking every year as a minimum time interval

unit, first fix the discrete time interval to one year, and

the transfer intensity is uniformly distributed over the

interval, that is, it is a constant, assuming that the

transfer intensity from health to disease is the same as

the transfer intensity from health to death.

2) Assuming that the strength of death at each age

is constant, i.e., constant over an age interval, the

strength of transfer from health to death is also

constant (Chunjuan et al 2023).

3) Under the premise that the transfer intensity is

constant, this paper can take the negative logarithm of

the morbidity rate to derive the transfer intensity of the

health state to the disease state.

Pricing of critical illness insurance, often that the

insurance liability includes major diseases and death

of two, so the pricing of critical illness insurance using

the following formula:

11 12 11 14

( ) ( )

AB t t

X n t x x t x x

A P t v dt P t v dt





(3)

P represents the transfer probability between states,

the two numbers on its superscript represent the

transfer from the initial state to another state, for

example,

represents the probability that the initial

state is i, and at the next moment the state is



DAML 2023 - International Conference on Data Analysis and Machine Learning

the transfer intensity, similar to our understanding of

the deadweight force in the life insurance actuarial,

then similarly



represents the intensity of the initial

state of i, and at the next moment the state of j. The

transfer probability between states is the probability

that the initial state is i, and at the next moment the

state is j. The first letter or number is generally a

transferable state, and the second letter or number is

generally a non-transferable state.

5 CONCLUSION

This paper uses traditional insurance pricing

calculations to see that premiums gradually increase

with age, peaking in the 61-70 age group. With age,

the body's function declines, immunity weakens, and

the risk of malignant tumors increases, so the premium

calculation results are in line with common sense.

Through the case study in this paper, this paper

found that this paper can develop and optimize in the

following areas in the future. In terms of data-driven

precision pricing, with the development of big data

technology, actuarial research on insurance pricing

will pay more attention to the in-depth analysis of the

incidence rate, mortality rate, and treatment cost of

patients with malignant tumors by using big data

technology, so as to realize the precision of pricing

malignant tumor insurance. By mining and analyzing

a large amount of data, insurance companies can be

provided with a more scientific and reasonable basis

for pricing, reducing the risk exposure of insurance

companies and improving the competitiveness of

insurance products. In terms of comprehensive

protection solutions, future actuarial research on

insurance pricing will focus more on the development

of comprehensive malignant tumor insurance products,

covering a variety of treatment modalities, such as

chemotherapy, radiotherapy and surgery, to provide

customers with all-around protection. In addition,

cooperation with related industries such as medical

care and rehabilitation can also be considered to

provide customers with a full range of services from

prevention, and treatment to rehabilitation. Finally, in

terms of policy support and regulation, government

policy support and regulation in malignant tumor

insurance pricing will have a positive impact on

actuarial research. The government can encourage

insurance companies to develop insurance products

for malignant tumors by adjusting tax policies and

providing financial subsidies. The theory of major

disease insurance pricing based on the Markov model

can be used as a basic model for practical application.

Under the premise of data support, according to the

algorithmic process of this paper, more states (e.g.,

healthy, mild, moderate, severe, and death) can be

considered to be added, which has a positive reference

significance to the industry's pricing of critical illness

insurance.

In conclusion, future actuarial research on

insurance pricing in China in terms of malignancy

insurance pricing is expected to achieve precision,

personalization, synthesis, innovation, and

standardization to meet market demand, reduce

patient burden, and promote the healthy development

of the insurance market.

REFERENCES

S. M. Adyani, E Gol-Alizadeh. The Need for

Complementary Health Insurance in Iran and

Suggestions for Its Development. Hospital Practices and

Research, 2018, pp. 146.

C. C. Koay. Development of Critical Illness Insurance in

Selected Markets, 2003.

F. Baione, S. Levantesi. A health insurance pricing model

based on prevalence rates: Application to critical illness

insurance. insurance, Insurance Mathematics and

Economics, 2014, vol. 58, pp. 174-184.

BL. Jone. Modeling Multi-State Processes using a Markov

Assumption. Actuarial Research Clearing House,1993,

vol.1.

E. Pitacco. Actuarial models for pricing disability benefits:

Towards a unifying approach. Insurance: Mathematics

and Economics, 1995, vol. 16, pp. 39-62.

M. C. Christiansen. Multistate Models in Health Insurance.

AStA Advances in Statistical Analysis, 2012, vol. 96,

no. 2, pp. 155‒186.

Z. Hailong. Research on pricing of critical illness insurance

under the new critical illness table. Shanxi University of

Finance and Economics, 2023.

S. Yaling. Pricing research on China's critical illness

insurance under the new critical illness table. Hunan

University, 2022.

US. Pasaribu, H. Husniah, RRKN. Sari, et al. Pricing critical

illness insurance premiums using multiple state

continous markov chain model. Journal of Physics:

Conference Series. IOP Publishing, 2019, vol. 1366, no.

1, 012112.

Q. Chunjuan, L. Yinhuan, T. Xinyue, et al. A study on

pricing of critical illness insurance in the framework of

Markov modeling-estimation based on mortality

effectiveness and morbidity intensity. Statistical

Research, 2023, vol. 40, no. 05, pp. 152-160.

Critical Illness Insurance Pricing and Markov Optimization Model: Based on the Analysis of Severe Malignancies in China