Multiverse: A Deep Learning 4X4 Sudoku Solver

Chaim Schendowich

, Eyal Ben Isaac

and Rina Azoulay

Dept. Computer Sciences, Lev Academic Center, Jerusalem, Israel

Dept. Data Mining, Lev Academic Center, Jerusalem, Israel

Keywords:

Sudoku, Deep Learning, One-Shot Prediction, Sequence Completion.

Abstract:

This paper presents a novel deep learning-based approach to solving 4x4 Sudoku puzzles, by viewing Su-

doku as a complex multi-level sequence completion problem. It introduces a neural network model, termed as

”Multiverse”, which comprises multiple parallel computational units, or ”verses”. Each unit is designed for

sequence completion based on Long Short-Term Memory (LSTM) modules. The paper’s novel perspective

views Sudoku as a sequence completion task rather than a pure constraint satisfaction problem. The study

generated its own dataset for 4x4 Sudoku puzzles and proposed variants of the Multiverse model for compar-

ison and validation purposes. Comparative analysis shows that the proposed model is competitive with, and

potentially superior to, state-of-the-art models. Notably, the proposed model was able to solve the puzzles

in a single prediction, which offers promising avenues for further research on larger, more complex Sudoku

puzzles.

1 INTRODUCTION

In this paper we propose a deep learning model for

solution of 4X4 Sudoku puzzles and show that the

model can solve over 99 percent of the puzzles pro-

vided to it in just a single prediction while state-of-

the-art systems needed more prediction iterations to

attain similar results.

The Sudoku puzzle was ﬁrst introduced in the

1970s in a Dell magazine. It became fairly known

throughout Japan. In the early 2000s, the puzzle

started becoming extremely popular in Europe and

then in the United States, igniting an interest not only

in the form of competitions but also in the form of

scientiﬁc research (see (Hayes, 2006) for a detailed

background). The popularity of the puzzle caused a

lot of research to be done regarding its logic-based

properties and the diverse methods for solving it.

The Sudoku puzzle is composed of a square of

cells with o

rows and o

columns for some natural

constant o called the order of the puzzle. The square

is subdivided into its o

primary o × o squares called

boxes or sub-squares. The boxes divide the rows and

columns into o sets of rows and o sets of columns

called row groups and column groups respectively.

The puzzle begins with some placement of values

1· · · o

in some of the cells called givens or hints. The

object of the puzzle is to ﬁll the rest of the cells with

(a) Boxes. (b) Row Groups. (c) Column Groups.

Figure 1: Depiction of the Sudoku variables.

values so that every row, column, and sub-square will

have all the values from 1 · · · o

. A block is either a

row, a column or a sub-square interchangeably.

Sudoku is considered a logic based puzzle. In fact,

there are many types of logic that must be combined

to solve the hardest of puzzles, ranging from trial and

error to deduction and from inference to elimination.

A Sudoku can, technically, have more than one

correct solution. A Well Posed Sudoku is a puzzle that

has only one correct solution. A puzzle can be easier

to solve if there are redundant hints, namely givens

that can be deduced from one or more other givens. A

puzzle with no redundant hints is called Locally Min-

imal (Simonis, 2005). Figures 2 and 3 demonstrate

examples of the types of puzzles and their solutions.

The puzzle in Fig. 2a is locally minimal because re-

moving any of the numbers will cause it to have more

than one solution thus no longer being well posed. For

example, removing the 2 will cause Fig. 3b to be a

valid solution as well; removing the 1 will make Fig.

Schendowich, C., Ben Isaac, E. and Azoulay, R.

Multiverse: A Deep Learning 4X4 Sudoku Solver.

DOI: 10.5220/0012232500003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 15-22

ISBN: 978-989-758-680-4; ISSN: 2184-433X

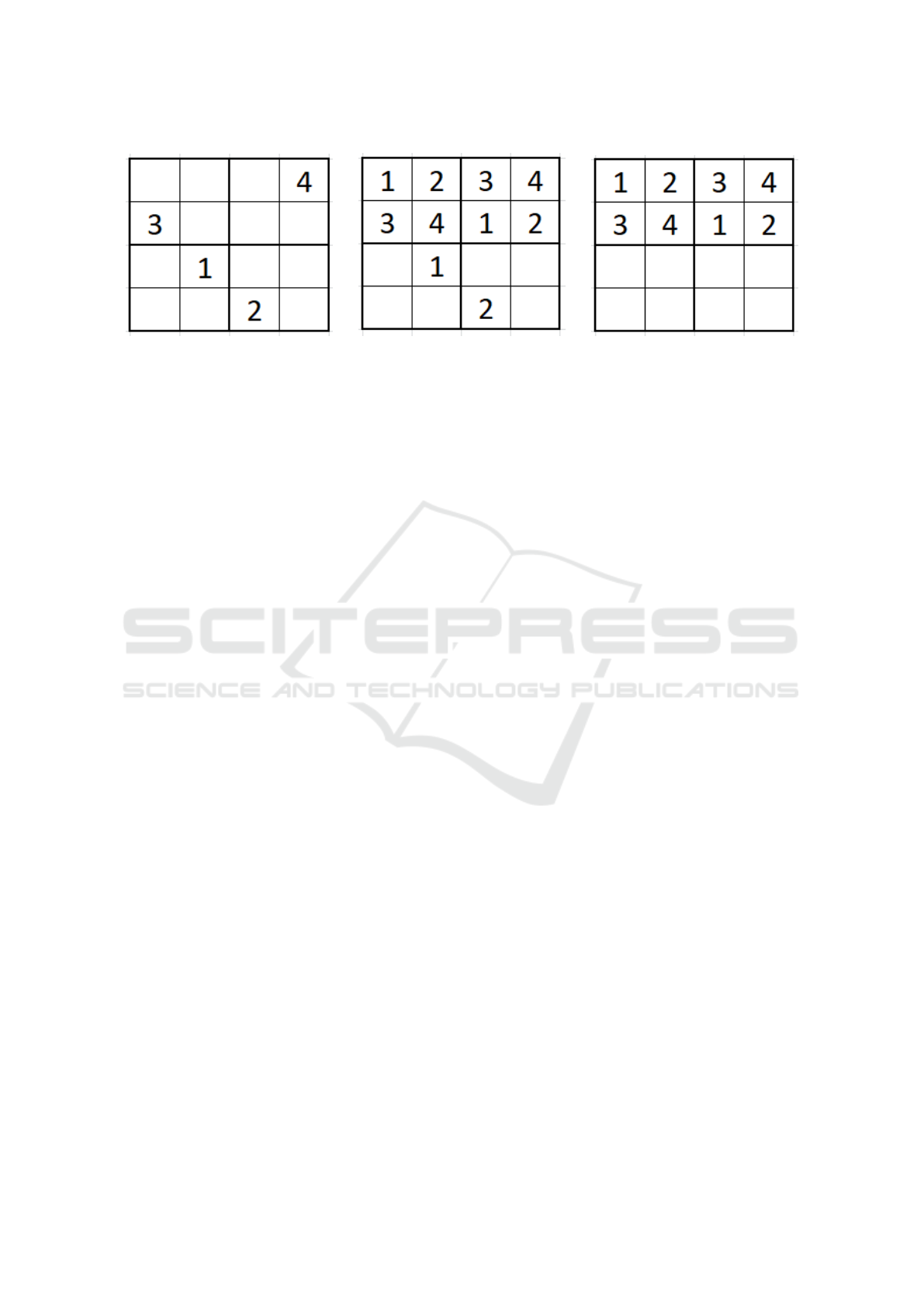
(a) Well posed, locally minimal. (b) Only well posed. (c) Not well posed (4 solutions).

Figure 2: Examples for well posed and locally minimal puzzles.

3d be a valid solution, and so on.

Sudoku can further be classiﬁed as a discrete con-

straint satisfaction problem (CSP). In particular, Su-

doku is a special case of CSPs called an exact cover

problem, where each constraint must be satisﬁed by

only one variable in the solution assignment. Any al-

gorithm that can solve discrete CSPs or exact cover

problems will be able to provide a solution for a Su-

doku, albeit usually in exponential run-time.

Sudoku can also be approached as a Machine

Learning problem, thus described as a multi-class

multi-label classiﬁcation problem, meaning that a

given puzzle has multiple values that need to be deter-

mined (namely the values of the unassigned cells) and

each of those is one discrete value of a shared domain

of integers. Therefore, there are various machine

learning and deep learning methods that might be ap-

plicable to it. Unfortunately, a very high level of gen-

eralization is required for learning the implicit con-

nections between the cells so simple methods are not

good enough here (Palm et al., 2018). Some progress

has been made in this avenue of research, particularly

combining deep learning with other methods (Wang

et al., 2019) or using networks with recurrent predic-

tion steps (Palm et al., 2018; Yang et al., 2023).

In this study, we introduce a novel approach to

tackle Sudoku solving by leveraging a neural network

architecture. Our methodology is rooted in the notion

that Sudoku puzzles share similarities with intricate

sequential data completion problems. To address this,

we devised a specialized sequential completion unit

based on Long Short-Term Memory (LSTM) and in-

terconnected multiple such units in a parallel fashion.

Remarkably, our resultant model exhibits comparable

competence to state-of-the-art models, while obviat-

ing the need for multiple prediction iterations. No-

tably, we demonstrate a substantial disparity between

our model and existing approaches in terms of perfor-

mance when such iterations are excluded.

Drawing upon the notion that Sudoku represents a

complex sequential data completion task, we adopted

bespoke deep learning techniques to tackle its solu-

tion. Recognizing that the puzzle’s completion pro-

cess entails a multi-dimensional sequence, our pro-

posed model incorporates multiple parallel computa-

tional units. For the sake of simplicity, our investiga-

tion primarily focuses on training the model on 4x4

puzzles that exhibit local minimality. Through one-

shot prediction, we achieved an impressive comple-

tion rate exceeding 99 percent, effectively showcas-

ing the neural network’s capacity to grasp the abstract

relationships among the puzzle’s cells.

To the best of our knowledge, even though Large

Language Models (LLMs) have been used for Sudoku

solving, there has not been previous research based on

the premise that Sudoku is a sequential completion

problem. We show that this approach is effective and

justiﬁable.

2 RELATED WORKS

Since solution by logic based algorithms has proven

intractable for difﬁcult puzzles of high order, auto-

mated Sudoku solving has become the object of a

large amount of highly varied research.

Simonis (Simonis, 2005) did a thorough job deﬁn-

ing the basic constraints in Sudoku puzzles. He also

showed that these constraints can be described in var-

ious ways, creating additional redundant constraints

with which the puzzles can be solved more efﬁciently.

In his paper, he compares 15 different strategies based

on constraint propagation and showed that the well

posed puzzles in his dataset can all be solved by an

all-different hyperarc solver, if the execution starts

with one shaving move.

Hunt et al. (Hunt et al., 2007) took this one step

further by showing that the constraints can be real-

ized in a binary matrix solvable by the DLX algorithm

provided by Knuth (Knuth, 2000) and that many of

the common logical solving techniques can be sum-

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

(a) The solution for Fig. 2. (b) 2nd solution for Fig. 2c. (c) 3rd solution for Fig. 2c. (d) 4th solution for Fig. 2c.

Figure 3: Solutions for puzzles in Fig. 2.

marized in a singe theorem based on that matrix. The

advantages of using DLX is that the algorithm is faster

than other backtracking algorithms and also provides

the number of possible solutions thus giving indica-

tion if a puzzle is well posed or not. The disadvantage

in using DLX is that since it is a backtracking algo-

rithm its run-time is exponential by nature.

Another related approach can be found in the

works of Weber (Weber, 2005), Ist et al. (Ist

et al., 2006) and Posthoff and Steinbach (Posthoff

and Steinbach, 2010) who all model Sudoku as a

SAT problem and use various SAT solvers to solve

it. This method utilizes powerful existing systems

but requires explicit deﬁnition of the rules and lay-

out of each puzzle, a number of clauses which could

expand exponentially with more complex puzzles. In

our study we favoured machine learning because it

obviates the need of explicit description of the logic

problem.

As mentioned in the introduction, deep learning is

also a good candidate for Sudoku solving. The advan-

tage of machine learning systems in general and deep

learning systems in particular is that they can gener-

alize a direct solution for a problem without having

to use algorithms of exponential or worse runtimes

to solve particular instances of the problem. Once

trained, such a model could be signiﬁcantly better

even than the DLX algorithm.

Park (Park, 2018) provides a model based on a

standard convolutional neural network that can solve

a Sudoku in a sequence of interdependent steps. It

solved 70 percent of the puzzles it was tested on, us-

ing a loop that predicted the value of the one highest

probability cell in each iteration.

Palm et al. (Palm et al., 2018) created a graph

neural network that solves problems that require mul-

tiple iterations of interdependent steps and showed

that it solved more than 96 percent of the Sudokus

presented to it, including very hard ones as well, al-

though the solution in this method had to be done in

a sequence of interdependent steps. While the results

achieved are noteworthy, it’s important to acknowl-

edge that they necessitated both an understanding of

the problem structure coded manually and a series of

predictive steps towards a solution. In contrast, our

study eliminates the need for prior knowledge of the

problem’s architecture and successfully resolves the

puzzles in a single prediction step.

Wang et al. (Wang et al., 2019) combined a SAT

solver with neural networks to add logical learning

methods that can overcome the difﬁculty traditional

neural networks have with global constraints in dis-

crete logical relationships. Using that combination

they succeeded in attaining a 98.3 percent comple-

tion rate without any hand coded knowledge of the

problem structure. This approach differs from our ap-

proach in that it requires the use of a SAT solver to

complement the prediction provided by the network.

Moreover, Chang et al. (Chang et al., 2020) showed

that the good results presented by Wang et al. (Wang

et al., 2019) are limited to easy puzzles and the results

are signiﬁcantly worse than those of Palm et al. (Palm

et al., 2018) when trying to solve hard puzzles.

Mehta (Mehta, 2021) created a reward system for

a Q-agent and achieved 7 percent full puzzle com-

pletion rate in easy Sudokus and 2.1 and 1.2 per-

cent win rates in medium and hard Sudokus respec-

tively all with no rules provided. She did this un-

aware of Poloziuk and Smrkovska (Poloziuk and Sm-

rkovska, 2020) who tested more complex Q-based

agents and Monte-Carlo Tree Search (MCTS) algo-

rithms and came to the conclusion that they require

too much computation power to be used reasonably

to solve Sudoku. With MCTS they performed a small

number of experiments achieving 35-46 percent ac-

curacy and called it a success, even though the results

are fairly low, considering that in each experiment the

training took them days to perform.

Du et al. (Du et al., 2021) used a Multi Layered

Perceptron (MLP) to solve order 2 puzzles. They cre-

ated a small 4 layer dense neural network and per-

formed their prediction stage by stage each time ﬁll-

ing in only the one highest probability cell. Their

dataset included puzzles none of which were locally

minimal - all missing between 4 and 10 values. Their

model solved more than 99 percent of the puzzles

Multiverse: A Deep Learning 4X4 Sudoku Solver

tested. However, the vast majority of the puzzles

tested were not locally minimal and the number of

prediction iterations they required were equal to the

number of missing values. In our study, we not only

performed experiments on locally minimal puzzles

with 10, 11, or 12 missing values - the hardest well

posed order 2 puzzles - and attained a completion rate

greater than 99 percent, but did so in a single predic-

tion step, albeit with a more intricate model.

Yang et al. (Yang et al., 2023) trained a generative

pre-trained transformer (GPT) based model with the

dataset used by Palm et al. (Palm et al., 2018) and

tested it with iterative predictions. They had supe-

rior results, solving more than 99 percent of the puz-

zles, although when restricted to the hardest puzzles

achieved a 96.7 percent completion rate. However,

Yang et al. (Yang et al., 2023) required a sequence

of prediction steps to reach the solution and did not

provide a solution in one end-to-end prediction. They

needed 32 prediction iterations to achieve their results

in order 3 puzzles. The baseline for our study is the

model used by Yang et al. (Yang et al., 2023) modi-

ﬁed for order 2 puzzles. We show that our model has

competitively good results in less prediction iterations

than required by their model.

As can be seen above, the signiﬁcant results so

far have been achieved only in systems that integrate

sequences of interdependent prediction stages. In this

paper we propose a model that achieves competent

results in a single prediction stage.

3 DEEP LEARNING METHODS

Our paper introduces a deep learning approach specif-

ically targeted at tackling order 2 Sudoku puzzles.

These are 4x4 puzzles that, while smaller in scale

compared to the standard order 3 Sudokus, present a

unique appeal for scientiﬁc investigation. Given their

relative simplicity, both in terms of representation and

analysis, focusing our research on order 2 puzzles en-

ables more rapid training and facilitates quicker at-

tainment of results.

We consider Sudoku to be akin to a sophisticated,

multi-layered sequence completion problem. With

this perspective, we developed a deep learning neu-

ral network that leverages LSTM modules designed

for sequence completion. This approach has yielded

results that are on par with current leading models.

While our demonstrated results are limited to or-

der 2 puzzles, we maintain the belief that these puz-

zles are sufﬁciently complex to serve as a sound foun-

dation for creating a successful model for higher-

order Sudoku problems. The importance of study-

Table 1: Well Posed Order 2 Puzzle Count.

H WP LM H WP LM

4 25728 25728 10 2204928 0

5 284160 58368 11 1239552 0

6 1041408 1536 12 522624 0

7 2141184 0 13 161280 0

8 2961024 0 14 34560 0

9 2958336 0

H - The number of hints in the puzzle.

WP - Well Posed, LM - Locally Minimal.

ing 4x4 puzzles lies in the opportunity they provide to

build, test and reﬁne models that could be efﬁciently

scaled to more intricate Sudoku variants. This makes

them an essential stepping stone in advancing deep

learning methodologies for solving larger and more

complex problems.

In this section we bring the technical information

of our methods, in particular the data composition and

the structure of our models.

3.1 Datasets

Since most of the research into Sudoku was on order

3 puzzles, we did not ﬁnd an existing dataset of order

2 puzzles so we created our own.

There exist exactly 288 unique order 2 solved Su-

doku boards. Those boards represent 85632 puzzles

which are both well posed and locally minimal, each

containing only 4, 5, or 6 hints. It is possible to create

a larger number of well posed puzzles by adding more

hints, although those puzzles are not locally minimal.

Figures 2 and 3 demonstrate examples for the various

possible types of puzzles and their solutions. Table 1

shows the full number of well posed puzzles with 4 to

14 hints and how many of them are locally minimal.

Our primary dataset consists of all 85632 well

posed and locally minimal order 2 puzzles. Details

on the generation process of the puzzles is provided

in the appendix. The training of our models was per-

formed on a subset of 77069 puzzles using 9-fold

cross validation (We divided the puzzles into 10 sub-

sets and left one out of the process).

The puzzles and their solutions are composed of

strings of digits, where missing values are denoted as

zeros. Since the values are discrete and categorical,

we one-hot encoded them into ﬁve digit binary vec-

tors in order to make processing easier.

3.2 Machine Learning Models

Below we describe the models used in this study. The

ﬁrst section describes our main model, a neural net-

work architecture we call the Multiverse, which is

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

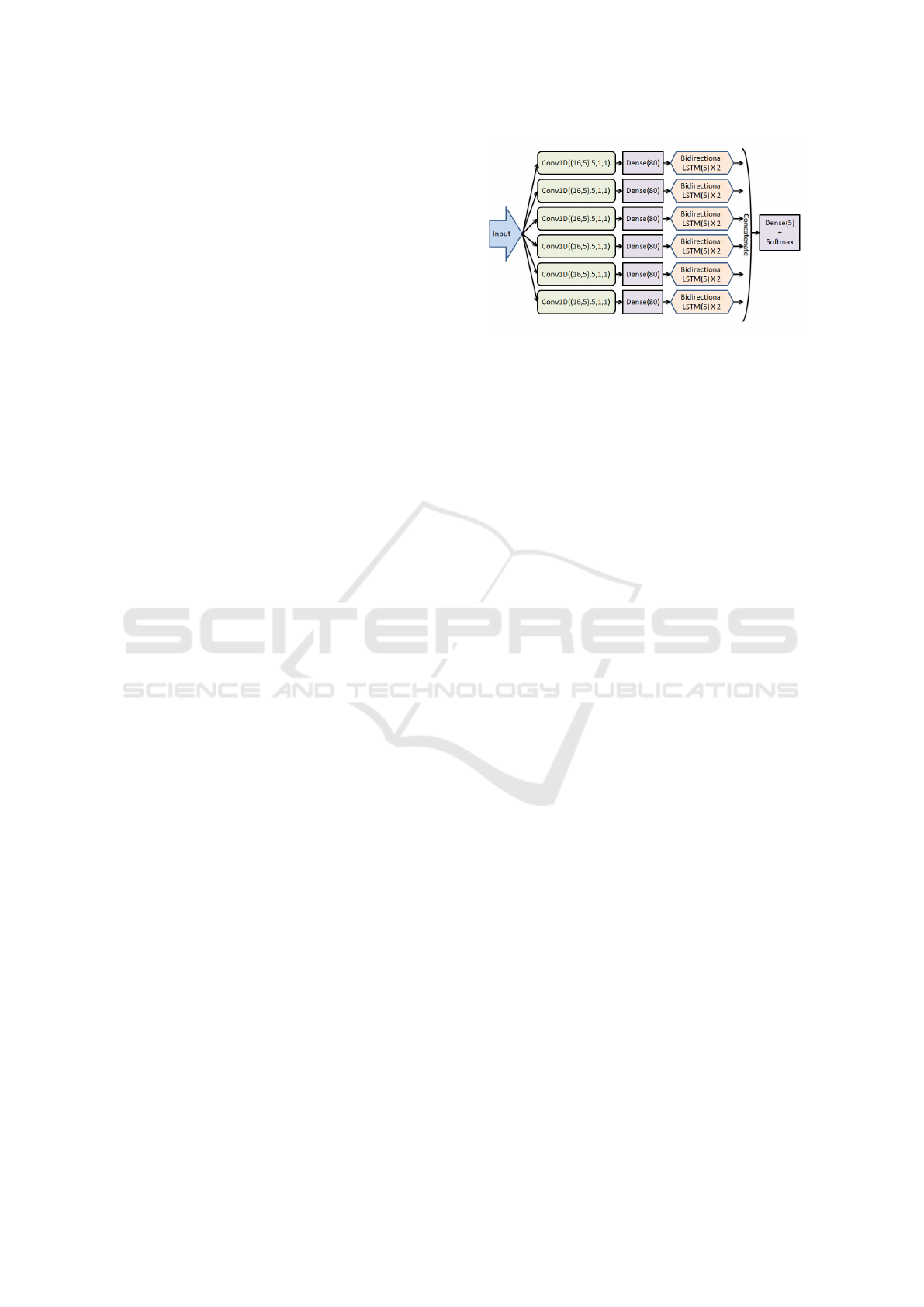
composed of a set of parallel computational units.

The next two sections describe variants of the Mul-

tiverse model that we used for our convergence study

and our ablation study. These studies show that all

the parts of each computational unit are important for

the results attained and the results are competent with

state-of-the-art models. The last section describes the

model we used as a baseline for our study.

Multiverse Model

In the model description below, we use the following

variables. o is the order of the puzzle (o = 2 for all

the tests in this study). r is the size of the range of

values possible in a given puzzle (r = 5 for all the

tests in this study, to include the 4 possible values and

zero). s is the length of a side of a given puzzle (s = o

always). a is the number of cells in a given puzzle

(a = s

always).

Sudoku in many respects is a sequence completion

problem. Each row must be completed with a permu-

tation of the values in the range. Each column and box

must be completed likewise. Each value must have a

location in each row forming a sequence of value-in-

row location indices that requires completion. Sim-

ilarly, such sequences are also formed by values in

columns and boxes. There may exist more aspects of

Sudoku puzzles that can also be viewed as completion

problems but that is subject for a separate study.

Our initial sequence completion unit (below re-

ferred to as a “verse”) is the following sequence of

deep learning layers, with reshape layers between

them where necessary:

1. Conv1D, where: input size = (a, r), output size =

(a, r), ﬁlters = r, kernel size = 1, strides = 1

2. Dense, where: input size = (a × r), output size =

(a × r)

3. Bidirectional LSTM, where: input size = (a, r),

output size = (a, 2 × r), return sequences is set to

true.

4. Bidirectional LSTM, where: input size = (a, 2 ×

r), output size = (a, 2 × r), return sequences is set

to true.

Our complete model is composed of a number

of parallel verses with their output concatenated into

a dense softmax termination layer (hence the name

“Multiverse”). A Multiverse model for order 2 puz-

zles with 6 parallel verses (M6) is depicted in Fig-

ure 4. The motivation for this architecture is that the

combination of the convolutional and the dense layers

provide a basic embedding feature that allows for dif-

ferent interpretations for the parallel verses. The Bidi-

rectional LSTM is a good sequencing modeler when

Figure 4: An order 2 Multiverse model with 6 parallel verse

modules.

the direction is unimportant. Unlike NLP problems,

Sudoku data is discrete and all-different removing the

semantic related aspects from the problem, so other

techniques that have greater effect when used on text

related problems are not required here.

Convergence Study Models

Some of the conﬁgurations of the baseline model sur-

passed a 99 percent completion rate, albeit with more

than one prediction, so we performed a study testing

the number of verses required to attain such presti-

gious results in one-shot predictions. This study was

performed on Multiverse models with 6 (See Fig. 4),

10 and 12 parallel verses (called M6, M10, and M12

respectively). M6 was our ﬁrst robust model with sig-

niﬁcantly good results. We based most of our study

around that model, but also tested the more powerful

M10 and M12 models to show that results achieved

by the baseline are attainable by our model as well.

The results themselves will be detailed in Section 4.

Ablation Study Models

We performed our ablation study on the following in-

complete Multiverse models with 6 verses:

• M6 - 6 complete verses.

• No Conv - 6 verses that have no Conv1D layers.

• No Dense - 6 verses that have no Dense layers.

• No LSTM - 6 verses that have no LSTM layers.

• One LSTM - 6 verses that have only the ﬁrst

LSTM layer.

• M5 - Only 5 verses, all complete.

Results will be detailed in Section 4.

Baseline Model

As a baseline we modiﬁed the transformer based

model provided by Yang et al. (Yang et al., 2023) to

Multiverse: A Deep Learning 4X4 Sudoku Solver

ﬁt our order 2 data. The model is based on a MinGPT

module (Karpathy, 2020) set to the input of a Su-

doku puzzle. MinGPT performs the computations on

sparse categorical data. Therefore, the input is not

one-hot encoded, rather left in numerical format with

one change: all the values in the solution that corre-

spond to hints were changed to -100. We maintained

this data format in our modiﬁed model.

For a convincing comparison with our model we

ran tests on the baseline model with a variety of set-

tings for the following parameters:

• Recurrences - The number of prediction itera-

tions. We refer to this parameter by the name It-

erations so as not to confuse with RNN.

• Heads - The number of transformer heads used.

• Embedding - The size of the puzzle embedding.

The outcomes will be elaborated upon in Section 4.

4 RESULTS

This section contains the experiments performed in

our study and the results they yielded. The ﬁrst ex-

periment recorded highlights the effectiveness of our

approach by yielding an impressive completion rate

greater than 99 percent in a single prediction itera-

tion. The second experiment determines the neces-

sity of all the components of our model by showing

the vast improvement each component contributes to

the results. Finally, we present a baseline experiment

resulting with a favorable comparison with state-of-

the-art models. All the training and the testing was

performed using Google Colaboratory.

The metric used in all the tests is the completion

rate, namely the percent of puzzles completed cor-

rectly out of the grand total.

4.1 Convergence Study

With the intent of maximizing the completion rate

of order 2 Sudoku puzzles, our study has produced

compelling ﬁndings. The performance of our model,

demonstrated in Table 2 and Figure 5, underscores

the strength of our research approach. Our 12 verse

model successfully achieves an impressive comple-

tion rate of over 99 percent within just 22 epochs, all

within a solitary prediction iteration.

This highlights the ability of our model to effec-

tively tackle nearly all order 2 puzzles, demanding

only a single predictive step for solution. This ro-

bust performance does not only exemplify the model’s

precision, but also its proﬁciency in rapidly deriving

solutions.

Table 2: Convergence Study Results.

Model No. Epochs Completion Rate

M6 100 92 percent

M10 28 97 percent

M12 22 >99 percent

Figure 5: Completion percentages of M6, M10 and M12

models by number of training epochs.

4.2 Ablation Study

In the ablation study our intent is to show that all the

parts of the model are required and important for the

results achieved.

Table 3 shows the results of the ablation study.

When using complete verses, the completion rates are

higher than when using partial verses, as illustrated

by the M5 completion rate which is higher than all the

completion rates attained by incomplete M6 variants.

As far as the components of each verse are concerned,

The LSTM layers and the dense layer have the great-

est effect on the results as shown by the signiﬁcantly

low completion rates attained by the No LSTM and

the No Dense models, while the convolutional layer

also has an important role to play as shown by the rel-

atively low completion rates attained by the No Conv

model.

Table 3: Ablation Study Results.

Epochs

Model 5 10 15

M12 87.63 96.25 98.21

M10 86.3 93.25 95.14

M6 73.19 83.18 86.53

No Conv 49.22 68.49 76.11

No Dense 1.69 5.73 9.34

No LSTM 9.5 9.26 9.23

One LSTM 66.01 77.53 81.43

M5 67.04 78.41 82.4

Results are in percent of completion rate.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

4.3 Baseline

We now compare our method with the state-of-the art

model. To do so we made use of a modiﬁed version

of the model used be Yang et al. (Yang et al., 2023).

Table 4 shows the results of the tests done on the

baseline model over 15 epochs. The original order 3

model had Embedding set to 128 and Heads set to 4.

Since the order 2 problems are simpler than order 3

problems we tried using less complex models with-

out signiﬁcant results. Since our M6 model might be

comparable with a 6 head transformer model, we also

tested some models that have 6 heads.

Table 4: Baseline Results.

Iterations

Embedding Heads 1 2

16 2 0 0

16 4 0 0.0011

32 2 0.5189 24.41

32 4 0.8822 41.96

128 2 13.17 89.8

128 4 25.06 >99

24 6 2.42 5.28

96 6 27.06 >99

All tests were performed over 15 epochs.

As can be seen, none of the tests reached signiﬁ-

cant results when Iterations was set to 1. In fact, we

continued the 128 embedding 4 heads model up to

200 epochs (the number of epochs used for order 3

in (Yang et al., 2023)) and the results were still only

37.19 percent completion and rising really slowly in

contrast with the 98.21 percent achieved by M12 in

just 15 epochs of training and one prediction itera-

tion, and the 86.53 percent and 82.4 percent achieved

by M6 and M5 respectively (See Table 3).

With 2 iterations the 128 embedding 4 heads

model and the 96 embedding 6 heads model both

achieved >99 percent completion. Even though these

results are excellent, it must be noted both models re-

quired 2 prediction iterations and the results attained

in just one iteration were very poor. This is in con-

trast with our convergence study in which we showed

that the M12 model can achieve a similar >99 percent

completion rate with just one iteration.

5 CONCLUSION

In this paper we approached the Sudoku problem as

a sophisticated sequence completion problem and de-

scribed models for solving 4X4 Sudoku puzzles.

To the best of our knowledge, previous studies

have refrained from using regular end-to-end deep

learning for Sudoku solving because of the implicit

logical connections necessary for the solution. In our

research, we show that when addressing the problem

as a multi-dimensional sequence completion problem

it is possible to reach competent results even with only

a single prediction.

On order 2 puzzles, our M12 model successfully

reached an over 99 percent completion rate with a sin-

gle prediction, a result which required another predic-

tion iteration by the baseline model. The implication

of this result is that not only our model is capable of

solving Sudoku puzzles despite their complexity, but

may prove to have greater competence in this ﬁeld

than the state-of-the-art models.

Future studies should focus on trying to scale up-

ward to order 3 puzzles, to see if the existing datasets

used in other studies are enough to reach signiﬁcant

results in less prediction iterations. The described

model is easily scalable to higher-order Sudoku puz-

zles by adjusting the value of o and adding more

verses. However, two key challenges need to be ad-

dressed: the availability of data, as higher-order puz-

zles have a vast number of possible solutions mak-

ing it difﬁcult to compute and store them, and the re-

source requirements - including signiﬁcant memory

drain and longer training times when scaling up to

higher-order puzzles. These issues taken into account,

it would be interesting to see if competitive results

could still be reached with less predictions.

Future research could also attempt to solve well

posed exact cover problems using the Mutiverse

model. Although the DLX algorithm is capable of

solving such problems, deep learning could reduce

the prediction process to polynomial runtime. The bi-

nary constraint matrix that describes an exact cover

problem could be approached as an extractive se-

quence summary problem, where only those variable

assignments that are relevant for the solution are ex-

tracted from the partially complete list of possible as-

signments that remain after applying the givens of

the problem. The factors contributing to our model’s

strong performance in sequence completion may also

be applicable to extractive sequence summary.

REFERENCES

Chang, O., Flokas, L., Lipson, H., and Spranger, M. (2020).

Assessing satnet’s ability to solve the symbol ground-

ing problem. Advances in Neural Information Pro-

cessing Systems, 33:1428–1439.

Du, H., Gao, L., and Hu, X. (2021). A 4× 4 sudoku solving

model based on multi-layer perceptron. In 2021 Inter-

national Conference on Electronic Information Engi-

Multiverse: A Deep Learning 4X4 Sudoku Solver

neering and Computer Science (EIECS), pages 306–

310. IEEE.

Hayes, B. (2006). Unwed numbers. American scientist,

94(1):12.

Hunt, M., Pong, C., and Tucker, G. (2007). Difﬁculty-

driven sudoku puzzle generation. The UMAP Journal,

29(3):343–362.

Ist, I. L., Lynce, I., and Ouaknine, J. (2006). Sudoku as

a sat problem. In Proceedings of the International

Symposium on Artiﬁcial Intelligence and Mathemat-

ics (AIMATH), pages 1–9.

Karpathy, A. (2020). mingpt.

Knuth, D. E. (2000). Dancing links. arXiv preprint

cs/0011047.

Mehta, A. (2021). Reinforcement learning for constraint

satisfaction game agents (15-puzzle, minesweeper,

2048, and sudoku). arXiv preprint arXiv:2102.06019.

Palm, R., Paquet, U., and Winther, O. (2018). Recurrent

relational networks. Advances in neural information

processing systems, 31.

Park, K. (2018). Can convolutional neural networks crack

sudoku puzzles.

Poloziuk, K. and Smrkovska, V. (2020). neural networks

and monte-carlo method usage in multi-agent systems

for sudoku problem solving. Technology audit and

production reserves, 6(2):56.

Posthoff, C. and Steinbach, B. (2010). The solution of dis-

crete constraint problems using boolean models-the

use of ternary vectors for parallel sat-solving. In In-

ternational Conference on Agents and Artiﬁcial Intel-

ligence, volume 2, pages 487–493. SCITEPRESS.

Simonis, H. (2005). Sudoku as a constraint problem. In CP

Workshop on modeling and reformulating Constraint

Satisfaction Problems, volume 12, pages 13–27. Cite-

seer.

Wang, P.-W., Donti, P., Wilder, B., and Kolter, Z. (2019).

Satnet: Bridging deep learning and logical reasoning

using a differentiable satisﬁability solver. In Interna-

tional Conference on Machine Learning, pages 6545–

6554. PMLR.

Weber, T. (2005). A sat-based sudoku solver. In LPAR,

pages 11–15.

Yang, Z., Ishay, A., and Lee, J. (2023). Learning to solve

constraint satisfaction problems with recurrent trans-

former. In The Eleventh International Conference on

Learning Representations.

APPENDIX

Order 2 Puzzle Dataset Generation

The generation process of locally minimal well posed

order 2 puzzles and their solutions was a 3 stage pro-

cess. The ﬁrst stage entailed creating a ﬁle contain-

ing all the 288 unique solutions for order 2 puzzles

(solutions). We also needed to create a ﬁle with all

the 65534 possible 16 bit binary strings except for an

all-0 string which is an empty puzzle and obviously

not well posed and an all-1 string which is a com-

pleted solution (bitmasks). The bitmasks ﬁle was cre-

ated in descending order of the amount of zeroes in

the strings. In the ﬁnal stage, for each solution in so-

lutions we iterated over bitmasks and ﬁltered the well

posed and locally minimal puzzles resulting with a

ﬁle with all the 85632 well posed and locally minimal

puzzles and their respective solutions (puzzles).

Stage 1: Order 2 Solutions

Since there are only 288 unique solutions for the or-

der 2 Sudoku problem, this stage is very straightfor-

ward. We simply took an empty puzzle, applied to it

the DLX algorithm, and saved to a ﬁle all the resulting

solutions.

Stage 2: Binary Strings

Creation of the bitmasks ﬁle was done with array ma-

nipulation. We created empty arrays and added to

them indices of locations where a bit in a mask should

be ‘1’, by gradually appending to the arrays more ar-

rays that are based on them and have more indices

added to them. After that we scanned the arrays and

transformed them into bit strings.

The algorithm runs in Θ(2

) for order 2 puz-

zles, and if modiﬁed for order o puzzles its runtime

is Θ(2

area

), where area = side

and side = o

. It uses

a similar amount of memory.

Stage 3: Order 2 Puzzles

This stage approaches the binary strings in bitmasks

as binary masks. We consider a mask a to cover

another mask b if for every i where b[i] =‘1’, also

a[i] =‘1’.

For each solution in solutions we iterate over the

binary masks in bitmasks and for each mask m we

check the following conditions:

• Has a puzzle already been added whose mask is

covered by m (and the refore the puzzle is not lo-

cally minimal)?

• Is the corresponding puzzle well posed?

If the ﬁrst condition is false and the second is true

we add the corresponding puzzle and its solution to

puzzles.

In order to check if a puzzle is well posed we ap-

ply to it the DLX algorithm and test if the number of

solutions is equal to 1.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence