Twisted Strategy Bolsters Minority Cooperator Populations

Akihiro Takahara

and Tomoko Sakiyama

Information Systems Science, Graduate School of Science and Engineering, Soka University, Tokyo, Japan

Department of Information Systems Science, Faculty of Science and Engineering, Soka University, Tokyo, Japan

Keywords: Spatial Prisoner’s Dilemma, Populations, Minority.

Abstract: Defectors tend to survive in the spatial prisoner's dilemma. Thus, many studies have sought to keep the

cooperator alive. Here, we aimed to enhance the survival of the cooperator by considering the memory length

in the spatial prisoner's dilemma. In the proposed model, all players are assigned a memory length. Based on

this memory length, players updated their strategies to those that were harder to choose in the past only when

the score of each neighbor with the same strategy was high. This above strategy update rule therefore

alleviates a disadvantageous situation for the player. In this paper, we focused on two cases where the

cooperators were initially in the minority and observed their evolution over time. The results showed that the

model eventually strives to maintain the cooperator population even when it was initially low.

1 INTRODUCTION

Cooperative behaviors are characteristic of several

animals including humans (Smith and Price, 1973).

Game theory presents the evolution of cooperation

among defective players (Nowak and May 1992,

Marko et al. 2022). In classical game theory, players

have two different strategies: the cooperative strategy

or the defector strategy. Defectors earn higher payoffs

against the opponent if the opponent is cooperative.

However, defectors earn a low payoff against the

defector opponent (Doebeli and Hauert, 2004, Hauert

and Doebeli, 2005). On the other hand, cooperators

share payoffs with each other if they mutually interact

with each other. Using the payoff matrix, classical

game theory has revealed that cooperators cannot

survive under some conditions (Doebeli and Hauert,

2004). To this end, many models have been

developed for the sake of the evolution of cooperative

players (Qin et al. 2018, Sakiyama and Arizono,

2019, Sakiyama, 2021).

Recently, we developed a spatial prisoner’s

dilemma (SPD) model called the twisted PD (TPD)

model, where players considered the past occurrence

of each strategy for themselves and sometimes

ignored the classical strategy update rule (Takahara

and Sakiyama, 2023). At that time, players adopted

an unlikely strategy. As a result, the TPD model

https://orcid.org/0000-0002-2687-7228

outperformed the classical SPD. In fact, studies have

revealed that introducing memory to players in the

system facilitates cooperation (Danku et al. 2019,

Deng et al. 2017, Javarone, 2016).

In this paper, we analyzed the flexibility of the

TPD model by considering a situation where the

cooperator population was a minority in the initial

spatial distribution. In other words, most of the

population was a defector. Under these conditions, a

cooperative population developed in the TPD model

over time.

2 METHODS

2.1 Simulation Environments

A 100 × 100 square lattice was formed. Players were

placed in all cells and initially assigned a cooperator

initial distributions of strategies: one where the value

of initial density of defector r was set to 0.5, 0.9, 0.95,

or 0.99 while a random uniform distribution was used

for the players, and one where cooperators were

placed on the center cell and its neighboring four cells

in a fixed distribution, while the remaining players

were defectors. We therefore assessed the

Takahara, A. and Sakiyama, T.

Twisted Strategy Bolsters Minority Cooperator Populations.

DOI: 10.5220/0012262000003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 1, pages 175-178

ISBN: 978-989-758-680-4; ISSN: 2184-433X

175

performance of the model where cooperators were

initially in the minority.

Payoff was set to T = b, R = 1, and S = P = 0 based

on the payoff matrix shown in Table 1, where T > R

> P > S. The parameter b that determines T was set to

1 < b < 2 (Nowak & May, 1992). A player with

strategy D received T if the neighboring player was

assigned strategy C. A player with strategy C received

S if the neighboring player was assigned strategy D.

If both strategies were D, the player earned P.

However, if both strategies were C, the player

received R. We used the Neumann neighborhood and

periodic boundary conditions. Individual players

interacted with players above, below, and to the left,

and right of them. Each trial was included 1000 time

steps.

Table 1: Payoff matrix.

nei

hbo

C D

Player C

𝑅1 𝑆0

𝑇𝑏 𝑃0

2.2 Model Description of SPD

The iteration was initiated after a strategy was

assigned to each player, who compared

neighborhoods, and strategies based on the payoff

matrix and calculated a score. After completing this

task, they compared score with their neighbors and

memorized the strategy of the neighbor with the

highest score. The strategy of each player was then

synchronously updated to the learned strategy.

However, the strategy was not updated if there were

multiple nearby players with the same highest score

but different strategies.

2.3 Model Description of the TPD

Model

Here, we describe the twisted Prisoner’s Dilemma

model (TPD model) (Takahara & Sakiyama, 2023),

where every player is assigned a length of memory of

value p that was constant between trials. After the

score was calculated, each player reflected on his or

her previous strategy. The length of the past

considered is from t (current) to t −p, and the number

of experienced cooperative strategies was recorded in

the parameter Count_c.

If neighboring players had the same strategy while

the player had a lower score, the player updated their

strategy using one of the two following probabilities:

The player will update its strategy to C with the

following probability:

1- (Count_c)/p

The player will update its strategy to D with the

following probability:

(Count_c)/p

If the above conditions were not satisfied, the rule

of the SPD model was applied for the strategy update.

The strategy of each player synchronously

updated. In this model, the strategy update rule to use

the values of p that was different from the SPD model

rules was not executed until t was greater than p. The

proposed model was based on the following concept:

the player changes their behavior when their score is

lower than that of neighbors who have the same

strategy.

3 RESULTS

3.1 Defector Density

First, the r was set to 0.5, 0.9, 0.95, and 0.99, whereas

p was fixed at 10. The defector density over 1000 time

steps was calculated by averaging 10 trials. The

results are shown in Figure 1. We found that an

initially large defector populations did not affect the

evolution of cooperators, though cooperators did not

survive if r was set to 0.99. This is perhaps because

not enough cooperators are placed, and they cannot

interact with each other.

Figure 1: Defector density for various values of r (0.5, 0.9,

0.95, 0.99).

Next, we switched the initial distribution of

players to the second condition, where each

cooperator was placed on the center cell and its

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

176

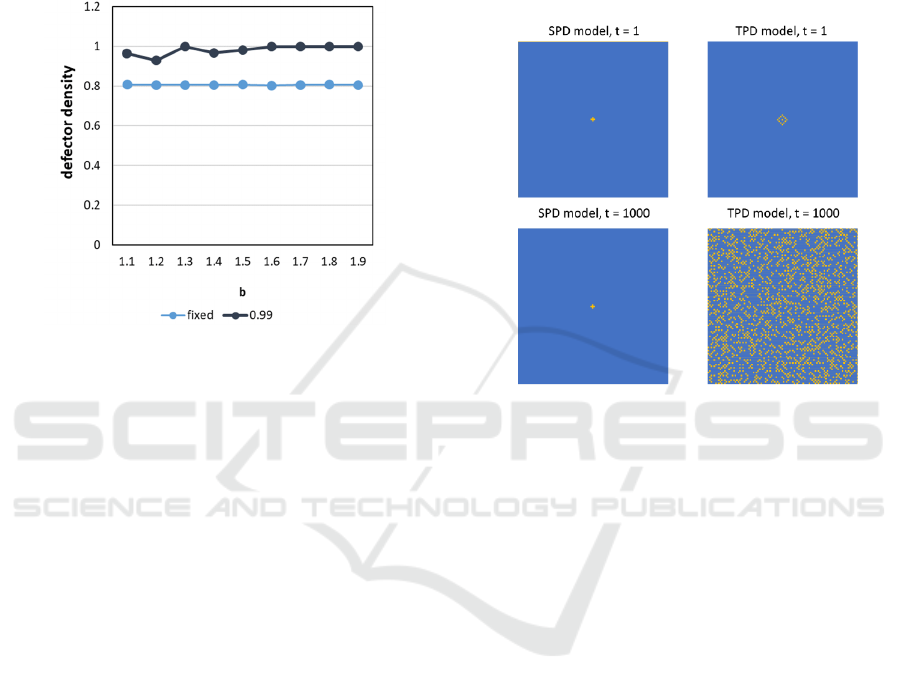
neighboring four cells. The remaining players were

defectors. Results were compared with r = 0.99 as

shown in Figure 2, where the defector density was

lower than r = 0.99 and remained around 0.80 for any

value of b. Although the initial density was much

higher than r = 0.99 in the density with a fixed initial

distribution, the defector did not increase as much as

r = 0.99.

Figure 2: Defector density of the two initial distributions.

3.2 Spatial Distribution

Next, we compared the spatial distribution of the

fixed initial distribution between the TPD model and

the SPD model. Here, we set the parameter b = 1.9.

As shown in Figure 3, the distribution of

cooperators in the TPD model was spread out from

the center at t = 10 but sparse at t = 1000. However,

the distribution remained constant over time in the

SPD model.

In both models, the score of the player at the

center was 4 at t = 1, and the neighbors of the centered

player adopted strategy C. Their strategy did not

change because the player in the neighborhood with

the highest score is the one in the center. In the TPD

model, this process is repeated until t = 9 according

to the SPD model rule where p = 10. Therefore, the

distribution of strategies did not change until t = 9.

However, neighbors of the centered player

considered previous strategies and followed an

unusual update rule because their own strategy earned

a score lower than that of the centered player, even

though their strategies were the same at t = 10. As a

result, they adopted strategy D according to the rules

of the TPD model.

Even though players outside of the region of

interest described above adopted strategy D, their

scores were lower than the player whose strategy was

D and who neighbors the player in C, so those players

were likely to change their strategy to C. As a result,

a diamond-like shape formed, and repeated many

times; a constant number of players with strategy C

survived at t = 1000. However, in the SPD model, the

strategy distribution maintained its shape and did not

deviate from the initial distribution even at t = 1000.

Therefore, the cross-like shape in the spatial

distribution of the TPD model during early stages

contributed to cooperator survival.

Figure 3: Spatial distribution of fixed initial density in two

models.

4 CONCLUSIONS

In this paper, we evaluated the TPD model in two

cases where cooperators were in the minority of the

population. In the first case, players of each strategy

were randomly distributed according to the defector

density parameter r. As we considered cooperative

populations as a minority group, the parameter r had

high values. We found that cooperators could evolve

despite their low initial density. A fixed distribution

was used in the second case, where only five players

in the center of the system adopted cooperative

strategies while others were initially defectors.

However, the number of cooperators increased over

time. Interestingly, the initial number of cooperators

in the second condition was lower than that of the first

condition with r = 0.99, and the final cooperator

population in the former was higher than the latter,

suggesting that the initial placement of cooperators

influences outcomes.

Twisted Strategy Bolsters Minority Cooperator Populations

177

REFERENCES

Danku, Z., Perc, M., Szolnoki, A. (2019). Knowing the past

improves cooperation in the future. Scientific Reports.

9, 262.

Deng, Z., Ma, C., Mao, X., Wang, S., Niu, Z., Gao, L.

(2017). Historical payoff promotes cooperation in the

prisoner’s dilemma game. Chaos, Solitons & Fractals.

104, 1–5.

Doebeli, M., Hauert, C. (2005). Models of cooperation

based on the Prisoner’s Dilemma and the Snowdrift

game. Ecology Letters. 8, 748–766.

Hauert, C., Doebeli, M. (2004). Spatial structure often

inhibits the evolution of cooperation in the snowdrift

game. Nature. 428, 643–646.

Javarone, M. A. (2016). Statistical physics of the spatial

prisoner’s dilemma with memory-aware agents. The

European Physical Journal B. 89, 1–6.

Jusup, M., Holme, P., Kanazawa, K., Takayasu, M., Romić,

I., Wang, Z., Geček, S., Lipić, T., Podobnik, B., Wang,

L., Luo, W., Klanjšček, T., Fan, J., Boccaletti, S., Perc,

M. (2022). Social physics. Physics Reports. 948, 1–148.

Smith, J. M., Price, G. R. (1973). The logic of animal

conflict. Nature. 246, 15–18.

Nowak, M. A., May, R. M. (1992). Evolutionary games and

spatial chaos. Nature. 359, 826–829.

Qin, J., Chen, Y., Fu, W., Kang, Y., Perc, M. (2018).

Neighborhood diversity promotes cooperation in social

dilemmas. IEEE Access. 6, 5003–5009.

Sakiyama, T. (2021). A power law network in an

evolutionary hawk–dove game. Chaos, Solitons &

Fractals. 146, 110932.

Sakiyama, T., Arizono, I. (2019). An adaptive replacement

of the rule update triggers the cooperative evolution in

the Hawk–Dove game. Chaos, Solitons & Fractals.

121, 59–62.

Takahara, A., Sakiyama, T. (2023). Twisted strategy may

enhance the evolution of cooperation in spatial

prisoner’s dilemma. Submitted.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

178