VP-DARTS: Validated Pruning Differentiable Architecture Search

Tai-Che Feng and Sheng-De Wang

Department of Electrical Engineering, National Taiwan University, Taipei, Taiwan

Keywords:

Deep Learning, Model Optimization, Neural Architecture Search, Differentiable Architecture Search, Model

Compression, Model Pruning, Soft Pruning.

Abstract:

Recently Differentiable Architecture Search (DARTS) has gained increasing attention due to its simplicity

and efﬁcient search capability. However, such search methods have a signiﬁcant chance of encountering

overﬁtting, which can result in the performance collapse problem of the discovered models. In this paper, we

proposed VP-DARTS, a validated pruning-based differentiable architecture search method using soft pruning,

to address this issue. Firstly, unlike previous search methods, we consider the differentiable architecture

search process as a model pruning problem. It prunes or removes unimportant operations from the supernet

that contains all possible architectures to obtain the ﬁnal model. We also show that the traditional hard

pruning method would gradually reduce the capacity of the search space during training, leading to local

optimal results. To get better architectures than hard pruning, we proposed using a parameterized soft pruning

approach in our training process. Secondly, the original DARTS method selects the operation with the

maximum architecture parameter on each edge to form the ﬁnal architecture after training. But we found

that this approach cannot truly reﬂect their importance. Therefore, we estimate the impact on the supernet of

each candidate operation by using a subset of the validation set to evaluate its degree of importance. Finally,

we implement our method on the NAS-Bench-201 search space, and the experimental results show that VP-

DARTS is a robust search method that can obtain architectures with good performance and stable results.

1 INTRODUCTION

Early machine learning models were all manually

crafted by experts, and these models achieved great

success in tasks such as image recognition, includ-

ing ResNet (He et al., 2016), VGG (Simonyan and

Zisserman, 2015), MobileNet (Howard et al., 2017;

Sandler et al., 2018), and others. However, designing

these neural networks requires a lot of expertise

and time. To address this issue, neural architecture

search (NAS) has gradually gained attention. Its

main objective is automatically to search for the

most suitable model architecture without requiring

specialized knowledge.

However, since the search space of NAS is not

continuous, early methods could only rely on Re-

inforcement Learning (Zoph and Le, 2017) or Ge-

netic Algorithms (Real et al., 2019), which require

a lot of computing resources and time. H. Liu (Liu

et al., 2019b) proposed a differentiable method called

DARTS to reduce search costs. The method still has

some limitations. First, during the training process,

skip connections are more likely to appear in the ﬁnal

architecture. This phenomenon is called performance

collapse, which can decrease the stability and accu-

racy of the network. Secondly, since the training is

done through continuous relaxation, each candidate

operation is assigned a trainable architecture parame-

ter, which is used to determine the ﬁnal architecture

by choosing the one with the highest value after

training. However, we found that these parameters do

not truly represent the importance of the operations.

In this paper, we propose using a portion of validating

set to estimate the degree of importance of operations

in the supernet.

The proposed approach is called VP-DARTS and

includes the following three main concepts: 1) con-

sidering the differentiable architecture search training

process as a model pruning problem, 2) using a

general parameterized soft pruning techniques based

on soft pruning (He et al., 2018) to solve the problem,

and 3) using a portion of validating set to estimate the

degree of importance of operations in the supernet. In

summary, our contributions are as follows:

• We found that the training process of the differen-

tiable architecture search method can be viewed

as a model pruning problem. And, a generalized

Feng, T. and Wang, S.

VP-DARTS: Validated Pruning Differentiable Architecture Search.

DOI: 10.5220/0012296700003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 2, pages 47-57

ISBN: 978-989-758-680-4; ISSN: 2184-433X

software pruning approach is proposed to solve

the problem.

• The previous methods of selecting operations can-

not correctly reﬂect their true importance. There-

fore, we propose estimating the impact of each

candidate operation on the supernet by using a

subset of the validation set to validate the supernet

rather than simply using the values of their archi-

tecture parameters.

2 RELATED WORKS

2.1 DARTS

DARTS (Liu et al., 2019b) aims to solve the problem

of discontinuous search space for NAS. It uses the

cell-based search space to narrow the search range

and maps the discrete optimization space to a contin-

uous interval.

In this cell-based search space, each searched cell

can be viewed as a directed acyclic graph (DAG),

where each node represents a feature map, and each

edge represents a type of operation performed. The

method ﬁrst constructs a supernet that contains all

possible architectures, where each edge (i, j) be-

comes a mixed operation o

(i, j)

(x) of all candidate

operations o ∈ O, with an architecture parameter α

(i, j)

assigned to it. These architecture parameters α on

the same edge will pass through a Softmax activation

function, as shown in Equation 1. Through the

continuous relaxation approach, NAS can be trained

simply using gradient descent. This reduces the train-

ing cost signiﬁcantly compared to the Reinforcement

Learning or Genetic Algorithm approaches.

(i, j)

(x) =

∑

o∈O

exp(α

(i, j)

)

∑

′

∈O

exp(α

(i, j)

′

)

o(x) (1)

At the end of the search, these architecture pa-

rameters can be regarded as the index of importance

of each operation on the corresponding edge since

a larger value α represents a higher proportion of

the results produced by that operation on the edge.

Therefore, we only need to select the best one based

on the maximum architecture parameter on each edge

after training to form the ﬁnal architecture. This

approach reduces the search cost from thousands of

GPU days to just hours and achieves comparable or

even better results to other non-differentiable NAS

methods.

2.2 Soft Pruning

Hard pruning (Han et al., 2015; Han et al., 2016;

Guo et al., 2020; Liu et al., 2019a; Liu et al., 2019c;

He et al., 2020) is the most common pruning tech-

nique. Generally, the importance scores are computed

based on certain criteria at a speciﬁc stage, and those

weights that do not satisfy are directly removed.

Afterward, the remaining weights are ﬁne-tuned to

recover the performance of the pruned model.

Soft pruning (He et al., 2018; He et al., 2019;

Cai et al., 2021) is another pruning technique. The

main difference between soft and hard pruning is that

the pruned weights are not permanently removed but

were allowed to participate in the iterative update

of the next epoch. Those considered unimportant

components have a second chance to regain their

importance at the latter training stage. Therefore,

the model capacity can be restored from the pruned

model during training, allowing the discovery of

better models that achieve higher accuracy. On the

other hand, in hard pruning, the pruned weights are

permanently removed, reducing the model’s capacity

during training and causing a loss in performance.

It also increases the probability that the ﬁnal search

result will be unstable. Since if different components

are removed, the subsequent training will search from

diverse remaining search spaces, resulting in signiﬁ-

cant differences in the search result. Furthermore, soft

pruning does not need to ﬁne-tune the pruned model

after training. This approach signiﬁcantly saves time

compared to the ﬁne-tuning stage required by hard

pruning.

In the original soft pruning method (He et al.,

2018), the unimportant weights are set to zero for

the next epoch. However, directly setting the pruned

weights to zero may be too aggressive. Thus, to grad-

ually discard the pruned weights, SofteR Pruning (Cai

et al., 2021) is introduced, which gradually increases

the pruning strength for these pruned weights during

the training process with a monotonic decreasing

parameter, leading to better pruning results.

3 APPROACH

3.1 DARTS Pruning

While in the differentiable architecture search

method, the goal is to choose the most considerable

operation on each edge to form the ﬁnal architecture.

Assuming we look from a different perspective, the

operation selection problem can be considered a

model pruning problem. In other words, we prune the

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

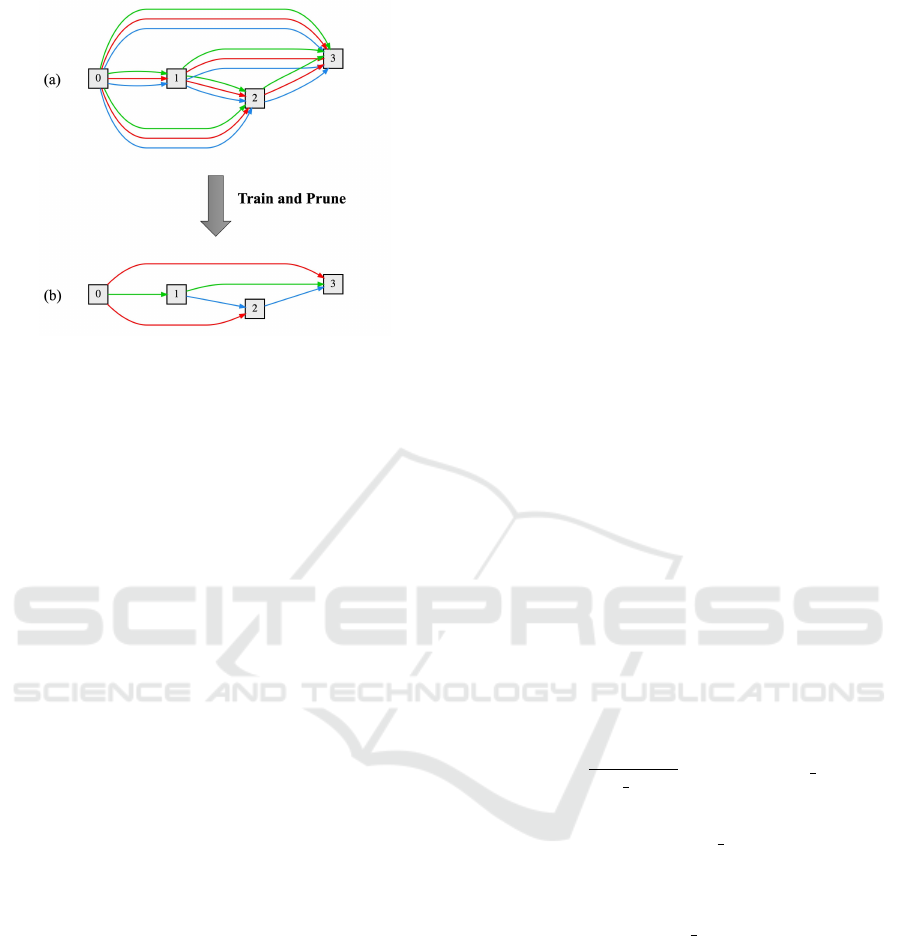
Figure 1: The pruning concept of DARTS (a) DARTS

constructs a supernet that contains all possible sub-networks

and is trained using continuous relaxation (b) After

training, operation-level pruning is performed to remove all

unimportant operations at once from the supernet, leaving

only one between each pair of nodes.

unimportant operations on each edge and keep the

best one, and these remaining operations become the

ﬁnal architecture. In the case of DARTS (Liu et al.,

2019b), as shown in Figure 1, the simplest pruning

method was employed. It sets the pruning ratio to

the maximum and prunes all unimportant operations

at the same time. However, the drawback of this

approach is that it may easily remove some crucial

components and lead to unstabilized results.

Therefore, it is necessary to change the pruning

technique to improve the search for more suitable

architectures in DARTS. One possible solution is

to avoid directly setting the pruning ratio to the

maximum but use a progressive approach, increasing

the pruning ratio step by step so that unimportant op-

erations can be removed gradually from the supernet

in the training process. This approach is adopted in

the Search Space Approximation of PDARTS (Chen

et al., 2019) and SGAS (Li et al., 2020), which aims to

search for better architectures by gradually selecting

the edge operations.

However, these various hard pruning approaches

still cannot solve the problem of excessive skip con-

nections. After conducting experiments, we found

that although the gradual pruning approach can in-

deed ﬁnd better combinations of operations than the

original DARTS with one-time pruning, skip connec-

tions still frequently appear in the ﬁnal architecture,

which suffers from the performance collapse prob-

lem. Moreover, these gradual pruning approaches

use a similar greedy algorithm to decide which op-

erations to prune at each step and heavily rely on

the current training results. Once the unimportant

ones are pruned, they are permanently removed and

cannot appear in the ﬁnal architecture. This reduces

the search space and compromises the performance

during training, leading to an unstable search result.

3.2 Soft Pruning-Based DARTS

Therefore, to address the problem of performance

collapse and stabilize the search results, we adopts

the soft pruning (He et al., 2018; He et al., 2019;

Cai et al., 2021) approach as the pruning technique

in differentiable architecture search. The reason is

that in this type of model architecture search, our

goal is to ﬁnd the best combination of operations. If

we use the traditional hard pruning, those considered

unimportant operations at the selection moment will

be permanently removed. It reduces the capacity

of the search space and the diversity of operation

combinations in the later stages of training.

These unimportant operations will not perma-

nently remove if soft pruning is used. Instead, the

values of their coefﬁcients will reduce or set to 0 in

each epoch and continue to be trained. As shown in

Figure 2, these operations still exist in the supernet

and allow iterative updates giving those unimportant

ones to regain their importance. This approach also

ensures the capacity of the search space and the

diversity of operations combination during training,

avoiding the aforementioned problems and enabling

us to search for better architectures.

The generalized soft pruning decay strategy for-

mula can be written as Equation 2.

= α

(1 −

max epoch

) , 0 ≤ K < max epoch (2)

where α

represents the original value, α

repre-

sents the pruned value, max epoch represents the

total number of pruning epochs, and the coefﬁcient

K represents the reduced rate of value, which can

control the decaying speed in each epoch. As we

ﬁxed the value of K as max epoch during the training

process, the original soft pruning (He et al., 2018)

approach is used. That is, the unimportant operation

coefﬁcients will be set to zero at the beginning of

each epoch. On the other hand, since directly setting

the pruned weights to zero may be too aggressive,

SofteR Pruning (Cai et al., 2021) gradually increases

the pruning strength during the training process, in

which the value of K is adjustable. This approach

improves the drawbacks of the original soft pruning

since the value of the operation coefﬁcients will not be

directly set to 0. In this case, the operation can regain

their importance more easily and the search can retain

more promising architectures.

VP-DARTS: Validated Pruning Differentiable Architecture Search

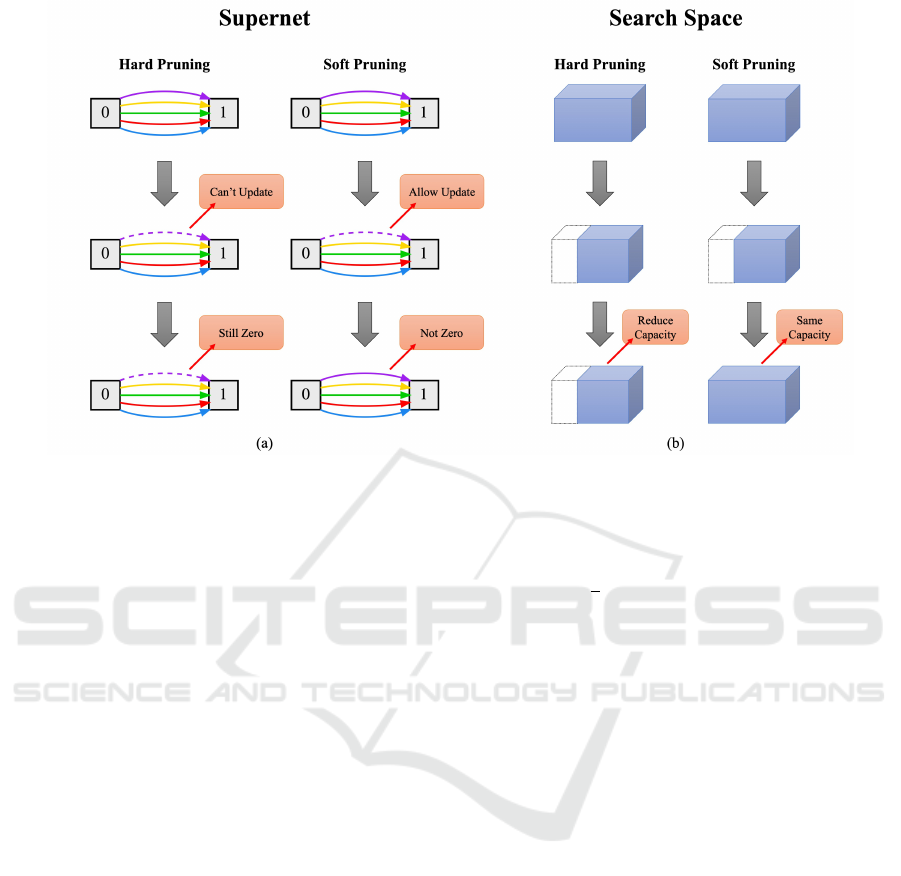
Figure 2: Hard pruning vs. soft pruning in DARTS. In the soft pruning training process, (a) no operation is removed from

the supernet during the middle of the training. Instead it is allowed to be continuously updated and let the unimportant

operations recover their importance; (b) the capacity of the search space will not decrease, and all possible architectures will

exist throughout the training process.

For example, as shown in Figure 3(a), the pruning

strength can be set up as the ratio between the cur-

rent epoch and the total number of pruning epochs.

This method is known as the linear decay strategy

in SofteR Pruning. Another strategy is called the

exponential decay strategy. However, compared to

ﬁlter pruning, the convergence speed is signiﬁcantly

slower in the differentiable architecture search train-

ing process, where operation-based pruning is per-

formed. If the exponential decay strategy is used,

the coefﬁcient values will drop in the early stages

of training signiﬁcantly, as shown in Figure 3(b),

reducing the chances of recovering operations that are

considered unimportant. Therefore, we only consider

using the linear decay strategy to attempt to train

better architectures. The difference between these

two approaches is shown in Figure 4, where the ﬁxed

value K will directly set the coefﬁcient to 0, and

the adjustable K will set the value according to the

decaying strategy.

Furthermore, since we treat the selection of op-

erations in DARTS as a model pruning problem, we

consider the architecture parameters as general model

weights just like others, rather than the probability

distribution on each edge. Therefore, we do not

use softmax to normalize the architecture parameters.

Instead, we train the unnormalized weights directly,

as shown in Equation 3.

(i, j)

(x) =

∑

o∈O

(i, j)

o(x) (3)

There are two beneﬁts while not using Softmax.

First, since softmax normalizes the weights and forces

the sum of all values to 1, when one value increases,

the others are compressed and become smaller. This

emphasizes the importance of the operations having

higher values. While this is ﬁne for fair compe-

tition in other methods, skip connections make the

competition unfair in DARTS, as some papers (Chen

et al., 2019; Chu et al., 2020) have pointed out

that its convergence speed is much faster than other

operations. Therefore, using softmax only makes

the architecture parameters of skip connections grow

faster, making it difﬁcult for other operations to be

selected. Moreover, since softmax is applied to

the architecture parameters on the same edge, it’s

unable to distinguish the importance between two

operations located on different edges and leads to

unfair comparisons between operations in the search

process.

3.3 Determine Operation Strength

Using Validation Set

In the original DARTS method, the importance of

each operation is determined based on the magnitude

of its architecture parameter. However, according to

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

Figure 3: Different decay strategy while using adjustable K.

Figure 4: Comparison of using ﬁxed K and adjustable K.

Figure 5: Comparison of Kendall τ coefﬁcient between

using the magnitude of architecture parameters α, the re-

maining supernet validation accuracy without the operation,

and the real ranking.

some studies (Zhou et al., 2021; Wang et al., 2021),

these coefﬁcients do not accurately reﬂect their true

importance. The operation with the highest coefﬁ-

cient may not be the most important one. Therefore,

we attempt to address this issue by estimating the

impact of all operations on the supernet instead of

directly looking at their architecture parameters.

Algorithm 1: Determine Operation Strength Using

Validation Accuracy.

Input : Supernet S; Two operations o

, o

Output: The more important operation o

, o

Val

= Validation accuracy of the remaining

supernet S when o

is removed;

Val

= Validation accuracy of the remaining

supernet S when o

is removed;

if Val

> Val

then

is more important than o

;

return o

;

end

else

is more important than o

;

return o

;

end

VP-DARTS: Validated Pruning Differentiable Architecture Search

We used the Kendall τ coefﬁcient (Kendall, 1938)

to verify the above situation. The Kendall τ co-

efﬁcient is a commonly used measurement of the

correlation between two rankings. It can be calculated

Kendall τ =

C − D

C + D

(4)

where C represents the number of concordant pairs,

and D represents the number of discordant pairs. The

resulting correlation value always falls between -1

and 1, where -1 and 1 represent perfect negative and

positive correlations, respectively, and 0 indicates that

the two rankings are completely independent.

Therefore, if we wish the predicted ranking to be

similar to the actual rank, the calculated Kendall τ

coefﬁcient should be as high as possible. As shown

in Figure 5, we calculated the Kendall τ coefﬁcient

between the magnitude of architecture parameters, the

supernet validation accuracy without the operation,

and the actual rank after the DARTS training method.

We random sample 100 cell architectures and replace

the edges to be evaluated for importance with all

candidate operations. We sort them based on the

accuracy of the models they construct and calculate

the average rank, which serves as the actual ranking

for those operations on that edge.

After experiments, we found that using the valida-

tion accuracy to determine the importance can better

reﬂect the operations ranking. Using the magnitude

of architecture parameters resulted in a Kendall τ

value of -0.2 while using validation accuracy as the

measurement achieved a value of 0.6. This result

shows that using the original magnitude of the ar-

chitecture parameters cannot correctly determine the

importance, leading to select the wrong operations to

form the ﬁnal architecture.

Therefore, according to the above ﬁndings, we

propose estimating the impact on the supernet of each

candidate operation to determine their importance.

The overall process is summarized in Algorithm 1.

If the validation accuracy decreases signiﬁcantly after

removing one of the operations from the supernet,

it indicates that the removed one is quite important

because the model performance can only improve by

adding it back. On the other hand, if the difference

in accuracy before and after removing an operation

is negligible, the importance of that operation is

relatively low because even without it, the model can

still maintain its performance.

3.4 VP-DARTS: Validated Pruning

Differentiable Architecture Search

In summary, this study uses the soft pruning approach

to conduct the differentiable architecture search

method and change the way of determining the

importance of operations by estimating their impact

on the supernet using the validation set. We name

the approach Validated Pruning Differentiable

Architecture Search (VP-DARTS). The whole VP-

DARTS method is shown in Figure 6, with the

following steps:

• To ensure fair competition between all operations,

a warmup strategy is employed in the early train-

ing, where all architecture parameters are frozen,

and only the weights on the model are trained.

• While the warmup stage is completed, at the

beginning of each epoch, all candidate opera-

tions are removed individually from the super-

net, and the validation accuracy of the remaining

model is measured to determine their importance.

Since testing with the entire validation set is time-

consuming, we randomly sample a subset in each

epoch to reduce the search cost.

• After every operation strength has been deter-

mined, the soft pruning method is used to remove

all operations that are considered unimportant

temporarily. This approach sets their architecture

parameters to α

with parameter K as shown

in Equation 2, which allows them to participate

in the next iteration update to regain their im-

portance. It ensures the search space and the

model capacity are not reduced during training,

which allows all possible operation combinations

to continue existing and ﬁnd better architectures.

• Repeat the above two steps in each epoch until

the training is complete. After training, remove

each operation and test the validation set accuracy

again to determine the importance of each one,

and select the best one with the lowest accuracy

to form the ﬁnal cell architecture.

4 EXPERIMENTS

4.1 Search Space: NAS-Bench-201

NAS-Bench-201 (Dong and Yang, 2020) is a widely-

used benchmark for neural architecture search, which

ﬁxes the hyperparameters such as the size of search

space, the number of candidate operations, the value

of learning rate, and data augmentation techniques

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

Table 1: Results of VP-DARTS on NAS-Bench-201.

Method

CIFAR-10 CIFAR-100 ImageNet16-120 Search Cost

validation test validation test validation test (h)

Random (baseline) 90.93 ± 0.36 93.70 ± 0.36 70.93 ± 1.09 71.04 ± 1.07 44.45 ± 1.10 44.57 ± 1.25 -

Reinforce (Zoph and Le, 2017) 91.09 ± 0.37 93.85 ± 0.37 71.61 ± 1.12 71.71 ± 1.09 45.05 ± 1.02 45.24 ± 1.18 -

Genetic (Real et al., 2019) 91.19 ± 0.31 93.92 ± 0.30 71.81 ± 1.12 71.84 ± 0.99 45.15 ± 0.89 45.54 ± 1.03 -

DARTS (1st) (Liu et al., 2019b) 39.77 ± 0.00 54.30 ± 0.00 15.03 ± 0.00 15.61 ± 0.00 16.43 ± 0.00 16.32 ± 0.00 2.0

DARTS (2nd) (Liu et al., 2019b) 39.77 ± 0.00 54.30 ± 0.00 15.03 ± 0.00 15.61 ± 0.00 16.43 ± 0.00 16.32 ± 0.00 -

SNAS (Xie et al., 2019) 90.10 ± 1.04 92.77 ± 0.83 69.69 ± 2.39 69.34 ± 1.98 42.84 ± 1.79 43.16 ± 2.64 -

PCDARTS (Xu et al., 2020) 89.96 ± 0.15 93.41 ± 0.30 67.12 ± 0.39 67.48 ± 0.89 40.83 ± 0.08 41.31 ± 0.22 -

SGAS (Li et al., 2020) 85.06 ± 0.00 88.33 ± 0.03 70.80 ± 0.65 70.76 ± 1.29 42.97 ± 2.53 43.04 ± 2.76 -

iDARTS (Zhang et al., 2021) 89.86 ± 0.60 93.58 ± 0.32 70.57 ± 0.24 70.83 ± 0.48 40.38 ± 0.59 40.89 ± 0.68 -

ReNAS (Xu et al., 2021) 90.90 ± 0.31 93.99 ± 0.25 71.96 ± 0.99 72.12 ± 0.79 45.85 ± 0.47 45.97 ± 0.49 -

DARTS- (Chu et al., 2021) 91.03 ± 0.44 93.80 ± 0.40 71.36 ± 1.51 71.53 ± 1.51 44.87 ± 1.46 45.12 ± 0.82 -

DrNAS (Chen et al., 2021) 91.55 ± 0.00 94.36 ± 0.00 73.49 ± 0.00 73.51 ± 0.00 46.37 ± 0.00 46.34 ± 0.00 3.9

β-DARTS (Ye et al., 2022) 91.55 ± 0.00 94.36 ± 0.00 73.49 ± 0.00 73.51 ± 0.00 46.37 ± 0.00 46.34 ± 0.00 3.2

VP-DARTS (Fixed K)

VP-DARTS (Fixed K) 91.34 ± 0.06

91.34 ± 0.06

91.34 ± 0.06 94.15 ± 0.07

94.15 ± 0.07

94.15 ± 0.07 72.64 ± 0.94

72.64 ± 0.94

72.64 ± 0.94 72.77 ± 0.57

72.77 ± 0.57

72.77 ± 0.57 45.81 ± 0.28

45.81 ± 0.28

45.81 ± 0.28 45.91 ± 0.43

45.91 ± 0.43

45.91 ± 0.43 2.8

2.8

VP-DARTS (Adjustable K)

VP-DARTS (Adjustable K) 91.55 ± 0.00

91.55 ± 0.00

91.55 ± 0.00 94.36 ± 0.00

94.36 ± 0.00

94.36 ± 0.00 73.49 ± 0.00

73.49 ± 0.00

73.49 ± 0.00 73.51 ± 0.00

73.51 ± 0.00

73.51 ± 0.00 46.37 ± 0.00

46.37 ± 0.00

46.37 ± 0.00 46.34 ± 0.00

46.34 ± 0.00

46.34 ± 0.00 2.8

2.8

Optimal 91.61 94.37 73.49 73.51 46.77 47.31

Figure 6: Overview of VP-DARTS.

during the search stage, providing a fair competi-

tion platform for all NAS methods in three datasets:

CIFAR-10, CIFAR-100 and ImageNet16-120, an Im-

ageNet subset down-sampled version. The objective

of the search space is to ﬁnd the best cell architecture,

which can be represented as a directed acyclic graph

(DAG) consisting of four nodes and six edges. The

search space consists of ﬁve candidate operations: Ze-

roize, Skip Connection, 1x1 Convolution, 3x3 Con-

volution, and 3x3 Avg Pooling. For more detailed

settings, please refer to the NAS-Bench-201 paper

(Dong and Yang, 2020).

4.2 Implementation Details

We conducted 20 warmup epochs at the beginning of

the search, where we froze all architecture parameters

and only trained the weights of the supernet itself, and

since skip connection has a faster convergence speed,

we added dropout with the probability of 0.2 behind

to suppress it, to ensure fair competition among all

operations. After the warmup stage, we applied

the soft pruning approach for the last 30 epochs by

random sampling 50% of validation sets accuracy

in each epoch to determine the importance. The

ﬁnal pruning ratio is used during the whole search

phase, which means that the training is performed

by considering four unimportant operations to be

masked on each edge in every epoch. We set K =

max epoch in Equation 2 as the ﬁxed K approach. For

the adjustable K approach, we use the linear decay

strategy mentioned in Section 3.2 to determine the

strength of pruning in each epoch. We performed

both search methods on CIFAR-10 and evaluated the

performance on all datasets.

4.3 Search Results

The experimental results are shown in Table 1, where

we conducted ﬁve search processes with different

random seeds and reported their average accuracy ±

variance. The results show that VP-DARTS, while

using the ﬁxed parameter K achieves comparable

performance on all datasets in NAS-Bench-201 with

94.15% test accuracy on CIFAR-10, 72.77% test

accuracy on CIFAR-100, and 45.91% test accuracy

VP-DARTS: Validated Pruning Differentiable Architecture Search

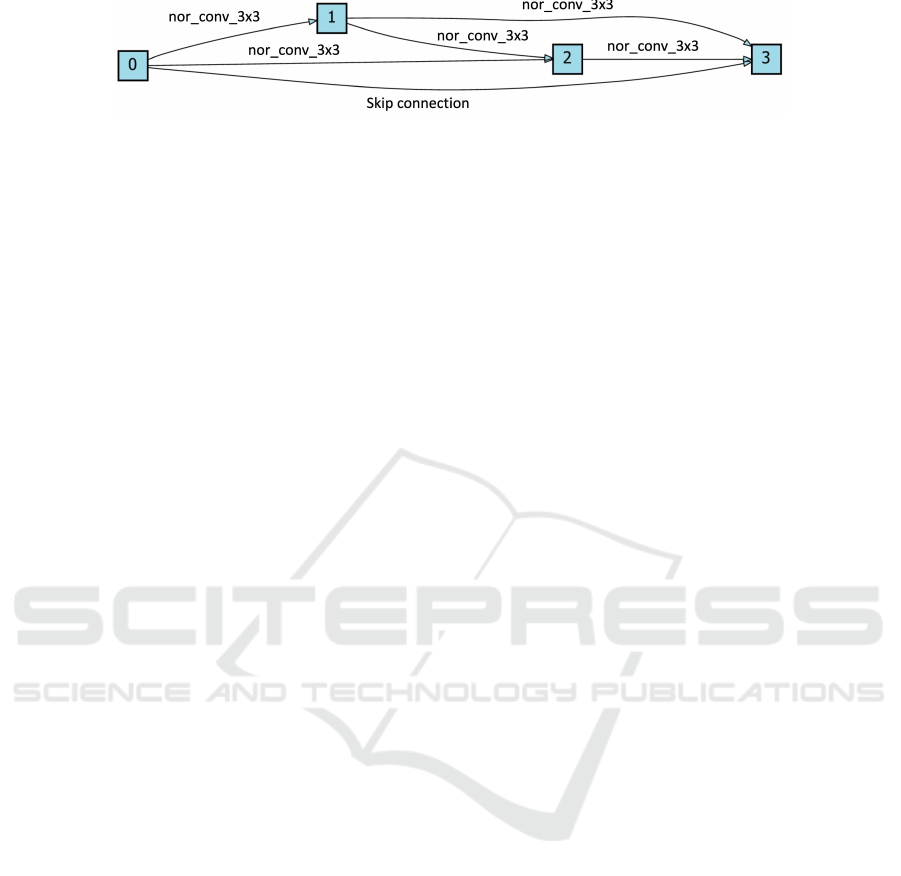
Figure 7: The searched cell of VP-DARTS (adjustable K) on NAS-Bench-201 with CIFAR-10.

on ImageNet16-120, which is better than most of the

search methods using the hard pruning approach, such

as DARTS and SGAS.

Furthermore, VP-DARTS using the adjustable K

approach can achieve even better results than the

ﬁxed value K, which could ﬁnd better architectures

on all datasets with 94.36% test accuracy on CIFAR-

10, 73.51% test accuracy on CIFAR-100 and 46.34%

test accuracy on ImageNet16-120. This approach

achieves state-of-the-art performance and completes

the search process in just 2.8 hours, requiring less

time than other methods. The searched architecture

of VP-DARTS using adjustable K is shown in Figure

7, from which we observe that VP-DARTS effectively

solves the problem of excessive skip connections

in DARTS, resulting in well-performing searched

architectures. Moreover, since using the adjustable

K does not directly set the architecture parameters of

unimportant operations to zero, it is easier to let them

regain importance at the beginning of the training

process and select the more suitable and stable one.

Therefore, adjustable K can get more stable results

than the ﬁxed value.

In summary, compared to using hard pruning

methods like DARTS or SGAS, VP-DARTS, which

uses the soft pruning approach, maintains the ca-

pacity of the search space unchanged during train-

ing, enabling the discovery of better and more sta-

ble architectures. Moreover, using the adjustable

K approach, VP-DARTS achieves superior results

by gradually increasing the pruning strength during

the search process with less training cost than other

search methods. These results indicate that applying

soft pruning in differentiable architecture search with

directly estimating the impact on the supernet can

obtain excellent architectures.

5 ABLATION STUDY

5.1 Soft Pruning vs. Hard Pruning

In this paper, we proposed VP-DARTS, which utilizes

the technique of generalized soft pruning to reduce

unimportant weights and the validated accuracy as

the operation selection criterion. In contrast, tradi-

tional hard pruning methods determine the strength

of the operations by the architecture parameter on the

current training status and permanently remove them

from the search space.

Here we conducted an ablation study to compare

the differences between soft pruning and hard pruning

in DARTS on NAS-Bench-201 search space. Both

methods are trained with the same settings mentioned

in Section 4.2, 50 epochs search phase with a 20

epochs warmup at the beginning, dropout rate of 0.2,

and using 50% of the validation set accuracy to deter-

mine the importance of operations. In traditional hard

pruning, we prune all unimportant ones at the end of

the training, similar to DARTS. In progressive hard

pruning, we use the Search Space Approximation

from PDARTS (Chen et al., 2019) and divide the later

search phase into three stages. The search space size

is set to 5, 3, and 2, respectively, gradually pruning

unimportant operations in the search phase.

We used different random seeds for ﬁve search

processes and reported their average accuracy ± vari-

ance. As shown in Table 2, the experiment results

demonstrate that utilizing hard pruning as the search

strategy in DARTS leads to lower performance in the

obtained network architecture, regardless of whether

traditional hard pruning or progressive hard pruning is

employed. Moreover, using soft pruning also shows a

more stable result. The experiment shows that using

the soft pruning approach to maintain the capacity

of the search space during training is helpful for the

differentiable architecture search method.

5.2 Validation Accuracy vs. Alpha

Value

In Section 3.3, we mentioned that using the same

approach as DARTS to directly determine the impor-

tance of operations based on the magnitude of α may

not accurately reﬂect the actual ranking compared

to using validation accuracy. Here, we compare

the impact of using these two approaches again.

We use the ﬁxed value K approach in VP-DARTS

while changing the way of directly determining the

importance of operations based on the magnitude of

α and compare it with the original method of using

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

Table 2: Comparison between using hard pruning and soft pruning approach.

Method

CIFAR-10 CIFAR-100 ImageNet16-120

validation test validation test validation test

Hard Pruning 87.97 ± 3.58 91.41 ± 2.24 67.67 ± 5.10 67.97 ± 5.23 40.42 ± 7.95 37.99 ± 53.90

Gradually Hard Pruning 89.79 ± 0.15 93.11 ± 0.10 69.88 ± 1.04 70.29 ± 1.66 42.74 ± 5.36 43.55 ± 4.93

Soft Pruning (Fixed K)

Soft Pruning (Fixed K) 91.34 ± 0.06

91.34 ± 0.06

91.34 ± 0.06 94.15 ± 0.07

94.15 ± 0.07

94.15 ± 0.07 72.64 ± 0.94

72.64 ± 0.94

72.64 ± 0.94 72.77 ± 0.57

72.77 ± 0.57

72.77 ± 0.57 45.81 ± 0.28

45.81 ± 0.28

45.81 ± 0.28 45.91 ± 0.43

45.91 ± 0.43

Table 3: Comparison of using the magnitude of α and validation accuracy determining the importance of operations.

Method

CIFAR-10 CIFAR-100 ImageNet16-120

validation test validation test validation test

α Value 85.27 ± 1.50 88.86 ± 1.49 62.47 ± 7.53 62.99 ± 9.45 35.90 ± 11.78 35.11 ± 12.37

Val Accuracy

Val Accuracy 91.34 ± 0.06

91.34 ± 0.06

91.34 ± 0.06 94.15 ± 0.07

94.15 ± 0.07

94.15 ± 0.07 72.64 ± 0.94

72.64 ± 0.94

72.64 ± 0.94 72.77 ± 0.57

72.77 ± 0.57

72.77 ± 0.57 45.81 ± 0.28

45.81 ± 0.28

45.81 ± 0.28 45.91 ± 0.43

45.91 ± 0.43

validation accuracy.

The experimental results are shown in Table 3.

From the result, we can observe that utilizing vali-

dation accuracy enables us to discover architectures

with superior performance. It achieves accuracy

rates exceeding 5% across all datasets and even 10%

accuracy boosts on CIFAR-100 and ImageNet16-120.

This once again conﬁrms that directly determining the

importance of operations based on the magnitude of α

cannot accurately represent the actual ranking.

5.3 The Impact of Validation Set

Proportion

Since we use validation accuracy to determine the

importance of operations, a large amount of validation

set testing is required in each epoch. Here we

compare the inﬂuence of using different proportions

of validation set sizes to determine the importance of

operations on the ﬁnal results. For the cases that use

a partial subset, we randomly sampled the validation

set during each epoch instead of using a ﬁxed subset.

The results are shown in Figure 8. We can observe

that employing a higher proportion of the validation

set for testing leads to better and more stable results of

the searched architecture. On the contrary, a smaller

proportion of the validation set results in decreased

accuracy and stability of the searched architecture

since different parts of the validation set are used each

time. However, it can signiﬁcantly reduce the search

time since fewer data are used for testing each time

when determining the importance of operations.

The search results are relatively consistent when

the proportion is 50% or above but would experience

a signiﬁcant drop when it is below 50%. Therefore,

our method chooses to use the 50% ratio, which

strikes a balance between training cost and accuracy.

6 CONCLUSION

In this paper, we propose VP-DARTS, a differentiable

architecture search method based on soft pruning,

and determining the importance of each operation by

directly estimating its impact on the supernet using

validation accuracy. This method effectively solves

the issue of excessive skip connections causing the

performance collapse problem and can result in better

architectures. With the ﬁxed value K of VP-DARTS,

we achieved a comparable result on the NAS-Bench-

201 search space, with accuracy rates of 94.15%,

72.77%, and 45.91% on CIFAR-10, CIFAR-100, and

ImageNet-16-120, respectively. It outperformed other

NAS methods using the hard pruning approach in the

training process.

Moreover, using the adjustable value K, VP-

DARTS can achieve even better results than the

ﬁxed value, obtaining accuracy rates of 94.36% on

CIFAR-10, 73.51% on CIFAR-100, and 46.34%

on ImageNet-16-120. It achieves state-of-the-art

performance with stable results and lower search

costs than other NAS methods. Furthermore, in the

ablation study, we showed that soft pruning could

obtain better and stable results than traditional hard

pruning among differentiable architecture search

methods. The main reason is that the software

pruning does not reduce the capacity of search

space during training while hard pruning does. The

experiments show that VP-DARTS is a robust search

method and can ﬁnd neural architectures with good

performance.

REFERENCES

Cai, L., An, Z., Yang, C., and Xu, Y. (2021). Softer pruning,

incremental regularization. In 25th International

VP-DARTS: Validated Pruning Differentiable Architecture Search

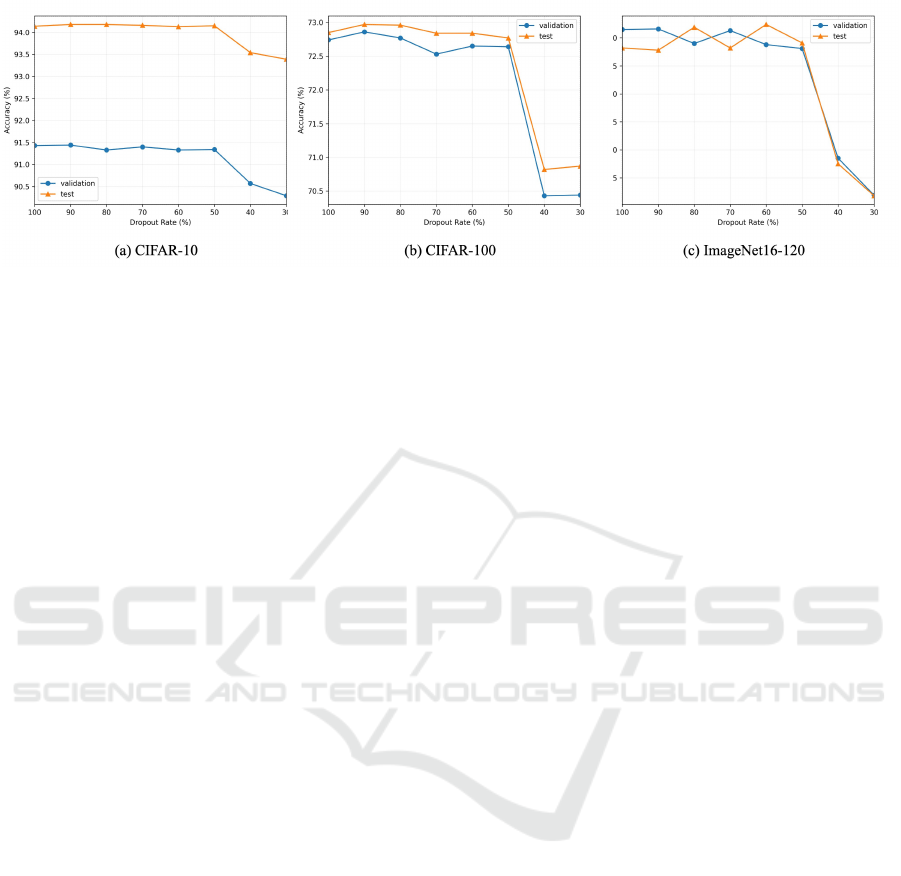
Figure 8: Comparison of VP-DARTS with ﬁxed value K using different validation set proportions.

Conference on Pattern Recognition (ICPR), pages

224–230. IEEE.

Chen, X., Wang, R., Tang, X., and Hsieh, C.-J. (2021).

DrNAS: Dirichlet neural architecture search. In

International Conference on Learning Representation

(ICLR).

Chen, X., Xie, L., Wu, J., and Tian, Q. (2019). Progressive

differentiable architecture search: Bridging the depth

gap between search and evaluation. In Proceedings of

the IEEE/CVF international conference on computer

vision, pages 1294–1303.

Chu, X., Wang, X., Zhang, B., Lu, S., Wei, X., and Yan,

J. (2021). DARTS-: Robustly stepping out of perfor-

mance collapse without indicators. In International

Conference on Learning Representations (ICLR).

Chu, X., Zhou, T., Zhang, B., and Li, J. (2020).

Fair DARTS: Eliminating Unfair Advantages in

Differentiable Architecture Search. In 16th European

Conference On Computer Vision (ECCV).

Dong, X. and Yang, Y. (2020). Nas-bench-201: Extending

the scope of reproducible neural architecture search.

In International Conference on Learning Representa-

tions (ICLR).

Guo, J., Zhang, W., Ouyang, W., and Xu, D. (2020). Model

compression using progressive channel pruning. IEEE

Transactions on Circuits and Systems for Video

Technology, 31(3):1114–1124.

Han, S., Mao, H., and Dally, W. J. (2016). Deep

compression: Compressing deep neural networks

with pruning, trained quantization and huffman

coding. International Conference on Learning

Representations (ICLR).

Han, S., Pool, J., Tran, J., and Dally, W. J. (2015).

Learning both weights and connections for efﬁcient

neural networks. In Proceedings of the 28th Interna-

tional Conference on Neural Information Processing

Systems-Volume 1, pages 1135–1143.

He, K., Zhang, X., Ren, S., and Sun, J. (2016).

Deep residual learning for image recognition. In

Proceedings of the IEEE conference on computer

vision and pattern recognition (CVPR), pages 770–

778.

He, Y., Ding, Y., Liu, P., Zhu, L., Zhang, H., and

Yang, Y. (2020). Learning ﬁlter pruning criteria

for deep convolutional neural networks acceleration.

In 2020 IEEE/CVF Conference on Computer Vision

and Pattern Recognition (CVPR), pages 2006–2015.

IEEE.

He, Y., Dong, X., Kang, G., Fu, Y., Yan, C., and Yang,

Y. (2019). Asymptotic soft ﬁlter pruning for deep

convolutional neural networks. IEEE Transactions on

Cybernetics, pages 1–11.

He, Y., Kang, G., Dong, X., Fu, Y., and Yang, Y. (2018).

Soft ﬁlter pruning for accelerating deep convolutional

neural networks. In International Joint Conference on

Artiﬁcial Intelligence (IJCAI), pages 2234–2240.

Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D.,

Wang, W., Weyand, T., Andreetto, M., and Adam, H.

(2017). Mobilenets: Efﬁcient convolutional neural

networks for mobile vision applications. arXiv

preprint arXiv:1704.04861.

Kendall, M. (1938). A new measure of rank correlation.

Biometrika, 30(1/2):81–93.

Li, G., Qian, G., Delgadillo, I. C., M

uller, M., Thabet,

A., and Ghanem, B. (2020). SGAS: Sequential

greedy architecture search. In Proceedings of

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR).

Liu, C., Liu, P., Zhao, W., and Tang, X. (2019a). Visual

tracking by structurally optimizing pre-trained cnn.

IEEE Transactions on Circuits and Systems for Video

Technology, 30(9):3153–3166.

Liu, H., Simonyan, K., and Yang, Y. (2019b). DARTS:

Differentiable architecture search. In International

Conference on Learning Representations (ICLR).

Liu, Z., Sun, M., Zhou, T., Huang, G., and Darrell,

T. (2019c). Rethinking the value of network

pruning. In International Conference on Learning

Representations (ICLR).

Real, E., Aggarwal, A., Huang, Y., and Le, Q. V. (2019).

Regularized evolution for image classiﬁer architecture

search. In Proceedings of the AAAI conference on

artiﬁcial intelligence, volume 33, pages 4780–4789.

Sandler, M., Howard, A., Zhu, M., Zhmoginov, A.,

and Chen, L.-C. (2018). Mobilenetv2: Inverted

residuals and linear bottlenecks. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 4510–4520.

Simonyan, K. and Zisserman, A. (2015). Very deep

convolutional networks for large-scale image recog-

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

nition. In International Conference on Learning

Representations (ICLR).

Wang, R., Cheng, M., Chen, X., Tang, X., and Hsieh,

C.-J. (2021). Rethinking architecture selection in

differentiable NAS. In International Conference on

Learning Representations (ICLR).

Xie, S., Zheng, H., Liu, C., and Lin, L. (2019). SNAS:

stochastic neural architecture search. In International

Conference on Learning Representations (ICLR).

Xu, Y., Wang, Y., Han, K., Tang, Y., Jui, S., Xu, C.,

and Xu, C. (2021). ReNAS: Relativistic evaluation

of neural architecture search. In Proceedings of the

IEEE/CVF conference on computer vision and pattern

recognition, pages 4411–4420.

Xu, Y., Xie, L., Zhang, X., Chen, X., Qi, G.-J., Tian,

Q., and Xiong, H. (2020). PC-DARTS: Partial

channel connections for memory-efﬁcient architecture

search. In International Conference on Learning

Representations (ICLR).

Ye, P., Li, B., Li, Y., Chen, T., Fan, J., and Ouyang,

W. (2022). β-DARTS: Beta-decay regularization

for differentiable architecture search. In 2022

IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR), pages 10864–10873.

IEEE.

Zhang, M., Su, S. W., Pan, S., Chang, X., Abbasnejad,

E. M., and Haffari, R. (2021). iDARTS: Differentiable

architecture search with stochastic implicit gradients.

In International Conference on Machine Learning,

pages 12557–12566. PMLR.

Zhou, Y., Xie, X., and Kung, S.-Y. (2021). Exploiting oper-

ation importance for differentiable neural architecture

search. IEEE Transactions on Neural Networks and

Learning Systems, 33(11):6235–6248.

Zoph, B. and Le, Q. (2017). Neural architecture search with

reinforcement learning. In International Conference

on Learning Representations (ICLR).

VP-DARTS: Validated Pruning Differentiable Architecture Search