KAIME: Central Bank Digital Currency with
Realistic and Modular Privacy
Ali Dogan
1,2 a
and Kemal Bicakci
1 b
1
Computer Engineering Department and Informatics Institute, Istanbul Technical University, Istanbul, Turkey
2
Blockchain Technologies Unit, T
¨
UB
˙
ITAK B
˙
ILGEM, Kocaeli, Turkey
Keywords:
CBDC, Privacy, Cryptography, Zero Knowledge Proofs, Threshold Cryptography, Realistic Privacy,
Regulatory Mechanism, AML, KYC, CFT.
Abstract:
Recently, with the increasing interest in Central Bank Digital Currency (CBDC), many countries have been
working on researching and developing digital currency. The most important reasons for this interest are that
CBDC eliminates the disadvantages of traditional currencies and provides a safer, faster, and more efficient
system. These benefits also come with challenges, such as safeguarding individuals’ privacy and ensuring reg-
ulatory mechanisms. While most research address the privacy conflict between users and regulatory agencies,
they miss an essential detail. Important parts of a financial system are banks and financial institutions. Some
studies ignore the need for privacy and include these institutions in the CBDC system, no system currently
offers a solution to the privacy conflict between banks, financial institutions, and users. In this study, while
we offer a solution to the privacy conflict between the user and the regulatory agencies, we also provide a
solution to the privacy conflict between the user and the banks. Our solution, KAIME (the name given to the
first banknote issued by the Ottoman Empire) alsa has a modular structure. In the transaction, the sender and
receiver can be hidden if desired. Compared to previous related research, security analysis and implementation
of KAIME is substantially simpler because simple and well-known cryptographic methods are used. Addi-
tionally, the zero-knowledge proofs employed can function without the assistance of a trusted third party.
1 INTRODUCTION
Blockchain technology has gained popularity with the
emergence of cryptocurrencies. Many people have
started to adopt and use these cryptocurrencies. Mo-
tivated by the prevalence and success of blockchains,
there is a race between central banks for the develop-
ment of Central Bank Digital Currency (CBDC). CB-
DCs could be a revolution in terms of payment sys-
tems worldwide. Several central banks, including the
Swedish central bank (Riksbank, 2020) and the Bank
of England (Bank of England, 2020), have shown in-
terest in developing their own digital currencies. The
People’s Bank of China (Zhao, 2020) has already be-
gun testing the digital yuan. Moreover, several cen-
tral banks, in collaboration with the Bank for Interna-
tional Settlements (BIS), have described the key con-
cepts and characteristics of a CBDC. However, this
revolution also brings problems, such as protecting
a
https://orcid.org/0009-0009-4191-2982
b
https://orcid.org/0000-0002-2378-8027
private life and harmonizing regulations. How dig-
ital currencies can balance privacy and regulation is
one of the focuses of recent research.
Many people are worried that introducing CBDCs
may result in the central bank having continuous ac-
cess to transactional data, making it a ”panopticon.”
This concern is not unique to CBDCs and has also
been expressed regarding first-generation cryptocur-
rencies like Bitcoin and Ethereum, which are only
pseudonymous. To address this, privacy-enhanced
cryptocurrencies such as ZCash (Sasson et al., 2014)
and Monero (Van Saberhagen, 2018) were developed
to provide a higher level of anonymity by hiding the
value of transactions and making them unlinkable.
However, this anonymity could also attract those who
wish to use these systems for illegal activities, such
as money laundering and financing terrorism. As a
result, privacy-preserving systems using such tech-
niques may pose challenges in regulatory compliance
settings.
Related Work. Chaum introduced the initial
framework for anonymous electronic cash in his work
672
Dogan, A. and Bicakci, K.
KAIME: Central Bank Digital Currency with Realistic and Modular Privacy.
DOI: 10.5220/0012308600003648
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 10th International Conference on Information Systems Security and Privacy (ICISSP 2024), pages 672-681
ISBN: 978-989-758-683-5; ISSN: 2184-4356
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

(Chaum, 1983), which emphasized protecting the
sender’s anonymity while revealing the recipient’s
identity and the amount of money transferred. With
this system, a user can obtain a coin from a bank by
creating a distinctive serial number and obtaining a
blind signature to keep the serial number concealed
from the bank. The user can then unblind the sig-
nature and use the coin for payments. When a mer-
chant receives payment, they can deposit the coin at
the bank, which will verify whether the serial num-
ber has been utilized previously. If the serial number
is already used, the payment is rejected; if not, it is
accepted. Camenisch et al. (Camenisch et al., 2006)
introduced a method of electronic payment based on
tokens, where the bank can impose specific regula-
tions such as payment limits for individual users. De-
spite this, the privacy of those who send transactions
is preserved; however, the recipient’s identity and the
payment amount are revealed.
Another related work, PRCash is more relevant to
our solution that addresses the privacy conflict (W
¨
ust
et al., 2019) and presents a solution that utilizes ZKPs
to enable efficient implementation of a receiving limit
for anonymous transactions within a specific time in-
terval or epoch. Additionally, the regulation mecha-
nism of PRCash requires linking multiple transactions
within a time limit, which can potentially compromise
user privacy.
Androulaki et al. presented a token management
system that is both privacy-preserving and auditable
(Androulaki et al., 2020). Their proposed system em-
ploys a UTxO (Unspent Transaction Output) model
in a permissioned blockchain. Their solution is tai-
lored for business-to-business scenarios and does not
provide a comprehensive approach to regulatory com-
pliance.
Gross et al. proposed a modified version of Ze-
rocash to create a ”privacy pool” for CBDC (Gross
et al., 2021). This modified Zerocash protocol (Sas-
son et al., 2014) can ensure the privacy of CBDC
transactions by hiding the identities of the transacting
parties while maintaining the integrity of the CBDC
system. It utilizes proofs of inclusion in a Merkle tree
to verify transactions. This means the system uses a
Merkle tree data structure to efficiently prove that a
transaction is valid and that its inputs have not been
previously spent.
W
¨
ust et al. introduced Platypus, a privacy-
preserving and centralized payment system (W
¨
ust
et al., 2022). Platypus is not decentralized, which
means it cannot continue to function effectively in the
event of a single point of failure.
Tomescu et al. proposed a decentralized payment
system known as UTT, which relies on a Byzantine
fault-tolerant infrastructure (Tomescu et al., 2022).
Additionally, UTT limits the amount of money that
can be anonymously sent monthly.
PEReDi (Kiayias et al., 2022) provides support
for regulatory compliance, including Know Your Cus-
tomer (KYC), Anti-Money Laundering (AML), and
Combating Financing of Terrorism (CFT) require-
ments. In the PEReDi, a committee of several au-
thorities can revoke privacy or trace transactions from
a specific user. The committee does so by decrypting
the ciphertext stored in the ledger. Both users must be
online for the transaction to occur on PEReDi.
Contributions. The paper presents the following
contributions:
1. To the best of our knowledge, we propose a
CBDC system that does not only address the
privacy conflict between the user and regulatory
agencies but also resolves the privacy conflict be-
tween the bank and the user by including all stake-
holders (users, banks, financial institutions, reg-
ulatory agencies, central bank) for the first time.
This system also supports regulatory mechanisms
such as KYC, AML, and CFT, which are critical
requirements that should be included in a CBDC
system.
2. In KAIME, sender and receiver privacy can be
added or removed as features from the system de-
pending on the requirements. This adds modular-
ity to our solution.
3. Since simple and known cryptographic algorithms
are used, security analysis and implementation of
KAIME is much easier than other related works.
In addition, the zero-knowledge proofs can work
without needing a trusted party.
2 OVERVIEW
In this section, we present a summary of our solution.
We begin by discussing our motivation and our re-
quirements. Next, we describe our system model and
then give the details of the cryptographic techniques
we have employed to develop our solution.
2.1 Motivation
In a report by the Swiss National Bank (Chaum et al.,
2021), ”mass surveillance” is specifically identified
as a potential risk associated with a CBDC. This un-
derscores the importance of ensuring strong privacy
protections. Furthermore, a survey conducted by the
European Central Bank (Bank, 2021) revealed that
KAIME: Central Bank Digital Currency with Realistic and Modular Privacy
673

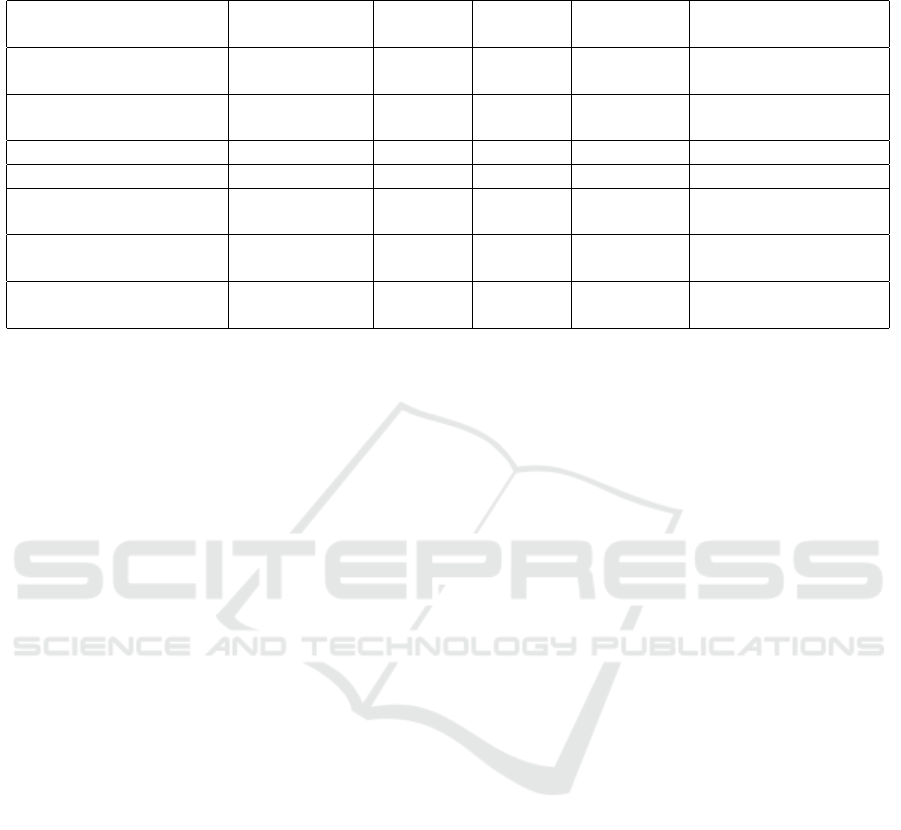
Table 1: The first column shows whether the system is UTxO or account-based. The last column shows the cryptographic
techniques used. The other columns show whether the sender, receiver, and transaction details are hidden.
Reference
UTxO or
Account Based
Sender
Privacy
Receiver
Privacy
Transaction
Privacy
Cryptographic
Technique
(W
¨
ust et al., 2019) UTxO Yes Yes Yes
ZKP , ElGamal Enc.,
Ped. Com.
(Androulaki et al., 2020) UTxO Yes Yes Yes
VRF, ElGamal Enc.,
PS Sig., Ped. Com.
(Gross et al., 2021) UTxO Yes Yes Yes Commitment, ZKP
(W
¨
ust et al., 2022) Account Yes Yes Yes Commitment, ZKP
(Tomescu et al., 2022) UTxO Yes Yes Yes
MPC, Commitment,
ZKP
(Kiayias et al., 2022) Account Yes Yes Yes
MPC, ZKP,
PS Sig., Elgamal Enc.
KAIME Account Optional Optional Yes
Elgamal Enc., ZKP,
MPC, Anon. Set
privacy was considered the most critical aspect of a
CBDC.
While CBDCs are expected to provide a criti-
cal feature, such as privacy, CBDCs must accommo-
date some regulatory requirements for financial sta-
bility and government security. Regulatory require-
ments for CBDCs are the enforcement of anti-money-
laundering (AML), know-your-customer (KYC), and
counter-financial-terrorism (CFT) (Allen et al., 2020).
On the other hand, this contradicts the objective of en-
hancing payment privacy.
There is a suggestion that this conflict can be re-
solved by allowing anonymous payments up to a spe-
cific limit per unit of time (Bank, 2019). Previous
works have proposed this idea (W
¨
ust et al., 2019),
(Garman et al., 2017), (W
¨
ust et al., 2022). The idea
does not meet the requirements. Government offi-
cials may not mind evading a $100 tax, but when it
comes to a criminal or murderer, payment informa-
tion is critical. Various suggestions for solving this
conflict are summarized in the related work section.
These solutions include various cryptographic tech-
niques such as zero-knowledge proof, commitment
scheme, threshold cryptography, and blind signature.
In (Auer et al., 2023), the authors stated that these so-
lutions do not explicitly address the privacy conflict
between stakeholder groups (merchants, banks and
payment providers, government). In the article, Auer
et al. mentioned not only the privacy conflict between
the user and the government but also the high level
of conflict between other groups. They have also di-
vided the situations in which the user’s data should be
accessed and the stakeholder who wants to access it,
layer by layer.
Based on the motivation to provide both the pri-
vacy of users and regulatory requirements and the
idea of bringing other stakeholders into the system,
our first aim is to design a system in which a per-
son suspected by the regulatory agencies can track all
transactions retrospectively and provide this tracking
by exceeding the threshold number. Our second goal
is to include banks and companies that use financial
data in the system and to solve the privacy conflict
between them and the user.
CBDC can be recorded in a distributed ledger us-
ing blockchain technology. This technology is used
to ensure that CBDCs are traded in a secure, transpar-
ent, and reliable manner. Blockchain technology can
help prevent fraudulent or misleading transactions as
transactions are recorded irreversibly. In addition to
such benefits, we use a permissioned blockchain to
easily access the transaction details of the stakehold-
ers, except the users in the system, and to prevent a
single point of failure.
2.2 Balance Between Soft and Hard
Privacy
Auer et al. divided the privacy methods in CBDC sys-
tems into three (Auer et al., 2023). These are hard pri-
vacy, soft privacy, and privacy with a balance between
soft and hard. The stakeholders in the system have
been divided into shells according to the monitoring
status of the transactions and the request to review the
transactions.
Hard privacy argues that all stakeholders in the
system cannot see the transactions and that only the
person with the private key can see the plaintext, that
is, the user. Unfortunately, this will lead to the disap-
pearance of regulatory mechanisms and is undesirable
for CBDCs. On the other hand, soft privacy addresses
the ability of payment information to move freely be-
tween different parties yet still protects it from exter-
nal attacks through point-to-point encryption. While a
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
674

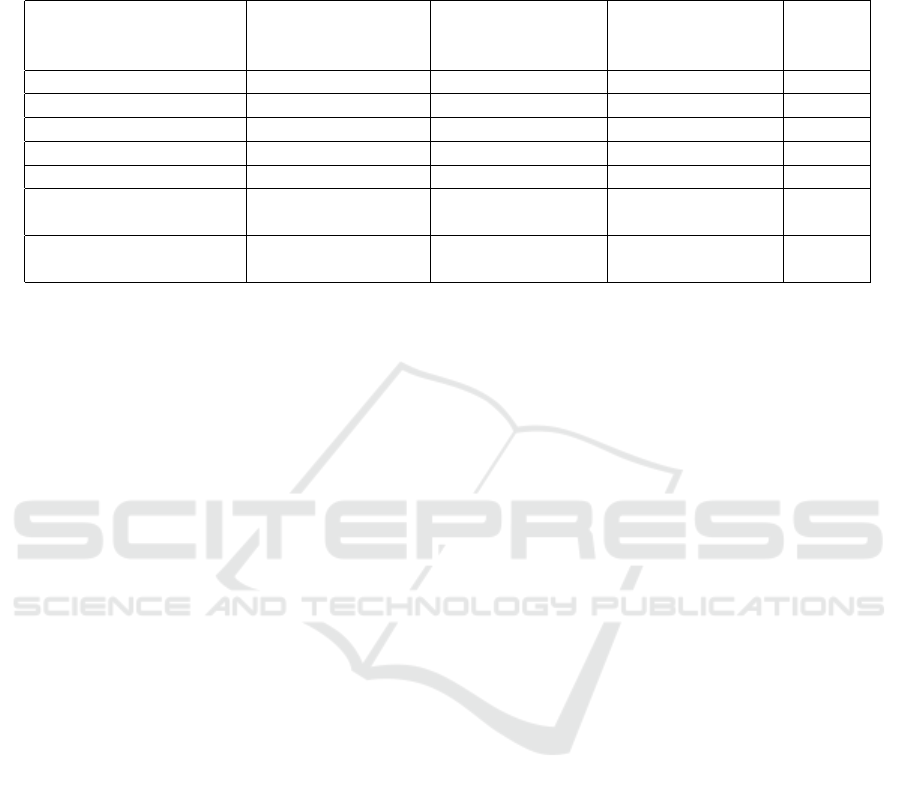
Table 2: The table compares the related work dealing with the privacy conflict and our solution. The second column shows
under what conditions and by whom the regulation mechanism is executed. The third and fourth columns show for which
stakeholders a solution to the privacy conflict is offered. The last column shows whether the papers were written for CBDC
purposes.
References
Regulation
Mechanism
Solution to Privacy
Conflict Between
User- Reg. Agen.
Solution to Privacy
Conflict Between
User- Fin. Ins.
For
CBDC?
(W
¨
ust et al., 2019) Balance Limit Yes No No
(Androulaki et al., 2020) Single Reg. Agency Yes No No
(Gross et al., 2021) Balance Limit Yes No Yes
(W
¨
ust et al., 2022) Balance Limit Yes No Yes
(Tomescu et al., 2022) Balance Limit Yes No Yes
(Kiayias et al., 2022)
More than One
Reg. Agency
Yes No Yes
KAIME
More than One
Reg. Agency
Yes Yes Yes
system like this can be highly effective in terms of ef-
ficiency, its privacy features will not differ from those
of current payment networks. As a result, it may not
meet the privacy needs of users who are particularly
concerned about protecting their information.
We use hard privacy techniques between regula-
tory agencies and users in KAIME; we use a tech-
nique that converges to soft privacy, although we can-
not say precisely soft privacy between the bank and
the user.
2.3 Security and Privacy Requirements
In this section, we define the privacy and security re-
quirements that should be in KAIME.
Transaction Integrity. It should not be possi-
ble for any person to transact on behalf of someone
else and change their balance. Following a success-
ful transaction between two users, it is imperative to
update the accounts of both parties accurately, taking
into account all relevant parameters. The transaction
must occur even if the receiving party is offline. The
balance increases and decreases on the sender, and re-
ceiver sides must be the same.
Regulatory Mechanism. Regulation mecha-
nisms such as KYC, AML, and CFT should be in-
cluded in the system. Regulatory agencies should be
able to see the details of the process and review them
retrospectively when needed. In order for these mech-
anisms to be quickly processed, the sender should not
be stored encrypted in the ledger.
Bank and Financial Institutions Tasks. The du-
ties of these institutions in traditional systems should
also be provided in the solution. The user should be
able to share the details of the past transaction with
the institution without deceiving the institution. How-
ever, the institution cannot monitor past transactions
without user permission.
Identity and Transaction Privacy. When a trans-
action is given, the recipient and the transaction value
should not be detected in cases other than auditing. In
addition, the user balance should be kept encrypted in
the ledger, and the balance should not be detected.
Unlinkability. Given a transaction, the ownership
of the assets used by the current transaction should
not be linked to past transactions. It should not be
possible to connect the receiver to another payment
in the same system where the sender or receiver is
located.
Non-Repudiation. Once a sender has made a
payment, she should not be able to deny it later.
2.4 Stakeholders & Roles
In this section, we describe the entities involved and
their respective roles. We would like to point out that
the central bank, banks, and regulatory agencies are
responsible for the operation of the blockchain.
• Central Bank. The digital currency is issued
by the central bank, which is accountable for the
monetary policy and has the authority over the
monetary supply at any point. However, the cen-
tral bank has no control over the status of all users’
accounts and lacks trust in privacy due to the pos-
sibility of mass surveillance. This means the cen-
tral bank cannot disclose the transferred values
associated with a particular transaction. For the
role of the central bank, we refer to (Chaum et al.,
2021).
• Users. As with any digital currency system, users
of the system can take on the role of either the
sender or the recipient when participating in a
transaction involving digital currency. Users have
KAIME: Central Bank Digital Currency with Realistic and Modular Privacy
675

no choice against regulatory agencies to protect
the privacy of their past transactions. If the regu-
latory agencies decide that the user is a potential
criminal, they can abort the user’s privacy with the
help of threshold cryptography. In addition, users
have the ability to allow banks and financial insti-
tutions to review transactions.
• Banks and Financial Institutions. Banks are
responsible for making the user registration pro-
cess. In the traditional banking system, banks
also have various responsibilities, such as giving
a credit score to the user and determining a credit
card limit. In order to perform these functions,
banks need to learn the balance and past transac-
tions of the user. They can perform this operation
cryptographically in line with the user’s consent.
Likewise, financial institutions need to access the
user’s transaction details to fulfill their duties in
the traditional system. The user can share trans-
action details with financial institutions upon re-
quest.
• Regulatory Agencies. Our approach involves en-
trusting a group of authorized institutions, which
we call regulatory agencies, with the task of con-
ducting different audit procedures required for en-
suring regulatory compliance. Regulatory agen-
cies can access the data of the user’s transactions
in case of doubt by joint decision. They can trans-
late the encrypted transaction data into plaintext
with the help of threshold cryptography and ac-
cess the transaction details.
3 SYSTEM DETAILS
In the following section, we will provide a more de-
tailed explanation of our solution. Our approach in-
volves the integration of various cryptographic tech-
niques as fundamental components. For additional
clarity, we have included further information about
these techniques in the Appendix.
3.1 System Initialization
Regulatory Agencies. An encryption keypair
(pk
R
, sk
R
) = (g
sk
R
, sk
R
) for Threshold Elgamal En-
cryption is generated by the regulatory agencies, and
the public keys are made available to the system setup.
We apply a variant of Pedersen Distributed Key Gen-
eration (Pedersen, 1991) to generate private key so
that a single agency does not have the authority to see
the transaction details. In KAIME, there are n regu-
latory agencies and we will display the private key of
each of them with sk
R,i
and the threshold number of
regulatory agencies required to construct a private key
is t. This means that in order to see the details of the
transactions, at least t agency agencies must reach an
agreement.
Central Bank. The central bank is registered in
the ledger, and the signature key pair is generated like
a user. The key pair is used for validation in the cur-
rency issue function.
Banks and Financial Institutions. Banks and fi-
nancial institutions will register in the system as a
user. They are responsible for the operation of the
blockchain and have access to the user’s ciphertext.
3.2 User Registration
By verifying the KYC step, the user is registered to
the system through the bank. Then, the user needs
to generate two key pairs. One is for signature; the
other is to keep the balance in the ledger as encrypted
and increase the received balances homomorphically
encrypted balance.
The bank then creates the ElGamal ciphertext with
a balance of 0 using the encryption public key pk
U
created by the user for encryption and saves it to the
ledger. The bank performs the same operation for
public key of regulatory agencies. The bank also adds
the proof that the plaintexts of the ciphertexts are 0
(see Appendix).
3.3 Currency Issue
The central bank encrypts the value v, which it wants
to issue, with the public key of the user and the pub-
lic key of the regulatory agencies. Then, the central
bank creates a Proof of Encryption Equality-1 (see
Appendix) that the values in these two ciphertexts are
the same and signs the transaction and proofs, and
then sends these to the ledger. The ledger is updated
by checking the validity of the proofs and signature.
3.4 Payment
To start the payment process, the sender must first
have the public key of the receiver and the public
key between the receiver and the bank. This initial
step can be accomplished with a QR code. When
the sender wants to send v value to the receiver, he
encrypts v under the public keys of the receiver, the
sender and regulatory agencies.
To ensure that three ciphertexts are decrypted to
the same value, the sender creates two Proofs of
Equality (see Appendix). In order to prevent any pos-
sibility of creating value out of thin air and verify that
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
676

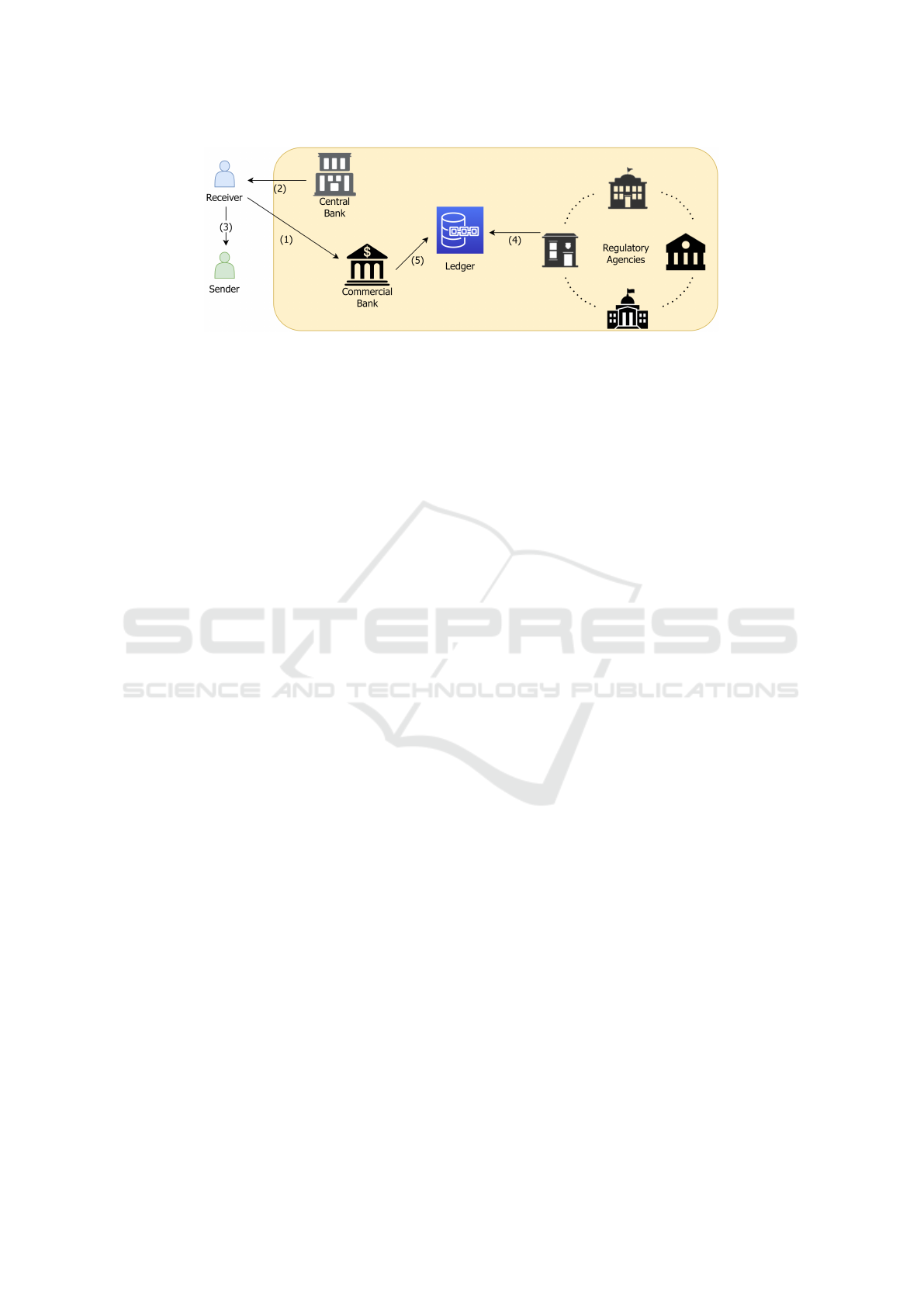
Figure 1: The System consists of commercial banks (or any financial institutions) responsible for user registration and tradi-
tional bank tasks, the central bank responsible for currency issues and monetary policy, and regulatory agencies responsible
for regulatory compliance. All entities are responsible for executing the validity of transactions and the blockchain network.
The direction of the arrows and the numbers in the figure do not indicate a specific order. The purpose of the arrows is to
show the functions that take place between the entities. (1) represents User Registration, (2) represents Currency Issue, (3)
represents Payment, (4) represents Abort Transaction Privacy, and (5) represents Abort Transaction Privacy for Bank.
the sender has sufficient balance in her account, he
also adds two range proofs. To prepare these range
proofs, he needs to keep track of the random values
used while encrypting the amounts. However, there is
no way for the user to keep track of the encrypted bal-
ance in the ledger (since the random value will change
as homomorphic addition occurs). For this reason, it
must replace the encrypted balance in the ledger with
an encrypted balance using a random value it knows.
In doing so, he creates Proof of Encryption Equality-
2. In this way, he will have the random value in the
ciphertext in the ledger. This method was first used in
PGC (Chen et al., 2019). Finally, the sender signs the
transaction with the private key and sends the proofs
and ciphertexts to the blockchain.
After proofs and sign are verified, the sender’s en-
crypted balance decreases homomorphically, and the
receiver’s encrypted balance increases homomorphi-
cally.
3.5 Abort Transaction Privacy
Regulatory agencies apply the abort privacy transac-
tion function on the transaction or balance related to
their shared ElGamal encryption keys to see the con-
tent of transactions they consider suspicious. How-
ever, for this to happen, a sufficient number of reg-
ulatory agencies must reach a consensus. The user’s
transaction history and account balance can then be
decrypted using threshold encryption. Details are de-
scribed in the Appendix.
3.6 Abort Transaction Privacy for Bank
and Financial Institutions
When the user wants to receive service from the bank
or institution, the institution that will provide the ser-
vice needs the details of the user’s past transactions.
The user can give the encryption private key to the
bank in order to present the contents of the encrypted
transactions on the ledger to the bank, but in such a
scenario, the bank will have the ability to see the fu-
ture transactions of the user.
Firstly, a bank or financial institution creates a
one-time public key for this function and sends it
to the user. The user encrypts the balance and val-
ues of all previous transactions with this public key.
After this step, the user creates Proof of Encryption
Equality-1 for all past encrypted transactions and the
encrypted texts it creates with the one-time public key
and sends it to the bank. The reason for creating this
proof is to prevent the user from cheating the bank.
After the bank has verified the proofs, it can access
the user’s transaction values and balance.
4 TRUST ASSUMPTION
Our paper does not address protection for network-
based deanonymization attacks, such as linking an IP
address to multiple transactions. Clients who wish to
protect themselves against such attacks can employ
measures.
We make the assumption that the clients en-
gage in communication through secure channels,
and all cryptographic operations employed conform
to the standard definitions of their security: It
is assumed that signatures are unforgeable, zero-
knowledge proofs provide soundness and are zero-
knowledge, and encryption is CPA-secure.
We assume that regulatory agencies do not want
to see the transaction details arbitrarily. They run the
abort privacy transaction function only for people and
transactions they think are suspicious.
KAIME: Central Bank Digital Currency with Realistic and Modular Privacy
677

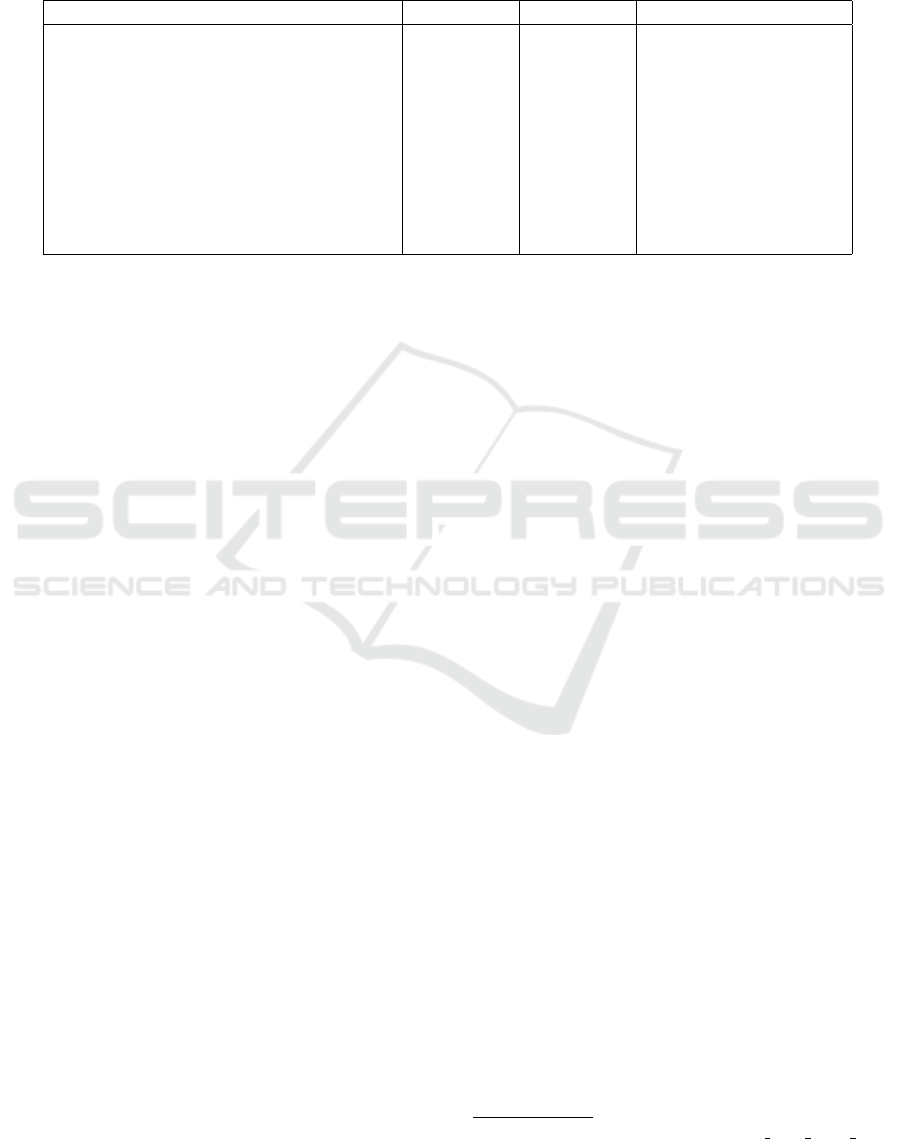
Table 3: The ”Algorithm” column specifies the cryptographic operation being measured, while the ”Prover” and ”Verifier”
columns show the time it takes for the prover and verifier to complete the operation in milliseconds. Additionally, the ”Number
of uses in a TX” column indicates how many times each operation is utilized within a transaction. Since zero proof is not
used in the transaction, it is shown with ”-” in the column. The results of the tests performed on a computer with i7-1165g7
@ 2.80ghz and 16gb.
Algorithm Prover Verifier Number of uses in a TX
Proof of Encryption Equality-1 (ed25519) 0.130 ms 0.243 ms 2
Proof of Encryption Equality-2 (ed25519) 0.201 ms 0.156 ms 1
Range Proof (ed25519) 32.209 ms 18.072 ms 2
Zero Proof (ed25519) 0.121 ms 0.252 ms -
ElGamal Encryption (ed25519) 0.147 ms - 3
Proof of Encryption Equality-1 (P256) 1.216 ms 2.309 ms 2
Proof of Encryption Equality-2 (P256) 1.989 ms 1.503 ms 1
Range Proof (P256) 292.965 ms 121.516 ms 2
Zero Proof (P256) 0.672 ms 1.749 ms -
ElGamal Encryption (P256) 1.083 ms - 3
5 ANONYMITY
In this section, we will give an anonymous version
of our solution. This version not only hides the
transferred amount but also hides the receiver. How-
ever, it comes at the expense of additional costs.
The complexity of the zero-knowledge proofs re-
quired for transfer will increase linearly the size of
the anonymity set, but with the method (Diamond,
2020) proposes, the complexity will increase loga-
rithmically. The complexity of the process can be re-
duced using this method. A similar solution was used
in Zether (B
¨
unz et al., 2020).
Because of the limited amount of available space,
we will only introduce it as an overview. An anony-
mous transaction allows a sender who wishes to send
a value v to a receiver with a public key pk
r
, to con-
ceal both the identity of the receiver among a larger
set of users with public keys {pk
1
, pk
2
,.....pk
n
}, as
well as the transferred value v. The sender sends 3n
ciphertexts, and all of them encrypt 0 except three.
Only three ciphertexts represent the real transaction;
the rest are fake transactions. Since the sent values in
the fake transaction are 0, the balance of the sender
and the users in the anonymity set does not change.
By using ring signatures, both the sender, the
receiver, and the transaction details can be hidden.
However, we do not recommend hiding the sender
so that the regulation mechanism can work better, al-
though it may differ according to the requirements.
6 IMPLEMENTATION AND
SECURITY ANALYSIS
In the scope of this study, we have implemented cryp-
tographic algorithms described in previous sections
using the Go programming language. To evaluate
the performance of these implementations, we pro-
vide the corresponding test results in Table 3. Fur-
thermore, the open-source tests and implementations
of these algorithms can be accessed via GitHub
1
.
We will show that zero knowledge proofs provide
completeness, special soundness and special honest
verifier zero knowledge properties in the full version
of the paper (Dogan and Bicakci, 2023).
7 CONCLUSIONS
This study showed that cryptographic protocols, as in
related works, are an effective tool for providing pri-
vacy and regulation to CBDCs. In addition, our study
also addressed the privacy between the user and the
banks and showed that cryptographic protocols pro-
tect this privacy. It also enabled banks to fulfill their
tasks. Future work may focus on further refining these
protocols and better protection of privacy and regula-
tion of CBDCs.
ACKNOWLEDGEMENTS
We would like to express our gratitude to T
¨
UB
˙
ITAK
B
˙
ILGEM employees Taner Dursun,
˙
Ilker Bedir, and
1
https://github.com/midmotor/kaime cbdc proof test
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
678

Abdulhamit Kumru for their valuable contributions
to this study. Additionally, we thank T
¨
UB
˙
ITAK
B
˙
ILGEM for financially supporting this study.
REFERENCES
Allen, S.,
ˇ
Capkun, S., Eyal, I., Fanti, G., Ford, B. A., Grim-
melmann, J., Juels, A., Kostiainen, K., Meiklejohn,
S., Miller, A., et al. (2020). Design choices for central
bank digital currency: Policy and technical considera-
tions. Technical report, National Bureau of Economic
Research.
Androulaki, E., Camenisch, J., Caro, A. D., Dubovit-
skaya, M., Elkhiyaoui, K., and Tackmann, B. (2020).
Privacy-preserving auditable token payments in a per-
missioned blockchain system. In Proceedings of the
2nd ACM Conference on Advances in Financial Tech-
nologies, pages 255–267.
Auer, R., B
¨
ohme, R., Clark, J., and Demirag, D. (2023).
Mapping the privacy landscape for central bank digital
currencies. Communications of the ACM, 66(3):46–
53.
Bank, E. C. (2019). Exploring anonymity in central bank
digital currencies. In Focus, 4:1–11.
Bank, E. C. (2021). Eurosystem report on the public con-
sultation on a digital euro.
Bank of England, U. (2020). Central bank digital
currency. opportunities, challenges and de-
sign. URL: https://www. bankofengland. co.
uk/-/media/boe/files/paper/2020/centralbank-digital-
currency-opportunities-challenges-and-design. pdf.
Bellare, M. and Rogaway, P. (1993). Random oracles are
practical: A paradigm for designing efficient proto-
cols. In Proceedings of the 1st ACM Conference on
Computer and Communications Security, pages 62–
73.
B
¨
unz, B., Agrawal, S., Zamani, M., and Boneh, D. (2020).
Zether: Towards privacy in a smart contract world.
In Financial Cryptography and Data Security: 24th
International Conference, FC 2020, Kota Kinabalu,
Malaysia, February 10–14, 2020 Revised Selected Pa-
pers, pages 423–443. Springer.
B
¨
unz, B., Bootle, J., Boneh, D., Poelstra, A., Wuille, P.,
and Maxwell, G. (2018). Bulletproofs: Short proofs
for confidential transactions and more. In 2018 IEEE
symposium on security and privacy (SP), pages 315–
334. IEEE.
Camenisch, J., Hohenberger, S., and Lysyanskaya, A.
(2006). Balancing accountability and privacy using e-
cash. In Security and Cryptography for Networks: 5th
International Conference, SCN 2006, Maiori, Italy,
September 6-8, 2006. Proceedings 5, pages 141–155.
Springer.
Chaum, D. (1983). Blind signatures for untraceable pay-
ments. In Advances in Cryptology: Proceedings of
Crypto 82, pages 199–203. Springer.
Chaum, D., Grothoff, C., and Moser, T. (2021). How to
issue a central bank digital currency. arXiv preprint
arXiv:2103.00254.
Chen, Y., Ma, X., Tang, C., and Au, M. H. (2019). Pgc:
pretty good decentralized confidential payment sys-
tem with auditability. Cryptology ePrint Archive.
Diamond, B. E. (2020). Many-out-of-many proofs and ap-
plications to anonymous zether. Cryptology ePrint
Archive, Paper 2020/293. https://eprint.iacr.org/2020/
293.
Dogan, A. and Bicakci, K. (2023). Kaime: Central bank
digital currency with realistic and modular privacy.
Cryptology ePrint Archive.
Garman, C., Green, M., and Miers, I. (2017). Accountable
privacy for decentralized anonymous payments. In Fi-
nancial Cryptography and Data Security: 20th Inter-
national Conference, FC 2016, Christ Church, Barba-
dos, February 22–26, 2016, Revised Selected Papers
20, pages 81–98. Springer.
Gross, J., Sedlmeir, J., Babel, M., Bechtel, A., and
Schellinger, B. (2021). Designing a central bank digi-
tal currency with support for cash-like privacy. Avail-
able at SSRN 3891121.
Kiayias, A., Kohlweiss, M., and Sarencheh, A. (2022).
Peredi: Privacy-enhanced, regulated and distributed
central bank digital currencies. Cryptology ePrint
Archive.
Komlo, C. and Goldberg, I. (2020). Frost: Flexible round-
optimized schnorr threshold signatures. Cryptology
ePrint Archive, Paper 2020/852. https://eprint.iacr.
org/2020/852.
Kurosawa, K. (2002). Multi-recipient public-key encryp-
tion with shortened ciphertext. In Public Key Cryp-
tography, volume 2274, pages 48–63. Springer.
Pedersen, T. P. (1991). A threshold cryptosystem with-
out a trusted party. In Advances in Cryptol-
ogy—EUROCRYPT’91: Workshop on the Theory and
Application of Cryptographic Techniques Brighton,
UK, April 8–11, 1991 Proceedings 10, pages 522–
526. Springer.
Riksbank, S. (2020). The riksbank’s e-krona pilot. Sveriges
Riksbank.
Sasson, E. B., Chiesa, A., Garman, C., Green, M., Miers, I.,
Tromer, E., and Virza, M. (2014). Zerocash: Decen-
tralized anonymous payments from bitcoin. In 2014
IEEE symposium on security and privacy, pages 459–
474. IEEE.
Tomescu, A., Bhat, A., Applebaum, B., Abraham, I., Gueta,
G., Pinkas, B., and Yanai, A. (2022). Utt: Decen-
tralized ecash with accountable privacy. Cryptology
ePrint Archive.
Van Saberhagen, N. (2018). Cryptonote v 2.0 (2013). URL:
https://cryptonote. org/whitepaper. pdf. White Paper.
Accessed, pages 04–13.
W
¨
ust, K., Kostiainen, K.,
ˇ
Capkun, V., and
ˇ
Capkun, S.
(2019). Prcash: fast, private and regulated transac-
tions for digital currencies. In Financial Cryptography
and Data Security: 23rd International Conference,
FC 2019, Frigate Bay, St. Kitts and Nevis, February
18–22, 2019, Revised Selected Papers 23, pages 158–
178. Springer.
W
¨
ust, K., Kostiainen, K., Delius, N., and Capkun, S.
(2022). Platypus: A central bank digital currency with
KAIME: Central Bank Digital Currency with Realistic and Modular Privacy
679

unlinkable transactions and privacy-preserving regu-
lation. In Proceedings of the 2022 ACM SIGSAC Con-
ference on Computer and Communications Security,
pages 2947–2960.
Zhao, W. (2020). Chinese state-owned bank offers test inter-
face for pboc central bank digital currency. CoinDesk.
Accessed July, 7:2022.
APPENDIX
Homomorphic Elgamal Encryption
The difficulty of solving the discrete logarithm prob-
lem is ensuring the security of the Elgamal encryp-
tion scheme. The encryption consists of the following
three algorithms:
1. KeyGen. Assuming that p is a prime number and
g is a generator of Z
∗
p
. Then private key sk is ran-
domly selected sk
$
←− Z
∗
p
and public key pk = g
sk
is calculated.
2. Encryption. To encrypt the v value, a random r is
selected r
$
←− Z
∗
p
and c is calculated.
(φ
L
, φ
R
) = (g
r
, g
v
· pk
r
)
3. Decryption. To decrypt the ciphertext, φ
R
/φ
sk
L
is
calculated.
g
v
= φ
R
/φ
sk
L
Then, the value b is found with brute force.
Distributed Key Generation
Distributed Key Generation (DKG) is a cryptographic
process in which multiple parties collaboratively gen-
erate a cryptographic key without any one party hav-
ing complete knowledge of the key. We use the same
DKG is used in FROST (Komlo and Goldberg, 2020).
We delete details for simplicity. The process is as fol-
lows:
1. Every participant P
i
(regulatory agencies in our
cases) chooses t random value and uses them
as coefficients to define polynomial f
i
(x) =
∑
t−1
j=0
a
i j
x
j
.
2. Each P
i
calculates a proof of knowledge for the
constant term in the polynomial.
3. Each P
i
computes a commitment
⃗
C
i
=

α
i0
,...,α
i(t−1)

, where α
i j
= g
a
i j
and broadcasts
⃗
C
i
and the proof.
4. Each P
i
, after receiving
⃗
C
ℓ
and the proof, verifies
the proof.
5. Each P
i
securely sends to other participants a se-
cret (ℓ, f
i
(ℓ)).
6. Each P
i
verifies their shares by calculating:
g
f
ℓ
(i)
?
=
∏
t−1
k=0
α
i
k
ℓk
mod q, after that calculates pri-
vate sharing key by computing sk
i
=
∑
n
ℓ=1
f
ℓ
(i)
7. The group public key is computed
pk =
∏
α
j0
Threshold ElGamal Encryption
∏
j̸=i
−x
j
x
i
−x
j
is the Lagrange coefficient. We represent
it with λ
i
. Suppose the ElGamal private key sk is dis-
tributed to n parties. That is,
sk =
∑
sk
i
λ
i
To decrypt a ciphertext, i-party publishes φ
sk
i
L
, and
the proof is generated in order to demonstrate the hon-
est contribution of the party. g
v
is calculated after
summing the values from the parties.
g
b
= φ
R
/
∏
φ
sk
i
λ
i
L
b is found by applying brute force to g
b
.
Fiat-Shamir Technique
Fiat-Shamir is a technique used to make an interac-
tive protocol non-interactive (Bellare and Rogaway,
1993). This technique uses an algorithm that gener-
ates a result using a hash function instead of a tradi-
tional protocol where two parties (prover and verifier)
share information and interact with each other. The
Fiat-Shamir technique eliminates interactivity in the
proofs described in this section. How to use the Fiat-
Shamir Technique in proofs is not shown for simplic-
ity.
Proof of 0 Encryption
The definition of the Proof of 0 Encryption relation is
as follows:
{(g, pk, φ
L
, φ
R
; r) : φ
L
= g
r
∧ φ
R
= g
0
· pk
r
}
With this proof, the prover proves that the value in the
ciphertext is 0. The protocol is shown in Figure 2.
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
680

Prover Verifier
u ∈
R
Z
n
a
1
←− g
u
a
2
←− (pk
1
/pk
2
)
u
a
1
, a
2
−−−−−−−−−−→
φ ∈
R
Z
q
c
←−−−−−−−−−−
z ←−
n
u + c.r
z
−−−−−−−−−−→
g
z
?
= a
1
.φ
c
1,L
(pk
1
/pk
2
)
z
?
= a
2
.(φ
1,R
/φ
2,R
)
c
Figure 2: Proof of 0 Encryption.
Proof of Encryption Equality-1
In the ElGamal encryption, Kurosawa demonstrated
that it is possible to use the same random values to en-
crypt data for multiple ciphertexts (Kurosawa, 2002).
This idea is applied in our solution to enhance the ef-
ficiency of the Proof of Encryption Equality-1. The
relation is as follows:
{(g, pk
1
, pk
2
, φ
1,L
, φ
1,R
, φ
2,R
;v, r) :
φ
1,L
= g
r
∧ φ
1,R
= g
v
· pk
r
1
∧ φ
2,R
= g
v
· pk
r
2
}
Proof of Encryption Equality-1 shows that two cipher-
texts commit to the same plaintext. The protocol is
shown in Figure 3.
Prover Verifier
u ∈
R
Z
n
a
1
←− g
u
a
2
←− (pk
1
/pk
2
)
u
a
1
, a
2
−−−−−−−−−−→
c ∈
R
Z
q
c
←−−−−−−−−−−
z ←−
n
u + c.r
z
−−−−−−−−−−→
g
z
?
= a
1
.φ
c
1,L
(pk
1
/pk
2
)
z
?
= a
2
.(φ
1,R
/φ
2,R
)
c
Figure 3: Proof of Encryption Equality-1.
Proof of Encryption Equality-2
The definition of the Proof of Encryption Equality-2
relation is as follows:
{(g, pk, φ, φ
′
; r, v, x) : φ
R
= g
v
· pk
r
∧ φ
′
R
= g
v
· pk
r
′
}
Proof of Encryption Equality-2 shows that the
plaintexts of two different ciphertexts are equal to
each other. This proof is used to keep track of
the random value by refreshing the ciphertext in the
ledger.The protocol is shown in Figure 4.
Range Proof
Bulletproofs (B
¨
unz et al., 2018) are utilized for the
range proof in our solution. The definition of the
Prover Verifier
u ∈
R
Z
n
a
1
←− g
u
a
2
←− (φ
L
/φ
′
L
)
u
a
1
, a
2
−−−−−−−−−−→
c ∈
R
Z
q
c
←−−−−−−−−−−
z ←−
n
u + c.x
z
−−−−−−−−−−→
g
z
?
= a
1
.pk
c
(φ
L
/φ
L
′
)
z
?
= a
2
.(φ
R
/φ
′
R
)
c
Figure 4: Proof of Encryption Equality-2.
range-proof relation is as follows:
{(g, pk,φ
R
; v,r) : φ
R
= g
v
· pk
r
∧ v ∈ [0, 2
32
− 1]}
g, pk and φ
R
are open parameters, v and r are wit-
ness values. With range proof, a prover can prove that
the value of v in a ciphertext is greater than 0 and less
than 2
32
− 1.
KAIME: Central Bank Digital Currency with Realistic and Modular Privacy
681