Biodegradable Biodevices: A Design Approach Based on Cellular

Automaton

William Solórzano-Requejo

, Carlos Aguilar

, Gabriel Callejo and Andrés Díaz Lantada

Department of Mechanical Engineering, ETSI Industriales, Universidad Politécnica de Madrid,

c/ José Gutiérrez Abascal 2, 28006 Madrid, Spain

Keywords: Biodegradable Medical Devices, Biodegradable Materials, Degradation Modelling, Simulation of Medical

Devices, Cellular Automata.

Abstract: This innovative study introduces a comprehensive methodology to simulate the two-dimensional degradation

of biodegradable materials, a crucial aspect in biodevice design. Several PVA specimens of diverse shapes

were created, and their degradation was computationally modelled using cellular automaton. Deterministic

and probabilistic transition rules were explored to identify the most accurate in the simulation of PVA

degradation. The results highlight the effectiveness of the probabilistic exponential rule, derived from Markov

Chains, for reliable degradation simulation. Furthermore, this approach was successfully applied to the

analysis of specific medical devices, enabling a detailed in silico assessment of degradation patterns in

coronary stents, tissue engineering scaffolds and craniosynostosis implants. This methodology deepens our

fundamental understanding of degradation and provides valuable information for engineers and medical

professionals, facilitating the creation of devices that integrate optimally with surrounding biological tissues.

1 INTRODUCTION

Cellular automaton (CA) are discrete, local

dynamical systems that can be considered in several

ways: as a mathematical idealization of natural

systems, a discrete caricature of microscopic

dynamics, a parallel algorithm, or a discretization of

partial differential equations. From an engineering

perspective, CAs are networks composed of finite-

state machines, also known as cells, that operate

through localized interactions. These cells evolve

collectively, and the evolution of the system is

determined by the interaction of their individual

components (Dascălu, 2018).

In essence, CAs are conceptualized as sets of cells

arranged in grids. Over sequential steps or iterations,

these grids are dynamically transformed according to

specific predefined rules. During these iterations, the

state of each cell changes, influenced by both the

predetermined rules and the previous states of

neighbouring cells. If all cells are updated

simultaneously, the automaton is called synchronous.

https://orcid.org/0000-0002-2989-9166

https://orcid.org/0000-0003-0291-3041

https://orcid.org/0000-0002-0358-9186

On the other hand, if only one cell is updated per

iteration, it is called asynchronous (Agapie et al.,

2014; Dascălu, 2018).

Furthermore, CA can vary in terms of

randomness. A deterministic automaton has no

randomness; the evolution of the cells strictly follows

predetermined rules. However, if the cell to be

updated is chosen randomly and/or the local transition

rule involves probabilities, the automaton is classified

as probabilistic (Agapie et al., 2014; Dascălu, 2018).

In the 1950s, Konrad Zuse, Stanislav Marcin

Ulam and John von Neumann formulated the first

theories of CA in their strictest sense (Deutsch &

Dormann, 2017). These pioneers used CA to model

real-world phenomena, and von Neumann was

particularly inspired by the self-reproduction

capability observed in biological organisms (Von

Neumann & Burks, 1966). His fascination with the

inherent ability of living entities to create similar

beings led him to explore artificial life. This

exploration laid the foundation for the emergence of

artificial life as a distinct field of study, connecting it

Solórzano-Requejo, W., Aguilar, C., Callejo, G. and Díaz Lantada, A.

Biodegradable Biodevices: A Design Approach Based on Cellular Automaton.

DOI: 10.5220/0012313600003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 1, pages 34-41

ISBN: 978-989-758-688-0; ISSN: 2184-4305

with artificial intelligence and genetic algorithms.

These disciplines share a common thread of natural

inspiration, as each replicates certain characteristics

or constructive principles found in natural systems

(Dascălu, 2018).

In 1970, John Conway presented the Game of Life

automaton, a seemingly simple but profoundly

meaningful representation of the processes of birth

and death. This creation quickly became an icon in

the field of CA, capturing the public imagination with

its easily understood rules and captivating

simulations. The Game of Life demonstrated the

extraordinary ability of minimal, localized rules to

generate intricate, self-organizing patterns (Gardner,

1970). It served as a paradigmatic example of the

fundamental concept underlying CA: a basic, regular

structure capable of giving rise to a wide variety of

phenomena, even from initially chaotic states.

CA has been widely applied in diverse fields to

model dynamical systems that exhibit organized

behaviour, including areas such as statistical physics,

biology, medicine, ecology, and socioeconomic

interactions (Agapie et al., 2014). Interestingly, CAs

have also found utility in the medical device design

process. These automata have been used to represent

a patient's mental state by integrating information

from electroencephalogram analysis (Colafiglio

et al., 2023), for neuronal image segmentation

(Kalkhof et al., 2023), simulation of cells colonizing

tissue engineering scaffolds (Díaz Lantada et al.,

2023), optimization of biomimetic cell culture

systems (Ballesteros Hernando et al., 2019), and even

metamaterial design (Z. Liu et al., 2023).

Regarding the design of biodegradable and

bioabsorbable implants made from polymers or

metals, it is crucial to understand and quantify the

degradation of the material and how its behaviour

affects the biodesign. In this context, this article

delves into the detailed explanation of a methodology

that uses CA to two-dimensionally model the

degradation of polymeric specimens.

2 MATERIALS AND METHODS

2.1 Test Bench and Specimens

To investigate the influence of neighbourhood on CA

dynamics, various test specimens were utilized,

including circular, triangular, hexagonal,

quadrilateral, D and 4-shape geometries (Figure 1),

all with maximum dimensions of 30 x 30 x 2 mm for

the analysis of their two-dimensional degradation.

These probes were designed using Autodesk

Fusion

360 (Autodesk Inc., San Rafael, CA, USA).

Figure 1: PVA test specimens.

For the fabrication of the samples, Poly (vinyl

alcohol) (PVA) was chosen as the material due to its

rapid solubility in water, which facilitated the testing

process outlined in this research. This thermoplastic

material was purchased from Smart Materials 3D

(Pol. Ind. El Retamar, c/ Tomillo 7, 23680 Alcalá la

Real, Jaén, Spain) in form of monofilaments with a

1.75 mm diameter. The specimens were

manufactured using fused deposition modelling

(FDM), employing a Bambu Lab X1 Carbon Combo

3D printer equipped with a 0.4 mm diameter hardened

steel nozzle.

To generate the tool path for printing, Bambu

Studio (Austin, TX, USA), an open-source slicing

software based on Prusa Slicer, was employed. The

print parameters were consistently configured for all

printed specimens: a layer thickness of 0.2 mm, a

print speed of 40 mm/s, a bed temperature of 50 °C, a

nozzle temperature of 220 °C, two perimeters, and a

100% rectilinear infill pattern.

To investigate degradation, a 12.0-megapixel

high-resolution optical sensor with an f/1.5 lens and

an optical photo stabiliser was used to capture test

images at regular one-minute intervals and merge

them all into a video. To ensure consistent results and

avoid localised degradation, the samples were

carefully placed inside a glass container,

proportionally submerged in water. To prevent water

ingress from the top to the bottom, PETG discs were

used. This ensures that the degradation is two-

dimensional, specifically from the sides of the

specimen. The container was filled with 600 mL of

water, and maintained at a constant temperature of

27°C.

2.2 Image Processing

Frames were extracted from the video of each

experiment, revealing the appearance of bubbles due

to specimen degradation. Subsequently, it was

necessary to segment the PVA specimen, as this

segmentation allowed defining the CA transition

rules. To distinguish between the background, the

bubbles and the PVA in each frame, the K-Means

algorithm was used. This unsupervised algorithm

analysed the unlabelled image and grouped pixels

Biodegradable Biodevices: A Design Approach Based on Cellular Automaton

with similar characteristics. The result was a mask

divided into 3 zones (K = 3). Unfortunately, K-Means

was insufficient to extract the degraded PVA, so it

was complemented with Morphological Geodesic

Active Contour (MGAC). MGAC is especially

suitable for images with visible contours, even in

cases where these contours are noisy, cluttered, or

partially blurred, however, it requires preprocessing

to highlight these contours (Caselles et al., 1997). In

this case, K-Means segmentation was used to

highlight the contours, penalizing the areas belonging

to the background and the bubbles by multiplying

their pixel values by 0 and 0.5 respectively, and

highlighting the region with degraded material by

preserving their pixel values (Figure 2). In addition,

all images were aligned by changing their perspective

to avoid deformations that may result in erroneous

compression of the degradation. This whole process

was done in Python

3.7.14 (Phyton Software

Foundation) using OpenCV and scikit-image

libraries.

Figure 2: Image processing steps.

2.3 Cellular Automaton

CA is specified by a grid composed of cells, a set of

states characterizing the cells ( 𝜀), an interaction

neighbourhood (𝒩) and a rule (𝑅) which determines

the dynamics (Deutsch & Dormann, 2017). To model

the degradation of PVA samples, it is necessary to

define all these parameters since the complexity of

the model depends on them. Moreover, the higher

generality of the probabilistic CA (PCA) makes this

model more efficient compared to the deterministic

one (Agapie et al., 2014). In the following

subsections, each of the components of the CA will

be explained in detail.

2.3.1 Grid, Boundary Condition and States

A grid, denoted ℒ, is composed of a set of cells

represented by 𝑟. This grid ℒ establishes the spatial

framework in which the automaton operates and can

assume a finite or infinite nature. In our model, the

CA grid is the initial already processed grayscale

image captured after the experiments performed on

each sample (Figure 3A).

Figure 3: (A) Grids, (B) states and (C) neighbourhood of

the CA model.

In this scenario, the cells correspond to individual

pixels of the image. This discrete spatial

representation is crucial for CAs. In this case it is

possible to quantify the pixel dimensions, each pixel

measuring 50 x 50 µm. This accurate spatial analysis

is essential in the computational framework, because

if the pixel size dimensions change, the transition

rules could differ, and the model would have to be

recalibrated.

The CA model has two states: "live" (𝜀1),

which indicates the presence of PVA material in the

cell, and "dead" (𝜀0), which indicates the absence

of material or the presence of water causing PVA

degradation (Figure 3B). This simplifies the

complexity of the model, as it only considers these

two states.

Since the CA mesh is finite, it is necessary to

impose boundary conditions that specify the

interaction neighbourhood of the cells at the boundary

of the mesh. That boundary can be periodic, implying

that the mesh is closed, reflective, the state of the cells

at the mesh boundary is replicated, or fixed, one state

is defined for the entire boundary. In this case, the

fixed boundary was chosen and defined with the dead

state because it favours material degradation.

2.3.2 Neighbourhood and Rule

An interaction neighbourhood 𝒩



𝑟



defines the cells

that impact the state dynamics of a specific cell

𝑟



𝑖,𝑗



∈ℒ. In two-dimensional CA, two prevalent

types of neighbourhoods are widely used: the von

Neumann neighbourhood, encompassing the four

neighbouring cells along the vertical and horizontal

axes, and the Moore neighbourhood (𝒩



) comprising

both side neighbours and corner cells. When

considering degradation processes, all surrounding

cells influence the degradation of the central cell

(𝑟𝑖,𝑗), leading to the incorporation of the Moore

neighbourhood in CA degradation models (Figure

3C). This choice reflects the comprehensive influence

of adjacent and diagonal cells on the degradation

BIODEVICES 2024 - 17th International Conference on Biomedical Electronics and Devices

dynamics of the focal cell, providing a more accurate

representation of the system's behaviour.

𝒩





𝑖,

𝑗





𝑟



𝑖1,

𝑗



,𝑟



𝑖1,

𝑗

1



,𝑟



𝑖,

𝑗

1



𝑟



𝑖1,

𝑗

1



,𝑟



𝑖1,

𝑗



,𝑟



𝑖1,

𝑗

1



𝑟



𝑖,

𝑗

1



,𝑟



𝑖1,

𝑗

1





(1)

The rule can be probabilistic or deterministic. The

deterministic approach is simple: if a neighbouring

cell is dead, the central cell will be dead in that

iteration. In contrast, PCA introduces complexity.

According to this scenario, if 𝑛 cells surrounding the

central cell are dead, there is a chance of degradation

with a probability of 𝑃



. Clearly, as the number of

degraded cells around the central cell increases, the

probability of going from a living to a dead state

increase. How to obtain the probabilities in each case

is detailed in the Results section. Furthermore, in the

CA degradation model, all cells are updated

simultaneously, so it is a synchronous automaton.

3 RESULTS

3.1 Modelling of PVA Specimens

In the Materials and Methods section, all the

parameters involved in the creation of the CA for

modelling the degradation of the PVA were

described, except the rule that regulates the dynamics

of the system. In this case, it is interesting to compare

the deterministic approach with the probabilistic one;

the latter requires the transition probabilities as a

function of the neighbourhood, but because the

current state is the only one responsible for the next

state, CA becomes the perfect candidate for using

Markov Chains (MC) to regulate the probabilities

(Agapie et al., 2014).

First, it is important to understand the degradation

phenomena. For this purpose, an analysis of the

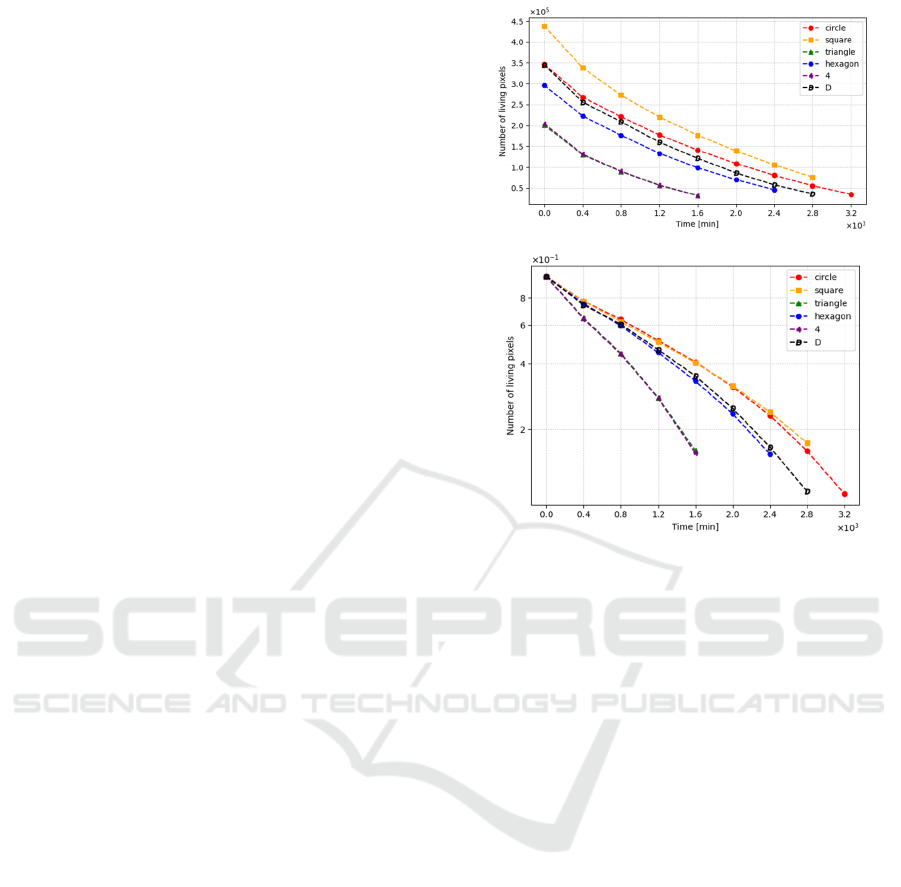
evolution of living pixels was carried out. Figure 4A

summarises the decreasing exponential trend of the

live pixels over time. To determine whether the

degradation rate is constant or not, the scale was

changed to exponential, and the number of live pixels

was normalised (Figure 4B). This graph demonstrates

two important aspects: the degradation rate is not

constant, and the geometry of PVA specimens

influences the degradation process because similar

shapes exhibit almost the same degradation rate. For

this reason, circular, triangular, and hexagonal

specimens were chosen to apply the MC model and

obtain the transition matrix, which defines the

probabilities of the CA.

(a)

(

)

Figure 4: Graphical representation of living pixel dynamics,

showing (A) dimensional and (B) dimensionless data.

MCs are stochastic processes characterised by a

finite set of states. For these processes, the transition

probabilities between states, denoted as 𝑝



, depend

exclusively on the current state of the system. These

probabilities are organised in a positive square

transition matrix 𝑃𝑝





,,



. In this context, the

"dead" state (𝜀0) is absorbing, since once the

system enters this state (𝑝



1), it can never leave.

By calculating the 𝑝



transition probability from

the ratio of the total number of cells to live cells, it is

evident that this MC is heterogeneous because the

transition matrix changes over time.

Therefore, the average value of the live-to-dead

transition probability was calculated for each of the

samples under study, considering only their

degradation information every 400 minutes until the

system is 80% degraded. Since the average transition

probability is 0.254, the following rule is established:

if the central cell is surrounded by at least one dead

cell, the degradation probability is 0.254 (𝑅



). In

addition, using the standard deviation information,

two probabilities were calculated: 0.17 and 0.41. Two

additional rules are defined considering that the

probability follows an exponential (𝑅



) or linear

(𝑅



) function, with 0.17 corresponding to the

Biodegradable Biodevices: A Design Approach Based on Cellular Automaton

probability of degradation if one of the neighbouring

cells is dead and 0.41 if six cells are dead.

In addition, two other rules are established using

linear (𝑅

__

) and exponential distributions

(𝑅

__

). The probability starts at 0.1 when one of

the cells is degraded and increases to 0.9 when six of

them are degraded. It is important to note that when

there are six degraded neighbours, it means that the

cell is attached to the specimen only by one live pixel,

and if there are seven dead cells, it implies that this

pixel is isolated. In both cases, it is determined that

the central cell will be degraded in that iteration.

Furthermore, all these rules are compared with the

deterministic one (𝑅



), which establishes that if at

least one of the neighbours is degraded, the central

cell will also be degraded. The whole CA was

programmed in Python

and the rules were applied if

the central cell is alive and if the transition

probability, which depends on the number of dead

neighbours, is greater than a random number.

Figure 5 compares the images obtained from the

experiments with the simulations of the CA with the

different rules. To determine the similarity between

the experimental images and those obtained through

the simulation, the mean square error (MSE) metric

was used, then, the iteration that presented the highest

similarity with the image of the degraded PVA

specimen at each moment was selected. This metric

also allowed us to quantify which of the rules

provides the most morphologically reliable

simulation. From the information provided by Figure

5 and the MSE analysis, it is concluded that the

exponential rule (𝑅



) obtained from the information

found in the Markov chain is the most reliable.

3.2 Simulation of Medical Devices

Degradation

Biodegradable implants offer several advantages for

medical professionals. First, they eliminate the need

for a second surgical intervention for removal, which

saves time and resources. In addition, biodegradation

can offer other significant advantages, for example,

rigid, non-biodegradable titanium implants can cause

problems such as refractures when removed, as the

bone has not been able to bear sufficient load during

the healing process. In contrast, biodegradable

implants can degrade slowly, gradually transferring

the load to the healing bone.

In tissue engineering, biodegradable scaffolds are

essential to provide adequate mechanical support for

damaged tissue and degrade gradually as new tissue

grows. However, the challenge lies in finding

materials with specific mechanical properties and

degradation rates for different tissues, as well as being

able to fabricate customized scaffolds with precise

pore interconnections (Y.-Y. Liu et al., 2023).

For coronary stents, a meticulous approach is

required to optimize mechanical properties and

degradation rate. These biodegradable stents offer a

promising advantage over traditional metallic stents

in that they dissolve completely in the body after a

period, thus reducing long-term adverse effects such

as restenosis. The ability to remove a foreign object

from the body after treatment of an obstruction is

especially attractive given current demographic

trends, which indicate that people are living longer

after a percutaneous coronary intervention procedure

(Tabares Ocampo et al., 2023). Traditionally,

biodegradable stents require a thicker strut compared

to conventional stents due to the weaker nature of the

degradable materials. However, a thicker strut leads

to worse patient outcomes.

As mentioned in both cases, it is essential to

consider the degradation of the medical device as an

essential design variable. This degradation is not only

dependent on the material and the environment, but

also on the geometry of the device and must be in

balance with tissue regeneration. The device must

disintegrate completely once it has fulfilled its

mechanical function. About this characteristic, the

degradation of the material leads to a loss of

properties that must be quantified. In some cases, this

loss may be beneficial, while in others it may be

detrimental. Therefore, controlling degradation

ensures a stable mechano-biological response.

To estimate in silico how the calibrated model

could aid in biodevice design, CT-like axial slices

were generated using Chitubox

v1.9. 0 (Chitubox,

Zhongcheng Future Industrial Park, Hangcheng

Avenue, Baoan District, Shenzhen, Guangdong,

China 518128) of a personalized coronary stent

exposed in the study by (Solórzano-Requejo et al.,

2023) and a tissue-engineered gyroid scaffold

designed using the open-source software MS Lattice

(Al‐Ketan & Abu Al‐Rub, 2021). Figure 6 shows the

slice degradation process for each of the medical

devices. By performing the conversion from

iterations to time, considering that 68 iterations equal

to approximately 400 minutes, the designer would be

able to analyze whether the implant degrades in the

right time frame and which areas are most prone to

degrade rapidly. Moreover, this is achieved at a very

low computational cost, as the CA model is very

optimal in that aspect.

BIODEVICES 2024 - 17th International Conference on Biomedical Electronics and Devices

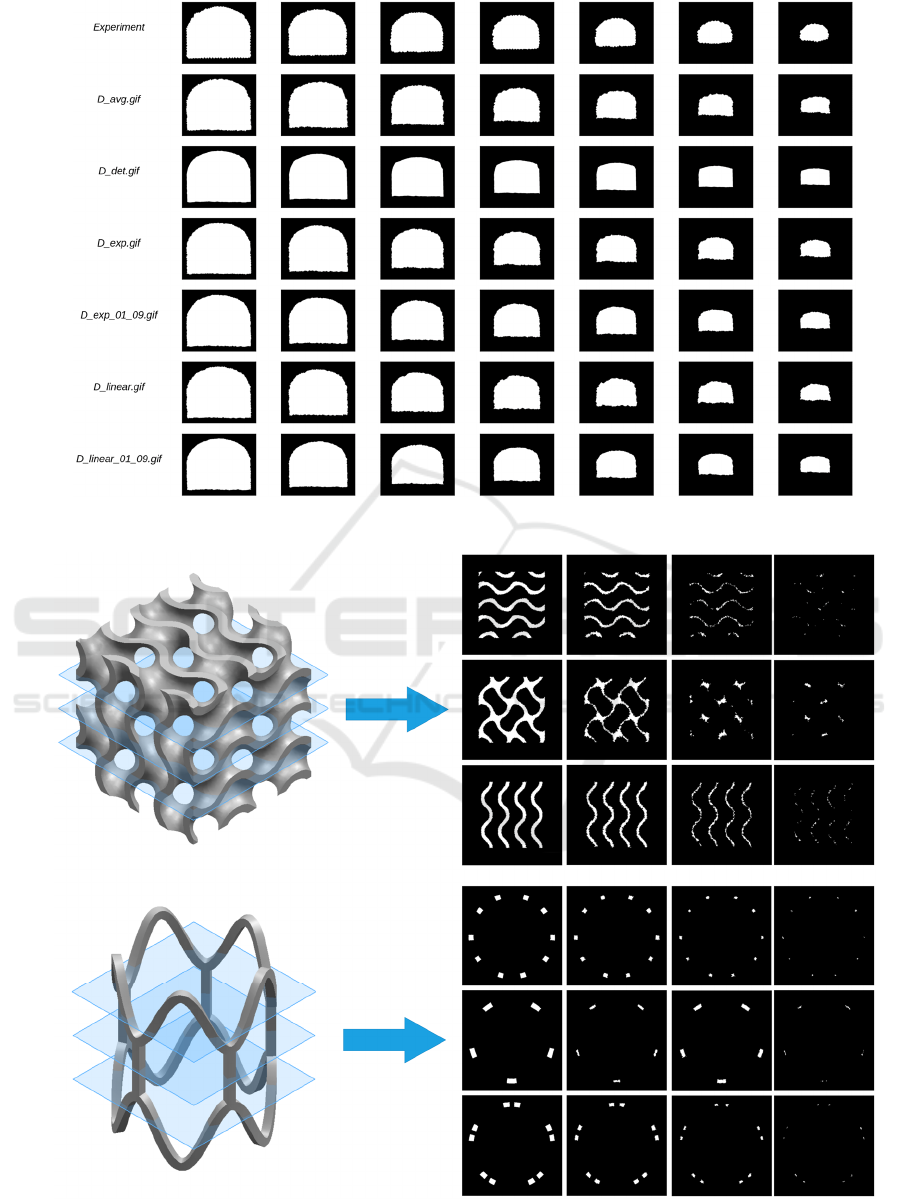
Figure 5: Comparison between experimental results and simulations with different rules for the D-shaped specimen.

Figure 6: PCA simulation of axial slices of a tissue engineering scaffold and coronary stent.

Biodegradable Biodevices: A Design Approach Based on Cellular Automaton

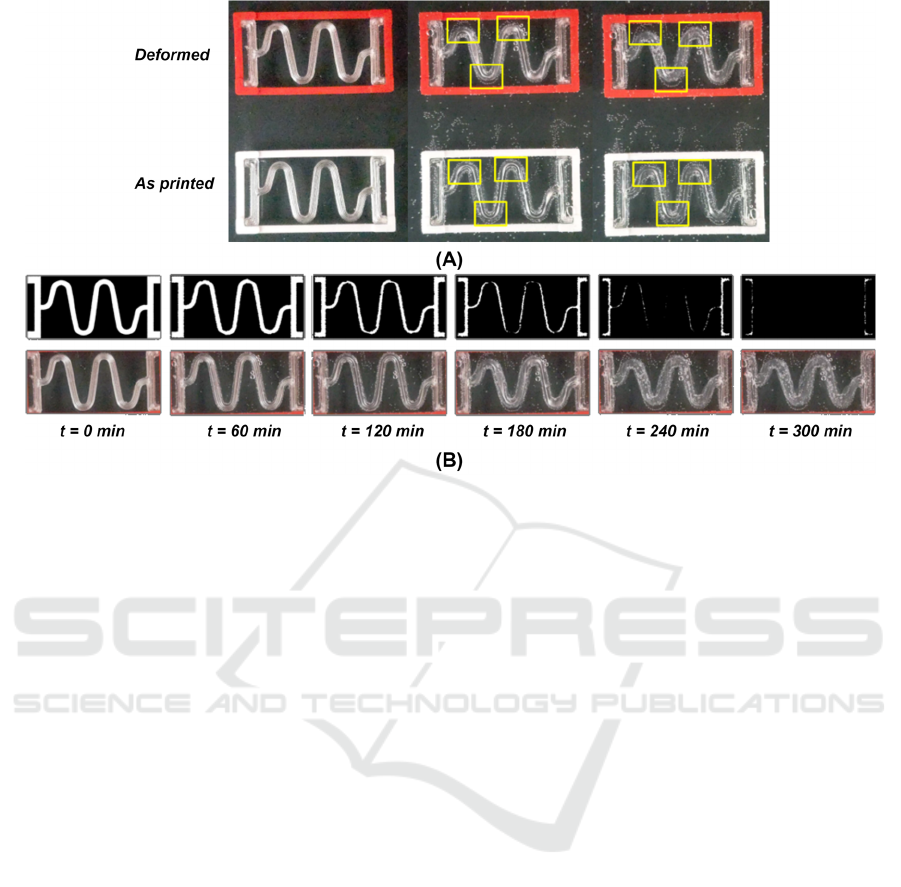
Figure 7: (A) Comparison of the degradation between two springs: one deformed by a framework during the degradation

process and the other printed directly with the deformed shape. (B) Simulation using the CA whose rules are influenced by

the stress state.

4 FUTURE PROPOSALS

In this study, a calibrated model capable of capturing

the complex two-dimensional interactions in medical

devices has been developed. However, to accurately

assess the degradation of these devices, it is essential

to adopt a three-dimensional perspective. By

connecting this model to finite element software, it is

possible to analyze how mechanical properties, such

as stiffness and creep, are affected by the progressive

degradation of the structure.

In the context of the mechanical state of the

material, it is crucial to consider how stresses and

strains impact the degradation rate. Therefore, it is

possible to use information obtained from a structural

analysis to define the rules of the CA model. These

rules should not only depend on the neighborhood,

but also on the stress state of the structure. More

mechanically loaded areas will experience faster

degradation compared to less stressed areas.

Additionally, in this study, experiments have been

carried out with PVA serpentine springs, which serve

as a prototype of implants for craniosynostosis,

aiming to promote brain growth. To test the influence

of the stress state, the degradation of two springs, one

deformed by a frame during degradation and the other

printed directly with the deformed shape obtained

from the finite element software as an STL file, was

compared. The results were revealing: the

degradation was noticeably more pronounced in the

curved regions that were highly deformed. Then, the

probabilities calibrated in our model were adjusted

as a function of the deformation of the springs

(Figure 7).

This finding suggests that it is possible to

hybridize both methodologies, using a three-

dimensional CA model within finite element software

meshed with hexahedral elements. In this approach,

each mesh element can represent a cell, and the

degradation probabilities would depend on the

specific stress state of each cell. This would allow

accurate simulation of how the material behaves

when the stress state varies, especially in

biodegradable biomedical devices under varying

loads.

5 CONCLUSIONS

This study presents a methodology for accurate

simulation of two-dimensional biodegradable

specimens, representing a significant advance in the

accurate simulation of degradation in medical

devices. Detailed results and meticulous comparisons

of CA rules have revealed that the exponential rule

BIODEVICES 2024 - 17th International Conference on Biomedical Electronics and Devices

(𝑅



) derived from Markov chains offers a highly

reliable simulation of PVA degradation.

This approach not only deepens our fundamental

understanding of degradation, which is influenced by

material, environment, and part geometry, but also

has practical applications in the design of

biodegradable medical devices. By simulating

devices such as coronary stent, tissue engineering

scaffold and prototypes of implants for

craniosynostosis, their degradation can be assessed in

silico, providing valuable information for engineers

and medical professionals.

In addition, this study has clearly pointed to future

research directions. The adoption of a three-

dimensional approach, integrating CA with finite

element models, promises to offer even more accurate

simulation, especially when considering the stress

state of each cell. This hybrid approach could unlock

new insights into how devices respond to different

loads, essential for the design of devices that integrate

optimally with the surrounding biological tissue.

ACKNOWLEDGEMENTS

This project has received funding from the European

Union’s Horizon Europe research and innovation

programme under grant agreement No 101047008

(BIOMET4D). Views and opinions expressed are

however those of the authors only and do not

necessarily reflect those of the European Union or the

European Innovation Council and SMEs Executive

Agency (EISMEA). Neither the European Union nor

the EISMEA can be held responsible for them.

REFERENCES

Agapie, A., Andreica, A., & Giuclea, M. (2014).

Probabilistic Cellular Automata. Journal of Computa-

tional Biology, 21(9), 699-708. https://doi.org/10.1089/

cmb.2014.0074

Al‐Ketan, O., & Abu Al‐Rub, R. K. (2021). MSLattice: A

free software for generating uniform and graded lattices

based on triply periodic minimal surfaces. Material

Design & Processing Communications, 3(6).

https://doi.org/10.1002/mdp2.205

Ballesteros Hernando, J., Ramos Gómez, M., & Díaz

Lantada, A. (2019). Modeling Living Cells Within

Microfluidic Systems Using Cellular Automata

Models. Scientific Reports, 9(1), 14886.

https://doi.org/10.1038/s41598-019-51494-1

Caselles, V., Kimmel, R., & Sapiro, G. (1997). Geodesic

Active Contours. International Journal of Computer

Vision, 22(1), 61-79. https://doi.org/10.1023/A:10079

79827043

Colafiglio, T., Lofù, D., Sorino, P., Festa, F., Di Noia, T.,

& Di Sciascio, E. (2023). Exploring the Mental State

Intersection by Brain-Computer Interfaces, Cellular

Automata and Biofeedback. IEEE EUROCON 2023 -

20th International Conference on Smart Technologies,

461-466. https://doi.org/10.1109/EUROCON56442.20

23.10198964

Dascălu, M. (2018). Cellular Automata and

Randomization: A Structural Overview. En R. Lopez-

Ruiz (Ed.), From Natural to Artificial Intelligence—

Algorithms and Applications. IntechOpen.

https://doi.org/10.5772/intechopen.79812

Deutsch, A., & Dormann, S. (2017). Cellular Automaton

Modeling of Biological Pattern Formation. Birkhäuser

Boston. https://doi.org/10.1007/978-1-4899-7980-3

Díaz Lantada, A., Urosa Sánchez, M., & Fernández

Fernández, D. (2023). In silico Tissue Engineering and

Cancer Treatment Using Cellular Automata and Hybrid

Cellular Automata-Finite Element Models:

Proceedings of the 16th International Joint Conference

on Biomedical Engineering Systems and Technologies,

56-63. https://doi.org/10.5220/0011742300003414

Gardner, M. (1970). Mathematical Games. Scientific

American, 223(4), 120-123.

Kalkhof, J., González, C., & Mukhopadhyay, A. (2023).

Med-NCA: Robust and Lightweight Segmentation with

Neural Cellular Automata. En A. Frangi, M. De

Bruijne, D. Wassermann, & N. Navab (Eds.),

Information Processing in Medical Imaging (Vol.

13939, pp. 705-716). Springer Nature Switzerland.

https://doi.org/10.1007/978-3-031-34048-2_54

Liu, Y.-Y., Blazquez, J. P. F., Yin, G.-Z., Wang, D.-Y.,

Llorca, J., & Echeverry-Rendón, M. (2023). A strategy

to tailor the mechanical and degradation properties of

PCL-PEG-PCL based copolymers for biomedical

application. European Polymer Journal, 198, 112388.

https://doi.org/10.1016/j.eurpolymj.2023.112388

Liu, Z., Fang, H., Xu, J., & Wang, K.-W. (2023). Cellular

automata inspired multistable origami metamaterials

for mechanical learning. https://doi.org/10.48550/

ARXIV.2305.19856

Solórzano-Requejo, W., Aguilar, C., Zapata Martínez, R.,

Contreras-Almengor, O., Moscol, I., Ojeda, C., Molina-

Aldareguia, J., & Diaz Lantada, A. (2023). Artificial

Intelligence and Numerical Methods Aided Design of

Patient-Specific Coronary Stents: Proceedings of the

16th International Joint Conference on Biomedical

Engineering Systems and Technologies, 37-45.

https://doi.org/10.5220/0011639000003414

Tabares Ocampo, J., Marín Valencia, V., Robledo, S. M.,

Upegui Zapata, Y. A., Restrepo Múnera, L. M.,

Echeverría, F., & Echeverry-Rendón, M. (2023).

Biological response of degradation products of PEO-

modified magnesium on vascular tissue cells,

hemocompatibility and its influence on the

inflammatory response. Biomaterials Advances, 154,

213645. https://doi.org/10.1016/j.bioadv.2023.213645

Von Neumann, J., & Burks, A. W. (1966). Theory of self-

reproducing automata. IEEE Transactions on Neural

Networks, 5(1), 3-14.

Biodegradable Biodevices: A Design Approach Based on Cellular Automaton