Data Quality Aware Approaches for Addressing Model Drift of Semantic

Segmentation Models

Samiha Mirza

, Vuong D. Nguyen

, Pranav Mantini

and Shishir K. Shah

Quantitative Imaging Lab, Dept. of Computer Science, University of Houston, Texas, U.S.A.

Keywords:

Model Drift, Semantic Segmentation, Image Quality Assessment Metrics, Feature Learning, Data Selection,

Quality-Aware Models.

Abstract:

In the midst of the rapid integration of artiﬁcial intelligence (AI) into real world applications, one pressing

challenge we confront is the phenomenon of model drift, wherein the performance of AI models gradually

degrades over time, compromising their effectiveness in real-world, dynamic environments. Once identiﬁed,

we need techniques for handling this drift to preserve the model performance and prevent further degradation.

This study investigates two prominent quality aware strategies to combat model drift: data quality assessment

and data conditioning based on prior model knowledge. The former leverages image quality assessment met-

rics to meticulously select high-quality training data, improving the model robustness, while the latter makes

use of learned feature vectors from existing models to guide the selection of future data, aligning it with the

model’s prior knowledge. Through comprehensive experimentation, this research aims to shed light on the

efﬁcacy of these approaches in enhancing the performance and reliability of semantic segmentation models,

thereby contributing to the advancement of computer vision capabilities in real-world scenarios.

1 INTRODUCTION

In recent years, the integration of artiﬁcial intelli-

gence (AI) into various domains has experienced a

remarkable surge, transforming the way we interact

with technology. The proliferation of AI applications,

ranging from natural language processing to com-

puter vision (Khaldi et al., 2022), has led to break-

throughs in numerous industries. Among the many

AI applications, semantic segmentation plays a piv-

otal role in object recognition, scene understanding,

and image analysis. It aims to assign class labels

to individual pixels within an image, thus enabling a

deeper understanding of the visual content. Seman-

tic segmentation ﬁnds practical application in diverse

ﬁelds, including autonomous driving, medical imag-

ing, robotics, and remote sensing, among others.

When these segmentation models are trained and

deployed in real-world settings, they undergo con-

stant updates and retraining using recently collected

datasets in conjunction with their existing training

https://orcid.org/0000-0003-3754-6894

https://orcid.org/0000-0002-2369-8793

https://orcid.org/0000-0001-8871-9068

https://orcid.org/0000-0003-4093-6906

Figure 1: Occurrence of model drift. It may happen due to

a variety of reasons, with one major reason being the degra-

dation of the quality of the new data.

datasets (Tsymbal, 2004). Often, an issue arises when

these models are retrained, where their performance

tends to deteriorate with the addition of new data,

Mirza, S., Nguyen, V., Mantini, P. and Shah, S.

Data Quality Aware Approaches for Addressing Model Drift of Semantic Segmentation Models.

DOI: 10.5220/0012316000003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

333-341

ISBN: 978-989-758-679-8; ISSN: 2184-4321

333

Figure 2: Comparison of model predictions between the original model, initially trained with initial datasets, and the updated

model, which incorporates both the initial datasets and newly acquired data. The updated model exhibits an increased occur-

rence of false positives and a corresponding reduction in F-score values when compared to the original model.

a phenomenon commonly referred to as model drift

(Whang et al., 2023). For instance, consider a salt

layer segmentation model in the oil and gas indus-

try (Devarakota et al., 2022). These models are ini-

tially trained and deployed for real-time prediction,

and are continuously updated (retrained) periodically

as more data is gathered. If the new data has a dif-

ferent distribution compared to the original data or

is of poor quality, the model performance progres-

sively degrades, resulting in numerous false predic-

tions. This phenomenon, as depicted in Figure 1, is

a manifestation of model drift, wherein the effective-

ness of AI models diminishes over time due to the in-

fusion of new data into the training pipeline (Whang

et al., 2023).

Figure 2 shows an example of model drift in a

vehicle segmentation model trained on autonomous

driving datasets (Zhou et al., 2017) (Zhou et al.,

2019), (Cordts et al., 2016), (Everingham et al.,

2010). In this case, two models are trained: the ﬁrst

using the original dataset and the latter using both the

original and new data. As illustrated in Figure 2, we

observe a decline in model performance, character-

ized by an increase in false positives and a subse-

quent decrease in F-scores following the addition of

new data. This prompts the fundamental question of

how to select future data that does not compromise

model performance.

One reason for the degradation is due to addition

of poor quality data. When low-quality or noisy data

is included, the model could learn from incorrect or

misleading information, leading to suboptimal per-

formance (Zha et al., 2023). Another cause for de-

cline in performance is when the distribution of the

new data differs from that of the old data and fails to

adequately represent the underlying domain (Bayram

et al., 2022). Recognizing these drifts is essential for

continuous model maintenance and, once these drifts

are recognized, we need techniques to combat and

handle this shift to prevent further model degradation.

In this paper, we investigate two major approaches

to address the issue of model drift over time. If the

model encounters unexpected data quality issues in

retraining that were not present in the old training

data, it may perform poorly. Thus, spanning from the

idea that the performance shift is due to the addition of

noisy or distorted data, the ﬁrst investigated approach

considers the intrinsic quality of the data itself (Jo-

hannes et al., 2023). Our second approach involves

conditioning data selection based on the model’s ex-

isting knowledge. We use the learned feature vectors

from these models as a guide for selecting future data

that aligns with its prior knowledge. This creates a

more harmonious connection between the model’s in-

sights and the selected data.

Our main contributions are as follows: (1) to con-

sider the data quality for updating the models, we pro-

pose the use of IQA metrics to select new data for

retraining the models; (2) we propose retaining the

knowledge from the current production model by se-

lecting future data based on the features learnt by this

current model; and (3) we present extensive experi-

ments on multiple benchmark datasets, to highlight

the effectiveness of these approaches.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

334

2 RELATED WORKS

In literature, studies have explored two main types

of model drift: concept drift and data drift (Bayram

et al., 2022). Concept drift arises when the statisti-

cal properties of the target variable, data distribution,

or underlying relationships between variables change

over time, rendering previously learned concepts less

relevant or outdated (Webb et al., 2016). An example

is observed in email spam detection, where evolving

spammer tactics can impact model performance over

time (Guerra-Manzanares et al., 2022). Data drift,

on the other hand, occurs when the statistical prop-

erties of new data have changed (Ackerman et al.,

2020). This change may result from signiﬁcant dif-

ferences between test and training data or variations

in the quality of new data compared to existing train-

ing data, which is investigated in this paper.

2.1 Concept Drift

Signiﬁcant research has been conducted on identify-

ing concept drift (Lu et al., 2018). Wang et al. (Wang

et al., 2022) introduced the Noise Tolerant Drift De-

tection Method (NTDDM) to identify concept drifts

in data streams, addressing noise commonly present

in real-world applications like those from the Inter-

net of Things. NTDDM employs a two-step approach

to distinguish real drifts from noise-induced false

alarms. Lacson et al. (Lacson et al., 2022) addressed

model drift in a machine learning model for predict-

ing diagnostic testing, employing two approaches: re-

training the original model with augmented recent

data and training new models. Their ﬁndings indicate

that training models with augmented data provided

better recall and comparable precision. Other re-

searches, such as (Wang and Abraham, 2015), (Dries

and R

uckert, 2009), and (Klinkenberg and Joachims,

2000), also explore methods to identify concept drift.

2.2 Data Drift

Rahmani et al. (Rahmani et al., 2023) explored var-

ious scenarios of data drift in clinical sepsis predic-

tion, encompassing changes in predictor variable dis-

tribution, statistical relationships, and major health-

care events like the COVID-19 pandemic. The study

suggests that properly retrained models, particularly

eXtreme Gradient Boosting (XGB), outperform base-

line models in most scenarios, highlighting the pres-

ence of data drift. Davis et al. (Davis et al., 2019)

addressed model drift in clinical prediction using non-

parametric methods. Their approach involves a two-

stage bootstrapping method to update models, miti-

gating overﬁtting impact in recommendations. The

second stage assesses predictions on samples of the

same size as the updating set, considering uncertainty

linked to the updating sample size in the decision-

making process. Other works, such as (Ackerman

et al., 2021) and (Hofer and Krempl, 2013), also in-

vestigate data drift.

In this paper, we investigate drift due to data qual-

ity changes. While prior research has predominantly

centered around concept drift, data drift’s impact, par-

ticularly in segmentation, has been overlooked. We

aim to ﬁll this gap by emphasizing the importance

of data quality in model pipeline. Notably, our ap-

proach uses quality-aware metrics, providing solu-

tions to tackle the challenges associated with data

drift and enhancing the robustness of segmentation.

3 PROPOSED METHODS

Problem Formulation. Our objective is to develop

methods for selecting suitable images or data to add

to our dataset pipeline for model retraining, all while

mitigating degradation in model performance. As

illustrated in Figure 3 let’s consider that we pos-

sess an initial training dataset, denoted as S

old

,···D

}, which is used for training model

old

. We have new data S

new

= {D

,···D

} to incor-

porate into our pipeline, so we can update our model

new

, using S

old

and appropriate data from S

new

. To

establish a criterion for selecting the appropriate data

select

, we need to ﬁnd a function G that obtains S

select

(which prevents model degradation) from S

new

as fol-

lows:

selected

= G (S

new

), (1)

where S

selected

⊆ S

new

, and G denotes an approach to

select data from S

new

. The following two approaches

give our proposed criteria for this selection.

3.1 Data Quality Based Approach

This section outlines the methodology for enhancing

the performance of a baseline U-Net (Ronneberger

et al., 2015) model (M

old

) by incorporating a data

quality-based approach. The core idea behind this ap-

proach is to leverage quantitative image quality as-

sessment (IQA) metrics to assess the quality of each

image within the training dataset and subsequently se-

lect a subset of matched quality data from the new

data for model reﬁnement. To evaluate the quality of

individual images within a set of available datasets

all

, we employ IQA metrics. For each image I

all

, we compute a quantitative quality value, denoted

as σ

, using these metrics, computed as:

Data Quality Aware Approaches for Addressing Model Drift of Semantic Segmentation Models

335

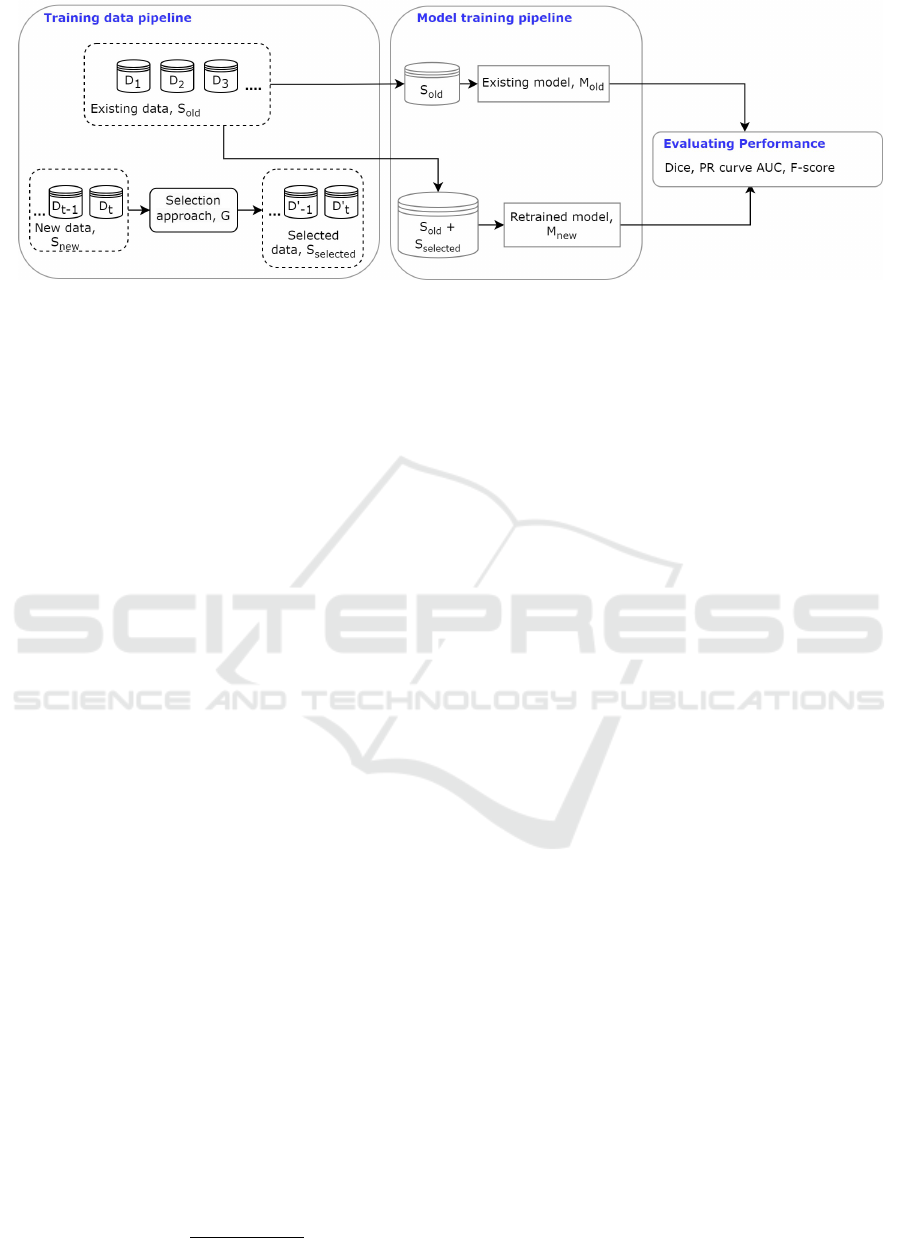
Figure 3: Incorporating quality-aware data selection into the ML pipeline: Existing model M

old

is trained with S

old

, and new

data S

new

needs integration. Criterion G explores data selection from S

new

without causing negative effects, preventing model

drift. Two criteria are investigated: data quality-based and feature learning-based. We compare performance between M

old

and updated model M

new

= F (I

), (2)

where, F represents a function that encapsulates the

investigated IQA metrics, generating a scalar value σ

for each image I

∈ D

all

With the set of quality values S

{σ

,σ

,...σ

},n = |D

all

| computed for all im-

ages in D

all

, we proceed to analyze the distribution

of these values. We aim to distinguish between

high-quality and low-quality images based on a

predeﬁned quality threshold T . Formally, we deﬁne a

binary selection function S(σ

) as follows:

S(σ

) =

(

1, if σ

≥ T

0, if σ

< T

(3)

Images for which S(σ

) = 1 are considered high-

quality and are chosen for model training, while those

for which S(σ

) = 0 are deemed low-quality and are

discarded. This technique relies on an optimal selec-

tion of T which avoids two scenarios: (1) too high

threshold, which causes the model to stop learning;

and (2) too low threshold, which causes the model to

capture noise.

Blind/Referenceless Image Spatial Quality Eval-

uator (BRISQUE). In this work, we investigated

BRISQUE (Mittal et al., 2012), a no-reference IQA

algorithm designed to evaluate the quality of digital

images without requiring a reference image for com-

parison. It operates by analyzing statistical properties

of the image such as luminance, texture, compression

etc. It spans from the idea that the distribution of pixel

intensities of natural images differs from that of dis-

torted images. First, a Mean Subtracted Contrast Nor-

malization (MSCN) is performed as follows:

I(i, j) =

I(i, j) − µ(i, j)

σ(i, j) +C

, (4)

where i = 1, 2, ..., M and j = 1,2,...,N are the spa-

tial indices, M and N are the image height and width

respectively,

I is the resulting MSCN image. µ(i, j)

is local mean ﬁeld which is the Gaussian Blur of the

original image. σ(i, j) is the local variance ﬁeld which

is the squared difference of original image and µ.

MSCN normalization is effective for pixel intensities,

but considering pixel relationships is crucial. So, pair-

wise products of MSCN image with a shifted version

of the MSCN image along four orientations: Hori-

zontal (H), Vertical (V), Left-Diagonal (D1), Right-

Diagonal (D2). The resulting ﬁve images are ﬁtted

to a Generalized Gaussian Distribution (GGD) to cre-

ate a feature vector. These statistical features serve as

input for a pretrained regression model, trained on a

large dataset annotated by human subjects, to predict

the BRISQUE score.

3.2 Feature Vector Learning Based

Approach

In order to ensure the reliability and improvement of

the training data as we gather more data for the mod-

els, we investigate another approach, depicted in Fig-

ure 4, where we incorporate a conditioning mecha-

nism that takes into account the data on which the cur-

rent model was trained. We make use of feature vec-

tors having the richest information extracted from the

bottleneck layers of the segmentation network to train

a simple Support Vector Machine (SVM) that learns

to distinguish the true and false predictions made by

the trained network on the test data. The purpose of

this network is to guide the feature learning of the re-

trained models on newly acquired dataset.

Consider that we have a baseline model M

trained

by an initial dataset which is assumed to be represen-

tative of our domain of interest. Then we test M

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

336

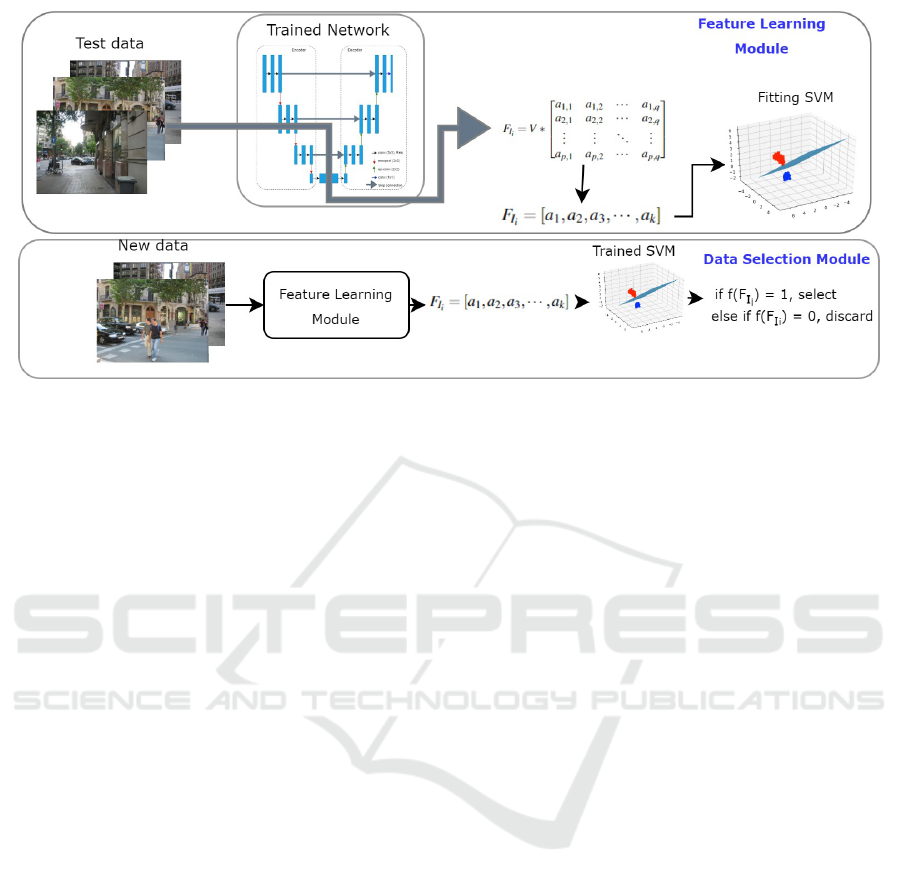
Figure 4: Illustration of the proposed approach. In the feature learning module, the feature vector representation are ﬁrst learnt

using an SVM on the prior segmentation network in production. Then any new data that needs to be added for retraining the

segmentation net, passes through the feature learning module and is ﬁt to the trained SVM to predict if it must be selected for

further model training or discarded.

our evaluation dataset D

test

to obtain the prediction

masks. Dice metric is computed to measure the ac-

curacy of the obtained masks. For each I

∈ D

test

, the

dice value is evaluated against a threshold to catego-

rize each result as true or false. After passing D

test

through the trained model M

we also take the output

from the bottleneck layer of the U-net and obtain a

feature vector set for image I

∈ D

test

, given as:

= V ∗







1,1

1,2

··· a

1,q

2,1

2,2

··· a

2,q

p,1

p,2

··· a

p,q







(5)

After obtaining V vectors of size p × q we apply spa-

tial pyramid pooling (He et al., 2015) to partition and

pool information from different regions of the fea-

ture maps, and this gives an aggregated representation

that retains vital contextual and positional informa-

tion while reducing the dimensionality to a 1D vector

for every I

∈ D

test

= [a

,··· , a

] (6)

Once we obtain the 1D vector, we use it as features

to train an SVM model that learns to distinguish the

vector representations for true and false predictions.

Subsequently, new data is then passed through the

SVM, allowing for the data selection of true predic-

tions that are then chosen for further model training.

By conditioning the selection of future data on this

network, we theorize that we are ﬁne tuning the new

data on the current model. Hence, we ensure that the

prior knowledge of the model is preserved leading to

retaining the model performance.

4 EXPERIMENTS

4.1 Datasets and Evaluation Methods

Datasets Used. We use three benchmark datasets

for semantic segmentation namely the Adverse Envi-

ronment Conditions dataset (ADE20K) (Zhou et al.,

2017) (Zhou et al., 2019), Cityscapes (Cordts et al.,

2016), and PASCAL Visual Object Classes (VOC)

(Everingham et al., 2010) dataset. ADE20K consists

of 480 × 600 images belonging to nearly 150 classes.

Cityscapes contains annotations for 30 classes and

VOC comprises 20 classes. For the sake of testing our

approach, we focus on segmenting one object of inter-

est from these datasets. Before passing the images to

train the model, they are resized to 256 × 256 with 3

channels. In total the training data comprises of 800

images from ADE20K, 800 from Cityscapes and 300

from VOC. The test dataset D

test

is created by taking

100 images from each of these 3 datasets that are not

part of the training data. The initial results obtained

on D

test

using the U-net model trained with different

combinations of the 3 datasets as training sets is given

in Table 3.

Evaluation Metrics. To evaluate the models we

employ three main metrics: the dice coefﬁcient, the

Area Under the Curve (AUC) of Precision-Recall

Data Quality Aware Approaches for Addressing Model Drift of Semantic Segmentation Models

337

Table 1: Comparing the performance of the baseline model trained with D

orignal

which consists of all the initial undistorted

images from Cityscapes, ADE, and VOC to the performance of the model trained with 70% of images from D

orignal

having

low BRISQUE and 30% from D

distorted

having high BRISQUE score. The model performance drops when high BRISQUE

scored images are added for training.

No. Training Dataset Dice PR score F-score

1 D

orignal

(Baseline) 0.404864 0.589132 0.289338

2 2/3 D

orignal

+ 1/3 D

distorted

0.369254 0.549964 0.36924

Table 2: Comparing the performance of the model trained with D

distorted

which consists of distorted versions of all images

from Cityscapes, ADE, and VOC to the performance of the model trained with D

′

distorted

which contains selected images

having BRISQUE < 60, meaning higher quality images. The model performance better when we prune images having high

BRISQUE.

No. Training Dataset Dice PR score F-score

1 D

distorted

0.309860 0.386605 0.208074

2 D

′

distorted

0.371031 0.484460 0.260145

(PR score), and the F-score. The dice coefﬁcient

quantiﬁes the degree of overlap between our model’s

predicted binary segmentation mask and the ground

truth, providing a measure of segmentation quality.

Meanwhile, the AUC of the PR curve offers a com-

prehensive assessment of binary classiﬁcation per-

formance, capturing the trade-off between precision

and recall at various thresholds. Lastly, the F-score,

which is the harmonic mean of precision and recall,

provides a balanced evaluation, particularly valuable

when dealing with class imbalances.

4.2 Model Architecture

The semantic segmentation model architecture on

which all the experiments are performed is the U-

net (Ronneberger et al., 2015). The U-net fol-

lows an encoder-decoder architecture, wherein the

encoder extracts high-level features through a con-

tracting path involving operations like convolution

and max-pooling. The decoder, mirroring the en-

coder, employs transposed convolutions to gradually

increase spatial dimensions. Skip connections to cor-

responding encoder layers aid in preserving details.

During training the binary cross-entropy loss function

is minimized.

5 RESULTS AND DISCUSSION

5.1 Approach 1: Results on IQA

Metrics Based Selection

To test the IQA metric based selection, we ﬁrst need

to assess where our data stands in terms of quantita-

tive quality. Hence we compute the BRISQUE, for

all the images in the three datasets as shown in Figure

5. This distribution shows that the perceptual qual-

ity of these images is good. However, this is not al-

ways the case in real world scenarios where we might

end up acquiring severely degraded data and retrain-

ing the model using this noisy data. Hence, to assess

if using IQA metrics aids in ﬁltering out the noisy

data, we ﬁrst distort theses images to degrade their

quality. Consider our original data pool denoted by

original

, with every image of dimension M × N, i.e.

M×N

∈ D

original

, we perform a pyramidal downscal-

ing followed by a pyramidal upscaling. For each pixel

(i, j) in the downscaled image I

′

, the corresponding

pixel value is computed by averaging the values of

the four neighboring pixels in I as follows:

′

(i, j) =

I(i − 1, j + 1) + I(i + 1, j + 1)

(11)

I(i − 1, j − 1) + I(i + 1, j − 1)

where i = 1, ..., M/2 and j = 1, ..., N/2. Then, in up-

scaling, for each pixel (i, j) in the desired upscaled

image I

′′

(where i ranges from 1 to M and j ranges

from 1 to N), the corresponding pixel value is directly

copied from the nearest pixel in the downscaled im-

age I

′

as follows:

′′

(i, j) = I

′

((i/2),( j/2)),i ∈ M, j ∈ N (12)

The ﬁnal distorted image I

′′

will have a blurring

effect. The IQA metric values for the distorted set

distorted

are depicted in Figure 5, where we can see

a clear degradation in the values reﬂecting this reduc-

tion in quality.

To investigate how adding high valued BRISQUE

scored images to the dataset pipeline affect the model

performance, we perform an experiment where we in-

clude 70% images from D

orignal

, and 30% of images

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

338

Table 3: Initial performance on D

test

of the U-net model trained using different combinations of the three datasets.

No. Training Dataset Dice PR score F-score

1 Cityscapes 0.375370 0.580734 0.307178

2 ADE 0.513763 0.645072 0.391683

3 VOC 0.245870 0.459835 0.154959

4 Cityscapes + VOC 0.286961 0.545884 0.186165

5 Cityscapes + ADE 0.493080 0.645643 0.370273

6 ADE + VOC 0.389131 0.617254 0.276805

7 Cityscapes + VOC + ADE 0.404864 0.589132 0.289338

Table 4: Performance of trained U-nets on D

test

using the feature vector learning approach. The ﬁrst row shows the initial

performance of the model on ADE dataset. As more data is added to the pipeline without any data selection strategy, the

model performance degrades as seen in row 2, due to noisy data. Upon applying the selection strategy on the new datasets,

we see that it preserves the prior knowledge and prevents further performance degradation in row 3.

No. Training Dataset Dice PR score F-score

1 ADE 0.513763 0.645072 0.391683

2 ADE + Cityscapes + VOC (Baseline Model) 0.404864 0.589132 0.289338

3 ADE + (Cityscapes +VOC)

SelectedData

0.462565 0.618605 0.342391

Figure 5: Distribution of original images, D

original

BRISQUE scores and BRISQUE scores for images after

image degradation (D

distorted

). Lower BRISQUE score in-

dicate better quality. The original images distribution re-

ﬂects an overall high perceptual quality images. After

degradation, we see an overall increase in BRISQUE due

to a poor quality.

from D

distorted

. The performance achieved by con-

ducting this experiment is demonstrated in Table 1. It

is observed that when we have images having high

BRISQUE scores (meaning poor quantitative qual-

ity), the model performance degrades as we see the

PR score drops to 0.549964 from 0.589132 as com-

pared to the baseline model trained purely with all

orignal

. This indicates a decreased ability to correctly

classify true positives while maintaining a similar rate

of false positives, due to the introduction of lower-

quality images.

Further investigations explore the impact of data

quality on model training, focusing on distorted im-

ages in datasets D

distorted

and D

′

distorted

. The for-

mer includes distorted versions of Cityscapes, ADE,

and VOC images, while the latter selectively includes

high-quality images with BRISQUE scores below 60.

Table 2 summarizes the model’s performance on these

datasets. Training with D

distorted

yields a dice coefﬁ-

cient of 0.309860, a PR score of 0.386605, and an F-

score of 0.208074. Contrastingly, utilizing D

′

distorted

results in signiﬁcantly improved metrics: a dice coef-

ﬁcient of 0.371031, a PR score of 0.484460, and an

F-score of 0.260145. This improvement underscores

the substantial beneﬁt of data curation using IQA met-

rics, ensuring high-quality inputs for model training.

5.2 Approach 2: Results on Feature

Learning Based Method

In this approach, we ﬁrst perform a systematic ex-

ploration of various training datasets for U-Net mod-

els and examine their performance on our test dataset

test

. Our initial objective is to identify a bench-

mark model for our proposed method. To this end,

we trained and evaluated multiple U-Net models us-

ing different combinations of three diverse datasets,

ADE, Cityscapes, and VOC. The performance results

of these models are given in Table 3. Among these,

we observed that the U-Net model trained solely

on the ADE dataset exhibits the best performance,

achieving a dice coefﬁcient of 0.513763, PR score of

0.645072, and and F-score of 0.391683. Hence, we

consider this model as our preferred choice for the

initial production model in our deployment environ-

ment.

Data Quality Aware Approaches for Addressing Model Drift of Semantic Segmentation Models

339

Table 5: Comparing results of the two approaches: (Cityscapes +V OC)

uses feature learning, and (Cityscapes +VOC)

involves quality-based selection with BRISQUE T < 40. Both are compared to the baseline model.

No. Training Dataset Dice PR score F-score

1 ADE+ Cityscapes + VOC (baseline) 0.404864 0.589132 0.289338

2 ADE+ (Cityscapes +VOC)

0.462565 0.618605 0.342391

3 ADE+ (Cityscapes +VOC)

0.437014 0.626327 0.322737

Table 6: Dataset size statistics.

Data # of Images

ADE 800

Cityscapes + VOC 1100

Selected from Cityscapes + VOC 550

Spanning from our initial formulated problem,

we add Cityscapes and VOC, to the initial dataset

pipeline, which was trained using only ADE. It can

be seen that the model suffers degradation in perfor-

mance, shown by the dice value falling from from

0.513763 to 0.404864 and the PR score dropping

from 0.645072 to 0.589132. To handle this drop,

we introduce our feature vector learning approach,

which involves leveraging the ADE-trained U-Net as

a base for selecting images from additional datasets,

Cityscapes and VOC, to be added to the retraining of

the model.

The results of this selection are illustrated in Ta-

ble 4. Table 6 presents the number of images selected

by this approach. Applying the feature-based data se-

lection strategy to new datasets yields substantial per-

formance improvements, evident in higher dice coef-

ﬁcient, PR, and F-score metrics. This improvement

surpasses the baseline model (ADE + Cityscapes +

VOC), which uses all available images without any

selection. Our method not only maintains high per-

formance with the ADE dataset but also adapts effec-

tively to diverse data sources. This adaptability is cru-

cial in real-world scenarios with continuous dataset

updates, showcasing the robustness and practical ap-

plicability of our proposed methodology for semantic

segmentation tasks. Some prediction visualizations

are depicted in Figure 6.

5.3 Comparing the Two Approaches

Both approaches demonstrate an overall perfor-

mance improvement, as shown in Table 5. The

quality-based method excels in reducing false

positives, as indicated by slight improvements in

PR scores and F-scores. On the other hand, the

feature vector learning-based approach enhances

dice, F-score, and reduces false predictions, though

not as prominently as the quality-based method. If

the primary goal is to minimize false predictions, the

Figure 6: Visualizing predictions made by the trained mod-

els. Approach 2 predictions are shown in the last column

of the image, where we see a visual reduction of the false

positives compared with the baseline model predictions.

quality-based approach appears to be the preferred

choice, showcasing its efﬁcacy.

6 CONCLUSIONS

In this work we investigate two strategies to handle

model drift: data quality assessment and data condi-

tioning based on prior model knowledge. The former

relies on image quality metrics to meticulously select

high-quality training data, thereby bolstering model

robustness. In contrast, the latter leverages learned

feature vectors from existing models to guide the se-

lection of future data, aligning it with the model’s

prior knowledge. Through extensive experimentation,

we provide valuable insights into the effectiveness of

these approaches in enhancing the performance and

reliability of semantic segmentation models. These

ﬁndings underscore the signiﬁcance of data quality

and alignment with prior knowledge in sustaining the

efﬁcacy of AI models in dynamic real-world environ-

ments, thus contributing to the ongoing advancement

of computer vision capabilities.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

340

REFERENCES

Ackerman, S., Farchi, E., Raz, O., et al. (2020). Detec-

tion of data drift and outliers affecting machine learn-

ing model performance over time. arXiv preprint

arXiv:2012.09258.

Ackerman, S., Raz, O., Zalmanovici, M., and Zlotnick, A.

(2021). Automatically detecting data drift in machine

learning classiﬁers. arXiv preprint arXiv:2111.05672.

Bayram, F., Ahmed, B. S., and Kassler, A. (2022). From

concept drift to model degradation: An overview on

performance-aware drift detectors. Knowledge-Based

Systems.

Cordts, M., Omran, M., Ramos, S., Rehfeld, T., et al.

(2016). The cityscapes dataset for semantic urban

scene understanding. In CVPR.

Davis, S. E., Greevy Jr, R. A., Fonnesbeck, C., Lasko, T. A.,

et al. (2019). A nonparametric updating method to

correct clinical prediction model drift. Journal of the

American Medical Informatics Association.

Devarakota, P., Gala, A., Li, Z., Alkan, E., et al. (2022).

Deep learning in salt interpretation from r&d to de-

ployment: Challenges and lessons learned. In Second

International Meeting for Applied Geoscience & En-

ergy.

Dries, A. and R

uckert, U. (2009). Adaptive concept drift

detection. Statistical Analysis and Data Mining: The

ASA Data Science Journal.

Everingham, M., Van Gool, L., Williams, C. K., et al.

(2010). The pascal visual object classes (voc) chal-

lenge. International journal of computer vision.

Guerra-Manzanares, A., Luckner, M., and Bahsi, H. (2022).

Android malware concept drift using system calls: de-

tection, characterization and challenges. Expert Sys-

tems with Applications.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Spatial pyra-

mid pooling in deep convolutional networks for visual

recognition. IEEE transactions on pattern analysis

and machine intelligence.

Hofer, V. and Krempl, G. (2013). Drift mining in data: A

framework for addressing drift in classiﬁcation. Com-

putational Statistics & Data Analysis.

Johannes, J., Michael, V., Niklas, K., et al. (2023). Data-

centric artiﬁcial intelligence.

Khaldi, K., Mantini, P., and Shah, S. K. (2022). Unsuper-

vised person re-identiﬁcation based on skeleton joints

using graph convolutional networks. In International

Conference on Image Analysis and Processing.

Klinkenberg, R. and Joachims, T. (2000). Detecting concept

drift with support vector machines. In ICML.

Lacson, R., Eskian, M., Licaros, A., et al. (2022). Machine

learning model drift: predicting diagnostic imaging

follow-up as a case example. Journal of the Ameri-

can College of Radiology.

Lu, J., Liu, A., Dong, F., et al. (2018). Learning under con-

cept drift: A review. IEEE transactions on knowledge

and data engineering.

Mittal, A., Moorthy, A. K., and Bovik, A. C. (2012). No-

reference image quality assessment in the spatial do-

main. IEEE Transactions on image processing.

Rahmani, K., Thapa, R., Tsou, P., Chetty, S. C., Barnes,

G., et al. (2023). Assessing the effects of data drift

on the performance of machine learning models used

in clinical sepsis prediction. International Journal of

Medical Informatics.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In MICCAI.

Tsymbal, A. (2004). The problem of concept drift: deﬁ-

nitions and related work. Computer Science Depart-

ment, Trinity College Dublin.

Wang, H. and Abraham, Z. (2015). Concept drift detection

for streaming data. In IJCNN.

Wang, P., Jin, N., Woo, W. L., et al. (2022). Noise tolerant

drift detection method for data stream mining. Infor-

mation Sciences.

Webb, G. I., Hyde, R., Cao, H., et al. (2016). Characterizing

concept drift. Data Mining and Knowledge Discovery.

Whang, S. E., Roh, Y., Song, H., and Lee, J.-G. (2023).

Data collection and quality challenges in deep learn-

ing: A data-centric ai perspective. The VLDB Journal.

Zha, D., Bhat, Z. P., Lai, K.-H., Yang, F., et al. (2023). Data-

centric artiﬁcial intelligence: A survey.

Zhou, B., Zhao, H., Puig, X., Fidler, S., et al. (2017). Scene

parsing through ade20k dataset. In CVPR.

Zhou, B., Zhao, H., Puig, X., Xiao, T., et al. (2019). Se-

mantic understanding of scenes through the ade20k

dataset. International Journal of Computer Vision.

Data Quality Aware Approaches for Addressing Model Drift of Semantic Segmentation Models

341