Privacy Preservation in Image Classification Using Seam Doppelganger
Nishitha Prakash
a
and James Pope
b
Department of Engineering Mathematics, University of Bristol, Bristol, U.K.
Keywords:
Privacy Preservation, Seam Doppelganger, Image Classification, Structural Similarity, Histogram of Gradient.
Abstract:
Cloud storage usage continues to increase and many cloud storage sites use advanced machine learning models
to classify user’s images for various purposes, possibly malicious in nature. This introduces very serious pri-
vacy concerns where users want to store and view their images on the cloud storage but do not want the models
to be able to accurately classify their images. This is a difficult problem and there are many proposed solu-
tions including the seam doppelganger algorithm. Seam Doppelganger uses the seam carving content-aware
resizing approach to modify the image in a way that is still human-understandable and has been shown to
reduce model accuracy. However, the approach was not tested with different classifiers, is not able to provide
complete restoration, and uses a limited dataset. We propose several modifications to the Seam Doppelganger
algorithm to better enhance the privacy of the image while keeping it human-readable and able to be fully
restored. We modify the energy function to use a histogram of gradients, comprehensively compare seam se-
lection, and evaluate with several pre-trained (on ImageNet and Kaggle datasets) image classification models.
We use the structural similarity index measure (SSIM) to determine the degree of distortion as a proxy for
human understanding. The approach degrades the classification performance by 70% and guarantees 100%
restoration of the original image.
1 INTRODUCTION
In recent years, the field of machine learning has wit-
nessed remarkable advancements and sophistication.
Techniques such as text recognition, speech recog-
nition, image recognition, image classification, etc.
have indeed unlocked several new features and op-
portunities like facial recognition, and automatic edit-
ing tools, but they also lead to the creation of new
challenges. Once an image is uploaded to an online
platform, knowingly or unknowingly, we grant public
access to our data. Apart from using it for personal-
ized curation, it is also used as a valuable source of
digital information for modern marketing strategies.
Obviously, there are several existing solutions to
address these problems. Techniques like encryption,
watermarking, and obfuscation were the best-known
novel techniques used for privacy preservation in the
early 2000s (Dang and Chau, 2000). Later, more ad-
vanced techniques like attribute selection, discretiza-
tion, fixed-data perturbation, probability distribution,
and randomization were used to modify the sensitive
attributes for privacy preservation (Li et al., 2003). To
a
https://orcid.org/0009-0007-1210-0577
b
https://orcid.org/0000-0003-2656-363X
provide a comprehensive solution, technologies like
watermarking, steganography, content protection, and
copyright management (Potdar et al., 2005) were in-
troduced. As machine learning models continued to
evolve, there was an increased demand for enhanced
privacy preservation methods, leading to the develop-
ment of several advanced techniques.
Even though privacy preservation techniques were
constantly evolving, recent advancements in the field
of image recognition machine learning approaches
such as deep learning to handle data augmentation
(Perez and Wang, 2017) and Hyperspectral image
classification (Yang et al., 2018) have strengthened
the efficiency of a classifier. The hyperspectral image
classifier uses the entire spectrum of each pixel in an
image to identify and discriminate the target features.
Moreover, recent advancements have also facilitated
the classification of noisy data with remarkable ac-
curacy. As described by (Yang et al., 2023) the pro-
posed solution still maintains to deliver a remarkable
prediction accuracy even for a noisy data set. Such
results have led to a hypothesis that privacy preserva-
tion techniques need to be constantly improved and
adapted in response to the evolution of new machine
learning techniques.
342
Prakash, N. and Pope, J.
Privacy Preservation in Image Classification Using Seam Doppelganger.
DOI: 10.5220/0012316100003660
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages
342-349
ISBN: 978-989-758-679-8; ISSN: 2184-4321
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

Due to the enhancements and exciting features
supported by the application, many users also prefer
to utilize the cloud platform and its resources, lead-
ing to a situation where they expect the images to
be in a format that humans can understand and ma-
chine learning models cannot. This introduces the
concept of Adversarial Perturbations, a technique that
intends to modify or alter the input data, specifically
images, to mislead or deceive the machine learning
model (Poursaeed et al., 2018). The existing seam
doppelganger approach intends to confuse the ma-
chine learning model by modifying the images us-
ing Seam Carving, a content-aware image resizing
technique (Avidan and Shamir, 2007). It identifies
and replaces the irrelevant seams of pixels in an im-
age to modify it. They are then applied over an im-
age classifier which classifies the image. The exist-
ing approach does impact the quality of classification
(Pope and Terwilliger, 2021), especially since it was
only tested on generic datasets. Moreover, the altered
images weren’t fully reconstructed. To handle these
challenges, the proposed solution aims to refine the
structure of the conventional seam doppelganger ap-
proach, aiming for better overall results. The contri-
butions of the paper are as follows.
• Proposed modifications to the seam doppelganger
algorithm to make it more effective and able to
fully restore images.
• Evaluated the HOG energy image and which
seams are the most effective for image privacy.
• Evaluated the optimal degree of distortion using
the SSIM.
• Validated the modified algorithm on both generic
and task-specific data sets. ImageNet dataset
is used for validating generic categories and the
Kaggle bird image dataset is used for validating
task-specific categories.
2 MODEL ARCHITECTURE
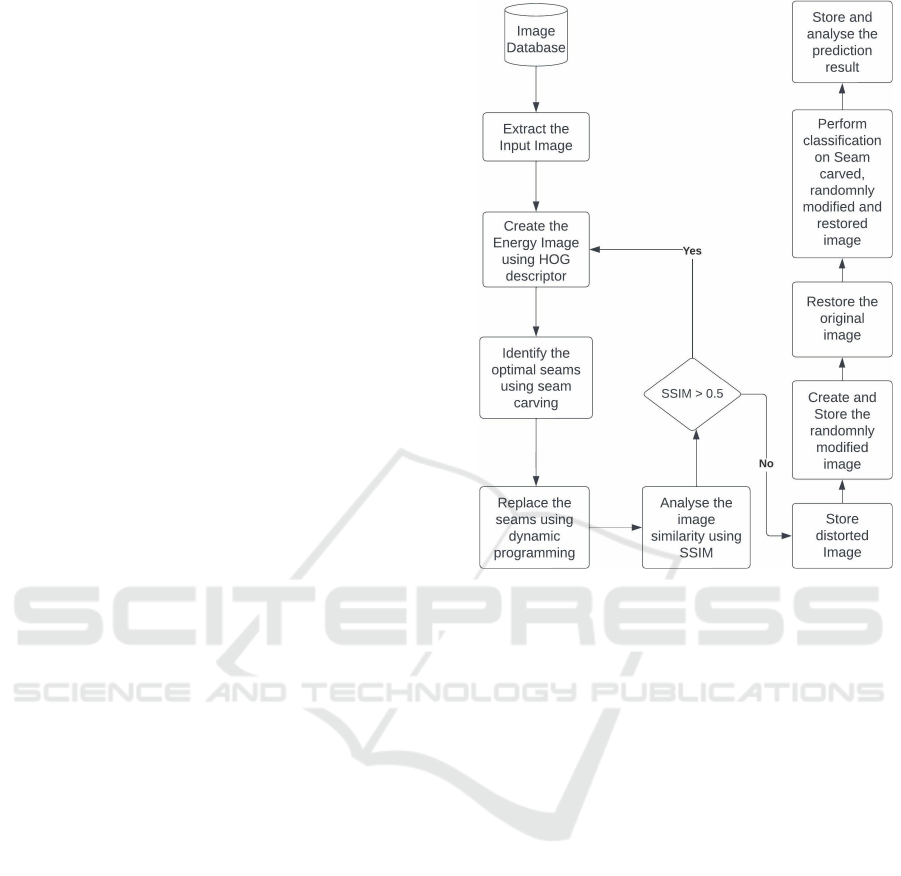
The workflow of the proposed solution is represented
as a two-step process. The first step involves image
modification and the second step involves image clas-
sification. Each step consists of a list of operations
to perform the desired task which is explained in the
later part of the section with the help of the workflow
diagram 1.
2.1 Image Modification
Image modification is the process of altering the im-
age to confuse the machine learning models. To be-
Figure 1: Workflow of Seam Doppelganger Model.
gin with, the images are extracted from the image
database. As discussed earlier, the ImageNet and
Kaggle datasets are used for extracting input images.
Over 1.2 million generic images and 524 unique bird
species images were used to validate the approach re-
spectively.
2.1.1 Energy Image Creation Using HOG
The first step towards image modification is the cre-
ation of an energy image. The original image is trans-
formed into an energy image which represents the im-
portance of each pixel. It is required to obtain the
salient features from the image. It can be created us-
ing several energy functions like gradient magnitude,
entropy, etc. In this work, the histogram of gradient
is used as the energy function. It represents the ori-
entation of the gradient magnitude in the local areas
of an image. The idea behind HOG is to capture the
object orientation, color, silhouettes, etc. based on the
gradient information for object detection. It results in
representing the image as a feature vector, a form that
displays only the important information in an image.
The first step in the process of creating a his-
togram is preprocessing the input image. The image
must be resized to a format required by the model.
The number of blocks and cells per block is adjusted
according to the specific task. Secondly, the gradient
Privacy Preservation in Image Classification Using Seam Doppelganger
343

difference between each pixel is computed along the
x and y direction. It is calculated by subtracting the
pixel value below from the pixel and above from the
pixel in both directions. Let’s say we need to find the
gradient difference in pixel p2, 2, the equations can
be given by 1 and 2
G(x) = p(2,3) − p(2,1) (1)
G(y) = p(3,2) − p(1,2) (2)
Where G(x) is the gradient change in the x-
direction and G(y) is the gradient change in the y-
direction. Finally, the magnitude and orientation of
the pixel are calculated using the formula 3 and 4
µ =
q
[(Gx)
2
+ (Gy)
2
] (3)
Θ = tan
−1
(Gy/Gx) (4)
Using the obtained values, the HOG is generated
by creating a magnitude bucket for each block of an
image. The bin size used for the buckets changes
depending on the complexity of the task. For this
project, each bucket has a bin size of 9 and a cell size
of (8,8). This ensures that the images are processed
as 8 ∗ 8 blocks and for each block, a magnitude ma-
trix is created of size 9 ∗ 1. Now that we have the
histogram for 8 ∗ 8 cells, the value is normalized to
obtain the histogram of the image in 16 ∗ 16 cells. It
is mainly done to overcome the imbalance in gradi-
ent difference. The values of all possible 8 ∗ 8 blocks
are combined into a single 16∗ 16 using the following
equations,
vector = [a1, a2,a3,...,a36], (5)
k =
q
(a1)
2
+ (a2)
2
+ (a3)
2
+ ... + (a36)
2
, (6)
normalized vector =

a
1
k
,
a
2
k
,...,
a
36
k

. (7)
Finally, the resulting matrix is used to generate the
energy image.
2.1.2 Seam Identification and Replacement
Using the energy image, the horizontal and vertical
seam is determined. It refers to the connected path of
pixels that identifies the features of an image. Usu-
ally, it is recognized as a connected path of low-
intensity pixels since it is primarily used for image
resizing. Here, it is identified as the high-intensity
path that represents the important features of the im-
age. The proposed model aims to iterate over all pos-
sible seams and identify the optimal seam using op-
timization techniques. Here, the optimal seam is the
one with high intensity or weight. After identification,
the values of the seam pixels are manually updated
to zero (min intensity value) to avoid identifying the
same seam during the next iterations. It is also saved
to restore back the original image.
After identifying the vertical and horizontal seam,
the seam’s pixel value is updated to produce a new
image. Two different approaches are tested to mod-
ify the original image. The first approach replaces
the pixel value with a solid color and the second ap-
proach replaces the pixel value by inverting it. Even
though both approaches showed similar results, the
former was technically complex. The seam informa-
tion and the original pixel value need to be stored to
restore the original image. Hence the seam is replaced
using the color inversion technique. The function in-
puts the seam array and the original image. The origi-
nal image is converted into an ImageDraw object to
enable modification. The input array is iterated to
access each seam index and the values are inverted.
This is done by subtracting 255 from the correspond-
ing pixel value. Here, 255 refers to the maximum in-
tensity value for an 8-bit image channel. Finally, the
modified image is returned in the form of a PIL in-
stance.
The process is repeated until the image is partially
modified. To iterate the process, the entire workflow
is repeated again including the generation of energy
images. The overall process of seam doppelganger is
explained in detail using 1
In addition to image modification by seam re-
placement, it is also distorted by replacing random
pixels. It is done to justify the use of a dedicated
technique for image modification. A random pixel
for the image is selected and replaced by a random
RGB value. Again, the process is repeated until the
similarity between the original and modified image is
less than 0.5. The classification results obtained using
both techniques are compared in later sections.
2.1.3 Image Restoration
In addition to image distortion, the original image
can also be restored by reversing the technique. The
same approach used for image modification is re-
peated to perform the restoration. The seams iden-
tified and stored during the replacement process are
modified back to the original pixel value. Since the
pixel values were inversed during replacement, re-
inversing them would generate the original image.
The proposed model not only provides a simple solu-
tion but also achieves 100% image restoration, unlike
the traditional seam doppelganger approach. The only
drawback of this approach is the additional memory
and computational time required to store the modified
seam during the image modification process.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
344

Procedure: Seam Doppelganger
Data: energy image matrix
Result: distored image, randomnly replaced image, restored image
while similarity score > 0.5 do
horizontal seam, vertical seam, distorted image, energy map = findSeam(original image,
energy map)
randomnly replaced image = randomReplacement(original image)
horizontal seam array = store horizontal seam
vertical seam array = store vertical seam
end
restored image = restore image(distorted image, horizontal seam array, vertical seam array )
return distored image, randomnly replaced image, restored image
Procedure: Seam Identification
Data: original image, energy map
Result: horizontal seam, vertical seam
for each row and col in energy map do
cumulative energy = findCumulativeEnergy(energy map)
seam = np.argmax(cumulative energy)
seam.setValue(argmin)
return seam
end
Procedure: Seam Replacement
Data: original image, seam array
Result: distorted image
for each row and col in seam array do
color = original image.getPixel(col,row)
color inverse = tuple(255 - component for component in colour)
original image = original image.overlay(color inverse)
end
Algorithm 1: Seam Doppelganger Algorithm.
2.2 Image Classification
In between image modification and restoration,
the workflow represents two primary functionalities
which include image classification and prediction
analysis. The primary goal of image modification is
to ensure privacy preservation. This objective is met
when the model cannot recognize the original class
label. To verify that, the CNN classifier, trained us-
ing ImageNet (Net, ) and Kaggle datasets (Gerry, )
respectively, is applied over the original and modified
image. The obtained results are stored and analyzed
to validate the quality of the application.
ResNet50 model, trained on millions of ImageNet
datasets, is used to test the generic feature of the ap-
plication. Along with that, a class-specific validation
is also carried out by using the EfficientNetB0 model.
It is trained on the Kaggle bird species dataset. Over
84,635 images were used to train the model and 2,625
images were used to validate and fine-tune it. Both
features are available as a separate functionality to the
users. Once the images are distorted and saved on the
directory, they can be fed into ResNet50 or Efficienet-
NetB0 model. However, ResNet50 can be used for
any image prediction whereas EfficientNetB0 can be
used only for bird images. Since the latter is trained
only on bird images, it is mandatory to validate only
bird image predictions.
The classifier outputs a text file that contains the
top 3 prediction classes along with the probability of
the seam, restored, and random versions of images.
Privacy Preservation in Image Classification Using Seam Doppelganger
345

Table 1: Hyperparameters used for initializing the HOG
function.
Orientation Pixels per Cell Cells per Block
9 (8,8) (2,2)
3 EXPERIMENTAL RESULTS
AND EVALUATION
The paper aims to improvise the existing seam dop-
pelganger architecture by experimenting with several
approaches. In this section, a comprehensive discus-
sion of the experimental results obtained using the ap-
proaches and the analysis conducted based on these
findings are explained in detail.
3.1 Hyper-Parameter Tuning for
Energy Image Creation
To generate the energy image, the HOG object is cre-
ated by trying out different parameter values. They
are fine-tuned according to the requirements. Three
primary parameters used for model creation include
orientation, pixels per cell, and cells per block. Fig-
ure 2 shows the energy image of Abbotts Babbler us-
ing the various hyperparameter values. As we ob-
serve, each pixel in the image is represented as ar-
rows or lines that denote the magnitude and orien-
tation. The length (or sometimes the brightness) of
these lines or arrows is proportional to the amount of
gradient magnitude in that orientation bin. The direc-
tion of each arrow represents the orientation of gradi-
ent change and the size represents the magnitude of
the change. Darker regions represent the less impor-
tant part of the image and the lighter region represents
the main subject, the bird in our case.
While analyzing and comparing other images, the
image on the top right is generated by setting the bin
size to 6. The resulting image is almost similar to the
actual hog image with a slight decrease in the overall
intensity. The bottom-left image is created with bin
size=6 and cell size = (4,4). Changing the cell size
decreases the size of the lines resulting in indistinct
detailing. Similarly, increasing the cell size to (10,10)
increases the size of lines resulting in the same issue.
Hence, the energy image is generated by using the
hyperparameter values mentioned in Table 1.
3.2 Identifying Seam from the Energy
Image
Using the energy image, the vertical and horizontal
seams are identified by applying dynamic program-
Figure 2: Energy image of Abbotts Babbler using various
hyperparameter values. Top-left: Energy image after hy-
perparameter tuning, Top-right: Energy Image with larger
bin size, Bottom-left: Energy Image with smaller cell size,
Bottom-right: Energy Image with larger cell size.
ming. Here, experiments are conducted to analyze
the modification rate using both the least and most
informative seams since the aim is not limited to im-
age resizing. Table 2 shows results comparing the
seam identification process using both approaches. It
contains the number of iterations to partially modify
the images and the prediction accuracy obtained us-
ing those images. The partial modification is achieved
by assessing the image similarity after each seam re-
placement iteration and the prediction accuracy is ob-
tained by applying the ResNet50 classifier over the
modified images. The accuracy here denotes the pre-
diction probability of the image. As evident from the
table, the image altered using LIS is recognized as Ja-
camar with a probability of 0.2471. In contrast, the
image modified using MIS has a much lower proba-
bility of 0.0016 of being classified as Jacamar. Simi-
lar results are seen for other image categories as well
which proves that modifying the image using MIS is
more effective than LIS. Even though the number of
iterations required to modify the images using MIS
is slightly higher than LIS, the difference in the pre-
diction probability adds more value. Hence to effec-
tively modify the image, the most informative seams
are identified from the energy image and replaced for
image modification.
3.3 Image Modification Using Color
Inversal
Each seam identified is updated to easily modify the
image structure. As discussed earlier, two different
approaches are tested to modify the original image.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
346

Table 2: Analysis of Seam Replacement using Least and Most Informative Seams.
Input Image Iteration
count using
LIS
Iteration
count using
MIS
Accuracy using LIS Accuracy using MIS Original Accuracy
Jacamar 35 22 0.2471 0.0016 0.5863
Golden Retriever 18 21 0.0429 0.1348 0.5775
Gold Fish 16 18 0.0138 0.0006 0.9999
Bald Eagle 16 18 0.1015 0.0001 0.9993
Indigo Finch 12 15 0.1235 0.0314 0.9919
Wood Rabbit 11 14 0.0652 0.0001 0.7247
Figure 3: Updated Jacamar image using solid color overlay
(left) and color inversion (right).
Figure 3 shows the image of Jacamar modified using
solid color overlay and color inversion. Clearly, all
the images are still human-readable. Both approaches
tend to perform well with image classification. How-
ever, changing the pixel value to a common color
would require us to store additional information hence
it is not preferred as the ideal technique.
3.4 Restoring the Original Image
The original image is restored by iterating over the re-
placed pixel and inverting it to the original value. Fig-
ure 4 shows the restored image (right) and the original
image of Abbott Babbler (left). The similarity score
between the original and restored image is 0.9466.
Technically, the method attains full restoration as the
similarity score is nearly 1.0, and visually, it’s chal-
lenging to identify any difference with the naked eye.
However, as we observe, the image quality has dete-
riorated due to several processing steps. The image is
resized to effectively generate the energy image and
identify seams. Hence, the proposed solution tries to
achieve 100% restoration while compromising on the
image quality. The process terminates by storing the
seam-replaced image, randomly replaced image, and
restored image in a directory for image classification.
Figure 4: AbbottsBabbler Restored (left) and Original
(right).
Table 3: Performance of ResNet50 model on Generic
dataset (same level of distortion, SSIM=0.5).
Image Category Total
Images
Images
Cor-
rectly
Pre-
dicted
Images
Wrongly
Predicted
Accuracy
Random 193 40 153 20.12%
Seamed 193 1 192 0.52%
3.5 Image Classification Performance
on Generic Dataset
ResNet50 model is trained over millions of data ex-
tracted from ImageNet that includes generalized cat-
egories. Ten image classes are used for the analysis
which includes Dog, Cat, Lizard, GuineaPig, Ham-
ster, Bird, Rabbit, Turtle, Fish, and Horse. They are
taken from the Kaggle dataset. Each image category
consists of 20 test images which are all used for clas-
sification. Table 3 shows the results of the experi-
ment. It clearly shows that modifying the image using
seam carving reduces the performance of the classi-
fier. However, randomly modified images don’t con-
fuse the classifier much. It is to be noted that both
images are distorted equally, the SSIM score between
the original and modified image is 0.5. The accuracy
of the model on random images is 20.1240% and on
seamed images is nearly 0. This proves that seamed
images tend to confuse the model better.
Privacy Preservation in Image Classification Using Seam Doppelganger
347

Table 4: Performance of EfficientNetB0 model on Bird
dataset (same level of distortion, SSIM=0.5).
Image Category Total
Number
of Im-
ages
Images
Cor-
rectly
Pre-
dicted
Images
Wrongly
Pre-
dicted
Accuracy
Random 2619 2282 337 87.13%
Seamed 2619 711 1908 27.15%
Figure 5: AbbottsBabbler Top-left: Original, Top-right:
randomly replaced, Bottom-left: Seam replaced, Bottom-
right: Restored.
3.6 Image Classification Performance
on Bird Dataset
EfficientNetB0 is trained exclusively on the bird im-
age dataset from Kaggle. The goal is to guarantee
that the model is not easily misled. Being trained
on task-specific data, it should find it difficult to clas-
sify the seam-carved images. To achieve this, the bird
images of 524 different bird species are used. Each
species consists of 5 test images and all the images are
used for classification. Like the previous approach,
the model makes predictions of the test images and
the results are stored in a text file. While analyzing
the results shown in Table 4, it is again evident that
seamed images reduce the efficiency of the classifier.
Out of 2619 images only 711 images were correctly
classified to their actual label, the remaining 1908 im-
ages were wrongly predicted by the model. The ac-
curacy of the EfficientNet50 model on seam carved
images is 27.1374%, which is 69.85% less than the
actual accuracy of the model (90%). It can be con-
cluded that the proposed solution reduces the perfor-
mance of the model by 69.85% even if it is trained on
task-specific data. Randomly replaced images show a
decent degradation in the model performance. Out of
2619 images 2282 were correctly classified. The ac-
curacy of the model on random images is 87.1324%.
Table 5: Prediction result of AbbottsBabbler using Effi-
cientNetB0 model.
Image Category Predicted Class Probability
Austral Canas-
tero
0.99114
Random Golden Bower
Bird
0.00155
Abbotts Bab-
bler
0.00108
Abbotts Bab-
bler
0.99817
Original Northern
Beardless
Tyrannulet
0.00048
Red Legged
Honeycreeper
0.00018
Alberts Towhee 0.27483
Seam Great Xenops 0.09549
Back Throated
Huet
0.08200
The image classification results obtained for Ab-
botts Babbler are presented in Table 5 and Figure
5. The seam-carved image successfully confuses the
classification model, as we see, the prediction prob-
ability is reduced from 0.998 to a value lesser than
0.08200 since we can’t even find Abbotts Babbler
in the top three prediction results. Randomly re-
placed images also tend to confuse the model well,
but not better than seam-carved images. It classified
the image correctly but with a reduced probability of
0.00108.
Almost 80% of the seam-carved images tend to
confuse the classifier. However, few results show that
the proposed approach might not always work. Ta-
ble 6 shows the prediction result of Campo Flicker.
Unexpectedly, the classifier classifies the seamed im-
age correctly as Campo Flicker with a probability
of 0.9944. The randomly replaced image is also
correctly classified by the model with a probability
of 0.9977. The original and processing images are
shown in Figure 6.
3.7 Future Work
Certain limitations impact the performance of the
model. Firstly, as seen in Figure 4, the quality of the
restored image is not on par with the original. This
is due to the various preprocessing steps the image
undergoes. Although the method accomplishes 100%
restoration, it doesn’t ensure the same quality as the
original image. To handle that, new techniques need
to be experimented which does not deteriorate the
quality of the image. Secondly, the proposed work
focuses on validating the approach on model trained
using task-specific data. It aims to prove that modi-
fying the images using a specialized technique would
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
348

Figure 6: CampoFlicker Top-left: Original, Top-right: ran-
domly replaced, Bottom-left: Seam replaced, Bottom-right:
Restored.
Table 6: Prediction result of CampoFlicker using Efficient-
NetB0 model.
Image Category Predicted Class Probability
Campo Flicker 0.99772
Random Lesser Adjutant 0.00022
Andean Lap-
wing
0.00008
Campo Flicker 0.99900
Original Greater Prairie
Chicken
0.00006
Lesser Adjutant 0.00005
Campo Flicker 0.99448
Seam Yellow
Breasted
Chat
0.00105
Gurneys Pitta 0.00067
definitely confuse the classifier even if it’s restricted
to bird images. Due to this reason, the concentra-
tion of the project was completely on image modi-
fication and not image classification. In the future,
the CNN model can be more robust by giving impor-
tance to technical details like hyperparameter tuning,
architecture modification, learning rate adjustments.,
etc. Finally, future work also includes validating the
approach on different image categories. Like birds,
other ImageNet categories can be evaluated.
4 CONCLUSIONS
The aim of the project is achieved by develop-
ing an improvised version of seam doppelganger
which proves to work better than the traditional ap-
proach. The model is updated by incorporating
better-performing techniques. Additionally, it is also
proven robust by validating both generic and task-
specific datasets. The traditional approach used only
ResNet50 to validate the solution. Results show that
the accuracy dropped to 3% on 50% distorted im-
ages. The proposed solution achieves an accuracy of
0.5180% on 50% distorted images after improving the
model architecture proving the enhanced efficiency of
the seam doppelganger approach. Finally, the updated
architecture also guarantees 100% image restoration,
unlike the traditional approach.
ACKNOWLEDGEMENTS
I wish to express my deepest gratitude to Dr. James
Pope at the University of Bristol, for his guidance and
assistance throughout this project. Despite the project
not being entirely within my primary area of exper-
tise, he helped me understand the fundamental prin-
ciples of seam carving and image processing. His in-
sightful feedback has not only been enlightening but
also served as a strong motivation for me to explore
beyond my boundaries.
REFERENCES
Avidan, S. and Shamir, A. (2007). Seam carving for
content-aware image resizing. ACM Transactions on
Graphics (TOG), 26(3):10.
Dang, P. and Chau, P. (2000). Image encryption for secure
internet multimedia applications. IEEE Transactions
on Consumer Electronics, 46(3):395–403.
Gerry. Birds 400 - species image classification.
Li, J., Shaw, M., Lin, F.-R., and Lin, F. (2003). Privacy
Protection in Data Mining.
Net, I. Imagenet.
Perez, L. and Wang, J. (2017). The effectiveness of data
augmentation in image classification using deep learn-
ing. arXiv:1712.04621 [cs].
Pope, J. and Terwilliger, M. (2021). Seam carving for image
classification privacy. Proceedings of the 10th Inter-
national Conference on Pattern Recognition Applica-
tions and Methods.
Potdar, V., Han, S., and Chang, E. (2005). A survey of
digital image watermarking techniques. In INDIN ’05.
2005 3rd IEEE International Conference on Industrial
Informatics, 2005., pages 709–716.
Poursaeed, O., Katsman, I., Gao, B., and Belongie, S.
(2018). Generative adversarial perturbations.
Yang, C.-H. H., Hung, I.-T., Liu, Y.-C., and Chen, P.-Y.
(2023). Treatment learning causal transformer for
noisy image classification.
Yang, X., Ye, Y., Li, X., Lau, R. Y. K., Zhang, X., and
Huang, X. (2018). Hyperspectral image classifica-
tion with deep learning models. IEEE Transactions on
Geoscience and Remote Sensing, 56(9):5408–5423.
Privacy Preservation in Image Classification Using Seam Doppelganger
349