Uncertain Formal Concept Analysis for the Study of a Text Corpus
Guillaume Petiot
CERES, Catholic Institute of Toulouse, 31 rue de la Fonderie, 31068, Toulouse, France
Keywords:
Data Analysis, Formal Concept Analysis, Natural Language Processing, Possibility Theory, Uncertainties.
Abstract:
The analysis of a corpus by an expert takes a relatively long time. The development of digital tools made it
possible to generate instantly a summary of information contained in the corpus. In this paper, we will focus on
the contribution of formal concept analysis (FCA) to the analysis of a corpus. FCA makes it possible to build a
model also called the Hasse diagram which can be queried to find relevant formal concepts. Uncertainties can
be present in all steps of the processing from the corpus processing to the visualization of the results. Indeed,
if the words of the corpus are misspelled or additional quantitative variables are associated with the corpus,
then uncertainties can appear. Uncertainties may also arise in queries when human knowledge is imprecise.
Possibility theory allows us to represent and process these imperfections. The combination of textual analysis
solutions and FCA allow us to present more relevant results that take into consideration uncertainties.
1 INTRODUCTION
A corpus is a collection of documents. These doc-
uments come from books, articles, transcripts of in-
terviews, open questions in a questionnaire, websites,
etc. The analysis of the lexicon of a corpus can be
a time-consuming task for an expert. Indeed, when
the corpus grows, it becomes more and more difficult
to analyze the lexicon and accurately represent the
relationships between words. The methods of Text
Mining (Hotho et al., 2005) or lexicometry (Salem,
1986) make it possible to summarize a corpus more
efficiently. Lexicometry (Salem, 1986) deals with the
quantitative analysis of the lexicon using statistical
methods. Many software tools have been proposed to
summarize text corpora. Alceste and Iramuteq soft-
ware, for example, are particularly interesting. In
these software, a dictionary is previously built after
a preprocessing of the corpus. The preprocessing can
be a pipeline of operations leading to a corpus clean-
ing, followed by lemmatization to reduce the size of
the dictionary. Then, a segmentation of the corpus is
performed. These tools make it possible to calculate
statistical summaries, to perform classification, facto-
rial correspondence analysis, similarity analysis, etc.
Finally, the latter offers graphical representations that
highlight previous results.
The Iramuteq software performs a text segmenta-
tion of the corpus into segments. Then we can apply
a factorial correspondence analysis and hierarchical
clustering proposed by Reinert (Reinert, 1983). We
obtain on the one hand a classification of terms and
on the other hand a representation of terms on the first
two principal components. Tables are presented in the
tool and allow us to explore intermediate data and all
results. For example, the result of the classification
makes it possible to consult for each class the words
associated with it as well as the χ
2
distance and the
p-value. A concordancer allows you to consult the
segments of text that contain the words selected by
the user. The similarity analysis (SA) (Degenne and
Verg
`
es, 1973) proposed in this tool greatly contributes
to the analysis of the link between terms by gradually
representing the links in a graph.
The representation of a document-term matrix
(DTM) is very close to the formal context of formal
concept analysis (FCA). Indeed, it is possible to bi-
narize the DTM or to define linguistic variables or
classes concerning the frequencies of words. If we
use possibility distributions of possibility theory to
represent linguistic variables, we can compute de-
grees of necessity for each modality. We can also
represent the uncertainty of words by a degree of ne-
cessity. Indeed, during lemmatization, a misspelled
word can be associated with several words because
the spelling of the words is very close. We can choose
the word with the highest possibility. This, however,
generates an uncertainty that must be propagated in
the analysis.
The variables of different kinds – binary, qualita-
218
Petiot, G.
Uncertain Formal Concept Analysis for the Study of a Text Corpus.
DOI: 10.5220/0012316400003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 3, pages 218-225
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

tive (nominal or ordinal) or quantitative – can be as-
sociated with the texts of the corpus. The process-
ing of variables is mandatory to represent them with
the terms (the words of the corpus) in an uncertain
context that gathers all information. Applications of
FCA have already been proposed to analyze a corpus
(Cimiano et al., 2005; Tovar et al., 2015), however,
uncertainties and additional variables are rarely dis-
cussed in these studies.
In this research, we will focus our interest on pro-
cessing uncertainties. We will extend the work al-
ready done in our previous research (Petiot, 2019).
We will propose a new approach to analyzing a cor-
pus by using uncertain formal concept analysis. We
will combine traditional textual analysis approaches
such as factorial correspondence analysis and similar-
ity analysis with FCA.
To do this, we will in the first part recall the ba-
sis of the possibility theory and FCA. Then we will
describe the steps of the corpus processing. We will
distinguish the preliminary analysis of the context and
the analysis of the formal concepts. We will present
an example of a graphical query language that al-
lows us to select pertinent formal concepts and to im-
prove the visualization of information. Finally, we
will show an example of the Hasse diagram leading
to the computation of rules that highlight the depen-
dence of terms.
2 POSSIBILITY THEORY
Possibility theory (Zadeh, 1978) is an extension of the
fuzzy sets theory proposed by L. A. Zadeh in 1965. It
makes it possible to represent imprecise knowledge
by distributions of possibility (noted π) and to com-
pute degrees of certainty. It also offers a representa-
tion of ignorance. There are two important measures
defined on the powerset of a universe Ω denoted P(Ω)
in [0,1]:
• The measure of possibility Π
∀A ∈ P(Ω),Π(A) = sup
x∈A
π(x). (1)
• The measure of necessity N
∀A ∈ P(Ω),N(A) = 1 − Π(
¯
A). (2)
The conditioning in possibility theory was dis-
cussed by researchers D. Dubois and H. Prade in
(Dubois and Prade, 1988). They proposed the follow-
ing solution for the conditioning:
Π(A|B) =
(
Π(A ∩ B) if Π(A ∩ B) < Π(B),
1 if Π(A ∩ B) = Π(B).
(3)
3 FORMAL CONCEPT ANALYSIS
Formal concept analysis is a method of data analy-
sis proposed by R. Wille (Wille, 1982) which con-
sists in describing the formal concepts present in a
given context. Formal concepts encompass recurring
features of the context. This method is an applica-
tion of lattice theory that allows formal concepts to be
represented by a Hasse diagram when a partial order
relation is defined. Two solutions can be proposed
to explore the formal concepts: a navigation in the
Hasse diagram and the consideration of a formal con-
cept and its neighbours. The second solution is to
perform queries to search relevant formal concepts.
Many applications exist concerning FCA (Poelmans
et al., 2013; Poelmans et al., 2014; Sn
´
a
ˇ
sel et al.,
2008; B
ˇ
elohl
´
avek et al., 2007; Fernandez-Manjon and
Fernandez-Valmayor, 1998) in text mining, linguis-
tics, social media, education, bioinformatics, psychol-
ogy, ontology engineering, etc.
A formal concept has two sets: the intension and
the extension. The intension represents the set of
common properties that the objects of the concept
have, and the extension represents the set of objects to
which they apply. Mathematically, a formal context is
a triplet (O,P,ℜ) where O =
{
o
1
,...,o
n
}
is the set of
objects, P =
{
p
1
,..., p
m
}
the set of properties, and ℜ
a binary relation such that ℜ ⊆ O × P. If (o, p) ∈ ℜ
then the object o has property p. A context is often
represented by a table where the rows are objects and
the columns are properties. The cells in the table rep-
resent the relation ℜ between the object and the prop-
erty: 0 if (o, p) /∈ ℜ or 1 if (o, p) ∈ ℜ. One can define
a function ϑ(o, p) that returns the value of the table
for an object o and a property p. A formal concept
of (O, P, ℜ) is a couple (O
i
,P
i
) such that O
i
∈ O and
P
i
∈ P such that P
i
is the set of properties shared by
the set of objects of O
i
. It can be noted O
↑
i
= P
i
or
P
↓
i
= O
i
. For example ({o
1
,o
4
,o
5
},{p
1
, p
2
}) is a for-
mal concept of the following binary context:
Table 1: Example of formal context.
Objects
Properties
p
1
p
2
p
3
o
1
1 1 0
o
2
1 0 1
o
3
0 1 1
o
4
1 1 0
o
5
1 1 1
Definition 3.1. The set of all formal concepts of
(O,P,ℜ) is denoted χ(ℜ).
We have the following property for
each formal concept (O
i
,P
i
) of χ(ℜ) :
Uncertain Formal Concept Analysis for the Study of a Text Corpus
219

n
(O
i
,P
i
)|O
↑
i
= P
i
,P
↓
i
= O
i
o
. It is possible to
compare formal concepts with each other by defining
a partial order:
Definition 3.2. Let be two formal concepts
(O
1
,P
1
),(O
2
,P
2
) of χ(ℜ). We define a partial order
≤ such that (O
1
,P
1
) ≤ (O
2
,P
2
) if and only if O
1
⊆
O
2
or P
2
⊆ P
1
.
The set χ(ℜ) with the partial order ≤ is used to
build a concept lattice that can be visualized by us-
ing a Hasse diagram. If the properties of the con-
text are quantitative or multivalued, a transformation
of the context must be performed to obtain a binary
formal context. If it is not certain that an object has a
property, it is necessary to adapt FCA. The study by
(B
ˇ
elohl
´
avek, 2004) focused on the use of fuzzy sets to
represent imprecise properties. The authors (Dubois
et al., 2007; Dubois and Prades, 2015; Ait-Yakoub
et al., 2016) propose to use possibility theory to take
into account imprecision and uncertainties. The same
authors also propose a solution to manage uncertain-
ties and to provide a frame to represent ignorance
which can be partial or total. A pair of necessity mea-
sures (α(o, p), β(o, p)) with α(o, p) = N((o, p) ∈ ℜ)
and β(o, p) = N((o, p) /∈ ℜ) is used to represent un-
certainties. N((o, p) ∈ ℜ) is the necessity that the ob-
ject o has the property p and N((o, p) /∈ ℜ) is the ne-
cessity that the object o does not have the property p.
The pair of necessity measures is required because of
the equation 2. Each necessity measure is computed
by using the possibility of the contrary event. The
necessity measures α and β must satisfy the property
min(α(o, p),β(o, p)) = 0 of possibility theory. The
(1,0) and (0,1) pairs denote a property or its lack. If
1 > max(α(o, p),β(o, p)) > 0, the ignorance is par-
tial. If one of the pair is (0,0), then ignorance is total.
Definition 3.3. An uncertain formal context can be
defined as follows (Dubois and Prades, 2015):
ℜ
′
=
{
(α(o, p),β(o, p))|o ∈ O, p ∈ P
}
(4)
To compute formal concepts we can replace the
(α(o, p),0) by 1 and (0,β(o, p)) by 0 to obtain a bi-
nary formal context. Then we can compute formal
concepts by using an existing algorithm.
Definition 3.4. The necessity measure (certainty) of a
formal concept C = (O
i
,P
i
) can be computed by using
the following formula:
N(C) = min
o∈O
i
,p∈P
i
N((o, p) ∈ ℜ) (5)
To illustrate the certainty computation we propose
the following example:
Table 2: Example of an uncertain formal context.
Objects
Properties
p
1
p
2
p
3
o
1
(0,1) (0,1) (0.4,0)
o
2
(0,0.3) (1,0) (1,0)
o
3
(0,0.7) (1,0) (0,0.6)
o
4
(1,0) (0.5,0) (0.8,0)
o
5
(1,0) (0,0.5) (1,0)
By transforming this context we obtain a binary
context:
Table 3: Uncertain formal context to binary formal context.
Objects
Properties
p
1
p
2
p
3
o
1
0 0 1
o
2
0 1 1
o
3
0 1 0
o
4
1 1 1
o
5
1 0 1
In this example, we can see that
({o
4
,o
5
},{p
1
, p
3
}), ({o
4
},{p
1
, p
2
, p
3
}),
({o
2
,o
4
},{p
2
, p
3
}),({o
2
,o
3
,o
4
},{p
2
}) and
({o
1
,o
2
,o
4
,o
5
},{p
3
}) are the formal concepts
of this formal context. We computed the certainty of
these formal concepts:
Table 4: Computation of certainty.
Formal Concepts Certainties
({o
4
,o
5
},{p
1
, p
3
}) 0.8
({o
4
},{p
1
, p
2
, p
3
}) 0.5
({o
2
,o
4
},{p
2
, p
3
}) 0.5
({o
2
,o
3
,o
4
},{p
2
}) 0.5
({o
1
,o
2
,o
4
,o
5
},{p
3
}) 0.4
We propose another example to illustrate the pro-
cessing of quantitative properties. We consider the
following context:
Table 5: Multivalued context example.
Objects
Properties
Age Gender
o
1
5 Man
o
2
35 Woman
o
3
50 Man
o
4
19 Man
o
5
80 Woman
We propose to use possibility theory and a linguis-
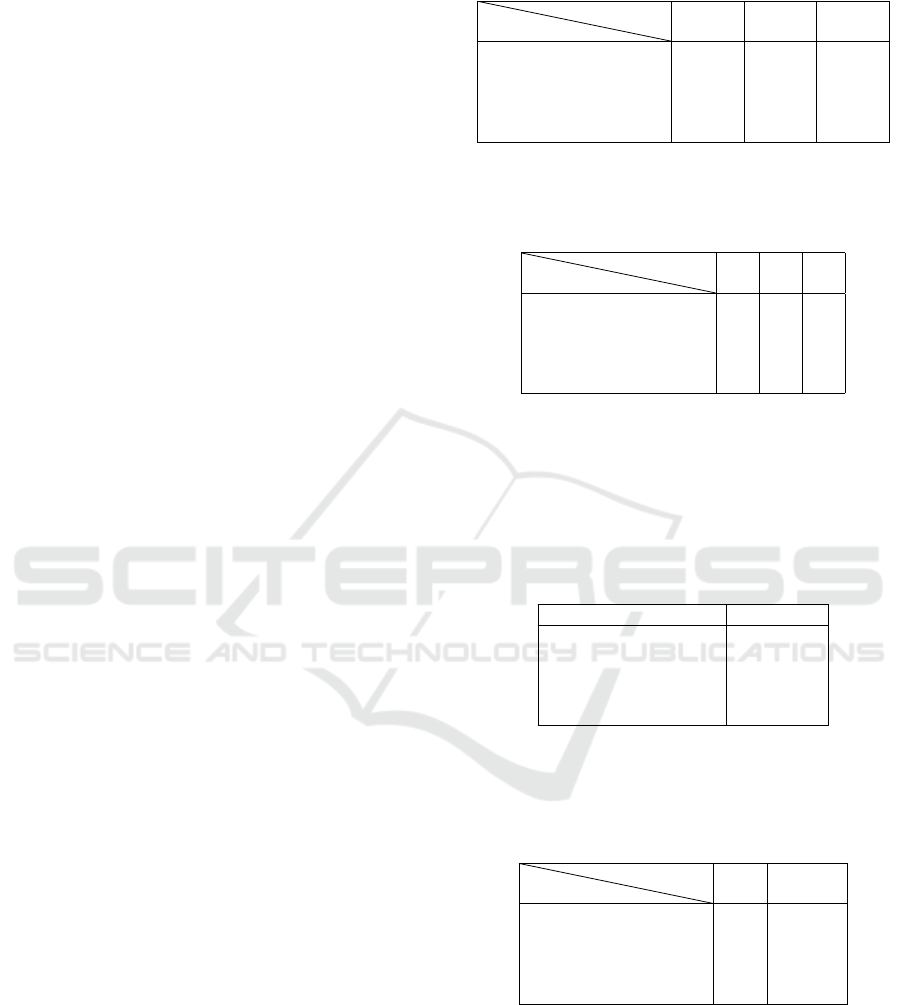
tic variable to transform the multivalued property con-
cerning age. We define for example three distributions
of possibility for age (young, adult and old):
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
220

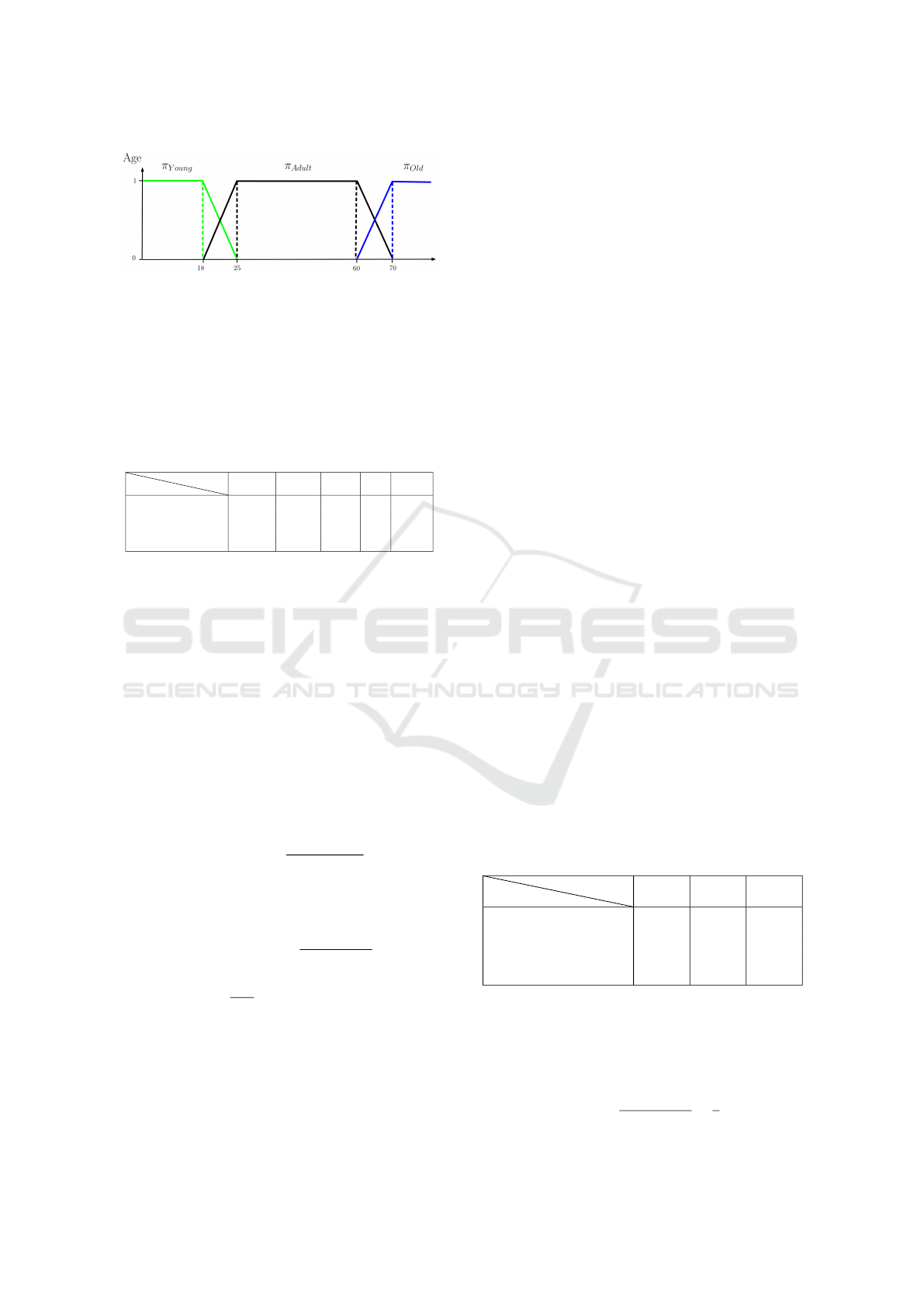
Figure 1: Linguistic variable.
We compute the membership degree of the three
possibility distributions, then we perform a renormal-
ization before computing the measure of necessity.
When the property is qualitative (nominal or ordinal),
we create as many properties as modalities. If we ap-
ply this to our example, we obtain:
Table 6: Transforming multivalued context into uncertain
context.
Objects
Properties
Age
Young
Age
Adult
Age
Old
Man Woman
o
1
(1,0) (0,1) (0,1) (1,0) (0,1)
o
2
(0,1) (1,0) (0,1) (0,1) (1,0)
o
3
(0,1) (1,0) (0,1) (1,0) (0,1)
o
4
(0.83,0) (0,0.83) (0,1) (1,0) (0,1)
o
5
(0,1) (0,1) (1,0) (0,1) (1,0)
Many algorithms can be used to compute all for-
mal concepts (S. O. Kuznetsov, 2003). We chose for
our experiment to use a parallel recursive algorithm
(Kraj
ˇ
ca et al., 2008). This algorithm takes in input a
binary context and computes all the formal concepts.
From the concept lattice, we can extract associa-
tion rules that represent the dependencies between the
properties.
Definition 3.5. An association rule is a pair of item-
set written P
1
→ P
2
where P
1
and P
2
are two sets of
properties such as P
1
∩ P
2
= ⊘. P
1
is the condition of
the rule and P
2
is the conclusion.
Definition 3.6. We define the support of the rule noted
σ(P
1
→ P
2
) by using the following formula:
σ(P
1
→ P
2
) =
∥(P
1
∪ P
2
)
↓
∥
∥O∥
(6)
Definition 3.7. The confidence of the rule con f (P
1
→
P
2
) can be computed as follows:
con f (P
1
→ P
2
) =
σ(P
1
→ P
2
)
σ(P
1
)
(7)
With ‘σ(P
1
) =
∥P
↓
1
∥
∥O∥
We consider in this research only the properties
that satisfy N((o, p) ∈ ℜ) > 0 for the computation of
the support and confidence. Usually, there are two
thresholds θ
σ
and θ
con f
that allow us to select relevant
association rules. If con f (A → B) = 1 then the rule is
exact, else the rule is approximate. If θ
σ
= 1 then the
rule has at least one object with this profile. Finally,
another measure can be proposed that corresponds to
the necessity of the rule.
Definition 3.8. The necessity degree of the rule noted
N(P
1
→ P
2
) can be computed as follows:
N(P
1
→ P
2
) = N(¬P
1
∪ P
2
) = 1 − Π(P
1
∩ ¬P
2
) (8)
P
1
and P
2
are conjunctions of properties. This
equation involves a discussion concerning Π(P
1
∩
¬P
2
) and Π(P
1
∩P
2
). The rule requires that the propo-
sition P
1
∩ P
2
is more possible than the proposition
P
1
∩ ¬P
2
. If Π(P
1
∩ P
2
) > Π(P
1
∩ ¬P
2
) then the rule
P
1
→ P
2
is true. In fact we have 1 − Π(P
1
∩ P
2
) <
1 − Π(P
1
∩ ¬P
2
) so N(¬P
1
∪ ¬P
2
) < N(¬P
1
∪ P
2
) and
finally N(P
1
→ ¬P
2
) < N(P
1
→ P
2
). This constraint
means that the certainty of having P
2
if P
1
is true
is higher than the certainty of having not P
2
if P
1
is true leading to the rule P
1
→ P
2
. For example if
Π(P
1
∩ P
2
) = 1 and Π(P
1
∩ ¬P
2
) = α then N(P
1
→
P
2
) = 1 − α and N(P
1
→ ¬P
2
) = 0.
If we consider the simple rule p → q where p and
q are two different properties of a formal context, we
compute the certainty of the rule as follows:
N(p → q) = min
o∈O
[1 − Π((o, p) ∈ ℜ ∩ (o, q) /∈ ℜ)] (9)
By using the property Π(A ∩ B) ≤
min(Π(A),Π(B)) and if we consider that the
minimum is the maximum value of the possibility
Π(A ∩ B) then we propose:
N(p → q) = min
o∈O
[1 − min(Π((o, p) ∈ ℜ),Π((o,q) /∈ ℜ))] (10)
This formula can be easily generalized for sev-
eral properties in the condition and conclusion of the
rule. For example, we consider the following uncer-
tain context and we want to compute the certainty of
the rule N(p
2
→ p
3
).
Table 7: Example of uncertain formal context.
Objects
Properties
p
1
p
2
p
3
o
1
(0,1) (0,1) (0.4,0)
o
2
(0,0.3) (1,0) (1,0)
o
3
(0,0.7) (1,0) (0.6,0)
o
4
(1,0) (0.5,0) (0.8,0)
o
5
(1,0) (0,0.5) (1,0)
By applying the previous formula we obtain:
N(p
2
→ p
3
) = min(1,1, 0.6,0.8,1) = 0.6 (11)
We can also compute the support of this rule:
σ(p
2
→ p
3
) =
∥(p
2
∪ p
3
)
↓
∥
∥O∥
=
3
5
= 0.6 (12)
Uncertain Formal Concept Analysis for the Study of a Text Corpus
221

We can see that the support of the rule p
2
→ p
3
is
the frequency of the rule in the context. It is also the
probability that an object has the properties p
2
and p
3
.
Then we compute the confidence of the rule:
con f (p
2
→ p
3
) =
σ(P
2
→ P
3
)
σ(P
2
)
=
0.6
0.6
= 1.0 (13)
We can deduce from the above formula that the
confidence of the rule p
2
→ p
3
is the percentage of
objects that have the property p
3
when they have the
property p
2
.
4 EXPERIMENTATION WITH A
TEXT CORPUS IN FRENCH
4.1 Preprocessing and Context
Generation
The goal of preprocessing is to gather variables that
represent exogenous information and the texts of the
corpus into an uncertain formal context. Variables
can be quantitative and qualitative. We can repre-
sent knowledge about a quantitative variable by using
a linguistic variable. Multivalued variables are also
transformed. Segmentation can be performed to di-
vide the initial texts into segments. Each segment in-
herits the values of the variables associated with the
initial text. A processing is applied to clean the new
corpus of texts made up of segments. This clean-
ing consists in changing the case and eliminating un-
wanted characters, punctuation, numbers, and unnec-
essary words. Below, we present a summary of the
processing:
Figure 2: Corpus processing.
Then we apply a lemmatization that significantly
reduces the size of the dictionary. To do this, we used
an existing French lexicon that associates each word
with its lemma. The synonyms were not considered in
this study. When a word is not found in the lexicon,
we look for the closest word. For each word of the
lexicon we associate a degree of possibility computed
by using the Jaro-Winkler (Winkler, 1999) distance
between the current word and the word in the lexicon.
The word of the lexicon with the highest degree of
possibility is chosen. If the possibility of this word is
less than a threshold, the original word is kept, lead-
ing to a pair of necessity measures (1,0) in the context
if the word is in a segment. Otherwise, the word is
replaced by the lemma of the lexicon. Then we renor-
malise the degrees of possibility before computing a
measure of necessity noted α. The pair of necessity
degrees is (α, 0) if the lemma is present in a segment
of text. The uncertain context is then generated from
the segments of texts and variables transformed into
properties.
4.2 Context Information
The uncertain formal context can be first analysed by
using usual data analysis tools before applying for-
mal concept analysis. To provide some examples of
results, we propose to analyse the computer science
curriculum in French high schools in 2019. We do
not use additional variables in this study. The cor-
pus is split into segments and we consider only the
50 most frequent terms of the corpus to generate the
uncertain context. The properties are the terms of the
corpus and the object the segment identifier. First,
it is possible to compute a co-occurrence matrix of
properties from the uncertain context. Then, we per-
form a similarity analysis and generate a similarity
graph. By computing the maximum spanning tree we
obtain a much more readable graph. We compute the
uncertainty I(m
1
,m
2
) (noted I) of the co-occurrence
between two properties m
1
and m
2
of the uncertain
context (O,P, ℜ) by using the following formula:
I = min
o∈O
[min(N((o, m
1
) ∈ ℜ),N((o,m
2
) ∈ ℜ))] (14)
A descending hierarchical classification (DHC) of
the segments makes it possible to highlight the terms
that are often found together in the segments. We pro-
pose a visualization of the classification on the first
two principal components of the factorial correspon-
dence analysis. For example we obtain:
Figure 3: DHC on the first two principal components with
7 classes.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
222

In this graph, proximity between the terms reveals
their links in the corpus when the quality of projection
is good. It is also possible to look for an interpretation
of the factorial axes. We can visualize the dendrogram
of the classification as follows:
Figure 4: Dendrogram with 7 classes.
The dendrogram represents all words in classes
and can be very useful for data analysis.
4.3 Formal Concepts Analysis
We consider now all terms to generate the uncertain
context. Formal concepts can be used to represent
terms that are present together in text segments. We
have developed several visualization tools. First of
all, we propose a visualization of the formal concepts
in a table that can be sorted according to the num-
ber of objects, number of properties, certainty, or the
relevance score computed from a query. Next, we
propose a representation with a Hasse diagram of the
concept lattice. We also propose for a formal con-
cept the similarity graph of the properties of the for-
mal concept to represent the links between the prop-
erties. Finally, we propose to visualize the properties
of a formal concept in the first two principal compo-
nents. When the number of formal concepts becomes
very important, visualization tools do not necessarily
allow us to see the information we are looking for.
We therefore propose two solutions. The first is to
consider only the words with a frequency above the
threshold. This makes it possible to limit the size
of the dictionary without losing the most important
words. The second solution we propose is the use
of queries in a relatively simple graphical language.
Indeed, the graphical language makes it possible to
take into account criteria of the presence or absence
of a property or an object. It is possible to perform
a multicriteria combination by using AND, OR and
NOT operators. We also propose functions that cal-
culate, for example, cardinality (the number of prop-
erties or objects in a formal concept), a score defined
in (Petiot, 2019). Criteria can be applied to the results
of these functions. Our solver can manage binary cri-
teria or uncertain criteria. The solver generates a pos-
sibilistic network before evaluating the query. Com-
bination operators are uncertain logical gates (Petiot,
2019) that can represent traditional logical combina-
tions and uncertain logical combinations. We compile
the query into a circuit to improve the computation
time and we compute a relevance score for each for-
mal concept. This solution allows us to manage the
uncertainties of the query which is illustrated by the
following example:
Figure 5: Graphical query to search formal concepts.
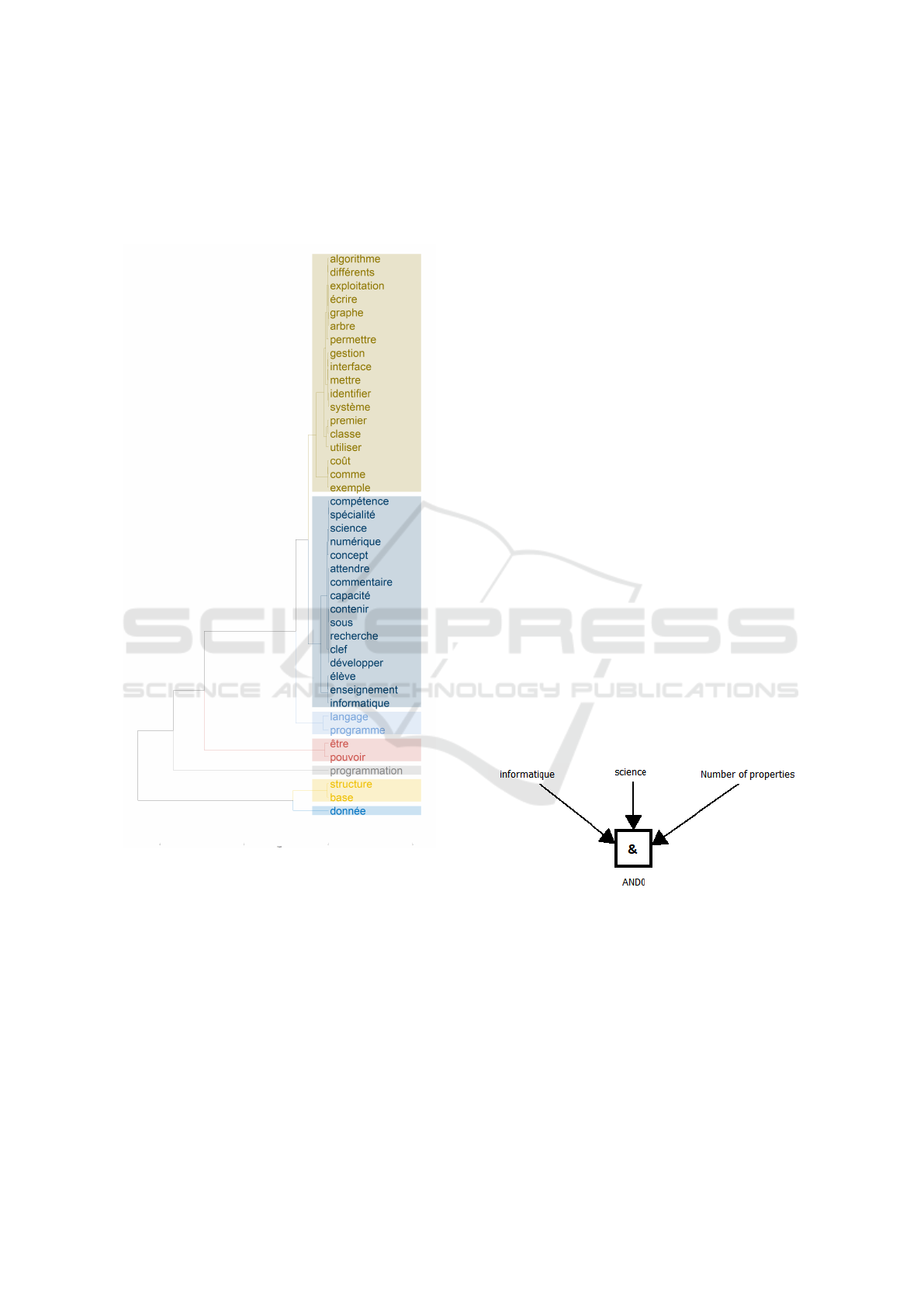
In this query, we want to retrieve the formal con-
cepts that contain the French words ”informatique”
and ”science”. We also want to keep only formal
concepts with a limited number of properties because
the visualization would be degraded. To translate this
constraint we used two possibility distributions that
represent the states of the variable ”Number of prop-
erties”:
Uncertain Formal Concept Analysis for the Study of a Text Corpus
223

Figure 6: Possibility distributions of the variable ”Number
of properties”.
The criterion true allows us to select only the for-
mal concepts that satisfy the constraint. Moreover, we
can see that formal concepts with less than 60 prop-
erties are accepted and others rejected. In the same
way, we can define states for variables associated with
the terms, for example here the terms ”informatique”
and ”science”. The result of the query evaluation is
as follows:
Figure 7: Query result.
We can deduce the similarity graph for each for-
mal concept of the query result. For the formal con-
cept denoted C7 we obtain the similarity graph below:
Figure 8: Similarity graph with uncertainties.
In the graph, the edges between the words are rep-
resented by a gradient of colours proportional to the
co-occurrence index. A maximum tree can also be
computed.
Figure 9: Maximum tree with uncertainties.
It is possible to generate a Hasse diagram with the
certainty of the formal concepts.
Figure 10: Hasse diagram with uncertainties.
Finally, we can deduce the rules from the Hasse
diagram. The rules are presented with their quality
measures: confidence, support and certainty.
Figure 11: Example of the first five rules.
5 CONCLUSION
In this research, our goal was to combine text analysis
with formal concept analysis to propose a new mixed
data analysis solution. We associated each text of the
corpus with a set of variables that can be qualitative
or quantitative. Next, we performed a lemmatization
of the corpus to reduce the vocabulary of the dictio-
nary. Quantitative variables were replaced by linguis-
tic variables. This made it possible to calculate cer-
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
224

tainty for each modality. Qualitative variables were
transformed into binary variables. Finally, we ob-
tained a representation of the corpus and variables in
an uncertain context. We computed uncertain formal
concepts and showed that it was possible to visualize
the links between words in a formal concept by us-
ing similarity analysis. By projecting formal concepts
on the first two principal components of factorial cor-
respondence analysis we visualized the relationships
between terms. Finally, the graphical queries made it
possible to highlight the essential terms. Moreover,
they improve computation time and they reduce ex-
ploration time for the user. Our perspective is to ex-
periment and improve this approach. We will improve
and compare the solutions for the preprocessing of the
corpus. We plan to collaborate with researchers in the
humanities to test our solution with practical applica-
tions.
REFERENCES
Ait-Yakoub, Z., Djouadi, Y., Dubois, D., and Prade, H.
(2016). From a possibility theory view of formal
concept analysis to the possibilistic handling of in-
complete and uncertain contexts. In 5th International
Workshop ”What can FCA do for Artificial Intelli-
gence?” (FCA4AI 2016) co-located with ECAI 2016,
pages 79–88.
B
ˇ
elohl
´
avek, R. (2004). Concept lattices and order in fuzzy
logic. In Annals of Pure and Applied Logic, volume
128, pages 277–298.
B
ˇ
elohl
´
avek, R., Sklenar, V., Zacpal, J., and Sigmund, E.
(2007). Evaluation of questionnaires by means of for-
mal concept analysis. In Int. Conference on Concept
Lattices and Their Applications, pages 100–111. J. Di-
atta, P. Eklund, M. Liquiere (Eds.): CLA 2007.
Cimiano, P., Hotho, A., and Staab, S. (2005). Learning con-
cept hierarchies from text corpora using formal con-
cept analysis. In Journal of Artificial Intelligence Re-
search, volume 24, pages 305–339.
Degenne, A. and Verg
`
es, P. (1973). Introduction
`
a l’analyse
de similitude. In Revue franc¸aise de sociologie
[Sciences Po University Press, Association Revue
Franc¸aise de Sociologie], volume 14, pages 471–512.
Dubois, D., de Saint-Cyr, F. D., and Prade, H. (2007). A
possibility-theoretic view of formal concept analysis.
In Fundamenta Informaticae, IOS Press, volume 75,
pages 195–213.
Dubois, D. and Prade, H. (1988). Possibility theory - an
approach to computerized processing of uncertainty.
Dubois, D. and Prades, H. (2015). Formal concept analysis
from the standpoint of possibility theory. In J. Baix-
eries, C. Sacarea, M. Ojeda-Aciego (eds) Formal Con-
cept Analysis. ICFCA 2015. Lecture Notes in Com-
puter Science, Springer, volume 9113, pages 21–38.
Fernandez-Manjon, B. and Fernandez-Valmayor, A. (1998).
Building educational tools based on formal concept
analysis. In Journal of Education and Information
Technologies, volume 3, pages 187–201.
Hotho, A., N
¨
urnberger, A., and Paass, G. (2005). A brief
survey of text mining. In LDV Forum - GLDV Journal
for Computational Linguistics and Language Technol-
ogy, volume 20, pages 19–62.
Kraj
ˇ
ca, P., Outrata, J., and Vychodil, V. (2008). Parallel
recursive algorithm for FCA. In In: Proc. CLA 2008,
CEUR WS, pages 71–82.
Petiot, G. (2019). Information retrieval in a concept lat-
tice by using uncertain logical gates. In Proceedings
of the 11th International Joint Conference on Knowl-
edge Discovery, Knowledge Engineering and Knowl-
edge Management, IC3K 2019, volume 1, pages 289–
296.
Poelmans, J., Ignatov, D., Kuznetsov, S. O., and Dedene, G.
(2013). Formal concept analysis in knowledge pro-
cessing: A survey on applications. In Expert Systems
with Applications, volume 40, pages 6538–6560.
Poelmans, J., Ignatov, D., Kuznetsov, S. O., and Dedene, G.
(2014). Fuzzy and rough formal concept analysis: A
survey. In International Journal of General Systems,
volume 43.
Reinert, A. (1983). Une m
´
ethode de classification descen-
dante hi
´
erarchique : application
`
a l’analyse lexicale
par contexte. In Cahiers de l’analyse des donn
´
ees 8.2,
pages 187–198.
S. O. Kuznetsov, S. A. O. (2003). Comparing performance
of algorithms for generating concept lattices. In J. Ex-
perimental & Theoretical Artificial Intelligence, vol-
ume 14, pages 189–216.
Salem, A. (1986). Segments r
´
ep
´
et
´
es et analyse statistique
des donn
´
ees textuelles, etude quantitative
`
a propos du
p
`
ere duchesne de h
´
ebert. In Histoire & Mesure, Ed.
du CNRS, volume 1.
Sn
´
a
ˇ
sel, V., Hor
´
ak, Z., and Abraham, A. (2008). Under-
standing social networks using formal concept anal-
ysis. In 2008 IEEE/WIC/ACM International Confer-
ence on Web Intelligence and Intelligent Agent Tech-
nology, pages 390–393.
Tovar, M., Pinto, D., Montes, A., Serna, G., and Vilari
˜
no,
D. (2015). Patterns used to identify relations in corpus
using formal concept analysis. In Arrasco-Ochoa, J.,
Martinez-Trinidad, J., Sossa-Azuela, J., Olvera L
`
opez,
J., Famili, F. (eds) Pattern Recognition. MCPR 2015.
Lecture Notes in Computer Science, Springer, volume
9116, pages 236–245.
Wille, R. (1982). Restructuring lattice theory: an approach
based on hierarchies of concepts. In I. Rival, (ed.)
Ordered Sets. Reidel, Dordrecht-Boston, pages 445–
470.
Winkler, W. E. (1999). The state of record linkage and cur-
rent research problems. In Statistical Research Divi-
sion, U.S. Bureau of the Census.
Zadeh, L. A. (1978). Fuzzy sets as a basis for a theory
of possibility. In Fuzzy Sets and Systems, volume 1,
pages 3–28.
Uncertain Formal Concept Analysis for the Study of a Text Corpus
225