Multi-Agent Monocular SLAM

Pieter Beerten

, Charles Hamesse

1,2

and Rob Haelterman

Department of Mathematics, Royal Military Academy, Belgium

imec - IPI - URC, Ghent University, Belgium

Keywords:

SLAM, Bundle Adjustment, Multi-Agent, Monocular Vision, Optimization.

Abstract:

This article describes the development of an optimization method for multi-agent monocular SLAM systems.

These systems allow autonomous robots to create a map of an unknown environment and to simultaneously

localize themselves within it. The proposed multi-agent system combines measurements made by independent

agents to increase the accuracy of the estimated poses of the agents and the created map. Our method is based

on the single-agent monocular ORB-SLAM2 framework, and we develop a complete multi-agent optimization

post-processing algorithm, effectively reﬁning all camera trajectories and map points. Our experiments on the

EuRoC machine hall dataset show that we can successfully combine the information of multiple SLAM agents

to increase the accuracy of the estimated trajectories.

1 INTRODUCTION

Autonomous robots are more popular today than ever

in our modern society. To name a few, the ﬁelds of

automotive, civil engineering, security, and leisure all

reveal a dynamic landscape of innovation where au-

tonomous robots play an important role. The progress

in 3D perception hardware allows robots to map, un-

derstand, and navigate within various types of envi-

ronments. They have the ability to perform tasks that

were typically tedious, dangerous, or complex for hu-

mans, such as surveying construction sites, monitor-

ing the health of agriculture ﬁelds, or moving boxes

and packages. In all of these applications, the robot

needs a way to know, at any given time, where it is

with respect to its surroundings, that is, to localize it-

self. For these robots to be able to do so and safely

navigate through unknown territories, different algo-

rithms have been developed over the course of the last

decades. One very popular method for this is Simulta-

neous Localization And Mapping, or SLAM in short.

This technique allows a robotic agent to determine its

location within an unknown environment based on the

input it captures via one or multiple onboard sensors.

Simultaneously, the locations of distinct points in the

environment are estimated, thus creating a map of the

scene.

The goal of this work is to develop an optimiza-

tion pipeline that reﬁnes the accuracy of the pose es-

timates and the created map, based on the application

of bundle adjustment to a combination of measure-

ments of multiple agents. To this end, ORB-SLAM2

(Mur-Artal et al., 2017) is used as a baseline to obtain

the initial SLAM measurements. The popular EuRoC

dataset (Burri et al., 2016) is used to test and vali-

date the proposed algorithm, rather than relying on

our own measurements.

The article is structured as follows: ﬁrst, in Sec-

tion 2, a theoretical introduction to the concept of

SLAM and the considered optimization method will

be provided. Next, in Section 3 the single-agent bun-

dle adjustment pipeline will be discussed. This will

serve as a building block to ﬁnally arrive at the multi-

agent bundle adjustment pipeline. In Section 4, the

results for both bundle adjustment algorithms will be

discussed. This article concludes with a general con-

clusion of the results and some suggestions for further

research.

2 RELATED WORK

We start with a broad overview of SLAM, then dive

deeper into bundle adjustment, the optimization tech-

nique on which our multi-agent optimization pipeline

relies.

Beerten, P., Hamesse, C. and Haelterman, R.

Multi-Agent Monocular SLAM.

DOI: 10.5220/0012320000003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 1, pages 213-220

ISBN: 978-989-758-680-4; ISSN: 2184-433X

213

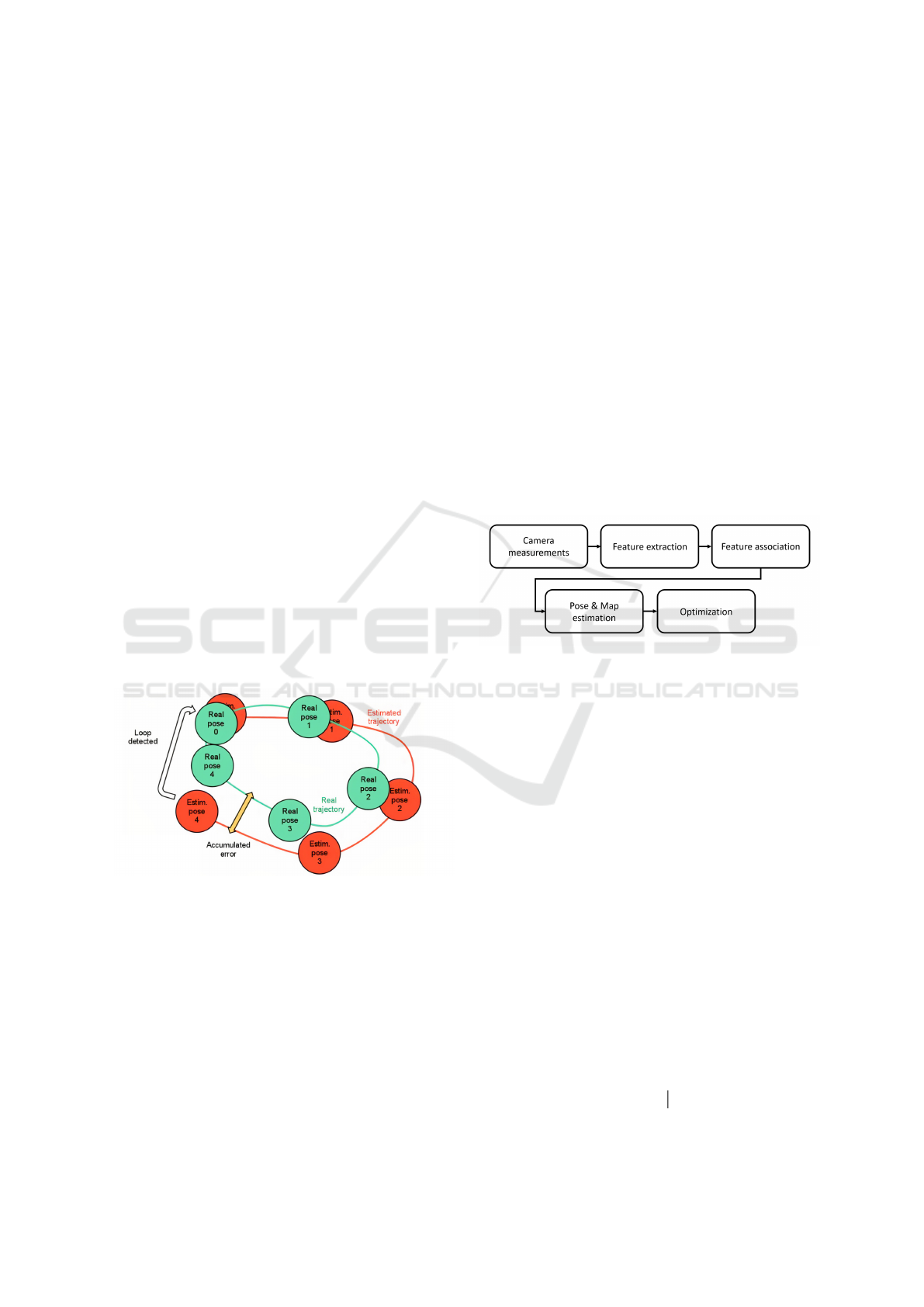
2.1 SLAM

SLAM algorithms are used to estimate the pose

(position + orientation) of an agent in an (unknown)

environment, while simultaneously building a map of

this environment. This allows autonomous agents to

navigate safely through the environment and to create

a map that can be used for various applications. To

this end, SLAM algorithms use data provided by

onboard sensors, such as visual sensors, GPS, lidar,

or radar. In this work, a single monochrome camera

(in the visual part of the spectrum) is used to provide

the necessary data.

One of the main issues at hand for SLAM algo-

rithms is the dual nature of the problem they are ad-

dressing. Indeed, to create a map based on data cap-

tured by an agent, the complete pose of the agent

should be known. However, to know the exact pose of

the agent, an accurate map is needed. Consequently,

errors in the pose will inevitably lead to errors in the

map, and vice versa. This can easily lead to accumu-

lating or drifting errors. An illustration of this accu-

mulating effect is given in Figure 1. To address this

issue, map reﬁnement techniques, such as pose graph

optimization, can be used to signiﬁcantly reduce the

drifting error. This is indicated by the white arrow.

However, in this work, bundle adjustment is chosen

as the optimization technique to reﬁne the estimates

and reduce the error.

Figure 1: Illustration of the accumulating error. (Wong,

2014).

As said, our work relies on monocular visual

SLAM algorithms. In general, these algorithms can

be broken down into ﬁve major parts, as represented

schematically in Figure 2. The work carried out for

this paper can be situated in the ”Optimization” part.

The visual variant of SLAM has been a subject of ex-

tensive research and development over the years. The

inception of monocular SLAM can be traced back to

2007 when Davison introduced MonoSLAM (Davi-

son et al., 2007). This algorithm utilized an extended

Kalman ﬁlter (EKF) to achieve real-time localization

by leveraging large image patch features and sparse

prior scene knowledge. Although Kalman ﬁlter-based

odometry systems are relatively simple and elegant,

optimization-based methods have been introduced to

increase accuracy. Odometry systems based on bun-

dle adjustment optimization have been adopted with

great success, albeit at the cost of increased computa-

tional complexity (an increase that can be controlled

with a smart use of keyframe-based and sliding win-

dow optimization). VINS-Mono (Qin et al., 2018) is

a robust visual-inertial odometry estimation system

that maintains recent states of map points and cam-

eras in a sliding window, optimized with local bun-

dle adjustment. Visual features are tracked using KLT

and optical ﬂow. ORB-SLAM (Campos et al., 2021)

uses ORB features and a descriptor-based approach

for matching, which is more expensive computation-

ally but can offer better long-term data association

performance.

Figure 2: Key components of a visual SLAM algorithm.

2.2 Bundle Adjustment

Bundle adjustment, often abbreviated as BA, can be

considered a general optimization technique for the

estimated trajectory and map. In robotics terms, it is

a state estimation technique used to jointly reﬁne the

estimates of the 3D location of the observed points

and the camera poses. This reﬁnement is performed

by minimizing the reprojection error, which expresses

the difference between the projection of the estimated

3D map points in the camera image and the actual

location in the image where the point is observed, as-

suming that the exact pose of the cameras and the co-

ordinates of the points in the environment are known.

By combining the data captured in several consecu-

tive frames, the estimates of the camera poses and the

World Coordinates of the observed features can be si-

multaneously optimized. Mathematically, the expres-

sion of the initial situation for a bundle adjustment

problem is given in (1):









= K · R ·



3×3







(1)

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

214

The 3 × 1 column vector (u v w)

at the left-hand

side of this equation represents the three-dimensional

pixel coordinates of an observed point. Note that the

third component is added to express the vector in ho-

mogeneous coordinates. On the right-hand side, the

3 × 3 matrix K is the intrinsic matrix of the camera,

the 3 × 3 matrix R is the rotational matrix, and the

3 × 1 column vector t represents the translation of the

camera center. I

3×3

represents the identity matrix of

dimension 3. The ﬁnal 4 × 1 column vector (X

represents the observed 3D point in homogeneous

coordinates in the World Coordinate System.

Moreover, the residual r can be expressed as:

r =





−









(2)

where (x y)

represents the observed pixel coordi-

nates of a feature. These coordinates will be pro-

vided as input to the BA algorithm. The second

vector





is calculated from the estimated ho-

mogeneous coordinates of the point in the three-

dimensional WCS and represents the reprojection of

an observed point in the image plane. By changing

the values of K, R and t, these reprojected coordi-

nates will vary accordingly.

In essence, a bundle adjustment algorithm will per-

form a nonlinear least squares (NLLS) optimization

in order to minimize the sum of the squared residuals

r over all considered points and camera poses:

min

C,X

∑

|| u

i j

− π(C

, X

) ||

(3)

In (3), u

i j

represents the observations in pixel coor-

dinates. This is inherently equal to (x y)

deﬁned in

(2). π(C

, X

) represents the projection of a point X

into the camera plane of camera C

. Hence, this term

corresponds to





deﬁned in (2). Note that this

is a nonlinear operation.

3 METHOD

As a ﬁrst building block, a pipeline to perform bun-

dle adjustment based on the measurements made by a

single agent is proposed. This is referred to as Single-

Agent Bundle Adjustment (SABA). We start with a

description of this algorithm, before moving on to the

Multi-Agent Bundle Adjustment (MABA) system.

3.1 Single-Agent Bundle Adjustment

As illustrated by (3), the ﬁrst step is to reproject the

observed features in the camera plane. This can be

Figure 3: MABA algorithm pipeline.

easily achieved by multiplying the estimated World

Coordinates of the points with the camera pose matrix

T ∈ SE(3), then with the camera intrinsic matrix to

obtain the pixel coordinates that are ultimately used

to calculate the residual.

Once all features are transformed to the Pixel Co-

ordinate System (PCS), the actual bundle adjustment

is carried out using the Ceres library. This library al-

lows for the solution of NLLS problems using various

solution methods, such as the Gauss-Newton method

or the Levenberg-Marquardt algorithm. Optionally,

the resulting camera trajectory can be smoothed to

reduce the effect of outliers, caused by an incorrect

pose estimation. This will result in a smaller Abso-

lute Pose Error (APE) and Relative Pose Error (RPE)

between the estimated trajectory and the ground truth.

When calculating the optimal camera poses and point

locations in the map, the algorithm can be run in two

different modes. The most intuitive approach is to

run the algorithm in the so-called ’unbounded’ mode,

which imposes no additional constraints on the re-

ﬁned parameters. While being the least constrained

problem, it might result in some camera positions be-

ing heavily displaced in order to minimize the global

cost function. To avoid this effect, which has a neg-

ative impact on the APE and RPE after alignment

with the ground truth, the algorithm can be run in the

’bounded’ mode. Now, the displacement of the cam-

era poses and the point coordinates is limited to avoid

huge outliers. In any of the three principal directions,

the maximal displacement of the camera positions is

clamped to [−δ, δ], where δ ∈ R

is a user-input pa-

rameter. Camera rotations and 3D point coordinates

are clamped in a similar manner.

While imposing additional constraints to the opti-

mization problem, this method tends to avoid having

great outliers, hence improving the alignment of the

estimated trajectory with the ground truth.

Multi-Agent Monocular SLAM

215

Figure 4: Illustration of point correspondences between images captured by different sequences. The colored lines connect

the matching features in the images.

3.2 Multi-Agent Bundle Adjustment

The goal of this algorithm is to combine the data from

multiple sequences such that the estimates of the cam-

era poses and the coordinates of the points are reﬁned

jointly for these sequences. By relying on measure-

ments obtained with multiple agents, the uncertainty

of the estimates can be reduced, which should lead to

more accurate results.

A key component of our pipeline is the Scaled

Point Cloud Registration (SPCR) system that we use

to make the outputs of each agent’s SLAM system co-

herent. In fact, monocular SLAM suffers from scale

ambiguity. Moreover, the different sequences do not

share the exact same initial pose. Therefore, we need

to apply a Similarity transform (Sim(3): an SE (3)

transformation with an extra degree of freedom for

scale) to the poses and map points to make the monoc-

ular SLAM outputs of different agents coherent.

In Figure 3, the pipeline of the MABA algorithm

is presented. The ﬁrst step will be to match the de-

scriptors of the points of the different sequences based

on a multi-dimensional distance metric. Once the

point correspondences are established correctly, the

SPCR is performed between the matching points in

order to estimate the rigid transformation parameters

that map the points observed by one sequence to the

reference frame of the other.

3.2.1 Descriptor Extraction and Matching

Every point considered by ORB-SLAM2 is given a

32-element descriptor vector. These vectors can be

used to establish point correspondences by calculat-

ing the minimum distance between the points seen in

different sequences. As ORB uses binary descriptors,

the Hamming distance is considered as a metric in this

article.

To increase the robustness of the point matching,

Lowe’s ratio test (Lowe, 2004) is implemented, which

discards ambiguous matches. In a practical applica-

tion, the distance between the closest and the second-

closest neighbor for a certain query descriptor is of-

ten very small. Consequently, incorrect matches often

occur whenever there is noise in the considered im-

ages. The idea behind this ratio test is that a match is

only accepted if the ratio of the distance to the closest

and second closest neighbor is smaller than a certain

threshold:

Accept if r =

SNN

< threshold (4)

where d

represents the minimal (Hamming) dis-

tance (Nearest Neighbor) between a query descriptor

and all descriptors against which it is matched. d

SNN

represents the second lowest distance (Second Near-

est Neighbor). If this ratio is smaller than the accep-

tance threshold, one can assume that the matching has

overcome the effects of noise or other sources of in-

consistencies in the calculation of the descriptors.

An example of point correspondences between

two images captured by different sequences is pro-

vided in Figure 4.

3.2.2 Pose Transformation Based on Established

Point Correspondences

We describe the Scaled Point Cloud Registration

(SPCR) system that we use to make the outputs of

each agent’s SLAM system coherent. Since the cam-

era poses and the estimated point positions for each

agent are expressed relative to their ﬁrst camera pose,

considered as the origin, the different sequences are

often expressed in totally different coordinate frames,

making it difﬁcult to compare the poses or the points

in an absolute way. To overcome this issue, the rigid

pose transformation parameters are estimated from a

set of matching points. By deﬁnition, these match-

ing points should have the exact same coordinates

when expressed in a common coordinate frame. This

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

216

knowledge can be used to estimate a Sim(3) trans-

form, i.e., 3 × 3 rotation matrix R, a 3 × 1 translation

vector t and a 3 × 1 scale vector s that map the points

from one coordinate system to the other:



′



= diag([s, 1])·



R t

0 1







(5)

where X and X

′

represent the point coordinates in the

original reference frame and the transformed coordi-

nates, respectively.

The results of the SPCR algorithm for the point

correspondences visualized in Figure 4 are presented

in Figure 5. There is indeed an apparent initial scale

difference between the estimated point coordinates

for the two sequences. However, after the transforma-

tion, both sets of points coincide almost perfectly. In

this ﬁgure, the source points represent the points that

should be transformed to a different coordinate sys-

tem. The target points are the points from the other

sequence with which the source points match.

Finally, the estimated transformation can be ap-

plied to the camera poses as well in order to transform

them to a common reference frame.

Figure 5: Illustration of the SPCR algorithm.

3.2.3 Combination of Keyframes and Points in a

Common Data Structure

Once all data is transformed to the same reference

system, a common data structure can be created for

the different sequences. This way, the multi-agent

problem is translated to one larger optimization prob-

lem, that involves the data of multiple sequences. The

observations of matched points are combined, while

unique points are individually added to the optimiza-

tion problem. An illustration of the combined trajec-

tory of sequences MH01 and MH02 is given in Figure

6. Notice the similarity in scale between the two se-

quences, enforced by the SPCR algorithm.

Figure 6: Resulting combined trajectory after SPCR.

4 EXPERIMENTS AND

DISCUSSION

As explained in the introduction, ORB-SLAM2 is

used to obtain the initial estimates of the camera poses

and the locations of the points in the created map for

each agent. Our system is evaluated on the EuRoC

dataset (Burri et al., 2016). Since ORB-SLAM2 re-

sults do not typically exhibit signiﬁcant drifting errors

(longer data sequences would be needed to better ob-

serve accumulating errors), our proposed system will

be validated through the deliberate addition of noise.

Figure 7: Illustration of the random walk noise.

Two different noise models are used to distort

the original estimates. First, a zero-mean Gaussian

noise is applied to the data, for which the effects

of the standard deviation of the applied noise on

the obtained results are analyzed. In a second set

of experiments, a random walk noise is applied to

the camera positions. This simulates the effect of an

accumulating error, which results in a more realistic

noise. This effect is illustrated by the red and purple

curves in Figure 7.

In Table 1, an overview of the different scenarios

is given.

Multi-Agent Monocular SLAM

217

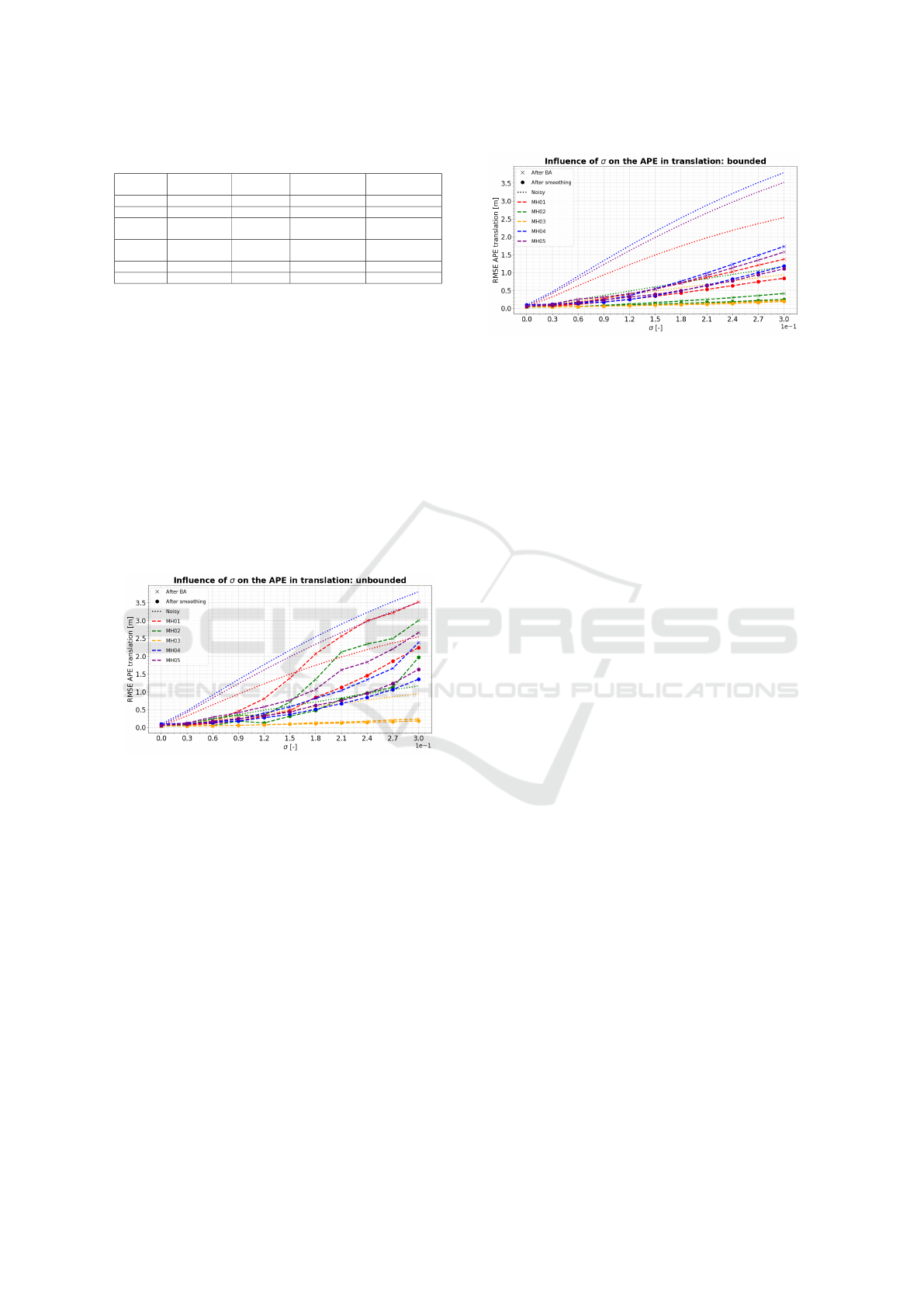
Table 1: Overview of the considered scenarios.

Scenario Noise type BA type

Discussed

noise parameter

Affected

quantity

Scenario 1 Gaussian Motion-only σ Camera positions

Scenario 2 Gaussian Motion-only σ Point coordinates

Scenario 3 Gaussian Full σ

Camera positions

Point coordinates

Scenario 4 Random Walk Motion-only

Camera positions

Scenario 5 Random Walk Motion-only σ Point coordinates

Scenario 6 Random Walk Full σ Point coordinates

4.1 Results for the SABA Algorithm

In Figure 8, the results of a sensitivity analysis of the

unbounded SABA algorithm are given for scenario

1. Note that for this scenario, the algorithm is run in

the motion-only mode, indicating that only the cam-

era poses are reﬁned. Especially for sequences MH01

and MH02, it is clear that the algorithm does not per-

form accurately for values of σ > 0.15. In these cases,

the APE after optimization is larger than before, due

to the presence of extreme outliers in the optimized

camera trajectory. By applying the smoothing ﬁlter,

which reduces the effect of these outliers, the APE is

indeed considerably smaller.

Figure 8: Results of the unbounded SABA algorithm for

scenario 1.

The estimates can be further improved by apply-

ing the bounded SABA algorithm, as shown in Fig-

ure 9. In all of our experiments, the bound parameter

is set to δ = 0.3. Now, even for the largest value of

σ, the APE after optimization is signiﬁcantly smaller

than the APE of the noisy trajectory, which suggests

the reﬁned trajectory is closer to the ground truth after

alignment.

4.2 Results for the MABA Algorithm

Finally, the bundle adjustment algorithm can be ap-

plied to the common data structures as explained in

Section 3.2.3. To guarantee a maximal overlap be-

tween the sequences, a combination of sequences

MH01 and MH02, and sequences MH04 and MH05

has been chosen in this article. For each of these, the

Figure 9: Results of the bounded SABA algorithm for sce-

nario 1.

coordinate system and scale of the ﬁrst sequence, re-

spectively MH01 and MH04, have been chosen as a

reference.

A comparison of the performance of the SABA

and MABA algorithm for scenario 1 is visualized in

Figure 10. There, it is clear that the resulting APE is

lower for the unbounded MABA algorithm than for

the single-agent variant for the same value of σ, in-

dicating that the extension to multiple agents indeed

has a positive effect on the optimized trajectory. How-

ever, for the bounded algorithm, the difference be-

tween SABA and MABA is negligible. This is due

to the higher level of limitation of the mathematical

problem, which reduces the potential to increase the

accuracy of the estimates by applying an optimization

algorithm.

For scenario 3, which considers the ’full’ bundle

adjustment algorithm, results tend to show a trend

similar to scenario 2. This is visualized in Figure

11. Now, the improvements are especially apparent

when the unbounded algorithm is applied to sequence

MH01, at values of σ > 0.09. For the bounded

algorithm, the difference is again negligible.

Notice that while the results obtained with the

MABA algorithm are generally better than for the

SABA algorithm, the computation time is signiﬁ-

cantly (∼10×) larger for the MABA algorithm, com-

puting the optimized poses and points for all agents

simultaneously.

5 CONCLUSION

This article discusses a bundle adjustment pipeline to

improve the estimated camera poses and locations of

points in the map, either based on measurements pro-

vided by a single agent or by combining the mea-

surements of multiple agents. For a setup involving

monocular visual SLAM, it is shown that the accuracy

of the estimates, after the deliberate addition of noise,

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

218

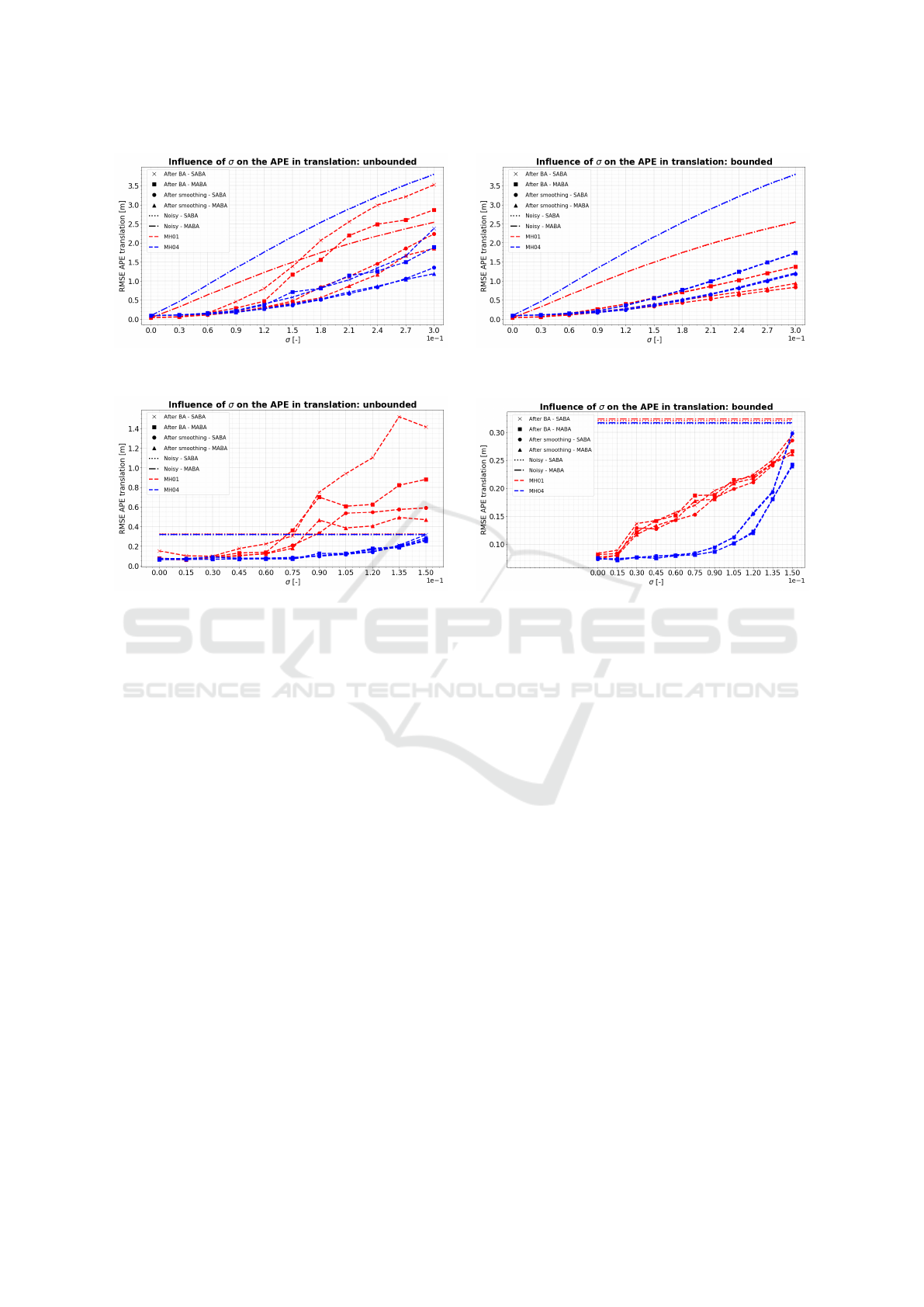
(a) (b)

Figure 10: Scenario 1: Comparison of the results of the SABA and MABA algorithm for the APE in translation.

(a) (b)

Figure 11: Scenario 3: Comparison of the results of the SABA and MABA algorithm for the APE in translation.

improves when the data of multiple agents are con-

sidered. However, a trade-off between the improved

accuracy and an increase in computation time should

always be considered.

6 FUTURE WORK

In this article, a multi-agent bundle adjustment

pipeline has been proposed for monocular visual

SLAM systems. In further research, this could be ex-

tended to integrate the data of other sensors, such as

GPS, IMU, or lidar, to improve the accuracy of the

estimates. Moreover, an analysis of the scalability

of the algorithm could be performed. As explained,

the computation time increases with a factor 10 when

the algorithm is expanded to consider two indepen-

dent sequences. Although the extension to additional

agents should be straightforward, computation time

might become an issue when too many agents are

considered. Therefore, future research could focus

on speed improvements for descriptor matching and

the solution of the nonlinear least-squares optimiza-

tion problem. A ﬁnal suggestion would be to per-

form an analysis of the parameters of the Ceres solver.

Fine-tuning these parameters, such as the type of lin-

ear solver, the step size of the Levenberg-Marquardt

solver, or the type of loss function, could signiﬁcantly

impact the results. Conducting a comprehensive sen-

sitivity analysis of these parameters across diverse

datasets would therefore be valuable to determine the

best settings for different scenarios.

REFERENCES

Burri, M., Nikolic, J., Gohl, P., Schneider, T., Rehder, J.,

Omari, S., Achtelik, M., and Siegwart, R. (2016). The

euroc micro aerial vehicle datasets. The International

Journal of Robotics Research.

Campos, C., Elvira, R., Gomez, J. J., Montiel, J. M. M.,

and Tardos, J. D. (2021). ORB-SLAM3: An accu-

rate open-source library for visual, visual-inertial and

multi-map SLAM. IEEE Transactions on Robotics,

37(6):1874–1890.

Davison, A. J., Reid, I. D., Molton, N., and Stasse, O.

(2007). Monoslam: Real-time single camera slam.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 29:1052–1067.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Mur-Artal, J., Montiel, R., and Tard

os, J. (2017). Orb-

slam2: an open-source slam system for monocular,

Multi-Agent Monocular SLAM

219

stereo and rgb-d cameras. IEEE Transactions on

Robotics, 33(5):1255–1262.

Qin, T., Li, P., and Shen, S. (2018). Vins-mono: A robust

and versatile monocular visual-inertial state estimator.

IEEE Transactions on Robotics, 34(4):1004–1020.

Wong, W. (2014). Autonomous 3d mapping and exploration

using a micro aerial vehicle. pages 138–142.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

220