Equilibrium Analysis and Social Optimization of a Selectable Single or

Time-Based Batch Service

Ayane Nakamura

and Tuan Phung-Duc

2 a

Graduate School of Science and Technology, University of Tsukuba, Tsukuba, Ibaraki, Japan

Institute of Systems and Information Engineering, University of Tsukuba, Tsukuba, Ibaraki, Japan

Keywords:

Queueing Game, Mode Choice, Batch Service, Clearing System, Nash Equilibrium, Social Optimization,

Social Optimal Pricing.

Abstract:

In current transportation systems, a common road is shared by multiple types of vehicles with different capac-

ities. To consider this phenomenon, we propose a model in which customers can strategically select a single

or batch service, and then receive a common service in a single-server queue with exponential service times.

Customers potentially arrive at the system according to a Poisson process and choose whether to join the queue

directly or wait for a batch service. The batch service commences periodically according to a Poisson process

and the capacity of the batch is determined by a geometric distribution. The optimization of such a model has

not been studied despite being an important social issue. We derive the unique equilibrium strategy of cus-

tomers, socially optimal strategy, and socially optimal relationship of fees for both services. Furthermore, we

demonstrate that these optimal fees exhibit linear relationships. In terms of practical application, this system

will allow us to consider the effects of road congestion on transportation platforms.

1 INTRODUCTION

In modern society, batch service systems, such as

buses or trains, are frequently employed in transporta-

tion, where customers are transported in groups. Re-

cently, batch service queueing models with strategic

customers have been studied to obtain insights from

an economic perspective.

There are generally two types of batch service

queues. The ﬁrst is a system in which the service is

conducted using a constant batch (see, e.g., (Boun-

tali and Economou, 2017; Bountali and Economou,

2019a; Bountali and Economou, 2019b)). The other

is a system in which customers are served in a batch

periodically according to a given interval distribu-

tion, called a clearing system (see, for example,

(Economou and Manou, 2013; Manou et al., 2014;

Manou et al., 2017)).

Furthermore, an interesting topic in batch service

queues is modeling the routing behavior of strate-

gic customers. Several studies have been conducted

on the strategic choice among inﬁnite server systems

with batches and single-server systems of a single

service (Calvert, 1997; Aﬁmeimounga et al., 2005;

https://orcid.org/0000-0002-5002-4946

Aﬁmeimounga et al., 2010; Chen et al., 2012; Wang

and Ziedins, 2018). These studies have presented

interesting Downs–Thomson and Braess-type para-

doxes through equilibrium analyses of the model.

In this study, we propose a model in which cus-

tomers select a single service or time-based (clear-

ing system-type) batch service strategically, and both

types of customers receive services in a common

single-server queue (see the detailed explanation in

Section 2). Note that customers who choose the batch

service receive a common service as one batch. From

an application perspective, different types of vehicles,

for example, cars and buses, often coexist on the same

road. Some studies have attempted to model trafﬁc

ﬂow using queueing theory (see, e.g., (Van Woensel

and Vandaele, 2007)). In these studies, part of a road

is modeled as a service station, which is a single-

server queuing model.

The model proposed in this study can be used to

study the trade-off problem between the total time in

a common queue and the waiting time for batch ser-

vice customers. As more customers choose a single

service, trafﬁc congestion is induced in the common

queue. However, as more customers choose the batch

service, the total waiting time for batch service of all

customers accumulates.

Nakamura, A. and Phung-Duc, T.

Equilibrium Analysis and Social Optimization of a Selectable Single or Time-Based Batch Service.

DOI: 10.5220/0012323800003639

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 92-100

ISBN: 978-989-758-681-1; ISSN: 2184-4372

Based on the above, this study aimed to deter-

mine the pricing policy for the two types of services

to achieve a socially optimal state. As relevant re-

search on the pricing of multiple types of services,

several studies have been conducted on queues with

priorities that can be purchased by additional fees

for taking over ordinary customers (see, for example,

Chapter 4 in (Hassin and Haviv, 2003), and (Afeche

and Mendelson, 2004; Li et al., 2020)). Both social

optimization and revenue maximization in priority

queues have been considered in (Afeche and Mendel-

son, 2004). However, to the best of our knowledge,

the optimization of a model in which customers can

select a single or batch service under pricing control

has not been studied, although it is a socially impor-

tant issue.

The remainder of this paper is organized as fol-

lows. First, we describe the model setting in Sec-

tion 2. Subsequently, the equilibrium strategy of cus-

tomers is derived in Section 3, and the socially opti-

mal strategy and pricing policy are discussed in Sec-

tion 4. Furthermore, we present the ﬁndings of some

numerical results in Section 5. Finally, some conclud-

ing remarks are given in Section 6.

2 SETTING OF THE MODEL

This section presents the detailed setting of the se-

lectable model for single and batch services. Cus-

tomers arrive at the system according to a Poisson

process at a rate λ. If a customer chooses the single

service, then the customer immediately joins a single

server queue whose service time is exponentially dis-

tributed with parameter µ. The batch corresponds to a

bus system having a ﬁnite capacity. If the batch ser-

vice is selected, then the customer must wait in the

waiting room until the batch service commences. We

assume that the interval of occurrences of the batch

service follows an exponential distribution with rate γ

and that the capacity for the batch is X, which follows

with probability 0 < α < 1:

:= P(X = c) = (1 − α)

c−1

α, c = 1,2,··· ,

for the tractability of the probability generating func-

tion (PGF). When the batch service commences, at

most X customers from the head in the waiting room

visit the same server with a single service and receive

the common service (the service time also follows an

exponential distribution with rate µ). We assume that

unserved customers (owing to capacity) immediately

abandon the system.

From an application perspective of the transporta-

tion system, a single server is considered to be a ser-

vice station on the road, as proposed in (Van Woensel

and Vandaele, 2007). In (Van Woensel and Vandaele,

2007), part of the road is regarded as a service station,

which is a single-server queueing model, and trafﬁc

congestion is expressed by the performance measures

of the service station.

For stability of the system in any case, we assume

µ > λ + γ. We deﬁne the fees for single and batch

services as τ

and τ

, respectively. The reward for

receiving service in the common server is R, and the

time cost per unit time is C. We also make the follow-

ing assumptions regarding τ

and τ

Assumption 1.

0 ≤ τ

≤ R −

µ − γ

and R −

µ − γ

≥ 0.

Assumption 2.

0 ≤ τ

≤ R −

µ − λ − γ

−

and

R −

µ − λ − γ

−

≥ 0.

These assumptions yield positiveness of fees and

avoid situations in which no one obtains positive util-

ity by receiving each type of service. Naturally, we

assume the following:

Assumption 3. τ

≥ τ

If τ

≤ τ

, then choosing a batch service does not

yield the best response (see the detailed proof of The-

orem 1). Assumption 3 excludes this case, except

for τ

= τ

(note that we include τ

= τ

to con-

sider the case in which fees are not imposed; that is,

= τ

= 0). This model is a two-stage game between

the monopolist and customers; that is, in the ﬁrst stage

of the game, the monopolist selects admission fees for

a single service τ

and batch service τ

. In the second

stage, the customers determine the strategy (p

, p

where p

and p

denote the joining probabilities for a

single service and batch service, respectively. We as-

sume that the system is unobservable and that balking

is not allowed; that is, p

+ p

= 1 always holds true.

Under the condition that customers follow strat-

egy (p

, p

), the mean waiting time for batch ser-

vice E[W

] and the mean sojourn time in the common

queue E[S] can be calculated as follows:

E[W

] =

, and E[S] =

µ − (p

λ + γ)

Therefore, the expected total time for batch service

customers who can receive the service, E[T

], is given

E[T

] =

µ − (p

λ + γ)

Equilibrium Analysis and Social Optimization of a Selectable Single or Time-Based Batch Service

The expected total time for all customers (including

customers who abandon the batch service) is calcu-

lated as

E[T ] =

µ − (p

λ + γ)

+ p



batch

)

µ − (p

λ + γ)



where P

batch

) denotes the ratio of the expected

number of customers served in a service cycle to the

expected number of customers joining the batch ser-

vice waiting room. According to (Manou et al., 2014),

batch

) is given by:

batch

) = 1 − Π



λp

+ γ



where Π(z) denotes the PGF of the batch size distri-

bution.

Π(z) =

∞

∑

c=1

αz

1 − z(1 − α)

Therefore, P

batch

) in the present model is calcu-

lated as

batch

) =

αλp

+ γ

3 EQUILIBRIUM STRATEGY

Theorem 1 presents the Nash equilibrium strategy for

customers.

Theorem 1. Under Assumptions 1 and 2, the unique

equilibrium strategy for customers (p

, p

) is

• Case 1: τ

≤ τ

. Then, a unique equilibrium

strategy (p

, p

) exists:

, p

) = (1,0).

• Case 2: τ

≤ τ

αλ + γ

−

αλ

αλ + γ

µ − γ

αλ

αλ + γ

R +

. Then, a unique

equilibrium strategy (p

,1 − p

) exists where

−A

−

)

− 4A

, (1)



R − τ



αλ

= −(R − τ

)(αλ + γ)λ − (R − τ

)(µ − γ)αλ

+Cαλ + (R − τ

)γλ −

λ(αλ + γ)

−

(µ − γ)αλ,

= Rαλ(µ − γ) − τ

(µ − γ)(αλ + γ) + τ

γ(µ − γ)

−Cαλ +

(µ − γ)(αλ + γ).

• Case 3: τ

≥ τ

αλ + γ

−

αλ

αλ + γ

µ − γ

αλ

αλ + γ

R +

. Then, a unique equilibrium

strategy (p

, p

) exists:

, p

) = (0,1).

Proof. Given that the dominant customer adopts

strategy (p

, p

), the expected utility for a tagged cus-

tomer who adopts strategy (p

′

, p

′

) is given by

U((p

′

, p

′

);(p

, p

)) = p

′



R − τ

−

µ − (p

λ + γ)



+ p

′



(R − τ

batch

) −

batch

)

µ − (p

λ + γ)

−



(2)

We then ﬁnd that the tagged customer must solve the

problem

max

′

)∈([0,1],[0,1])

U((p

′

, p

′

);(p

, p

))

under p

+ p

= 1 and p

′

+ p

′

= 1. Here, it is obvi-

ous that U((p

′

, p

′

);(p

, p

)) is linear with respect to

′

and p

′

. Therefore, the tagged customer bases his

decision on the following two quantities:

ind

) = (R − τ

) −

µ − (p

λ + γ)

ind

, p

) = (R − τ

batch

) −

batch

)

µ − (p

λ + γ)

−

(3)

The set of best responses against (p

, p

), that is,

BR(p

, p

), is given by

BR(p

, p

) =







(1,0), if S

ind

) ≥ S

ind

, p

(0,1), if S

ind

, p

) ≤ S

ind

(a,1 − a), if S

ind

) = S

ind

, p

(4)

where a ∈ [0, 1]. We can conﬁrm the equilibrium strat-

egy using the following procedure:

Strategy (1, 0) is an equilibrium strategy if and

only if (1,0) ∈ BR(1,0); that is, S

ind

(1) ≥ S

ind

(1,0),

which reduces to

R − τ

≥

µ − λ − γ



(R − τ

) −

µ − λ − γ



−

(5)

Strategy (0, 1) is an equilibrium strategy if and

only if (0,1) ∈ BR(0, 1); that is, S

ind

(0) ≤ S

ind

(0,1),

which reduces to

R − τ

≤

µ − γ



(R − τ

) −

µ − γ



αλ + γ

−

(6)

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

Here, using Assumption 1, we can easily ﬁnd that

µ − γ



R − τ

−

µ − γ



αλ + γ

−

µ − λ − γ

−



R − τ

−

µ − λ − γ



µ − γ



R − τ

−

µ − γ



−

µ − λ − γ

−



R − τ

−

µ − λ − γ



= 0,

(7)

which implies that τ

satisfying both (5) and (6) si-

multaneously does not exist. Therefore, the equilib-

rium strategies (1,0) and (0,1) cannot simultaneously

be in equilibrium.

Finally, the strategy (p

,1 − p

) is an equilibrium

strategy if and only if (p

,1 − p

) ∈ BR(p

,1 − p

i.e., S

ind

) = S

ind

,1 − p

). This necessary and

sufﬁcient condition is equivalent to p

satisfying the

following condition:

(R − τ

) −

µ − p

λ − γ



(R − τ

) −

µ − p

λ − γ



αλ(1 − p

) + γ

−

=⇒ A

+ A

= 0,

(8)

where A

, A

, and A

are deﬁned in Theorem 1. Sub-

sequently, let F(p

) denote

F(p

) = (R − τ

) −

µ − p

λ − γ

−



(R − τ

) −

µ − p

λ − γ



αλ(1 − p

) + γ

(9)

Then, we obtain

′

) = −

λC

(µ − p

λ − γ)

αλ(1 − p

)

αλ(1 − p

) + γ

−



(R − τ

) −

µ − p

λ − γ



γαλ

(αλ(1 − p

) + γ)

(10)

Assumption 2 indicates that F

′

) < 0 is true for 0 ≤

≤ 1. Therefore, F(p

) = 0 has a unique root as (1)

within 0 ≤ p

≤ 1 if F(0) ≥ 0 and F(1) ≤ 0; that is,

the following is satisﬁed:

−

αC

µ − λ − γ

+ αR +

≤ τ

αλ + γ

−

α(γ + λ)

αλ + γ

µ − γ

α(γ + λ)

αλ + γ

R +

(11)

Remark 1. When τ

= τ

holds, the unique equilib-

rium strategy (p

, p

) is (p

, p

) = (1,0). This is be-

cause (5) holds true if τ

= τ

. This result is natural

because batch-service customers must wait, and there

is a possibility that they are not served while they do

not occur on single-service customers. Therefore, if

fees are not imposed (i.e., τ

= τ

= 0), the unique

equilibrium is to choose the single service. However,

as the fee for the batch service becomes less than that

for the single service, the equilibrium shifts in favor

of the batch service being used more.

Moreover, we obtain the following theorem:

Theorem 2. The model is an avoid-the-crowd (ATC)

type.

Proof. The increase in utility when a customer

chooses the single service (compared to the batch

service) is given by F(p

). As has already shown,

F(p

) decreases monotonically within 0 ≤ p

≤ 1,

from which the ATC property follows.

Remark 2. A comparison of Theorems 2 and The-

orem 4.5 in (Hassin and Haviv, 2003) is of inter-

est. The latter theorem shows that an unobservable

single-server queue with a priority (an additional fee)

is of the follow-the-crowd (FTC) type. Note that mul-

tiple equilibria often exist in an FTC setting, and this

trend also applies to basic unobservable queues with

priority. In comparison, our model has a unique equi-

librium; therefore, this is more tractable for consider-

ing the social optimization problem in Section 4.

The reasons for these differences are as follows.

In the priority queue, an ordinary (not buying prior-

ity) customer may be overtaken by successive prior-

ity customers after their decision is completed. Thus,

customers tend to buy more priorities to avoid this

situation as the arrival rate increases. On the other

hand, batch service customers (lower fee and longer

waiting time) are never overtaken after their batch

enters the queue. In addition, recall that batch ser-

vices occur periodically; therefore, it is guaranteed

that batch service customers can line the queue within

a certain amount of time, as long as the capacity is not

exceeded.

4 SOCIAL OPTIMIZATION

Next, we consider the social planner’s point of view.

First, we present Theorem 3:

Theorem 3. For the social planner’s admission prob-

lem, a unique socially optimal strategy (p

, p

) is

given by

Equilibrium Analysis and Social Optimization of a Selectable Single or Time-Based Batch Service

• Case 1:

R ≤

µ − γ

1 −

(αλ + γ)



αλ + γ

(µ − γ)

−



Then, a unique socially optimal strategy (p

, p

)

exists:

, p

) = (0,1).

• Case 2:

R ≥

µ − γ

1 −

(αλ + γ)



αλ + γ

(µ − γ)

−



and

(µ − λ − γ)

−

≥ 0.

Then, a unique socially optimal strategy (p

,1 −

) exists where p

is a unique solution of

λ(αλ(1 − p

) + γ)

− λγ

(αλ(1 − p

) + γ)



R −

µ − p

λ − γ



−

λp



αλ(1 − p

) + γ



+ λ(1 − p

)γ

αλ(1 − p

) + γ

λC

(µ − p

λ − γ)

λC

= 0.

(12)

• Case 3:

(µ − λ − γ)

−

≤ 0. Then, a unique

socially optimal strategy (p

, p

) exists:

, p

) = (1,0).

Proof. Assuming that all customers follow strategy

, p

), The mean number of single-service cus-

tomers and batch-service customers, E[C

] and E[C

in the common queue is given by

E[C

] =

µ − p

λ − γ

, E[C

] =

µ − p

λ − γ

E[B],

respectively, where E[B] is the mean number of cus-

tomers (who choose the batch service) in a batch,

E[B] =

batch

According to Little’s law, the mean number of waiting

customers for the batch service is given by

E[N

] =

Therefore, social welfare per unit time is given by

soc

, p

)

= λ



+ p

αλp

+ γ



R −

µ − p

λ − γ



−

λC

(13)

Using the normalization condition p

+ p

= 1,

soc

, p

) can be rewritten as

soc

) = λp



R −

µ − p

λ − γ



λ(1 − p

)γ

αλ(1 − p

) + γ



R −

µ − p

λ − γ



−

(1 − p

)λC

(14)

Here, the social planner must solve for

max

∈[0,1]

soc

). We obtain the following

differentiation form for p

∂S

soc

)

∂p

λ(αλ(1 − p

) + γ)

− λγ

(αλ(1 − p

) + γ)



R −

µ − p

λ − γ



−

λp

{

αλ(1 − p

) + γ

}

+ λ(1 − p

)γ

αλ(1 − p

) + γ

λC

(µ − p

λ − γ)

λC

(15)

∂

soc

)

∂

= −



1 −

(αλ(1 − p

) + γ)



2λ

(µ − p

λ − γ)

−

2λ

(µ − p

λ − γ)

−

2αλ

(αλ(1 − p

) + γ)



R −

µ − p

λ − γ



−

λ(1 − p

)γ

αλ(1 − p

) + γ

2λ

(µ − p

λ − γ)

From Assumption 1, it is clear that

∂

soc

)

∂

< 0 holds

for 0 ≤ p

≤ 1, indicating the concavity of S

soc

Hence, the socially optimal strategy (p

, p

) becomes

(0,1) if

∂S

soc

)

∂p



≤ 0, i.e.,

R ≤

µ − γ

1 −

(αλ + γ)



αλ + γ

(µ − γ)

−



(16)

the socially optimal strategy (p

, p

) becomes (1, 0)

∂S

soc

)

∂p



≥ 0, i.e.,

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

(µ − λ − γ)

−

≤ 0,

(17)

and the socially optimal (p

, p

) becomes (p

,1− p

)

where p

is a unique solution of (15) in the other case.

Here, due to Assumption 1, we have

0 ≤

αλ + γ

(µ − γ)

−

if (16) holds. As the following:

αλ + γ

(µ − γ)

≤

(µ − λ − γ)

is clear, the inequalities (16) and (17) cannot be sat-

isﬁed simultaneously. Thus, the strategy becomes the

unique strategy.

Remark 3. From Theorem 3, we consider that the

socially optimal probability for a single service in-

creases as R increases as long as λ/(µ − λ − γ)

−

1/γ ≥ 0 is satisﬁed. When R is small, the cost of the

waiting time, i.e., C, is considered to be signiﬁcant.

Thus, in this case, it is socially optimal for customers

to wait for batch services and to prevent trafﬁc con-

gestion in the common queue. On the other hand,

when R is high, the risk of batch service in which

customers may not be served because of the capacity

is considered to be signiﬁcant because unserved cus-

tomers obtain zero reward. Therefore, choosing the

single service becomes socially optimal. In the case

of λ/(µ − λ − γ)

−1/γ ≤ 0, the arrival of buses is too

infrequent which results in choosing the single service

with probability 1 becomes social optimal.

Based on Theorems 1 and 3, we consider the so-

cially optimal relationship between τ

and τ

. To this

end, we put forth the following assumption:

Assumption 4. If multiple patterns exist in the rela-

tionship between τ

and τ

, the social planner adopts

the relationship such that the difference between τ

and τ

is the smallest.

From Assumption 4, we obtain Theorem 4.

Theorem 4. The socially optimal relationship be-

tween the admission fees (τ

and τ

) for single and

batch services satisﬁes the following linear equation:

• Case 1:

R ≤

µ − γ

1 −

(αλ + γ)



αλ + γ

(µ − γ)

−



Then, τ

and τ

satisfy

αλ + γ

−

αλ

αλ + γ

µ − γ

αλ

αλ + γ

R +

• Case 2:

R ≥

µ − γ

1 −

(αλ + γ)



αλ + γ

(µ − γ)

−



and

(µ − λ − γ)

−

≥ 0.

Then, τ

and τ

satisfy

= T

+ T

where

αλ(1 − p

) + γ

= R −

µ − p

λ − γ

−



R −

µ − p

λ − γ



αλ(1 − p

) + γ

• Case 3:

(µ − λ − γ)

−

≤ 0. Then, τ

and τ

satisfy

= τ

Proof. In Case 1, the socially optimal strategy is

(0,1). Thus, the social planner sets a fee such that the

equilibrium strategy becomes (0,1) under Assump-

tion 4. The same argument holds true for Case 3. In

Case 2, the socially optimal strategy is (p

,1 − p

where p

is a unique solution to (12). Therefore, we

obtain the result by substituting p

into the equation

for the equilibrium strategy, that is, (1).

Remark 4. From Theorem 4, we ﬁnd that that τ

/τ

(the amount of τ

relative to τ

) decreases as R in-

creases as long as λ/(µ − λ − γ)

− 1/γ ≥ 0 is satis-

ﬁed. This can be explained as follows. When R is

large, the single service is socially preferable, as dis-

cussed in Remark 3. Therefore, it is optimal for the

social planner to set τ

relatively low and induce cus-

tomers to use the single service more often, and vice

versa.

5 NUMERICAL EXAMPLES

This section provides some numerical results for the

social welfare and socially optimal relationship be-

tween the fees for single and batch services. Note that

all experiments were conducted under the condition

that Assumptions 1, 2, and 3 are satisﬁed. We show

some examples under that λ/(µ − λ − γ)

− 1/γ ≥ 0

is satisﬁed. The detailed parameter settings are de-

scribed in each ﬁgure caption.

Equilibrium Analysis and Social Optimization of a Selectable Single or Time-Based Batch Service

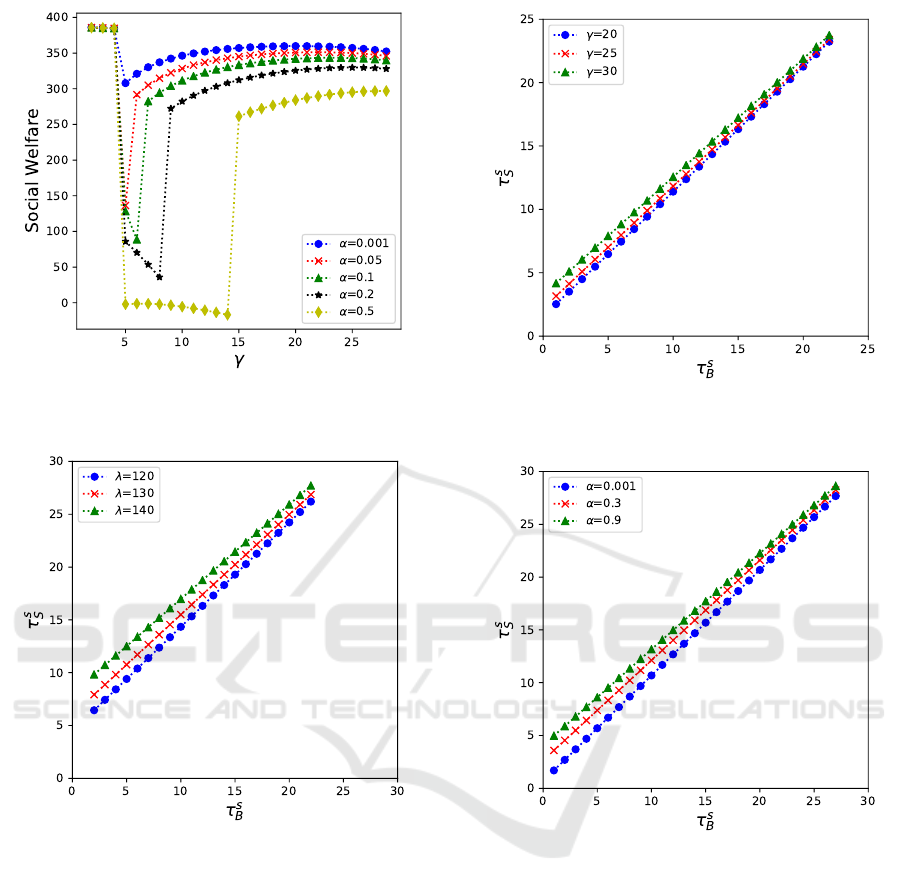
Figure 1: Social welfare for γ and α. The other parameters

are λ = 10, µ = 40,R = 40,C = 40,τ

= 20,τ

= 10.

Figure 2: τ

vs. τ

for λ. The other parameters are µ =

160,α = 0.1, γ = 10, R = 40,C = 20.

5.1 Social Welfare

In this subsection, the results for Social Welfare, i.e.,

(13), are presented.

Figure 1 depicts Social Welfare with regard to the

batch service, that is, the rate of the exponential distri-

bution for the interval of the batch service occurrences

γ, and the geometric distribution of the capacity α.

Here, the expected batch size becomes 1/α because

of the mean of the geometric distribution. Thus, the

expected batch size increases as α decreases.

Figure 1 illustrates an intriguing tendency. The

graphs behave as decreasing, increasing, and decreas-

ing again, against γ. This trend can be interpreted

as follows. When γ is low, choosing the batch ser-

Figure 3: τ

vs. τ

for γ. The other parameters are λ =

25,µ = 100, α = 0.2,R = 40,C = 40.

Figure 4: τ

vs. τ

for α. The other parameters are λ =

25,µ = 60, γ = 30,R = 40,C = 20.

vice rarely becomes the equilibrium strategy. There-

fore, although γ is increased slightly, this only just in-

duces the congestion level of the common queue (al-

though few customers choose the batch service), and

Social Welfare is decreased. When γ reaches a cer-

tain level, customers often start to use the batch ser-

vice, and Social Welfare increases. However, when γ

increases further, its effect on the congestion of the

common queue becomes stronger than the total re-

ward for batch service customers.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

5.2 Relationship Between Fees of Single

and Batch Services

In the following section, we discuss the socially op-

timal relationship between fees for single and batch

services; that is, Theorem 4. Figures 2–4 show τ

when the horizontal axis represents τ

We observe that both fees become closer as τ

in-

creases. This is natural from the form of Theorem 4.

Fees become dominant in the linear equations as they

increase. Recall that balking is not allowed in this

model. This assumption may allow even large fees

to become socially optimal. Therefore, the develop-

ment of a model in which balking is allowed would

be meaningful in future work.

It is conﬁrmed in Figure 2 that τ

becomes larger

as λ increases for the same τ

. This result implic-

itly suggests that the batch service becomes socially

preferable when the arrival rate is high, and it is bet-

ter for the social planner to set τ

low to induce cus-

tomers to use the batch service. It follows that con-

gestion in the common queue becomes signiﬁcant if

too many customers use the single service.

Figures 3 and 4 show the results for the batch ser-

vice parameters. As the maximum throughput of the

batch service increases, that is, γ increases or α de-

creases, a lower cost of τ

becomes socially prefer-

able. This naturally implies that it is socially optimal

for customers to use more batch services when the

performance of the batch service is superior; thus, the

social planner must set τ

lower.

6 CONCLUSION

In this study, we proposed a model in which cus-

tomers can probabilistically select a single or batch

service. A novel feature of this model is that both

customer types join a common queue. From an appli-

cation perspective, this setting enables us to consider

the effects of road congestion on transportation plat-

forms.

We proved the existence of a unique equilibrium

strategy in this model. Moreover, we derived a so-

cially optimal strategy and demonstrated that using

batch services to alleviate the congestion of the com-

mon queue is socially desirable compared to the equi-

librium strategy. Based on these results, we derived

a socially optimal relationship between the fees for

both services. Interestingly, these optimal fees exhibit

a linear relationship.

In addition, we presented several numerical exam-

ples. In particular, the social welfare for the batch ser-

vice parameters (γ and α) in Figure 1 shows a unique

tendency. It can be interpreted from Figure 1 that in-

creasing the frequency and capacity of the batch ser-

vice does not necessarily lead to better results. Over-

all, the main managerial ﬁndings are summarized in

Remarks 1–4 and Section 5.

As potential extensions of this study, a model with

balking or an (partially) observable scheme can be

considered. In addition, the model should be fur-

ther studied under more general assumptions regard-

ing batch service occurrences and capacity.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Nos.

21K11765, 18K18006, and JST SPRING No. JP-

MJSP2124. In addition, this study was supported by

F-MIRAI: R&D Center for Frontiers of MIRAI in

Policy and Technology, the University of Tsukuba,

and Toyota Motor Corporation Collaborative R&D

Center.

REFERENCES

Afeche, P. and Mendelson, H. (2004). Pricing and priority

auctions in queueing systems with a generalized delay

cost structure. Management science, 50(7):869–882.

Aﬁmeimounga, H., Solomon, W., and Ziedins, I. (2005).

The downs-thomson paradox: existence, uniqueness

and stability of user equilibria. Queueing Systems,

49:321–334.

Aﬁmeimounga, H., Solomon, W., and Ziedins, I. (2010).

User equilibria for a parallel queueing system with

state dependent routing. Queueing Systems, 66:169–

193.

Bountali, O. and Economou, A. (2017). Equilibrium joining

strategies in batch service queueing systems. Euro-

pean Journal of Operational Research, 260(3):1142–

1151.

Bountali, O. and Economou, A. (2019a). Equilibrium

threshold joining strategies in partially observable

batch service queueing systems. Annals of Operations

Research, 277(2):231–253.

Bountali, O. and Economou, A. (2019b). Strategic cus-

tomer behavior in a two-stage batch processing sys-

tem. Queueing Systems, 93(1):3–2019.

Calvert, B. (1997). The downs-thomson effect in a markov

process. Probability in the Engineering and Informa-

tional Sciences, 11(3):327–340.

Chen, Y., Holmes, M., and Ziedins, I. (2012). Monotonic-

ity properties of user equilibrium policies for parallel

batch systems. Queueing Systems, 70:81–103.

Economou, A. and Manou, A. (2013). Equilibrium balk-

ing strategies for a clearing queueing system in alter-

nating environment. Annals of Operations Research,

208(1):489–514.

Equilibrium Analysis and Social Optimization of a Selectable Single or Time-Based Batch Service

Hassin, R. and Haviv, M. (2003). To queue or not to

queue: Equilibrium behavior in queueing systems,

volume 59. Springer Science & Business Media.

Li, Q., Guo, P., and Wang, Y. (2020). Equilibrium analysis

of unobservable m/ m/n priority queues with balking

and homogeneous customers. Operations Research

Letters, 48(5):674–681.

Manou, A., Canbolat, P. G., and Karaesmen, F. (2017).

Pricing in a transportation station with strategic cus-

tomers. Production and Operations Management,

26(9):1632–1645.

Manou, A., Economou, A., and Karaesmen, F. (2014).

Strategic customers in a transportation station: when

is it optimal to wait? Operations Research,

62(4):910–925.

Van Woensel, T. and Vandaele, N. (2007). Modeling trafﬁc

ﬂows with queueing models: a review. Asia-Paciﬁc

Journal of Operational Research, 24(4):435–461.

Wang, A. and Ziedins, I. (2018). Probabilistic selﬁsh rout-

ing in parallel batch and single-server queues. Queue-

ing Systems, 88:389–407.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

100