State-Aware Application Placement in Mobile Edge Clouds

Chanh Nguyen

, Cristian Klein

and Erik Elmroth

Department of Computing Science, Ume

a University, Sweden

Keywords:

Mobile Edge Clouds, Application Placement, Service Orchestration, Optimization.

Abstract:

Placing applications within Mobile Edge Clouds (MEC) poses challenges due to dynamic user mobility. Main-

taining optimal Quality of Service may require frequent application migration in response to changing user

locations, potentially leading to bandwidth wastage. This paper addresses application placement challenges

in MEC environments by developing a comprehensive model covering workloads, applications, and MEC

infrastructures. Following this, various costs associated with application operation, including resource utiliza-

tion, migration overhead, and potential service quality degradation, are systematically formulated. An online

application placement algorithm, App EDC Match, inspired by the Gale-Shapley matching algorithm, is in-

troduced to optimize application placement considering these cost factors. Through experiments that employ

real mobility traces to simulate workload dynamics, the results demonstrate that the proposed algorithm efﬁ-

ciently determines near-optimal application placements within Edge Data Centers. It achieves total operating

costs within a narrow margin of 8% higher than the approximate global optimum attained by the ofﬂine pre-

cognition algorithm, which assumes access to future user locations. Additionally, the proposed placement

algorithm effectively mitigates resource scarcity in MEC.

1 INTRODUCTION

The growth of mobile technology, coupled with the

rollout of 5G networks, paves the way for a new era

of applications characterized by stringent demands

for minimal jitter, low latency, and extensive band-

width. As an example, real-time gaming applications

necessitate response times of mere milliseconds to

forestall substantial Quality of Service (QoS) degra-

dation (Pantel and Wolf, 2002). Likewise, virtual

reality applications employing head-tracked systems

mandate latencies below 16 ms to maintain percep-

tual stability, preserving the illusion of reality (Ellis

et al., 2004).

In recent years, there has been a signiﬁcant shift

away from conventional centralized cloud comput-

ing data centers towards the adoption of a dis-

tributed computing infrastructure known as Mobile

Edge Clouds (MECs). MECs are designed to de-

centralize computing and storage resources to the

network edge, speciﬁcally within Edge Data Cen-

ters (EDCs) located in close proximity to end-users.

These EDCs are often strategically placed, such as

https://orcid.org/0000-0002-9156-3364

https://orcid.org/0000-0003-0106-3049

https://orcid.org/0000-0002-2633-6798

being colocated with central ofﬁce locations (Kavak

et al., 2015). Recent research efforts (Mehta et al.,

2016; Tong et al., 2016) have introduced the con-

cept of hierarchical MECs, incorporating heteroge-

neous costs and capacities. In this hierarchical struc-

ture, data centers (DCs) are organized into different

layers. DCs in higher layers offer greater compu-

tational capacities at lower cost but are situated far-

ther from end-users, resulting in increased latency and

bandwidth expenses. MECs offer exceptional ﬂexi-

bility, allowing for the placement of applications that

align with their speciﬁc requirements. This versatility

strikes a balance between cost-effective computation

and proximity to end-users. In fact, many algorithms

have been proposed for placing stateless applications

on MECs, including dynamic placement algorithms

for efﬁciently dealing with user mobility (Li et al.,

2022; Shang et al., 2022; Apat et al., 2023; Nguyen

et al., 2019). Nonetheless, a signiﬁcant number of en-

visioned MEC applications exhibit stateful character-

istics. Take, for instance, augmented reality applica-

tions, which entail the storage of generated meshes,

world data, textures, and more. Utilizing stateless

placement algorithms for such stateful applications

entails the risk of incurring unnecessary costs, primar-

ily attributed to the bandwidth needed to migrate user

Nguyen, C., Klein, C. and Elmroth, E.

State-Aware Application Placement in Mobile Edge Clouds.

DOI: 10.5220/0012326300003711

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Cloud Computing and Services Science (CLOSER 2024), pages 117-128

ISBN: 978-989-758-701-6; ISSN: 2184-5042

117

state from one EDC to another.

In this paper, we tackle the challenge of placing

stateful applications in an MEC environment. Our ap-

proach begins with a comprehensive modeling of the

various costs associated with hosting stateful applica-

tions on MECs. These costs encompass the resource

cost, which includes both computing and application

bandwidth expenses, as well as the QoS degradation

cost and migration costs. Subsequently, we introduce

an online state-aware application placement strategy,

denoted as App EDC Match, inspired by the well-

known Gale-Shapley matching algorithm (Gale and

Shapley, 1962). The primary objective of the pro-

posed strategy is to discover placement solutions that

match applications with EDCs, resulting in the lowest

resource cost and bandwidth consumption across the

physical network links.

We conducted a comprehensive evaluation of the

proposed algorithms within an MEC topology encom-

passing EDCs distributed throughout the San Fran-

cisco area. To simulate user mobility patterns, we em-

ployed real mobility traces derived from taxi move-

ment data in San Francisco. Additionally, we mod-

eled user transitions between applications using a

Markov model. The evaluation compared the total op-

erating costs generated by the App EDC Match algo-

rithm against those produced by a precognition place-

ment algorithm, which possesses knowledge of future

user locations. Furthermore, we conducted extensive

experimental comparisons of the proposed placement

algorithm’s performance and behavior across differ-

ent application types, including compute-intensive

and bandwidth-intensive applications.

The contributions of this paper are three-fold:

• A comprehensive cost model is provided for host-

ing stateful applications on MECs (see Section 2).

• An efﬁcient online state-aware placement strategy

for distributing applications among EDCs with

the goal of minimizing the overall operating costs

(see Section 3).

• Extensive experiments to evaluate the perfor-

mance of the proposed placement strategy (see

Section 5).

The experimental results show the efﬁciency of

the proposed online placement algorithm for optimiz-

ing application placements among EDCs. It achieves

a total operational cost only 8% higher than the ap-

proximate global optimum determined by the pre-

cognition ofﬂine algorithm. Furthermore, the pro-

posed algorithm effectively addresses workload bal-

ancing within MECs, mitigating resource scarcity

challenges.

2 PROBLEM DEFINITION

In this section, we ﬁrst describe models for each com-

ponent considered in the application placement prob-

lem, namely the MEC infrastructure, applications,

user mobility, workload and cost model. Based on

these models, we then formulate a formal statement

of the problem to be solved.

2.1 Mobile Edge Clouds

MECs with a hierarchy of geo-distributed EDCs have

proven to be efﬁcient infrastructures for meeting en-

visioned MEC workloads (Tong et al., 2016; Bar-

tolomeo et al., 2023; Yang et al., 2018; Wang et al.,

2017). We therefore focus on a MEC with EDCs

organized into a hierarchical topology in this work

(see Figure 1).

We model a MEC as a set of N EDCs geograph-

ically distributed within an area, denoted E = {i|i =

1,2,...,N}. Each EDC is identiﬁed by a geographic

location loc

and a layer that e

belongs to. In layer

1, every EDC e

is collocated with a cellular base

station or a WiFi access point, from which the end-

users send requests to an application hosted by the

MEC. Each EDC is equipped with a certain number

of servers that provide a pool of virtualized comput-

ing resources. EDCs in higher layers feature greater

computing capacities. We use C

to denote the com-

puting capacity of e

The interconnection between the EDCs is repre-

sented by the following network model. We denote

the set of all physical network links in the MEC as

L = { j| j = 1,2,...,M}. Each link l

connects e

with

its closest ancestor and is characterized by its network

delay d

and a maximum bandwidth – also known as

the bandwidth capacity – denoted B

. Thus, it is worth

noting that M = N − 1. Any pair of EDCs can com-

municate by following the shortest network path. Let

i,i

′

⊆ L be the set of all physical network links on

the shortest path between two EDCs e

, e

′

. Here, it is

worth noting that total bandwidth consumed on a par-

ticular physical network link l

is equal to the sum of

the bandwidth consumed on all paths P

i,i

′

containing

2.2 Application

Let A = {p|p = 1,2,..,P} be the set of applications

hosted in the MEC. An application p is characterized

by the following parameters:

• Compute ξ

describes the amount of computa-

tional resource units required by p to serve an end-

user. The unit is CPU × seconds/user.

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

118

Layer 1

Layer 2

Layer 3

l7 l8

Figure 1: Our model of an MEC, showing the organization

of EDCs into various layers and physical network linking

the EDCs.

• Bandwidth ξ

describes the amount of network

bandwidth required by p to serve an end-user. The

unit is KB/user.

• State ξ

describes the amount of state stored by

p for each served end-user. This is the amount

of network bandwidth required to transfer the ap-

plication from one EDC to another. The unit is

KB/user.

We use compute-bandwidth-usage-ratio per applica-

tion request (CPU-h/GB), denoted as A

(Mehta

et al., 2016), to determine whether a speciﬁc appli-

cation is compute-intensive or bandwidth-intensive.

takes values in the range [0.01,10]. To guaran-

tee the target QoS, the system must allocate resources

(both compute and bandwidth) that can handle the to-

tal workload generated by users.

2.3 User and Workload

We consider a set of users U = {k|k = 1,2,...,K} that

dynamically move around in the area covered by the

MEC. In time slot t, user k connects wirelessly to the

physically closest EDC, called the connecting EDC.

The access delay, i.e., the delay due to the wireless

network between k and the connecting EDC i is de-

noted as d

k,t

In each time slot t, user k connect to application

p ∈ A that is speciﬁed in λ

k,t

. After each time slot,

user k may continue using the same application or

change to a different application.

To serve the user, the placement algorithm must

allocate capacity to the application in a serving EDC.

Depending on the placement algorithm’s decision,

the serving EDC may or may not coincide with the

connecting EDC. Let s

k,t,i

denote the decision about

whether or not the requested application p of user k is

hosted on i at time slot t. Formally:

k,t,i

(

1, if p is hosted in EDC i for user k

0, otherwise

(1)

and

∑

k,t,i

= 1

(2)

Let tb

j,t

be the total bandwidth (i.e. the bandwidth

allocated for serving applications plus the bandwidth

needed to migrate applications) allocated from link j

in time slot t. This gives us the expression:

j,t

= ξ

j,t

+ ξ

j,t

(3)

whereas, ξ

j,t

is total bandwidth allocated on net-

work link j for serving applications in time slot t, and

j,t

is total bandwidth allocated on network link j for

migrating applications in time slot t.

2.4 Operating Cost

To serve the end-users, the system responsible for

placing applications hosted in MECs must take var-

ious costs into consideration:

• The Resource Cost:

This cost refers to the compute and bandwidth

cost, which abstract all the regular costs due to

hardware, service maintenance, energy consump-

tion, and so on. While real cloud computing sys-

tems employ intricate unit pricing functions, con-

sidering factors like supply and demand, resource

utilization, instance types, and pricing tiers, our

modeling approach simpliﬁes this by assuming

an inverse proportionality between the current ca-

pacities of compute resource at EDC i and net-

work link j with their respective unit prices. This

simpliﬁcation adheres to micro-economic prin-

ciples, particularly the law of supply and de-

mand (Moore, 1925), and acknowledges the inﬂu-

ence of economy-of-scale effects on energy and

maintenance costs. It is worth noting that the

resource unit price function (as deﬁned in equa-

tion 4 below) can be customized to align with

stakeholder deﬁnitions and speciﬁc scenarios.

Let g

∗

(.) be the function that determines the re-

source unit price:

∗

) = (u

max

− u

min

) × x

+ u

min

(4)

Here,







∑

k,t−1,i

×ξ

k,t−1

,for the compute resource

j,t−1

, for the bandwidth resource

(5)

and u

min

max

are the minimum and maximum re-

source unit price, which are predeﬁned differently

for each EDC i and network link j.

The resource cost Cost

res

is then calculated as be-

low:

State-Aware Application Placement in Mobile Edge Clouds

119

Cost

res

∑

k,t,i





× ξ

k,t

∑

j∈P

i,loc

× ξ

k,t





(6)

Here, P

loc

k,t

is the network path as deﬁned in Sec-

tion 2.1.

The total bandwidth allocated on a particular

physical network link j for serving applications

is equal to the sum of the bandwidth consumed

on paths P

loc

k,t

go through j, which is decided by

k,t,i

j,t

∑

j∈P

loc

k,t

k,t,i

× ξ

k,t

(7)

• The Migration Cost: This cost is associated with

migrations, i.e. the transfer of a user’s application

p hosted on EDC i at time t − 1 to another EDC

′

in time slot t. It is related to the size of the ap-

plication’s state data (or service proﬁle) for each

user. Transferring such data across EDCs requires

bandwidth from the inter-EDC-network connect-

ing i and i

′

We deﬁne the migration ﬂag as MF

k,t,i,i

′

, which

takes a value of 1 if and only if user k requests

the same application in successive time slots (i.e.,

k,t

= λ

k,t−1

), and that application is placed on

different EDCs in those time slots (i.e., ⟨s

k,t

k,t−1

⟩ = 0):

k,t,i,i

′











1, λ

k,t

= λ

k,t−1

and s

k,i

′

= 1

and s

k,i,t−1

= 1

0, otherwise

(8)

Here, i is the source EDC and i

′

is the destination

EDC of the migration.

Then, the total migration cost is calculated as:

Cost

mig

∑

′

(MF

k,t,i,i

′

∑

j∈P

i,i

′

× ξ

k,t

)

(9)

Here, the total bandwidth allocated on a network

link l

for application migrations is equal to the

sum of the bandwidth allocated to migrate appli-

cations on paths P

i,i

′

going through l

j,t

∑

′

k,t,i,i

′

∑

j∈P

i,i

′

k,t

(10)

• The Service Quality Degradation Cost: This

cost stems from delays due to three factors: i) the

start-up time of new virtual resources to host new

applications requested by users; ii) the wireless

network delay between user k and the connected

EDC e

; and iii) the delay due to data transmission

between network link l

(including data transmis-

sion due to an application’s state migration, if

any).

Given ξ

k,t−1

and ξ

k,t

, we calculate the increment

of the resource allocation for EDC e

between two

time slots t and t − 1 as below:

t,i

= max

(

∑



k,t,i

× ξ

k,t

− s

k,t−1,i

× ξ

k,t−1



)

(11)

Denoting the average start-up time for a new vir-

tual resource as st, we assume the new virtual re-

sources are invoked in parallel at each EDC e

each time slot t. The start-up time of the new

added virtual resources, d

st,t

, is thus given by the

following expression:

st,t

(

st, for δ

t,i

> 0

0, for δ

t,i

= 0

(12)

To model the relationship between the network la-

tency and the injection bandwidth for each phys-

ical link l

, we treat the relative latency as a

function of the offered trafﬁc for a simple net-

work. As shown previously (Moudi and Othman,

2020; Dally and Towles, 2004), the network la-

tency in an interconnection network rises to inﬁn-

ity as throughput approaches saturation. In such

cases, the relationship is well described by an ex-

ponential distribution. It is worth noting that in

our model, we constrain the total bandwidth allo-

cation on each link l

at time t to the link’s max-

imum bandwidth. Consequently, we do not ac-

count for potential waiting times, such as queuing

latency, that may be present in an actual network.

We model the network delay at link l

using an

exponential distribution:

delay

j,t



j,t



1 −

j,t

+ d

(13)

Let cc

qos

be the unit price of the service qual-

ity downgrade due to delay. The service quality

degradation cost, Cost

qos

, can then be calculated

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

120

as follows:

Cost

qos

= cc

qos

∑



st,t



∑

k,t

∑

delay



(14)

2.5 Cost Optimization Formulation

Having describing different costs of placing applica-

tions on MECs to serve end-users respecting to QoS.

The total cost is the sum of all the aforementioned

costs, i.e., Cost

res

+ Cost

mig

+ Cost

qos

. The applica-

tion placement optimization problem can be formal-

ized as:

minimize: P = Cost

res

+ Cost

mig

+ Cost

qos

(15)

subject to:

∑

k,t

× s

k,i,t

≤ C

,∀i,t, (16)

j,t

≤ B

,∀ j,t (17)

Here, constraints 16 and 17 ensure that the system’s

capacity limit is not exceeded (i.e. the load on each

EDC does not exceed its compute capacity; and the

trafﬁc through each network link does not exceed its

maximum bandwidth).

In summary, in each time slot t ∈ T , the system

must decide s

k,t,i

, i.e., on which EDCs to place the

requested application p of user k. These decisions de-

termine the total compute resource allocation at each

EDC e

, and total bandwidth usage at each link l

The decision should be made so as to guarantee that

the aggregated operating cost over time window T is

minimized.

3 ONLINE APPLICATION

PLACEMENT ALGORITHM

In this section, we ﬁrst present the mathematical

transformation to simplify the original placement

problem presented in Section 2. Subsequently, we

establish the NP-hardness of the placement prob-

lem, highlighting the impracticality of obtaining an

exact solution within polynomial time. In light of

these challenges, we introduce the App EDC Match

placement strategy, an online placement algorithm de-

signed to address the placement problem efﬁciently

within polynomial time.

3.1 Mathematical Transformation and

NP-Hardness Proof

It is undoubtedly true that in time slot t the place-

ment decisions made in previous time slots cannot be

changed. However, the placement of applications in

the preceding time slot t − 1 will impact the place-

ment decision at time t. Therefore, the original total

operation cost P from Equation (15) can be re-written

as follows (with T = [1, T ]):

t∈[1,T ]

= P

t∈[1,T −1]

+ P

t=T

(18)

Finding an optimal operating cost P

t∈[1,T ]

thus be-

comes a recursive process of ﬁnding an optimal oper-

ating cost P

t=T

based on the current system’s state,

and the assumption that the application placements

decided in the previous time slots t ≤ T − 1 are op-

timal. In each time slot t ∈ T , the total compute re-

source allocated at each EDC e

∑

k,t−1

× s

k,t−1,i

and the total bandwidth resource allocated at each net-

work link l

, tb

j,t−1

are known. These values together

with the users’ application requests and their loca-

tion during t are the inputs for the placement prob-

lem, P

t=T

. Therefore, the original placement prob-

lem transforms into an assignment problem: to which

EDC should each user’s requested applications be as-

signed so as to minimize the total operating cost at

every time slot t. This problem has been proven to be

NP-hard (Fisher et al., 1986).

Obtaining an optimal solution for the application

placement problem in polynomial time is considered

impossible unless P = NP. Consequently, our focus

shifts to the development of efﬁcient algorithms ca-

pable of delivering near-optimal solutions for min-

imizing P

t=T

within a polynomial time frame. In

pursuit of this goal, we present the App EDC Match

placement strategy, an efﬁcient heuristic algorithm in-

spired by the widely recognized Gale-Shapley match-

ing problem.

3.2 App EDC Match Placement

Strategy

In general, our problem of assigning requested appli-

cations to EDCs in each time slot t to minimize P

t=T

is analogous to the college admissions discussed by

Gale and Shapley (Gale and Shapley, 1962). In the

college admissions problem, each student proposes

to their most preferred available college, while col-

leges can only hold a limited number of proposals at

a time. Subsequently, a solution is derived to match

students with colleges based on their preferences and

constraints, with the goal of optimizing criteria such

as overall satisfaction or fairness. The set of n EDCs

State-Aware Application Placement in Mobile Edge Clouds

121

E can be compared to the set of n colleges, in which

each e

∈ E has a designated “quota” C

. Similarly,

the set of m requested applications, to be assigned to

the n EDCs, can be compared to the m applicants to

be assigned to the n colleges. Inspired by this parallel,

we introduce the App EDC Macth placement strategy

leveraging the Gale-Shapley algorithm as presented in

Algorithm 1.

The algorithm receives inputs that encompass the

application placement solution from time t − 1, com-

pute resource availability at each EDC, and band-

width availability at each network link up to time

t (line 1). Subsequently, the algorithm updates the

compute unit price and bandwidth unit price at each

EDC e

and network link l

respectively (line 2).

Moving forward, the algorithm proceeds to construct

the application preference matrix M

app

(n× m), where

each column p ranks EDCs in decreasing order of the

operating cost incurred when placing application p on

them (line 3). Similarly, the algorithm formulates an

EDC preference matrix M

edc

(m × n), where each col-

umn i ranks the requested applications in decreasing

order of the bandwidth consumption when placed on

EDC e

(line 4). This preference ensures that each ap-

plication is hosted on an EDC that minimizes network

congestion. Finally, it invokes the matching method

to perform the assignment, using the two matrices

above as inputs (line 5).

For n EDCs and m applications, the time com-

plexity of the App EDC Match placement strategy is

O(n × m).

1: Input: The application placement from t − 1,

Datacenters resource capacity up to t,

Network links bandwidth capacity up to t,

User locations u

and workload W = λ

k,t

at t

2: Update: compute unit price of each EDC i,

bandwidth unit price of each network link j

3: Calculate M

app

(n × m) – the application prefer-

ence matrix, in which each column p ranks EDCs

in the order of resulting lowest operating cost if

application p is placed on it

4: Calculate M

edc

(m × n) – the EDC preference

matrix, in which each column i rank applications

in the order of consuming least bandwidth

5: Matching (M

app

, M

edc

)

6: return s

k,i

, cost

Algorithm 1: App EDC Match placement strategy.

4 EXPERIMENTAL SETTING

This section presents our simulation-based evalua-

tion. First, we describe an MEC infrastructure with

EDCs distributed in a metropolitan area connected in

Figure 2: Distribution of 6 EDCs collocated with cellular

base stations in layer 1.

tree topology. Then, we describe the parameters of

simulated applications and end-users workload. Fi-

nally, we describe the implementation and setup of

our proposed placement algorithm, as well as the

baseline placement algorithm.

4.1 Infrastructure: an MEC Platform

We simulate a hierarchical MEC platform with EDCs

distributed over a metropolitan area, drawing on a pre-

viously reported MEC model (Mehta et al., 2016).

The capacities of EDCs in different layers and their

compute unit price (min, max) are presented in Ta-

ble 1 together with the capacities and prices of the net-

work links between subsequent layers. The physical

network links between layer 1 and layer 2 are mod-

eled as OC-3 (i.e., optical carrier level 3), while the

links between layer 2 and layer 3 are modeled as OC-

12.

EDCs in layer 1 are distributed across the area

and collocated with base stations, allowing end-users

to connect directly. The geo-coordinates of theses

EDCs are taken from a dataset of the real-world loca-

tions of cellular towers in San Francisco, US

. From

this dataset we selected 6 different tower locations as

layer 1 EDC deployment sites, as shown in Figure 2.

While datacenter deployment is not the main focus

of the current work, the locations were selected to

maximize the coverage of areas with high densities of

end-users in the experimental mobility trace dataset,

as discussed in Section 4.3.

http://www.city-data.com/towers/cell-San-Francisco-

California.html

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

122

Table 1: Experiment Conﬁguration.

MEC topology

Layer

Capacity

(#VMs)

Cost

($/CPU-h)

1 150 (0.115, 0.206)

2 1500 (0.091, 0.127)

3 15000 (0.075, 0.086)

Netwok Link

Link

Capacity

(Mbps)

Cost

($/GB)

OC3 155 (0.3078, 0.46)

OC12 622 (0.98, 1.47)

Application

(CPU-h/GB)

(0.01, 10)

4.2 Application

We simulate different applications speciﬁed by

their resource usage. We use the compute-

bandwidth-usage-ratio per user (CPU-h/GB), de-

noted as A

(Mehta et al., 2016), which is in range

of [0.01,10] to generate 10 different applications with

different CPU usage and bandwidth usage. Addition-

ally, each application has an average state size that

determines the bandwidth required to transfer the ap-

plication’s state during a migration action. In stateful

application migration, there is a general tendency that

links the size of the migrating operator with the in-

coming data rate: the higher the load, the larger the

saved state (Cardellini et al., 2016). Therefore, for

the sake of simplicity, we model the state size as a

linear function of the average bandwidth usage of the

application:

state size = ν × bandwidth usage

(19)

Here, ν is a uniform random deviate in the range

(0.5,1).

4.3 User Mobility and Workload

We use real mobility traces of San Francisco-based

Yellow cab vehicles (Piorkowski et al., 2009) to sim-

ulate user mobility because the data reﬂect the move-

ments of end-users (i.e., taxi) in the same geographic

area as our simulated MEC. Speciﬁcally, the dataset

traces the mobility behavior of 536 taxi cabs in the

San Francisco Bay area over 25 days starting on May

17th, 2008. The original dataset contains 4 attributes:

longitude, latitude, datetime, and number of people

in the car. We preprocess the trace to remove all

invalid records by setting a maximum velocity of

max

= 115km/h based on the relevant urban trafﬁc

regulations.

We assume that the locations of users do not

change within any given time slot t, but may change

from one time slot to another. We set the length of

a time slot to 1 minute. In each time slot t, a user

connects to an application hosted on the MEC. The

session length is the smallest integer greater than or

equal to an exponential random variable with a rate

parameter of:

rate =

average session length

(20)

where average session length is the average ses-

sion duration for users using a speciﬁc application.

This parameter was set to values corresponding to the

average session duration of virtual reality users in the

United States during the 2nd and 3rd quarters of 2019,

as reported in (Observer Analytics, 2022). For every

time slot t, we check if the current session is over.

If the session is over, the user uniformly selects an-

other application. The simulation records the follow-

ing data for each user in every time slot: the layer 1

EDC to which the user connects, the application to

which the user is linked, and the allocated amounts of

CPU, bandwidth, and state size.

4.4 Off-line Placement Strategy -

Precognition Strategy

To evaluate the performance of our algorithm, we

compare it to the following approximately optimal

off-line placement strategy. The strategy is precogni-

tion because it has access to complete future informa-

tion for the whole time window of T . Speciﬁcally, it

is aware of end-users’ locations, their requested appli-

cations, and the available capacity of each EDC and

network link at every time slot in T . While such fu-

ture information is not available in a real-world set-

ting, this approach allows us to determine how close

our proposed placement algorithm is to an approach

based on perfect information. To this end, we ap-

ply Simulated annealing (SA) (Van Laarhoven and

Aarts, 1987), a meta-heuristic technique, to ﬁnd the

approximate global optimum. In essence, given all

the above-mentioned information over time window

T , we transform the placement problem into a prob-

lem of ﬁnding the shortest path. We use a graph

G = (V , E) to represent all the possible placement

decisions within T , in which the weight put on each

edge between two vertices (in successive time slots)

is the operating cost returned for each time slot t ∈ T .

Hence, the shortest path from the starting vertex (i.e.,

when t = −1) to the end vertex (i.e., when t = T + 1)

corresponds to the minimum total operating cost for

the whole time window T . The pseudo-code of the

precognition strategy is presented in Line 2.

State-Aware Application Placement in Mobile Edge Clouds

123

The input of the algorithm are data on the MEC

system including the compute resource capacity of the

EDCs, the bandwidth capacity of the network links,

and complete workload information for a time win-

dow T . The Simulated Annealing algorithm also re-

quires the speciﬁcation of two parameters: the Tem-

perature T, which must be sufﬁciently high; and the

CoolingFactor c ∈ (0,1), which determines the ex-

pected time budget for the algorithm to seek solutions.

Initially, the algorithm takes the best solution returned

by the proposed algorithm as the starting point (line

2). This is done to initialize it with the best solution

found so far, avoiding the algorithm starting with a

worse solution. For each iteration of the loop (line 3 -

9), the algorithm generates a neighboring solution by

randomly shaking the current solution (i.e., changing

the placement at a speciﬁc time slot t). The algorithm

then determines whether the new solution will be ac-

cepted or not using a probability method (line 6). The

new solution is selected as the best solution if its cost

less than the best cost (line 7).

With N EDCs, K users, and a time window of

length T , there are in total (N

)

possible solutions

in the search space. Therefore, if these parameters are

set to large numbers, it is impossible for the precogni-

tion algorithm to ﬁnd the optimum solution in a ﬁxed

amount of time. Hence, we run the algorithm using

small values of these parameters in the experiments.

The approximate minimum operating cost returned by

the precognition strategy is taken as a benchmark for

evaluating how close the App EDC Match placement

strategy get to the global optimum.

4.5 Evaluation Metrics

We evaluate the performance of our approach based

on the following metrics:

• Total Cost: As previously deﬁned in Section 2,

this metric serves as a benchmark for the algo-

rithm’s effectiveness, with the goal of minimizing

overall costs P.

• Resource Usage: We measure the utilization of

EDCs and network links. This gives us an indi-

cation of the behavior of each placement strategy

and their ability to avoid capacity shortage.

• Mean Execution Time: This metric measures the

time required by the placement algorithm to make

placement decisions.

Our experiments were conducted on a single-threaded

PC equipped with an Intel i7-4790 CPU and 32 GB of

RAM.

1: Input: Temperature T ,

Cooling factor c,

Initial placement s

and its operating cost cost

Datacenters resource capacity,

Network links bandwidth capacity,

User locations and workload in the whole time

window W

2: Initialize: s

best

← s

cost

best

← cost

current

← s

cost

current

← cost

temp

current

← T

3: do

4: Create new solution s

new

by randomly

5: taking a neighbor of s

current

6: Calculate cost

new

for s

new

7: if Math.random() < e

cost

current

−cost

new

temp

current

then

current

← s

new

cost

current

← cost

new

end

8: if cost

current

< cost

best

then

best

← s

current

cost

best

← cost

current

end

9: temp

current

← temp

current

× c

10: while temp

current

> 1

11: return s

best

and cost

best

Algorithm 2: Precognition placement strategy.

5 RESULT AND DISCUSSION

In this section, we present the experimental results

obtained and provide a comprehensive discussion on

the efﬁcacy of the proposed placement strategy by ad-

dressing various questions below.

5.1 How Does the Achieved Total

Operating Cost Using the Proposed

Placement Algorithm Compare to

that of the Baseline Algorithm?

The goal of addressing this question is to quantita-

tively assess how well the proposed online placement

strategy performs in terms of cost savings compared

to the ofﬂine placement strategy. As mentioned ear-

lier, when dealing with a large search space, the pre-

cognition placement strategy cannot ﬁnd an approxi-

mate optimal solution within a reasonable time frame.

Therefore, we conduct experiments with a reduced

number of users and a shortened time window. To

achieve this, we randomly select an appropriate num-

ber of users and their corresponding workloads within

the reduced time window, all derived from the original

trace. For the precognition strategy, we set the Tem-

perature parameter to 10e+11, and the CoolingFac-

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

124

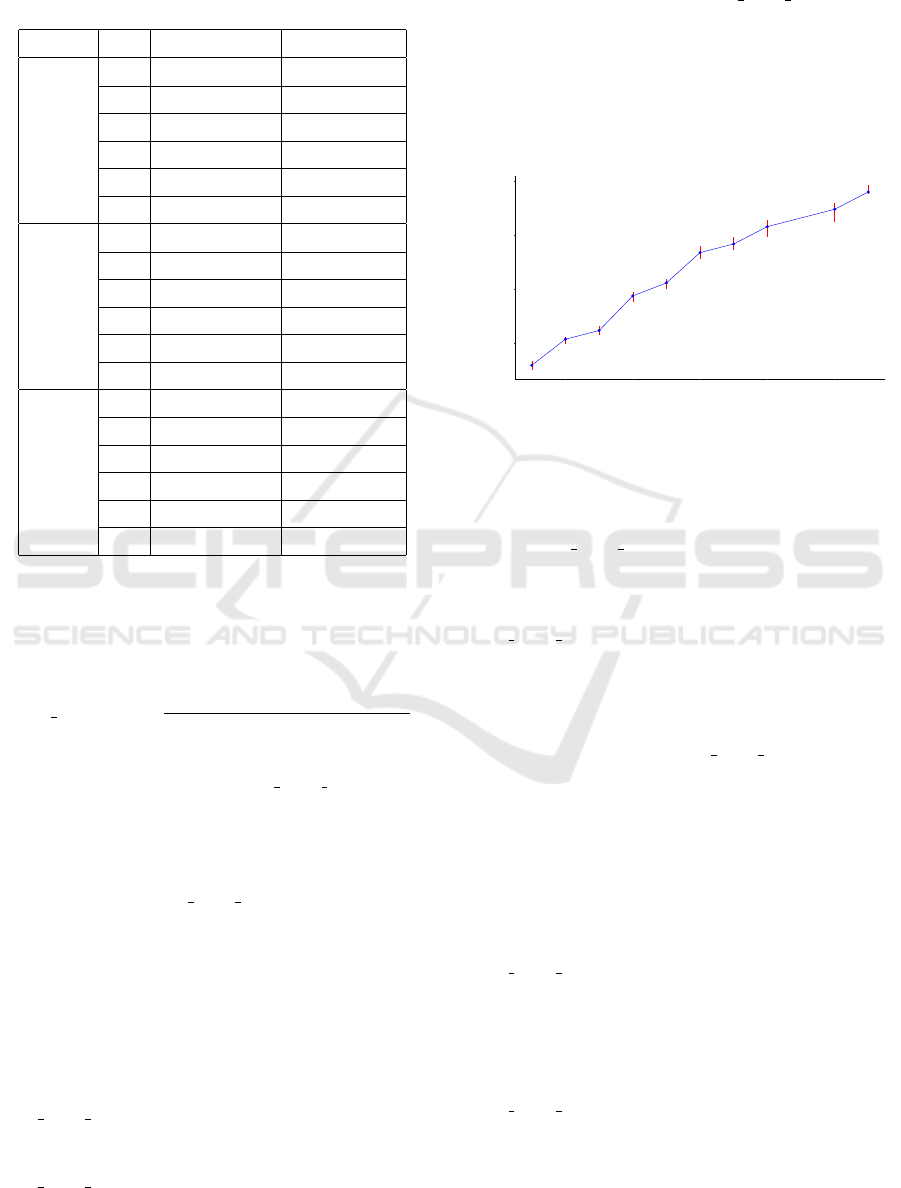
Table 2: The total operating cost difference between the

proposed strategy and the precognition strategy in differ-

ent experiment settings. CompInApp: Compute-intensive

application; BandInApp: Bandwidth-intensive application.

#User T CompInApp BandInApp

1 0 0

3 0.05 0.05

5 0.07 0.07

10 0.05 0.08

20 0.05 0.02

30 0.05 0.01

1 0 0

3 0.03 0.02

5 0.02 0.03

10 0.05 0.07

20 0.02 1.5e−3

30 0.01 0.01

1 0 0

3 0.04 0.03

5 0.05 0.06

10 4.8e−3 4.4e−3

20 0.03 0.03

30 0.03 0.02

tor parameter to 0.995, to ensure it obtains a solution

within a reasonable amount of time. We collect the re-

sults obtained from both algorithms and calculate the

deviation in total operating costs using the following

formula:

cost difference =

cost

(proposed)

− cost

(precognition)

cost

(precognition)

In Table 2, we show the differences in total operat-

ing costs achieved with the App EDC Match strat-

egy and the precognition strategy across different set-

tings of numbers of users (i.e., 3, 5, and 10 users)

and time window lengths (i.e., 1, 3, 5, 10, 20, and

30 time slots). As observed, the total operating costs

achieved with the App EDC Match placement strat-

egy are pretty close to the approximate optimal val-

ues returned by the precognition strategy, with a max-

imum deviation of approximately 8%.

5.2 What Are The Execution Times of

the Proposed Placement Algorithm?

We now evaluate the scalability of the

App

EDC Match placement strategy and its suit-

ability for real MECs, where real-time decision-

making is crucial. As presented in Section 3, the

App EDC Match strategy’s execution time depends

on the number of EDCs n and the number of users

m, i.e., its time complexity is O(n × m). To verify

that the execution time of App EDC Match scales

linearly with the number of users in a ﬁxed MEC

infrastructure, we measure the mean execution time

per time slot for the proposed strategy with varying

number of users. In essence, we use the same emu-

lated MECs as in previous experiments and increase

the number of users per experiment.

100

1000 2000 3000 4000 5000

# Number of Users

Mean Execution Time Per Time Slot (msec)

Figure 3: Mean execution time per time slot for the pro-

posed online placement strategy with the number of users

ranging from 500 to 5500. The red vertical line connects

the maximum and minimum observed execution times.

Figure 3 shows the mean execution time per time

slot of App EDC Match as the number of users is

raised from 500 to 5500 users. As observed, the exe-

cution time per time slot increases linearly with the

number of users. Moreover, the execution time of

App EDC Match starts off considerably lower but ex-

periences a rapid increase. Nonetheless, the execution

times per time slot remain reasonably small, staying

below 100 ms for the experiment with 5500 users,

which is well below the length of the time slots (1

minute). As a result, the App EDC Match algorithm

is well-suited for deployment in real MEC systems to

rapidly determine placement solutions that approach

the near-global optimum.

5.3 Where Are Applications Placed by

the Proposed Algorithm?

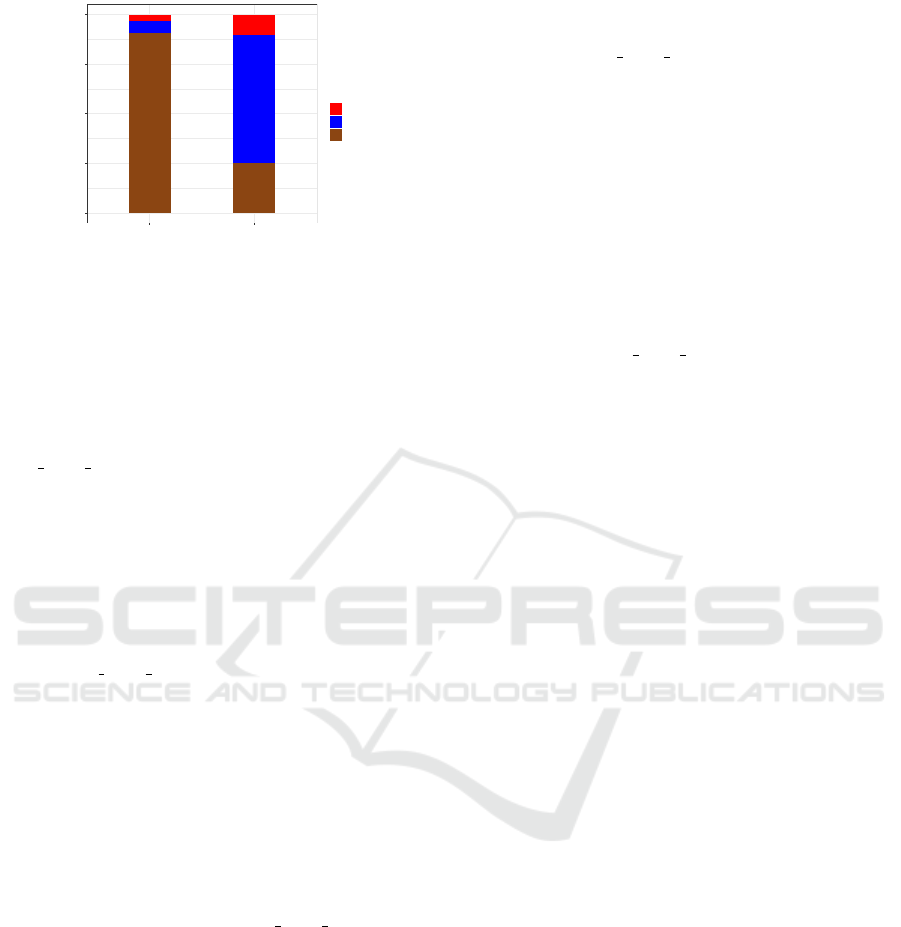
We analyse the results produced by the

App EDC Match placement strategy to better

understand its behavior. Figure 4 shows the dis-

tribution of applications throughout the entire

experiment. For the bandwidth-intensive applica-

tions, to minimize network bandwidth utilization

and thereby reduce overall operational costs, the

App EDC Match strategy prioritizes the placement

of applications on the EDC to which the application’s

users directly connected. Consequently, 91% of

bandwidth-intensive applications are placed on the

State-Aware Application Placement in Mobile Edge Clouds

125

0.00

0.25

0.50

0.75

1.00

BandwidthInt. ComputeInt.

Application Type

Percentage

Place_at

L−3

L−2

L−1

Figure 4: Behavior of the proposed placement strategy

with bandwidth-intensive (BandwidthInt.) and compute-

intensive (ComputeInt.) applications. L-1, L-2, L-3 denote

layers 1, 2, and 3 in the emulated MEC, respectively.

connecting EDCs of the users, while approximately

5.8% are placed on layer 2 EDCs, and the remaining

3.2% being placed on layer 3 EDCs.

In case of compute-intensive applications, the

App EDC Match strategy leverages higher-capacity

resources from EDCs in upper layers, which typi-

cally offer lower compute resources unit prices. More

speciﬁcally, approximately 25.1% of the compute-

intensive applications are placed on the EDCs directly

connected to users, while a larger portion, roughly

64.5% are placed on layer 2 EDCs, and the remain-

ing 10.4% of these applications are placed on layer

3 EDCs. These observed results show the effective-

ness of App EDC Match in achieving a balanced and

efﬁcient utilization of resources within MEC infras-

tructure.

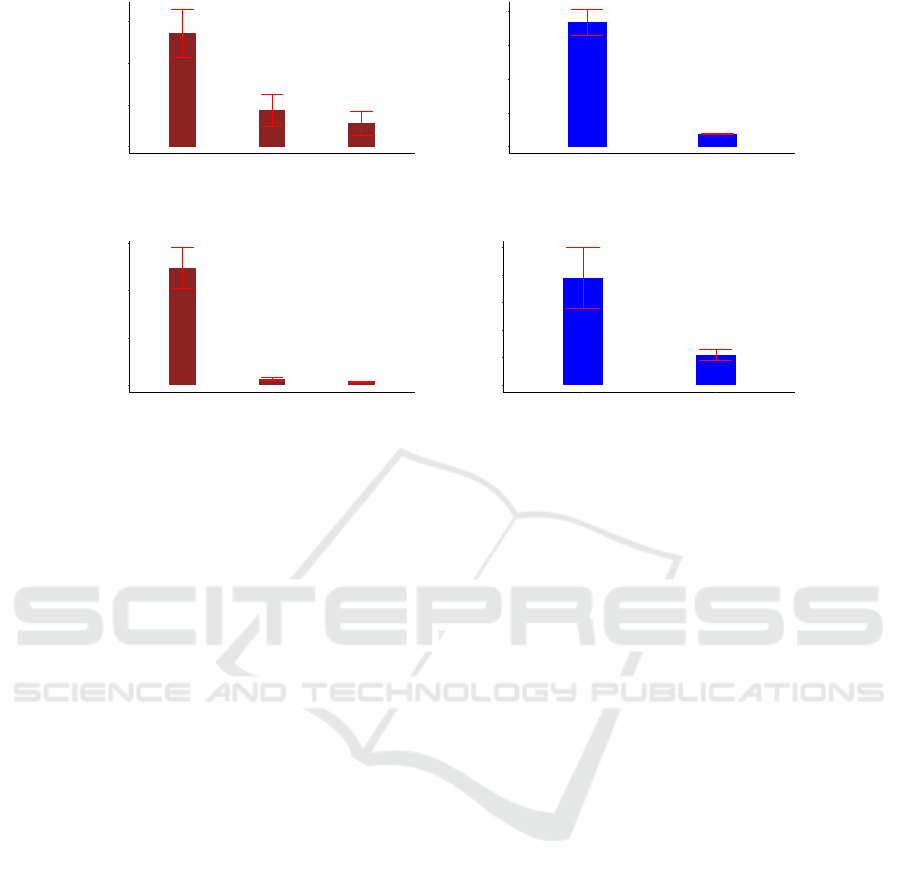
Taking the analysis a step further, we investigate

the utilization of compute resources within EDCs

at each layer and the utilization of network band-

width (expressed as a percentage of the total capac-

ity) in network links during a peak workload scenario

characterized by a high volume of concurrent users.

Figure 5 shows the experimental results with com-

pute intensive applications. In the previous exper-

iment, we observed that the App EDC Match strat-

egy effectively distributes compute intensive applica-

tions leveraging the greater computing capabilities of

EDCs in higher layers (layer 2 and 3). As a result, the

workload is not signiﬁcantly concentrated in EDCs in

layer 1, leading to average resource utilization rates

of 54.2% for EDCs in layer 1, 17.5% for EDCs in

layer 2, and 11.4% for EDCs in layer 3 (Figure 5a).

Regarding bandwidth usage, we observe an average

bandwidth usage of 11.9% on the links connecting

layer 2 and layer 3, while the links connecting layers

1 and 2 exhibited an average bandwidth utilization of

18.3% (Figure 5b).

Figure 6 presents the experimental results related

to bandwidth-intensive applications. Since these ap-

plications demand fewer compute resources, we ob-

serve that the App EDC Match strategy primarily uti-

lizes compute resources from EDCs in layer 1. This

results in an average resource usage of 24.8% for

EDCs in this layer, while the corresponding values

for EDCs in layers 2 and 3 are 1.3% and 0.8%, re-

spectively (Figure 6a). Consequently, this applica-

tion placement pattern impacts bandwidth usage in

the network links. There is a higher concentration of

bandwidth utilization on the links connecting layer 1

and layer 2, with an average of 3.9%. In contrast,

the links between layer 2 and layer 3 demonstrate

less concentrated bandwidth usage, averaging 1.1%

(Figure 6b). These results not only show the effec-

tiveness of the App EDC Match placement strategy,

but also provide further conﬁrmation of the ﬁndings

in (Mehta et al., 2016), which underscore the advan-

tages of introducing intermediate layers of EDCs, in-

cluding cost savings, prevention of compute capacity

shortages, and the mitigation of network congestion

within MECs environment.

6 RELATED WORK

In this section, we explore research efforts addressing

the MEC application placement problem.

Ouyang et al. (Ouyang et al., 2019) introduced an

online service placement method for MECs, priori-

tizing user latency and service migration cost. Their

approach utilizes a Thompson-sampling based on-

line learning algorithm to adaptively select service

locations based on user preferences, resulting in im-

proved performance compared to alternative methods,

as demonstrated through theoretical analysis and per-

formance evaluation. Farhadi et al. (Farhadi et al.,

2021) introduced a two-time-scale framework for op-

timizing service placement and request scheduling,

considering various constraints. Their algorithms

demonstrated efﬁcient polynomial-time performance

and consistently achieved high optimization levels.

Similarly, Gao et al. (Gao et al., 2021) addressed on-

line service placement in MECs, dividing it into se-

lecting the access network and determining service

deployment locations. They aimed to enhance QoS by

balancing factors like access and communication de-

lays, using an iterative-based algorithm to approach

optimality. Smolka et al. (Smolka et al., 2023) pro-

posed a decentralized method for dynamic edge ap-

plication placement. Each edge node autonomously

decides through auctions to minimize application la-

tency individually.

These previous works primarily focus on high-

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

126

L−1 L−2 L−3

Layer

Average Resource Usage %

a Compute resource usage.

L−1 to L−2 L−2 to L−3

Network Link

Average Bandwidth Usage %

b Bandwidth usage.

Figure 5: Experiment with compute-intensive applications.

L−1 L−2 L−3

Layer

Average Resource Usage %

a Compute resource usage.

L−1 to L−2 L−2 to L−3

Network Link

Average Bandwidth Usage %

b Bandwidth usage.

Figure 6: Experiment with bandwidth-intensive applications.

level abstractions of applications and are most efﬁ-

cient when dealing with general, stateless applica-

tions. Our work builds upon these existing efforts,

particularly in understanding the cost components as-

sociated with application placement operations. Nev-

ertheless, we incorporate additional aspects to our

approach to the problem. Firstly, we consider dy-

namic workloads that vary from one time slot to an-

other. Secondly, we explicitly incorporate data ex-

change costs, especially the bandwidth cost, along the

network path connecting the EDC co-located with the

nearest tower to the end-user and the EDC responsible

for managing the end-user’s workload.

7 CONCLUSION AND FUTURE

WORK

In this paper, we tackle the challenge of deploy-

ing stateful applications in MEC environments. Our

approach begins with a comprehensive modeling of

the anticipated workloads, applications, and MEC in-

frastructures. Subsequently, we deﬁne and analyze

the various costs associated with application opera-

tion, encompassing resource utilization costs, migra-

tion cost, and the costs incurred due to service qual-

ity degradation. Lastly, we introduce an efﬁcient on-

line placement algorithm driven by the Gale-Shapley

matching algorithm. The experiments reveal that the

proposed algorithm enables MECs to make swift de-

cisions on allocating capacity for applications, result-

ing in total operating costs that are no more than 8%

higher than the approximate global optimum obtained

from an ofﬂine precognition algorithm. Moreover, it

effectively facilitates workload balancing, mitigating

resource scarcity challenges for MECs.

We envision several promising directions for fu-

ture research. While the proposed placement algo-

rithm treats all applications equally, it is essential

to acknowledge that real-world scenarios often in-

volve mission-critical applications with strict local-

ity requirements. These applications necessitate be-

ing hosted on resources from EDCs in close proxim-

ity to end-users. As a result, we intend to enhance

the application model presented in this study to incor-

porate application priorities. Subsequently, we will

adapt our proposed placement algorithms to account

for these priority considerations. Secondly, we plan

to explore distributed placement algorithms designed

for deployment across all EDCs. Ideally, these dis-

tributed algorithms should exhibit execution times in-

dependent of the number of EDCs. This investiga-

tion aims to further optimize and scale our placement

strategies in large-scale MEC environments.

ACKNOWLEDGEMENTS

This work was partially supported by the Knut

and Alice Wallenberg Foundation, both directly and

through the Wallenberg AI, Autonomous Systems

and Software Program (WASP), as well as by the

State-Aware Application Placement in Mobile Edge Clouds

127

eSSENCE strategic research programme.

REFERENCES

Apat, H. K., Nayak, R., and Sahoo, B. (2023). A com-

prehensive review on internet of things application

placement in fog computing environment. Internet of

Things, page 100866.

Bartolomeo, G., Yosoﬁe, M., B

aurle, S., Haluszczynski,

O., Mohan, N., and Ott, J. (2023). Oakestra: A

lightweight hierarchical orchestration framework for

edge computing. In 2023 USENIX Annual Technical

Conference (USENIX ATC 23), pages 215–231.

Cardellini, V., Nardelli, M., and Luzi, D. (2016). Elastic

stateful stream processing in storm. In 2016 Interna-

tional Conference on High Performance Computing &

Simulation (HPCS), pages 583–590. IEEE.

Dally, W. J. and Towles, B. P. (2004). Principles and prac-

tices of interconnection networks. Elsevier.

Ellis, S. R., Mania, K., Adelstein, B. D., and Hill, M. I.

(2004). Generalizeability of latency detection in a

variety of virtual environments. In Proceedings of

the Human Factors and Ergonomics Society Annual

Meeting, volume 48, pages 2632–2636. SAGE Publi-

cations Sage CA: Los Angeles, CA.

Farhadi, V., Mehmeti, F., He, T., La Porta, T. F., Kham-

froush, H., Wang, S., Chan, K. S., and Poularakis, K.

(2021). Service placement and request scheduling for

data-intensive applications in edge clouds. IEEE/ACM

Transactions on Networking, 29(2):779–792.

Fisher, M. L., Jaikumar, R., and Van Wassenhove, L. N.

(1986). A multiplier adjustment method for the gen-

eralized assignment problem. Management science,

32(9):1095–1103.

Gale, D. and Shapley, L. S. (1962). College admissions and

the stability of marriage. The American Mathematical

Monthly, 69(1):9–15.

Gao, B., Zhou, Z., Liu, F., Xu, F., and Li, B. (2021). An on-

line framework for joint network selection and service

placement in mobile edge computing. IEEE Transac-

tions on Mobile Computing, 21(11):3836–3851.

Kavak, N., Wilkinson, A., Larkins, J., Patil, S., and Frazier,

B. (2015). The central ofﬁce of the ict era: Agile,

smart, and autonomous. Ericsson Technol. Rev, 93:1–

13.

Li, R., Zhou, Z., Zhang, X., and Chen, X. (2022). Joint

application placement and request routing optimiza-

tion for dynamic edge computing service manage-

ment. IEEE Transactions on Parallel and Distributed

Systems, 33(12):4581–4596.

Mehta, A., T

arneberg, W., Klein, C., Tordsson, J., Kihl,

M., and Elmroth, E. (2016). How beneﬁcial are inter-

mediate layer data centers in mobile edge networks?

In 2016 IEEE 1st International Workshops on Foun-

dations and Applications of Self* Systems (FAS* W),

pages 222–229. IEEE.

Moore, H. L. (1925). A Moving Equilibrium of Demand

and Supply. The Quarterly Journal of Economics,

39(3):357–371.

Moudi, M. and Othman, M. (2020). On the relation between

network throughput and delay curves. Automatika,

61(3):415–424.

Nguyen, C., Klein, C., and Elmroth, E. (2019). Multivari-

ate lstm-based location-aware workload prediction for

edge data centers. In 2019 19th IEEE/ACM Interna-

tional Symposium on Cluster, Cloud and Grid Com-

puting (CCGRID), pages 341–350. IEEE.

Observer Analytics (2022). Average session time of vr users

in the US q2 - q3 2019, by user type. Accessed on

12/12/2023.

Ouyang, T., Li, R., Chen, X., Zhou, Z., and Tang, X.

(2019). Adaptive user-managed service placement for

mobile edge computing: An online learning approach.

In IEEE INFOCOM 2019-IEEE Conference on Com-

puter Communications, pages 1468–1476. IEEE.

Pantel, L. and Wolf, L. C. (2002). On the impact of delay

on real-time multiplayer games. In Proceedings of the

12th international workshop on Network and operat-

ing systems support for digital audio and video, pages

23–29.

Piorkowski, M., Saraﬁjanovoc-Djukic, N., and Gross-

glauser, M. (2009). CRAWDAD dataset epﬂ/mobility

(v. 2009-02-24). Downloaded from https://crawdad.

org/epﬂ/mobility/20090224.

Shang, X., Huang, Y., Mao, Y., Liu, Z., and Yang, Y. (2022).

Enabling qoe support for interactive applications over

mobile edge with high user mobility. In IEEE INFO-

COM 2022-IEEE Conference on Computer Commu-

nications, pages 1289–1298. IEEE.

Smolka, S., Wißenberg, L., and Mann, Z.

A. (2023).

Edgedecap: An auction-based decentralized algo-

rithm for optimizing application placement in edge

computing. Journal of Parallel and Distributed Com-

puting, 175:22–36.

Tong, L., Li, Y., and Gao, W. (2016). A hierarchical edge

cloud architecture for mobile computing. In IEEE IN-

FOCOM 2016-The 35th Annual IEEE International

Conference on Computer Communications, pages 1–

9. IEEE.

Van Laarhoven, P. J. and Aarts, E. H. (1987). Simulated

annealing. In Simulated annealing: Theory and ap-

plications, pages 7–15. Springer.

Wang, S., Zafer, M., and Leung, K. K. (2017). Online place-

ment of multi-component applications in edge com-

puting environments. IEEE Access, 5:2514–2533.

Yang, B., Chai, W. K., Xu, Z., Katsaros, K. V., and Pavlou,

G. (2018). Cost-efﬁcient nfv-enabled mobile edge-

cloud for low latency mobile applications. IEEE

Transactions on Network and Service Management,

15(1):475–488.

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

128