Generating Products Placement in Warehouse Using

BLPSO and MIQCPs

Ayaka Sugiura

, Takahiro Suzuki

, Koya Ihara

2 a

, Takuto Sakuma

and Shohei Kato

1,2 b

Graduate School of Engineering, Nagoya Institute of Technology, Japan

NITech AI Research Center, Nagoya Institute of Technology, Japan

Keywords:

Optimization in Logistic Warehouse, Products Layout Generation, Particle Swarm Optimization, BLPSO,

Mixed Integer Quadratic Constraints Programming Problems.

Abstract:

Expansion of the e-commerce market due to the development of the Internet has increased in the volume of

distribution, and the number of operations in distribution warehouses had also increased. Picking operation

is one of the most important tasks, and companies are trying to make this task more efﬁcient by introducing

autonomous mobile robots (AMRs), which transports products manually picked to a depot. In this study,

we propose a method to generate product assignments that make picking operations more efﬁcient through

a two-step optimization process. First, product assignments for utilizing AMRs are generated using particle

swarm optimization. Next, in-shelf products layout is generated by mathematical optimization for the products

group assigned to the shelves. In product placement optimization, one of the approximate solution methods

of the metaheuristic, BLPSO, is fused with a class-based warehouse to obtain an optimal solution. In addi-

tion, the problem of in-shelf product layout is formulated in MIQCPs. The constraint expression is used to

generate a layout that considers preventing picking mistakes and ensuring the safety of the picker. We have

conducted placement optimization experiments using real-world logistic data and discuss the effectiveness of

the proposed method.

1 INTRODUCTION

Logistics is an indispensable part of human life, and

the development of e-commerce via the Internet has

led to the sale and purchase of a variety of goods. As

logistics volumes increase, large-scale logistics ware-

houses with high logistics efﬁciency are required. Lo-

gistics warehouses play a wide role as logistics bases;

in particular, picking operations account for more

than 50% of the total operational costs (Koster et al.,

2007).

Many companies are trying to make picking oper-

ations more efﬁcient by introducing low-cost Au-

tonomous Mobile Robots (AMRs). AMRs are robots

that move through a facility along a predetermined

route and carry products that have been manually

picked. They are easy to install and can also serve

as unloading points (drop-off points) for products col-

lected by pickers, allowing for more drop-off points.

It is expected to reduce the travel distance required

https://orcid.org/0000-0002-5473-0864

https://orcid.org/0000-0003-4130-2729

for picking. However, it is difﬁcult to use AMRs to

the fullest extent in existing product placement. In

addition, in order to make practical use of product as-

signment that can take advantage of AMR, it is nec-

essary to determine in-shelf product layout that can

make manual picking operations safe and efﬁcient. In

this study, product placement is generated through a

two-stage optimization process, shown in Figure 1,

to make efﬁcient manual picking operations possible.

First, particle swarm optimization (PSO) generates

product assignments to use AMRs to the fullest ex-

tent. Next, mixed integer quadratic constraints pro-

grammings (MIQCPs) is used to generate in-shelf

product layouts for the product groups generated by

product assignment optimization. For product assign-

ment optimization, we use BLPSO, a combination of

evy ﬂight and PSO. PSO is given four initial solu-

tions: two class-based storage, current placement, and

random placement, to compare picking costs before

and after optimization. Two class-based storage takes

into account two drop-off points and divides shelves

into classes. In-shelf product layout optimization us-

ing mathematical optimization generates an in-shelf

454

Sugiura, A., Suzuki, T., Ihara, K., Sakuma, T. and Kato, S.

Generating Products Placement in Warehouse Using BLPSO and MIQCPs.

DOI: 10.5220/0012359600003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 454-461

ISBN: 978-989-758-680-4; ISSN: 2184-433X

Figure 1: Overview of two-stage optimization.

(a) Placement with one class

in each aisle.

(b) Placement ordered by

closeness to depot.

Figure 2: Example of shelf classiﬁcations.

product layout that considers picker safety by plac-

ing heavy product in the lower rows and efﬁciency

by placing frequently shipped products in the middle

rows. The generated in-shelf product layout and the

value of the objective function are compared before

and after optimization, and discussed the effective-

ness. Section 2 describes the product assignment us-

ing PSO, and Section 3 presents the in-shelf product

layout using MIQCPs in detail.

1.1 Related Work

With respect to the product-assignment problem, var-

ious methods exist for assigning storage space, and

class-based storage is one of the most common meth-

ods (Koster et al., 2007). This method divides shelves

and products into classes and randomly assigns them

to the same class. Classes are often divided into

three categories and products are classiﬁed accord-

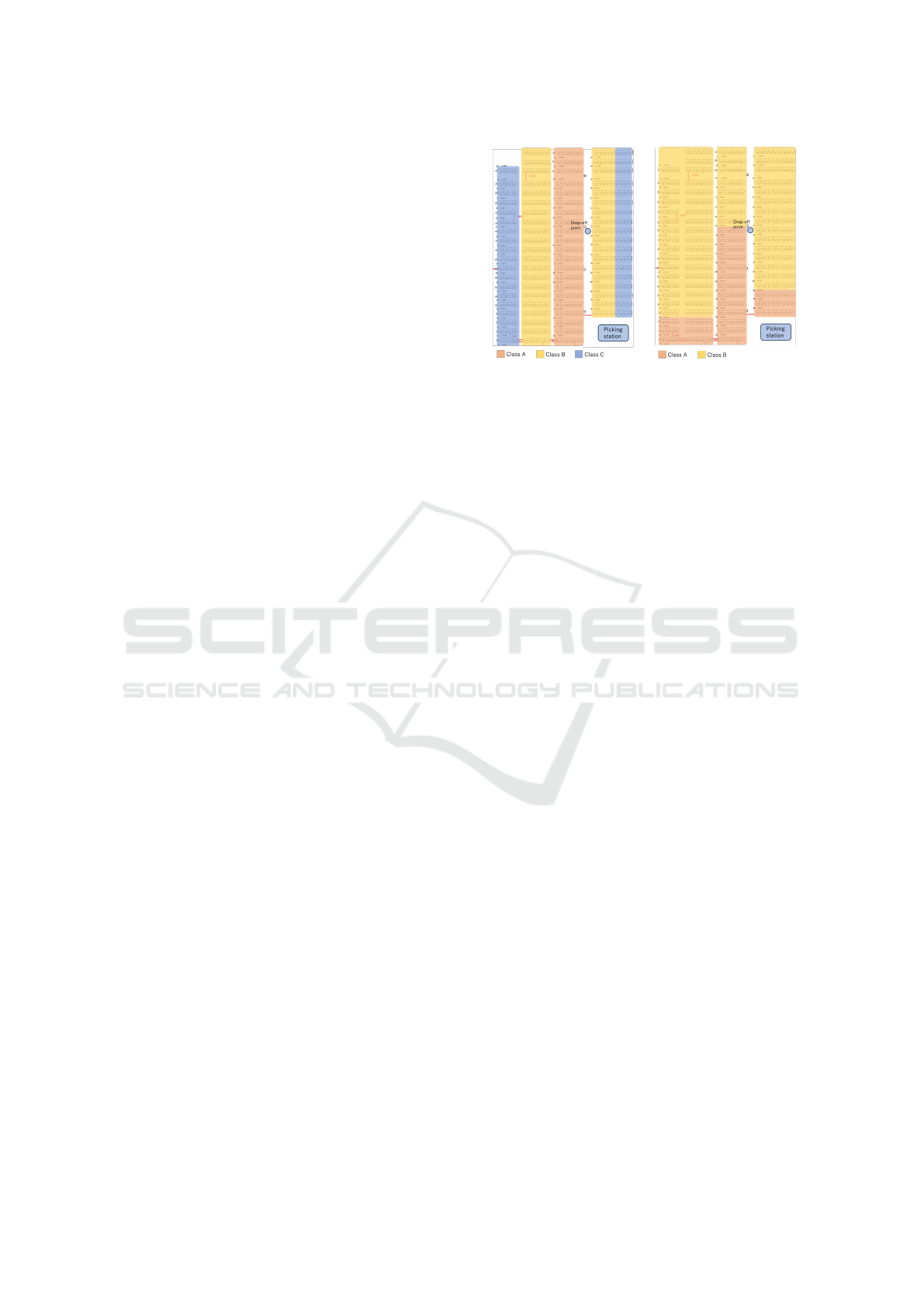
ing to their shipment frequency. Figures 2(a) and (b)

show example of a shelf classiﬁcation. Figure 2(a)

shows a placement in which each aisle contains only

one class, whereas Figure 2(b) shows a placement

in which all shelves containing the products of each

class are placed in the order of the nearest depot.

These placements are simple, yet demonstrate high

performance. However, class-based storage does not

consider the combination of product orders or the dis-

tance traveled between products when picking multi-

ple products in a sequence.

With respect to the in-shelf product layout prob-

lem, the facility layout problem (FLP) involves gen-

erating an optimal layout that ensures lower cost

and more efﬁcient production (P

erez-Gosende et al.,

2021). The layout includes the ﬂoor plan of a

house, the arrangement of rooms in the ofﬁce, or

even the arrangement of speciﬁc facilities, such as

hospitals, in the entire city. Depending on the con-

ditions deﬁned, single-row facility layout problems

(SRFLPs) (Meskar et al., 2020; Cravo and Amaral,

2019) and multi-row facility layout problems (MR-

FLPs) (Anjos and Vieira, 2021; Dahlbeck et al., 2020)

exist, and these methods also vary (Hosseini-Nasab

et al., 2018; Hungerl

ander and Rendl, 2013). Wu et

al. (Wenming et al., 2018) formulated a problem using

mixed integer quadratic programmings (MIQPs), one

of the mathematical optimization, to generate ﬂoor

plan candidates for open-ﬁeld facility layout prob-

lems. The rooms were rectangular polygons opti-

mized in a rectangular layout. Constraints such as

rooms that do not overlap with each other and rooms

placed within a boundary were expressed. Rectangles

were combined by labeling to represent rooms with

complex shapes, such as U- and L-shapes.

2 PRODUCT ASSIGNMENT

PROBLEM BY BLPSO

Product assignment optimization is formulated as

a combinatorial optimization problem. Because

the number of product assignment combinations is

large in the warehouses targeted in this study, meta-

heuristics were used to obtain approximate solu-

tions. Watanabe et al. (Watanabe et al., 2021) pro-

posed a system for product assignment optimization

using BLPSO, a particle swarm optimization algo-

rithm that incorporates l

evy ﬂight and is effective for

high-dimensional problems. The system proposed

by Watanabe et al. optimized the shelves to which

products are assigned, evaluates the candidate solu-

tions generated by the simulator, and updates the solu-

tions. Experimental results showed that BLPSO pro-

duced better solutions than class-based storage, the

current real warehouse placement. However, this sys-

tem does not consider the installation of AMRs or

multiple drop-off points. AMRs are assumed to be

another drop-off point (AP, AMR Point) in addition

to the conventional drop-off point (PS, Picking Sta-

tion).

2.1 Settings

Set of shelves and products with s

s = [s

,...,s

] and

m = [m

,...,m

], and we deﬁned the decision vari-

ables as shelves x

x = [x

,...,x

] where the products

are stored. When x

= s

, product m

is placed on shelf

. For order picking, a picking group (PG) is created

based on the order sheet, which is a group of prod-

ucts to be picked in one trip. Pickers travel around the

Generating Products Placement in Warehouse Using BLPSO and MIQCPs

455

storage area to pick up products by following the PGs

and deliver the collected items to the drop-off points

(PS or AP) by each of the four PGs. In this study, the

distance for picking all PGs G

G = [g

,...,g

] was de-

ﬁned as picking cost and used as objective function.

The objective function f was formulated as follows.

f (x) = distance(x

x,G

G), (1)

where distance(x

x,G

G) indicates the total distance trav-

eled by PG for the picking operation with respect to

product placement x

x. This includes the distance trav-

eled to and from the drop-off points. The volume of

shelf s

was denoted by C

, and the shelf-capacity con-

straint was formulated as follows:

≥ v

(i = 1,...,n

), (2)

∑

{ j|x

}

volume(m

), (3)

where v

is the total volume of products placed on

shelf s

, and volume(m

) is the volume occupied by

product m

2.2 Proposed System

In the current product placement, frequently ordered

products are often stored close to the PS because there

was only one place to drop off the collected products.

Therefore, we proposed a new product placement op-

timization system for efﬁcient use of the AMR in-

stalled in existing warehouses by integrating previous

research on class-based storage and the product as-

signment optimization method using PSO. First, one

of the candidate solutions (product placement) gener-

ated by the PSO algorithm was initialized with a prod-

uct placement created by referring to class-based stor-

age. It aims to place the bestselling products near the

AMR as well, and to optimize the placement. Initial-

ization of the PSO solution is discussed below. The

product assignment was then passed to the simulator,

which was designed by following the actual picking

method. In the simulator, order picking simulation

and constraint calculation were conducted based on

the order data in the product placement. Then, the

algorithm updated the solution by considering the ﬁt-

ness evaluations. Additionally, cargo carts were used

as the new drop-off point, and AMR was used to re-

trieve the cargo.

2.2.1 Updation of the Fitness Function Based on

the Distance Traveled

In this system, the solution was evaluated as the ex-

pected value. The picking cost was deﬁned as the

collection and round-trip distances. The collection

distance is the shortest distance between the products

in PG, and the round-trip distance is the distance be-

tween the products and PS. The round-trip distance

was evaluated based on the expected value. The ﬁt-

ness function f

was formulated as

(x) =

∑

{T SP(x

x,g

) +

dist(x

x,g

) × 2}, (4)

where T SP(x

x,g

) indicates the shortest distance for

collecting all products in PG g

at product place-

ment x

x and is obtained by solving traveling sales-

man problem. Also, n

denotes the total number of

PGs,

dist(x

x,g

) denotes average distances between

each drop-off points and products in g

and was for-

mulated as follows:

dist(x

x,g

) =



outward(PS)+ outward(AP)



+ return(PS,AP), (5)

where outward(PS) and outward(AP) denote out-

ward trip function which return the average dis-

tance between PS, AP and each products in g

return(PS,AP) denotes return trip function which re-

turns the average distance between the nearest drop-

off points (PS or AP) and each products in g

. The

picker returns to the drop-off points after every 4PG.

2.2.2 Initialization of the Particle’s Global Best

Solutions

The initialization effect enables an efﬁcient search

in the warehouse assignment optimization problem

in PSO-based optimization using hints to narrow the

search range without losing the diversity of the initial

population. In this study, multiple product placements

were provided as the initial values of the global solu-

tion gBest, and the product assignment optimization

problem was solved.

2.3 Particle Swarm Optimization

PSO is a stochastic optimization method based on

swarm intelligence and a multi-point search strategy.

Ihara et al. (Ihara et al., 2019) compared PSO with ε

constrained genetic algorithm (εGA), one of a heuris-

tic solution method, and conﬁrmed that PSO is sig-

niﬁcant. Furthermore, Ihara and Kato (Ihara and

Kato, 2020) proposed BLPSO, that extends binary-

PSO (BPSO), which used bit strings as position vec-

tors of particles in PSO, and improved the efﬁciency

of the search by controlling the step size of sampling

candidate solutions from the probability distribution

represented by the position and velocity of particles

by the l

evy distribution. L

evy ﬂight (Fogedby, 1994)

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

456

is a Random Walk whose step length follows the l

evy

distribution. The combination of PSO and l

evy ﬂight

was particularly effective when the number of dimen-

sions of the decision variables and the possible values

for each variable are large. This BLPSO was used to

optimize product assignment.

3 IN-SHELF PRODUCT LAYOUT

PROBLEM BY MIQCPS

The in-shelf product layout was formulated and op-

timized using MIQCPs, a mathematical optimization

method. A typical problem in mathematical optimiza-

tion is the knapsack problem. The problem is to max-

imize value or minimize cost under constraints such

as capacity. Mathematical optimization problems are

composed of constraints and objective functions, all

of which are expressed in mathematical formulas. A

problem in which both the objective function and the

constraints are represented in nonlinear form is called

an MIQCPs, which is an NP-hard problem.

3.1 Settings

Figure 3 shows the shelves used to solve this problem.

The shelves have K rows, and a set of shelves consist

of two shelves facing each other. The two shelves fac-

ing each other are represented by shelf 0 and shelf 1.

Figure 4 shows the product conﬁguration. The prod-

ucts are represented by rectangular polygons that are

small boxes. One face is deﬁned as the state when the

small box is stored as long as possible in the height

and depth directions. The number of faces is obtained

from the number of small boxes stored. In addition,

bulk bolts are particularly large and heavy. These

products should be placed at lower row for safety dur-

ing picking.

3.2 Formulation

It was formulated using an objective function and ﬁve

liner and nonlinear constraints. The inputs were as

follows:

W,H, D : indicate the width, height, and depth of the

shelf.

w, h, d : indicate the width, height, and depth of the

small box.

weight : indicates the weight of the small box.

SR : indicates the rank based on product shipping fre-

quency. We ranked the number of shipments made

in descending order, as calculated from the ship-

ment records.

Figure 3: Settings and size of the shelf to be assumed for

the real world situation(K = 5).

Figure 4: Description of product composition and face

length.

n : indicates the number of boxes to be stored.

α : indicates a combination of similar products. α is

represented by a binary value, and products i and

j are similar when α

i, j

= 1.

β : indicates a bulk bolt. β is represented by a binary

value, and the product i is a bulk bolt when β

= 1.

A rectangle is represented by four parameters

(x, f ace,ε,θ). x is the bottom-left corner x-coordinate

of the rectangle, f ace is the number of faces of the

product, ε is the shelf of the rectangle is stored, and

θ is the row where the product is stored. ε and θ are

deﬁned as a binary variable. These are subject to opti-

mization. The constraints and objective functions are

described in detail as follows:

Inside Constraints

To generate a valid layout, all the products must

be placed inside the shelf. The x-coordinates of

the four vertices of the rectangle representing the

merchandise reside inside the shelf. This con-

straint was formulated as follows:



·W ≤ x

≤ (1 + ε

) ·W

·W ≤ x

+ f ace

· w

≤ (1 + ε

) ·W,

(6)

where 1 ≤ i ≤ N denotes the number of products

assigned to the shelf.

Face Length Constraints

Because the height of the rows varies, the num-

Generating Products Placement in Warehouse Using BLPSO and MIQCPs

457

ber of faces and products that can be stored in

the height direction varies depending on the row

where the product is stored. Product i is placed in

the kth row when θ

i,k

= 1. The face length con-

straint was formulated as follows:

f ace

= round(n

) + 1, (7)

= round(H

) × round(D, d

), (8)

where round(a,b) indicates the integer part of the

a/b quotient, and 1 ≤ k ≤ K denotes the number

of rows in the shelf.

Nonoverlap Constraints

The two rectangles have two directions: right, left,

as determined by the auxiliary binary variable σ.

Rectangle i exists to the right (left) of rectangle j

when σ

i, j



i, j



= 1. The nonoverlap constraint

is formulated as follows:



≥ x

+ f ace

· w

− M(1 − σ

i, j

)

+ f ace

· w

≤ x

+ M(1 − σ

i, j

(9)

∑

{i, j|θ

i,k

=1∩θ

j,k

=1}

{γ∈{right,le f t}}

i, j

= 1, (10)

where M is a large constant and M = W × D.

Then σ

i, j



i, j



= 0, the ﬁrst (second) inequality

is always satisﬁed. Equation (10) ensures that

one of the top two inequalities should be satisﬁed

if product i and product j are same row. The

auxiliary variable σ is automatically assigned

during optimization, and this method is also used

with other constraints.

Weight Constraints

To ensure picking safety, the rows in which heavy

goods are stored must be limited. Bulk bolts

should be placed in below the k

th row, and prod-

ucts other than bulk bolts with a weight of Weight

or more should be placed in rows other than the

1st row. The weight constraint is formulated as

follows:

∑

{i|β

=1}

≥k≥K}

i,k

= 1, (11)

∑

{i|weight

≥Weight}

{2≥k≥K}

i,k

= 1. (12)

Nonadjacent Constraints

Similar products are placed separately to prevent

mix-ups during the picking operation. Figure 5

shows the area in which adjacency is prohibited

Figure 5: Description of the area where product i prohibits

adjacency.

for product i. The non-adjacent constraint, ex-

pressed in terms of the auxiliary binary variable

ρ, is formulated as follows:



· α

i, j

≥ (x

+ 2 f ace

· w

− Mρ

i, j

) · α

i, j

+ 2 f ace

· w

) · α

i, j

≤ (x

+ M(1 − ρ

i, j

)) · α

i, j

{i, j|θ

i,k

= 1 ∩ θ

j,k

(13)



· α

i, j

≥ (x

+ f ace

· w

− Mρ

i, j

) · α

i, j

+ f ace

· w

) · α

i, j

≤ (x

+ M(1 − ρ

i, j

)) · α

i, j

{i, j|θ

i,k

= 1 ∩ θ

j,k+1

(14)

Objective Function

The objective function deﬁnes that items with

high shipment frequency are placed in the prior-

ity row and that heavy items are not placed in the

1st row. The objective function is expressed by as-

signing a penalty for disobedience. The objective

function is deﬁned as follows:

min λ(P

shipment

width

)+(1 −λ)P

weight

, (15)

where λ is the weight that controls the tradeoff

between (P

shipment

width

) and P

weight

. The prod-

uct with the large number of shipments is placed

in the highest priority row. The order of priority

is determined by priority. A penalty is assigned

proportional to the rank of the number of products

shipments and the priority of the row. P

shipment

formulated as follows:

shipment

∑



· θ

i,priority

× k



× φ

(16)

where φ = [φ

,φ

] is the weight that aligns the

value range of the three penalties.

width

is a penalty for placing more products in

highest priority row. P

width

is formulated as fol-

lows:

width

2W −

∑

f ace

· w

· θ

i,priority

× φ

(17)

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

458

weight

is a penalty for the weight of the product

and is applied when a heavier product weighing

less than Wight

is placed in the highest row. The

penalty is proportional to the weight. P

weight

formulated as follows:

weight

∑

(Weight

· θ

i,1

)

× φ

. (18)

4 EXPERIMENTS

We experiment with product data from a logistics

warehouse company. The in-shelf layout is optimized

using the results of product assignment optimization.

Product assignment is implemented in java, and in-

shelf layout is implemented in Python using a solver

”gurobi optimizer”(gur, ). The CPU used in the ex-

periments was AMD Ryzen Threadripper 3970X.

4.1 Experimental Setting

For product assignment optimization, the ﬁtness func-

tion is optimized to minimize. No contingencies are

considered in the simulation environment. Four dif-

ferent product assignments are assigned to the parti-

cles as the initial gBest of the PSO. Data were col-

lected at logistic warehouse of collaborative company

for three months (from December 1, 2021 to February

28, 2022), which was the experimental period. The

ε-constraint method (Tetsuyuki Takahama, 2005) is

employed to handle the capacity constraints. For the

PSO parameters, the group size is set to 10, maxi-

mum number of iterations to 30,000, maximum ve-

locity Vmax to 10.0, and the recommended value in

(Kennedy and Eberhart, 1995). For the l

evy ﬂight,

the scale parameters α = 1.0 and β = 1.5 are set ac-

cording to (Xin-She Yang, 2010). Four different ini-

tial solution gBest placements are given to the PSO

particles. The current placement, within-aisle storage

(WAS), two-class, and random placement. WAS and

two-class classify the shelves into classes, as shown

in the Figure 6. The total volume of shelves in each

class is calculated, and products that ﬁt in the volume

are classiﬁed into the same class according to their or-

der frequency. The shelves and products with match-

ing classes in the current placement are unchanged.

Products whose classes do not match are randomly

assigned to shelves within the class.

The in-shelf product layout generates an in-shelf

layout for each shelf based on the solution obtained

from product assignment. Set parameters based on

real world warehouse: the weight λ = 0.3 and φ =

[0.001,0.01,0.0001] for the objective function. As-

sume that the number of rows K = 5, width W = 820,

(a) Shelf classiﬁcation of

WAS.

(b) Shelf classiﬁcation of

two-class.

Figure 6: Example of shelf classiﬁcations.

height H = [365,300,300,350,360], depth D = 480,

and priority = [3,2,4,5,1]. The parameter Weight

4000 [g] and k

= 3 for heavy products.

4.2 Experimental Results

Table 1 summarizes the results of product assignment,

showing the picking cost (TSP), the distance from the

drop-off point to the shelf, and the total distance be-

fore and after optimization for the four initial solu-

tions gBest. In parentheses are the standard devia-

tions. In the table, the picking cost TSP represents

the shortest distance to collect all the products in the

PG, and the drop-off to the shelf means the distance

between each drop-off point and the products. The re-

duction from gBest is shown in terms of distance and

percentage. The picking cost with the current place-

ment is 1009.0 km, and the experiment with the cur-

rent placement as the initial solution resulted in 965.1

km, a reduction of 43.8 km. On the other hand, for

the class-based WAS and two-class, the initial place-

ment costs were 853.4 km and 952.1 km. Both place-

ments resulted in lower picking costs than the current

placement optimization results. Furthermore, opti-

mizing these two class-based storages further reduced

the picking cost, resulting in a WAS of 845.1 km, the

lowest cost among all methods. When the initial so-

lution was random, the picking cost was large for the

initial placement and was not as high as any of the

methods when optimized. The reduction tended to be

larger the larger the initial picking cost, and the maxi-

mum reduction was 4.3% when the current placement

was used as the initial solution.

An example of the results generated by in-shelf

product layout optimization based on the product

groups determined by product assignment optimiza-

tion is shown in the Figures 7(a) and (b). They show

the results of in-shelf product layout for 45 products

Generating Products Placement in Warehouse Using BLPSO and MIQCPs

459

Table 1: Experimental result of product assignment optimization (SD).

Distance before optimization (km) Distance after optimization (km) Reduction

Total distance TSP

Drop-off

Total distance TSP

Drop-off Distance Percentage

to shelf to shelf (km) (%)

Current 1009.0 809.7 199.2 965.1(4.48) 767.6 197.5 43.8 4.3(0.44)

WAS-stay 853.4 685.2 168.2 845.1(0.95) 677.1 168.0 8.3 0.97(0.11)

Two-class 952.1 763.7 188.4 939.6(1.57) 751.6 188.1 12.4 1.3(0.16)

Random 1149.3 944.4 205.0 1106.3(6.72) 903.0 203.3 43.0 3.7(0.59)

(a) shelf 0. (b) shelf 1.

Figure 7: Result of generating in-shelf product layouts for

Shelf ’12B05Q’.

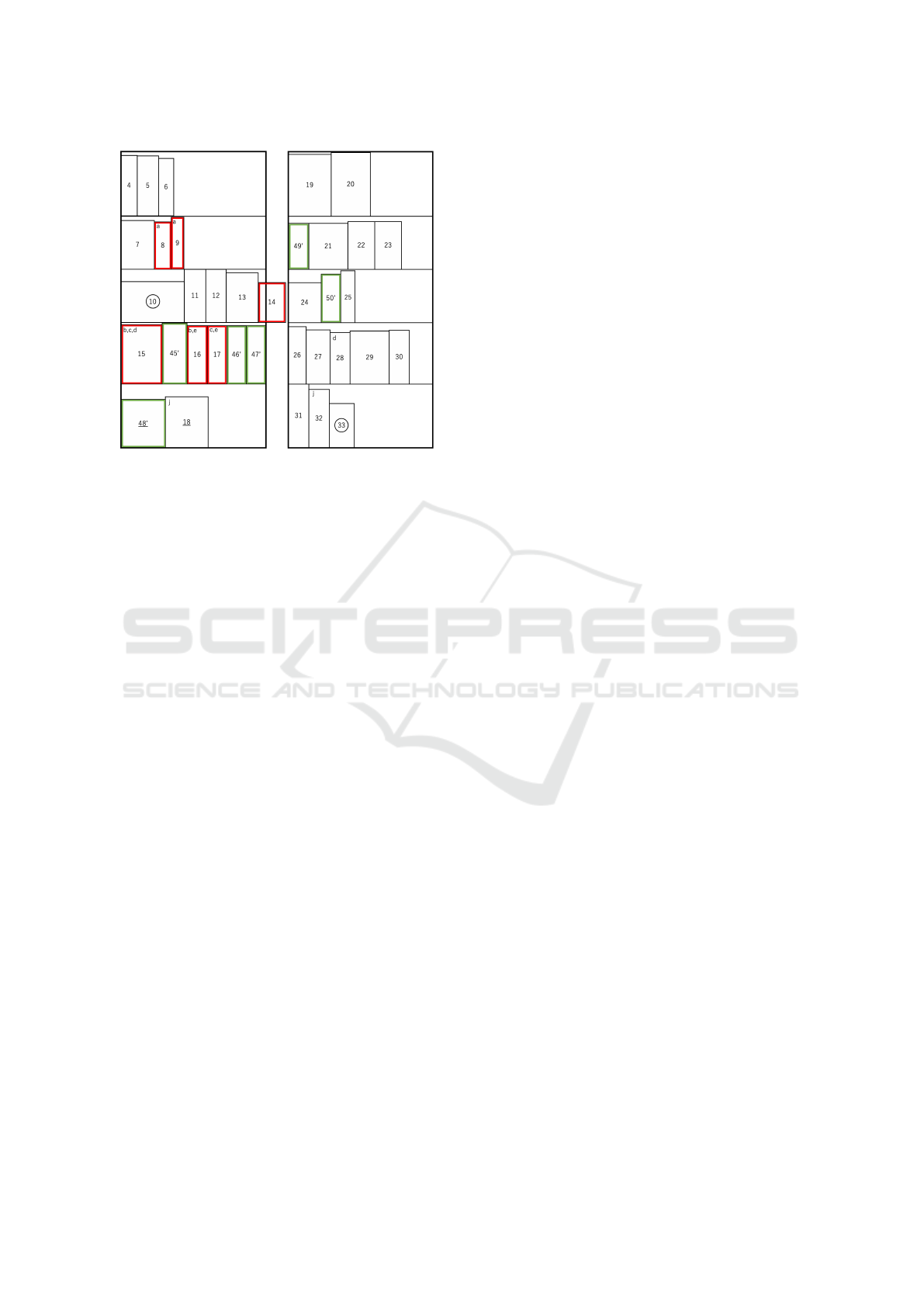
for randomly selected in Shelf ’12B05Q’. The num-

bers (0–44) indicate the index of 45 products, under-

lined numbers indicate bulk bolts, circled numbers in-

dicate products weighing more than 4000 [g] other

than bulk bolts, and the letters (a–j) in the upper left

corner indicate pairs of similar products. Compared

with the current layout, blue colored products (Prod-

uct 0-3 and 35-44) indicate products that were as-

signed to ’12B05Q’ from other shelves by product as-

signment. Also, all 45 products assigned to ’12B05Q’

were changed to their optimal positions by in-shelf

product layout optimization. The generated results

satisfy all the constraints.

In addition, Figures 8(a) and (b) show the objec-

tive function values before and after optimization of

the in-shelf layout for the 10 shelves closest to PS

and AP. The average values for the 10 shelves near

PS were 78.2 before and 8.8 after optimization, while

the average values for the 10 shelves near AP were

113.5 before and 8.1 after optimization.

4.3 Discussion

The results in the Table 1 show that the TSP was

reduced after product assignment optimization with

(a) 10 shelves near PS. (b) 10 shelves near AP.

Figure 8: Comparison of objective function values pre- and

post-optimization.

BLPSO from the current arrangement. In particular,

the TSP was the smallest when WAS was used as the

initial solution. The combination of class-based and

BLPSO produced the lowest cost product assignment.

Figures 9(a) and (b) show the in-shelf product layout

of ’12B05Q’ before optimization. Products colored

green indicate products assigned to shelves other than

’12B05Q’ by the product assignment optimization.

Products colored red are those that violate constraints.

Product 14 is placed outside of the shelf and violates

the inside constraint. Products 8, 9, 15, 16, and 17

violate the nonadjacent constraint. It can be said that

in-shelf product layout optimization has generated an

effective in-shelf product layout. In the comparison of

the objective functions, the t-test conﬁrmed a signiﬁ-

cant difference (p < 0.01) between the pre- and post-

optimization results for the 10 shelves that are close to

both PS and AP. In conclusion, the proposed method

is effective and has potensial to generate feasible and

efﬁcient product layouts for picking operations.

5 CONCLUSION AND FUTURE

WORK

We proposed the method for generating product as-

signments to make efﬁcient manual picking opera-

tions in a distribution warehouse, which consists of

two stages of optimization. First, PSO is used to gen-

erate a product assignment to maximize the utiliza-

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

460

(a) shelf 0. (b) shelf 1.

Figure 9: Pre-optimize in-shelf product layouts for Shelf

’12B05Q’.

tion of AMRs. Based on the product assignments,

in-shelf product layout is generated by mathematical

optimization. The generated in-shelf product layout

is an effective layout, which allows for more efﬁcient

and safer picking than the pre-optimized placement.

In the future, we will investigate methods that allow

interaction between the two optimization stages, such

as performing multiple product assignment optimiza-

tions only on shelves where the objective function

value is not improved, even though the two optimiza-

tion stages are independent. We will also discuss the

results of ongoing demonstration experiments using

real-world logistic data.

ACKNOWLEDGEMENTS

This work was supported in part by the Ministry of

Education, Culture, Sports, Science and Technology-

Japan, Grant–in–Aid for Scientiﬁc Research under

grant #JP19H01137 and #JP20H04018, and part

by the commissioned research by National Insti-

tute of Information and Communications Technology

(NICT), JAPAN. We are grateful to Yahata Neji Cor-

poration for providing us with real logistics operation

data.

REFERENCES

Gurobi optimizer homepage. https://www.gurobi.com/,

Last accessed 24 Jul 2023.

Anjos, M. F. and Vieira, M. V. (2021). Mathematical opti-

mization approach for facility layout on several rows.

Optimization Letters, 15(1):9–23.

Cravo, G. L. and Amaral, A. R. S. (2019). A grasp algo-

rithm for solving large-scale single row facility lay-

out problems. Computers & Operations Research,

106:49–61.

Dahlbeck, M., Fischer, A., and Hungerl

ander, P. (2020). A

study of the relation between the single-row and the

double-row facility layout problem. Working paper.

Fogedby, H. C. (1994). L

evy ﬂights in random environ-

ments. Physical review letters, 73(19):2517.

Hosseini-Nasab, H., Fereidouni, S., Ghomi, S. M. T. F., and

Fakhrzad, M. B. (2018). Classiﬁcation of facility lay-

out problems: a review study. The International Jour-

nal of Advanced Manufacturing Technology, 94:957–

977.

Hungerl

ander, P. and Rendl, F. (2013). A computational

study and survey of methods for the single-row facil-

ity layout problem. Computational Optimization and

Applications, 55:1–22.

Ihara, K. and Kato, S. (2020). Improving distribution-

based discrete particle swarm optimization using l

evy

ﬂight. Australasian Joint Conference on Artiﬁcial In-

telligence, pages 189–200.

Ihara, K., Kato, S., Nakaya, T., Ogi, T., and Masuda, H.

(2019). Application of pso-based constrained combi-

nation optimization to segment assignment in shield

tunneling. Agents and Artiﬁcial Intelligence: 11th

International Conference, ICAART 2019, pages 166–

182.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. 4:1942–1948.

Koster, R. D., Le-Duc, T., and Roodbergen, K. J. (2007).

Design and control of warehouse order picking: A lit-

erature review. 182(2):481–501.

Meskar, M., Eshghi, K., et al. (2020). An algorithm for

solving generalized single row facility layout prob-

lem. American Journal of Operations Research,

10(06):299.

erez-Gosende, P., Mula, J., and D

ıaz-Madro

nero, M.

(2021). Facility layout planning. an extended litera-

ture review. International Journal of Production Re-

search, 59(12):3777–3816.

Tetsuyuki Takahama, S. S. (2005). Constrained optimiza-

tion by ε constrained particle swarm optimizer with

ε-level control. In Soft computing as transdisciplinary

science and technology, pages 1019–1029.

Watanabe, M., Ihara, K., Kato, S., and Sakuma, T. (2021).

Initialization effects for pso based storage assignment

optimization. pages pp. 494–495.

Wenming, W., Lubin, F., Ligang, L., and Peter, W. (2018).

Miqp-based layout design for building interiors. Com-

puter Graphics Forum, 37(2).

Xin-She Yang, S. D. (2010). Engineering optimisation by

cuckoo search. International Journal of Mathemati-

cal Modelling and Numerical Optimisation, 1(4):330–

343.

Generating Products Placement in Warehouse Using BLPSO and MIQCPs

461