
Foundations of Dispatchability for Simple Temporal Networks with
Uncertainty
Luke Hunsberger
1 a
and Roberto Posenato
2 b
1
Computer Science Department, Vassar College, Poughkeepsie, NY, U.S.A.
2
Dipartimento di Informatica, Universit
`
adegli Studi di Verona, Verona, Italy
Keywords:
Planning and Scheduling, Temporal Constraint Networks, Dispatchability, Real-Time Execution.
Abstract:
Simple Temporal Networks (STNs) are a widely used formalism for representing and reasoning about tem-
poral constraints on activities. The dispatchability of an STN was originally defined as a guarantee that a
specific real-time execution algorithm would necessarily satisfy all of the STN’s constraints while preserv-
ing maximum flexibility but requiring minimal computation. A Simple Temporal Network with Uncertainty
(STNU) augments an STN to accommodate actions with uncertain durations. However, the dispatchability of
an STNU was defined differently: in terms of the dispatchability of its so-called STN projections. It was then
argued informally that this definition provided a similar real-time execution guarantee, but without specifying
the execution algorithm. This paper formally defines a real-time execution algorithm for STNUs that similarly
preserves maximum flexibility while requiring minimal computation. It then proves that an STNU is dispatch-
able if and only if every run of that real-time execution algorithm necessarily satisfies the STNU’s constraints
no matter how the uncertain durations play out. By formally connecting STNU dispatchability to an explicit
real-time execution algorithm, the paper fills in important elements of the foundations of the dispatchability of
STNUs.
1 INTRODUCTION
Temporal networks are formalisms for representing
and reasoning about temporal constraints on activi-
ties. Many kinds of temporal networks differ in the
kinds of constraints and uncertainty that they can ac-
commodate. Typically, the more expressive the net-
work, the more expensive the corresponding compu-
tational tasks.
Simple Temporal Networks (STNs) are the most
basic and most widely used kind of temporal net-
work (Dechter et al., 1991). An STN can repre-
sent deadlines, release times, duration constraints,
and inter-action constraints. The basic computational
tasks associated with STNs can be done in polyno-
mial time. An STN is consistent if it has a solution
(as a constraint-satisfaction problem). But, imposing
a fixed solution in advance of execution (i.e., before
any actions are actually performed) is often unneces-
sarily inflexible. Instead, it can be desirable to post-
pone, as much as possible, decisions about the pre-
a
https://orcid.org/0009-0005-8603-4803
b
https://orcid.org/0000-0003-0944-0419
cise timing of actions to allow an executor to react to
unexpected events without having to do expensive re-
planning. In other words, it can be desirable to take
advantage of the inherent flexibility afforded by the
STN representation. However, postponing execution
decisions invariably requires real-time computations
to, for example, propagate the effects of such deci-
sions throughout the network. An effective real-time
execution algorithm, responsible for saying when ac-
tions should be done, must therefore limit the amount
of real-time computation. A Real-Time Execution
(RTE) algorithm that preserves maximum flexibility
while requiring minimal computation has been pre-
sented for STNs (Muscettola et al., 1998). Unfortu-
nately, the RTE algorithm does not necessarily suc-
cessfully execute all consistent STNs (i.e., it does not
guarantee the satisfaction of all of the STN’s con-
straints). However, it has been shown that every con-
sistent STN can be converted into an equivalent net-
work that the RTE algorithm will necessarily success-
fully execute—no matter how the algorithm chooses
to exploit the network’s flexibility (Muscettola et al.,
1998). Such networks are called dispatchable. They
provide applications with both flexibility and compu-
Hunsberger, L. and Posenato, R.
Foundations of Dispatchability for Simple Temporal Networks with Uncertainty.
DOI: 10.5220/0012360000003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 2, pages 253-263
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
253

tational efficiency.
Simple Temporal Networks with Uncertainty
(STNUs) augment STNs to accommodate actions
with uncertain durations (Morris et al., 2001). Al-
though more expressive than STNs, the basic com-
putational task associated with STNUs can also be
done in polynomial time (Morris, 2014; Cairo et al.,
2018). An STNU is dynamically controllable (DC)
if there exists a dynamic strategy for executing its
actions such that all of its constraints will be sat-
isfied no matter how the uncertain action durations
play out—within their specified bounds. An execu-
tion strategy is dynamic in that it can react to ob-
servations of action durations as they occur. Un-
like solutions for consistent STNs, dynamic strate-
gies for DC STNUs typically require exponential
space and thus cannot be computed in advance. In-
stead, the relevant portions of such strategies can be
computed incrementally, during execution. As with
STNs, it is important to preserve maximal flexibil-
ity while requiring minimal computation during ex-
ecution. Hence, the notion of dispatchability has
also been defined for STNUs (Morris, 2014). How-
ever, unlike for STNs, the dispatchability of an STNU
was not specified as a constraint-satisfaction guaran-
tee for a particular real-time execution algorithm, but
instead in terms of the dispatchability of its STN pro-
jections. (A projection of an STNU is the STN that
results from assigning a fixed duration to each ac-
tion.) Since STN dispatchability can be checked by
analyzing the associated STN graph (Morris, 2016),
this definition is attractive. However, it was only ar-
gued informally that dispatchability for an STNU, de-
fined in this way, would provide a similar constraint-
satisfaction guarantee in the context of real-time exe-
cution. Nonetheless, polynomial algorithms for con-
verting DC STNUs into equivalent dispatchable net-
works have been presented (Morris, 2014; Huns-
berger and Posenato, 2023).
Since the primary motivation for dispatchability
is to provide a real-time execution guarantee, it is im-
portant to formally connect STNU dispatchability to
a real-time execution algorithm. This paper provides
such a connection. First, it defines a real-time exe-
cution algorithm for STNUs, called RTE
∗
, that pre-
serves maximal flexibility while requiring minimal
computation. Then it proves that an STNU is dis-
patchable if and only if every run of the RTE
∗
al-
gorithm necessarily satisfies its constraints, no mat-
ter how the uncertain durations turn out. In this way,
the paper fills an important gap in the foundations of
STNU dispatchability.
The rest of the paper is organized as follows. Sec-
tion 2 summarizes the main definitions and results
C
Z
A
Y
X
3
−2
−1
−7
10
−1
1
−1
Figure 1: A sample STN graph.
for the dispatchability of Simple Temporal Networks
(STNs). Section 3 reviews Simple Temporal Net-
works with Uncertainty (STNUs) and how the con-
cept of dispatchability has been extended to them
using Extended STNUs (ESTNUs). Section 4 in-
troduces a real-time execution algorithm for EST-
NUs, called RTE
∗
, and proves its correctness. Sec-
tion 5 summarizes the contributions of the paper and
sketches possible future work.
2 STN DISPATCHABILITY
A Simple Temporal Network (STN) is a pair, (T , C),
where T is a set of real-valued variables called time-
points (TPs) and C is a set of binary difference con-
straints, called ordinary constraints, each of the form
Y − X ≤ δ, where X,Y ∈ T and δ ∈ R (Dechter et al.,
1991). Typically, we let n = |T | and m = |C |. With no
loss of generality, it is convenient to assume that each
STN has a special timepoint Z whose value is fixed
at zero (or some other convenient timestamp) and is
constrained to occur at or before every other time-
point.
1
Each STN has a corresponding graph, (T ,E),
where the timepoints in T serve as nodes and each
constraint Y − X ≤ δ in C corresponds to a labeled di-
rected edge X
δ
Y in E, called an ordinary edge. For
convenience, such edges will be notated as (X,δ,Y ).
Figure 1 shows a sample STN graph. An STN is con-
sistent if it has a solution as a constraint satisfaction
problem. An STN is consistent if and only if its graph
has no negative cycles (Dechter et al., 1991).
Although checking the consistency of an STN is
important and can be done in polynomial time, fixing
a solution in advance undermines the inherent flexi-
bility of the STN representation. Instead, it can be de-
sirable to preserve as much flexibility as possible until
actions are actually performed (i.e., during the “real-
time execution”), while minimizing real-time compu-
tation.
Toward that end, consider the Real-Time Exe-
cution (RTE) algorithm for STNs given in Algo-
1
It is not hard to show that in any consistent STN (see
below) there is at least one TP that can play the role of Z
(i.e., constrained to occur at or before every other TP).
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
254

Algorithm 1: RTE: real-time execution for STNs.
Input: (T , C ), an STN with graph (T ,E)
Output: A function, f : T → [0,∞) or fail
1 foreach X ∈ T do
2 TW(X) = [0, ∞)
3 U := T ; now = 0
4 Enabs := {X ∈ T | X has no outgoing
negative edges}
5 while U 6= {} do
6 if Enabs =
/
0 then
7 return fail
8 ` := min{lb(W ) | W ∈ Enabs}
9 u := min{ub(W ) | W ∈ Enabs}
10 if [`,u] ∩ [now, ∞) =
/
0 then
11 return fail
12 Select any X ∈ Enabs | TW(X) ∩ [now, u]6=
/
0
13 Select any t ∈ TW(X) ∩ [now, u]
14 Remove X from U
15 f (X) := t; now := t
16 Propagate f (X) = t to X’s neighbors in E
17 Enabs := {Y ∈ U | all negative edges from
Y terminate at TPs not in U}
18 return f
rithm 1 (Muscettola et al., 1998).
2
It provides max-
imum flexibility by maintaining for each timepoint
X a time window TW(X) (initially [0, ∞), Line 2),
and providing freedom for which timepoint to exe-
cute next and when to execute it (Lines 8 to 13). To
minimize real-time computation, the effects of each
execution decision, X = t (represented in the pseu-
docode by setting f (X) = t at Line 15) are propagated
only locally, to the neighbors of X in the STN graph
(i.e., the timepoints connected to X by a single edge)
(Line 16).
After initializing the time windows (Line 2), the
RTE algorithm initializes the current time now to 0
and the set U of unexecuted timepoints to T (Line 3);
and then the set of enabled timepoints to those having
no outgoing negative edges (Line 4). (A timepoint Y
is enabled for execution if it is not constrained to oc-
cur after any unexecuted timepoint—equivalently, if
there are no negative edges from Y to any unexecuted
timepoint.) Each iteration of the while loop (Lines 5
to 17) begins by computing the interval [`, u], where
` is the minimum lower bound of the time windows
among the enabled timepoints (i.e., the earliest time
2
Muscettola et al. (1998) refer to their algorithm as ei-
ther the Time Dispatching Algorithm (TDA) or the Dis-
patching Execution Controller (DEC). The RTE algorithm
presented here is equivalent, although organized somewhat
differently and using different notation.
at which something could happen) and u is the min-
imum upper bound among those same time windows
(i.e., the deadline by which something must happen)
(Lines 8 and 9).
3
The algorithm fails if that interval
does not include times at or after now (Line 10). Next
(Line 12), it selects one of the enabled timepoints X
whose time window TW(X) has a non-empty intersec-
tion with [now,u], and then (Line 13) selects any time
t ∈ TW(X) ∩ [now, u] at which to execute it. (If [`, u] ∩
[now,∞) is non-empty, then there must be such an X.)
After assigning X to t (Line 15), it then propagates the
effects of that assignment to X ’s neighbors in the STN
graph (Line 16). In particular, for any non-negative
edge (X, δ,V ) ∈ E, it updates the time window for
V as follows: TW(V ) := TW(V ) ∩ (−∞,t + δ]. Simi-
larly, for each negative edge (U, −γ,X), it updates U’s
time window: TW(U) := TW(U)∩[t + γ,∞). Finally,
it updates the set of enabled timepoints (Line 17) in
preparation for the next iteration.
The RTE algorithm for STNs provides maximal
flexibility in that any solution to a consistent STN can
be generated by an appropriate sequence of choices
at Lines 12 to 13. In addition, it requires minimal
computation by performing only local propagation (at
Line 16). However, it does not provide a constraint-
satisfaction guarantee for all runs on consistent STNs,
as illustrated by the sample run-through of the algo-
rithm shown in Table 1(a), which motivates the work
on STN dispatchability, as follows.
Definition 1 (Dispatchability Muscettola et al.
(1998)). An STN S = (T , C) is dispatchable if every
run of the RTE algorithm (Algorithm 1) on the corre-
sponding STN graph G = (T , E) necessarily gener-
ates a solution for S.
Muscettola et al. (1998) showed that for consis-
tent STNs, the all-pairs, shortest-paths (APSP) graph
is necessarily dispatchable, but its O(n
2
) edges can-
cel the benefits of local propagation. Their O(n
3
)-
time edge-filtering algorithm computes an equiv-
alent minimal dispatchable STN by starting with
the APSP graph, then removing dominated edges
(i.e., edges not needed for dispatchability). A
faster O(mn + n
2
logn)-time algorithm accumulates
undominated edges without first building the APSP
graph (Tsamardinos et al., 1998).
Morris (2016) later found a graphical characteri-
zation of STN dispatchability in terms of vee-paths.
Definition 2 (Vee-path (Morris, 2016)). A vee-path
comprises zero or more negative edges followed by
zero or more non-negative edges.
3
In Algorithm 1, lb(X) and ub(X) respectively denote
the lower and upper bounds from X’s time window, TW(X).
Foundations of Dispatchability for Simple Temporal Networks with Uncertainty
255
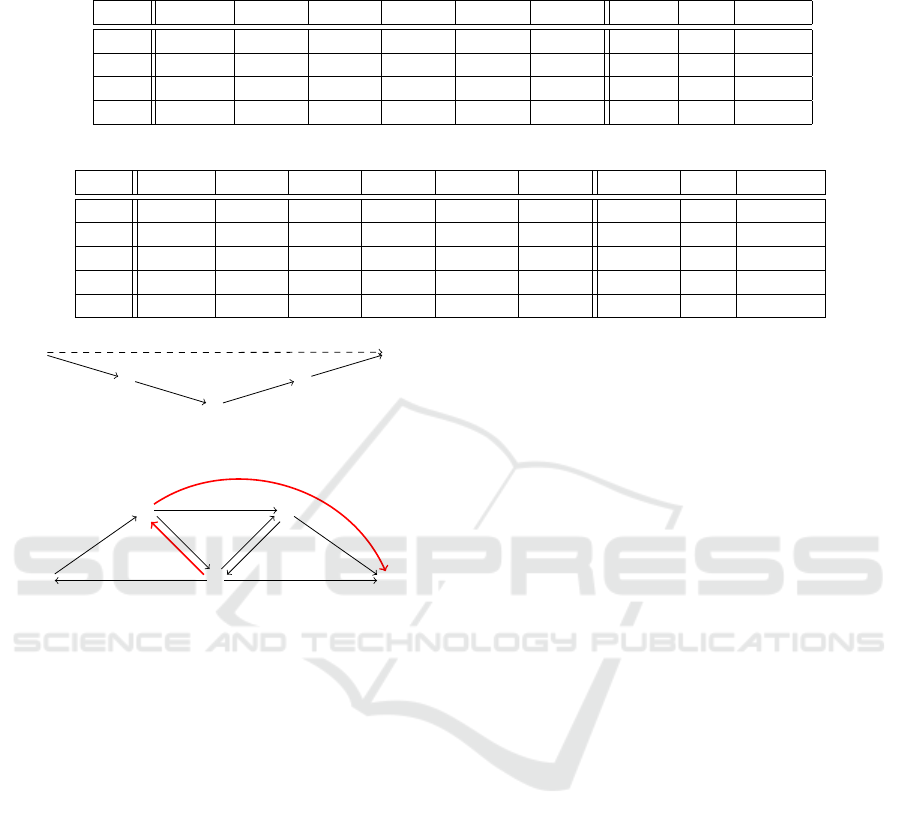
Table 1: Sample runs of the RTE algorithm.
(a) A sample run of the RTE algorithm on the consistent STN from Figure 1.
Iter. Enabs TW(Z) TW(A) TW(C) TW(X) TW(Y ) [`,u] now Exec.
Init. {Z} [0,∞] [0, ∞) [0,∞) [0,∞) [0, ∞) [0,∞) 0 Z := 0
1 {A,Y } — [1,∞) [7,∞) [0,∞) [1, ∞) [0,∞) 0 Y := 4
2 {A, X} — [1, ∞) [7,5] [6,∞) — [1,∞) 4 A := 8
3 {C, X } — — [9,5] [6,∞) — [6,5] 8 fail
(b) A sample run of the RTE algorithm on the dispatchable STN from Figure 3.
Iter. Enabs TW(Z) TW(A) TW(C) TW(X) TW(Y ) [`, u] now Exec.
Init. {Z} [0,∞) [0,∞) [0, ∞) [0,∞) [0,∞) [0, ∞) 0 Z := 0
1 {A,Y } — [1, ∞) [7,∞) [0,∞) [6, ∞) [1, ∞) 0 A := 8
2 {C,Y } — — [9, 18] [0, ∞) [8,∞) [8,18] 8 C := 15
3 {Y } — — — [0, 18] [8, 16] [8, 16] 15 Y := 16
4 {X} — — — [18, 18] — [18, 18] 16 X := 18
X
A
B
C
D
−7
−3
1
4
−5
Figure 2: A sample vee-path that dominates a direct edge.
C
Z
A
Y
X
3
−2
10
−1
1
1
0
−1
−7
−6
Figure 3: An equivalent dispatchable STN graph.
Figure 2 shows a sample vee-path from X to Y that
dominates the (dashed) direct edge from X to Y . For
this vee-path, the enablement condition (Line 12) en-
sures that the RTE algorithm will execute B before A,
and A before X; hence, local propagation ensures the
satisfaction of the edges (X, −7, A) and (A, −3, B).
On the other side, if the algorithm executes C before
B, then the edge (B, 1,C) is automatically satisfied;
otherwise, local propagation ensures its satisfaction.
Similarly, the RTE algorithm necessarily satisfies the
edge (C,4,D). Since the algorithm satisfies all the
edges in the vee-path, it also satisfies the direct edge
(X,−5,Y ). Hence that edge is not needed to ensure
dispatchability.
Theorem 1 (Morris (2016)). An STN is dispatchable
iff for each path from any X to any Y in the STN graph,
there is a shortest path from X to Y that is a vee-path.
Figure 3 shows a dispatchable STN that is equiv-
alent to the STN from Figure 1 (new edges are thick
and red). It is easy to check that each path has a cor-
responding vee-path that is a shortest path. Table 1(b)
shows a sample run of the RTE algorithm on this dis-
patchable STN, which necessarily generates a solu-
tion.
RTE Complexity. With appropriate data structures,
the RTE algorithm can be implemented to run in
O(n
2
) worst-case time, while allowing for maximum
flexibility in the selection of the timepoint X to exe-
cute next and the time t at which to execute it. The
local propagations involve m updates, each done in
constant time. The set of enabled timepoints can be
implemented by keeping, for each timepoint, a count
of its outgoing negative edges. Whenever a negative
edge is processed, the count for the source of that edge
is decremented. When the count for a given time-
point reaches 0, that timepoint becomes enabled. To
compute the values of ` and u, it suffices to maintain
two min priority queues (Cormen et al., 2022), one
for ` and one for u. When a TP X becomes enabled,
it is inserted into both queues using its lb(X) and
ub(X) values as keys. To compute the desired min-
imum values requires only “peeking” at the current
minimum value. TPs need not be extracted from the
queues when executed, but instead can be extracted
lazily, as follows. Whenever a “peek” reveals a value
based on an already-executed TP, that TP can be ex-
tracted at that time; and subsequent peek/extractions
can be done until a peek reveals a value based on a
not-yet-executed TP. In this way, each TP is inserted
and extracted exactly once which, together with at
most m “decrease key” updates, yields a total cost of
O(m + n logn). The peeks can be done in constant
time and so don’t affect the overall time. For full
flexibility, O(n) worst-case time is required for select-
ing the timepoint X to execute next, which drives the
overall O(n
2
) worst-case time. The selection of the
time t at which to execute X, if done randomly, can be
done in constant time. Of course, an application may
have domain-specific criteria that would make the se-
lections of X and t more time-consuming, but that is
beyond the purview of the RTE algorithm.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
256
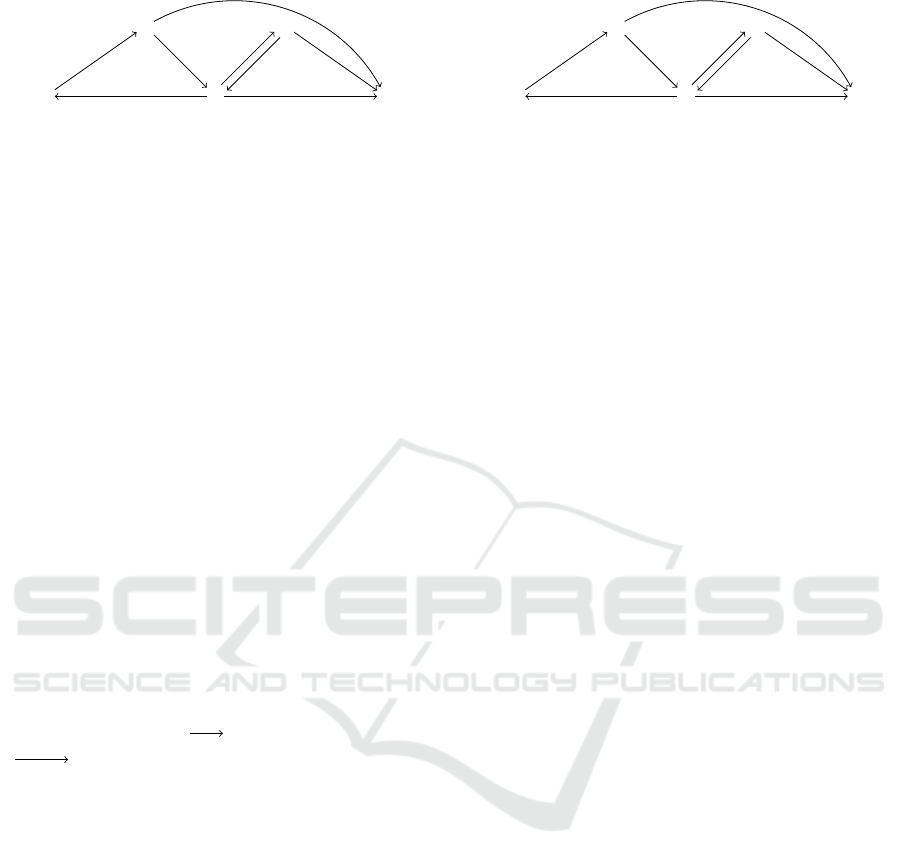
C
Z
A
Y
X
−7
c:1
C: − 10
1
−2
3
−1
−1
Figure 4: A sample STNU.
3 STNU DISPATCHABILITY
A Simple Temporal Network with Uncertainty
(STNU) augments an STN to include contingent
links that can represent actions with uncertain du-
rations (Morris et al., 2001). An STNU is a triple
(T , C, L) where (T , C) is an STN, and L is a set of
contingent links, each of the form (A,x, y,C), where:
A ∈ T is the activation timepoint (ATP); C ∈ T is the
contingent timepoint (CTP); and 0 < x < y < ∞ spec-
ifies bounds on the duration C − A. Typically, an ex-
ecutor controls the execution of A, but not C. The ex-
ecution time for C is only learned in real time, when
it happens, but is guaranteed to satisfy C − A ∈ [x, y].
We let k = |L|; and notate the set of contingent time-
points as T
c
; and the non-contingent (i.e., executable)
timepoints as T
x
= T \T
c
.
Each STNU (T , C , L) has a corresponding graph,
(T , E ∪ E
lc
∪E
uc
), where: (T , E) is the graph for the
STN (T ,C ); E
lc
is a set of lower-case (LC) edges;
and E
uc
is a set of upper-case (UC) edges. The LC
and UC edges correspond to the contingent links in L,
as follows. For each contingent link (A,x, y,C) ∈ L,
there is an LC edge A
c:x
C in E
lc
and a UC edge
C
C:−y
A in E
uc
, respectively representing the uncon-
trollable possibilities that the duration C − A might
take on its lower bound x or its upper bound y. For
convenience, such edges may be notated as (A,c:x,C)
and (C,C:−y, A). Figure 4 shows a sample STNU
graph with a contingent link (A,1, 10,C).
An STNU is dynamically controllable (DC) if
there exists a dynamic strategy for executing its non-
contingent timepoints such that all of the constraints
in C will necessarily be satisfied no matter how the
contingent durations turn out—within their specified
bounds (Morris et al., 2001; Hunsberger, 2009). A
strategy is dynamic in that it can react in real time
to observations of contingent executions, but its ex-
ecution decisions cannot depend on advance knowl-
edge of contingent durations. As is common in the
literature, this paper assumes that strategies can re-
act instantaneously to observations. Morris (2014)
presented the first O(n
3
)-time DC-checking algorithm
for STNUs. Cairo et al. (2018) gave a O(mn + k
2
n +
kn logn)-time algorithm that is faster on sparse net-
C
Z
A
Y
X
−7
4
−4
1
−2
3
−1
−1
Figure 5: The projection of the sample STNU onto ω = (4).
works.
Most DC-checking algorithms generate a new
kind of edge, called a wait, that represents a condi-
tional constraint. A wait edge (Y,C:−w, A) represents
the conditional constraint that as long as C has not yet
executed, Y must wait until at least w after A. In this
paper, a wait labeled by the contingent timepoint C is
called a C-wait. Following Morris (2014), we define
an extended STNU (ESTNU) to include a set C
w
of
conditional wait constraints, and an ESTNU graph to
include a corresponding set E
w
of wait edges. (While
wait edges are not necessary for DC-checking, they
are typically necessary for dispatchability.)
Morris (2014) defined the dispatchability of an
ESTNU in terms of its STN projections. A projection
of an ESTNU is the STN that results from assigning
fixed durations to its contingent links (Morris et al.,
2001; Morris, 2014; Hunsberger and Posenato, 2023).
Definition 3 (Projection). Let S = (T , C, L, C
w
) be
an ESTNU, where L = {(A
i
,x
i
,y
i
,C
i
) | 1 ≤ i ≤
k}. Let ω = (ω
1
,ω
2
,. .. , ω
k
) be any k-tuple such that
x
i
≤ ω
i
≤ y
i
for each i. Then the projection of S onto
ω is the STN S
ω
= (T , C ∪ C
ω
lc
∪ C
ω
uc
∪ C
ω
w
) given by:
C
ω
lc
= {(A
i
,ω
i
,C
i
) | 1 ≤ i ≤ k}
C
ω
uc
= {(C
i
,−ω
i
,A
i
) | 1 ≤ i ≤ k}
C
ω
w
= {(X , −min{w,ω
i
},A
i
) |
(X,C
i
: − w,A
i
) ∈ C
w
}
The constraints in C
ω
lc
∪ C
ω
uc
together fix the duration
of each contingent link (A
i
,x
i
,y
i
,C
i
) to C
i
− A
i
= ω
i
.
Each wait edge (X,C
i
:−w, A
i
) ∈ C
w
projects onto ei-
ther the STN edge (X, −w, A
i
) if w ≤ ω
i
(i.e., if the
wait expires before C
i
executes) or the STN edge
(X,−ω, A
i
) (i.e., if C
i
executes before A
i
+ w).
Figure 5 shows the projection of the sample STNU
from Figure 4 onto ω = (4). Note that this projection
is not dispatchable (as an STN) since, for example,
there is no shortest path from C to Y that is a vee-path.
Definition 4 (ESTNU dispatchability (Morris, 2014)).
An ESTNU is dispatchable if all of its STN projections
are dispatchable (as STNs).
Morris (2014) argued informally that a dispatchable
ESTNU (Definition 4) would provide a real-time ex-
ecution guarantee, but did not specify an RTE al-
gorithm for ESTNUs. However, he showed that
Foundations of Dispatchability for Simple Temporal Networks with Uncertainty
257
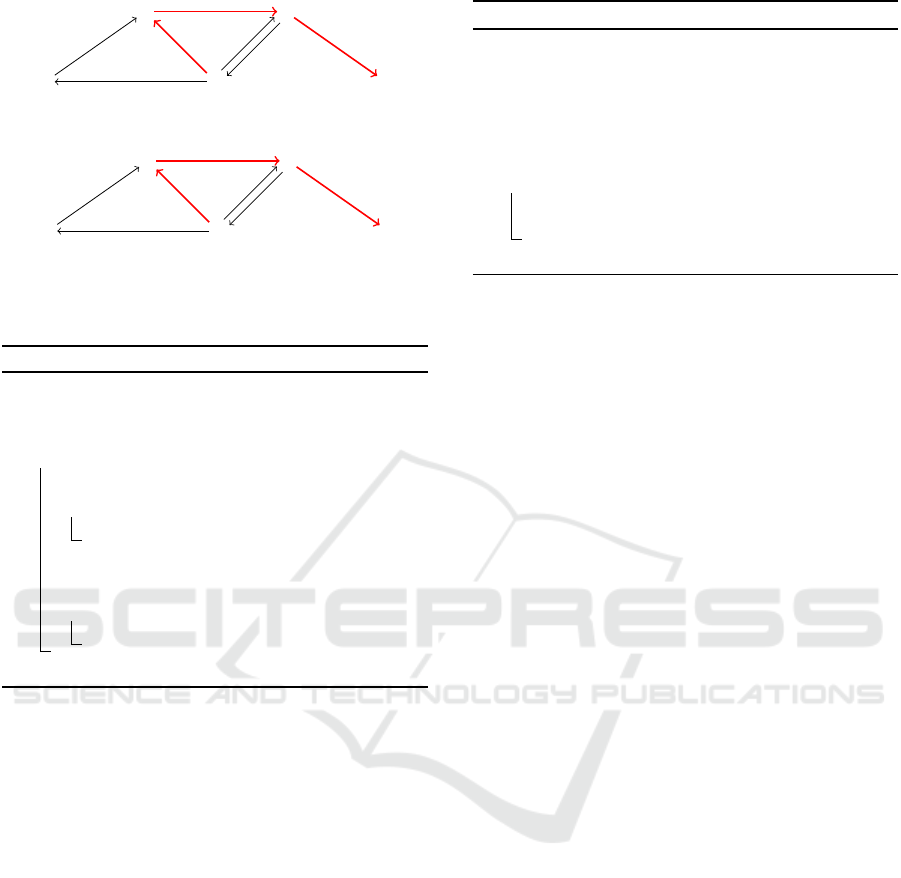
C
Z
A
Y
X
−6
c:1
C: − 10
C: − 9
−2
3
1
(a) Dispatchable ESTNU.
C
Z
A
Y
X
−6
4
−4
−4
−2
3
1
(b) Its projection onto ω = (4).
Figure 6: A dispatchable ESTNU (top) that is equivalent to
the STNU from Figure 4 and one of its projections (bottom).
Algorithm 2: RTE
∗
: real-time execution for ESTNUs.
Input: S = (T
x
∪ T
c
,C , L, C
w
), an ESTNU
Output: A function f : (T
x
∪ T
c
) → R or fail
1 D := RTE
∗
init
(T
x
,T
c
) // Initialization
2 while D.U
x
∪ D.U
c
6=
/
0 do // Some TPs unexec.
3 ∆ := RTE
∗
genD
(D)// Generate exec. decision
4 if ∆ = fail then
5 return fail
6 (ρ,τ) := Observe
c
(S, D, ∆)// Obser ve CTPs
7 D := RTE
∗
update
(D,∆, (ρ, τ))// Update in D
8 if D = fail then
9 return fail
10 return D. f
his O(n
3
)-time DC-checking algorithm, modified to
generate wait edges, outputs an equivalent dispatch-
able ESTNU when given a DC input. Hunsberger
and Posenato (2023) recently provided an O(mn +
kn
2
+ n
2
logn)-time algorithm that is faster on sparse
graphs.
Figure 6(a) shows a dispatchable ESTNU that is
equivalent to the STNU from Figure 4. Figure 6(b)
shows its projection onto ω = (4), which is dispatch-
able (as an STN).
4 RTE ALGORITHM FOR
ESTNUs
This section specifies a real-time execution algorithm
for ESTNUs, called RTE
∗
, whose high-level iterative
operation is given as Algorithm 2.
On each iteration, the algorithm first generates an
execution decision (Line 3). Next, it observes whether
any contingent TPs happened to execute (Line 6).
Since, as discussed below, the execution of contingent
Algorithm 3: RTE
∗
init
: Initialization.
Input: T
x
, executable TPs; T
c
, contingent TPs
Output: D, initialized RTEdata structure
1 D = new(RTEdata)
2 D.U
x
:= T
x
; D.U
c
:= T
c
; D.now = 0; D. f =
/
0
3 D.Enabs
x
={X ∈ T
x
| X has no
outgoing negative edges}
4 foreach X ∈ T
x
do
5 D.TW(X) := [0, ∞)
6 D.AcWts(X) :=
/
0
7 return D
TPs is not controlled by the RTE
∗
algorithm, observa-
tion is represented here by an oracle, Observe
c
. Af-
terward, the RTE
∗
algorithm responds by updating in-
formation (Line 7). In successful instances, the RTE
∗
algorithm returns a complete set of variable assign-
ments for the timepoints in T (equivalently, a func-
tion f : T → R).
The RTE
∗
algorithm maintains information in a
data structure, called RTEdata, that has the following
fields:
• U
x
(the unexecuted executable timepoints),
• U
c
(the unexecuted contingent timepoints),
• Enabs
x
(the enabled executable timepoints),
• now (the current time),
• f (a set of variable assignments),
• for each executable timepoint X ∈ T
x
, TW(X) =
[lb(X),ub(X)] (time window for X),
• AcWts(X) (the activated waits for X , see below).
A new RTEdata instance, D, is initialized by the
RTE
∗
init
algorithm (Algorithm 3). Note that for ES-
TNUs, an executable timepoint X is enabled if all of
its outgoing negative edges—including wait edges—
point at already executed timepoints.
Activated Waits. A wait edge such as (X,C:−w, A)
represents a conditional constraint that as long as C
has not yet executed, X must wait at least w after A.
Once the activation timepoint A for the contingent
link (A, x, y,C) has been executed, say, at some time
a, we say that the wait edge has been activated, which
the RTE
∗
algorithm keeps track of by inserting an en-
try (a + w,C) into the set AcWts(X). There are two
ways for this wait to be satisfied: C can execute early
(i.e., before a + w) or the wait can expire (i.e., the cur-
rent time passes a + w). In response to either event,
the entry (a + w,C) is removed from AcWts(X). In
general, if AcWts(X ) is non-empty, X cannot be exe-
cuted.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
258

Algorithm 4: RTE
∗
genD
: Generate execution decision.
Input: D, an RTEdata structure
Output: Exec decn: Wait or (t,V ); or fail
1 if D.Enabs
x
=
/
0 then
2 return Wait
3 foreach X ∈ D.Enabs
x
do
// Maximum wait time for X
4 wt(X) = max{w | ∃(w, ) ∈ D.AcWts(X)}
// Greatest lower bound for X
5 glb(X) = max{D.lb(X), wt(X )}
// Earliest possible next execution
6 t
L
= min{glb(X ) | X ∈ D.Enabs
x
}
// Latest possible next execution
7 t
U
= min{D.ub(X ) | X ∈ D.Enabs
x
}
8 if [t
L
,t
U
] ∩ [D.now, ∞) =
/
0 then
9 return fail
10 Select any V ∈ D.Enabs
x
for which
[glb(X),ub(X)] ∩ [D.now,t
U
] 6=
/
0
11 Select any t ∈ [glb(V ), ub(V )] ∩ [D.now,t
U
]
12 return (t,V )
Generate Execution Decision. Hunsberger (2009)
formally characterized dynamic execution strategies
for STNUs in terms of real-time execution decisions
(RTEDs). An RTED can have one of two forms: Wait
or (t, χ). A Wait decision can be glossed as “wait for
a contingent timepoint to execute”. A (t, χ) decision
can be glossed as “if no contingent timepoints exe-
cute before time t, then execute the timepoints in the
set χ”. Given the assumption about instantaneous re-
activity, it suffices to limit χ to a single timepoint.
Algorithm 4 computes the next RTED for one it-
eration of the RTE
∗
algorithm. First, at Line 1, if
there are no enabled timepoints, then the only viable
RTED is Wait. Otherwise, the algorithm generates
an RTED of the form (t,V ) for some t ∈ R and some
enabled TP V . Lines 3 to 5 compute, for each enabled
TP X , the maximum wait time wt(X) among all of
X’s activated waits (or −∞ if there are none), and then
compares that with the lower-bound lb(X ) from X’s
time window to generate the earliest time, glb(X), at
which X could be executed.
4
Then, at Line 6, it com-
putes the earliest possible time t
L
that any enabled TP
could be executed next. Line 7 computes the latest
time at which the next execution event could occur.
The algorithm fails if the interval between the earliest
possible time and the latest does not include times at
or after now (Line 9). Otherwise, it selects any one
of the enabled timepoints V whose time window in-
cludes times in [D.now,t
U
] (Line 10); and any time
4
D.lb(X) and D.ub(X) respectively denote the lower and
upper bounds of X’s time window, D.TW(X ).
Algorithm 5: Observe
c
: Oracle.
Input: S = (T
x
∪ T
c
,C , L, C
w
), an ESTNU; D,
an RTEdata structure; ∆, an RTED
Output: (ρ, τ), where ρ ∈ R and τ ⊆ D.U
c
1 f := D. f ; now := D.now
// Get ACLs: currently active contingent links
2 ACLs := {(A,x, y,C) ∈ L | f (A) ≤ now,
f (C) = ⊥}
// Waiting forever
3 if ACLs =
/
0 and ∆ = Wait then
4 return (∞,
/
0)
// No CTPs execute at or before time t
5 if ACLs =
/
0 and ∆ = (t,V ) then
6 return (t,
/
0)
// Compute bounds for possible contingent executions
7 lb
c
:= min{ f (A) + x | (A, x, y,C) ∈ ACLs}
8 ub
c
:= min{ f (A) + y | (A, x, y,C) ∈ ACLs}
9 Select any t
c
∈ [lb
c
,ub
c
]
// Oracle decides not to execute any CTPs yet
10 if ∆ = (t,V ) and t
c
> t then
11 return (t,
/
0)
// Oracle decides to execute one or more CTPs
12 τ
∗
:= {C | (A,x, y,C) ∈ ACLs,t
c
∈ [a + x, a + y],
where a = f (A)}
13 Select τ: any non-empty subset of τ
∗
14 return (t
c
,τ)
t ∈ [glb(V ), ub(V )] ∩ [D.now,t
U
] at which to execute
it (Line 11). (Note the flexibility inherent in the se-
lection of both V and t.) The algorithm outputs the
RTED (t,V ) (Line 12).
Observation. Once the RTE
∗
algorithm generates
an execution decision (e.g., “If nothing happens be-
fore time t, then execute V ”), it must wait to see
what happens (e.g., whether some contingent time-
points happen to execute). Since the execution of
contingent TPs is not controlled by the RTE
∗
algo-
rithm, we represent it within the algorithm by an or-
acle, called Observe
c
, whose pseudocode is given in
Algorithm 5.
The oracle, Observe
c
, non-deterministically de-
cides whether to execute any contingent TPs and, if
so, when. At Line 2, it computes the set of currently
active contingent links (i.e., those whose activation
TPs have been executed, but whose contingent TPs
have not yet). If there are none, then no CTPs can exe-
cute. In that case, Observe
c
returns (∞,
/
0) in response
to a wait decision (Line 4), or (t,
/
0) in response to
a (t,V ) decision (Line 6). Otherwise (i.e., there are
some active contingent links), Observe
c
computes
the range of possible times for the next contingent
Foundations of Dispatchability for Simple Temporal Networks with Uncertainty
259
Algorithm 6: RTE
∗
update
: update information in D.
Input: S , an ESTNU; D, an RTEdata structure;
∆, an RTED (Wait or (t,V )); (ρ,τ), an
observation, where ρ ∈ R and τ ⊆ D.U
c
Output: Updated D or fail
// Case 0: Failure (waiting forever)
1 if ρ = ∞ then
2 return fail
// Case 1: Only contingent timepoints executed
3 if ∆ = Wait or (∆ = (t,V ) and ρ < t) then
4 HCE(S, D, ρ,τ)
5 else
// Case 2: Executable timepoint V executes at t
6 HXE(S, D,t,V )
// Case 3: CTPs also execute at t
7 if τ 6=
/
0 then
8 HCE(S, D,t, τ)
9 D.now := ρ
10 return D
execution event and arbitrarily selects some time t
c
within that range (Lines 7 to 9). Now, if the pending
RTE
∗
decision is (t,V ), and t
c
happens to be greater
than t, then the oracle has effectively decided not to
execute any contingent TPs yet (Line 10). Other-
wise, it computes the set τ
∗
of CTPs that could ex-
ecute at time t
c
(Line 12) and then arbitrarily selects a
non-empty subset of τ
∗
to actually execute at time t
c
(Line 13).
Update. The response of the RTE
∗
algorithm to its
observation of possible CTP executions is handled by
the RTE
∗
update
algorithm (Algorithm 6). If ρ = ∞,
which can only happen when a Wait decision was
made but there were no active contingent links, then
the RTE
∗
algorithm would wait forever and, hence,
fail (Line 2). Otherwise, ρ < ∞. If the decision was
wait, then one or more contingent TPs must have ex-
ecuted at ρ (and no executable TPs), whence (Lines 3
to 4) the relevant updates are computed by the HCE
algorithm (Algorithm 7). The same updates are also
needed if the decision was (t,V ), where ρ < t (Lines 3
to 4).
The HCE algorithm (Algorithm 7) updates D in
response to contingent executions as follows. Lines 2
to 3 record that C occurred at ρ by adding the vari-
able assignment (C, ρ) to D. f and removing C from
D.U
c
. Line 4 updates the time windows for neigh-
boring timepoints, exactly like the RTE algorithm for
STNs. Since the execution of C automatically satis-
fies all C-waits, Line 5 removes any C-waits from the
D.AcWts sets. Finally, Line 6 updates the set of en-
Algorithm 7: HCE: Handle contingent executions.
Input: S , an ESTNU; D, an RTEdata; ρ ∈ R,
an execution time; τ ⊆ U
c
, CTPs to
execute at ρ
Result: D updated
1 foreach C ∈ τ do
2 Add (C,ρ) to D. f
3 Remove C from D.U
c
4 Update time windows for neighbors of C
5 Remove C-waits from all D.AcWts sets
6 Update D.Enabs
x
due to incoming
neg. edges to C or any deleted C-waits
Algorithm 8: HXE: Handle a non-contingent execu-
tion.
Input: S , an ESTNU; D, an RTEdata structure;
t ∈ R; V ∈ U
x
Result: D updated
1 Add (V,t) to D. f
2 Remove V from D.U
x
3 Update time windows for neighbors of V
4 Update D.Enabs
x
due to any negative incoming
edges to V
5 if V is activation TP for some CTP C then
6 foreach (Y,C:−w,V ) ∈ E
w
do
7 Insert (t + w,C) into D.AcWts(Y )
abled executable TPs in case the execution of C or the
deletion of C-waits enables some new TPs.
In the remaining cases (Lines 5 to 8) of RTE
∗
update
(Algorithm 6), the decision is (t,V ) and ρ = t. In
other words, no contingent TPs executed before time
t and, so, the executable timepoint V must be exe-
cuted at t. The corresponding updates are handled by
the HXE algorithm (Algorithm 8). The HXE updates
are the same as those done by the RTE algorithm for
STNs, except that if V happens to be an activation TP
for some contingent TP C, then information about all
C-waits must be entered into the appropriate AcWts
sets (Lines 5 to 7).
Finally, in the (extremely rare) case (of Algo-
rithm 6, Line 8) where one or more CTPs happen to
execute precisely at time t (i.e., simultaneously with
V ), the HCE algorithm (Algorithm 7) performs the
needed updates, as in Case 1. Finally, Algorithm 6
updates the current time to ρ (Line 9).
Table 2 shows sample runs of the RTE
∗
algorithm
on the dispatchable ESTNU from Figure 6(a). In Ta-
ble 2(a), C executes early (at A + 5); in Table 2(b), C
executes late (at A + 10). Both runs result in variable
assignments that satisfy all of the constraints in C.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
260
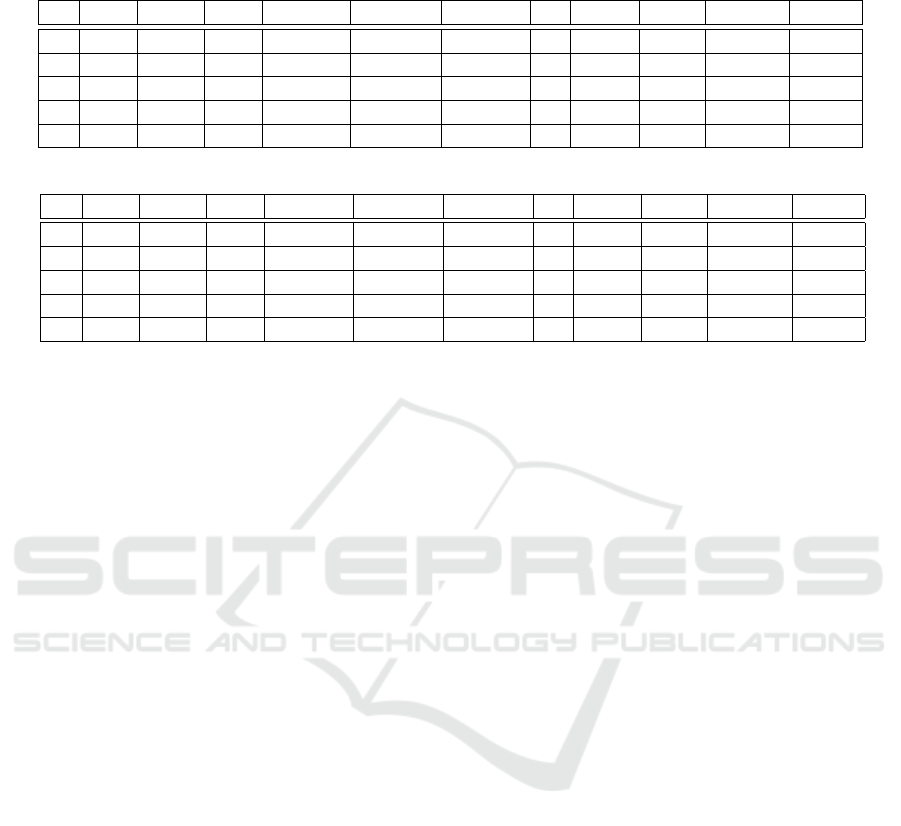
Table 2: Sample runs of the RTE
∗
algorithm on the dispatchable ESTNU from Figure 6(a).
(a) Sample run where C executes early (at A + 5).
Iter. TW(A) TW(X) TW(Y ) AcWts(A) AcWts(X) AcWts(Y ) now Enabs
x
RTED Obs Exec
Init. [0, ∞) [0,∞) [0, ∞)
/
0
/
0
/
0 0 {Z} (0, Z) (0,
/
0) Z := 0
1 [6,∞) [0, ∞) [0,∞)
/
0
/
0
/
0 0 {A} (7, A) (7,
/
0) A := 7
2 — [0,∞) [0,∞) —
/
0 {(16,C)} 7 {Y } (16,Y ) (12, {C}) C := 12
3 — [0,15] [0,13] —
/
0
/
0 12 {Y } (13,Y ) (13,
/
0) Y := 13
4 — [15,15] — —
/
0 — 13 {X} (15,X) (15,
/
0) X := 15
(b) Sample run where C executes late (at A + 10).
Iter. TW(A) TW(X) TW(Y ) AcWts(A) AcWts(X) AcWts(Y ) now Enabs
x
RTED Obs Exec
Init. [0, ∞) [0,∞) [0, ∞)
/
0
/
0
/
0 0 {Z} (0, Z) (0,
/
0) Z := 0
1 [6,∞) [0, ∞) [0,∞)
/
0
/
0
/
0 0 {A} (7, A) (7,
/
0) A := 7
2 — [0,∞) [0,∞) —
/
0 {(16,C)} 7 {Y } (16,Y ) (16,
/
0) Y := 16
3 — [18, ∞) — —
/
0 — 16 {X} (22,X) (17,{C}) C := 17
4 — [18,20] — —
/
0 — 17 {X} (19,X) (19,
/
0) X := 19
RTE
∗
Complexity. The worst-case complexity of
the RTE
∗
algorithm is similar to that of the RTE al-
gorithm except for the maintenance of the AcWts sets
(which is handled by the HCE and HXE algorithms).
The AcWts sets can also be implemented using min
priority queues. Since there are at most nk wait edges,
each of which gets inserted into an AcWts set exactly
once, and also gets deleted exactly once, the worst-
case complexity over the entire RTE
∗
algorithm is
O(nk + (nk) log(nk)) = O(nk log(nk)). This assumes
that the deletions are done lazily, as described earlier
for the other min priority queues. Therefore, the over-
all complexity is O(m+nlog n +nk log(nk)) = O(m +
nk log(nk)). Finally, although we provide pseudocode
for the Observe
c
oracle, that was just to highlight the
range of possible observations. From the perspective
of the RTE
∗
algorithm, the oracle presents observa-
tions in real time and, hence, there is no computation
cost associated with them.
4.1 Main Theorem
Theorem 2. Let S = (T , C , L, C
w
) be an ESTNU. Ev-
ery run of the RTE
∗
algorithm on S corresponds to
a run of the RTE algorithm for STNs on some STN
projection S
ω
of S, yielding the same variable assign-
ments to the timepoints in T .
The following definitions, closely related to defi-
nitions in Morris (2016) and Hunsberger (2009), are
used in the proof.
Definition 5 (Execution sequence). A (possibly
partial) execution sequence is any sequence of
the form σ = ((X
1
,t
1
),(X
2
,t
2
),. .., (X
h
,t
h
)) where
{X
1
,X
2
,. .. , X
h
} ⊆ T and t
1
≤ t
2
≤ .. . ≤ t
h
. For any
(X,t) ∈ σ, we write σ(X) = t. For any X that doesn’t
appear in σ, we write σ(X) = ⊥. In addition, we let
max(σ) = t
h
notate the time of the latest execution
event in σ.
Note that the “functions” D. f and f that are incremen-
tally computed by the RTE
∗
and RTE algorithms may
be viewed as execution sequences; and that D.now =
max(D. f ) and now = max( f ).
Definition 6 (Pre-history). The pre-history π
σ
of
an execution sequence σ = ((X
1
,t
1
),. .., (X
h
,t
h
))
is a set that specifies the duration, σ(C) − σ(A),
of each contingent link (A, x, y,C) for which
σ(A),σ(C) ≤ max(σ), and constrains the duration
of any currently active contingent link (A
0
,x
0
,y
0
,C
0
),
where σ(A
0
) ≤ max(σ) but σ(C
0
) = ⊥, to C
0
− A
0
≥
max(σ) − A
0
(i.e., C
0
≥ max(σ)).
Definition 7 (Respect). A projection S
ω
respects a
pre-history π if it is consistent with the constraints on
the durations specified by π.
Definition 8 (RTE-compliant). A (possibly partial)
execution sequence σ is RTE-compliant for an ES-
TNU S if it can be generated by some run of the
RTE algorithm on every projection S
ω
that respects
the pre-history π
σ
.
Proof. This proof incrementally analyzes an arbi-
trary execution sequence generated by the RTE
∗
al-
gorithm on the ESTNU S, placing no restrictions on
the choices it makes along the way, while construct-
ing in parallel a corresponding run of the RTE algo-
rithm on an incrementally specified projection of S
such that, in the end, both algorithms generate the
same set of variable assignments. In what follows,
information computed by RTE
∗
is prefixed by D; non-
prefixed terms by RTE. The proof uses induction to
show that at the beginning of each iteration the fol-
lowing invariants hold:
Foundations of Dispatchability for Simple Temporal Networks with Uncertainty
261

(P1) D. f = f (i.e., the current, typically partial exe-
cution sequences are the same); and
(P2) f is RTE compliant for S.
Base Case. D. f =
/
0 = f , and
/
0 is trivially RTE-
compliant for S.
Recursive Case. Suppose (P1) and (P2) hold at the
beginning of some iteration. First, note that D. f = f
implies that D.U
x
∪D.U
c
= U. In the case where these
sets are both empty, both algorithms terminate, sig-
naling that D. f = f is a complete assignment. Other-
wise, both sets are non-empty and we must show that
(P1) and (P2) hold at the start of the next iteration.
Note that D.now = max(D. f ) = max( f ) = now.
Next, we show that D.Enabs
x
= Enabs ∩U
x
. This fol-
lows because each negative edge in S is either an ordi-
nary edge or a wait edge, both of which project onto
negative edges in every projection. Since D.Enabs
x
only includes executable TPs, the equality holds.
Case 1: D.Enabs
x
=
/
0. Therefore, Enabs ⊆ U
c
.
Then the RTE
∗
algorithm generates a Wait decision.
Now, Enabs =
/
0 would cause RTE to fail (Algo-
rithm 1, Line 7), contradicting the dispatchability of
any STN projection from this point onward. There-
fore, Enabs 6=
/
0 and, thus, there exists at least one
enabled CTP C which, given the negative edge from
C to its activation TP, implies that its contingent link
is currently active. Therefore, Lines 7 to 13 of the or-
acle (Algorithm 5) would select an observation of the
form (t
c
,τ), where τ 6=
/
0.
Now, by (P2), f is RTE-compliant; hence it can
be generated by any projection that respects the pre-
history π
f
. Next, let f
0
be the execution sequence
obtained by executing the CTPs in τ at time t
c
; and
let π
f
0
be the corresponding pre-history. Among the
projections that respect the pre-history π
f
are those
that also respect π
f
0
. Since the RTE algorithm, when
applied to any of those projections, must execute the
CTPs in τ at time t
c
, it follows that f
0
is RTE com-
pliant for S (i.e., (P2) holds at the start of the next
iteration). And since the HCE algorithm executes the
CTPs in τ at t
c
, it follows that (P1) holds at the start of
the next iteration. Finally, the other updates done by
HCE are equivalent to those done by RTE, as follows.
Removing any C-waits for C ∈ τ corresponds to the
satisfaction of the corresponding projected constraints
since, for example, a C-wait (W,C:−8, A) projects to
the negative edge (W, −5, A) in the projection where
C − A = 5, whose lower bound of A + 5 is automati-
cally satisfied when C executes at A + 5. And RTE
∗
’s
updating of D.Enabs
x
is equivalent to RTE’s updating
of Enabs given that wait edges project onto ordinary
negative edges.
Case 2: D.Enabs
x
6=
/
0. Here, the RTE
∗
genD
algo-
rithm (Algorithm 4) would, at Lines 3 to 12, gener-
ate an execution decision of the form (t,V ). Now, for
any (executable) X ∈ Enabs
x
, its upper bound is com-
puted based solely on propagations from executed
TPs along non-negative edges. Given that D. f = f , it
follows that D.ub(X) = ub(X) for each X ∈ D.Enabs
x
,
regardless of the f -respecting projection that RTE is
applied to. Similar remarks apply to the lower bound
for each X except that D.glb(X) ≥ lb(X). To see this,
note that although propagations along ordinary nega-
tive edges done by RTE
∗
are identical to those done
by RTE, the activated waits in AcWts(X) may impose
stronger constraints. For example, consider an acti-
vated wait edge (X,C
i
:−7,A
i
), which imposes a lower
bound of A
i
+ 7 on X. In a projection where ω
i
= 4 <
7, this edge projects onto the ordinary negative edge
(X,−4, A
i
), which imposes the weaker lower bound
of A
i
+ 4 on X. In contrast, in a projection where
ω
i
= 9 ≥ 7, the wait edge projects onto the ordinary
negative edge (X,−7, A
i
), which imposes the lower
bound of A
i
+ 7 on X. In general, it therefore follows
that [D.glb(X ), D.ub(X)] ⊆ [lb(X),ub(X)]. To ensure
that the RTE
∗
genD
algorithm does not fail at Line 9, we
must show that D.glb(X) ≤ D.ub(X). To see why, let
S
ω
be any projection that respects f , but also spec-
ifies maximum durations for all of the currently ac-
tive contingent links. In S
ω
, all C-waits project onto
negative edges of the same length, which implies that
D.glb(X) = lb(X) ≤ ub(X) = D.ub(X), since the dis-
patchability of all projections ensures that RTE cannot
fail, and hence [D.tl, D.ul]∩[D.now,∞) 6=
/
0. Therefore,
RTE
∗
genD
will generate an RTED of the form (t,V ).
Case 2a: A (ρ,τ) observation, where ρ < t. This
case can be handled similarly to Case 1.
Case 2b: A (t,
/
0) observation.. Here, RTE
∗
ex-
ecutes V at time t. Since t ∈ [D.glb(V ),D.ub(V )] ⊆
[lb(V ), ub(V )] it follows that executing V at t is a vi-
able choice for the RTE algorithm for every projec-
tion that (1) respects f ; and (2) constrains the dura-
tion of each active contingent link (A,x, y,C) to satisfy
C − A ≥ t − f (A). (And such projections exist, since
otherwise the oracle could not have generated the ob-
servation (t,
/
0).) Therefore, (P1) and (P2) will neces-
sarily hold at the start of the next iteration, when RTE
is restricted to such projections. Finally, note that the
updates done by the HXE algorithm are exactly the
same as those done by RTE, except for the updating
of the activated waits in the case where V happens
to be an activation timepoint. However, inserting an
entry (t + w,C
i
) into the set D.AcWts(Y ) in response
to a wait edge (Y,C
i
:−w,V ), merely ensures that the
bound for the corresponding projected edge (Y, −γ,V )
will be respected by RTE
∗
, where γ = min{w, ω
i
} and
ω
i
specifies the duration of the relevant contingent
link.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
262

Case 2c: A (t, τ) observation, where τ 6=
/
0. This
case is similar to a combination of Case 1 (with ρ = t)
and Case 2b.
Corrolary 1. An ESTNU S is dispatchable if and only
if every run of the RTE
∗
algorithm on S outputs a so-
lution for the ordinary constraints in S.
Proof. By Theorem 2, S is dispatchable if and only
if each run of RTE
∗
generates a complete assignment
that can also be generated by a run of RTE on some
projection S
ω
. But by Definitions 4 and 1, S is dis-
patchable if and only if every one of its STN projec-
tions is dispatchable (i.e., every run of RTE on any of
the STN projections generates a solution).
5 CONCLUSION
The main contributions of this paper are:
1. to provide a formal definition of a real-time
execution algorithm for ESTNUs, called RTE
∗
,
that provides maximum flexibility while requiring
only minimal computation; and
2. to formally prove that an ESTNU
S = (T , C, L, C
w
) is dispatchable (according
to the definition in the literature) if and only if
every run of RTE
∗
on S necessarily satisfies all of
the constraints in C no matter how the contingent
durations play out in real time.
In so doing, the paper fills an important gap in the al-
gorithmic and theoretic foundations of the dispatcha-
bility of Simple Temporal Networks with Uncertainty.
Since the worst-case complexity of the RTE
∗
algo-
rithm is O(m + nk log(nk)), future work will focus on
generating equivalent dispatchable ESTNUs having
the minimum number of (ordinary and wait) edges.
REFERENCES
Cairo, M., Hunsberger, L., and Rizzi, R. (2018). Faster
Dynamic Controllablity Checking for Simple Tempo-
ral Networks with Uncertainty. In 25th International
Symposium on Temporal Representation and Reasoning
(TIME-2018), volume 120 of LIPIcs, pages 8:1–8:16.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2022). Introduction to Algorithms, 4th Edition. MIT
Press.
Dechter, R., Meiri, I., and Pearl, J. (1991). Temporal Con-
straint Networks. Artificial Intelligence, 49(1-3):61–95.
Hunsberger, L. (2009). Fixing the semantics for dynamic
controllability and providing a more practical character-
ization of dynamic execution strategies. In 16th Interna-
tional Symposium on Temporal Representation and Rea-
soning (TIME-2009), pages 155–162.
Hunsberger, L. and Posenato, R. (2023). A Faster Algo-
rithm for Converting Simple Temporal Networks with
Uncertainty into Dispatchable Form. Information and
Computation, 293(105063):1–21.
Morris, P. (2014). Dynamic controllability and dispatcha-
bility relationships. In CPAIOR 2014, volume 8451 of
LNCS, pages 464–479. Springer.
Morris, P. (2016). The Mathematics of Dispatchability Re-
visited. In 26th International Conference on Automated
Planning and Scheduling (ICAPS-2016), pages 244–252.
Morris, P., Muscettola, N., and Vidal, T. (2001). Dynamic
control of plans with temporal uncertainty. In IJCAI
2001: Proc. of the 17th international joint conference
on Artificial intelligence, volume 1, pages 494–499.
Muscettola, N., Morris, P. H., and Tsamardinos, I. (1998).
Reformulating Temporal Plans for Efficient Execution.
In 6th Int. Conf. on Principles of Knowledge Representa-
tion and Reasoning (KR-1998), pages 444–452.
Tsamardinos, I., Muscettola, N., and Morris, P. (1998). Fast
Transformation of Temporal Plans for Efficient Execu-
tion. In 15th National Conf. on Artificial Intelligence
(AAAI-1998), pages 254–261.
Foundations of Dispatchability for Simple Temporal Networks with Uncertainty
263
