Assessment of the Academic Load in a Curriculum Through an

Optimization Model: Case Study of a Master Program

Myriam Gaete

and Marcela C. González-Araya

Doctorado en Sistemas de Ingeniería, Faculty of Engineering, Universidad de Talca, Campus Curicó,

Camino a Los Niches, km 1, Curicó, Chile

Departament of Industrial Engineering, Faculty of Engineering, Universidad de Talca, Campus Curicó,

Camino a Los Niches km 1, Curicó, Chile

Keywords: Optimization Model, Academic Load, Linear Programming, Curriculum, Mathematical Modeling.

Abstract: The evaluation of academic load is necessary and constitutes a fundamental process in the design and redesign

of programs. This is because an excessive academic load can have academic consequences such as lag, as

well as effects on mental health, including depression, anxiety, burnout, self-esteem problems, among others.

Academic load is a complex and dynamic topic, resulting in the absence of a single approach to its study and

measurement. In this sense, this work proposes a mathematical model of linear programming. The case study

evaluated in Magister, a Chilean university. The results reveal an even distribution of academic load between

semesters and courses within the program. As the semesters progress, the academic load tends to increase

gradually. Integrated courses, such as Course 10 and Course 11, have higher loads compared to others. In the

third semester there is variability in the academic load, with one course concentrating most of the study hours.

In total, 294 hours of study are required to complete the program. A comprehensive review of academic load

distribution is recommended to ensure an equitable and manageable educational experience for students.

1 INTRODUCTION

The academic load of a curriculum is a critical issue

for educational institutions because it is necessary to

guarantee the competences and skills established in

an outcome profile (undergraduate or graduate

profile). Therefore, the curriculum seeks to achieve

the outcome profile through the definition of course

contents and training periods. In this topic, the

academic load of a course represents the total time

that an average student must spend attending classes

and studying independently (i.e., making lectures,

projects, self-study, trainee, etc.) for obtaining the

learning outcomes (Ünal and Uysal, 2014). For this

reason, designing a curriculum involves several

complexities, such as the challenge of ensuring

accessibility and effectiveness of learning for all

students, considering their diversity in terms of

abilities, prior knowledge, learning styles, and special

needs (Dantas & Cunha, 2020; Woodcock et al.,

2022); the inclusion of excessive contents, generating

https://orcid.org/0000-0001-5917-5217

https://orcid.org/0000-0002-4969-2939

curricular overload (Chen et al., 2023); the necessity

of periodic curriculum reviews and updates for

ensuring its relevance and effectiveness (Chen et al.,

2023).

Regarding the academic load, optimization

models have been proposed in the literature for

establishing it. According to Lambert et al. (2006),

one of the first models that dealt with this topic was

the balanced academic curriculum problem (BACP)

introduced by Castro and Manzano, (2001). The

proposed model was an integer linear programming

model, which sought to design a balanced academic

curriculum by assigning courses to periods,

guaranteeing a similar academic load in each period.

The model was executed using synthetic instances,

concluding that it could solve medium size problems.

A few years later, Hnich et al., (2004) presented a

hybrid modelling approach that combines a mixed

integer linear programming model with a data-driven

model. Additionally, the authors used machine

learning techniques in order to forecast the course

Gaete, M. and González-Araya, M.

Assessment of the Academic Load in a Curriculum Through an Optimization Model: Case Study of a Master Program.

DOI: 10.5220/0012365400003639

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 269-276

ISBN: 978-989-758-681-1; ISSN: 2184-4372

269

demand. These authors also applied their approach to

synthetic instances. They concluded that the hybrid

model could increase the complexity of the problem.

However, they did not mention conclusions about

improvements in the academic load related to their

approach. Based on the model presented by Castro

and Manzano (2001), Lambert et al. (2006) developed

a method for solving it, which combines two solution

techniques: genetic algorithms (Holland, 1992) and

constraint propagation (Jaffart et al., 1987). Genetic

algorithms are used to generate solutions for the

model of Castro and Manzano (2001), and to explore

the solution space, while constraint propagation

method is applied to improve the solutions, and to

ensure the feasibility of the solutions. In 2012,

Chiarandini et al. (2012) presented a generalized

version of the balanced academic curriculum problem

(BACP) proposed by Castro and Manzano, (2001)

The new version of the model considers different

curricula and professors’ preferences and was solved

by using a local search metaheuristic (Hoos, 2004). In

this study, the authors used a real case study,

corresponding to the curricula of an engineering

school of Italy. The new model aimed to balance the

academic curricula of all the engineering careers of

the school simultaneously. Therefore, some

limitations of the model discussed by the authors

were: i) a course established in the curriculum for

different engineering careers, one was scheduled for

each career instead of defining only one for all

careers; ii) the model did not balance the academic

load of professors; iii) the increase in the number of

elective courses made the model more complex; iv)

engineering students could have some terms without

courses because the model does not force that a

course be carried out every term. Later, Ünal and

Uysal (2014) presented a bi-objective mixed integer

linear programming model, which was called relevant

course balancing problem (RBCB). This model also

seeks to balance a curriculum but considers two

objective functions. One objective function

minimizes the distance (relevant score) of relevant

courses among periods, prioritizing scheduling these

courses in a same period (zero distance). The other

objective function minimizes the bias of the academic

load per term. In this study, the authors used a real

case study, corresponding to the curriculum of an

undergraduate career from the industrial engineering

department of Fatih University in Turkey. The

proposed model enables consolidating loads of

students per semester, meeting the prerequisite

conditions. Furthermore, the authors compared their

model with the BACP, where the RBCB generated

better course timetabling solutions than the BACP.

About this comparison, they concluded that the

BACP can be solved faster than the RBCB.

Nevertheless, the RBCB obtained optimal solutions

in about 3–15 minutes, which is a reasonable time. It

is important to highlight that none of the studies

presented in the literature took into account the

specific knowledges that need to be incorporated in

each course, which are directly related to the

academic load of a curriculum.

Regarding the taxonomy for classifying

knowledges, the current literature has dealt with this

issue as a peripheral topic (Tuma & Nassar, 2021). In

education, the taxonomy is relevant because it

classifies educational objectives into various

cognitive levels, from the simplest to the most

complex. The most known taxonomy is the Bloom’s

Taxonomy, proposed by Benjamin Bloom in 1956

(Choi-Koh, 2003), and it has had a significant impact

on education by offering a well-organized framework

for both curriculum design and the evaluation of

learning (Tuma & Nassar, 2021). Moreover, this

classification defines six levels of cognitive

complexity, which are: remembering (remember facts

and concepts); understanding (understand and

explain the meaning of the information); applying

(apply knowledge in new or specific situations);

analyzing (divide the information into parts and

understand their relationships); evaluating (judging

the validity of information, arguments or methods);

and creating (combining elements to form a new

whole or create something new).

In the current study, a methodology that includes

the development of a linear programming model for

designing a curriculum is proposed. In this way, the

developed model seeks to allocate knowledges to

courses, where the courses have been pre-defined for

each term. The objective of this allocation is to

guarantee the achievement of competences and skills

outlined in the graduate profile.

This article is structured as follows. Section 2

describes the proposed methodology to estimate the

academic load. Section 3 presents a real case study,

belonging to a Chilean university. Finally, the main

conclusions are presented in Section 4.

2 METODOLOGY

The proposed methodology of this study has three key

stages, which are described as follows.

• Step 1. Rating Knowledges by an Expert

Team. In this step, the knowledges need to be

rated for incorporating them as input parameters

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

270

of the proposed linear programming model.

Therefore, a multidisciplinary expert team is

required to rate them. The rating process can be

carried out by using the “developing a

curriculum methodology.”

• Step 2. Execution of the Optimization Model

for Estimating the Academic Load. In this step,

the proposed mathematical programming model

is executed by using the parameters determined

in the previous step. The model allows allocating

the minimum number of knowledges to the

courses, maintaining the defined academic load

of each course, that is, the established academic

credits of each course. Thus, excessive, or low

academic load per term is avoided.

• Step 3. Comparison of Results with the

Current Curriculum. The purpose of this

comparison is to evaluate the quality and

consistency of the current curriculum, and to

propose improvements.

2.1 Model Knowledge-Based

Curriculum Balance (BKCP)

For contextualizing the terms used in the proposed

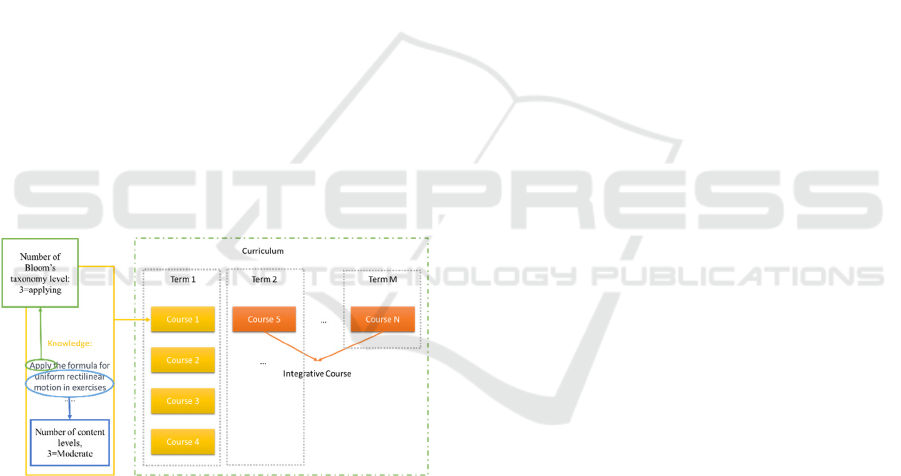
mathematical model, a schematic representation of a

curriculum is shown in Figure 1.

Figure 1: Schematic representation of a curriculum.

In Figure 1, the concepts as term, credit, content

levels and Taxonomy Bloom’s levels. A term consists

in a group of courses dictated in the same period.

Every course is associated with a specific set of

knowledges. Furthermore, each knowledge is

characterized by a action verb, quantified according

to the Bloom’s Taxonomy, that is, from 1 to 6. It is

important to notice that every knowledge has a

content, which is also assessed by experts regarding

to its level of complexity, by using a scale from 1 to

6. On the other hand, in a curriculum, there are

integrative courses designed to comprehensively

address and evaluate the concepts’ learning. These

courses aim to foster the integration of knowledges

and skills from diverse content areas.

Two examples regarding the different

complexities of a content are described as follows.

For example, a student could need more time to solve

Quantum Physics exercises than Uniform Rectilinear

Motion problems because the first content requires

more knowledges. The similar situation can be

observed in the taxonomic level. For example,

memorizing axioms of probability requires less time

than applying them. Finally, the academic period also

influences the time required by a student for learning.

For example, a first-year student may spend more

time making a Python coding assignment than a

senior student.

The proposed model seeks to assign knowledge

assigned in each course and period of the program

curriculum according to a Bloom j taxonomy level, at

a content level of each knowledge. As mentioned

previously, the objective of the proposed model is to

allocate the minimal quantity of knowledges to

courses, while guaranteeing the academic load

requirements. In this way, it allows distributing the

academic load of a curriculum to comply with the

knowledges declared at graduation profile.

The linear programming model developed in this

study, called as knowledge-based curriculum balance

(BKCP), which is applied in the Step 2, is detailed as

follows.

Definition of Parameters:

𝐼= Number of courses,

𝐽= Number of Bloom’s taxonomy levels, where 1 =

remembering, 2= understanding, 3= applying, 4=

analyzing, evaluating=5 and 6=creating,

𝑀= Number of terms in the curriculum,

𝐾= Number of content levels, where 1= Very Easy,

2=Easy, 3=Moderate, 4=Difficult, 5= Very

Challenging and 6= Extremely Difficult,

𝐴 = Set of integrative courses,

𝐵



= Set of terms from which the course i is excluded,

i=1,…I,

𝐶𝐴



= Number of credits per course i, i = 1, …, I,

SC = Minimum number of knowledge elements

required per credit in the curriculum,

𝑝



= Percentage of slack accepted between the

declared credits and the credits assigned according to

the model,

𝑉

,,

= The number of hours required by the student

to acquire knowledge based on course I, Bloom's

taxonomy level j, content level k, and term m, j = 1,

…, J, k=1, …, K and m=1, …, M,

𝑀𝐷 = The maximum number of knowledges of the

same course and content within a specific term.

Assessment of the Academic Load in a Curriculum Through an Optimization Model: Case Study of a Master Program

271

Definition of the Decision Variables:

𝑥

,,,

= number of knowledge elements in course i

with a Bloom’s taxonomy level j, at a content level k,

in a term m, i=1, …, I, j = 1, …, J, k=1, …, K and

m=1, …, M.

Mathematical Formulation:

Minimize𝑥

,,,



















(1)

𝑉

,,

𝑥

,,,













≤𝑝



𝐶𝐴



∀𝑖=1,…,𝐼

(2)

𝑉

,,

𝑥

,,,













≥𝑝



𝐶𝐴



∀ 𝑖 = 1,…,𝐼

(3)

𝑥

,



,,













−𝑥

,



,,













≤𝑀𝐷,∀

𝑗



𝑗



(4)

𝑥

,,,













=0,∀

𝑗

=1,…,

𝐽

(5)

𝑥

,,,













≥𝑆𝐶×𝐶

𝐴



∀ 𝑖 = 1,…𝐼

(6)

𝑥

,,,





−𝑥

,,,





≤0,

∀ 𝑖=1,…𝐼,𝑚=1,…𝑀,𝑘=1,…𝐾

(7)

𝑥

,,,











=0 ,∀𝑖=1,…𝐼,𝑚 𝜖 𝐵



(8)

𝑥

,,,















−𝑥

,,,















≥0,∀ 𝑘



,𝑘



=1,…𝐾

(9)

𝑥

,,,

≥0









∀ 𝑘=1,…𝐾,𝑚=1,…𝑀

(10)

𝑥

,,,

∈ 



,∀𝑖,

𝑗

,𝑚,𝑘.

(11)

The objective function seeks to minimize the

number of knowledge elements in the study plan.

Constraint (2) ensures that each course has at least p

percentage of the academic load defined in the

program. Constraint (3) ensures that courses cannot

have more than p

percentage of the academic load

defined in the program. Constraint (4) ensures that the

number of knowledge elements by taxonomy is

similar at different levels. Constraint (5) ensures that

the course has knowledge elements according to the

level where the course is located. Constraint (6)

ensures that each course has at least SC knowledge

elements for each of the assigned credits. Constraint

(7) ensures that courses in the first period cannot have

more knowledge elements of the highest taxonomy

level than the sum of the knowledge elements of

lower levels. Constraint (8) ensures equitable content

coverage, while Constraint (9) ensures that the

content is distributed equally across all semesters of

the program. Constraint (10) guarantees the inclusion

of all the required contents in each term. Constraint

(11) establishes the nature of the decision variables.

It is important to notice that in the BKCP model,

the parameter V represents the number of hours

required by a student to acquire knowledges and

skills. This parameter considers the complexity of the

contents, the taxonomic levels, and the current

academic period (term).

3 CASE STUDY

Below are the results, evaluating a 4-semester study

program at Magister a Chilean university. The

program consists of 98 SCT credits and 12 courses (of

which the 11th and 12th are integrative courses), and

the parameters can be found in the annexes of this

work.

Each course has a different number of credits,

integrative courses have a greater academic load, as

can be seen in Table 1. Regarding the number of

knowledges, currently the program has 101

knowledge. By analyzing this knowledge by

semester, we can see that the curriculum has a large

amount of high-level knowledge according to

Bloom's taxonomy, in the first semesters of the

program. The courses with the highest number of

credits are in turn those with the lowest number of

knowledges, which shows an imbalance in the

academic load.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

272

Table 1: Number of knowledges per course of the study

program.

Semester Course Credit

Bloom's Taxonomy

Total

1 2 3 4 5 6

1 5 4 5 2

1 12

2 5

3 5 2

1 2 2 7

4 5

4 4 8

Total 1

20 4 7 12 1 7 6 37

5 5 1

6 2 1 10

6 5

7 5

3 3 6

8 2

9 5 1 1 1 3 6

Total 2 22 2 0 7 15 5 6 35

10 2 3 1 4

11 26 1 8 9 18

Total 3

28 0 1 0 0 11 10 22

4 12 28 3 4 7

Total 4

28 0 0 0 0 3 4 7

Total

98 6 8 19 16 26 26 101

3.1 Model BKCP Results

The results reveal a substantial redistribution of

knowledge, with a notable increase from 101 to 336

units of knowledge. This increase is primarily

attributed to the higher levels of Bloom's taxonomy

(levels 4, 5, and 6). In terms of knowledge allocation

per course, those with 5 credits are associated with 15

units of knowledge distributed across various levels

Table 2: Model BKCP results.

Semester

Course

Bloom's Taxonomy

Total 1 2 3 4 5 6

3 3 9 15

5 1 1 8 15

3 1 2 9 15

1 14 15

Total 1

0 7 6 20 1 26 60

5 7 3 15

4 1 10 15

1 1 12 1 15

4 11 15

1 5 6

Total 2

1 5 10 19 13 18 66

24 42 12 78

2 4 6

Total 3

0 24 2 4 42 12 84

55 20 38 13 126

Total 4

55 20 38 13 126

Total

56 56 56 56 56 56 336

When considering the knowledge distribution in

integrative courses, the model suggests an increase of

over 70 units of knowledge. This substantial increase

is due to the considerably higher load of these courses

compared to other courses in the curriculum.

3.2 Comparison of Model Results with

the Current Learning Path

The current program has only one-third of the

knowledge items that the mathematical model

identified as optimal. According to the comparison

presented in Table 1, the existing pathway

demonstrates a notably lower quantity of high-level

cognitive knowledge. As a result, from a curricular

perspective, questions may arise regarding students'

achievement of the specified competency levels.

In analyzing the distribution of knowledge by

Bloom's Taxonomy and content, we can appreciate

that the results of the BKCP model diversify the

distribution of the academic load. This translates to

none of the 6 identified contents being at the highest

level of Bloom's Taxonomy (Figure 2 and 3).

Figure 2: Number of knowledges Number of knowledges

per Bloom's Taxonomy and content of the study program.

Figure 3: Number of knowledges Number of knowledges

per Bloom's Taxonomy and content of Model BKCP.

Furthermore, a disparity in the quantity of

knowledge among courses in the first and second

semesters is noticeable, despite all these courses

having the same number of credits.

Assessment of the Academic Load in a Curriculum Through an Optimization Model: Case Study of a Master Program

273

On the other hand, when we analyze courses 10

and 11, which were defined as integrative knowledge

courses, the number of knowledge items is low.

4 CONCLUSIONS

There is an unequal distribution of academic load

across different semesters and courses. Notably,

courses like Course 6 in the second semester and

Course 10 in the third semester exhibit significantly

higher loads compared to others.

Certain courses, such as Course 10 and 12, carry

notably heavier academic burdens compared to their

counterparts. This demands special attention to

ensure students can effectively manage their load.

Across all semesters and courses, a total of 336

areas of knowledge is required, providing a

comprehensive overview of the complete academic

load within the program.

Concerning the distribution of academic load

based on Bloom’s taxonomy, it becomes evident that

knowledge at the lower taxonomy levels is

predominantly concentrated in the first two

semesters, while higher-level knowledge in Bloom’s

taxonomy is predominantly concentrated in the later

semesters.

For future research, it is advisable to consider the

incorporation of additional variables into the model,

including soliciting student feedback on their courses.

In addition, the inclusion of prerequisites for each

course would be considered, as has carried out in the

study of Lambert et al., (2006).

ACKNOWLEDGEMENTS

MSc Myriam Gaete G. would like to thank

CONICYT PFCHA/BECA DE DOCTORADO

NACIONAL/2021 under Grant 21211324 for its

financial support. Moreover, DSc Marcela González-

Araya would like to thank FONDECYT Project

1191764 (Chile) for its financial support.

REFERENCES

Castro, C., & Manzano, S. (2001). Variable and Value

Ordering When Solving Balanced Academic

Curriculum Problems. Proceedings of 6th Workshop of

the ERCIM WG on Constraints (Prague, June 2001), 1–

12. https://doi.org/https://doi.org/10.48550/arXiv.cs/

0110007

Chen, A. M. H., Brown, S., Mark, K., & McBane, S. (2023).

An overview of Instructional approaches and decision-

making strategies to curtail curricular overload. In

American journal of pharmaceutical education (Vol.

87, Issue 8, p. 100013). NLM (Medline).

https://doi.org/10.1016/j.ajpe.2022.12.001

Chiarandini, M., Di Gaspero, L., Gualandi, S., & Schaerf,

A. (2012). The balanced academic curriculum problem

revisited. Journal of Heuristics, 18(1), 119–148.

https://doi.org/10.1007/s10732-011-9158-2

Choi-Koh, S. S. (2003). Effect of a Graphing Calculator on

a 10th-Grade Student’s Study of Trigonometry. In

Source: The Journal of Educational Research (Vol. 96,

Issue 6).

Dantas, L. A., & Cunha, A. (2020). An integrative debate

on learning styles and the learning process. Social

Sciences and Humanities Open, 2(1).

https://doi.org/10.1016/j.ssaho.2020.100017

Hnich, B., Kiziltan, Z., Miguel, I., & Walsh, T. (2004).

Hybrid Modelling for Robust Solving. Annals of

Operations Research, 130, 19–39. www.csplib.org

Holland, J. H. (1992). Adaptation in Natural and Artificial

Systems. The MIT Press. https://doi.org/10.7551/

mitpress/1090.001.0001

Hoos, H. (2004). Stochastic Local Search - Methods,

Models, Applications (Elsevier).

Jaffart, J., Lassez, J.-L., Thomas, I. B. M., Watson, J.,

Center, R., & Heights, Y. (1987). Constraint Logic

Programming. Constraint Logic Programming. In

Proceedings of the 14th ACM SIGACT-SIGPLAN

Symposium on Principles of Programming Languages,

111–119.

Lambert, T., Castro, C., Monfroy, E., & Saubion, F. (2006).

Solving the Balanced Academic Curriculum Problem

with an Hybridization of Genetic Algorithm and

Constraint Propagation.

Tuma, F., & Nassar, A. K. (2021). Applying Bloom’s

taxonomy in clinical surgery: Practical examples.

Annals of Medicine and Surgery, 69.

https://doi.org/10.1016/j.amsu.2021.102656

Ünal, Y. Z., & Uysal, Ö. (2014). A new mixed integer

programming model for curriculum balancing:

Application to a Turkish university. European Journal

of Operational Research, 238(1), 339–347.

https://doi.org/10.1016/j.ejor.2014.03.015

Woodcock, S., Sharma, U., Subban, P., & Hitches, E.

(2022). Teacher self-efficacy and inclusive education

practices: Rethinking teachers’ engagement with

inclusive practices. Teaching and Teacher Education,

117. https://doi.org/10.1016/j.tate.2022.103802.

APPENDIX A

Valuation of academic load by type of knowledge.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

274

Bloom’s Taxonomy Content Semester Value

1 1 1 54,00

2 1 1 27,00

3 1 1 18,00

4 1 1 13,50

5 1 1 10,80

6 1 1 9,00

1 2 1 27,00

2 2 1 13,50

3 2 1 9,00

4 2 1 6,75

5 2 1 5,40

6 2 1 4,50

1 3 1 18,00

2 3 1 9,00

3 3 1 6,00

4 3 1 4,50

5 3 1 3,60

6 3 1 3,00

1 4 1 13,50

2 4 1 6,75

3 4 1 4,50

4 4 1 3,38

5 4 1 2,70

6 4 1 2,25

1 5 1 10,80

2 5 1 5,40

3 5 1 3,60

4 5 1 2,70

5 5 1 2,16

6 5 1 1,80

1 6 1 9,00

2 6 1 4,50

3 6 1 3,00

4 6 1 2,25

5 6 1 1,80

6 6 1 1,50

1 1 2 48,00

2 1 2 24,00

3 1 2 16,00

4 1 2 12,00

5 1 2 9,60

6 1 2 8,00

1 2 2 24,00

2 2 2 12,00

3 2 2 8,00

4 2 2 6,00

5 2 2 4,80

6 2 2 4,00

1 3 2 16,00

2 3 2 8,00

3 3 2 5,33

4 3 2 4,00

5 3 2 3,20

6 3 2 2,67

1 4 2 12,00

2 4 2 6,00

Bloom’s Taxonomy Content Semester Value

3 4 2 4,00

4 4 2 3,00

5 4 2 2,40

6 4 2 2,00

1 5 2 9,60

2 5 2 4,80

3 5 2 3,20

4 5 2 2,40

5 5 2 1,92

6 5 2 1,60

1 6 2 8,00

2 6 2 4,00

3 6 2 2,67

4 6 2 2,00

5 6 2 1,60

6 6 2 1,33

1 1 3 42,00

2 1 3 21,00

3 1 3 14,00

4 1 3 10,50

5 1 3 8,40

6 1 3 7,00

1 2 3 21,00

2 2 3 10,50

3 2 3 7,00

4 2 3 5,25

5 2 3 4,20

6 2 3 3,50

1 3 3 14,00

2 3 3 7,00

3 3 3 4,67

4 3 3 3,50

5 3 3 2,80

3 3 2,33

1 4 3 10,50

2 4 3 5,25

3 4 3 3,50

4 4 3 2,63

5 4 3 2,10

6 4 3 1,75

1 5 3 8,40

2 5 3 4,20

3 5 3 2,80

4 5 3 2,10

5 5 3 1,68

6 5 3 1,40

1 6 3 7,00

2 6 3 3,50

3 6 3 2,33

4 6 3 1,75

5 6 3 1,40

6 6 3 1,17

1 1 4 36,00

2 1 4 18,00

3 1 4 12,00

4 1 4 9,00

Assessment of the Academic Load in a Curriculum Through an Optimization Model: Case Study of a Master Program

275

Bloom’s Taxonomy Content Semester Value

5 1 4 7,20

6 1 4 6,00

1 2 4 18,00

2 2 4 9,00

3 2 4 6,00

4 2 4 4,50

5 2 4 3,60

6 2 4 3,00

1 3 4 12,00

2 3 4 6,00

3 3 4 4,00

4 3 4 3,00

5 3 4 2,40

6 3 4 2,00

1 4 4 9,00

2 4 4 4,50

3 4 4 3,00

4 4 4 2,25

5 4 4 1,80

6 4 4 1,50

1 5 4 7,20

2 5 4 3,60

3 5 4 2,40

4 5 4 1,80

5 5 4 1,44

6 5 4 1,20

1 6 4 6,00

2 6 4 3,00

3 6 4 2,00

4 6 4 1,50

5 6 4 1,20

6 6 4 1,00

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

276