Partial Tensorized Transformers for Natural Language Processing

Subhadra Vadlamannati

and Ryan Solgi

Mercer Island High School, 9100 SE 42nd St, Mercer Island, U.S.A.

Department of Electrical and Computer Engineering, University of California Santa Barbara, Santa Barbara, U.S.A.

Keywords:

Neural Networks, Machine Learning, Natural Language Processing, ALIGN, Tensor-Train Decomposition,

Vision-Language Modelling.

Abstract:

The transformer architecture has revolutionized Natural Language Processing (NLP) and other machine-

learning tasks, due to its unprecedented accuracy. However, their extensive memory and parameter require-

ments often hinder their practical applications. In this work, we study the effect of tensor-train decomposition

to improve the accuracy and compress transformer vision-language neural networks, namely BERT and ViT.

We focus both on embedding-layer compression and partial tensorization of neural networks (PTNN) through

an algorithmic approach. Our novel PTNN approach signiﬁcantly improves the accuracy of existing models

by up to 5%, all without the need for post-training adjustments, breaking new ground in the ﬁeld of tensor

decomposition.

1 INTRODUCTION

The transformer architecture has been extremely in-

ﬂuential in the ﬁeld of Natural Language Process-

ing (NLP) by achieving state-of-the-art performance

in multiple downstream tasks (Brown et al., 2020).

Speciﬁcally, transformer-based models have achieved

state-of-the-art performance in machine translation,

sentence representation, and language generation

(Brown et al., 2020). However, due to the multi-head

self-attention layers present in such architectures and

the sheer number of parameters present in each layer

(upwards of a million parameters during each forward

pass of the model), transformers are computationally

demanding in terms of both memory and computation

time (Gu et al., 2022).

Effective network compression for convolutional

neural networks with fully-connected networks is

still an open research question. Therefore, com-

pressing Transformer networks is essential for their

use on edge devices and in low-resource environ-

ments. Tensor Decomposition works by represent-

ing higher-order tensors as a series of low-rank fac-

tors(Oseledets, 2011).

Tensor Decomposition (TD) works by represent-

ing higher-order tensors as a series of simpler, lower-

order tensors via elementary operations (Oseledets,

2011). There are a variety of methods proposed to

express tensors in a low-rank format factored form,

including CANDECOMP PARAFAC (CP), tucker,

and tensor-train decomposition (Bacciu and Mandic,

2020).

Several studies have explored the application of

tensor decomposition methods to reduce the size of

neural networks and improve their efﬁciency. For ex-

ample, CP decomposition has been utilized to factor-

ize weight matrices as the sum of rank-1 tensors, re-

ducing the model’s memory requirements and speed-

ing up inference time 8x (Maldonado-Chan et al.,

2021).

Techniques like tensorized training can be applied

to neural networks to achieve both faster model in-

ference and also a large reduction in the number of

parameters. More recently, tensorized training ap-

proaches have explored the possibility of updating the

factored tensors of the weights of deep neural net-

works during the forward pass instead of the model

weights directly (Bacciu and Mandic, 2020).

In the ﬁeld of natural language processing, while

tensor decomposition methods have been extensively

studied for text-based neural networks, their appli-

cation to multimodal neural networks has received

limited attention. Multimodal neural networks such

as ALIGN (Jia et al., 2021b) and VisualBERT (Li

et al., 2019), have gained signiﬁcant attention in re-

cent years due to their remarkable ability to process

both text and image data. These dual-encoder archi-

tectures require a larger number of parameters com-

Vadlamannati, S. and Solgi, R.

Partial Tensorized Transformers for Natural Language Processing.

DOI: 10.5220/0012366500003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 543-547

ISBN: 978-989-758-680-4; ISSN: 2184-433X

543

pared to traditional text-based models due to their

need to capture information from many modalities.

While there has been existing research on apply-

ing traditional tensor decomposition methods to re-

duce the size of neural networks, their application on

multimodal neural networks has been severely lim-

ited (Maldonado-Chan et al., 2021). Existing methods

have demonstrated that tensor decomposition meth-

ods can effectively reduce memory time and increase

efﬁciency on neural networks while maintaining min-

imal accuracy loss (Zhong 2019; Bacciu and Mandic

2020).

In this paper, we focus on vision-language

transformer-based models as prime candidates for

models that require compression, as these models em-

ploy a dual-encoder architecture that requires double

the amount of parameters traditional text-based mod-

els use. These models must encode both text and im-

age data and then generate a latent space that can be

employed on a variety of downstream tasks includ-

ing visual question-answering, visual common-sense

reasoning, natural language for visual reasoning, and

region-to-phrase grounding. Vision-language tasks

have a wide range of practical applications, including

closed-captioning for the hard-of-hearing and screen

reading capabilities (Morris et al., 2018).

This paper aims to advance the ﬁeld of multi-

modal language processing by applying state-of-the-

art tensor decomposition techniques to compress pop-

ular networks such as ViT and BERT while maintain-

ing model accuracy. We additionally study the effect

of tensor size and hyperparameter values during ten-

sorized training.

2 METHODS

2.1 Data

We use the ImageNet dataset to train ViT. ImageNet is

a collection of 80 million tiny images for image clas-

siﬁcation. Instead of using the entire dataset, we use

the standard 1000 image test set of ImageNet known

as CIFAR10 (Krizhevsky, 2009) to evaluate the com-

pressed model.

2.2 Tensor-Train Decomposition

We use tensor-train (TT) decomposition throughout

this paper to compress weight tensors. In the tensor

train (TT) format (Oseledets, 2011), a d-way tensor

W ∈ R

×....×n

is approximated with a set of d cores

G = {G

, G

, ..., G

} where G

∈ R

j−1

×n

×r

, r

’s

for j = 1, ..., d −1 are the ranks, r

= r

= 1, and each

element of Y is approximated by the following equa-

tion:

W [i

, ..., i

] =

∑

,...,l

, i

, l

]...G

d−1

, i

, l

With a prescribed error tolerance (ε), the fun-

damental components, denoted as G

, are obtained

through a sequence of (d − 1) consecutive Singular

Value Decompositions (SVDs) performed on auxil-

iary matrices derived from the unfolding of the tensor

Y along various axes. This decomposition method,

referred to as TT-SVD, is detailed in Algorithm 1.

Input: d-way tensor Y , error bound ε.

Output:

G = {G

, G

, ..., G

}

σ =

d−1

∥Y ∥

= 1, r

= 1, W = reshape(Y , (n

|Y |

))

for j = 1 to j = d − 1 do

W = reshape(W, (r

j−1

|W|

j−1

))

Compute σ-truncated SVD:

W = USV

+ E, where ∥E∥

≤ σ

= the rank of matrix W based on

σ-truncated SVD

= reshape(U, (r

j−1

, n

, r

))

W = SV

end

= reshape(W, (r

d−1

, n

, r

))

Return

G = {G

, G

, ..., G

}

Algorithm 1: TT-SVD.

2.3 Models and Pretraining

2.3.1 Models

We perform an analysis on the effects of various mod-

els to encode both visual and textual data. For the text

encoder, we focus on BERT (Liu et al., 2019) which

applies the bi-directional training of the Transformer

to create in-context word embeddings. To test BERT

on image classiﬁcation, we pair it with EfﬁcientNet

for the visual encoding, which is consistent with the

implementation in the dual-encoder network ALIGN

(Jia et al., 2021a). BERT has 12 layers, a hidden layer

size of 768, and around 120 million parameters.

For the visual encoder we focus on ViT (Dosovit-

skiy et al., 2021). ViT is an image processor based on

the Transformer architecture.

2.3.2 Pre-Compression Training

We ﬁne-tune the image encoder ViT as it’s trained on

a much larger, more general dataset ImageNet. Ad-

ditionally, this ﬁne-tuning improves baseline model

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

544

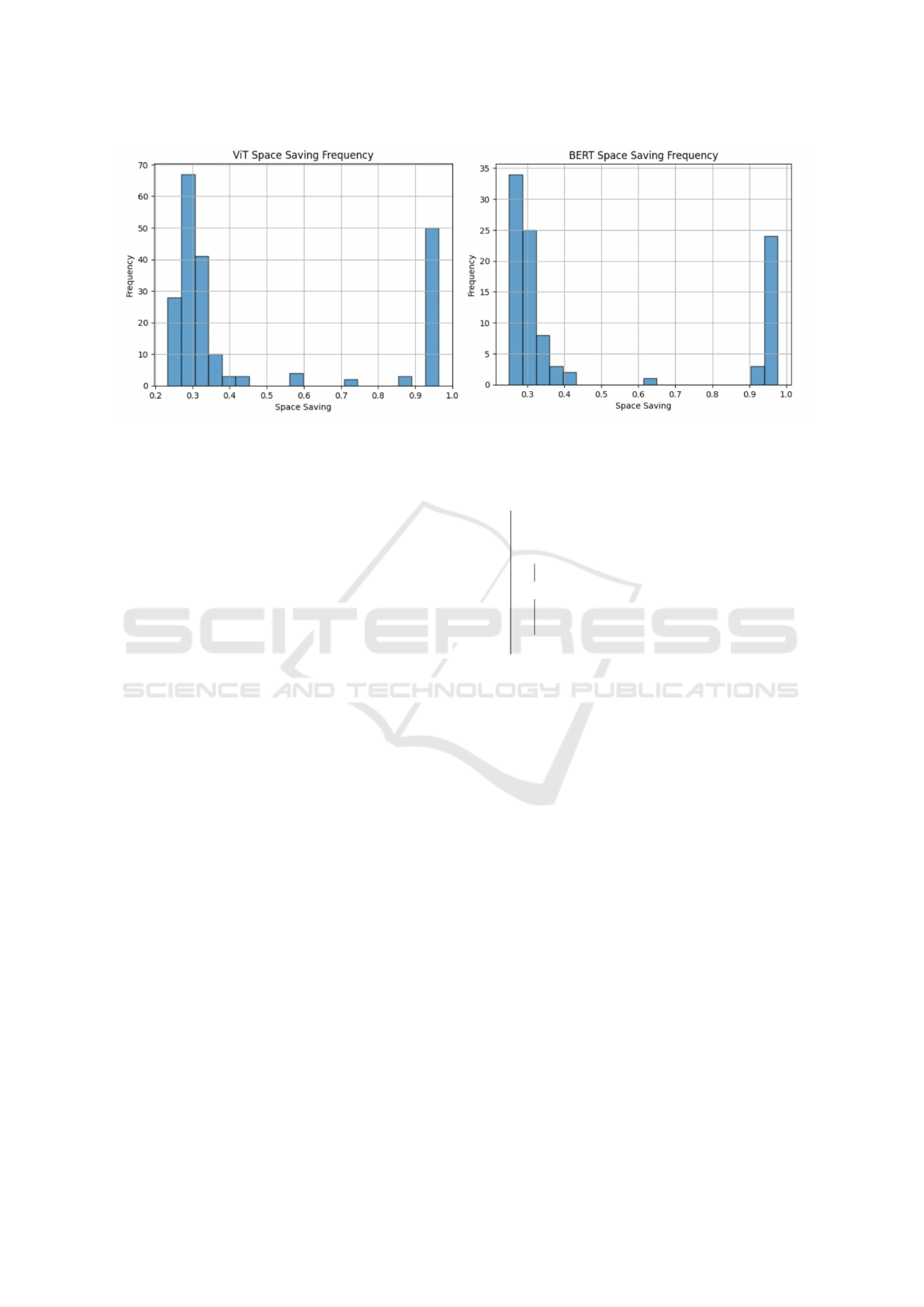
Figure 1: Bimodal Space-saving distribution for the two models.

accuracy which ensures that our post-training adjust-

ments truly improve model accuracy. Speciﬁcally, we

ﬁne-tune ViT on the CIFAR10 train set with 50,000

images and hyperparameters as outlined in Section 4.

Post ﬁne-tuning, we achieve an accuracy of 97.89%, a

validation loss of 0.2564 and a training loss of 0.4291.

2.4 Embedding Layer Tensorization

Due to the relatively large size of the embedding

layer, comprising around 28% of BERT’s total param-

eters, and around 40% of ViT’s total parameters, we

ﬁrst explore the effects of embedding layer tensoriza-

tion. Following the aforementioned approach in 2.2,

we compress the embedding layers of the model and

study the effects on model accuracy.

2.5 Partially Tensorized Neural

Network (PTNN)

As the compression of the embedding layer caused

the accuracy of the network to increase, as men-

tioned in 3.1, we continue exploring this accuracy

improvement for the rest of the model using our

method in 2.4. In this case, we do not perform post-

training adjustments (like retraining). Initially, we ex-

tract model weights from all relevant encoders. We

compress every layer by initially transforming the

weight’s 2D matrix into a tensor of higher dimension

with the same volume as the original matrix. Tensor-

train decomposition is then used to decompose model

weights with a given error bound. Lastly, we re-

shape the tensor back into the original dimensions of

the 2D weight matrix. To perform this iteratively as

described in Algorithm 2, we re-initialize the model

with the decomposed weights and perform the same

process to compress the remaining model weights.

while not at the end of the model do

compress layers 0 to n using TT decomp;

if model accuracy ≥ 5% of the original

accuracy then

proceed to layer n + 1;

else

leave layer n uncompressed;

move to layer n + 1;

end

Algorithm 2: Iterative model tensorization.

2.6 Decomposition Evaluation

We evaluate the effectiveness of the decomposition

using commonly known metrics like compression ra-

tio and space saving, as described in Equation (1).

We additionally evaluate the memory saved and

time complexity of our decomposed models. For

memory reduction, we simply multiply the percent-

age space saving with the total number of parameters

in the non-decomposed matrix. Then, we divide this

over the total number of parameters in the model.

For time complexity, we use a standard approach

to ﬁnd the O(n) based on the rank of the Tensor-

Train decomposed matrices as outlined in (Oseledets,

2011).

3 RESULTS

We evaluate both models on both the train (50,000)

and test (10,000) image split of the CIFAR10 dataset.

The ViT model has 98 weight tensors while BERT

Partial Tensorized Transformers for Natural Language Processing

545

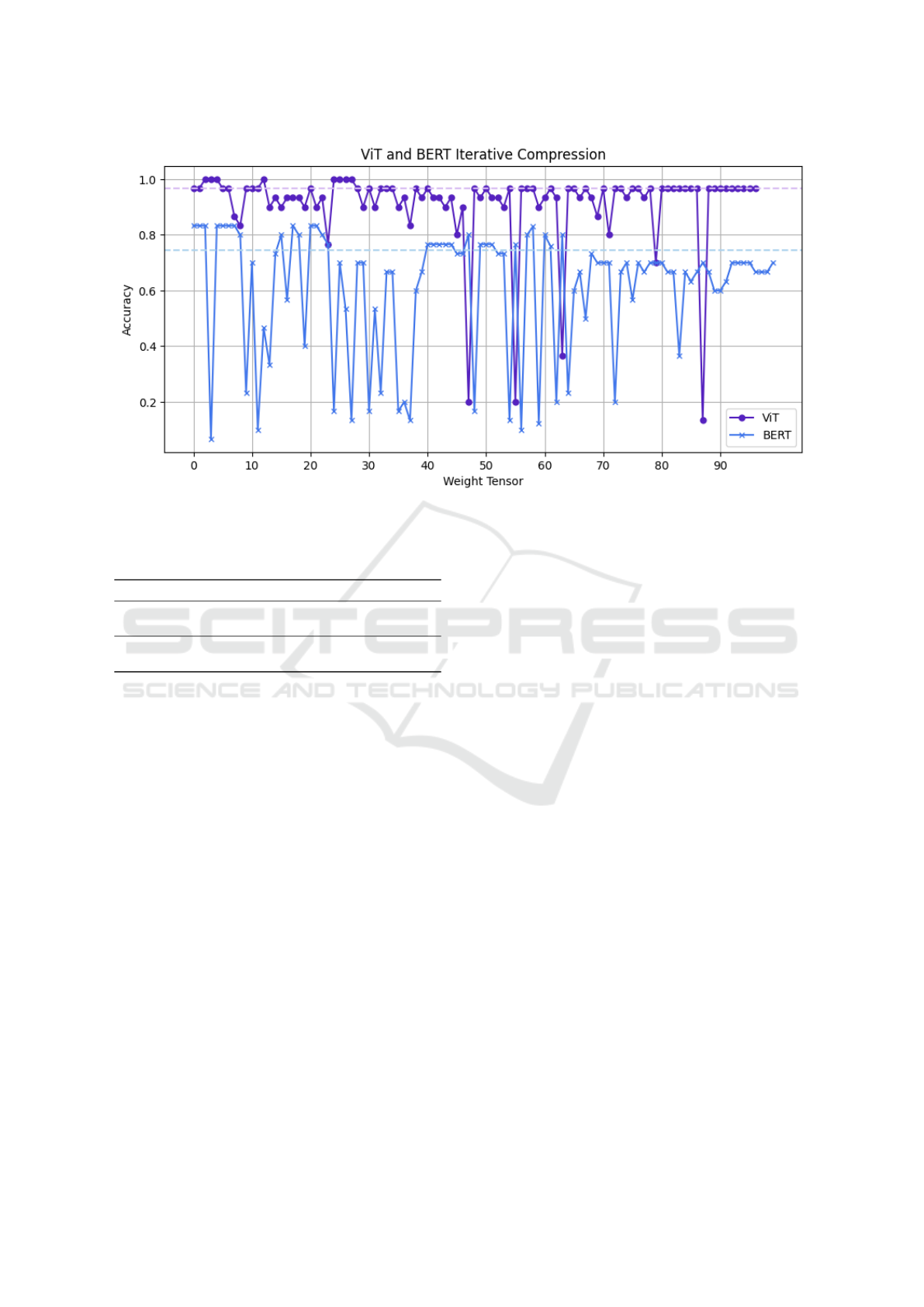
Figure 2: BERT and ViT model iterative compression with exclusion of low-accuracy layers. Lighter color corresponding

dashed lines indicate baseline accuracy.

Table 1: Embedding Layer Decomposition Results.

Model Train Test Space-saving

Decomposed ViT 0.986 0.966 0.267

Base ViT 0.960 0.960 NA

Tensorized BERT (ALIGN) 0.767 0.833 0.269

Base BERT (ALIGN) 0.750 0.746 NA

contains 99 weight tensors. All layers are compressed

with an epsilon of 0.5 and 3D projections are con-

structed with lowest norms.

3.1 Embedding Layer Decomposition

The results of embedding layer decomposition are

presented in Table 1. Embedding layer decomposi-

tion results in an accuracy increase of around 2% and

still provides us with a noticeable parameter reduc-

tion. Even though we are not able to achieve high

space-saving on these layers (i.e. only around 26%),

the success of this approach in maintaining or even

improving accuracy leads us to apply this technique

to compress more layers of the model.

As seen in 3.1, decomposing the embedding layer

of BERT provides an accuracy gain over baseline

comparisons. Following these promising results, we

follow the methodology in Algorithm 2 to determine

the amount of BERT that can be compressed whilst

still maintaining overall accuracy.

3.2 Iterative and Individual

Decomposition

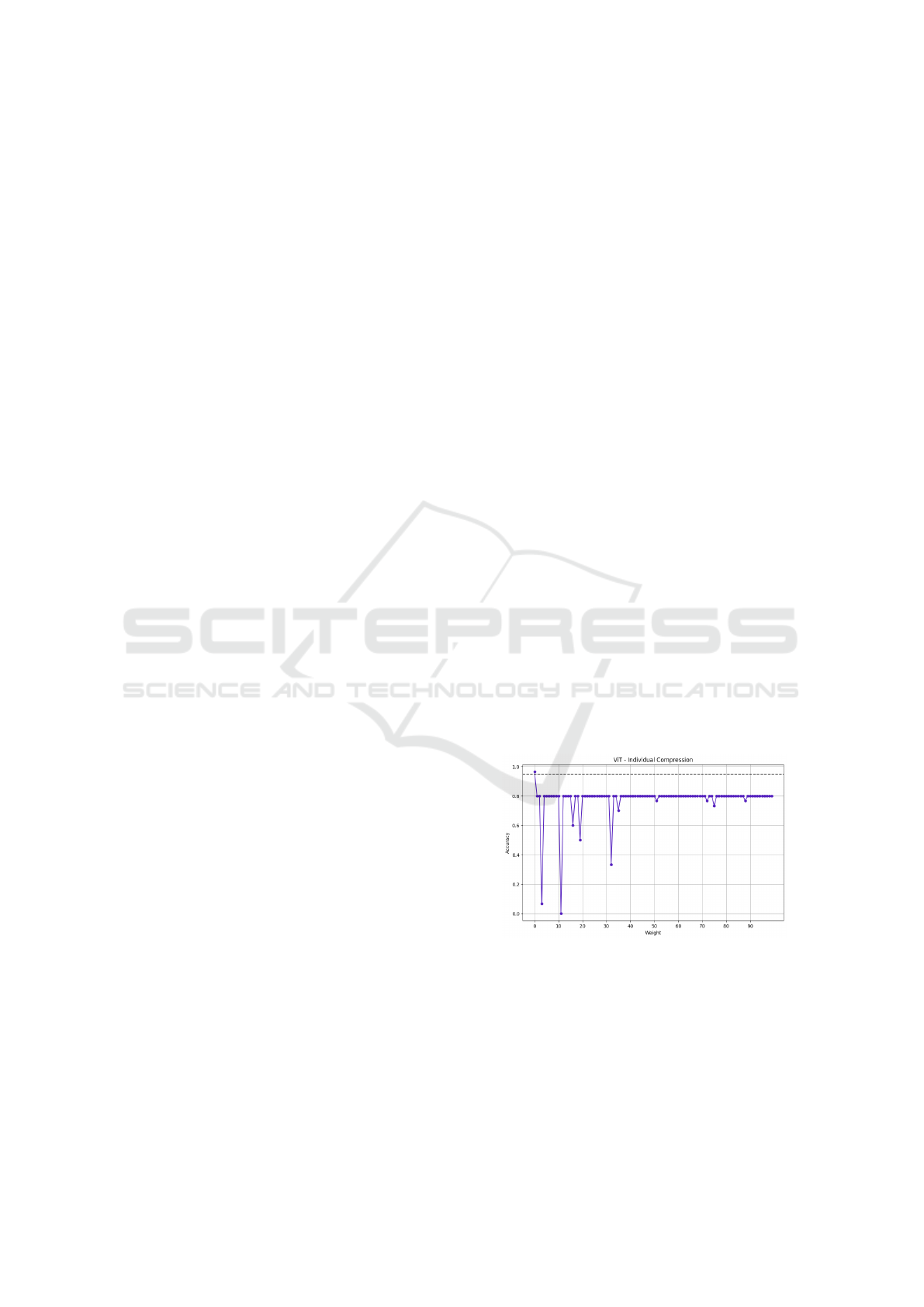
We ﬁrst individually compressed ViT’s weight ten-

sors, but did not saw decreases in model accuracy af-

ter the embedding layer (results found in 4). There-

fore, individual decomposition was not tested exten-

sively on BERT due to computational limitations. In-

stead, we rather focused on the synergistic effects be-

tween layers of the model as mentioned in 2.5.

After compressing both models utilizing the pro-

cess described in Algorithm 2, the results are seen in

2. In general, we see accuracy improvements even

while compressing around half of the model’s pa-

rameters (53% in BERT and around 49% in ViT).

This is achieved all without post-training adjustments.

Most notably, more layers in BERT tend to have an

improved accuracy, however in ViT, compression of

many layers does not change the baseline accuracy,

while still resulting in a parameter reduction.

TT-decomposition can be an effective way to

improve the accuracy of transformer-based models.

While some layers vastly decrease the accuracy of the

model, we can still achieve a high compression even

when not including such layers in the overall decom-

position.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

546

4 CONCLUSIONS

This paper introduces a novel approach to compress-

ing transformer-based vision-language neural net-

works using TensorTrain decomposition. By applying

this method to popular models like ViT and BERT, we

achieved signiﬁcant improvements in accuracy, up to

5%, without the need for post-training adjustments.

The iterative compression of model layers, coupled

with retraining, enables us to preserve model accu-

racy while reducing up to 53% of the model’s pa-

rameters. In the future, we would like to general-

ize our approach to other dual encoder models and

test our approach on other multimodal tasks like vi-

sual question answering and caption generation. This

work represents a valuable advancement in the ﬁeld

of multimodal language processing and contributes to

our broader goal of making transformer-based mod-

els more efﬁcient and practical for real-world appli-

cations.

ACKNOWLEDGEMENTS

The ﬁrst author would like to extend her gratitude to

Dr. Lina Kim and the Research Mentorship Program

Cohort for their support throughout the research pro-

cess.

REFERENCES

Bacciu, D. and Mandic, D. P. (2020). Tensor decomposi-

tions in deep learning. Computational Intelligence.

Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J.,

Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G.,

Askell, A., Agarwal, S., Herbert-Voss, A., Krueger,

G., Henighan, T., Child, R., Ramesh, A., Ziegler,

D. M., Wu, J., Winter, C., and Amodei, D. (2020).

Language models are few-shot learners. arXiv.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,

M., Heigold, G., Gelly, S., Uszkoreit, J., and Houlsby,

N. (2021). An image is worth 16x16 words: Trans-

formers for image recognition at scale. arXiv.

Gu, J., Keller, B., Kossaiﬁ, J., Anandkumar, A., Khailany,

B., and Pan, D. Z. (2022). Heat: Hardware-efﬁcient

automatic tensor decomposition for transformer com-

pression. arXiv.

Jia, C., Yang, Y., Xia, Y., Chen, Y., Parekh, Z., Pham,

H., Le, Q. V., Sung, Y., Li, Z., and Duerig, T.

(2021a). Scaling up visual and vision-language repre-

sentation learning with noisy text supervision. CoRR,

abs/2102.05918.

Jia, C., Yang, Y., Xia, Y., Chen, Y.-T., Parekh, Z., Pham,

H., Le, Q. V., Sung, Y., Li, Z., and Duerig, T. (2021b).

Scaling up visual and vision-language representation

learning with noisy text supervision. arXiv.

Krizhevsky, A. (2009). Learning multiple layers of features

from tiny images.

Li, L. H., Yatskar, M., Yin, D., Hsieh, C.-J., and Chang,

K.-W. (2019). Visualbert: A simple and performant

baseline for vision and language. arXiv.

Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D.,

Levy, O., Lewis, M., Zettlemoyer, L., and Stoyanov,

V. (2019). Roberta: A robustly optimized bert pre-

training approach. arXiv.

Maldonado-Chan, M., Mendez-Vazquez, A., and

Guardado-Medina, R. O. (2021). Multimodal

tucker decomposition for gated rbm inference.

Applied Sciences, 11(16):16.

Morris, M. R., Johnson, J., Bennett, C. L., and Cutrell,

E. (2018). Rich representations of visual content for

screen reader users. In Proceedings of the 2018 CHI

Conference on Human Factors in Computing Systems,

pages 1–11.

Oseledets, I. V. (2011). Tensor-train decomposition. SIAM

Journal on Scientiﬁc Computing, 33(5):2295–2317.

APPENDIX

ViT Fine-Tuning Hyperparameters

Learning Rate: 5

Train/Evaluation Batch Size: 32

Optimizer: Adam, linear learning rate

Epoch(s): 1

Individual Compression

Figure 3: ViT Individual Compression.

Partial Tensorized Transformers for Natural Language Processing

547