High Throughput Neural Network for Network Intrusion Detection on

FPGAs: An Algorithm-Architecture Interaction

Muhammad Ali Farooq

1, 2 a

, Syed Muhammad Fasih Ul Hassan

, Muhammad Umer Farooq

and

Abid Raﬁque

1, 2

RapidSilicon, Islamabad, Pakistan

School of Engineering, Hong Kong University of Science and Technology, Hong Kong, S.A.R.

School of Electrical Engineering and Computer Sciences, NUST, Islamabad, Pakistan

Keywords:

FPGA, Shallow Neural Networks, Machine Learning, Loss Function, Network Intrusion Detection.

Abstract:

With the increasing digitization of human activities, the risk of cyberattacks has increased. The resulting

potential for extensive harm underscores the need for robust detection mechanisms. Neural network-based

solutions deployed on FPGAs provide robust and fast solutions to this challenge by scrutinizing network

trafﬁc patterns to identify malicious behaviours. This paper introduces a novel loss function tailored for use

on the UNSW-NB15 dataset. This loss function allows a small, binarized neural network deployed on FPGAs

to function at high speed with competitive accuracy. This paper further introduces a model trained using this

method which has a maximum operating frequency of 1.028 GHz and LUT and ﬂip-ﬂop usage of 135 and

148 respectively, with an accuracy of 90.91% and an F1 score of 91.81%. The high operating frequency

and low LUT footprint provide avenues for further research, even though the accuracy and F1 score are not

groundbreaking.

1 INTRODUCTION

The rapid growth of the digital world provides in-

creased opportunities for attackers to prey upon indi-

vidual users and critical infrastructure (Ardagna et al.,

2022). Furthermore, the rapid increase in network

trafﬁc has led to the use of high-speed network in-

frastructure. Multiple avenues of attack detection are

being developed to provide security to the increas-

ingly high-speed network infrastructure. One such

avenue is that of a network intrusion detection system

(NIDS) which detects attacks in local trafﬁc. Cur-

rently, NIDS focus on attack detection through pat-

tern matching and statistical analysis. However, such

methods are slow and computationally intensive. As

such, current research focuses on the development

of machine learning (ML) based systems to achieve

the same effect. These include convolutional neural

networks (CNNs) (Azizjon et al., 2020; Jeune et al.,

2022; Wang et al., 2017), recurrent neural networks

(RNN’s) (Yin et al., 2017), and support-vector ma-

chines (SVNs) (Yang et al., 2021) for anomaly detec-

tion and attack classiﬁcation.

https://orcid.org/0009-0009-8138-8118

A common challenge across these methods is

dealing with imbalanced datasets where network at-

tacks are infrequent, leading to reduced detection ac-

curacy. Strategies to address this issue include over-

sampling (Zheng et al., 2015), undersampling (Tahir

et al., 2012), Synthetic Minority Oversampling Tech-

nique (SMOTE)(Wang and Huang, 2018), the use of

generative adversarial networks (GANs) to generate

additional minority samples (Andresini et al., 2021),

and Difﬁcult Set Sampling Technique (DSSTE) to

both reduce the data points of the majority class and

increase the number of minority samples (Liu et al.,

2021). Recent advancements propose loss functions

like the attack-sharing loss to handle class imbalance

effectively, especially in the realm of network intru-

sion detection (Dong et al., 2021; Ehmer et al., 2022).

The UNSW-NB15 is a popular choice for

hardware-deployed binary neural networks, and it is

discussed in depth in 4. An important point to note

is that it has a class imbalance, with more total attack

class samples as compared to normal samples in the

training data.

Another point to note is that most of the currently

explored strategies are prohibitively slow, with higher

Farooq, M., Fasih Ul Hassan, S., Umer Farooq, M. and Raﬁque, A.

High Throughput Neural Network for Network Intrusion Detection on FPGAs: An Algorithm-Architecture Interaction.

DOI: 10.5220/0012367800003648

In Proceedings of the 10th International Conference on Information Systems Security and Privacy (ICISSP 2024), pages 423-429

ISBN: 978-989-758-683-5; ISSN: 2184-4356

423

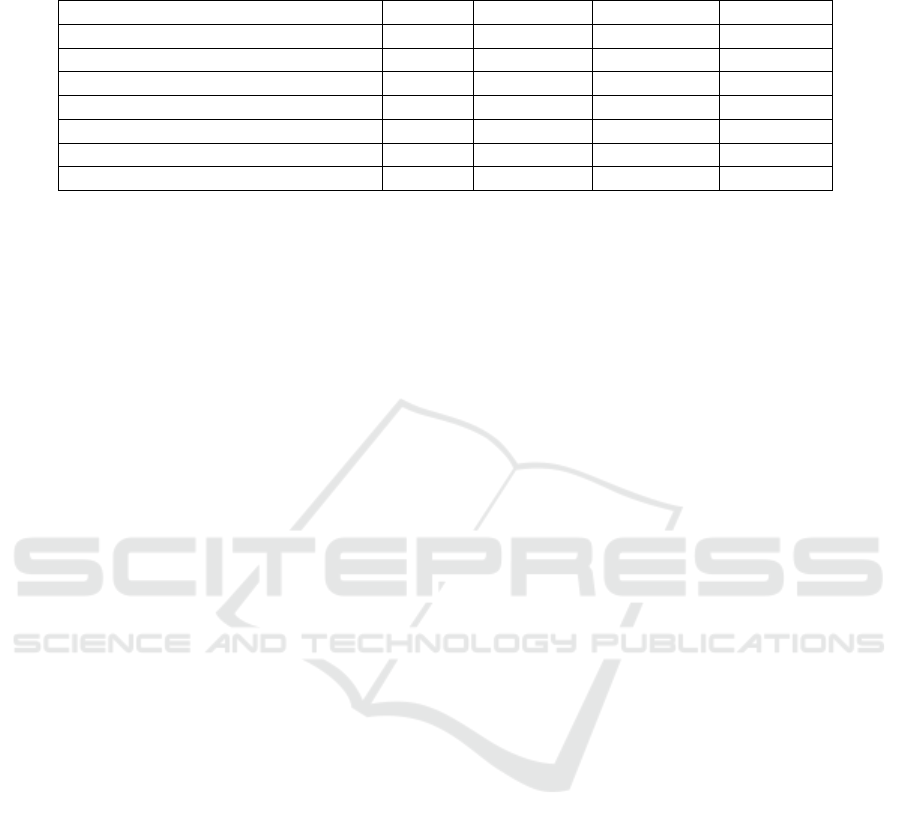
Table 1: Previous Work on BNN Based Network Intrusion Detection Systems Trained on UNSW-NB15.

Model Acc.(%) Latency(ns) No. of LUTs f

max

(MHz)

MPCBNN (Murovi

c and Trost, 2019) 90.74 19.6 51353 -

MPBNN (Murovi

c and Trost, 2021) 92.04 19 26879 -

BNN (Vre

ca et al., 2021) 82.1 91 26556 142.85

NID-S (Umuroglu et al., 2020) 83.88 3.70 3586 811

NID-M (Umuroglu et al., 2020) 91.3 10.5 15949 471

NID-S (Umoroglu et al., 2023) 90.5 3.96 650 758.15

NID-M (Umoroglu et al., 2023) 92.6 3.57 1649 839.63

NID-L (Umoroglu et al., 2023) 92.9 10.0 8106 498.26

accuracies in intrusion detection corresponding with

slower systems. One approach to solving the speed

challenge is to deploy and accelerate NIDS on ﬁeld

programmable gate arrays (FPGAs). While many ac-

celeration frameworks are in development (such as

Vitis AI by Xilinx (2023), hls4ml by Duarte et al.

(2018), and FINN by Umuroglu et al. (2017) and Blott

et al. (2018)), only LogicNets (Umuroglu et al., 2020)

is designed to cater towards the acceleration of mod-

els in scenarios where speed is of the highest priority.

In this paper, we introduce a loss function based

on a novel regularisation term. We further train a bi-

narized neural network on the UNSW-NB15 dataset

using the LogicNets framework and this new loss

function. Synthesis is performed for FPGA deploy-

ment and the results are discussed and compared with

other state-of-the-art solutions.

The rest of the paper is organised as follows. In

Section 2 we introduce related work, after which we

introduce the LogicNets framework in Section 3. Af-

ter detailing the speciﬁcs of the UNSW-NB15 in Sec-

tion 4, we present our experiment in Section 5 and the

results and appropriate discussion in Section 6. We

conclude our paper in Section 7 with a summary of

the results and possible directions for future work.

2 RELATED WORK

While network intrusion detection systems are not a

new concept, there has been a large research effort to

use machine learning to detect attacks (Buczak and

Guven, 2016). Most of these efforts are designed for

deployment on CPUs or GPUs. Such approaches can

not handle the high speeds of current network trafﬁc,

which can exceed 100 GBPS.

FPGAs provide an alternative platform for the

deployment of such models since they allow for

hardware implementation. Among FPGA-based im-

plementations of ML-based NIDSs, neural-network-

based architectures are popular. Ngo et al. ex-

plored various iterations of a neural network deployed

on an FPGA for the NSL-KDD dataset and IoT-23

dataset (Ngo et al., 2019, 2021). Murovi

c et al. pro-

posed and iterated upon a fully combinational Bi-

nary Neural Network (FCBNN) that is evaluated on

the UNSW-NB15 dataset (Murovi

c and Trost, 2019,

2020, 2021). Similarly, Umuroglu et al. proposed

LogicNets as a technique to deploy BNNs on FPGAs,

and demonstrated its potential by accelerating a NIDS

for UNSW-NB15 and further iterating on the design

(Umuroglu et al., 2020; Umoroglu et al., 2023). Vre

et al. (2021) also developed a BNN for the UNSW-

NB15 dataset.

We observe that BNNs are the fastest hardware ar-

chitectures when considering latency or throughput,

and have the smallest LUT footprints. These neural

networks are very small and feature a reduced com-

plexity. More complex architectures tend to intro-

duce a signiﬁcant cost in terms of hardware resources

and speed. We compare some state-of-the-art models

from past work in Table 1.

3 LOGICNETS FRAMEWORK

LogicNets is an approach developed by Umuroglu

et al. (2020) that specializes in crafting and deploy-

ing sparse, quantized neural networks using hardware

building blocks, delivering impressive levels of speed

and efﬁciency on FPGAs. At its core, LogicNets is

based on the concept of equating artiﬁcial neurons to

truth tables with quantized inputs and outputs. Take,

for example, an artiﬁcial neuron with C

inputs, each

spanning β-bits, and producing a single β-bit out-

put. Regardless of the neuron’s internal intricacies, its

function can always be represented by an X-input, Y-

output truth table, achieved by exhaustively enumer-

ating all possible 2

inputs and recording their respec-

tive outputs.

In the LogicNets framework, the Verilog imple-

mentation of these X : Y truth tables are referred to

as Hardware Building Blocks (HBBs), while trained

artiﬁcial neurons that can be converted into HBBs are

termed Neuron Equivalents (NEQs). The beauty of

NEQs lies in their ﬂexibility, allowing the addition

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

424

of components to simplify the DNN training process.

NEQs and HBBs are the cornerstones of LogicNets in

PyTorch and Verilog, respectively.

The design ﬂow begins with identifying X : Y val-

ues that yield HBBs with reasonable LUT cost and

deﬁning corresponding NEQs in PyTorch that comply

with sparsity and activation quantization constraints.

These NEQs can map to speciﬁc FPGA conﬁgura-

tions or generic X:Y truth tables for synthesis. Us-

ing these NEQs, a deep neural network topology is

constructed, followed by training in PyTorch, em-

ploying standard DNN optimization techniques. Post-

training, the network transforms into a Verilog netlist

of HBB instances and their sparse connections, al-

lowing for further optimization. Ultimately, this ap-

proach focuses on single-FPGA implementations for

high-throughput applications and concludes the pro-

cess with the generation of an FPGA bit ﬁle through

synthesis and place-and-route algorithms.

4 DATASET

The dataset used for training is UNSW-NB15, an up-

dated and enhanced version of the former KDD Cup

dataset. The KDD Cup dataset, which has become

obsolete, had numerous anomalies.

The UNSW-NB15 is relatively smaller in size

compared to other datasets, it stands out due to re-

duced redundancy, providing sufﬁcient data for train-

ing a reasonably accurate model. This dataset com-

prises ten distinct target classes, including one denot-

ing normal activity or benign behaviour, and nine rep-

resenting various forms of attacks.

The dataset consists of a total of 45 features, each

of signiﬁcant importance in accurately classifying the

aforementioned targets. Out of this dataset, 175,341

samples are used for training and 82,332 for test-

ing. The data distribution of the training and testing

dataset are displayed in Table 2.

We utilized the binarized version of UNSW-

NB15. In this version, all original features, includ-

ing data types like strings, categorical values, and

ﬂoating-point values have been systematically trans-

formed into a binary bit string consisting of 593 bits.

Each value within these features is discretized into

either ’0’ or ’1’ and stored as a uint8 value. These

uint8 values are conveniently represented as numpy

arrays and are distributed separately for both the train-

ing and test datasets, maintaining the same partition-

ing as the original dataset. The conclusive binary

value within each sample serves as an indicative rep-

resentation of the expected output. This binarized

dataset was used by both Murovi

c and Trost (2019)

Table 2: Data Set Record Distribution By Yang et al. (2019).

Category Training Testing

Dataset Dataset

Normal 56,000 37,000

Generic 40,000 18,871

Exploits 33,393 11,132

Fuzzers 18,184 6062

DoS 12,264 4089

Reconnaissance 10,491 3496

Analysis 2000 677

Backdoor 1746 583

Shellcode 1133 378

Worms 130 44

Total 175,341 82,332

and Umuroglu et al. (2020), and can be found online

(Umuroglu, 2021). Note the class imbalance between

the normal data packets and total attack packets in the

training and test distributions.

Our primary goal was to develop an accurate

model for binary classiﬁcation on this dataset. To ad-

dress the class imbalance issue and avoid losing the

variety of attacks in the dataset, we opted for a loss-

function-based approach.

5 PROPOSED SOLUTION

5.1 Loss Function

To address the pronounced data imbalance within our

dataset, we must ﬁrst examine the high contrast be-

tween the quantities of normal and attack samples

presented in Table 2. Speciﬁcally, we observe a to-

tal of 56, 000 normal samples in contrast to a signiﬁ-

cantly higher count of 119, 341 attack samples. This

notable disparity underscores the presence of a class

imbalance, which warrants our consideration regard-

ing its impact on our model’s performance.

It is imperative to recognize that such a substan-

tial class imbalance could impart a substantial bias to

our model’s predictions. This inherent skew in the

data distribution could result in a propensity for the

model to favour predictions in favour of the attack

class, due to the disproportionately higher number of

training samples allocated to this category, as com-

pared to the normal class. Consequently, this class

imbalance may lead the model to produce erroneous

predictions, particularly in the form of false positives

within the attack class.

To mitigate this issue, our work explores the uti-

lization of modiﬁed loss functions as a strategic ap-

proach. The focus of our study became the work of

Dong et al. Dong et al. (2021) and Ehmer et al. Ehmer

High Throughput Neural Network for Network Intrusion Detection on FPGAs: An Algorithm-Architecture Interaction

425

et al. (2022). The method suggested by Ehmer et al.,

shown in Equation 1 is as follows:

Loss = J

−

∑

i=1



α · I(y

(i)

, 1)log(p

(i)

)

∑

j=2

· I(y

(i)

, j)log(1 − p

(i)

)



(1)

Where:

I(a, b) =



1 if a = b

0 Otherwise

= β ·



1 −



And:

• J

is the binary cross-entropy loss,

• N is the number of samples in the batch,

• p

(i)

is the predicted probability of the majority

class for the i-th sample,

• y

(i)

is the prediction for the i-th sample,

• α is a scaling factor,

• β is a scaling factor,

• n

is the number of samples of the j-th minority

class in the batch,

• N

is the total number of minority samples in the

batch

This method does not adapt to binary classiﬁca-

tion, because the term for the scaling factor for the

minority class simpliﬁes to 0.

The method suggested by Dong et al. is as fol-

lows:

Loss = J

−

∑

i=1



I(y

(i)

, 1)log(p

(i)

)

∑

j=2

I(y

(i)

, j)log(1 − p

(i)

)



(2)

Where λ is a scaling factor. This method failed to

yield acceptable results using our small quantized

neural network architecture.

Drawing inspiration from the works of Dong et al.

and Ehmer et al., we created a loss function which

worked well for our small architecture. The goal in

mind was to penalize unconﬁdent predictions for the

minority class. The loss function we created is de-

tailed in Equation 3. In line with the speciﬁcs of

the UNSW-NB15 dataset discussed in Section 4, 0 is

the label for the minority class and 1 is the label for

the majority class. During our experiments, we set

λ = 0.5.

Loss = J

−

∑

i=1



λ · I(y

(i)

, 1)log(p

(i)

)

+ I(y

(i)

, 0)log(1 − log(1 − p

(i)

))



(3)

Where:

I(a, b) =



1 if a = b

0 Otherwise

• J

is the binary cross-entropy loss, computed us-

ing nn.BCEWithLogitsLoss(),

• N is the number of samples in the dataset,

• p

(i)

is the predicted probability of the majority

class for the i-th sample,

• y

(i)

is the binary prediction for the i-th sample (1

for attack, 0 for benign)

5.2 Our Network Topology

The artiﬁcial neural network employs a structured

three-layer conﬁguration, with a single hidden layer.

Keeping in line with the strategy maintained by

Umoroglu et al. Umuroglu et al. (2020), we ex-

clude the softmax layer at the output to tailor each

layer to speciﬁc computational needs. The founda-

tional layer consists of 49 neurons, each with 7 input

channels, akin to synapses in biological neural net-

works. These neurons output 2-bit data for nuanced

responses. In the second layer, featuring 7 neurons,

the input bit width expands to 7 for more complex

processing, while maintaining a 2-bit output. The top

layer, a single neuron, aggregates data from 7 inputs

and also provides a 2-bit output.

Figure 1 illustrates the overview of the artiﬁcial

neural network architecture used and also an exploded

view of the perceptron.

5.3 Training

We trained the model for 100 epochs with a learning

rate 10

−1

and batch size of 1023. The training was

performed on Intel(R) Core(TM) i7-10750H with 16

GB of RAM in Ubuntu 20.04. Results are discussed

in Section 6.

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

426

Figure 1: Network Topology.

5.4 Synthesis

Out-of-context synthesis was performed for an AMD

Xilinx Alveo U280 (part number xcu280-fsvh2892-

2L-e) on an Intel(R) Core(TM) i7-10750H with 16

GB of RAM in Ubuntu 20.04 using Vivado 2019.2.

The results of the synthesis are discussed in Section

6 RESULTS

We have rigorously evaluated our system to assess its

suitability for network intrusion detection, focusing

on both computational resource usage and classiﬁca-

tion accuracy.

6.1 System Performance Metrics

To begin, we examine the system’s performance in

terms of its maximum operating frequency and re-

source utilization. These metrics serve as essential

indicators of the system’s efﬁciency and practicality

for real-world deployment. Our system achieved an

impressive maximum operating frequency of 1.028

GHz, demonstrating its ability to process data rapidly

and efﬁciently. Additionally, the resource utilization

metrics reveal that the design is resource-efﬁcient,

with a consumption of 135 Look-Up Tables (LUTs)

and 148 Flip-Flops. A comparison of our synthesis re-

sults with past works is displayed graphically in Fig-

ure 2.

6.2 Classiﬁcation Performance

Evaluation

Our evaluation extends to the classiﬁcation perfor-

mance of the system, a critical aspect for applications

such as pattern recognition and anomaly detection.

We employed a binary confusion matrix to rigorously

analyze the system’s ability to correctly classify in-

stances.

As shown in Table 3, our proposed neural network

provides competitive accuracy with a near negligi-

ble LUT footprint at a maximum operating frequency

which crosses 1 GHz.

From the confusion matrix in Figure 3, we derived

the following essential performance metrics:

• True Positive (TP): The number of correct positive

classiﬁcations made by the system

• False Positive (FP): The number of incorrect pos-

itive classiﬁcations made by the system

• False Negative (FN): The number of incorrect

negative classiﬁcations made by the system

• True Negative (TN): The number of correct nega-

tive classiﬁcations made by the system

6.3 Accuracy and F1 Score

With these performance metrics in hand, we assess

the overall effectiveness of our classiﬁcation sys-

tem. Our results indicate an impressive accuracy of

90.91%, signifying the system’s ability to make ac-

curate predictions. Additionally, we achieved an F1

score of 91.82%, highlighting the system’s capability

200

400

600

800

1,000

LUT Count

Operating Frequency(MHz)

Our Work

NID-S (Umuroglu et al., 2020)

NID-S (Umoroglu et al., 2023)

NID-M (Umoroglu et al., 2023)

BNN (Vre

ca et al., 2021)

Figure 2: LUT Count vs. Operating Frequency.

High Throughput Neural Network for Network Intrusion Detection on FPGAs: An Algorithm-Architecture Interaction

427

Table 3: Comparison of Our Work With Select Previous Works.

Model Acc. (%) Latency LUT f (MHz)

MPBNN (Murovi

c and Trost, 2021) 92.04 19 ns 26879 -

NID-S (Umuroglu et al., 2020) 83.88 3.70 ns 3586 811

NID-S (Umoroglu et al., 2023) 90.5 3.96 ns 650 758.15

NID-M (Umoroglu et al., 2023) 92.6 3.57 ns 1649 839.63

Our Work 90.91 2.92 ns 135 1027.75

Figure 3: Confusion Matrix.

to balance precision and recall effectively. These out-

comes underscore the system’s robustness and its po-

tential to excel in a wide range of classiﬁcation tasks,

making it a valuable asset for applications that require

reliable decision-making.

To evaluate the classiﬁcation performance, we cal-

culate the accuracy and F1 score using the following

formulas:

Accuracy =

T P + T N

T P + T N + FP + FN

(4)

F1 =

2 · T P

2 · T P +FP +FN

(5)

So, using the values enumerated in Fig.3, the calcu-

lated values are as follows:

• Accuracy: 0.909137 (or 90.91%)

• F1 Score: 0.918195 (or 91.82%)

7 CONCLUSION AND FUTURE

WORK

We ﬁrmly advocate the need for further efforts in

devising innovative architectures and exploring logic

optimization techniques, particularly for parallel bi-

nary neural networks, which are essential in the high-

speed domain of network intrusion detection. Addi-

tionally, we stress the importance of studying the in-

teraction between algorithmic changes and the Logic-

Nets framework, as it can signiﬁcantly impact model

performance and logic reduction. This comprehen-

sive analysis will contribute to the continued advance-

ment of hardware-based machine learning in the ﬁeld

of network intrusion detection.

ACKNOWLEDGEMENTS

We are thankful for the support of Dr. Mazhar Ali, at

the University of Central Florida, and the guidance of

Dr. Hammond Pearce, at the University of New South

Wales.

REFERENCES

Andresini, G., Appice, A., De Rose, L., and Malerba, D.

(2021). Gan augmentation to deal with imbalance in

imaging-based intrusion detection. Future Generation

Computer Systems, 123:108–127.

Ardagna, C., Corbiaux, S., Impe, K. V., and Sfakianakis,

A. (2022). ENISA Threat Landscape 2022. Techni-

cal report, European Union Agency for Cybersecurity

ENISA.

Azizjon, M., Jumabek, A., and Kim, W. (2020). 1d cnn

based network intrusion detection with normalization

on imbalanced data. In 2020 International Conference

on Artiﬁcial Intelligence in Information and Commu-

nication (ICAIIC). IEEE.

Blott, M., Preußer, T. B., Fraser, N. J., Gambardella, G.,

O’brien, K., Umuroglu, Y., Leeser, M., and Vissers,

K. (2018). Finn- r: An end-to-end deep-learning

framework for fast exploration of quantized neural

networks. ACM Transactions on Reconﬁgurable Tech-

nology and Systems, 11(3):1–23.

Buczak, A. L. and Guven, E. (2016). A survey of data min-

ing and machine learning methods for cyber security

intrusion detection. IEEE Communications Surveys

I& Tutorials, 18(2):1153–1176.

Dong, B., Hui, W., Varde, A. S., Li, D., Samanthula, B. K.,

Sun, W., and Zhao, L. (2021). Cyber intrusion de-

tection by using deep neural networks with attack-

sharing loss.

Duarte, J., Han, S., Harris, P., Jindariani, S., Kreinar, E.,

Kreis, B., Ngadiuba, J., Pierini, M., Rivera, R., Tran,

N., and Wu, Z. (2018). Fast inference of deep neu-

ral networks in fpgas for particle physics. Journal of

Instrumentation, 13(07):P07027–P07027.

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

428

Ehmer, J., Granado, B., Denoulet, J., Savaria, Y., and David,

J.-P. (2022). Low complexity shallow neural network

with improved false negative rate for cyber intrusion

detection systems. In 2022 20th IEEE Interregional

NEWCAS Conference (NEWCAS). IEEE.

Jeune, L. L., Goedeme, T., and Mentens, N. (2022).

Feature dimensionality in cnn acceleration for high-

throughput network intrusion detection. In 2022 32nd

International Conference on Field-Programmable

Logic and Applications (FPL). IEEE.

Liu, L., Wang, P., Lin, J., and Liu, L. (2021). Intru-

sion detection of imbalanced network trafﬁc based on

machine learning and deep learning. IEEE Access,

9:7550–7563.

Murovi

c, T. and Trost, A. (2019). Massively parallel com-

binational binary neural networks for edge processing.

Elektrotehniski Vestnik, 86(1/2):47–53.

Murovi

c, T. and Trost, A. (2020). Resource-optimized com-

binational binary neural network circuits. Microelec-

tron. J., 97(C).

Murovi

c, T. and Trost, A. (2021). Genetically optimized

massively parallel binary neural networks for intru-

sion detection systems. Computer Communications,

179:1–10.

Ngo, D.-M., Temko, A., Murphy, C. C., and Popovici,

E. (2021). Fpga hardware acceleration framework

for anomaly-based intrusion detection system in iot.

In 2021 31st International Conference on Field-

Programmable Logic and Applications (FPL). IEEE.

Ngo, D.-M., Tran-Thanh, B., Dang, T., Tran, T., Thinh,

T. N., and Pham-Quoc, C. (2019). High-Throughput

Machine Learning Approaches for Network Attacks

Detection on FPGA, page 47–60. Springer Interna-

tional Publishing.

Tahir, M. A., Kittler, J., and Yan, F. (2012). Inverse ran-

dom under sampling for class imbalance problem and

its application to multi-label classiﬁcation. Pattern

Recognition, 45(10):3738–3750.

Umoroglu, Y., Fraser, N. J., and Akhauri, Y.

(2023). Xilinx/Logicnets. [online] Available:

https://github.com/Xilinx/logicnets.

Umuroglu, Y. (2021). The unsw-nb15 dataset with bina-

rized features.

Umuroglu, Y., Akhauri, Y., Fraser, N. J., and Blott,

M. (2020). Logicnets: Co-designed neural net-

works and circuits for extreme-throughput applica-

tions. In 2020 30th International Conference on Field-

Programmable Logic and Applications (FPL). IEEE.

Umuroglu, Y., Fraser, N. J., Gambardella, G., Blott,

M., Leong, P., Jahre, M., and Vissers, K. (2017).

Finn: A framework for fast, scalable binarized

neural network inference. In Proceedings of the

2017 ACM/SIGDA International Symposium on Field-

Programmable Gate Arrays, FPGA ’17. ACM.

Vre

ca, J., Ivanov, I., Papa, G., and Biasizzo, A. (2021). De-

tecting network intrusion using binarized neural net-

works. In 2021 IEEE 7th World Forum on Internet of

Things (WF-IoT). IEEE.

Wang, H. and Huang, H. (2018). Lad-smote: A new over-

sampling method based on locally adaptive distance.

In 2018 Ninth International Conference on Intelligent

Control and Information Processing (ICICIP). IEEE.

Wang, W., Zhu, M., Zeng, X., Ye, X., and Sheng, Y.

(2017). Malware trafﬁc classiﬁcation using convolu-

tional neural network for representation learning. In

2017 International Conference on Information Net-

working (ICOIN). IEEE.

Xilinx (2023). Vitis AI. [online] Available:

https://www.xilinx.com/products/design-

tools/vitis/vitis-ai.html.

Yang, K., Kpotufe, S., and Feamster, N. (2021). An efﬁcient

one-class svm for anomaly detection in the internet of

things. ArXiv, abs/2104.11146.

Yang, Y., Zheng, K., Wu, C., and Yang, Y. (2019). Improv-

ing the classiﬁcation effectiveness of intrusion detec-

tion by using improved conditional variational autoen-

coder and deep neural network. Sensors, 19(11):2528.

Yin, C., Zhu, Y., Fei, J., and He, X. (2017). A deep learning

approach for intrusion detection using recurrent neural

networks. IEEE Access, 5:21954–21961.

Zheng, Z., Cai, Y., and Li, Y. (2015). Oversampling method

for imbalanced classiﬁcation. Comput. Informatics,

34:1017–1037.

High Throughput Neural Network for Network Intrusion Detection on FPGAs: An Algorithm-Architecture Interaction

429