Mutually Exclusive Multi-Modal Approach for Parkinson’s Disease

Classiﬁcation

Arunava Chaudhuri

∗

, Abhishek Singh Sambyal and Deepti R. Bathula

∗

Department of Computer Science and Engineering, Indian Institute of Technology Ropar, Rupnagar, 140001, Punjab, India

Keywords:

Parkinson’s Disease, Multi-Modal, Classiﬁcation, Siamese Network, Deep Learning.

Abstract:

Parkinson’s Disease (PD) is a progressive neurodegenerative disorder that affects the central nervous system

and causes both motor and non-motor symptoms. While movement related symptoms are the most noticeable

early signs, others like loss of smell can occur quite early and are easy to miss. This suggests that multi-modal

assessment has signiﬁcant potential in early diagnosis of PD. Multi-modal analysis allows for synergistic

fusion of complementary information for improved prediction accuracy. However, acquiring all modalities

for all subjects is not only expensive but also impractical in some cases. This work attempts to address the

missing modality problem where the data is mutually exclusive. Speciﬁcally, we propose to leverage two

distinct and unpaired datasets to improve the classiﬁcation accuracy of PD. We propose a two-stage strategy that

combines individual modality classiﬁers to train a multi-modality classiﬁer using siamese network with Triplet

Loss. Furthermore, we use a Max-Voting strategy applied to Mix-and-Match pairing of the unlabelled test

sample of one modality with both positive and negative samples from the other modality for test-time inference.

We conducted experiments using gait sensor data (PhysioNet) and clinical data (PPMI). Our experimental

results demonstrate the efﬁcacy of the proposed approach compared to the state-of-the-art methods using single

modality analysis.

1 INTRODUCTION

Parkinson’s Disease, an incurable central nervous sys-

tem disorder, affects approximately 8.5 million indi-

viduals worldwide, gradually impairing motor activity.

Early symptoms encompass rigidity, tremors, slowed

movement, gait difﬁculties, and behavioral changes,

with intensiﬁcation in later stages. The disorder’s eti-

ology remains elusive, prompting researchers to in-

vestigate commonalities among PD (Emamzadeh and

Surguchov, 2018; Makarious et al., 2022) patients. Ad-

vanced stages present with manifestations such as mus-

cle stiffness, olfactory loss, rapid eye movement, and

sleep disturbances, signiﬁcantly impacting daily life.

Subtle early symptoms often go unnoticed, leading to

a progressive neurodegenerative condition. Challenges

in diagnosing the disease at its early stage arise from its

diverse manifestations, requiring extended observation

to discern symptoms.

Recent advancements in machine learning and

deep learning techniques show promise in assisting

the diagnosis of Parkinson’s disease. Researchers have

initiated investigations into the symptomatology of

∗

Corresponding Author

the disease. Initially, the focus centered on identi-

fying commonalities among patients. Subsequently,

it was observed that various factors impact the diag-

nostic process. Single-symptom experiments provide

accuracy for speciﬁc data types, disregarding potential

co-occurring symptoms. To address this, a proposed

framework for differential PD identiﬁcation takes into

account multiple symptoms in characterizing individu-

als as either Parkinson’s Disease (PD) or Healthy Con-

trol (HC) subjects. However, achieving the required

high accuracy remains challenging in healthcare. Clin-

ical diagnosis relies on tests, patient responses, and

neuroimaging, contributing to detection errors. Early

detection poses an additional challenge, marked by

brain structural changes preceding subtle symptoms.

Notably, the impact of Parkinson’s Disease on the sub-

stantia nigra and basal ganglia is evident in brain im-

ages, reﬂecting dopaminergic effects preceding motor

symptoms. Timely identiﬁcation facilitates interven-

tion with neuroprotective medication. Machine learn-

ing techniques (Archila J., 2022; Pahuja G., 2022),

increasingly popular over the past decade, aid in pat-

tern recognition within clinical data and images. In

this context, gait sensor data, along with motor and

236

Chaudhuri, A., Sambyal, A. and Bathula, D.

Mutually Exclusive Multi-Modal Approach for Parkinson’s Disease Classiﬁcation.

DOI: 10.5220/0012376100003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 1, pages 236-243

ISBN: 978-989-758-688-0; ISSN: 2184-4305

non-motor symptom data, is employed to classify PD

patients.

Given a comprehensive understanding of the afore-

mentioned challenges, we propose the development

of a multi-modal framework that utilizes various data

sources to improve disease classiﬁcation. Our goal

is to integrate gait analysis data and clinical data to

enhance the accuracy of categorizing Parkinson’s dis-

ease. Furthermore, we have implemented a robust

cross-validation technique to address over-ﬁtting com-

plexities within the machine learning model. Our con-

tributions can be summarized as follows:

•

We proposed a novel approach to jointly train two

mutually exclusive datasets within a multi-modal

framework. Additionally, we suggested an innova-

tive inference method utilizing embedding with a

triplet loss function.

•

We conducted a comprehensive evaluation of the

training and inference framework using a variety

of metrics and compared it with state-of-the-art

(SOTA) approaches.

•

Our approach demonstrated a signiﬁcant reduction

in error rates and an improvement in accuracy for

the diagnostic process.

2 LITERATURE SURVEY

Research studies that are based on machine learning

techniques have been done until now a can be catego-

rized into three parts. Those are summarized in the

following:

1. Studies to Discriminate PD and HC Using Ma-

chine Learning Techniques – Combining diverse

data modalities, including images and clinical data,

while accommodating varying measurement scales,

has emerged as a promising avenue. (Prashanth et al.,

2016) advocate for a comprehensive analysis, integrat-

ing cerebrospinal ﬂuid (CSF), non-motor attributes,

and images, enhancing preclinical PD diagnosis. Like-

wise, (Glaab E et al., 2019) establish the value of

merging blood sample data with PET images, enhanc-

ing the distinction between PD and healthy controls.

(H. Hirschauer et al., 2015) propose an innovative

methodology, utilizing neuro-pathological brain data

alongside motor and non-motor symptom data within

an enhanced probabilistic neural network. Impres-

sively, this approach surpasses classical machine learn-

ing algorithms, yielding signiﬁcantly higher accuracy

than previous experiments. These endeavors collec-

tively underscore the potential of multi-modal data

fusion in advancing PD diagnosis and classiﬁcation

accuracy.

2. Studies on Different Diagnoses of PD Using

Machine-Learning Techniques – Variability within

Parkinson’s disease (PD) necessitates distinct treat-

ment approaches, prompting recent investigations.

Leveraging Dopaminergic images, structural MRI,

functional MRI, and diffusion tensor images, machine

learning techniques like SVM and logistic regression

effectively differentiated PD categories. However, the

amalgamation of multi-modal features emerges as a

promising avenue for classiﬁcation. This approach is

exempliﬁed in recent studies, such as (Cherubini A

and et al., 2014), who integrated DTI and voxel-based

morphometry using support vector machines to distin-

guish PSP and PD patients. This experiment highlights

the potential of automated pattern recognition for PSP

and PD detection. Moreover, (Du G. and et al., 2017)

demonstrated the utility of apparent transverse relax-

ation rate and DTI images as critical markers for PD

differential identiﬁcation. These ﬁndings collectively

underscore the viability of multi-modal data fusion in

enhancing PD variation differentiation.

3. Experiments on the Initial Phase Identiﬁcation

of PD Using ML Techniques – Numerous inves-

tigations have converged on the integration of im-

age and clinical data to enhance initial PD diagnosis.

(Long D. and et al., 2012) notably harnessed structural

and resting-state functional magnetic resonance imag-

ing (rsfMRI) data, extracting diverse characteristics

encompassing ALFF, RFCs, ReHo, as well as cere-

brospinal ﬂuid (CSF), gray matter (GM), and white

matter (WM). Employing a two-sample t-test in con-

junction with a Support Vector Machine (SVM), they

achieved an impressive 87% accuracy in early PD pa-

tient classiﬁcation, surpassing the efﬁcacy of single-

source image data. Another study by (Oliveira et al.,

2018) delved into SPECT imaging data, extracting

seven features from each brain hemisphere and leverag-

ing classical machine learning techniques. Strikingly,

by combining all features, they attained a remarkable

classiﬁcation accuracy of 97%, outperforming previ-

ous studies that employed individual features. These

collective investigations underscore the potential of

multi-modal data integration in substantially enhanc-

ing early PD diagnosis and classiﬁcation accuracy.

The preceding discussions reveal notable chal-

lenges. Clinical diagnosis data’s error susceptibility

warrants caution for PD patient classiﬁcation. Conse-

quently, unsupervised techniques are proposed to un-

veil data patterns, while handling image data encoun-

ters feature extraction limitations. Machine learning’s

Mutually Exclusive Multi-Modal Approach for Parkinson’s Disease Classiﬁcation

237

opaque nature conﬂicts with evidence-based medicine

principles, emphasizing the need to identify disease-

speciﬁc features. Over-ﬁtting poses a signiﬁcant con-

cern, with models excelling in training but struggling

in testing. Recent studies underscore the impact of ex-

cessive data heterogeneity on generalizability, even

with a single source. Addressing this entails aug-

menting data quantity and rigorous validation to en-

hance model generalization a comprehensive, aware

approach is pivotal for robust PD classiﬁcation and

understanding.

3 DATASETS

The two mutually exclusive or unpaired datasets cho-

sen for this work are described below:

3.1 Gait in Parkinson’s Disease

This dataset by PhysioNet (Goldberger and et al., 2000)

includes multi-channel gait sensor data collected from

93 patients with PD (mean age: 66.3 years; 63% men),

and 73 healthy controls (mean age: 66.3 years; 55%

men). The dataset captures vertical ground force mea-

surements as subjects walk normally for approximately

2 minutes on ﬂat terrain. Eight sensors beneath each

foot record force over time at a sampling frequency

of 100 Hz. Additionally, demographic information,

measure of disease severity and other related measures

are also included.

3.2 Parkinson’s Progression Markers

Initiative (PPMI)

This dataset has been captured by in-person clinical

assessments, covering people with a conﬁrmed diag-

nosis of PD, people who exhibit PD risk factors but

have not yet been diagnosed with PD, and healthy con-

trols. This repository contains data from more than

1500 participants of which, 423 participants exhibit

PD and 196 are healthy individuals. The clinical data

collection spanned 12 visits including clinical motor

assessment at three-month intervals during ﬁrst year,

transitioning to six-month intervals thereafter. Behav-

ioral and cognitive diagnoses are conducted annually

for all participants. 24-month visits for SWEDD par-

ticipants, and baseline recordings for healthy controls.

Blood sample collection followed a scheduled three-

month interval during the ﬁrst year, then transitions

to six-month intervals. Fourth, Cerebrospinal ﬂuid

(CSF) data are collected at 6-month and 12-month in-

tervals. And lastly, Urine testing was administered at

12-month intervals for all participants. As some of

this information is available only for a subset of the

participant population, we used data from initial visit

along with visits 2, 4, 6, 8, 10 and 12 for our analysis.

This generated a pool of 476 subjects with data in all

these visits.

4 METHODOLOGY

Given the constraints of mutually exclusive datasets,

our primary focus lies on expanding our sample size to

facilitate effective training of our proposed model. The

following section provides a detailed view of the tech-

niques employed for generating supplementary data

samples from our available dataset. This is followed

by an in-depth elucidation of our proposed framework.

4.1

Data Generation and Pre-Processing

This section is structured to enhance clarity by delin-

eating two pivotal steps which is also described in

Figure 1. We commence by streamlining gait sensor

data, simplifying its format for seamless integration

with PPMI data.

Data Separation Step – Initially, we apply seven

fundamental statistical techniques to each sensor data

column, including Minimum, Maximum, Mean, Me-

dian, Standard Deviation, Skewness, and Kurtosis.

Subsequently, we consolidate the complete time series

data for each subject into a uniﬁed row, resulting in

126 features (each attribute is transformed into seven

additional columns). In the case of the PPMI dataset,

we encompass data from seven visits, including the

baseline, capturing motor and non-motor symptoms,

thereby yielding a cumulative total of 1595 features.

As detailed in the dataset description, gait data com-

prises records from 93 PD patients and 73 HC patients,

while the PPMI dataset encompasses 294 PD patient

records and 154 HC patient records. Before amalga-

mation, data from both sources are stratiﬁed based on

class distribution.

Cross-Merging Step – The generation of the

merged dataset is accomplished through a cross-

merging operation involving corresponding class data

from both datasets. More precisely, it combines

the features of a single sample from the gait dataset

with the features of a corresponding sample from the

PPMI dataset, both belonging to the same class. For

model training, 50% of the merged data is used and

BIOIMAGING 2024 - 11th International Conference on Bioimaging

238

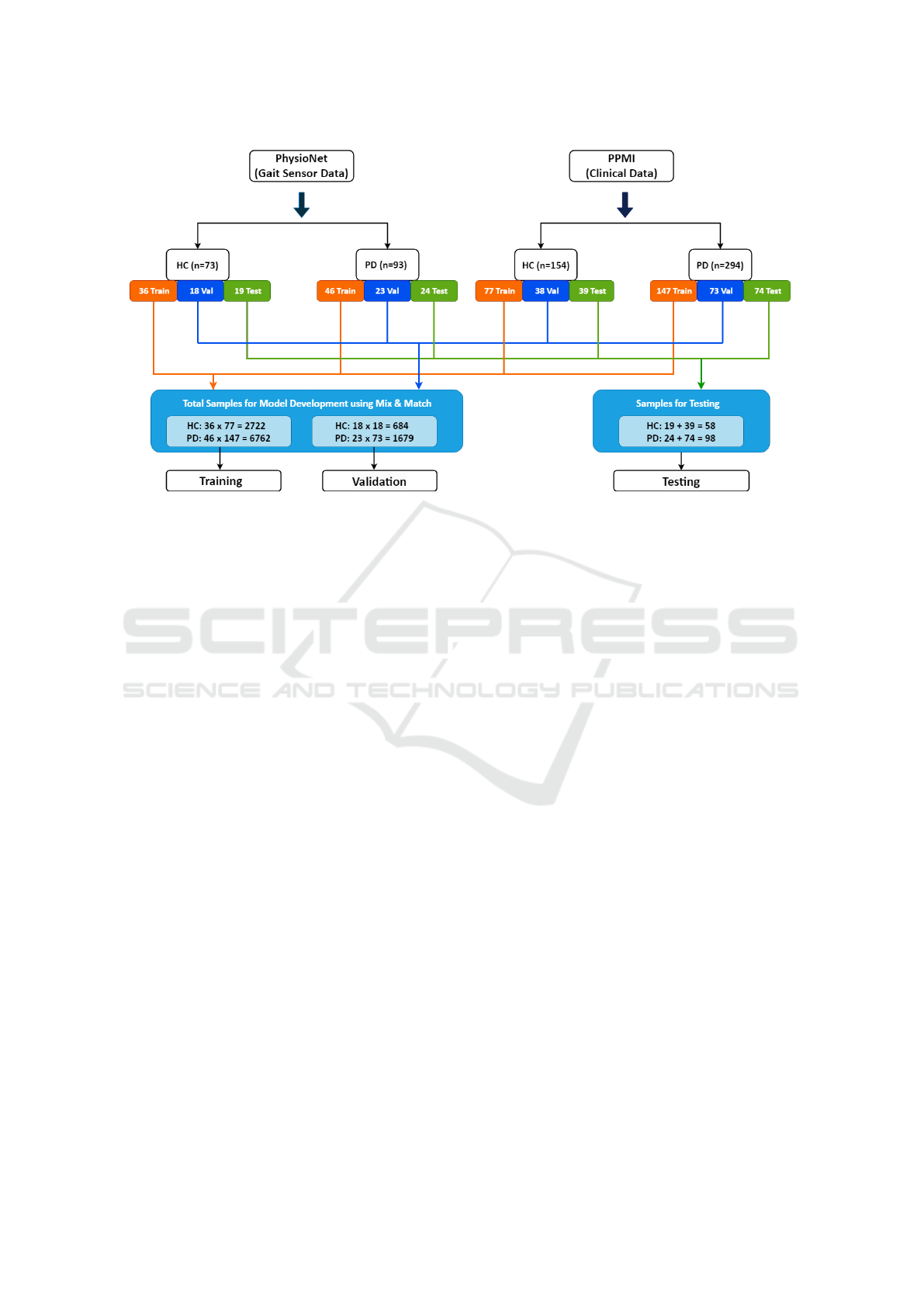
Figure 1: Data Generation Diagram. Each cohort is separated into two classes (mainly Parkinson’s Disease (PD) and Healthy

Control (HC)) and each class data of each cohort has been divided into 50%, 25% and 25% for the use of training, validation

and test. The orange line depicts the training data ﬂow, whereas the blue and green data ﬂows are for validation and test. The

ﬁrst blue-colored block is responsible for generating data for model development whereas the second one is for generalization.

Same colored block data coming for training or validation are crossed between same class (Exp: Orange colored cohort 1 HC

data is crossed with orange colored cohort 2 HC date and same for PD data also.) This process has been repeated for blue

colored types of data.

the remaining 50% is equally assigned to validation

and testing. As a result of these post-splitting and

cross-merging operations, the dataset comprises 9484

records for training, 2363 for validation, and 2517 for

testing, encompassing a total of 1721 features.

4.2 Proposed Mutually-Exclusive,

Multi-Modal Framework

Multi-modal analysis helps improve the accuracy of

machine learning algorithms by leveraging the com-

plementarity of heterogeneous data. However, acquir-

ing all modalities for all samples might not only be

expensive but also practically infeasible in some con-

ditions. Consequently, we propose an unpaired multi-

modal learning strategy that learns to extract beneﬁts

from mutually exclusive modalities. Our proposed

two-stage process along with training and inference

mechanisms are described below.

Individual Modality Networks. In stage one, we

used simple multi-layer perceptrons (MLPs) or fully

connected networks (four layers) for Parkinson’s dis-

ease prediction using individual modalities of gait

and clinical data. Each of the individual networks

were trained and optimized for best PD classiﬁcation

accuracy with one modality using categorical cross-

entropy. Once trained, the weights of these networks

were frozen and the output or features extracted from

the penultimate layer is considered as the latent space

representation of corresponding modalities.

Multi-Modal Network. In stage two, the feature

vectors encompassing the distinct attributes of gait and

clinical data modalities are concatenated and used as

input to train a multi-modal network. While we use

similar architecture with four fully connected layers,

we utilize it in a siamese network with Triplet loss

function. As siamese networks are designed to com-

pare pairs of feature embeddings rather than make a

prediction, they are suitable for small datasets. Fur-

thermore, the Triplet loss function helps the model to

recognize the similarity or differences between classes.

Triplet Loss. The objective of the triplet loss func-

tion is to learn from the distributed representation of

data points in a high-dimensional vector space. It

ensures that similar data points are projected closer

together, while dissimilar ones are pushed farther apart.

The loss function is deﬁned as:

L = max(d(a, p) − d(a, n) + margin, 0)

where ‘

’ represents the anchor sample, ‘

’ and ‘

’

denote the positive and negative samples respectively.

Mutually Exclusive Multi-Modal Approach for Parkinson’s Disease Classiﬁcation

239

Figure 2: Siamese Network Architecture. Complete pipeline to generate embedding using combination of gait and PPMI data.

The input block is used for send the data to baseline models. Network section contains two previously used baseline networks

(Gait and PPMI Network) which will take gait and PPMI data individually and will generate feature matrices (Blue arrow in

between network and features section the diagram) corresponding to each data. In features section, these two feature matrices

are combined into single matrix. The common network section (Siamese Network) takes the combined feature matrix as input

and generates embedding output in the output section.

Notably, the similarity between "

" and "

" should

exceed that between "

" and "

." An additional hyper-

parameter termed "margin" is integrated into the loss

function. This parameter dictates the degree of dissim-

ilarity required, aiding in the efﬁcient discrimination

of distinct samples.

Consequently, we compute gradients, which in turn

facilitate the adjustment of biases and weights within

the siamese network. Throughout the training phase,

we gather an anchor sample along with random posi-

tive and negative samples to compute loss and update

the network’s gradients.

Training Multi-Modality Network. As the two

datasets are mutually exclusive, there is no paired data

to train the multi-modal network. We address this

difﬁculty by pairing each sample of a particular class

in one dataset with every sample of the same class

in the other dataset. For instance,

samples of PD

in gait dataset and

samples of PD in PPMI dataset

generates a total of

× s

PD samples for training

the multi-modal network. This approach not only cap-

tures the variance in the modalities but also provides

implicit data augmentation. Such pairing is repeated

for samples of all classes and given the same label.

At each training step, triplets are composed by

ﬁrst randomly selecting a sample to represent the an-

chor. Next, another sample from the same class is

randomly chosen as the positive sample and a sam-

ple from different class is randomly chosen to be the

negative sample. All the samples are ﬁrst processed

using individual modality networks to extract modality

speciﬁc features. Features extracted for each sample

are concatenated to create input feature vectors to the

siamese network. The network operates by indepen-

dently processing the anchor, positive, and negative

losses, generating distinct embedding vectors for each

sample. Employing the triplet loss function, the model

computes the Euclidean distance between the anchor

and positive embedding, as well as between the an-

chor and negative embedding. These computations

facilitate the update of gradients within the siamese

network, thereby reﬁning the network’s performance.

Proposed Inference Technique. Conventional in-

ference approaches are unsuitable due to the absence

of a modality. Therefore, we propose a novel method

for predicting the label of a test instance, employing a

combination of the max-voting approach and mix-and-

match pairing. During inference, we utilize triplets of

anchor, positive, negative.

Anchor: We ﬁrst generate a test sample in the required

format for inference by combining a gait test sample

with ﬁve positive and ﬁve negative instances from the

PPMI training dataset. This process yields ten anchor

instances and removes the missing modality issue.

Positive and Negative: Each anchor instance is then

paired with one PD and one HC instance from the out-

BIOIMAGING 2024 - 11th International Conference on Bioimaging

240

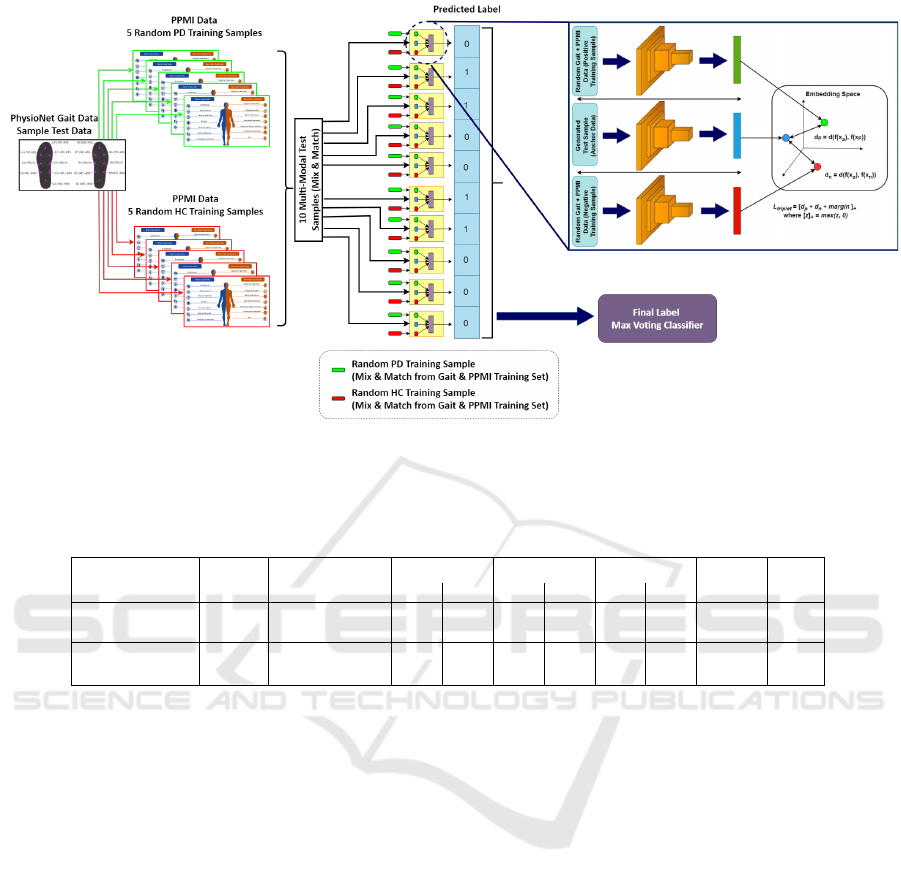
Figure 3: Model Inference Flow Diagram. The approach in the ﬁgure explains the classiﬁcation of gait test sample. Gait test

sample is combined with 5 random positive (PD) and 5 random negative (HC) samples of PPMI data from training set. The

curated samples are then used as an input to proposed multi-model. The output will be aggregated using max voting technique

and compared with the actual class label to measure accuracy.

Table 1: Performance comparison of Single modal vs. Multi-modal approach (Higher is better).

Model

Dataset

Accuracy (%) HC PD HC PD HC PD Kappa AUC

Single-Modality

Gait 83.33 1.00 0.77 0.61 1.00 0.76 0.87 0.64 0.81

PPMI 92.03 0.81 1.00 1.00 0.88 0.90 0.94 0.83 0.94

Multi-Modality

Gait 99.20 1.00 0.98 0.97 1.00 0.97 0.98 0.98 0.97

PPMI 99.12 1.00 0.99 0.97 1.00 0.99 0.99 0.98 0.97

Precision Recall F1-Score

put of the cross-merging step, serving as positive and

negative samples, respectively. The generated triplet

is then inputted into the triplet loss, predicting one of

the two classes (PD/HC). Applying a max-voting strat-

egy allows us to determine the ﬁnal prediction. Figure

3 illustrates the operation of the proposed inference

method.

5 RESULT

The multi-modality approach generally outperforms

single-modality for classiﬁcation, but it hasn’t been

much explored for Parkinson’s disease tasks. In

single-modality, we individually trained the gait

network and PPMI network (Figure 2) using separate

datasets. Our proposed multi-modality framework

(Figure 2) combines features from both models,

gait and PPMI, along with the inference technique

described in Section 4.2. In our experiments, we

evaluated both single-modality and multi-modality on

the test set using various performance metrics such

as accuracy, precision, recall, F1-score, Kappa, and

AUC. Table 1 shows that the multi-modality approach

achieves

≈

13% higher average accuracy compared

to its single-modality counterpart, also signiﬁcant

improvement in other metrics like precision and recall

afﬁrms the correctness and reduction in false negatives

which is essential in healthcare domain, making it

preferable for classiﬁcation tasks. Similar trends of

multi-modal superiority over single-modality are

observed in other performance metrics as well.

Comparison with SOTA Methods – To further an-

alyze the effectiveness of our proposed method, we

compared it with various methods in the literature us-

ing both the gait and PPMI datasets. Our goal is to

assess the method’s ability to classify data without

speciﬁc modalities. Table 2 and Table 3 describe the

comparisons for the PPMI and gait datasets, respec-

tively. In Table 2 for the PPMI dataset, our method

signiﬁcantly outperforms established accuracy bench-

marks, as well as other performance measures such

as AUC, Kappa Score, sensitivity, and speciﬁcity. For

gait dataset in Table 3, recent studies have achieved

accuracy levels exceeding 99%, leaving limited room

Mutually Exclusive Multi-Modal Approach for Parkinson’s Disease Classiﬁcation

241

Table 2: Performance comparison of the proposed approach with SOTA on PPMI dataset. (Higher is better).

Studies Model Accuracy (%) Sensitivity (%) Speciﬁcity (%) AUC Kappa

(Prashanth

et al., 2016)

Support Vector Machine (SVM)

[non-motor, CSF and imaging

markers]

96.40 97.03 95.01 0.98 NA

(Leger C,

2020)

Generalised Additive Model

(GAM) [Baseline Evaluation

with non-motor clinical and

biomarker features]

89.80 92.30 85 0.94 0.77

(MS Hema

and et al.,

2023)

Random Forest [Motor,

Non-Motor, Mental Health,

Semantic Features]

94.50 93.40 89.20 0.97 NA

Ours

Multi-Modal Siamese Network

(motor and non-motor)

99.12 ± 0.62 99 ± 0.007 97.43 ± 0.02 0.97 ± 0.01 0.98 ± 0.014

Table 3: Performance comparison of the proposed approach with SOTA on gait dataset. (Higher is better).

Studies Model Accuracy (%) Sensitivity (%) Speciﬁcity (%) F1 Score

(Zeng W and et al.,

2016)

Radial Basis Function (RBF)

Neural Networks

98.8 98.92 98.63 NR

(Acici K and et al.,

2017)

Random Forests 98 99.1 95.7 0.98

(Asuroglu T and

et al., 2018)

Locally Weighted Random

Forest (LWRF)

99 97.8 99.5 NR

(Zhao et al., 2018)

Long Short-Term Memory

(LSTM) and Convolutional

Neural Network (CNN)

98.61 NR NR NR

(Veeraragavan S and

SA., 2020)

Artiﬁcial Neural Network

(ANN)

97.7 97.05 97.41 0.97

(Xia Yand Yao Z and

N., 2020)

Long Short-Term Memory

(LSTM) and Convolutional

Neural Network (CNN)

99.07 99.1 99.01 NR

(Priya SJ and N.,

2020)

Logistic Regression 98.82 NR NR NR

(Ghaderyan and

Fathi, 2021)

Sparse NNLS coding

Method

97.22 98.22 95.86 NR

(Liu et al., 2021)

Long Short-Term Memory

(LSTM) and Convolutional

Neural Network (CNN)

99.22 98.04 100 0.99

(Tong J and S., 2021)

Support Vector Machine

(SVM)

99.23 NR NR NR

Ours

Multi-Modal Siamese

Network

99.20 ± 1.13 98.20 ± 0.01 99 ± 0.02 0.99 ± 0.01

for further improvement. Nonetheless, our method

demonstrates similar accuracy performance. When

comparing other metrics such as sensitivity, speciﬁcity,

and f1-score, we gain a deeper and more comprehen-

sive understanding of the model’s actual performance.

Our method also shows improvement across the ma-

jority of metrics when compared to other approaches

in the literature.

6 CONCLUSION

We proposed a novel technique that uses mutually

exclusive multi-modality training and inference ap-

proaches for classifying Parkinson’s disease (PD) in

scenarios with missing modalities. Our method in-

volves fusing features from a multi-modal network into

a combined feature vector, pairing reference modality

samples with positive and negative samples from other

modalities during inference, and using a voting scheme

for ﬁnal classiﬁcation. Comparing our multi-modal

approach to a single-modality approach, we observed

signiﬁcant performance improvements. Our method

also outperformed existing approaches on both PPMI

and gait datasets. This research has broader implica-

tions for addressing other disease detection scenarios

with missing modalities, enhancing prediction preci-

sion, and reducing the need for exhaustive datasets.

BIOIMAGING 2024 - 11th International Conference on Bioimaging

242

REFERENCES

Acici K, O. g. H. and et al. (2017). A random forest method

to detect parkinson’s disease via gait analysis. In Engi-

neering Applications of Neural Networks.

Archila J., M. A. . M. F. (2022). A multimodal parkinson

quantiﬁcation by fusing eye and gait motion patterns,

using covariance descriptors , from non-invasive com-

puter vision. In Computer Methods and Programs in

Biomedicine.

Asuroglu T, O. H. and et al. (2018). Parkinson’s disease

monitoring from gait analysis via foot-worn sensors.

In Biocybern Biomed Eng.

Cherubini A, M. M. and et al. (2014). Magnetic resonance

support vector machine discriminates between parkin-

son’s disease and progressive supranuclear palsy. In

International Parkinson and Movement Disorder Soci-

ety.

Du G., Lewis M., K. S. and et al. (2017). Combined diffu-

sion tensor imaging and apparent transverse relaxation

rate differentiate parkinson disease and atypical parkin-

sonism. In In American Journal of Neuroradiology.

Emamzadeh, F. N. and Surguchov, A. (2018). Parkinson’s

disease: Biomarkers, treatment, and risk factors. In

Frontiers in Neuroscience.

Ghaderyan, P. and Fathi, G. (2021). Inter-limb time-varying

singular value: A new gait feature for parkinson’s dis-

ease detection and stage classiﬁcation. Measurement,

177:109249.

Glaab E, Trezzi JP, D. N., C., E., and et al. (2019). Inte-

grative analysis of blood metabolomics and pet brain

neuroimaging data for parkinson’s disease. In Neuro-

biology of Disease.

Goldberger, A., S. H. E. and et al. (2000). Physiobank,

physiotoolkit, and physionet: Components of a new

research resource for complex physiologic signals. In

In Proc. CVPR.

H. Hirschauer, T. J., Adeli, B., and A., J. (2015). Computer-

aided diagnosis of parkinson’s disease using enhanced

probabilistic neural network. In In Journal of Medical

Systems.

Leger C, Herbert M, D. J. (2020). Non-motor clinical and

biomarker predictors enable high cross-validated accu-

racy detection of early pd but lesser cross-validated ac-

curacy detection of scans without evidence of dopamin-

ergic deﬁcit. In Frontiers in Neurology.

Liu, X., Li, W., Liu, Z., Du, F., and Zou, Q. (2021). A

dual-branch model for diagnosis of parkinson’s disease

based on the independent and joint features of the left

and right gait. Applied Intelligence, 51(10):7221–7232.

Long D., W. J. and et al. (2012). Automatic classiﬁcation of

early parkinson’s disease with multi-modal mr imaging.

In In PLOS ONE.

Makarious, M. B., Leonard, H. L., Vitale, D., and et al.

(2022). Multi-modality machine learning predicting

parkinson’s disease. npj Parkinson’s Disease, 8(1):35.

MS Hema, M Nageswara Guptha, V. P. and et al. (2023).

Prediction analysis for parkinson disease using mul-

tiple feature selection and classiﬁcation methods. In

Multimedia Tools and Applications.

Oliveira, F. P. M., Faria, and et al. (2018). Extraction, se-

lection and comparison of features for an effective

automated computer-aided diagnosis of parkinson’s

disease based on [123i]fp-cit spect images. European

Journal of Nuclear Medicine and Molecular Imaging,

45(6):1052–1062.

Pahuja G., P. B. (2022). Deep learning architectures for

parkinson’s disease detection by using multi-modal

features. In Computers in Biology and Medicine.

Prashanth, R., Dutta Roy, S., Mandal, P. K., and Ghosh,

S. (2016). High-accuracy detection of early parkin-

son’s disease through multimodal features and machine

learning. International Journal of Medical Informatics,

90:13–21.

Priya SJ, R. A. and N., U. (2020). Improving the prediction

accuracy of parkinson’s disease based on pattern tech-

niques. In 5th International Conference on Devices,

Circuits and Systems.

Tong J, Zhang J, D. E. and S., D. (2021). Severity classi-

ﬁcation of parkinson’s disease based on permutation-

variable importance and persistent entropy. In Multi-

media Tools and Applications.

Veeraragavan S, Gopalai AA, G. D. and SA., A. (2020).

Parkinson’s disease diagnosis and severity assessment

using ground reaction forces and neural networks. In

Front Physiol.

Xia Yand Yao Z, Y. Q. and N., C. (2020). A dual-modal

attention-enhanced deep learning network for quantiﬁ-

cation of parkinson’s disease characteristics. In IEEE

Trans Neural Syst Rehabil Eng.

Zeng W, Liu F, Z. Y. and et al. (2016). Parkinson’s dis-

ease classiﬁcation using gait analysis via deterministic

learning. In Neurosci Lett.

Zhao, A., Qi, L., Li, J., Dong, J., and Yu, H. (2018). A hybrid

spatio-temporal model for detection and severity rating

of parkinson’s disease from gait data. Neurocomputing,

315:1–8.

Mutually Exclusive Multi-Modal Approach for Parkinson’s Disease Classiﬁcation

243