
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using
Variable Subsampling and Randomized Measurements
Michael K
¨
olle
1
, Afrae Ahouzi
1,2
, Pascal Debus
2
, Robert M
¨
uller
1
, Dani
¨
elle Schuman
1
and Claudia Linnhoff-Popien
1
1
Institute of Informatics, LMU Munich, Munich, Germany
2
Fraunhofer AISEC, Garching, Germany
fi
Keywords:
Quantum Machine Learning, Anomaly Detection, OC-SVM.
Abstract:
Quantum computing, with its potential to enhance various machine learning tasks, allows significant advance-
ments in kernel calculation and model precision. Utilizing the one-class Support Vector Machine alongside a
quantum kernel, known for its classically challenging representational capacity, notable improvements in aver-
age precision compared to classical counterparts were observed in previous studies. Conventional calculations
of these kernels, however, present a quadratic time complexity concerning data size, posing challenges in prac-
tical applications. To mitigate this, we explore two distinct approaches: utilizing randomized measurements to
evaluate the quantum kernel and implementing the variable subsampling ensemble method, both targeting lin-
ear time complexity. Experimental results demonstrate a substantial reduction in training and inference times
by up to 95% and 25% respectively, employing these methods. Although unstable, the average precision of
randomized measurements discernibly surpasses that of the classical Radial Basis Function kernel, suggesting
a promising direction for further research in scalable, efficient quantum computing applications in machine
learning.
1 INTRODUCTION
In the prevailing digital landscape, anomaly detection
algorithms safeguard numerous systems by identify-
ing irregularities, such as unauthorized intrusion into
a network, unexpected machinery behavior, or abnor-
mal medical readings (Fernando et al., 2021; Boloka
et al., 2021). In e-commerce, these algorithms are
pivotal in protecting both customers and companies
from fraudulent transactions, which could precipitate
substantial financial losses (ECB, 2023). Anomaly
detection faces challenges, including the diverse and
rarely similar nature of anomalies, and often encoun-
ters high-dimensional, correlated, and sometimes un-
labeled data sets.
Quantum Machine Learning (QML), a synthe-
sis of machine learning and quantum computing,
promises potential solutions to some of these chal-
lenges by leveraging the capability of quantum al-
gorithms to compute classically challenging kernels
(Havl
´
ı
ˇ
cek et al., 2019). Some initiatives have aimed
at ameliorating existing anomaly detection methods
with quantum methods. A notable attempt (Kyriienko
and Magnusson, 2022) achieved a 20% elevation in
average precision using one-class support vector ma-
chine models with a quantum kernel, though con-
fronted quadratic scaling challenges with data size,
impacting both training and testing times.
Addressing the aforementioned time complexity
challenge, this work replicates the results from (Kyri-
ienko and Magnusson, 2022) and employs them as
benchmarks to explore the efficacy of two linear time
complexity methods based on data size: randomized
measurements for quantum kernel measurement and
an ensemble method termed variable subsampling.
The focus rests on two pivotal questions:
1. Can the quantum kernel extract superior informa-
tion from the data compared to the classical Ra-
dial Basis Function kernel, and thereby offer over-
all enhanced results?
2. Do randomized measurements and variable sub-
sampling models maintain the performance of the
quantum kernel derived through the inversion test,
while diminishing the time complexity related to
data size?
The evaluation engages synthetic data and the Credit
Card Fraud data set, inspecting performance and time
324
Kölle, M., Ahouzi, A., Debus, P., Müller, R., Schuman, D. and Linnhoff-Popien, C.
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements.
DOI: 10.5220/0012381200003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 2, pages 324-335
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

Input space
d
1
d
2
+
+
b −w ·Φ(x
i
)b −w ·Φ(x
i
)
bb
Separating hyperplaneSeparating hyperplane
AnomalousAnomalous
NormalNormal
Feature space
d
′
1
d
′
2
Feature Map
Φ
Figure 1: The linearly inseparable points on the input space
are mapped using a quantum feature Φ into a feature space
where they are linearly separable (Aggarwal, 2017).
complexities contingent on data size and qubit num-
ber. Our findings, diverging from (Kyriienko and
Magnusson, 2022), reveal that while attainable im-
provements in average precision and F1 score over
the classical kernel are discernible, they are min-
imally significant. Models utilizing variable sub-
sampling with the inversion test exhibited stability,
whereas those employing the randomized measure-
ment method presented high variance. Nevertheless,
variable subsampling did manifest considerable en-
hancements in training and testing times, indicating
potential performance elevation opportunities through
alternate hyperparameters. All Code and Experiments
can be found here
1
.
2 PRELIMINARIES
2.1 One-Class Support Vector Machines
The One-Class Support Vector Machine (OC-SVM),
originally presented by (Sch
¨
olkopf et al., 1999), of-
fers an unsupervised variant of the SVM for anomaly
and novelty detection. Differing from the conven-
tional SVM, which finds a maximum margin hyper-
plane to distinguish normal from anomalous data, the
OC-SVM presupposes that the origin represents the
anomalous class when labels are absent. It seeks to
maximize the margin b between origin and the input
data, penalizing points below the hyperplane (Fig. 1).
These are governed by a hyperparameter ν ∈ (0, 1]
which dictates the portion of points categorized as
anomalous.
min
w,b
1
2
w
2
+
1
νN
N
∑
i=1
max{b −w ·Φ(x
i
), 0}−b (1)
1
https://github.com/AfraeA/q-anomaly
To address non-linearly separable data, feature
maps Φ : X → F elevate data from input space X to
a higher dimensional feature space F . Since direct
calculations of feature maps are computationally in-
tensive, a kernel function k : X ×X → R is used to
ascertain data point similarity in the embedded fea-
ture space.
k(x
i
, x
j
) = ⟨Φ(x
i
), Φ(x
j
)⟩ (2)
The use of the kernel function, which can be
summed up in matrix form by the kernel matrix
G = [k(x
i
, x
j
)], facilitates a dual problem formulation.
Solving this dual problem leads to an implicit parame-
terization of the hyperplane based on the support vec-
tors α
i
.
Relying on this parameterization, scoring new
data depends on its relation to the separating hyper-
plane:
Score(x
new
) =
N
∑
i=1
α
i
·k(x
new
, x
i
) (3)
The label is determined by the score’s sign: neg-
ative connoting an anomaly and positive signifying
normalcy.
2.2 Quantum Kernel Embedding
Quantum feature maps allow for the embedding of
classical data into quantum states within Hilbert space
H through the use of data-dependent quantum unitary
gates U
Φ
(x), mathematically expressed as
|
Φ(x)
⟩
=
U
Φ
(x)
|
0
⟩
. The IQP-like (Instantaneous Quantum
Polynomial) feature map, recognized for being hard
to simulate classically (Havl
´
ı
ˇ
cek et al., 2019), en-
codes a d-dimensional input x
i
into d qubits as fol-
lows:
|
Φ(x
i
)
⟩
= U
Z
(x
i
)H
⊗d
U
Z
(x
i
)H
⊗d
0
d
E
,
U
Z
(x
i
) = exp
d
∑
j=1
λx
i j
Z
j
+
d
∑
j=1
d
∑
j
′
=1
λ
2
x
i j
x
i j
′
Z
j
Z
j
′
!
,
(4)
where λ, influenced by data reuploading counts, im-
pacts the kernel bandwidth analogously to γ (Shay-
dulin and Wild, 2022). We refer to FigureFig. 2a for a
visual representation. Upon data encoding, fidelity,
distilled to the overlap of states for pure quantum
states as F(x, x
′
) = |
⟨
Φ(x
′
)
|
Φ(x)
⟩
|
2
, quantifies data
similarity.
Two prominent methods for measuring fidelity are
the inversion and swap tests. The inversion test, de-
tailed in FigureFig. 2b, calculates the overlap of two
data points’ pure quantum states with O(n
2
) kernel
evaluations, but necessitates unitary feature maps and
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements
325

yields deeper circuits. Conversely, the swap test, de-
picted in FigureFig. 2c, is applicable to both pure and
mixed states but necessitates wider circuits. It is based
on the swap trick (Hubregtsen et al., 2022), which de-
duces the inner product from the tensor product of
density matrices ρ
i
and ρ
j
utilizing a swap gate S,
expressed in Eq. 5:
Tr(ρ
i
ρ
j
) = Tr(Sρ
i
⊗ρ
j
). (5)
2.3 Time Complexity for Quantum
Kernels
Quantum one-class Support Vector Machines provide
a nuanced method for detection but are hindered by
formidable time complexity, particularly given the ex-
isting operational frequencies of quantum hardware.
The intrinsic quadratic time complexity of one-class
SVMs is significantly amplified in a quantum com-
puting context, requiring a substantial number of rep-
etitions (shots) to accurately measure fidelity between
points due to its probabilistic nature; typically, at
least 1000 shots per circuit measurement are neces-
sary to obtain replicable results. Training a quantum
one-class SVM on a large dataset, exemplified by the
284,000 instances from the Credit Card dataset in our
experiments, would theoretically necessitate approxi-
mately 4 ×10
10
kernel function value calculations to
construct the symmetrical kernel matrix. This implies
a staggering requirement of 4 × 10
13
shots, which,
with a measurement rate of 5kHz (Haug et al., 2021),
equates to a minimum training time of 255 years us-
ing a swap or inversion test kernel.
Reducing the dataset may abbreviate training time
but risks degrading algorithmic performance and sta-
bility due to decreased representativity of training
samples. This diminution can result in less depend-
able support vectors and decision functions, jeopar-
dizing the reliability and consistency of the one-class
SVM, especially when training data substantially de-
viates from the overall distribution. The challenge
also permeates inference times, as predicting a new
point demands evaluating the kernel function against
all training points, elongating detection times and hin-
dering real-time applications like patient monitoring
and fraud prevention.
To surmount these obstacles, optimization of ker-
nel calculation algorithms and investigation into in-
novative quantum measurement techniques, which
could minimize the requisite shots, are pivotal. Viable
approaches may encompass adapting classical meth-
ods to minimize data needed for kernel matrix com-
putations while preserving performance, employing
clustering, and applying matrix decomposition and
approximation methods to avoid evaluating the kernel
across the entire training set.
3 RELATED WORK
3.1 Quantum Anomaly Detection
This work augments the methodology propounded in
(Kyriienko and Magnusson, 2022), amalgamating the
one-class SVM with a computationally intricate ker-
nel based on the IQP feature map (FigureFig. 2a) to
secure a 20% enhancement in average precision vis-
`
a-vis their classical benchmark. Subsequent exper-
iments herein adhere to this protocol as a quantum
yardstick, exploring two strategies to diminish the
time complexity relative to data size.
Hybrid quantum-classical models manifest as a
prominent archetype in anomaly detection research.
For instance, (Sakhnenko et al., 2022) innovatively
refines the auto-encoder (AE) hidden representation
by interfacing a parameterized quantum circuit (PQC)
with its bottleneck, segueing into an unsupervised
model post-training by substituting the decoder with
an isolation forest, and vetting performance across
multifarious data sets and PQC architectures. Concur-
rently, (Herr et al., 2021) pioneers an adaptation of the
classical AnoGAN (Schlegl et al., 2017) by deploying
a Wasserstein GAN, wherein the generator is substi-
tuted with a hybrid quantum-classical neural network,
and subsequently trained via a variational algorithm.
Contrastingly, quantum annealing approaches,
such as the QUBO-SVM presented in (Wang
et al., 2022), reformulate the conventional SVM
optimization predicament into a quadratic uncon-
strained binary optimization problem (QUBO) which
is amenable to resolution via quantum annealing
solvers. Although retaining the conventional SVM
optimization problem, this methodology expedites
accurate predictions through adept kernel function
identification, thereby facilitating plausible real-time
anomaly detection.
(Ray et al., 2022) explores hybrid ensembles, con-
structing an amalgamation of bagging and stacking
ensembles from assorted quantum and classical com-
ponents, each playing a pivotal role in the anomaly
detection framework. The amalgamated quantum
components encapsulate disparate variable quan-
tum circuit architectures, kernel-based, and quan-
tum annealing-based SVMs, while the classical con-
stituents encompass logistic regression, graph convo-
lutional neural networks, and light gradient boosting
models. Despite superficial similarity to the variable
subsampling utilized herein, it’s noteworthy that the
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
326
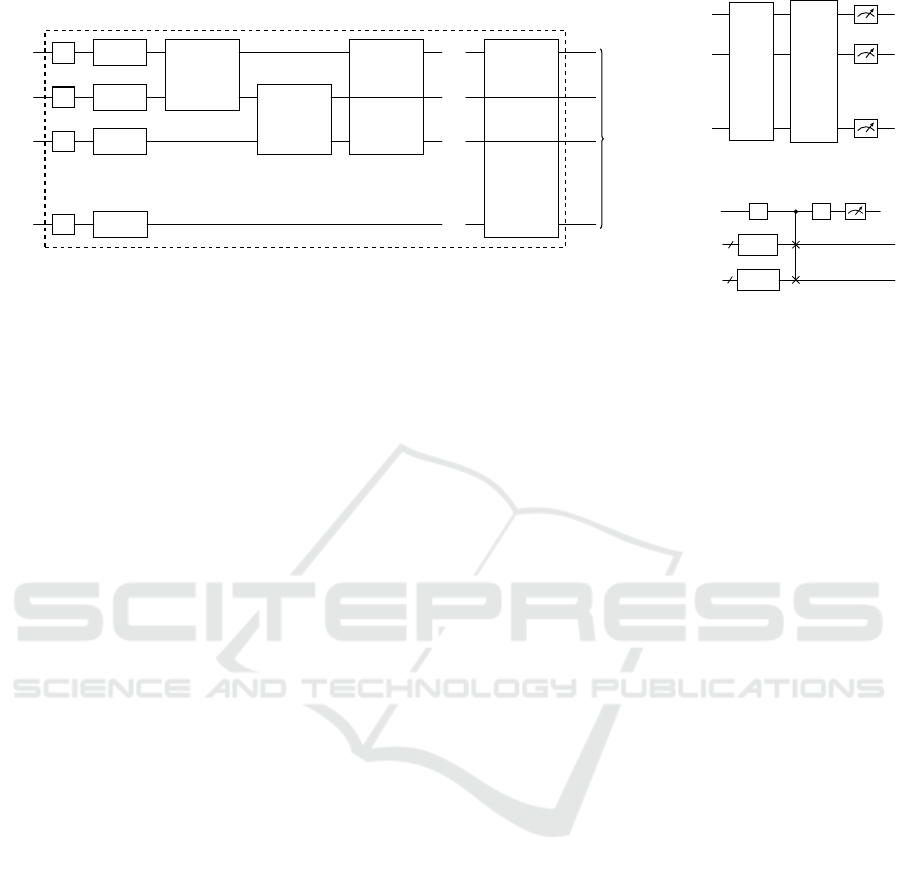
|
0
⟩
. . .
|
0
⟩
. . .
|
0
⟩
. . .
.
.
.
.
.
.
|
0
⟩
. . .
H
R
Z
(x
1
)
R
ZZ
(x
1
x
2
)
R
ZZ
(x
1
x
3
)
R
ZZ
(x
1
x
d
)
U
Φ
(x)
|
0
⟩
H
R
Z
(x
2
)
R
ZZ
(x
2
x
3
)
H
R
Z
(x
3
)
H
R
Z
(x
d
)
×2λ
(a) IQP-like feature map
|
0
⟩
|
0
⟩
.
.
.
.
.
.
|
0
⟩
U
Φ
(x)
U
†
Φ
(x
′
)
(b) Inversion test circuit
|
0
⟩
|
0
⟩
⊗d
|
0
⟩
⊗d
H H
U
Φ
(x)
U
Φ
(x
′
)
(c) Swap test circuit
Figure 2: Quantum circuits for IQP-like feature map, inversion test and swap test.
latter method’s adoption of varying sub-sample sizes
uniquely addresses the OC-SVM’s parameterization
dependence.
3.2 Efficient Gram Matrix Evaluation
Quantum kernel methods, pivotal for various quan-
tum machine learning applications, grapple with no-
table computational demands in matrix evaluations.
Approaches to mitigate this complexity are: (i)
Quantum-Friendly Classical Methods, reducing ker-
nel matrix elements to evaluate, and (ii) Quantum Na-
tive Methods, minimizing the shot requirements yet
necessitating classical post-processing, albeit feasibly
parallelizable or vectorizable.
Randomized measurement kernels, pioneered by
(Haug et al., 2021) and utilized with hardware-
efficient feature maps, achieved an expedited ker-
nel measurement while approximating Radial Basis
Function (RBF) kernels, demonstrated via both syn-
thetic and MNIST data. Conversely, the classical
shadow method, proposed by (Huang et al., 2020),
employs a similar quantum protocol but diverges in
classical post-processing to provide classical state
snapshots via the inversion of a quantum channel, of-
ten attaining reduced error in predicting second R
´
enyi
Entropy.
Variable subsampling, introduced by (Aggarwal
and Sathe, 2015), and its sophisticated counterpart,
variable subsampling with rotated bagging, offer an
efficient ensemble training approach, leveraging var-
ied sample sizes and rotational orthogonal axis system
projections respectively. These methods not only con-
fer computational efficiency but also harness an adap-
tive ensemble model training strategy, tested effica-
ciously with algorithms like local outlier factor (LOF)
models and the k-Nearest Neighbors algorithm.
The Distance-based Importance Sampling and
Clustering (DISC) approach, by (Hajibabaee et al.,
2021), and Block Basis Factorization, by (Wang
et al., 2019), represent variants of matrix decomposi-
tion based methods for kernel approximation. While
DISC employs cluster centroids as landmarks to for-
mulate approximation matrices and assumes kernel
matrix symmetry, block basis factorization avails ran-
domized spectral value decomposition on cluster sam-
ples and creates a smaller, computationally tractable
inner similarity matrix, demonstrating superior per-
formance relative to the k-means Nystr
¨
om method.
4 APPROACHES
In the preceding review of related work, several
methodologies of efficient gram matrix evaluation
were highlighted. However, moving forward, we will
focus on two specific approaches which can be ap-
plied to both symmetric training kernel matrices and
asymmetric ones used during prediction. Although
the classical shadows and block basis factorization
methods satisfy this criterion, we have decided to
explore randomized measurements and variable sub-
sampling methods because of their intuitive concep-
tual frameworks.
4.1 Randomized Measurements Kernel
Expanding upon the method of randomized measure-
ments, suggested for future exploration in (Kyriienko
and Magnusson, 2022), and practically employed in
kernel calculation for classification by (Haug et al.,
2021), this method endeavors to adeptly meld linear
and quadratic complexities concerning data size. This
is achieved respectively through acquiring measure-
ments of feature maps and subsequent classical post-
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements
327

processing. The method notably diminishes the req-
uisite quantum shots, thereby alleviating the overall
computational burden.
The inception of the fidelity calculation was mo-
tivated by the possibility of conceiving the swap op-
erator S as a quantum twirling channel Φ
(2)
N
(Elben
et al., 2019). Quantum twirling channels are opera-
tions commonly used in error correction. A 2-fold lo-
cal quantum twirling channel applied to an arbitrary
operator O is articulated by
Φ
(2)
N
(O) = (U
⊗2
)
†
OU
⊗2
, (6)
with . . . denoting the average over the unitaries U =
N
N
k
U
k
and U
k
sampled from a unitary 2-design. A
unitary t-design approximates property averages over
all possible unitaries using a finite set, while the
Haar measure provides a uniform sampling mecha-
nism across unitary matrices. (Elben et al., 2019)
demonstrate that the expectation value of applying
such a twirling channel on an operator O acting on
two copies of a quantum state ρ is obtainable from
the probability products P
U
resulting from the mea-
surements:
∑
s,s
′
O
s,s
′
P
U
(s)P
U
(s
′
) = Tr
Φ
(2)
N
(O) ρ ⊗ρ
(7)
The coefficients O
s,s
′
specific to the swap operator are
derived by employing Weingarten calculus of Haar
random unitaries and Schur-Weyl duality (Roberts
and Yoshida, 2017) to calculate the purity of the state
ρ, yielding:
O
s,s
′
= d
N
(−d)
D
(
s,s
′
)
. (8)
A formula for quantum fidelities in terms of random-
ized measurement probabilities is obtained by utiliz-
ing the swap trick, then employing Eq. 6 with the co-
efficients from Eq. 7.
Local Haar random unitaries U
Haar
are constructed
by tensoring sampled unitary U
k
∈ SU (2) for each
qubit. As illustrated in Fig. 3, each quantum circuit
leverages a unitary U
Φ
, corresponding to the quantum
feature map, and one of the r different local Haar ran-
dom unitaries U
Haar
. Every circuit requires s different
shots. This yields r sets of strings s
A
and their mea-
surement probabilities P
(i)
U
(s
A
) for the different ran-
dom basis rotations U
Haar
. Post-processing harnesses
the formula:
K(x
i
, x
j
) = Tr(ρ
i
ρ
j
)
= 2
d
∑
s
A
,s
′
A
(−2)
−D(s
A
,s
′
A
)
P
(i)
U
(s
A
)P
( j)
U
(s
′
A
)
(9)
The statistical error in fidelity measurement, quan-
tified as ∆G ≈
1
s
√
r
, necessitates error mitigation, par-
ticularly pertinent in noisy hardware scenarios. A fa-
cilitative aspect of the randomized measurements ap-
proach is its provision for straightforward error mit-
igation, involving purities calculated and recorded in
the diagonal of the training kernel matrix and exploit-
ing a minor computational overhead in the testing
phase for the asymmetrical kernel matrix.
The quantum kernel calculation segment, employ-
ing randomized measurements, presents a time com-
plexity of nrs (n: data size, r: basis rotation unitaries,
s: shots per rotation), while classical post-processing
demands n
2
complexity, albeit with an unfavorable
exponential time complexity concerning the number
of qubits (features). Implementation aligning with
(Haug et al., 2021) is accessible via the Large Scale
QML
2
GitHub repository, whereas randomized mea-
surement processing and combination utilize func-
tionalities from the qc optim
3
repository. Accommo-
dating the IQP-like feature map and enabling interim
kernel copy retention and calculation time-keeping
mandated the development of a novel implementa-
tion.
4.2 Variable Subsampling
Introduced by (Aggarwal, 2017), variable subsam-
pling addresses sensitivities in the one-class SVM to
kernel choice and hyperparameter ν values by exploit-
ing ensemble methods. Unlike bagging ensembles,
variable sampling ensembles, while utilizing random
subset selection for model training, employ varying
sub-sample sizes, permitting sampling over parame-
ter spaces, particularly those related to data size, like
the expected anomaly ratio ν in the one-class SVM.
Supposing a variable subsampling ensemble com-
prises 3 OC-SVMs trained with ν = 0.1 and sample
sizes of 53, 104, and 230, differing support vector
lower bounds among components yield varied deci-
sion boundaries. These can subsequently be com-
bined in a manner that diminishes the bias or variance
in predictions.
Ensemble construction commences with uni-
formly sampling c different subsample sizes between
50 and 1000. Data subsets, corresponding to sam-
pled sizes, are randomly selected from the dataset
and employed to train base model versions, here,
the quantum one-class SVM with inversion test. Al-
though subsamples may contain identical elements,
each avoids reusing data points to better reduce vari-
ance. Predictions are calculated by combining nor-
malized (to zero mean and unit standard deviation)
decision functions of all components, considering
2
https://github.com/chris-n-self/large-scale-qml
3
https://github.com/chris-n-self/qc optim
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
328
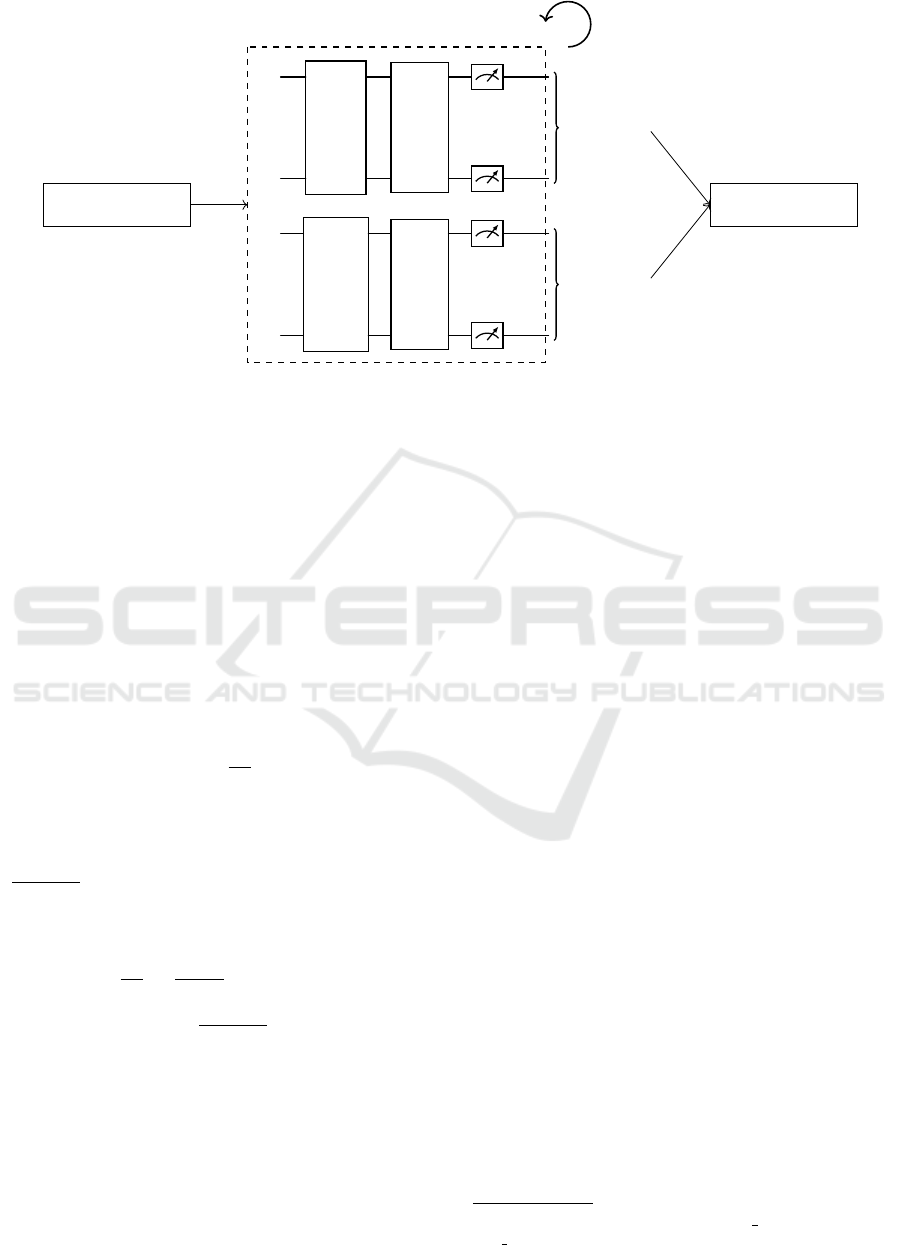
Sample r random
Haar unitaries U
Haar
|
0
⟩
.
.
.
.
.
.
|
0
⟩
|
0
⟩
.
.
.
.
.
.
|
0
⟩
U
Φ
(x)
U
Haar
s
A
, P
U
(s
A
)
U
Φ
(x
′
)
U
Haar
s
′
A
, P
U
(s
′
A
)
Classical Postpro-
cessing using Eq. 9
Repeat measurement for r Haar
random unitaries, each for s shots
Figure 3: The protocol and the circuit architecture for calculating quantum kernel functions using randomized measurement.
each is trained with distinct data sizes, thus possessing
varied decision function value ranges (Aggarwal and
Sathe, 2015). Simple averaging of outlier scores is ad-
vantageous for reducing variance and superior perfor-
mance with smaller datasets. Applying the maximum
score, conversely, curtails bias but elevates variance.
Post decision function value extraction, the threshold
function sgn(.) derives the class label.
More components and a higher maximum sub-
sample size facilitate optimal variance reduction, at
the expense of increased computational resource and
time demands. However, this trade-off can be man-
aged through wise hyperparameter selection. For ex-
ample, we choose a maximum subsample size of 100,
instead of the recommended 1000 points from the
original research, and use ⌊
n
100
⌋ components instead
of 100. While this may negatively affect performance,
it provides insight into the ensemble’s behavior when
scalability takes precedence.
The training phase exhibits approximately c ·
(
n
min
+n
max
2
)
2
time complexity, where c is the number
of ensemble components, and n
min
= 50 and n
max
=
100 are the minimum and maximum subsample sizes
respectively. Incorporating scalability modifications,
this becomes ⌊
n
100
⌋·
50+100
2
2
, indicating linear com-
plexity. Testing similarly maintains linear time com-
plexity, formulated as c·
n
min
+n
max
2
·n
test
, with n
test
rep-
resenting test samples.
5 EXPERIMENTAL SETUP
Ensuring the reproducibility of our experiments, this
section meticulously delineates implementation as-
pects, encompassing pre-processing, various kernel
calculation methodologies, and hyperparameter se-
lection. Two distinct experiment sets facilitate the
comparative analysis of our approaches:
1. The first set aspires to examine performance,
training, and testing durations with respect to data
size. Primarily, it endeavors to contrast the com-
putational efficiencies afforded by our methodolo-
gies, delineated in Section 4, and to comprehend
model responses to elevated data volumes.
2. Focusing on the relationship between perfor-
mance, computational time, and the number of
features (or qubits), the second experiment set
seeks not only to discern whether the methods im-
pose detrimental effects on performance but also
to elucidate the time feature/qubit relationship.
Experiments are conducted using 15 distinct
seeds, ranging from 0 to 14.
5.1 Datasets
Our experiments utilize two datasets, distinguished by
their synthetic or real-world origin, to investigate vari-
ous methodologies. The synthetic dataset is employed
exclusively in the first experiment set, given its two-
dimensional nature and the associated limitations in
exploring numerous features.
5.1.1 Synthetic Data
Our synthetic dataset is a bi-dimensional, non-
linearly separable dataset, derived by modifying an
SKlearn OC-SVM demonstration
4
to yield training
samples of diverse sizes. Testing samples consistently
4
https://scikit-learn.org/stable/auto examples/svm/
plot oneclass.html
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements
329

comprise 125 points, incorporating a 0.3 anomaly ra-
tio.
5.1.2 Credit Card Fraud Data
The credit card fraud data
5
encompasses approxi-
mately 284,000 datapoints, with 492 classified as
anomalous (class 1), across 31 features. Omitting
’time’ and ’amount’, 28 PCA-applied, anonymized
numerical features are retained. Each seed corre-
sponds to a unique data split. The size varies for
the set of experiments exploring the effects of data
size, while it is kept at a constant 500 data samples
for the set of experiments exploring the effects of
the qubit/feature number. Training data only contains
non-anomaly samples while the test set always con-
tains 125 points, which include 6 anomalies, achiev-
ing a 0.05 anomaly ratio.
5.2 Data Pre-Processing
Distinctive pre-processing methodologies were ne-
cessitated based on the quantum kernel measurement
technique applied and the data type (synthetic or real).
Radial Basis Function (RBF) Kernel. For imple-
mentations utilizing the RBF kernel, standard scaling
was executed post data partitioning into training and
test subsets, ensuring zero mean and unit standard de-
viation across all features. Subsequently, Principal
Component Analysis (PCA) was employed to consol-
idate the data into the requisite number of features.
Inversion Test Kernels. The application of inver-
sion test kernels warranted an additional step follow-
ing the pre-processing used for the RBF kernel. Given
that data was utilized as rotation angles within the
quantum circuit, a scaling by a factor of 0.1 was an
imperative post-PCA application.
Randomized Measurements Kernels. Adhering
to guidelines by (Haug et al., 2021), the randomized
measurements kernels necessitated a unique rescaling
approach. Post-PCA, a second round of standard
scaling was administered, succeeded by an additional
rescaling using factor
1
√
M
, with M representing the
post-PCA data dimensionality.
Note that while real data pre-processing was
adapted in accordance with the specific quantum ker-
nel measurement technique deployed, synthetic data
5
https://www.kaggle.com/datasets/mlg-ulb/
creditcardfraud
was subjected to pre-processing solely when imple-
menting the randomized measurement kernel, only re-
quiring a step of standard scaling with an additional
rescaling by factor
1
√
M
.
5.3 Baselines
For the real dataset, we aim to replicate the one-class
SVM results from (Kyriienko and Magnusson, 2022),
adopting them as quantum and classical benchmarks.
Lacking detailed insight into their sampling method
and explicit test set sizes, we employ random sam-
pling to generate data sets comprising 500 training
and 125 test data points, training the OC-SVM solely
on non-anomalous data, like the original authors. An
anomaly ratio of 0.05 is maintained in the test set.
The experiments concerning model responses to
various data sizes retain these architectures, holding
the number of PCA features steady while manipulat-
ing data sizes. Specifically, we utilize 2 features for
synthetic and 6 for real data sets, exploring data sizes
n ∈ {250, 500, 750, 1000, 1250, 1500}.
5.4 Models and Parameter Selection
Employing both classical and quantum versions of
the OC-SVM, we utilize OneClassSVM from the
SKlearn
6
library. All classical models adopt the RBF
kernel with γ =
1
N·Var(M)
and a consistent ν = 0.1.
Quantum circuits, pivotal for kernel calculations,
are crafted with the qiskit
7
library, simulated via
qiskit aer.QasmSimulator. Employing λ = 3 data
reuploadings for all quantum methods’ feature maps,
inversion test kernel elements are determined using
1000 shots each.
Randomized measurement circuits, realized with
r = 30 measurement settings and subjected to s =
9000 shots each, leverage crucial classical post-
processing, which emphasizes minimal embedded
loops and prioritizes efficient matrix operations. The
variable subsampling method, utilizing c = ⌊
n
100
⌋
components (n representing the training set size) and
a subsample size n
s
∈ [50, 100] to ensure scalable
model performance, invokes the inversion test for ker-
nel calculations with 1000 shots per element. Em-
ploying a consistent ν value, the desired kernel matrix
calculation function is passed as a callable kernel pa-
rameter, designed to accept two data sets and method-
specific hyper-parameters, subsequently returning the
computed kernel matrix.
6
https://scikit-learn.org/stable/modules/generated/
sklearn.svm.OneClassSVM.html
7
https://qiskit.org/
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
330

5.5 Performance Metrics for
Imbalanced Data Sets
Analyzing highly imbalanced data sets, prevalent in
anomaly detection, necessitates alternative metrics to
accuracy due to its incapability to reflect model per-
formance accurately across classes (Aggarwal, 2017).
Hence, derivatives of precision and recall like the F1
score and average precision gain prominence.
F1 Score: represents the harmonic mean of preci-
sion and recall, providing a balanced perspective on
model performance regarding false positives and neg-
atives. It is defined as
F1 score = 2 ·
Precision ·Recall
Precision + Recall
. (10)
Average Precision: quantifies the model’s capabil-
ity to discern anomalies, irrespective of threshold, by
measuring the area under the precision-recall curve.
Specifically,
AP =
∑
k
[Recall(k) −Recall(k + 1)] ·Precision(k).
(11)
An average precision equal to the data’s anomaly ratio
signifies a model with no anomaly detection capabil-
ity, while a score of 1 indicates a flawless detector.
Consequently, our analysis prioritizes average preci-
sion, complemented by precision, recall, and F1 score
insights.
6 RESULTS
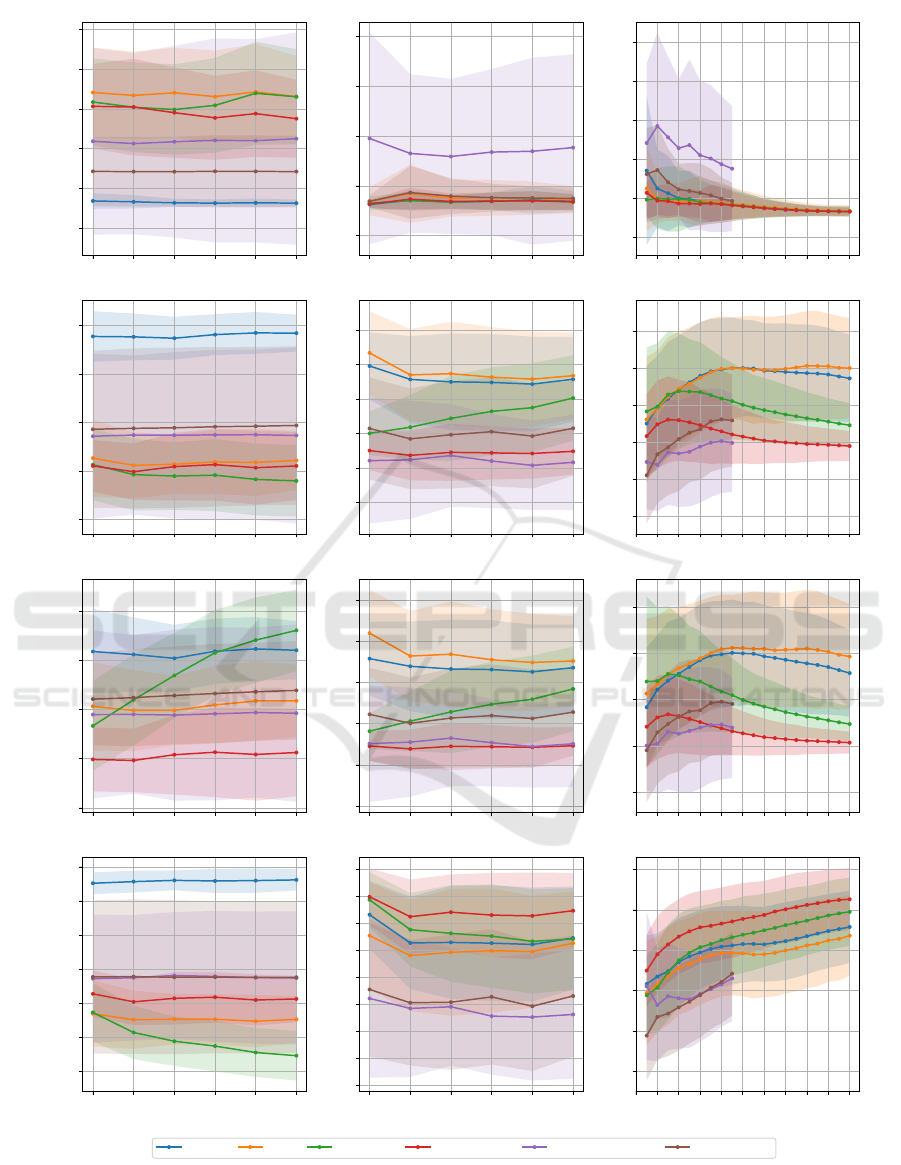
6.1 Performance Analysis Synthetic
Dataset
The performance results utilizing synthetic data are
presented in the first column of Fig. 4a. Quantum
methods demonstrate superior average precision com-
pared to classical Radial Basis Function (RBF) mod-
els with the synthetic data. Despite this, given the
anomaly ratio of 0.3, most methods underperform rel-
ative to a random detector, with inversion test and
variable subsampling (using the maximum score) as
exceptions. Variable subsampling not only surpasses
randomized measurements in average precision but
also exhibits comparable variance in ensemble results
across different combination functions. Notably, it
presents augmented results with the maximum over
the average function for data sizes exceeding 750
points.
Upon applying the sign as a threshold, classical
models outperform quantum models with the RBF
kernel models securing an approximate F1 score of
0.88 and demonstrating lower variance. The random-
ized measurements and inversion test models follow
in performance, with versions of the variable subsam-
pling ensemble trailing. Despite the mitigated version
of randomized measurements models achieving supe-
rior precision, F1 scores, and recall values were alike
between mitigated and unmitigated versions. Contrar-
ily, variable subsampling employing the maximum
score delivers superior precision but inferior recall
compared to its average score counterpart, suggest-
ing its unsuitability for anomaly detection using the
current threshold.
Although results might appear conflicting, dispar-
ities may stem from suboptimal threshold selection
for quantum methods. Given that average precision
operates independently of a threshold, findings might
imply an optimal threshold where quantum methods
supersede classical RBF.
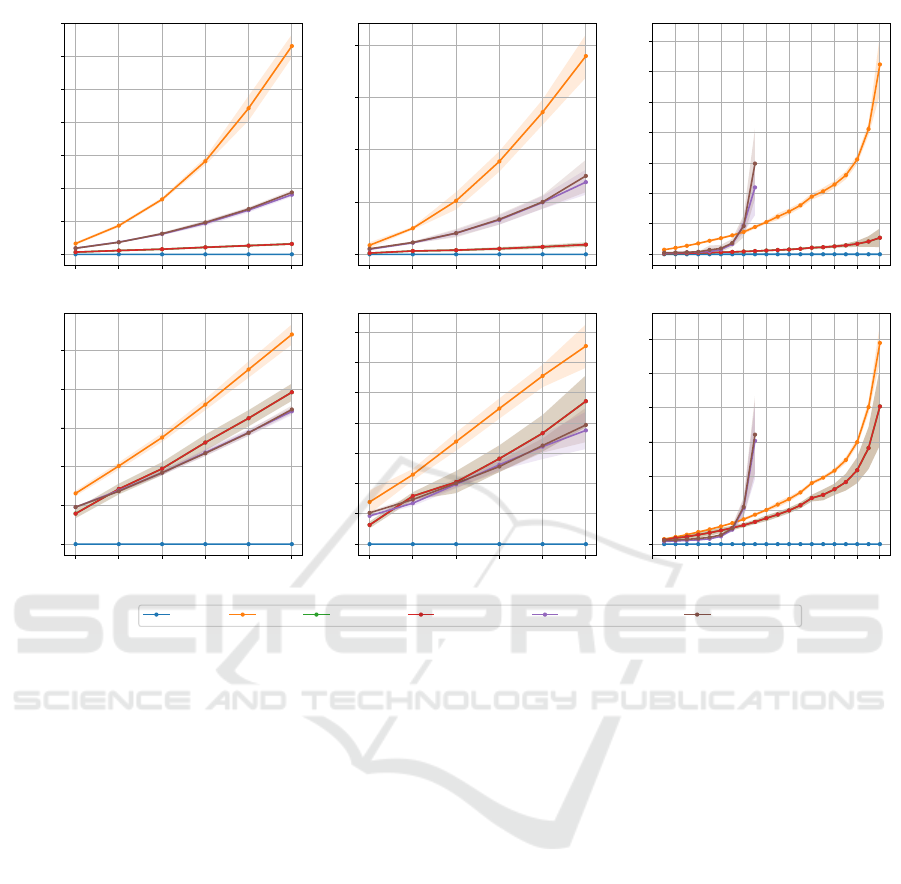
6.2 Training and Testing Durations
Synthetic Dataset
Fig. 5a depicts the notable efficiency of the variable
subsampling method in reducing training durations,
achieving the lowest among all employed quantum
methods for both VS Max and VS Average. Interest-
ingly, varied score functions do not impact the time
consumption. Variable subsampling not only realizes
linear time but also accomplishes a ∼ 95% reduction
in training time with 1500 data points, suggesting po-
tential similar results in significantly less time given
their average precision closely mirroring that of an
individual one-class SVM utilizing the inversion test
(Section 2). Furthermore, a ∼ 25% enhancement in
testing time is observed at 1500 training data points.
Mitigated and unmitigated randomized measure-
ments methods yielded analogous times, corroborat-
ing that error mitigation imposes minimal overhead.
While randomized measurements facilitate substan-
tial training time reduction, complexity is non-linear
relative to data size, attributed to the inclusion of clas-
sical post-processing in training time, which demands
quadratic time complexity. Albeit the training time
reduction from the randomized measurement method
falls below that of variable subsampling, it yet pro-
vides ∼ 35% and ∼ 12% reduced testing times com-
pared to the inversion test and variable subsampling
respectively at 1500 training data points.
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements
331
250 500 750 1000 1250 1500
Training data size
0.15
0.20
0.25
0.30
0.35
0.40
Average precision
(a) Synthetic Data by Size
250 500 750 1000 1250 1500
Training data size
0.00
0.05
0.10
0.15
0.20
(b) Credit Card Fraud Data by Size
0 2 4 6 8 10 12 14 16 18 20
Number of qubits/features
0.00
0.05
0.10
0.15
0.20
0.25
(c) Credit Card Fraud Data by Features
250 500 750 1000 1250 1500
Training data size
0.5
0.6
0.7
0.8
0.9
F1 score
250 500 750 1000 1250 1500
Training data size
0.1
0.2
0.3
0.4
0.5
0.6
0 2 4 6 8 10 12 14 16 18 20
Number of qubits/features
0.0
0.1
0.2
0.3
0.4
0.5
250 500 750 1000 1250 1500
Training data size
0.5
0.6
0.7
0.8
0.9
Precision
250 500 750 1000 1250 1500
Training data size
0.0
0.1
0.2
0.3
0.4
0.5
0 2 4 6 8 10 12 14 16 18 20
Number of qubits/features
0.0
0.1
0.2
0.3
0.4
250 500 750 1000 1250 1500
Training data size
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Recall
250 500 750 1000 1250 1500
Training data size
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0 2 4 6 8 10 12 14 16 18 20
Number of qubits/features
0.0
0.2
0.4
0.6
0.8
1.0
RBF IT VS Max VS Average Unmitigated RM Mitigated RM
Figure 4: The performance of the models trained using the different methods. The first column of the figure corresponds to
the synthetic dataset, used with 2 features and various data sizes. The second and third columns correspond to the Credit Card
dataset, with 6 as the number of features using various data sizes, then used with various numbers of features and a constant
data size of 500.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
332
250 500 750 1000 1250 1500
Training data size
0
2000
4000
6000
8000
10000
12000
14000
Training Time [s]
(a) Synthetic Data by Size
250 500 750 1000 1250 1500
Training data size
0
20000
40000
60000
80000
(b) Credit Card Fraud Data by Size
0 2 4 6 8 10 12 14 16 18 20
Number of qubits/features
0
20000
40000
60000
80000
100000
120000
140000
(c) Credit Card Fraud Data by Features
250 500 750 1000 1250 1500
Training data size
0
500
1000
1500
2000
2500
Testing Time [s]
250 500 750 1000 1250 1500
Training data size
0
2500
5000
7500
10000
12500
15000
17500
0 2 4 6 8 10 12 14 16 18 20
Number of qubits/features
0
10000
20000
30000
40000
50000
60000
RBF IT VS Max VS Average Unmitigated RM Mitigated RM
Figure 5: Training and testing durations in seconds, based on the data size.
6.3 Performance Analysis Relative to
Data Size Credit Card Data
Fig. 4b reveals a predominant equivalence to a ran-
dom detector across most models, with the unmiti-
gated randomized measurements kernel being a no-
table exception. Despite this hinting at a potential
performance threshold, the model’s notable variance
signifies an inherent instability.
At the utilized threshold, the inversion test and
classical RBF exhibit comparable F1 scores in
Fig. 4b, succeeded by variable subsampling models
employing maximum scoring, which seem to exhibit
an enhancement with increased data usage. Despite
affording the highest recall, both variable subsam-
pling variations grapple with suboptimal precision.
Meanwhile, both randomized measurement ker-
nels, under the current threshold, struggle with no-
tably low recall, undermining their utility for anomaly
detection.
6.4 Time Complexity Relative to Data
Size Credit Card Data
In Fig. 5b, we demonstrate that, analogous to syn-
thetic data outcomes, employing variable subsam-
pling assures linear time complexity and substantially
curtails training time. Furthermore, randomized mea-
surements realize up to a 50% reduction in training
time, even while tripling data utilization. Both vari-
able sampling and randomized measurements main-
tain comparable, and notably reduced, inference times
relative to the inversion test method.
6.5 Performance Analysis Concerning
Qubit Number - Credit Card Fraud
Dataset
In our endeavor to replicate the results from (Kyri-
ienko and Magnusson, 2022), we also explore ad-
ditional metrics including precision, recall, and
F1 score, employing thresholds in model evalua-
tion. The original study lacks explicit data selection
methodology for training and testing, along with ab-
sent details on the number of runs, prompting us to
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements
333

opt for a uniformly random data selection.
Our findings, notably divergent from (Kyriienko
and Magnusson, 2022), are presented in Fig. 4c.
Average Precision reveals considerably less favor-
able outcomes for classical RBF and quantum inver-
sion test than the aforementioned study, particularly
over 15 different runs, underperforming even a ran-
dom detector. Increasing feature/qubit usage evens
the average precision of the inversion test kernel, uti-
lizing the IQP-like kernel, to that of the classical
RBF, suggesting the original paper’s results might
hinge more on beneficial sample selection for the
quantum IQP-like kernel rather than demonstrating a
clear quantum advantage. Notably, models exhibit en-
hanced stability—diminishing average precision vari-
ance—with augmented feature/qubit use.
Thresholded metrics indicate marginal improve-
ment with inversion tests over classical methods, yet
a similar F1 score is attainable via the classical ker-
nel with fewer qubits. Variable subsampling, while
offering the highest recall and consistent results, un-
derachieves in F1 score due to suboptimal preci-
sion—potentially attributable to conservative hyper-
parameter selections. An exploration into its perfor-
mance with increased components and a larger maxi-
mum subsample could be interesting.
6.6 Time Complexity Concerning Qubit
Number - Credit Card Fraud
Dataset
Fig. 5c illustrates a quadratic relationship between the
training time and the number of qubits for the inver-
sion test. Despite a similar relationship, variable sub-
sampling effectively diminishes training time, poten-
tially attributed to its ensemble components utilizing
the inversion test independently of qubit number, con-
strained by limited and non-correlated component and
data sizes. Conversely, the randomized measurements
method sees escalated training times with 8 or more
qubits, hindering its utility for high-dimensional data
sets. A rise in testing times is also observed with in-
creasing qubit numbers.
7 CONCLUSION
This work explores two methodologies aimed at en-
hancing the scalability of the quantum one-class SVM
in a semi-supervised framework: (1) the randomized
measurements and (2) variable subsampling ensem-
ble methods. The former, inherently quantum, re-
alizes linear quantum time complexity but demands
a quadratically complex classical post-processing
based on data size. It generates kernel matrices by
combining measurements from quantum feature maps
of the data, executed through a randomized scheme.
The latter adopts an ensemble approach, training mul-
tiple base model instances on varied-sized data sub-
sets.
Two experimental datasets, synthetic and Credit
Card, were deployed, revealing a marginal average
precision improvement over the classical RBF for
all methods in the synthetic data. Discrepancies
emerged between outcomes from the Credit Card
Fraud dataset and those in (Kyriienko and Magnus-
son, 2022). While models utilizing the inversion
test and variable subsampling approximated the RBF
and were relatively stable, those yielding higher aver-
age precision, like unmitigated randomized measure-
ments, exhibited instability.
Future research trajectories include exploring the
integration of variable subsampling with random-
ized measurements kernels and employing random-
ized measurements or variable subsampling alongside
alternative kernels, such as learnable ones. Incorpo-
rating importance sampling in selecting the Haar ran-
dom unitaries (Rath et al., 2021), as suggested by
(Haug et al., 2021), could refine the randomized mea-
surements method. The classical shadow method, due
to its lower average error compared to randomized
measurements, and the examination of Nystr
¨
om and
block basis factorization approximations of a quan-
tum kernel, warrant further exploration. Finally, en-
hancing the quantum SVM’s performance through
the proposed variable sampling method, by utilizing
more components and enlarging maximum subsam-
ple sizes, remains a viable avenue, given the resultant
training and testing time reductions.
ACKNOWLEDGEMENTS
This research is part of the Munich Quantum Valley,
which is supported by the Bavarian state government
with funds from the Hightech Agenda Bayern Plus.
REFERENCES
Aggarwal, C. C. (2017). An introduction to outlier analysis.
Springer.
Aggarwal, C. C. and Sathe, S. (2015). Theoretical foun-
dations and algorithms for outlier ensembles. ACM
SIGKDD explorations newsletter, 17(1):24–47.
Boloka, T., Crafford, G., Mokuwe, W., and Eden,
B. V. (2021). Anomaly detection monitoring sys-
tem for healthcare. In 2021 Southern African
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
334

Universities Power Engineering Conference/Robotics
and Mechatronics/Pattern Recognition Association of
South Africa (SAUPEC/RobMech/PRASA), pages 1–6.
ECB (2023). Report on card fraud in 2020 and 2021.
Elben, A., Vermersch, B., Roos, C. F., and Zoller, P. (2019).
Statistical correlations between locally randomized
measurements: A toolbox for probing entanglement
in many-body quantum states. Physical Review A,
99(5):052323.
Fernando, T., Gammulle, H., Denman, S., Sridharan, S.,
and Fookes, C. (2021). Deep learning for medical
anomaly detection – a survey.
Hajibabaee, P., Pourkamali-Anaraki, F., and Hariri-
Ardebili, M. A. (2021). Kernel matrix approximation
on class-imbalanced data with an application to scien-
tific simulation. IEEE Access, 9:83579–83591.
Haug, T., Self, C. N., and Kim, M. (2021). Large-scale
quantum machine learning. arXiv e-prints, pages
arXiv–2108.
Havl
´
ı
ˇ
cek, V., C
´
orcoles, A. D., Temme, K., Harrow, A. W.,
Kandala, A., Chow, J. M., and Gambetta, J. M. (2019).
Supervised learning with quantum-enhanced feature
spaces. Nature, 567(7747):209–212.
Herr, D., Obert, B., and Rosenkranz, M. (2021). Anomaly
detection with variational quantum generative adver-
sarial networks. Quantum Science and Technology,
6(4):045004.
Huang, H.-Y., Kueng, R., and Preskill, J. (2020). Predicting
many properties of a quantum system from very few
measurements. Nature Physics, 16(10):1050–1057.
Hubregtsen, T., Wierichs, D., Gil-Fuster, E., Derks, P.-J. H.,
Faehrmann, P. K., and Meyer, J. J. (2022). Train-
ing quantum embedding kernels on near-term quan-
tum computers. Physical Review A, 106(4):042431.
Kyriienko, O. and Magnusson, E. B. (2022). Unsupervised
quantum machine learning for fraud detection. arXiv
preprint arXiv:2208.01203.
Rath, A., van Bijnen, R., Elben, A., Zoller, P., and Verm-
ersch, B. (2021). Importance sampling of randomized
measurements for probing entanglement. Physical Re-
view Letters, 127(20).
Ray, A., Guddanti, S. S., Ajith, V., and Vinayagamurthy, D.
(2022). Classical ensemble of quantum-classical ml
algorithms for phishing detection in ethereum trans-
action networks. arXiv preprint arXiv:2211.00004.
Roberts, D. A. and Yoshida, B. (2017). Chaos and com-
plexity by design. Journal of High Energy Physics,
2017(4).
Sakhnenko, A., O’Meara, C., Ghosh, K. J., Mendl, C. B.,
Cortiana, G., and Bernab
´
e-Moreno, J. (2022). Hybrid
classical-quantum autoencoder for anomaly detection.
Quantum Machine Intelligence, 4(2):1–17.
Schlegl, T., Seeb
¨
ock, P., Waldstein, S. M., Schmidt-Erfurth,
U., and Langs, G. (2017). Unsupervised anomaly de-
tection with generative adversarial networks to guide
marker discovery.
Sch
¨
olkopf, B., Williamson, R. C., Smola, A., Shawe-Taylor,
J., and Platt, J. (1999). Support vector method for nov-
elty detection. Advances in neural information pro-
cessing systems, 12.
Shaydulin, R. and Wild, S. M. (2022). Importance of ker-
nel bandwidth in quantum machine learning. Physical
Review A, 106(4).
Wang, H., Wang, W., Liu, Y., and Alidaee, B. (2022). In-
tegrating machine learning algorithms with quantum
annealing solvers for online fraud detection. IEEE Ac-
cess, 10:75908–75917.
Wang, R., Li, Y., Mahoney, M. W., and Darve, E. (2019).
Block basis factorization for scalable kernel evalua-
tion. SIAM Journal on Matrix Analysis and Applica-
tions, 40(4):1497–1526.
Towards Efficient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements
335
