
Disentangling Quantum and Classical Contributions in Hybrid Quantum
Machine Learning Architectures
Michael K
¨
olle, Jonas Maurer, Philipp Altmann, Leo S
¨
unkel, Jonas Stein and Claudia Linnhoff-Popien
Institute of Informatics, LMU Munich, Munich, Germany
fi
Keywords:
Variational Quantum Circuits, Autoencoder, Dimensionality Reduction.
Abstract:
Quantum computing offers the potential for superior computational capabilities, particularly for data-intensive
tasks. However, the current state of quantum hardware puts heavy restrictions on input size. To address this,
hybrid transfer learning solutions have been developed, merging pre-trained classical models, capable of han-
dling extensive inputs, with variational quantum circuits. Yet, it remains unclear how much each component
– classical and quantum – contributes to the model’s results. We propose a novel hybrid architecture: instead
of utilizing a pre-trained network for compression, we employ an autoencoder to derive a compressed version
of the input data. This compressed data is then channeled through the encoder part of the autoencoder to
the quantum component. We assess our model’s classification capabilities against two state-of-the-art hybrid
transfer learning architectures, two purely classical architectures and one quantum architecture. Their accu-
racy is compared across four datasets: Banknote Authentication, Breast Cancer Wisconsin, MNIST digits, and
AudioMNIST. Our research suggests that classical components significantly influence classification in hybrid
transfer learning, a contribution often mistakenly ascribed to the quantum element. The performance of our
model aligns with that of a variational quantum circuit using amplitude embedding, positioning it as a feasible
alternative.
1 INTRODUCTION
In recent years, remarkable progress has been made
in the field of machine learning, leading to break-
throughs in various areas such as image recognition
(Dosovitskiy et al., 2021) and speech recognition
(Schneider et al., 2019). With the advancement of
technology, the scale and complexity of data continue
to increase, posing significant challenges for classi-
cal computational methods, including the curse of di-
mensionality (Bellman, 1957). In this context, the use
of quantum computers promises performance advan-
tages.
However, we are currently in the Noisy
Intermediate-Scale Quantum (NISQ) era, char-
acterized by not only a restricted number of qubits
within the quantum circuit but also limitations on
circuit depth and the quantity of operations conducted
on the qubits (Preskill, 2018).
To overcome these limitations, approaches which
combine classical neural networks (NN) with quan-
tum circuits are subject to increased research – often
combined with transfer learning. Mari et al. (Mari
et al., 2020) propose the Dressed Quantum Circuit
(DQC), where a variational quantum circuit (VQC) is
framed by a classical pre-processing NN and a classi-
cal post-processing NN. This approach is then com-
bined with different transfer learning architectures,
whereby the most appealing one according to the au-
thors is classical to quantum transfer learning. Here a
classical pre-trained NN extracts features, which are
subsequently passed to a VQC. A major problem with
a hybrid approach like this is the uncertainty of the
actual contribution of the VQC to the classification
performance and whether it provides any additional
benefit over a purely classical NN as the VQC adds
additional calculation time and complexity.
Another approach which builds on transfer learn-
ing is Sequential Quantum Enhanced Training (SE-
QUENT) (Altmann et al., 2023). Here, the post-
processing layer is omitted and the training consists
of two steps: classical and quantum. In the classical
step, the model consists of a pre-processing layer and
a surrogate classical classifier. This proxy is replaced
by a VQC after pre-training and the corresponding
quantum weights are optimized while the classical
weights are frozen. Again, the influence of the re-
spective classical and quantum parts of the model is
Kölle, M., Maurer, J., Altmann, P., Sünkel, L., Stein, J. and Linnhoff-Popien, C.
Disentangling Quantum and Classical Contributions in Hybr id Quantum Machine Learning Architectures.
DOI: 10.5220/0012381600003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 3, pages 649-656
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
649

ambiguous.
In this work, we propose an alternative approach
to address the aforementioned challenges of the NISQ
era and the limitations of the just presented models.
Instead of using transfer learning, the encoder part of
an autoencoder (AE) is utilized to compress the input
data into a lower-dimensional space. Subsequently,
this reduced input is passed to a VQC, which then
classifies the data. By using an AE for the compres-
sion, we aim to provide a more transparent under-
standing of the actual classification performance of
the VQC. The performance of our approach is then
compared to a DQC, SEQUENT, a classical NN with
the uncompressed and compressed input, and even-
tually with a pure VQC, which uses amplitude em-
bedding. The models were trained and compared
with each other on the datasets Banknote Authenti-
cation, Breast Cancer Wisconsin, MNIST, and Au-
dioMNIST – ranging from medical to image and au-
dio data. Hence, our contributions can be summarized
as follows:
• We propose an alternative approach for handling
high-dimensional input data in quantum machine
learning (QML)
• We evaluate the individual performance of classi-
cal and quantum parts in hybrid architectures
All experiment data and code can be found here
1
.
2 VARIATIONAL QUANTUM
ALGORITHMS
One of the most promising strategies for QML al-
gorithms are variational quantum algorithms (VQA)
(Cerezo et al., 2021), which can be used e.g. as clas-
sifiers (Schuld et al., 2020; Farhi and Neven, 2018).
Generally, VQAs allow us to use quantum computing
in the NISQ era by utilizing a hybrid approach of a
quantum computer, but classical optimization strate-
gies in an iterative quantum-classical feedback loop.
A parametrized quantum circuit – a VQC – is used to
change qubit states with different gate operations and
a classical computer to optimize the parameters of the
circuit. Hybrid in this context does not mean that a
combined architecture with a classical and a quantum
part is applied, but rather that solely a quantum cir-
cuit is used in combination with classical optimiza-
tion strategies. The goal is to minimize a specified
cost function in the training process by finding the
optimal parameters for the quantum circuit (Cerezo
et al., 2021).
1
https://github.com/javajonny/AE-and-VQC
3 OUR APPROACH
In this chapter, we introduce our approach. First,
we will describe the architecture of the AE and the
VQC individually. Subsequently, we will illustrate
how these two components are combined to achieve
the desired reduction in dimensionality.
3.1 Autoencoder for Dimensionality
Reduction
An AE serves as a feature extractor by encoding
inputs into a smaller yet significant representation
(Goodfellow et al., 2016), addressing VQCs’ limi-
tations in the NISQ era by minimizing input dimen-
sions to the number of output classes for VQC in-
tegration. The encoder progressively halves dimen-
sions per layer, aligning the final layer’s neurons with
output classes, using ReLU for non-linear transfor-
mations (Nair and Hinton, 2010; Krizhevsky et al.,
2017; Ramachandran et al., 2017). A Sigmoid ac-
tivation function in the last layer ensures the output
range matches pre-processed inputs. The decoder
mirrors the encoder’s structure, reconstructing inputs
from compressed data with minimal loss, and also
employs Sigmoid after the final layer for consistent
output range.
Due to its simplicity and reliably good perfor-
mance in NNs (Ramachandran et al., 2017), we use
ReLU in this AE architecture after the input layer and
between the hidden layers. After the last layer, a Sig-
moid function is used as an activation function, which
converts any input to the range [0, 1] and therefore
aligns with our pre-processed input data.
3.2 Variational Quantum Circuit
In the following, we will explain the architecture of
the proposed VQC, which acts as a classifier. It con-
sists of the three components: state preparation, en-
tangling layers, and the measurement layer.
3.2.1 State Preparation
At first, the provided input in the range [0, 1] is con-
verted to the range [−
π
2
,
π
2
] to be within the range of
typical angles used in quantum gates. Our presented
VQC then uses angle embedding to encode the fea-
ture vector of dimension N into the rotation angles of
n qubits, with N ≤ n, in the quantum Hilbert space.
In the first step, a layer of single-qubit Hadamard
gates is applied to each qubit in the circuit and hereby
transforms the basis state |0⟩ to an equal superposition
|+⟩, making the quantum state unbiased with respect
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
650

to |0⟩ and |1⟩. In the second step, a Ry-gate is ap-
plied to each qubit, which performs the actual angle
embedding.
3.2.2 Entangling Layers
To save time in the optimization and training pro-
cess, weight remapping is applied (K
¨
olle et al., 2023a;
K
¨
olle et al., 2023b). The entangling layers apply
a sequence of trainable operations to the prepared
states, whereby the general architecture is inspired
by the model circuit (Schuld et al., 2020) and the ar-
chitecture of SEQUENT. Each of the entangling lay-
ers consists of a CNOT ladder resulting in entangle-
ment between qubits, followed by Ry-gates that apply
parametrized rotations around the y-axis.
3.2.3 Measurement Layer
The last component performs the measurements of
each wire in the computational basis. More specifi-
cally, the expectation value of the Pauli-Z operator is
calculated and returned for each wire.
3.3 Integration of the Autoencoder and
the Variational Quantum Circuit
The first step consists of data pre-processing, which is
followed by the initialization and training of the AE.
We selected the Mean Square Error (MSE) as the loss
function and the Adam optimizer algorithm (Kingma
and Ba, 2015) as the optimizer. After training the AE,
only the optimized encoder is used by passing the in-
put data to it and compressing the input dimension to
the number of labels.
In order to classify the reduced features, the VQC
must then be initialized, which is again followed by
the training of the same, for which classical optimiza-
tion techniques can be used in an iterative process
with a quantum-classical feedback loop. The Cross
Entropy Loss is taken as the criterion and the Stochas-
tic Gradient Descent for the optimization. Subse-
quently, the trained VQC is used for classification
tasks. An illustration of our proposed architecture can
be found in Fig. 1.
4 EXPERIMENTAL SETUP
In this chapter, the datasets, baselines, and the hyper-
parameter optimization are presented. For the AE, the
MSE as the reconstruction loss is the main evaluation
metric, and for our model and the baselines, the accu-
racy is most relevant.
4.1 Datasets and Pre-Processing
The four different datasets Banknote Authentication
(Lohweg, 2013), Breast Cancer Wisconsin (Wolberg
et al., 1995), MNIST (LeCun et al., 1998) and Au-
dioMNIST (Becker et al., 2019) were chosen to
demonstrate the versatility of the suggested approach.
Each dataset was split into a training set, a validation
set and a test set. The input values were then nor-
malized to the range [0, 1] and the output labels were
one-hot encoded. The images of the MNIST dataset
were first flattened to one-dimensional tensors. For
AudioMNIST, the initial audio files were converted
to Mel spectrograms. These were then converted to
images and subsequently flattened.
4.2 Baselines
Our presented model will be compared against the
following baselines: a VQC with amplitude embed-
ding, a DQC, SEQUENT, a classical NN, and an AE
in combination with a classical NN.
4.2.1 Variational Quantum Classifier
(Amplitude Embedding)
The VQC with amplitude embedding just differs in
the state preparation. Amplitude embedding encodes
the features of the input vector into the amplitudes of
the qubits and makes superposition its advantage: an
exponential number of features, 2
n
, can be mapped
into the amplitude vector of n qubits (Schuld and
Petruccione, 2018). It’s important to note that, for
cases where n is less than log
2
N, where N represents
the number of classical features, padding is applied
to the original input, i.e. fill the vector with zeros.
An additional requirement is the normalization of the
padded input to unit length: x
T
padded
· x
padded
= 1.
4.2.2 Dressed Quantum Circuit
The DQC as suggested by Mari et al. (Mari et al.,
2020) consists of three parts. A classical pre-
processing part, a VQC, and a post-processing part.
The pre-processing part is a NN, consisting of one
layer, which in our case reduces the input vector di-
rectly to the number of output classes, followed by
applying a Sigmoid activation function. This reduced
input is then passed to a VQC which has the same
architecture and number of layers as our reference
model. The post-processing part also consists of one
layer and maps the data from the dimension of the
VQC width to the number of output classes. In our
case, both dimensions are the same.
Disentangling Quantum and Classical Contributions in Hybrid Quantum Machine Learning Architectures
651
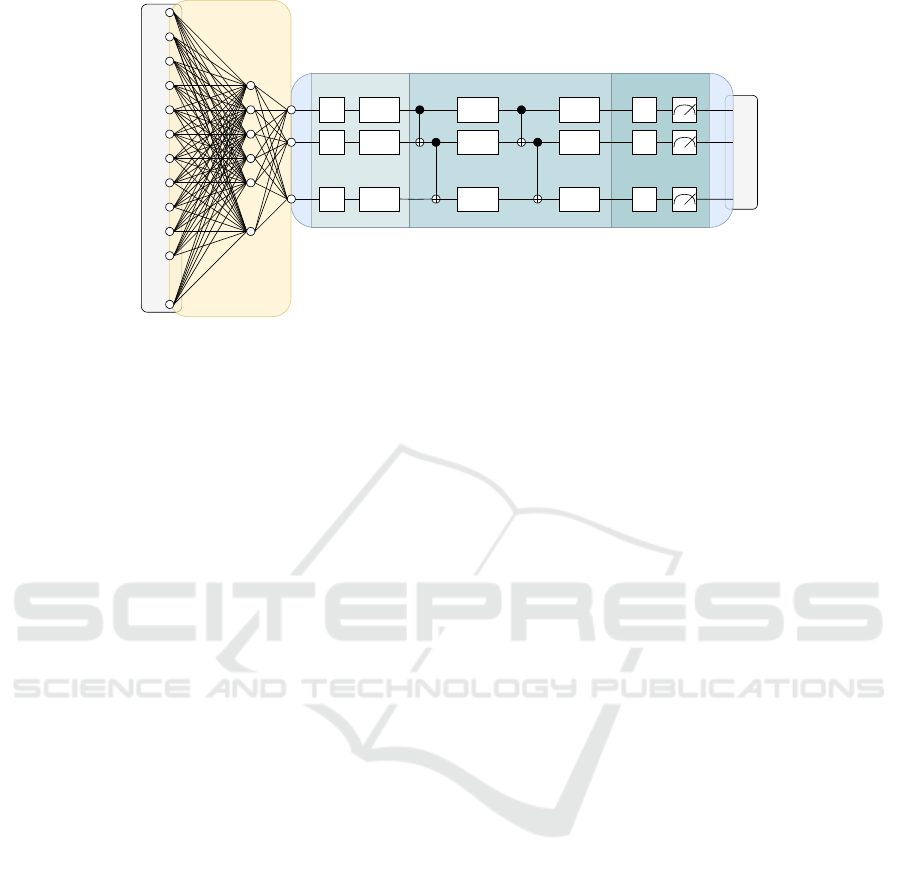
H
H
H
R
Y
(Φ
1,1
)
Z
Z
Z
𝕏
3) Measurement2)Entangling Layers1) State Preparation
ŷ
Encoder
VQC
R
Y
(z
1
)
R
Y
(z
2
)
R
Y
(z
n
)
R
Y
(Φ
2,1
)
R
Y
(Φ
n,1
)
R
Y
(Φ
2,δ
)
R
Y
(Φ
n,δ
)
R
Y
(Φ
1,δ
)
Figure 1: Architecture of our approach, which consists of an encoder and a VQC parametrized with φ. The input data is given
by X and the prediction targets by ˆy. The VQC has n qubits and consists of δ entangling layers.
The training consists of two stages. In the classical
stage, just the weights of the pre- and post-processing
are optimized. In the second stage – the quantum
stage – these classical weights are frozen and just the
parameters in the VQC are optimized.
We use this model as a baseline since the pre-
processing layer also reduces the input. Here the clas-
sical pre-processing layer already classifies. The dis-
advantage of the DQC is that the effect of the classical
and quantum parts is not separately assessable.
4.2.3 SEQUENT
The third baseline SEQUENT consists of a classical
compression layer and a classification part. The train-
ing takes place in two stages. In the classical stage,
the classification part is a classical surrogate feed for-
ward NN. We reduce the input directly to the number
of output classes in the classical compression layer
and then apply a Sigmoid activation function. This
reduced input is then passed to the second NN for
classification. The two parts are both trained and the
weights are optimized.
In the quantum training step, the classical weights
are frozen and the classical surrogate classification
network is replaced by a VQC. For the training, just
the quantum parameters are optimized. The VQC
is defined as in the DQC. Altmann et al. (Altmann
et al., 2023) argue that this two-step procedure in SE-
QUENT and DQC can be seen as transfer learning
because it is transferred from classical to quantum
weights. This model also has the same disadvantage
as the DQC in that the effect of the classical and quan-
tum components are not separately assessable.
4.2.4 Classical Feed Forward Neural Network
on Uncompressed Input
Another baseline is a classical feed forward NN,
which is introduced to verify if our model achieves
a quantum speedup. The NN for this paper consists
of one input layer, followed by a hidden layer and an
output layer. The ReLU activation function is applied
after the input layer. The number of neurons in the
hidden layer is chosen to match the number of train-
able parameters in our proposed approach.
4.2.5 Classical Feed Forward Neural Network
on Compressed Input
The last baseline is an AE, which compressed the in-
put data, in combination with a NN. The AE is the
same as for our introduced model. The classical NN
has the same architecture as the one just presented in
Section 4.2.4. The difference is the number of neu-
rons in the hidden layer – only the number of train-
able parameters of our VQC is relevant since the AE
is the same.
4.3 Optimization, Training and
Hyperparameters
The applied optimization technique was grid search
and all experiments were performed several times
for multiple seeds to obtain a more reliable and ro-
bust result. First the AE was optimized and then
the different models. The corresponding results can
be seen in Table 1 and Table 2. Python (v3.8.10)
with the frameworks PyTorch (v1.9.0+cpu) and Pen-
nyLane (v0.27.0) were used for all of our experi-
ments. For all plots in this paper, the exponential
moving average with a smoothing factor α = 0.6 was
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
652

used to display the curves.
Table 1: AE optimization with the test reconstruction loss
and 95% confidence interval for the best hyperparameter
combination per dataset..
Dataset Epochs Learning Rate Batch Size Test Loss
Banknote Authentication 500 0.1 128 0.0046 ± 0.0002
Breast Cancer Wisconsin 500 0.01 32 0.0077 ± 0.0034
MNIST 500 0.001 64 0.0198 ± 0.0012
AudioMNIST 500 0.001 128 0.0006 ± 0.0001
Table 2: Optimal learning rate for each model and dataset
obtained from the grid search.
Model AE+VQC (angle) VQC (amplitude) DQC SEQUENT AE+NN NN
Dataset
Banknote Authentication 0.01 0.01 0.1 0.1 0.1 0.1
Breast Cancer Wisconsin 0.1 0.01 0.1 0.1 0.1 0.1
MNIST 0.01 0.01 0.01 0.001 0.01 0.1
AudioMNIST 0.001 0.1 0.1 0.1 0.01 0.1
5 RESULTS
We selected optimal hyperparameters from our op-
timization process for each model and dataset (Ta-
ble 2), running ten experiments with varying seeds
(0-9). The VQC maintained six layers, and the batch
size was set at five, training for the same epochs as
optimization.
This section presents model performances per
dataset and overall results averaged across datasets.
Validation accuracies and test accuracies are shown in
Fig. 3 and Table 3, respectively. We verified the AE’s
non-classification assumption with tests. Addition-
ally, statistical analyses determined significant perfor-
mance differences between models, with follow-up
tests for pairwise analyses, assuming a significance
level of α = 0.05. Results focus on pairwise differ-
ences involving our model.
5.1 Banknote Authentication
For the Banknote Authentication dataset, the DQC
performed the best with an accuracy of 0.994, fol-
lowed by the classical NN on the uncompressed in-
put with 0.991, and SEQUENT with 0.979. The
VQC with amplitude embedding yielded an accuracy
of 0.847 and therefore performed better than our ap-
proach with an accuracy of 0.787. The classical NN
on the compressed input was the worst of the models
with 0.699.
The Friedman test indicates that the performance
differences of the approaches are significant, χ
2
(5) =
45.88, p < 0.001. The Wilcoxon signed-rank tests
show that our approach yielded significantly worse re-
sults than DQC (p < 0.001), SEQUENT (p = 0.028),
and the NN with uncompressed input (p = 0.001).
The differences of our model to the VQC with am-
plitude embedding and to the NN on the compressed
input are not significant.
5.2 Breast Cancer Wisconsin
For the Breast Cancer Wisconsin dataset, the classical
NN on the uncompressed input performed best with
an accuracy of 0.974. This performance is closely
followed by DQC and SEQUENT with an accuracy
of 0.972 for each. VQC with amplitude embedding
yielded a performance of 0.849, followed by the clas-
sical NN on the compressed input with 0.833. Our
approach achieved an accuracy of 0.816 and therefore
performed slightly worse than the VQC with ampli-
tude embedding.
The Friedman test indicates that the performance
differences of the approaches are significant, χ
2
(5) =
31.72, p < 0.001. The Wilcoxon signed-rank tests
show that our model performed significantly worse
than DQC (p = 0.042) and SEQUENT (p = 0.042).
The differences between our approach and the VQC
with amplitude embedding, the NN on the com-
pressed input, and the NN on the uncompressed input
are not significant.
5.3 MNIST
Also for dataset MNIST, the NN on the uncompressed
input obtained the best accuracy with 0.985. This is
followed by DQC with 0.896 and the classical NN
on the compressed input with 0.831. SEQUENT
achieved an accuracy of 0.508, marginally better than
our approach with 0.507. The worst accuracy of 0.444
was reached by the VQC with amplitude embedding.
The repeated measures ANOVA with
Greenhouse-Geiser corrected values (ε < 0.75)
indicates that there is a statistically significant
performance difference between the approaches,
F(2.77, 25.92) = 260.67, p < 0.001. Our model per-
formed significantly worse than DQC (p < 0.001),
the classical NN on the compressed input (p < 0.001),
and the NN on the uncompressed input (p < 0.001).
The difference between our approach and the VQC
with amplitude embedding and between SEQUENT
is not significant.
5.4 AudioMNIST
For the AudioMNIST dataset, the classical NN on the
uncompressed input performed the best with an ac-
curacy of 0.879, followed by SEQUENT with 0.385
Disentangling Quantum and Classical Contributions in Hybrid Quantum Machine Learning Architectures
653

and DQC with 0.356. The classical NN on the com-
pressed input achieved an accuracy of 0.298. The
VQC with amplitude embedding yielded a result of
0.257 and was therefore better than our approach with
an accuracy of 0.240. For DQC and SEQUENT, it
can be seen in Fig. 2 that the classical training step
achieved validation accuracies of about 0.8. In the
quantum training step, first an expected drop occurred
and then only a slight improvement of accuracy can
be observed visually for SEQUENT. The validation
accuracy of DQC deteriorates.
The Friedman test indicates that the performance
differences between the approaches are significant,
χ
2
(5) = 33.03, p < 0.001. The Wilcoxon signed-rank
tests show that our model performed significantly
worse than SEQUENT (p = 0.028) and the classi-
cal NN on the uncompressed input (p < 0.001). No
statistically significant difference can be obtained be-
tween our model and VQC with amplitude embed-
ding, DQC, and the classical NN on the compressed
input.
Figure 2: Validation accuracies for AudioMNIST. The clas-
sical and quantum validation accuracies are shown for the
two-step hybrid transfer learning of DQC and SEQUENT.
5.5 Overall Comparison
Averaged over all datasets, the classical NN on the
uncompressed input achieved an accuracy of 0.957,
followed by the DQC with 0.805 and SEQUENT with
0.711. The NN on the compressed input gives an ac-
curacy of 0.665. The VQC with amplitude embedding
had a marginally better performance with 0.599 than
our approach with 0.588.
The Kruskal-Wallis test indicates that the perfor-
mance differences of the approaches are significant,
χ
2
(5) = 80.75, p < 0.001. The Mann-Whitney tests
show that our approach performed significantly worse
than DQC (p < 0.001) and the NN on the uncom-
pressed input (p < 0.001). The observed difference
between our approach and SEQUENT falls just short
of achieving statistical significance (p = 0.052). Be-
tween our approach and the VQC with amplitude em-
bedding and the NN on the compressed input no sig-
nificant difference can be obtained.
5.6 Discussion
The NN on the uncompressed input, DQC, and SE-
QUENT achieved better results than our approach,
where the former was superior. Across DQC, SE-
QUENT, and our model the VQC shared the same ar-
chitecture and numbers of layers. In contrast to DQC
and SEQUENT, our compression part (AE) did not
classify which can be seen in Table 3. This leads to
the assumption that the classical compression layer
plays a pivotal role in the overall performance of these
hybrid transfer learning approaches and the role of the
VQC itself may be questioned. This assumption is
also supported by Fig. 2, which shows the respective
validation accuracies for the two-stage training pro-
cess of DQC and SEQUENT, exemplary for AudioM-
NIST. Already after the classical training step, a very
high validation accuracy can be seen for both models
over both datasets. After this training stage, a drop
in the accuracy can be observed because the quantum
weights were randomly initialized. The validation ac-
curacy subsequently did not increase any further in
the quantum training step, where just the weights of
the VQC were optimized – the validation accuracies
for DQC and SEQUENT after the complete training
are worse than the accuracies after the classical train-
ing stage. A possible explanation could be that the
extracted features of the pre-processing or compres-
sion layer do not contain enough information for fur-
ther classification, or that the VQC lacks the required
power or complexity to maintain the desired results.
The comparison between the VQC with amplitude
embedding and our model did not show any statisti-
cally significant difference in performance – making
our approach a valid alternative. To test the perfor-
mance of the AE, a classical NN that uses the reduced
input of the AE was introduced. This model achieved
good results for Breast Cancer Wisconsin and for
MNIST. However, especially for AudioMNIST an ac-
curacy of just 0.298 was achieved – compared to the
NN on the uncompressed input with 0.879. This sug-
gests that the proposed AE may not have been able
to adequately extract the essential information within
the latent space. It is hence possible that the architec-
ture is not able to adapt well to specific characteristics
of a dataset. Further research is needed to enhance
the effectiveness of the AE and come up with spe-
cialized architectures for datasets. Additionally, joint
training of the AE and the VQC in contrast to sequen-
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
654
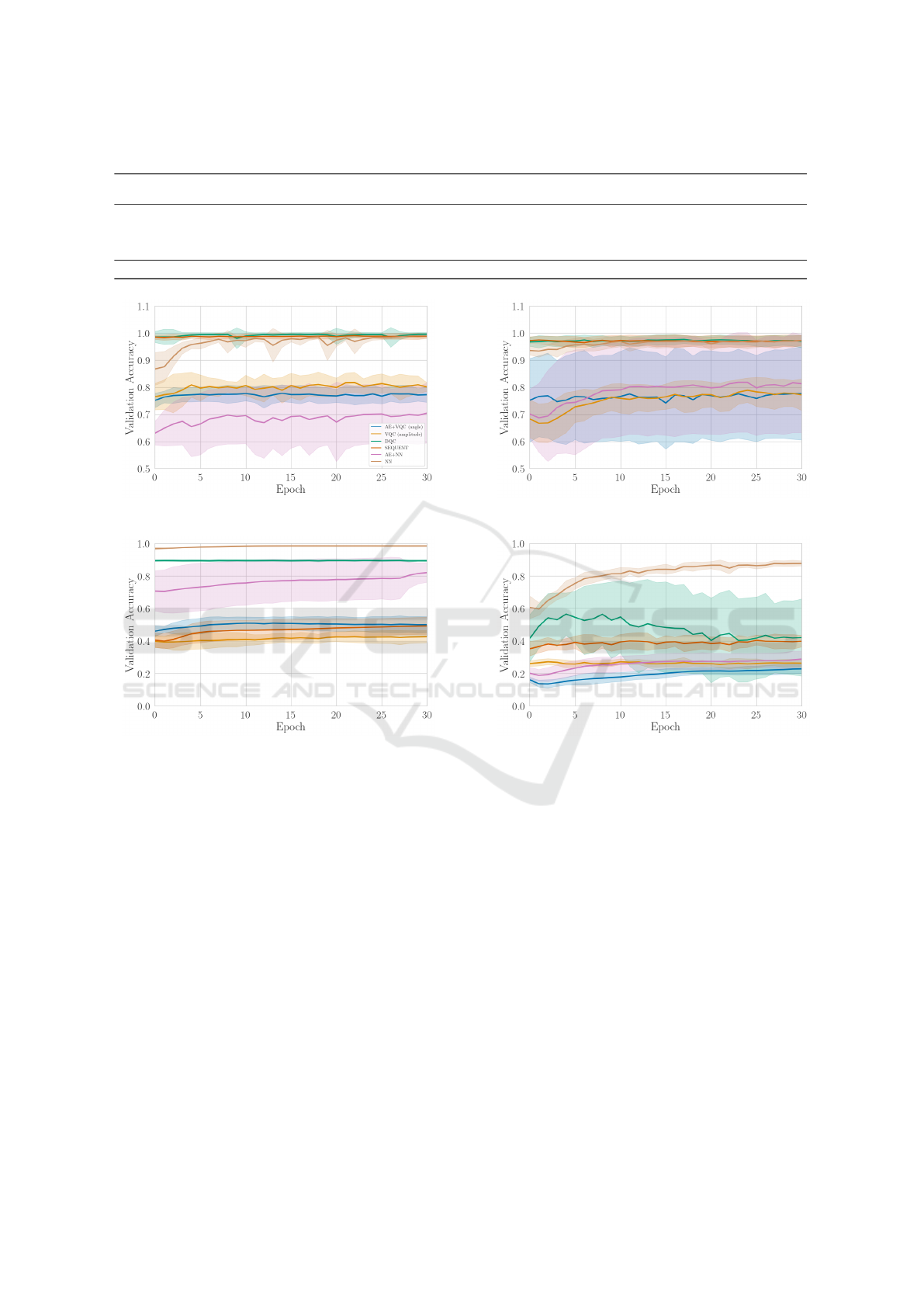
Table 3: Test accuracy and 95% confidence interval for all models.
Model AE+VQC (angle) VQC (amplitude) DQC SEQUENT AE+NN NN AE
Dataset
Banknote Authentication 0.787± 0.023 0.847 ± 0.036 0.994 ± 0.004 0.979 ± 0.009 0.699 ± 0.084 0.991 ± 0.008 0.172 ± 0.030
Breast Cancer Wisconsin 0.816 ± 0.114 0.849 ± 0.021 0.972 ± 0.018 0.972 ± 0.016 0.833 ± 0.121 0.974 ± 0.022 0.016 ±0.024
MNIST 0.507 ± 0.036 0.444 ± 0.033 0.896 ± 0.005 0.508 ± 0.046 0.831 ± 0.042 0.985 ± 0.001 < 0.001± < 0.001
AudioMNIST 0.240 ± 0.028 0.257 ± 0.025 0.356 ± 0.188 0.385 ± 0.036 0.298 ± 0.028 0.879 ± 0.039 < 0.001± < 0.001
Average 0.588 ± 0.430 0.599 ± 0.473 0.805 ± 0.480 0.711 ± 0.492 0.665 ± 0.402 0.957 ± 0.084 0.047 ± 0.133
(a) Banknote Authentication (b) Breast Cancer Wisconsin
(c) MNIST (d) AudioMNIST
Figure 3: Plots for the validation accuracies for all models over the first 30 epochs. The datasets Banknote Authentication,
Breast Cancer Wisconsin, MNIST, and AudioMNIST are displayed.
tial training should be considered. Interestingly, the
other models (except for the NN on the uncompressed
input) also did not exceed 40% accuracy either. This
indicates that the pre-processing of the AudioMNIST
dataset may not have been effective. Improving this
process could also be a promising direction for future
research.
Another limitation of the AE in our approach is
the additional effort for the training of the AE, es-
pecially compared to the VQC with amplitude em-
bedding. It is also worthwhile to consider other data
compression techniques, e.g. the principal component
analysis. As already mentioned, the architecture of
our VQC could pose a limitation. It can be benefi-
cial to allow for rotations across all three axes and to
increase the number of layers. Other techniques to
find the optimal hyperparameters of a model should
be considered.
6 CONCLUSION
We introduced an approach to tackle the issues of
the current NISQ era by using the encoder of an AE
to reduce the input dimension of a dataset. This
compressed input is fed to a VQC, which uses an-
gle embedding to map the data from the classical
to the Hilbert space. The performance was mea-
sured across the four datasets Banknote Authentica-
tion, Breast Cancer Wisconsin, MNIST, and AudioM-
NIST – ranging from medical to image and audio
samples. We then compared our model to other de-
signs: SEQUENT and DQC from the topic of clas-
sical to quantum transfer learning, VQC with ampli-
Disentangling Quantum and Classical Contributions in Hybrid Quantum Machine Learning Architectures
655

tude embedding as a purely quantum architecture and
a purely classical NN on the compressed and uncom-
pressed input.
Our results suggest that the classification perfor-
mance in hybrid transfer learning is mainly influenced
by the classifying compression layer and that the ac-
tual contribution of the VQC may be doubted. Ad-
ditionally, these approaches yield better results than
models where solely the VQC classifies.
Even though our model performs worse on aver-
age than the hybrid transfer learning models DQC and
SEQUENT, it allows for a more transparent and inter-
pretable analysis of the quantum circuit’s role in the
machine learning task because of the clear distinction
between the components. Additionally, our research
indicates that our approach with angle embedding on
the compressed input is a valid alternative to a VQC
with amplitude embedding on the original input.
ACKNOWLEDGEMENTS
This work is part of the Munich Quantum Valley,
which is supported by the Bavarian state government
with funds from the Hightech Agenda Bayern Plus.
This paper was partially funded by the German Fed-
eral Ministry for Economic Affairs and Climate Ac-
tion through the funding program ”Quantum Comput-
ing – Applications for the industry” based on the al-
lowance ”Development of digital technologies” (con-
tract number: 01MQ22008A).
REFERENCES
Altmann, P., S
¨
unkel, L., Stein, J., M
¨
uller, T., Roch, C.,
and Linnhoff-Popien, C. (2023). SEQUENT: Towards
Traceable Quantum Machine Learning using Sequen-
tial Quantum Enhanced Training. arXiv:2301.02601
[quant-ph].
Becker, S., Ackermann, M., Lapuschkin, S., M
¨
uller, K.-
R., and Samek, W. (2019). Interpreting and Explain-
ing Deep Neural Networks for Classification of Audio
Signals. arXiv:1807.03418 [cs, eess].
Bellman, R. (1957). Dynamic Programming. Princeton
University Press, Princeton, NJ.
Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C.,
Endo, S., Fujii, K., McClean, J. R., Mitarai, K.,
Yuan, X., Cincio, L., and Coles, P. J. (2021). Varia-
tional Quantum Algorithms. Nature Reviews Physics,
3(9):625–644. arXiv:2012.09265 [quant-ph, stat].
Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,
D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,
M., Heigold, G., Gelly, S., Uszkoreit, J., and Houlsby,
N. (2021). An Image is Worth 16x16 Words: Trans-
formers for Image Recognition at Scale. In Interna-
tional Conference on Learning Representations.
Farhi, E. and Neven, H. (2018). Classification with
Quantum Neural Networks on Near Term Processors.
arXiv:1802.06002 [quant-ph].
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. MIT Press.
Kingma, D. P. and Ba, J. (2015). Adam: A Method for
Stochastic Optimization. In Bengio, Y. and LeCun,
Y., editors, 3rd International Conference on Learn-
ing Representations, ICLR 2015, San Diego, CA, USA,
May 7-9, 2015, Conference Track Proceedings.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). Im-
ageNet classification with deep convolutional neural
networks. Communications of the ACM, 60(6):84–90.
K
¨
olle, M., Giovagnoli, A., Stein, J., Mansky, M. B., Hager,
J., and Linnhoff-Popien, C. (2023a). Improving Con-
vergence for Quantum Variational Classifiers using
Weight Re-Mapping. arXiv:2212.14807 [quant-ph].
K
¨
olle, M., Giovagnoli, A., Stein, J., Mansky, M. B., Hager,
J., Rohe, T., M
¨
uller, R., and Linnhoff-Popien, C.
(2023b). Weight Re-Mapping for Variational Quan-
tum Algorithms. arXiv:2306.05776 [quant-ph].
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Lohweg, V. (2013). banknote authentication. Published:
UCI Machine Learning Repository.
Mari, A., Bromley, T. R., Izaac, J., Schuld, M., and Killo-
ran, N. (2020). Transfer learning in hybrid classical-
quantum neural networks. Quantum, 4:340.
Nair, V. and Hinton, G. E. (2010). Rectified Linear Units
Improve Restricted Boltzmann Machines. In Proceed-
ings of the 27th International Conference on Interna-
tional Conference on Machine Learning, ICML’10,
pages 807–814, Madison, WI, USA. Omnipress.
Preskill, J. (2018). Quantum Computing in the NISQ
era and beyond. Quantum, 2:79. arXiv:1801.00862
[cond-mat, physics:quant-ph].
Ramachandran, P., Zoph, B., and Le, Q. V. (2017). Search-
ing for Activation Functions. arXiv:1710.05941 [cs].
Schneider, S., Baevski, A., Collobert, R., and Auli, M.
(2019). wav2vec: Unsupervised Pre-Training for
Speech Recognition. In Interspeech 2019, pages
3465–3469. ISCA.
Schuld, M., Bocharov, A., Svore, K., and Wiebe, N. (2020).
Circuit-centric quantum classifiers. Physical Review
A, 101(3):032308. arXiv:1804.00633 [quant-ph].
Schuld, M. and Petruccione, F. (2018). Supervised Learn-
ing with Quantum Computers. Quantum Science and
Technology. Springer Cham, 1 edition.
Wolberg, W. H., Mangasarian, O. L., and W. Nick Street
(1995). Breast Cancer Wisconsin (Diagnostic). Pub-
lished: UCI Machine Learning Repository.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
656
