Process-Aware Analysis of Treatment Paths in Heart Failure Patients:

A Case Study

Harry H. Beyel

1 a

, Marlo Verket

2 b

, Viki Peeva

1 c

, Christian Rennert

1 d

, Marco Pegoraro

1 e

Katharina Sch

utt

2 f

, Wil M. P. van der Aalst

1 g

and Nikolaus Marx

2 h

Chair of Process and Data Science (PADS), RWTH Aachen University, Aachen, Germany

Department of Internal Medicine I, RWTH Aachen University Hospital, Aachen, Germany

Keywords:

Process Mining, Healthcare, Heart Failure, Patient Cohort Analysis.

Abstract:

Process mining in healthcare presents a range of challenges when working with different types of data within

the healthcare domain. There is high diversity considering the variety of data collected from healthcare pro-

cesses: operational processes given by claims data, a collection of events during surgery, data related to

pre-operative and post-operative care, and high-level data collections based on regular ambulant visits with no

apparent events. In this case study, a data set from the last category is analyzed. We apply process-mining

techniques on sparse patient heart failure data and investigate whether an information gain towards several

research questions is achievable. Here, available data are transformed into an event log format, and process

discovery and conformance checking are applied. Additionally, patients are split into different cohorts based

on comorbidities, such as diabetes and chronic kidney disease, and multiple statistics are compared between

the cohorts. Conclusively, we apply decision mining to determine whether a patient will have a cardiovascular

outcome and whether a patient will die.

1 INTRODUCTION

Heart Failure (HF) is a complex chronic disease, and

the prevalence of HF continues to increase globally.

HF is one of the main causes of hospitalization for

subjects aged 65 years or older, resulting in high costs

and a major social impact. The management of multi-

modal treatment for patients with chronic HF is com-

plex. Despite good treatment, patients with HF still

have a poor prognosis, and about 15% to 25% die

within the ﬁrst ﬁve years after their diagnosis. In

the presence of comorbidities, such as diabetes and

chronic kidney disease, this rate rises at least by a 2-

fold factor to about 50%. (Romero-Gonz

alez et al.,

2020). With an abundance of clinical trials focus-

ing on treatment strategies to reduce Cardiovascular

https://orcid.org/0000-0002-6541-3848

https://orcid.org/0000-0002-3361-3722

https://orcid.org/0000-0001-7144-5136

https://orcid.org/0000-0003-4614-6171

https://orcid.org/0000-0002-8997-7517

https://orcid.org/0000-0002-0162-5219

https://orcid.org/0000-0002-0955-6940

https://orcid.org/0000-0001-6141-634X

Outcomes (COs), such as Hospitalization for Heart

Failure (HHF) and cardiovascular or all-cause mor-

tality (Sattar et al., 2021; Zelniker et al., 2019), it is

still hard to predict which patients respond positively

to treatment strategies and which do not. A possible

solution to gain insights into the treatment responses

of patients when data are recorded is process mining.

The process-mining discipline can generally be

split into three main areas: process discovery, confor-

mance checking, and process enhancement (van der

Aalst, 2016). Process-discovery techniques extract

a comprehensible process model that represents the

underlying behavior in the data. Conformance-

checking techniques quantify how well a process

model represents the behavior in the recorded data.

Process-enhancement techniques can decorate a pro-

cess model with additional information and insights

about the process, e.g., about time, frequency, and

explanations of decision points. While the ﬁeld of

process mining originated in the context of business

processes, it has been applied with remarkable suc-

cess to a number of other disciplines in recent years.

A prominent example of such disciplines is health-

care science (Mans et al., 2015; Munoz-Gama et al.,

2022). More speciﬁcally, the last few years have seen

506

Beyel, H., Verket, M., Peeva, V., Rennert, C., Pegoraro, M., Schütt, K., van der Aalst, W. and Marx, N.

Process-Aware Analysis of Treatment Paths in Heart Failure Patients: A Case Study.

DOI: 10.5220/0012392600003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 2, pages 506-515

ISBN: 978-989-758-688-0; ISSN: 2184-4305

Patient data

Event log

Process model

Differences in activity

frequencies

Cohort logs

Preprocessing and

transformation

Decision mining

Domain knowledge

Figure 1: Overview of our work.

a surge of process mining analyses of medical data,

propelled by advancements in healthcare information

systems and by the ever-increasing demand for data-

centric solutions to aid in the management of critical

situations such as epidemics (Pegoraro et al., 2021;

Benevento et al., 2022). Applications include the

analysis of clinical pathways, patient behavior, and

personnel tasks for a large array of diseases (Guzzo

et al., 2022).

In this paper, we contribute to the literature on pro-

cess mining in cardiology by reporting our ﬁndings

on data recorded for patients with HF treated within

the Aachen Longitudinal Heart Failure and Diabetes

Registry Study (ALIDIA). An overview of our work

is shown in Figure 1. First, we transform patient data

into an event log suitable for process mining. Second,

we discover a collection of patients’ treatment paths

and decide on a representative process model. Third,

we compare different subgroups of patients concern-

ing the frequency of events. Fourth, we discover rea-

sons for certain decisions in our process model.

The remainder of this paper is organized as fol-

lows. In Section 2, we present related work to this

study. In Section 3, we lay down preliminary con-

cepts. Subsequently, in Section 4, we present the col-

lected data. In Section 5, we preprocess the available

data to select the information we consider in the re-

mainder and transform the resulting data into an event

log suitable for process-mining techniques. Section 6

analyzes the treatment paths using alignment-based

conformance checking. In Section 7, we split the pa-

tients into different cohorts, considering whether they

suffer from diabetes or chronic kidney disease, and

analyze the similarities and dissimilarities between

the cohorts. Section 8 presents an analysis of the deci-

sion points in the treatment process. We report our re-

sults together with the challenges we faced analyzing

this type of data. Section 9 concludes the paper, sum-

marizing our ﬁndings, pointing out limitations, and

providing points for future work.

2 RELATED WORK

In (de Vries et al., 2017), a case study is pre-

sented showing how to apply process mining to

electronic-medical-record data when dealing with

sepsis. In (Back et al., 2020), patient ﬂows in a sur-

gical ward are mined. The identiﬁcation of disease

trajectory models is investigated in (Kusuma et al.,

2020). The authors apply transformations to an event

log to later apply process-mining tools. Also, process

mining has a substantial history in cardiology. Early

attempts (Mans et al., 2008) compared process mod-

els for the treatment process of stroke in different hos-

pitals and showed a process model for the pre-hospital

process.

There has also been a focus on developing mod-

els for HF. Frameworks for the 30-day re-admission

risk management and prediction of HF using ma-

chine learning, Divide-n-Discover, and applying data

mining techniques have been explored and applied.

(Kerexeta et al., 2018; Roy and Chin, 2014; Chin

et al., 2014). Additionally, a regression model for

time series using hospital admissions was developed

to understand better the impact of environmental fac-

tors, such as weather and air quality, from an open

dataset on HF (Artola et al., 2019). Other factors in

a patient’s therapy, like the feasibility and usability

of devices, have been summarized for telemedicine

(Zweth et al., 2018). Other systems, like Computer

Interpretable Guidelines, have been used to model

when a patient, during treatment of a comorbidity,

develops HF (Bottrighi et al., 2018). Furthermore,

the TranSMART tool and the Alfresco platform have

been applied to a workﬂow from patient data collec-

tion to data processing in identifying therapeutic tar-

gets for HF with preserved ejection fraction (Almeida

et al., 2020). There are several approaches in manag-

ing HF, in particular within the timeframe of 30-day

re-admission or providing frameworks for biomark-

ers. This paper aims to ﬁll the gap by attempting to

use different factors in the patient pathways, including

diabetes and chronic kidney disease as comorbidities.

Our goal is to kickstart an underexplored research di-

rection: the analysis of COs in heart failure patients

through a combination of process-aware and statisti-

cal analysis techniques, with the objective of under-

standing (and eventually preventing) the insurgence

of cardiovascular outcomes.

3 PRELIMINARIES

In this section, we formally introduce concepts that

are the basics of the techniques we introduce later.

Process-Aware Analysis of Treatment Paths in Heart Failure Patients: A Case Study

507

Table 1: Example event log.

RowID Case Activity Timestamp

1 1337 a 2023-01-21

2 1337 b 2023-02-15

3 1337 c 2023-05-05

4 1338 d 2023-06-01

5 1338 e 2023-06-19

6 1338 c 2023-07-20

Given a set X , a sequence σ ∈ X

∗

assigns an enumer-

ation to elements of the set. We denote this with σ =

⟨σ

, . . . , σ

⟩. In the remainder, we refer with σ

to the

sequence’s i-th element.To concatenate sequences, we

use the symbol ·, i.e., ⟨σ

, . . . , σ

⟩ · ⟨σ

′

, . . . , σ

′

⟩ =

⟨σ

, . . . , σ

, σ

′

, . . . , σ

′

⟩ for n ∈ N and m ∈ N. Given

a set X , B(X) denotes the set of all multisets over set

X. For example, if X = {x, y, z}, a possible bag is

[x, x, y] = [x

, y]. To combine multisets, we use ⊎, for

instance, [x, y] ⊎ [x, z] = [x, y, x, z] = [x

, y, z].

To apply process-mining techniques, we need an

event log. An event log consists of at least three

mandatory attributes: case identiﬁer, activty name,

and timestamp. We use U

case

as the universe of case

identiﬁers, U

act

as the universe of activity names, and

time

as the universe of timestamps. The following

deﬁnes an event log.

Deﬁnition 1 (Event Log). U

is the universe of

events. e ∈ U

is an event, π

act

(e) ∈ U

act

is the

activity of e, π

case

(e) ∈ U

case

is the case of e, and

time

(e) ∈ U

time

the timestamp of e. An event log

L ⊆ U

is a set of events. For simplicity, we assume

that other, here non-deﬁned, functions can be applied

to the event, resulting in more attributes.

An example event log is displayed in Table 1.

In the remainder of this work, we use Petri nets as

process model representations. Introduction to them

is provided in (van der Aalst, 2016; Reisig, 1985).

In this work, we refer to τ-transitions, respectively,

silent transitions. In Petri nets, silent transitions pro-

vide a ﬂexible and expressive mechanism for model-

ing various aspects of process behavior. They enable

the representation of internal actions, improving Petri

nets’ modeling capabilities. Silent transitions can act

as synchronization points, waiting for speciﬁc condi-

tions to be met before allowing subsequent transitions

to ﬁre. In our ﬁgures, they are represented as black

transitions. Besides, we use conformance-checking

techniques to measure a process model’s ﬁtness, pre-

cision, and generalization scores. (Carmona et al.,

2018) provide an introduction to these measurements.

4 DATA COLLECTION AND

PREPARATION

The data we analyze in this work consists of HF pa-

tients treated in the Aachen Longitudinal Heart Fail-

ure and Diabetes Registry Study (ALIDIA) between

April 2019 and May 2023. The original data are in

a tabular format and contain two disjoint sets of data

records for each patient: outpatient clinical visit infor-

mation and cardiovascular outcome. We joined these

two sets, resulting in one concise set capturing the

patient data. We deﬁne the following Cardiovascular

Outcomes (COs):

• Hospitalization for heart failure: The day of hos-

pitalization is deﬁned as when the patient is ad-

mitted to the emergency room due to clinical man-

ifestations of HF (new or worsening) (HF).

• Hospitalization for myocardial infarction: The

day of hospitalization is deﬁned as when the pa-

tient is admitted to the emergency room for non-

ST-elevation myocardial infarction or ST-segment

elevation myocardial infarction (MI).

• Hospitalization for stroke: The day of hospitaliza-

tion is deﬁned as when the patient is admitted to

the emergency room for a transient ischemic at-

tack or stroke (Stroke).

• Hospitalization for cardiovascular diseases: Hos-

pitalisations that were attributed to a cardiovascu-

lar disease (CV) cause and not attributed to other

previous categories were deﬁned as hospitaliza-

tion for CV diseases (CV).

• Death due to any cause: All deaths not attributed

to the category of HF were deﬁned as death due to

any cause (Death AnyCause).

• Death due to heart failure: When the death oc-

curred in the context of decompensation HF, this

death was deﬁned as due to HF (Death HF).

Moreover, the patient data captures medication in-

formation. To evaluate the changes in HF medica-

tion, the different substances within a drug class were

converted to unity value, using the HF guidelines

from the European Society of Cardiology (McDon-

agh et al., 2021). In the following, we describe the

features of the patient data in more detail. U

PatID

the universe of patient ids.

• PatID: unique identiﬁcation number allocated to a

speciﬁc patient (U

PatID

• LVEF: left ventricular ejection fraction is the per-

centage of the amount of blood in the left ventricle

pumped with each contraction.

HEALTHINF 2024 - 17th International Conference on Health Informatics

508

• HFrEF: HF with reduced ejection fraction is de-

ﬁned as LVEF ≤ 40% .

• HFmrEF: HF with mildly reduced ejection frac-

tion is deﬁned as LVEF between 40% and 49%.

• HFpEF: HF with preserved ejection fraction is

deﬁned as LVEF ≥ 50% and symptoms and signs

of HF.

• Weight: biomarker that provides an alert for wors-

ening HF, when rapid weight gain is present.

• HF diagnosis: the year the patient is diagnosed

with HF.

• NT pro-BNP: biomarker for diagnosing and sever-

ity of HF.

• Diabetes: underlying disease that may augment

CO.

• CKD: chronic kidney disease, an additional un-

derlying disease that may augment CO.

• Outcome: COs as deﬁned above, covering HF,

stroke, MI, CV, death due to any cause, and death

due to HF.

• WBC: white blood cell count, a biomarker for in-

dicating an infection or inﬂammation.

• hsTNT: high-sensitivity cardiac troponin T, a

biomarker for myocardial injury, including is-

chemia.

• IL-6: Interleukin-6 is a biomarker for inﬂamma-

tory response and is associated with the risk for

mortality and cardiovascular outcomes.

• Urea: a biomarker that indicates the kidney func-

tionality.

• Beta-blocker: HF medication to reduce mortality

and morbidity for patients with HF.

• ACE-I/ARNI: angiotensin-converting enzyme in-

hibitors (ACE-I) or an angiotensin receptor-

neprilysin inhibitor (ARNI), HF medication to re-

duce the risks of morbidity and mortality.

• SGLT-2: sodium-glucose co-transporter 2 in-

hibitors, HF medication to reduce HF-related hos-

pitalization and CV death.

• MRA: mineralocorticoid receptor antagonists, HF

medication to reduce mortality and the risk of hos-

pitalization for HF.

• Time: timestamp of record (U

time

)

The collected data consist of 240 different patients

and 1000 instance. An example of patient data is de-

picted in Table 2. Each row corresponds to a patient

data instance (U

). An absence of information is de-

noted with ⊥.

A formal representation of patient data is pre-

sented in the following.

Deﬁnition 2 (Patient Data and Sequences). U

the universe of patient data instances. d ∈ U

is a patient data instance. The previously intro-

duced domains and meaning of attributes hold, i.e.,

PatID

(d) ∈ U

PatID

is the patient id of d and π

time

(d) ∈

time

the timestamp of d. Additionally, π

LV EF

(d) is

the LVEF value of d, π

HFrEF

(d) signals if the instance

d is related to an HFrEF patient, etc. Patient data

P ⊆ U

is a set of patient data instances. The data

for a patient are stored in P

= {p ∈ P | π

PatID

(p) =

id}. seq

is the sequential representation of P

such

that for seq

= ⟨d

, . . . , d

⟩ of length n, the elements

∈ P

, . . . , d

∈ P

are sorted by timestamp from

earliest to latest, i.e., π

time

) ≤ ··· ≤ π

time

5 DATA PREPROCESSING AND

TRANSFORMATION

To make the data accessible for process mining, we

need to preprocess and transform the data. We pre-

process the data by abstracting the level of detail

and deriving new attributes based on existing ones.

For example, medication dose changes might be ab-

stracted to medication increase and medication de-

crease, or the values binned in several categories.

Similarly, the same procedure is done for measured

lab values. After pre-processing the data, we convert

our data to an event log to apply process-mining tech-

niques. This implies identifying case, activity, and

timestamp attributes. Concerning cases, we use the

provided patient id attribute. As a result, each case re-

ﬂects the treatment path of a patient. As timestamps,

we use the ones provided in the patient data. Deter-

mining the activity attribute is more challenging since

it is the only one of the primary attributes (case, ac-

tivity, timestamp), for which there is a multitude of

options to choose from, and choosing one or another

would result in different study focuses. In this work,

with the help of domain experts, we decided to focus

on a speciﬁc subset of COs. The transformations we

present in the rest of this section are made with this

goal in mind. We applied a rule-based approach. If a

datum in the patient data consists of a CO, we use the

outcome as an activity. Otherwise, for each patient,

we check whether a visit happens before or after such

an outcome. If it happens before, we assign it as activ-

ity “Visit before CO”; otherwise, we assign “Visit af-

ter CO”. We use the previously introduced sequences

(seq

) for the transformation process. First, we split

the sequences into two halves: the part before the ﬁrst

CO and the part containing the ﬁrst CO.

Process-Aware Analysis of Treatment Paths in Heart Failure Patients: A Case Study

509

Table 2: Example record of patient data.

RowID PatID LVEF HFrEF HFmrEF HFpEF Weight HF diagnosis NT pro-BNP Diabetes CKD Outcome WBC hsTNT IL-6 Urea Beta-Blocker ACE-I/ARNI SGLT-2 MRA Timestamp

1 007 50 0 0 1 80 2017 750.5 1 ⊥ ⊥ ⊥ 24.9 10.5 38 100 50 10 12.5 2023-02-20

2 007 50 0 0 1 80 2017 750.5 1 ⊥ HF ⊥ 24.9 10.5 38 100 50 10 12.5 2023-02-21

3 007 50 0 0 1 80 2017 750.5 1 ⊥ Death HF ⊥ 24.9 10.5 38 100 50 10 12.5 2023-02-20

4 008 10 1 0 0 99 2012 ⊥ ⊥ ⊥ ⊥ 10.2 24.9 10.5 ⊥ ⊥ ⊥ 15 ⊥ 2023-02-20

Deﬁnition 3 (Sequence Before and After Outcome).

Let P ⊆ U

be a set of patient data instances and P

and seq

be deﬁned as before. seq

= pre

· post

with seq

= ⟨d

, . . . , d

⟩ · ⟨d

i+1

, . . . , d

⟩, such that for

all d

∈ pre

, j ∈ {1, . . . , i}, π

Outcome

) = ⊥ and

Outcome

i+1

) ̸= ⊥.

For our example data (Table 2), there are the fol-

lowing sequences: pre

007

= ⟨1⟩, post

007

= ⟨2, 3⟩,

pre

008

= ⟨4⟩, post

008

= ⟨ ⟩.

In the following, we transform each datum in a

sequence before a CO into an event.

Deﬁnition 4 (Transformation Before Outcome). Let

P ⊆ U

be a set of patient data instances and P

and seq

and pre

be deﬁned as before. Let L ⊆ U

be an event log. There exists a function trans

pre

that

maps each element of the sequence pre

of length n,

∈ pre

, i ∈ {1, . . . , n}, to an event such that the

following holds:

• π

PatID

) = π

case

(trans

pre

))

• “Visit before CO” = π

act

(trans

pre

))

• π

time

) = π

time

(trans

pre

))

Moreover, the values for the different patient data at-

tributes for all d

∈ pre

are the same for the mapped

event.

Finally, we transform each datum in a sequence

after a CO into an event.

Deﬁnition 5 (Transformation After Outcome). Let

P ⊆ U

be a set of patient data instances and P

and seq

and post

be deﬁned as before. Let L ⊆ U

be an event log. There exists a function trans

post

that

maps each element of the sequence post

of length n,

∈ post

, i ∈ {1, . . . , n}, to an event such that the

following holds:

• π

PatID

) = π

case

(trans

post

))

• “Visit after CO” = π

act

(trans

post

)) if

Outcome

) = ⊥

• π

Outcome

) = π

act

(trans

post

)) if

Outcome

) ̸= ⊥

• π

time

) = π

time

(trans

post

))

Moreover, the values for the different patient data at-

tributes for all d

∈ post

are the same for the mapped

event.

We apply these steps to all patients contained in

the data. The result of applying these steps to the pa-

tient data portrayed in Table 2 is displayed in Table 3.

Visit before CO CV

Death_AnyCause

Visit after CO

Visit before CO

Visit after CO

Figure 2: De-facto model of treatment paths.

Applying these steps to our patient data leads to

an event log with 240 cases (i.e., patients) and 1000

events.

6 OBTAINING TREATMENT

PATHS

In this section, we investigate the nature and be-

havior of the treatment paths of patients obtained

in the previous section. To observe the treatment

paths, we use process models, in particular, the afore-

mentioned Petri nets. To validate whether the re-

ceived process models are representative and the data

is compliant, we apply conformance-checking tech-

niques. In particular, we measure ﬁtness by utiliz-

ing alignments with a standard cost function (Adri-

ansyah et al., 2011), computed precision (Adriansyah

et al., 2015) and generalization (Buijs et al., 2014)

scores, as well as the simplicity of the model (Weerdt

et al., 2010). In addition, we computed F1 scores

using the obtained ﬁtness and precision scores. To

receive process models, we applied several process

discovery algorithms to the transformed event log,

all implemented in ProM

. Moreover, we consulted

domain experts to construct a de-jure model. The

conformance-checking results are shown in Table 4.

As denoted, the process-discovery algorithms

yield various results. Four models have a ﬁtness score

of 1.0, and six models have a precision score of 1.0.

The best generalization score is 0.89, achieved by six

models. One model has a simplicity score of 1.0, far

better than the second-best score (0.9). Concerning

the F1 score, the best score is 0.95, achieved by the

model discovered by the directly-follows miner us-

ing all activities and 90% of paths. This model is de-

picted in Figure 2. However, this model has some

Available at https://promtools.org/.

HEALTHINF 2024 - 17th International Conference on Health Informatics

510

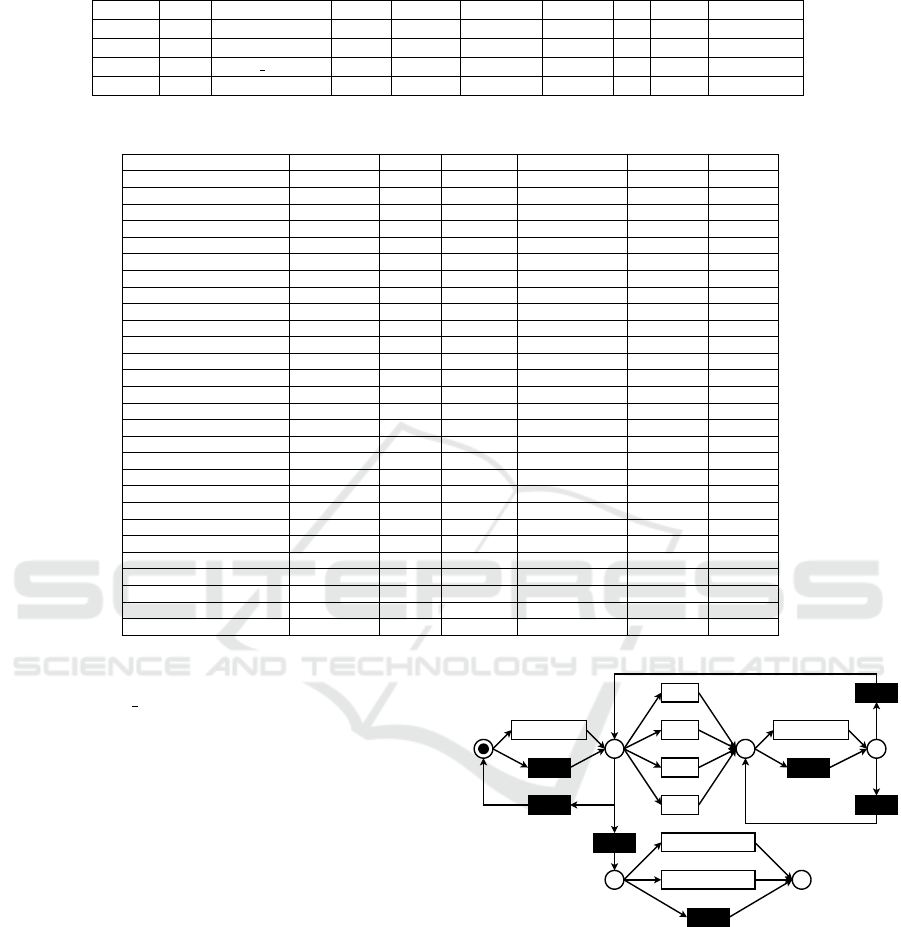
Table 3: Example transformed event log.

RowID Case Activity LVEF HFrEF HFmrEF HFpEF . . . MRA Timestamp

1 007 Visit before CO 50 0 0 1 . . . 12.5 2023-02-20

2 007 HF 50 0 0 1 . . . 12.5 2023-03-14

3 007 Death HF 50 0 0 1 . . . 12.5 2023-04-15

4 008 Visit before CO 10 1 0 0 . . . ⊥ 2023-06-18

Table 4: Conformance checking results.

Algorithm Parameters Fitness Precision Generalization Simplicity F1 score

Alpha - 0.39 0.44 0.70 0.85 0.41

Alpha+ - 0.39 0.44 0.70 0.85 0.41

Alpha++ - - - - - -

Alpha# - 0.96 0.57 0.78 1.00 0.72

Directly-follows Miner 0.0 (paths) - - - - -

Directly-follows Miner 0.1 (paths) 0.75 1.00 0.89 0.78 0.86

Directly-follows Miner 0.2 (paths) 0.75 1.00 0.89 0.78 0.86

Directly-follows Miner 0.3 (paths) 0.75 1.00 0.89 0.78 0.86

Directly-follows Miner 0.4 (paths) 0.75 1.00 0.89 0.78 0.86

Directly-follows Miner 0.5 (paths) 0.75 1.00 0.89 0.78 0.86

Directly-follows Miner 0.6 (paths) 0.75 1.00 0.89 0.78 0.86

Directly-follows Miner 0.7 (paths) 0.84 0.98 0.86 0.68 0.90

Directly-follows Miner 0.8 (paths) 0.91 0.96 0.84 0.63 0.93

Directly-follows Miner 0.9 (paths) 0.97 0.94 0.76 0.52 0.95

Directly-follows Miner 1.0 (paths) 1.00 0.72 0.48 0.47 0.83

Inductive Miner complete - 1.00 0.62 0.80 0.64 0.77

Inductive Miner frequent 0.0 1.00 0.63 0.80 0.63 0.77

Inductive Miner frequent 0.1 0.99 0.59 0.82 0.61 0.74

Inductive Miner frequent 0.2 0.96 0.55 0.82 0.60 0.70

Inductive Miner frequent 0.3 0.46 0.74 0.77 0.62 0.57

Inductive Miner frequent 0.4 0.45 0.74 0.77 0.64 0.56

Inductive Miner frequent 0.5 0.41 0.82 0.77 0.70 0.55

Inductive Miner frequent 0.6 0.41 0.82 0.77 0.70 0.55

Inductive Miner frequent 0.7 0.33 0.79 0.75 0.78 0.47

Inductive Miner frequent 0.8 0.33 0.79 0.75 0.78 0.47

Inductive Miner frequent 0.9 0.33 0.79 0.75 0.78 0.47

Inductive Miner frequent 1.0 0.27 0.67 0.66 0.90 0.38

De-jure model - 1.00 0.56 0.79 0.54 0.72

issues. First, not all activities are represented as ac-

tivities. “Death HF”, “MI”, and “Stroke” are miss-

ing. Second, the model does not show the possible

paths as given in the data. For example, a patient that

has an HF (p2) can never die. Third, the structure

of the process model limits us in applying process-

enhancement techniques such that conclusions for do-

main experts are possible. As a result, we use the de-

jure model. The advantage of this model is its struc-

ture, allowing for decision-mining applications inter-

esting for domain experts. The model is depicted in

Figure 3. In the following, we describe the behavior

captured in the model. Starting from the initial mark-

ing, there is a choice between having a visit or not.

Independently from the choice, the next place is p1.

In p1, there are multiple choices. First, one of the

cardiovascular outcomes may happen. Second, a visit

may happen again, potentially more than two times.

Third, the record of patients ends, either with their

death or there is no more record (p4). Firing one of

the cardiovascular outcomes leads to place p2. Next,

there is a choice between a visit or no visits, leading

to place p3. In place p3, there is a choice between

having another visit or switching to place p1.

Visit before CO

Stroke

Death_HF

Death_AnyCause

p1 p2

Visit after CO

p4 p5

Figure 3: De-jure model of treatment paths.

7 COHORT COMPARISON

In this section, we compare different patient cohorts

of our data. First, we present how we split up the

data and provide reasons. Second, we discover statis-

tically signiﬁcant differences concerning the amount

of activity frequencies.

Process-Aware Analysis of Treatment Paths in Heart Failure Patients: A Case Study

511

7.1 Dividing the Data

We divided the patient population based on three char-

acteristics: (1) which HF phenotype the patient ini-

tially exhibited; (2) whether the patient had diabetes

or not; (3) whether the patient had chronic kidney dis-

ease (CKD) or not. Patients with HF can be divided

into three groups: patients with reduced (HFrEF),

mildly reduced (HFmrEF), or preserved (HFpEF) left

ventricular ejection fraction (LVEF). All phenotypes

are based on LVEF with the presence of signs and

symptoms of HF. As introduced earlier, HFrEF is

classiﬁed with LVEF ≤40%, HFmrEF is deﬁned with

LVEF between 40% and 49%, and HFpEF is with

LVEF ≥50% (McDonagh et al., 2021). This group-

ing allows for tailored treatment strategies. CKD is

deﬁned as showing at least one marker of kidney dam-

age or persistently reduced estimated glomerular ﬁl-

tration (eGFR) rate of <60 ml/min per 1.73m

for

>3 months (Levin et al., 2013). CKD and HF are

concurrent diseases that accelerate the progression of

outcomes, thus leading to an increase in risk for hos-

pitalization and death. Furthermore, diabetes is de-

ﬁned as HbA1c value ≥ 6.5% (≥ 48 mmol/mol), or

when the patient is treated with anti-diabetic medica-

tion. There are two types of diabetes: Type 1 and Type

2. Over 90% of cases are Type 2 diabetes. Similarly

to CKD, patients with HF and diabetes have a higher

risk of cardiovascular mortality, including death due

to worsening HF, compared to those without diabetes.

We exclude patients with Type 1 diabetes.

7.2 Differences in Frequencies of

Activities

First, we count the occurrences for each activity in a

given case (i.e., a patient treatment path).

Deﬁnition 6 (Occurrence count: case). Let L ⊆ U

be an event log, act ∈ U

act

be an activity, and case ∈

case

be a case. count

is a function that counts how

often an activity occurs in a given case for a given log,

i.e., count

(act, case, L) = |{e ∈ L | π

case

(e) = case ∧

act

(e) = act}|.

In the next step, we perform this action on all

cases of a given event log, resulting in a multiset,

in which the cardinality of each element denotes the

number of occurrences of the given activity in a case.

Deﬁnition 7 (Occurrence count: event log). Let L ⊆

be an event log and act ∈ U

act

be an activity.

Then C

= {π

case

(e) | e ∈ L} provides all cases of an

event log L. count

is a function that returns a multiset

of case-wise occurrences of an activity in an event log,

i.e., count

(act, L) =

case∈C

[count

(act, case, L)].

Table 5: P-values after applying Kruskal-Wallis test

(Kruskal and Wallis, 1952) concerning diabetes (yes or no)

and different LVEF categories (HFrEF, HFmrEF, HFpEF),

resulting in six groups for each activity.

Activity p-value

Visit before CO 0.151

Visit after CO 0.566

Hosp CV 0.485

Hosp HF 0.205

Hosp Stroke 0.841

Hosp MI 0.225

Death AnyCause 0.137

Death HF 0.017

Table 6: P-values after applying Kruskal-Wallis test

(Kruskal and Wallis, 1952) concerning CKD (yes or no)

and different LVEF categories (HFrEF, HFmrEF, HFpEF),

resulting in six groups for each activity.

Activity p-value

Visit before CO 0.550

Visit after CO 0.549

Hosp CV 0.376

Hosp HF 0.113

Hosp Stroke 0.949

Hosp MI 0.213

Death AnyCause 0.287

Death HF 0.183

Applying this on the event log shown in Table 3

concerning activity “Visit before CO” leads to [1, 1],

concerning activity “HF” leads to [1, 0].

We apply this methodology considering all activ-

ities. We consider two greater cohorts: patients who

have or do not have diabetes and different LVEF cat-

egories (HFrEF, HFmrEF, HFpEF); and patients who

have or do not have CKD and different LVEF cate-

gories (HFrEF, HFmrEF, HFpEF). Each cohort con-

sists of six groups. We applied the Kruskal-Wallis

test (Kruskal and Wallis, 1952) to check for differ-

ences between groups for each cohort. The Kruskal-

Wallis test is a non-parametric version of the ANOVA

test (Fisher, 1992). If there is a statistically signiﬁcant

difference in the number of occurrences, we applied

Dunn’s test (Dunn, 1964) with Bonferroni adjustment

to check which group differs.

The results concerning Kruskal-Wallis tests

(Kruskal and Wallis, 1952) are shown in Tables 5

and 6.

We consider a difference statistically signiﬁcant if

a p-value is smaller than 0.05. In Tables 5 and 6, such

a value can only be noted in Table 5, when consid-

ering the activity ‘Death AnyCause”, diabetes (yes or

no), and different LVEF categories (0.017). As a re-

sult, Dunn’s test (Dunn, 1964) with Bonferroni ad-

HEALTHINF 2024 - 17th International Conference on Health Informatics

512

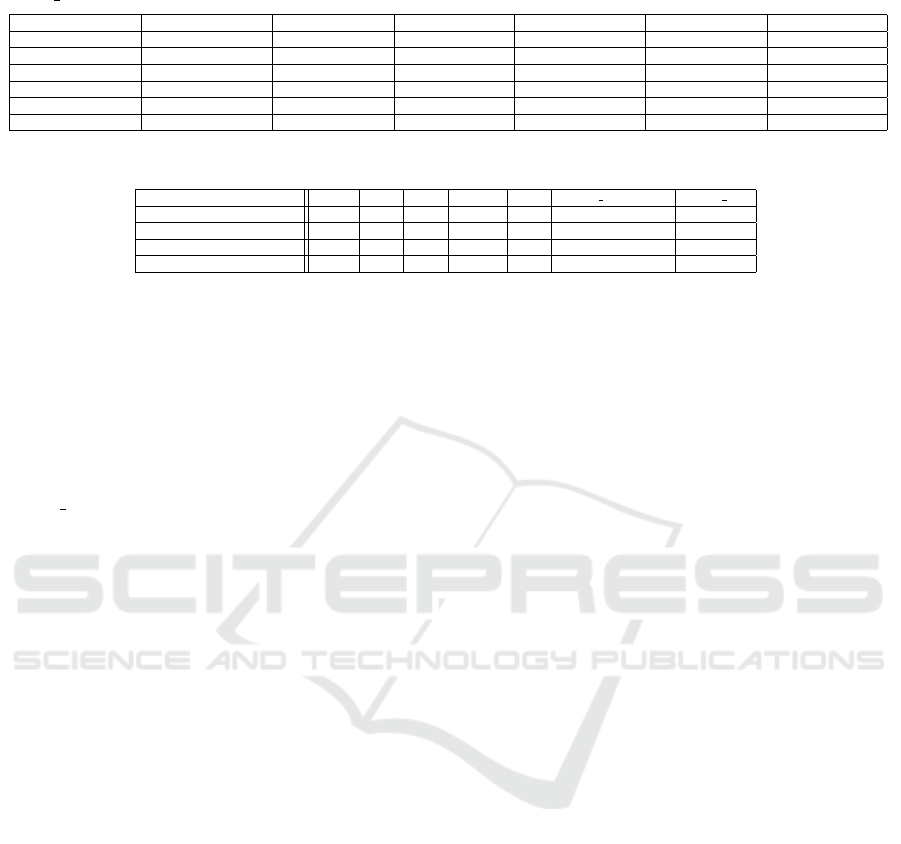
Table 7: Adjusted p-values after applying Dunn’s test (Dunn, 1964) with Bonferroni adjustment concerning the activity

“Death AnyCause”, diabetes (D, yes (1) or no (0)), and different LVEF categories.

D=0 and HFmrEF D=0 and HFpEF D=0 and HFrEF D=1 and HFmrEF D=1 and HFpEF D=1 and HFrEF

D=0 and HFmrEF 1.00 1.00 1.00 1.00 1.00 0.45

D=0 and HFpEF 1.00 1.00 1.00 1.00 1.00 0.11

D=0 and HFrEF 1.00 1.00 1.00 1.00 1.00 0.01

D=1 and HFmrEF 1.00 1.00 1.00 1.00 1.00 0.36

D=1 and HFpEF 1.00 1.00 1.00 1.00 1.00 1.00

D=1 and HFrEF 0.45 0.11 0.01 0.36 1.00 1.00

Table 8: Distribution of next activities for places p1 and p4.

Place and population None HF CV Stroke MI Death AnyCause Death HF

Place p1(all patients) 91.86 5.78 1.90 0.30 0.15 - -

Place p1 (HFrEF patients) 91.30 6.10 2.10 0.40 0.10 - -

Place p4 (all patients) 98.29 - - - - 1.39 0.33

Place p4 (HFrEF patients) 97.89 - - - - 1.71 0.40

justment is applied to observe which groups differ.

The result is displayed in Table 7.

As it can be noted, the group having diabetes and

being associated with HFrEF is different from nearly

all other groups. However, a stronger statistically sig-

niﬁcant difference can be noted between the men-

tioned group of patients and patients having no dia-

betes and being part of the HFrEF group. As a result,

“Death AnyCause” happens statistically signiﬁcantly

more often for HFrEF patients if they have diabetes.

8 INVESTIGATING REASONS

In this section, we investigate the reasons for deci-

sions in the model. To investigate the reasons, two

things are required: the transformed event log and at

least one decision point. A decision point is a place

in a Petri net with more than one outgoing arc. There

are two interesting decision points in the model shown

in Figure 3: places p1 and p4. The former is a deci-

sion point concerning COs. The latter points out the

decision between two death options and the end of a

patient’s record. Using the event log, we use the infor-

mation associated with the events to discover the rea-

sons behind the decision. Since HFrEF patients are in

a worse state than the others, we additionally applied

our approach to records containing patients with that

characteristic separately. The probability distribution

for the outcomes of the mentioned places considering

the whole population and the HFrEF patients is dis-

played in Table 8. We summarised the execution of

τ-transitions as “None”.

The results of applying various classiﬁcation tech-

niques are displayed in Table 9. In the following, we

investigate the different decision points in greater de-

tail.

8.1 Reasons for Cardiovascular

Outcomes

COs are highly interesting events in the strategy for

patients’ treatment. Understanding why they happen

can lead to improvements in the treatment process,

such that these outcomes are avoided. The choice be-

tween COs is taking place in place p1 in the Petri net

depicted in Figure 3. As shown in Table 8, a CO ac-

tivity rarely happens. Considering the whole popu-

lation, a non-CO activity is executed 91.86% of the

time. The algorithms adopt this behavior, conduct a

majority vote, and achieve similar accuracy, as shown

in Table 9. When we consider only HFrEF patients,

we observe that 91.3% of the time, a non-CO activity

is executed. At the same time, the accuracy of the al-

gorithms is slightly better, with an accuracy of 91.4%

(naive Bayes, decision trees, gradient-boosted trees,

and support vector machines). However, the differ-

ence is negligible. We conclude that predicting a CO

activity, given our data, is not possible. The distribu-

tion over the different classes is skewed, and sampling

was infeasible based on the limited data.

8.2 Reasons for Death

As stated, in place p4 in the model depicted in Fig-

ure 3, the decision between a patient’s death and the

end of a patient’s records takes place. In the follow-

ing, we analyze the reasons for the whole popula-

tion and HFrEF patients. Considering the distribu-

tion of activities, as shown in Table 8, a death activ-

ity happens rarely. Considering the whole population,

98.29% of the time, the records of patients end with-

out death. However, as shown in Table 9, the accu-

racy is at most 98%. When considering only HFrEF

patients, 97.89% of the time, the records of patients

end without death. The classiﬁers have an accuracy of

98.6%, which is better than the majority vote and our

Process-Aware Analysis of Treatment Paths in Heart Failure Patients: A Case Study

513

Table 9: Highest measured accuracy of prediction measured using multiple strategies for different places and patient popula-

tions in the model shown in Figure 3.

Place and population

Naive

Bayes

Generalized

Linear

Model

Logistic

Regression

Fast

Large

Margin

Deep

Learning

Decision

Tree

Random

Forest

Gradient

Boosted

Trees

Support

Vector

Machine

Place p1 (all patients) 91.8 91.8 - - 91.8 91.8 91.8 91.8 91.8

Place p1 (HFrEF patients) 91.4 86.3 - - 91.0 91.4 88.4 91.4 91.4

Place p4 (all patients) 98.0 98.0 - 98.0 98.0 98.0 98.0 98.0 98.0

Place p4 (HFrEF patients) 98.6 98.6 - 98.6 98.6 98.6 98.6 98.6 98.6

best offset to the greatest distribution value. However,

given the unbalanced classes, the accuracy is still not

satisfying. As for determining reasons for COs, we

do not have enough information on all classes.

9 CONCLUSION

Our work aimed to analyze the reasons for COs

and death during the treatment pathway of a patient

with HF. In general, we applied process mining-based

methodology to patient data for HF in a real-world

setting. We transformed patient data into an event log.

Subsequently, we applied process-mining techniques

to the transformed event log. We discovered pro-

cess models and applied conformance-checking tech-

niques to the discovered model and a de-jure model.

We investigated differences between different patient

cohorts. Finally, we performed decision mining using

the transformed event log and the de-jure model.

However, the results have to be treated with cau-

tion. First, the number of patients included is limited.

The records that we analyzed were for 240 patients.

Thus, we analyzed 1000 events, i.e., roughly four

events per patient in roughly four years. Second, pa-

tients’ data are usually sparse, and the dataset we ana-

lyzed is no exception. Types of sparseness include the

temporal sparseness that was previously mentioned,

but there is also an absence of information for some

attributes. Third, patients’ data and their treatment are

highly complex. The data we analyzed only cover in-

formation recorded at the RWTH Aachen University

Hospital. Information about the treatments in other

hospitals is limited. Thus, only CV-related hospital-

izations from other hospitals are included.

This case study allows for open questions and di-

rections for future research in the context of health-

care. First, the used activities are generic. The data

consists of biomarkers, which can be used to generate

more meaningful activity names. Second, for some

visits, there exist textual reports. Using text-mining

techniques, information can be extracted from these

reports, enabling a more precise description of the

record. Third, as previously stated, the data consist

of a small number of patients, for which most either

do not die or do not have a CO. Increasing the num-

ber of patient records such that more of these kinds

of patients appear in the data can increase the qual-

ity of the classiﬁcation algorithms and the forecasting

quality of these systems, leading to better treatment.

ACKNOWLEDGEMENTS

We thank the Alexander von Humboldt (AvH)

Stiftung for supporting our research. Dr. Sch

utt is

supported by the Deutsche Forschungsgemeinschaft

(German Research Foundation; TRR 219; Project-

ID 322900939 [C07]); Prof. Marx is supported by

the Deutsche Forschungsgemeinschaft (German Re-

search Foundation; TRR 219; Project-ID 322900939

[M03, M05]). Funded under the Excellence Strategy

of the Federal Government and the L

ander in support

of the “Computational Ecosystem for the Analysis

and Clinical Application of Multi-Organ Crosstalk”

(COAT) initiative of RWTH Aachen University.

REFERENCES

Adriansyah, A., Munoz-Gama, J., Carmona, J., et al.

(2015). Measuring precision of modeled behavior. Inf.

Syst. E Bus. Manag., 13(1):37–67.

Adriansyah, A., Sidorova, N., and van Dongen, B. F.

(2011). Cost-based ﬁtness in conformance checking.

In Caillaud, B., Carmona, J., and Hiraishi, K., editors,

International Conference on Application of Concur-

rency to System Design, pages 57–66. IEEE Computer

Society.

Almeida, J. R., Freire, P., Fajarda, O., et al. (2020). A com-

putational platform for heart failure cases research. In

HEALTHINF, pages 601–608.

Artola, G., Larburu, N.,

Alvarez, R., et al. (2019). The im-

pact of environmental factors on heart failure decom-

pensations. In HEALTHINF, pages 51–58.

Back, C. O., Manataki, A., and Harrison, E. M. (2020).

Mining patient ﬂow patterns in a surgical ward. In

HEALTHINF, pages 273–283. SCITEPRESS.

Benevento, E., Pegoraro, M., Antoniazzi, M., et al.

(2022). Process modeling and conformance checking

in healthcare: A COVID-19 case study - case study. In

HEALTHINF 2024 - 17th International Conference on Health Informatics

514

Process Mining Workshops - ICPM, pages 315–327.

Springer.

Bottrighi, A., Piovesan, L., Terenziani, P., et al. (2018). A

general framework for the distributed management of

exceptions and comorbidities. In HEALTHINF, pages

66–76.

Buijs, J. C. A. M., van Dongen, B. F., and van der Aalst,

W. M. P. (2014). Quality dimensions in process dis-

covery: The importance of ﬁtness, precision, general-

ization and simplicity. Int. J. Cooperative Inf. Syst.,

23(1).

Carmona, J., van Dongen, B. F., Solti, A., et al. (2018). Con-

formance Checking - Relating Processes and Models.

Springer.

Chin, S. C., Zolfaghar, K., Roy, S. B., et al. (2014). Divide-

n-discover: Discretization based data exploration

framework for healthcare analytics. In HEALTHINF,

pages 329–333. SciTePress.

de Vries, G., Neira, R. A. Q., Geleijnse, G., et al. (2017).

Towards process mining of EMR data - case study for

sepsis management. In HEALTHINF, pages 585–593.

SciTePress.

Dunn, O. J. (1964). Multiple comparisons using rank sums.

Technometrics, 6(3):241–252.

Fisher, R. A. (1992). Statistical Methods for Research

Workers. Springer New York, New York, NY.

Guzzo, A., Rullo, A., and Vocaturo, E. (2022). Process min-

ing applications in the healthcare domain: A compre-

hensive review. WIREs Data Mining and Knowledge

Discovery, 12(2).

Kerexeta, J., Artetxe, A., Escolar, V., et al. (2018). Predict-

ing 30-day readmission in heart failure using machine

learning techniques. In HEALTHINF, pages 308–315.

Kruskal, W. H. and Wallis, W. A. (1952). Use of ranks in

one-criterion variance analysis. Journal of the Ameri-

can Statistical Association, 47(260):583–621.

Kusuma, G. P., Sykes, S., McInerney, C., et al. (2020). Pro-

cess mining of disease trajectories: A feasibility study.

In International Joint Conference on Biomedical En-

gineering Systems and Technologies: HEALTHINF,

pages 705–712. SCITEPRESS.

Levin, A., Stevens, P. E., Bilous, R. W., et al. (2013). Kid-

ney disease: Improving global outcomes (kdigo) ckd

work group. kdigo 2012 clinical practice guideline for

the evaluation and management of chronic kidney dis-

ease. Kidney international supplements, 3(1):1–150.

Mans, R., Schonenberg, H., Leonardi, G., et al. (2008). Pro-

cess mining techniques: an application to stroke care.

In MIE, pages 573–578. IOS Press.

Mans, R., van der Aalst, W. M. P., and Vanwersch, R.

J. B. (2015). Process Mining in Healthcare - Eval-

uating and Exploiting Operational Healthcare Pro-

cesses. Springer Briefs in Business Process Manage-

ment. Springer.

McDonagh, T. A., Metra, M., Adamo, M., et al. (2021).

2021 ESC guidelines for the diagnosis and treatment

of acute and chronic heart failure. European Heart

Journal, 42(36):3599–3726.

Munoz-Gama, J., Martin, N., Fern

andez-Llatas, C., et al.

(2022). Process mining for healthcare: Characteristics

and challenges. J. Biomed. Informatics, 127:103994.

Pegoraro, M., Narayana, M. B. S., Benevento, E., et al.

(2021). Analyzing medical data with process min-

ing: A COVID-19 case study. volume 444 of Lec-

ture Notes in Business Information Processing, pages

39–44. Springer.

Reisig, W. (1985). Petri Nets: An Introduction, volume 4

of EATCS Monographs on Theoretical Computer Sci-

ence. Springer.

Romero-Gonz

alez, G., Ravassa, S., Gonz

alez, O., et al.

(2020). Burden and challenges of heart failure in pa-

tients with chronic kidney disease. a call to action. Ne-

frolog

ıa, 40(3):223–236.

Roy, S. B. and Chin, S.-C. (2014). Prediction and manage-

ment of readmission risk for congestive heart failure.

In HEALTHINF, pages 523–528. SciTePress.

Sattar, N., Lee, M. M. Y., Kristensen, S. L., et al. (2021).

Cardiovascular, mortality, and kidney outcomes with

GLP-1 receptor agonists in patients with type 2 dia-

betes: a systematic review and meta-analysis of ran-

domised trials. The Lancet Diabetes & Endocrinol-

ogy, 9(10):653–662.

van der Aalst, W. M. P. (2016). Process Mining - Data

Science in Action, Second Edition. Springer.

Weerdt, J. D., Backer, M. D., Vanthienen, J., et al. (2010).

A critical evaluation study of model-log metrics in

process discovery. In Business Process Management

Workshops, pages 158–169. Springer.

Zelniker, T. A., Wiviott, S. D., Raz, I., et al. (2019). SGLT2

inhibitors for primary and secondary prevention of

cardiovascular and renal outcomes in type 2 diabetes:

a systematic review and meta-analysis of cardiovascu-

lar outcome trials. The Lancet, 393(10166):31–39.

Zweth, J., Askari, M., Spruit, M., et al. (2018). Devices

used for non-invasive tele homecare for cardiovascular

patients: A systematic literature review. In HEALTH-

INF, pages 300–307. SciTePress.

Process-Aware Analysis of Treatment Paths in Heart Failure Patients: A Case Study

515