Compressing UNSAT CDCL Trees with Caching
Anthony Blomme
a
, Daniel Le Berre
b
, Anne Parrain
c
and Olivier Roussel
d
Univ. Artois, CNRS, Centre de Recherche en Informatique de Lens (CRIL), F-62300 Lens, France
Keywords:
Explainable AI, SAT Solver, Proof Compression.
Abstract:
We aim at providing users of SAT solvers with small, easily understandable proofs of unsatisfiability. Caching
techniques have been proposed to identify redundant subproofs and reduce the size of some UNSAT proof
trees. Branches are pruned when they correspond to subformulas that were proved unsatisfiable earlier in the
tree. A caching mechanism based on subgraph isomorphism was proposed as postprocessing step both in the
DPLL and CDCL architectures but the technique could only be integrated during the search on the DPLL
architecture. This paper presents how to integrate such caching mechanism during the search for the CDCL
case and presents a generalized caching mechanism for that architecture.
1 INTRODUCTION
SAT solvers are currently used to solve a wide range
of combinatorial problems (Biere et al., 2021). They
can be trusted since they can provide either a model
when a solution exists or a certificate of unsatisfiabil-
ity (Wetzler et al., 2014) that can be verified by an
independent checker. Both kinds of certificates allow
to check the answer provided by the SAT solver, but
it is usually not an explanation for the user of the SAT
solver. If there are more than one solution, why pro-
viding that one? If there are no solution, why is it the
case? In the former case, it will be difficult to answer
since the model found depends heavily on the imple-
mentation of the SAT solver used and has no logical
explanation. In the latter case, it is possible to find
a minimal subset of unsatisfiable clauses (MUS) (Ig-
natiev et al., 2015). However, there is no guarantee
that a MUS is smaller than the complete formula, and
a certificate can have an exponential number of steps.
In this work, we only consider unsatisfiable for-
mulas and our goal is to significantly compress the
search tree of a CDCL solver in order to obtain a
proof that is small enough to be given as explana-
tion to the user. To do so, we focus on finding re-
curring unsatisfiable patterns during the search be-
cause of their potentially huge impact on the tree size,
and also because they can be ”explained” individu-
a
https://orcid.org/0000-0001-5395-1625
b
https://orcid.org/0000-0003-3221-9923
c
https://orcid.org/0000-0001-7115-8022
d
https://orcid.org/0000-0002-9394-3897
ally and independently to the user. We use a cache
based on subgraph isomorphism detection to recog-
nize these patterns. If the current subformula was al-
ready explored and proved unsatisfiable, the current
branch can be pruned and a conflict clause must be
provided to the CDCL solver. That work has been
initiated in (Blomme et al., 2023), with a complete in-
tegration in the DPLL architecture but only as a post-
processing step in the CDCL architecture. This pa-
per extends that work with a complete integration in
a CDCL solver and a generalized caching mechanism
dedicated to that architecture.
This paper is organized as follows. In Section 2,
we define some basic notions and notations. In Sec-
tion 3, we summarize the previous work on this prob-
lem by (Blomme et al., 2023). In Section 4, we pro-
pose an integration of a cache for unsatisfiable formu-
las into a CDCL solver. Then, we present a more gen-
eral caching definition in Section 5. Some experimen-
tal results are presented in Section 6 and we discuss
the generation of reduced prrofs in Section 7. Finally,
we conclude and present some future works.
2 PRELIMINARIES
A Boolean variable v is either true or false. A literal is
a variable v or its negation ¬v. A clause is a disjunc-
tion of literals and a formula in Conjunctive Normal
Form (CNF) is a conjunction of clauses. An assign-
ment maps the set of variables to the truth values 0
(for false) or 1 (for true). A clause is satisfied by an
792
Blomme, A., Berre, D., Parrain, A. and Roussel, O.
Compressing UNSAT CDCL Trees with Caching.
DOI: 10.5220/0012393000003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 3, pages 792-799
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

assignment if it contains at least one literal l which is
assigned true. A formula is satisfied by an assignment
if and only if all its clauses are satisfied. Deciding if
there exists an assignment that satisfies a given for-
mula in CNF is known as the satisfiability problem
(SAT), which is NP-complete (Cook, 1971). The for-
mula is SAT if it is possible to find such an assignment
and it is UNSAT otherwise. Given an assignment I, F
|I
denotes the formula simplified by I: satisfied clauses
are removed from the formula and falsified literals are
removed from the remaining clauses. A unit clause is
a clause C which contains only one non falsified lit-
eral l, therefore l must be assigned true. In this case,
C is the reason for the assignment of l and will be
denoted r(l). Applying this operation until there re-
mains no unit clause is called unit propagation. Ex-
tending an assignment with a literal assignment with-
out reason is called a decision. A function DL(l) pro-
vides the level of l, which is the number of decisions
taken before l. SAT solvers are programs that solve
the satisfiability problem. In the 90’s, complete SAT
solvers were based on the Davis Putnam Logemann
Loveland (DPLL) architecture (Davis and Putnam,
1960)(Davis et al., 1962). In 2001, a new architec-
ture called Conflict Driven Clause Learning (CDCL)
(Silva and Sakallah, 1999; Moskewicz et al., 2001;
E
´
en and S
¨
orensson, 2003) appeared and made SAT
solvers commodity software oracles for solving NP-
Complete problems (Biere et al., 2021). SAT solvers
explore a search tree, in which a path from the root
to the leaves is a partial assignment, and leaves corre-
spond to falsified clauses (a so-called conflict) when
the formula is unsatisfiable. While DPLL solvers ex-
plore a binary tree by branching on variables, CDCL
solvers use conflict analysis and clause learning to
drive the search (Marques-Silva et al., 2021).
3 CACHING FOR COMPRESSING
3.1 Principle
In (Blomme et al., 2023), it was noticed that some
unsatisfiable problems have a specific structure that
can be used to reduce the search tree of a SAT solver.
A widely known academic problem with such prop-
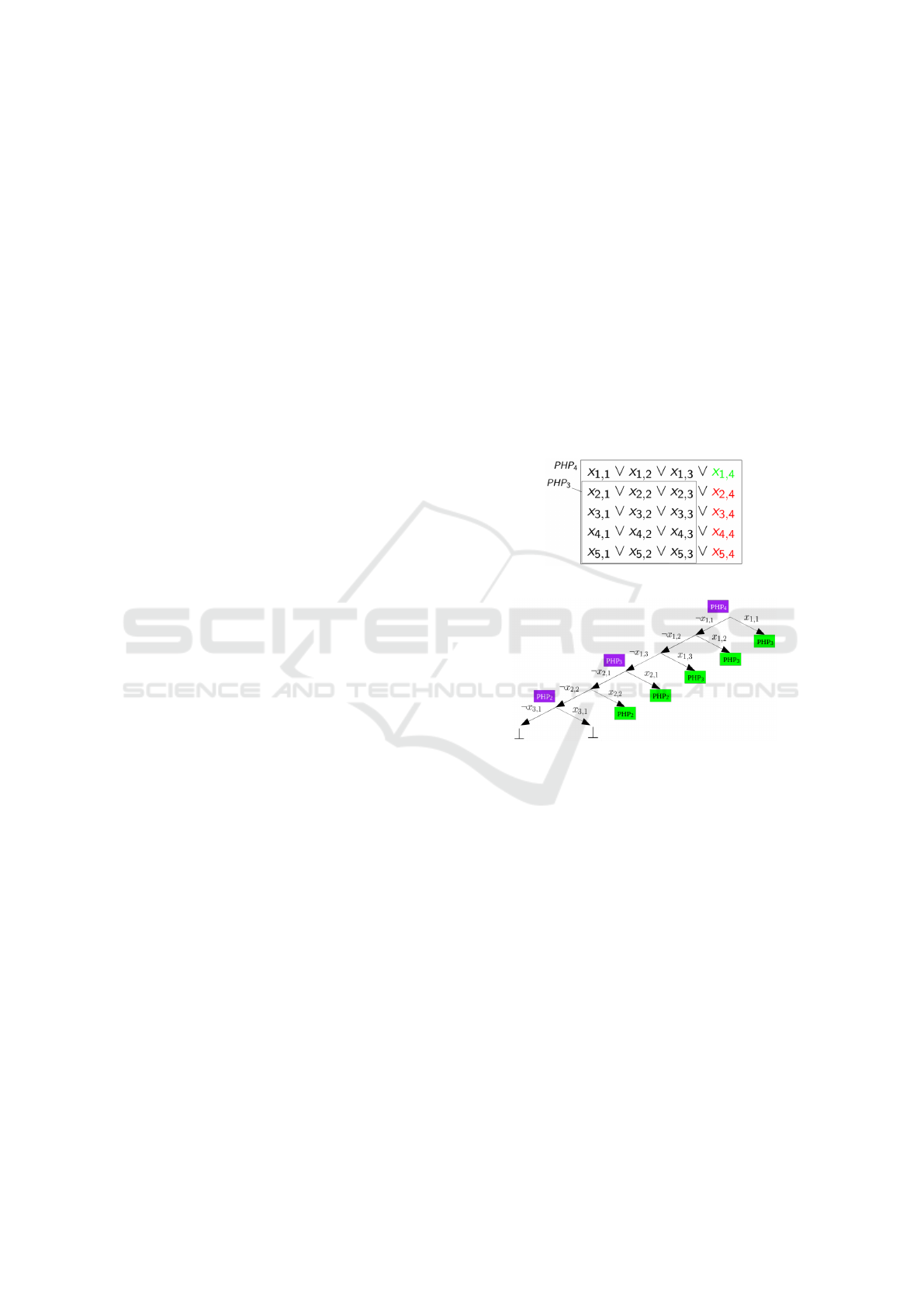
erty is the Pigeon Hole Principle (PHP), famous for
being hard for solvers and for featuring lots of sym-
metries (Haken, 1985). The problem is to assign
n + 1 pigeons to n holes with the constraints that a
pigeon has to be associated with one hole and a hole
cannot contain more than one pigeon. This prob-
lem is denoted PHP
n
and is defined by variables x
i,k
,
which state that pigeon i is assigned hole k. The
first constraint is encoded by using a clause of size
n for each pigeon: C
1,n
=
V
1≤i≤n+1
(x
i,1
∨ · ·· ∨ x
i,n
).
For the second constraint, we add the mutual exclu-
sions between two pigeons and for a specific hole:
C
2,n
=
V
1≤i< j≤n+1
V
1≤k≤n
(¬x
i,k
∨ ¬x
j,k
). It can be
noticed that PHP
n|x
1,n
is an instance of PHP
n−1
. This
occurs when exploring the n ways to place the first
pigeon. Once the first PHP
n−1
subproblem has been
explored, it can be recognized as soon as any of the
other x
1,k
is assigned true (this occurs n − 1 times).
This step can be repeated recursively until the prob-
lem PHP
2
is encountered. The latter only needs two
branches to be fully explored. Figure 1 shows an im-
bricated PHP subproblems of size 3 inside a PHP
problem of size 4. Figure 2 shows a reduced search
tree when PHP subproblems are recognized (propaga-
tions have been omitted).
Figure 1: Pigeon Hole Principle problem of size 4.
Figure 2: Expected single branch when solving PHP
4
.
3.2 Subformula Recognition
The different PHP problems in the previous examples
are not based on the same variables. As such, the
recognition mechanism needs to support the notion of
equality modulo a renaming of the literals. There is
also a specificity related to dealing with UNSAT for-
mulas: a formula is UNSAT if it contains an UNSAT
subformula. So it is also important to detect formulas
included in a target formula.
Inclusion and renaming can be implemented
by solving an NP-complete Subgraph Isomorphism
problem. For an UNSAT formula E and a current for-
mula F
|I
, one wants to determine if there exists a con-
sistent renaming σ of literals (i.e. a permutation of
literals such that if σ(l) = l
′
then σ(¬l) = ¬l
′
) such
that σ(E) ⊆ F
|I
. As such, (Blomme et al., 2023) pro-
posed to implement a caching mechanism for UNSAT
formulas based on subgraph isomorphism detection.
Compressing UNSAT CDCL Trees with Caching
793

3.3 Sources of Inconsistency
The caching mechanism presented in (Blomme et al.,
2023) is based on the notion of sources.
The sources of an unsatisfiable subformula F
|I
are
the initial clauses of F used by the solver to prove
the unsatisfiability of F
|I
. This set will be denoted
S(F, I). These sources are easily obtained in the solver
by gathering recursively the reason of each propaga-
tion leading to the conflicts. This process is in essence
the same as conflict analysis in a CDCL solver, except
that no resolution step is performed. One important
point is that the sources may only contain clauses of
the initial formula. In a CDCL solver, if a learned
clause appears in the sources, it is replaced by the set
of initial clauses that generated it. Formally, sources
are defined as follows in (Blomme et al., 2023).
Definition 1. We first define the source of a clause
S(C). When C is an initial clause, S(C) = {C} When
L is a learned clause, S(L) is the set of initial clauses
of F that appear in the derivation of L by resolution.
Let F
|I
be an unsatisfiable subformula and let
{I
1
, . . . I
m
} be the set of branches developed by the
solver to prove this inconsistency. Each F
|I
j
con-
tains a conflict C
j
. We define S
0
(F, I
j
) = {C
j
} and
S
i+1
(F, I
j
) = S
i
(F, I
j
) ∪{S(r(l))|l ∈ c ∧ c ∈ S
i
(F, I
j
) ∧
DL(l) ≥ DL(I
j
)}. This sequence has a least fixed-
point denoted S(F, I
j
). At last, the sources S(F, I) of
F
|I
are defined as S(F, I) = ∪
j
S(F, I
j
).
The cache of a CDCL solver is fed with the
sources of the conflicting clauses met during the
search.
4 CACHING FOR CDCL
CDCL solvers need a falsified clause to start the con-
flict analysis procedure. This is also the case when an
entry is recognized. In (Blomme et al., 2023), the au-
thors proposed to simply create a clause which is fal-
sified by all decisions on the path from the root to the
leaf. However, such an approach did not provide good
early experimental results. It is especially useless for
conflict analysis because no literal has a reason. As
such, the clause may contain literals unnecessary for
the conflict.
We propose an alternative approach, which takes
advantage of the notion of sources. When we have
collected the original clauses O that match the entry
in F
|I
, we can create a clause composed of all the falsi-
fied literals in O
|I
. Such a clause is by design falsified
by the current assignment I. Besides, we show that
this clause is entailed by the original formula, so it
Algorithm 1: CacheCDCL(φ).
Data: φ - a CNF formula
Result: Is φ SAT or UNSAT?
α ←
/
0;
while true do
con f lictFound ← f alse;
(α,C) ← Propagate(φ, α);
if C ̸= Unde f then
if CurrentDecisionLevel() = 0 then
return UNSAT;
con f lictFound ← true;
S ← CollectSourcesCon f lict(C);
else if (H ← HasIsomorphism(φ, α)) ̸=
/
0
then
if CurrentDecisionLevel() = 0 then
return UNSAT;
con f lictFound ← true;
C ← CreateCon f lictFromIso(H, α);
S ← CollectSourcesIsomorphism(H);
α ← Back jumpI f Needed(C, α);
if con f lictFound = true then
C
1
← AnalyzeCon f lict(C);
AddToCache(S, α);
φ ← φ ∪ {C
1
};
α ← Back jump(C
1
, α);
else
if needRestart then
Restart();
if needCleanDB then
CleanDB();
l ← Decide();
if l = Unde f then
return SAT ;
α ← α ∪ {l}
Algorithm 2: CollectSourcesConflict(C).
Data: C - a conflict clause
Result: S - the sources collected
S ← Sources(C);
for l ∈ C do
if r(l) ̸=
/
0 and !Used[var(l)] then
Used[var(l)] ← true;
S ← S ∪CollectSourcesCon f lict(r(l));
return S;
Algorithm 3: CollectSourcesIsomorphism(H).
Data: H - the clauses recognized
Result: S - the sources collected
S ←
/
0;
for C ∈ H do
S ← S ∪CollectSourcesCon f lict(C)
return S;
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
794

Algorithm 4: CreateConflictFromIso(O, α).
Data: O - the original clauses recognized, α - the
current assignment
Result: C - a generated conflict clause
con f lict ←
/
0;
for C ∈ O do
for l ∈ C such that α(l) = f alse do
con f lict ← con f lict ∪ {l};
return con f lict;
Algorithm 5: BackjumpIfNeeded(C, α).
Data: C - the generated conflict clause, α - the
current assignment
Result: α - the updated assignment
if DL(C) < CurrentDecisionLevel() then
α ← Back jumpUntil(DL(C), α);
return α;
is a conflict. We know that O
|I
⊆ F
|I
is unsatisfiable,
so O ∧ I |= ⊥. Suppose we call SELECT (O, I) the
literals from I that falsify a literal in a clause of O.
Then, we also have O ∧ SELECT (O, I) |= ⊥, hence
F |= O |= ¬SELECT (O, I) since literals from I satis-
fying clauses in O do not contribute to unsatisfiability.
So using ¬SELECT (O, I) as conflict clause when an
entry is detected is sound. Algorithm 1 is a modi-
fied CDCL procedure with the caching mechanism of
(Blomme et al., 2023) enabled and our conflict clause
generation procedure for caching hits. Those modi-
fications are highlighted in blue. The conflict clause
generation is given in Algorithm 4.
As an example, let us consider the problem PHP
3
with a heuristics that negatively decides the variables
in reverse order. Figure 3 illustrates the behaviour
of that heuristic. Here a blue arrow denotes a de-
cision, a black arrow represents a propagation with
an original clause and a red arrow represents a prop-
agation with a learned clause. The heuristics first
decides ¬x
4,3
and then ¬x
4,2
. This propagates x
4,1
,
¬x
1,1
, ¬x
2,1
and ¬x
3,1
. We end up now with a PHP
2
problem. After exploring it, we add it to the cache
and the solver learns the clause ¬x
4,1
, which makes
us backtrack to the root of the tree. After propagating
¬x
4,1
, the heuristics decides again ¬x
4,3
. The clause
x
4,1
∨ x
4,2
∨ x
4,3
propagates x
4,2
and then the mutual
exclusions propagate ¬x
1,2
, ¬x
2,2
, and ¬x
3,2
. We
end up again with a PHP
2
problem that we recognize
since it is in the cache. The clauses x
1,1
∨ x
1,2
∨ x
1,3
,
x
2,1
∨ x
2,2
∨ x
2,3
and x
3,1
∨ x
3,2
∨ x
3,3
and the required
mutual exclusion clauses match the entry. In these
clauses, we know that the literals x
1,2
, x
2,2
and x
3,2
have been falsified, so we can create the falsified
clause x
1,2
∨ x
2,2
∨ x
3,2
that will be given to the con-
flict analysis. By performing resolution on the clauses
¬x
1,2
∨ ¬x
4,2
, ¬x
2,2
∨ ¬x
4,2
and ¬x
3,2
∨ ¬x
4,2
, we can
learn the clause ¬x
4,2
, backtrack to the decision level
0, propagate ¬x
4,2
and then continue the search.
Figure 3: Example to illustrate the integration of the cache
system with the conflict analysis.
Note that if the current decision is unrelated to the
hit, then the proposed conflict clause may not con-
tain any literal from the current decision level, which
breaks one classical CDCL invariant. To restore it, we
compute the deepest decision level of the conflicting
clause and, if it is not the current decision level, we
backtrack to this level before performing the conflict
analysis (cf Algorithm 5).
5 GENERALIZED
ISOMORPHISMS DETECTION
We observed that the current formula F
|I
may contain
(up to a renaming of variables) an entry E of the cache
simplified by a subset I
1
of the current interpretation
I (i.e. σ(E)
|I
1
⊆ F
|I
). When this happens, since E is
unsatisfiable, σ(E)
|I
1
is also unsatisfiable hence, F
|I
is unsatisfiable. In practice, this may happen because
we look for isomorphisms only at each decision and
not after each unit propagation, which would be too
costly. It also happens if literals occurring in E are
assigned early on the branch. To detect this case, we
have to introduce a generalized isomorphisms.
As an example, let us consider the formula F con-
taining the clauses of PHP
4
where the first clause
x
1,1
∨ x
1,2
∨ x
1,3
∨ x
1,4
is extended with the fresh vari-
ables a and b. Let us further assume that the cache al-
ready contains PHP
4
and that x
2,4
was assigned false
early on the current branch. When both a and b are
assigned false, it is clear that PHP
4
is now contained
(in some way) in the current formula. However, syn-
tactically, this is not true if we consider the simplified
current formula. Indeed, this simplified formula does
not contain the second clause of PHP
4
because it was
reduced by x
2,4
. Hence, a regular isomorphism cannot
be identified. However, if a and b had been assigned
before x
2,4
, this identification would have been pos-
Compressing UNSAT CDCL Trees with Caching
795

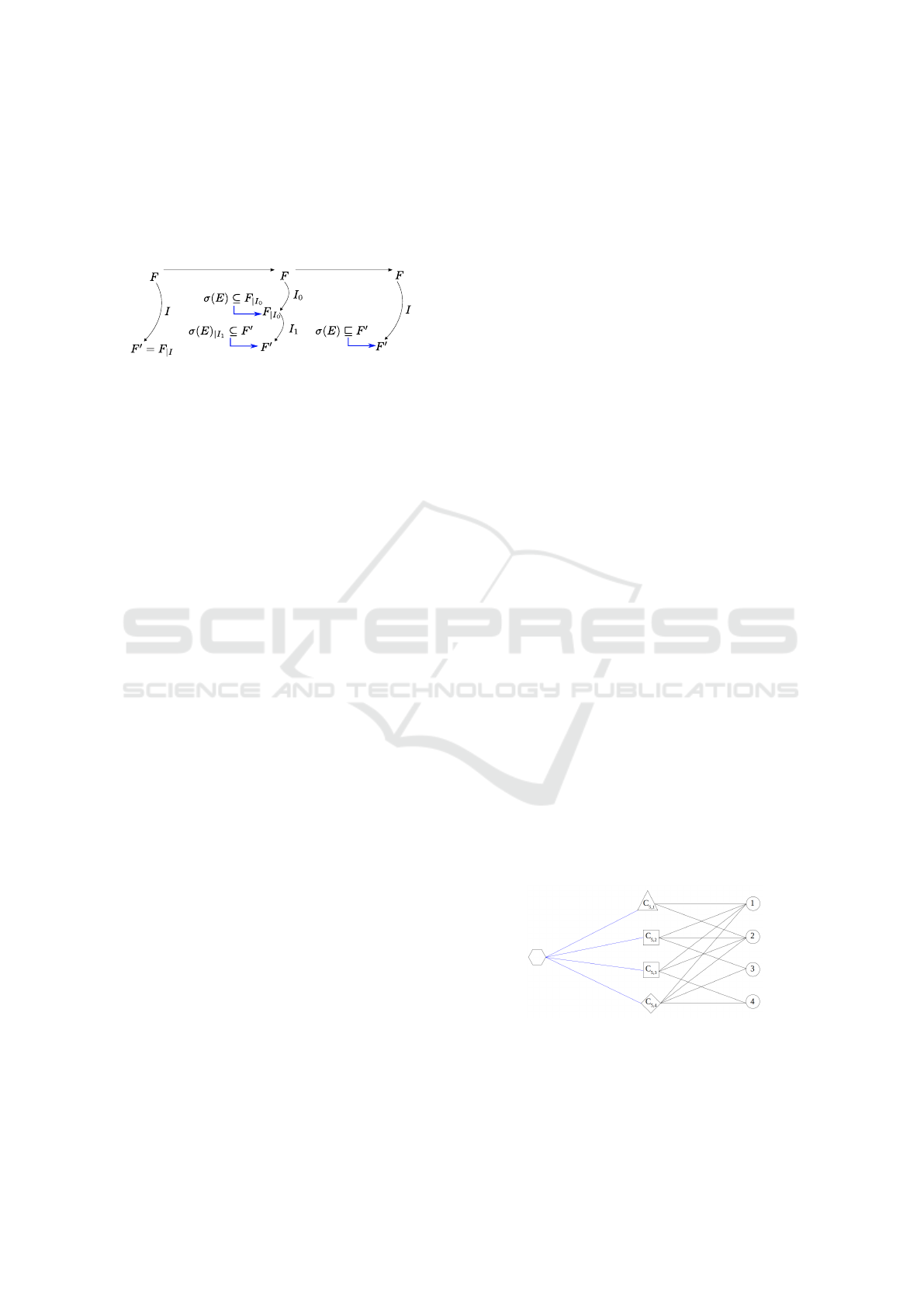
sible. Clearly, the method is highly sensitive to the
order of assignments, and this should be avoided.
5.1 Formal Definition
assignment reordering
test in theory
test in practice
Figure 4: Principle of the generalized isomorphism test.
Let F be the initial formula, I the current interpreta-
tion, F
′
= F
|I
the current formula and E an entry. We
want to determine if I can be partitioned into two sub-
sets I
0
and I
1
and such that σ(E)
|I
1
⊆ F
′
. I
1
is used to
simplify both σ(E) and F, I
0
is only used to simplify
F. In other words, we want to detect if by reorder-
ing the assignments, we could obtain at some point a
regular isomorphism: σ(E) ⊆ F
|I
0
. Figure 4 illustrates
the relation between the different formulas, interpre-
tations and tests. Obviously, I
0
and I
1
are unknown.
It should be noticed that I
1
may satisfy a clause C
of σ(E), but we have to make sure that C is indeed
present in F. Otherwise the current formula may con-
tain only a strict subset of E, which may be satisfiable.
This means that we have to keep satisfied clauses to
perform our tests. Besides, a clause C ∈ E may match
a clause C
′
in F even if C
′
contains additional literals,
as long as these are falsified by I
0
. To formalize this,
we introduce a specific inclusion relation ⊑ such that
σ(E) ⊑ F
′
implies ∃I
0
s.t. σ(E) ⊆ F
|I
0
.
Given a current interpretation I and two clauses C
and C
′
, C ⊑ C
′
iff C ⊆ C
′
and ∀l ∈ C
′
\C, I(l) = f alse
(l is assigned false by I). Given I the current interpre-
tation and two formulas F
1
and F
2
, F
1
⊑ F
2
iff every
clause C of F
1
maps to a clause C
′
of F
2
such that
C ⊑ C
′
. In this work, we consider only bijective map-
pings to simplify the tests. Obviously, σ(E) ⊑ F
′
im-
plies ∃I
0
s.t. σ(E) ⊆ F
|I
0
because ⊑ ignores falsified
literals, which belong either to I
0
, in which case we
want to simply ignore them, or they belong to I
1
, in
which case they are simplified in both σ(E) and F
′
.
Determining if such a generalized formula iso-
morphism exists is still in NP. Indeed, if we have an
oracle that returns a consistent generalized renaming
σ
′
that maps a literal l to a literal if l ̸∈ I
0
, or maps to
either true or false if l ∈ I
0
, then checking if σ(E) ⊑ F
′
(σ is σ
′
restricted to literals not in I
0
) amounts to
checking if σ
′
(E) ⊆ F
′′
where F
′′
is obtained by re-
moving from F every literal falsified by I
0
. This latter
check is obviously polynomial.
Identifying generalized isomorphisms could be
done in several ways, for example by adapting a sub-
graph isomorphism solver. In this work, we chose
the easier option of encoding the generalized isomor-
phism as a subgraph isomorphism problem, even if
the proposed encoding is not polynomial. Finding a
polynomial encoding is the subject of future work.
5.2 Generalized Encoding
To allow the possibility to assign some literals of an
entry to true or false, we have to adapt the graph en-
coding of (Blomme et al., 2023). Allowing some lit-
erals of a given clause to be satisfied is straightfor-
ward: we do not remove satisfied clauses before en-
coding the current formula. Allowing the literals of
a given clause to be falsified (guessing I
0
) is more
involved. Indeed, a falsified literal should either be
erased from the clause (if it belongs to I
0
) or kept
(if it belongs to I
1
) in order to match an entry in the
cache. As I
0
and I
1
are unknown, we have to con-
sider both cases, for all falsified literals. So, for each
clause with n falsified literals, we need to consider
2
n
variants of the initial clause obtained by erasing
some falsified literals (from no literal erased to each
falsified literal erased) and to make sure that we only
select one of them. This allows the subgraph isomor-
phism solver to identify which literal belongs to I
0
.
Note that the worst case corresponds to clauses used
as reason, since all the literals but one will be falsified
(there is no conflicting clause at this stage). In order
to avoid matching several variants of a same clause
for different clauses of an entry, we have to introduce
a new type of node in our graph representation. These
new nodes, that we will call exclusion nodes, will link
all the variants of a same clause in the graph repre-
sentation of the current formula. In the entry, since
there is no variant, we simply add one unique exclu-
sion node per clause. As an example, let us consider a
clause C
5
= (x
1
∨x
2
∨x
3
∨x
4
). If the literals x
3
and x
4
are falsified in the current assignment, then this new
encoding will create the 4 variants shown in Figure 5.
Figure 5: Graph representation of all the variants of the
clause C
5
= (x
1
∨ x
2
∨ x
3
∨ x
4
) when x
3
and x
4
are falsified.
A diamond represents a clause of size 4 and an hexagon rep-
resents an exclusion node.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
796

6 EXPERIMENTAL RESULTS
We implemented the proposed approaches on top of
MiniSat (E
´
en and S
¨
orensson, 2003). We disabled
database simplification and restarts. The Glasgow
Subgraph Solver (GSS for short) (McCreesh et al.,
2020) is called to compute subgraph isomorphisms,
i.e. to query our cache. We used the same 580 UN-
SAT instances as in (Blomme et al., 2023).
6.1 Caching, Regular Isomorphisms
We first used the regular isomorphisms and the cache
to immediately prune the search. We considered a
timeout of 2 seconds for each call to GSS and of 15
minutes per benchmark. An excerpt of the results
is shown in the left part of Table 1. For each in-
stance, we give the number of conflicts, the number
of entries created in the cache, the number of calls
to GSS that found an isomorphism (the number be-
tween parenthesis indicates the number of different
entries recognized by isomorphism), the total number
of calls to GSS, the time spent by the solver (with-
out isomorphism detection) and the cumulated time
of all the calls to GSS. All times are in seconds. Our
approach has solved 185 instances (113 for SAT’02
and 72 for SAT’03). We could generate a total of 63
single branch search trees (26 for SAT’02 and 37 for
SAT’03) with this approach, mainly on instances from
the families marg, Urquhart and xor
chain. Thus, we
can often obtain a good compression on these fami-
lies, with few branches in the search tree. We also
observed that this approach can solve in less than 15
minutes some SAT’02 Urquhart crafted instances that
MiniSat is unable to solve in more than 4 hours. The
heuristics used here is not exactly the same as MiniSat
because, in addition to the activity updates present in
the conflict analysis, the dedicated procedure that col-
lects the sources will also update the activity of the
variables it will find.
Since the number of entries keeps growing, and
those elements get larger and larger during the search,
trying to recognize an entry can become very expen-
sive. Moreover, as the subformulas can be very large
as well, finding an isomorphism may take more time
than the imposed limit. On large instances, some calls
to GSS may be aborted and we may miss some exist-
ing isomorphisms, hence some possible compression.
This occurs on problems bigger than PHP
16
.
6.2 Caching, Generalized Isomorphisms
As a second experiment, we have integrated the
generalized isomorphisms to immediately prune the
search tree. This time, as this encoding is much larger
than the regular one, we have imposed a time limit of
30 minutes for the solver and a time limit of 4 sec-
onds for each call to GSS (i.e. twice as much time
as for the regular isomorphism). Some results can
be found in the right part of Table 1. Our approach
has solved a total of 89 instances (51 for SAT’02 and
38 for SAT’03) and has generated a total of 31 single
branch search trees (9 for SAT’02 and 22 for SAT’03).
If we compare the two tables, and notably the in-
stance 3col40 5 4.cnf, we can see that the general-
ized isomorphisms can help to obtain smaller search
trees. However, we also note that the approach is
much slower due to the size of the encoding. Con-
cerning PHP problems, we could not retrieve single
branch search trees with these instances but the gen-
eralized isomorphism is able to detect more isomor-
phisms and also to develop a smaller search tree than
the regular one. Figure 6 shows the search tree de-
veloped by this approach for the problem PHP
5
with
both the regular and generalized isomorphisms. Red
leaves denote classical conflicts while green nodes de-
note hits. Compared to the regular isomorphisms, we
can see that the generalized isomorphisms are able to
detect more hits and also to develop a smaller tree.
6.3 Comparison with Previous Work
Here we compare our two contributions with the pre-
vious work (Blomme et al., 2023). Integrating the
cache within the CDCL solver increases the number
of instances solved and the number of single branch
search trees found compared to the post-processing
approach. However, DPLL with integrated cache al-
lows to find more single branch search trees than the
CDCL approach. This is in part due to the assign-
ment of some variables which prevented their detec-
tion. The generalized cache, even with a larger time-
out, does not scale. Indeed, it creates larger graphs
which limits its applicability on real benchmarks.
7 REDUCED UNSAT PROOFS
When an entry E of the cache is recognized in the
current formula F
|I
and the current branch (corre-
sponding to interpretation I) is pruned, we know that
F
|I
is unsatisfiable because if contains σ(E) where σ
is the renaming identified by the subgraph isomor-
phism. In some cases, this gives very short search
trees. However, this does not translate directly to very
short proofs of unsatisfiability, because the current
proof formats such as DRAT (Wetzler et al., 2014) or
VeriPB (Gocht and Nordstr
¨
om, 2021) do not include
Compressing UNSAT CDCL Trees with Caching
797

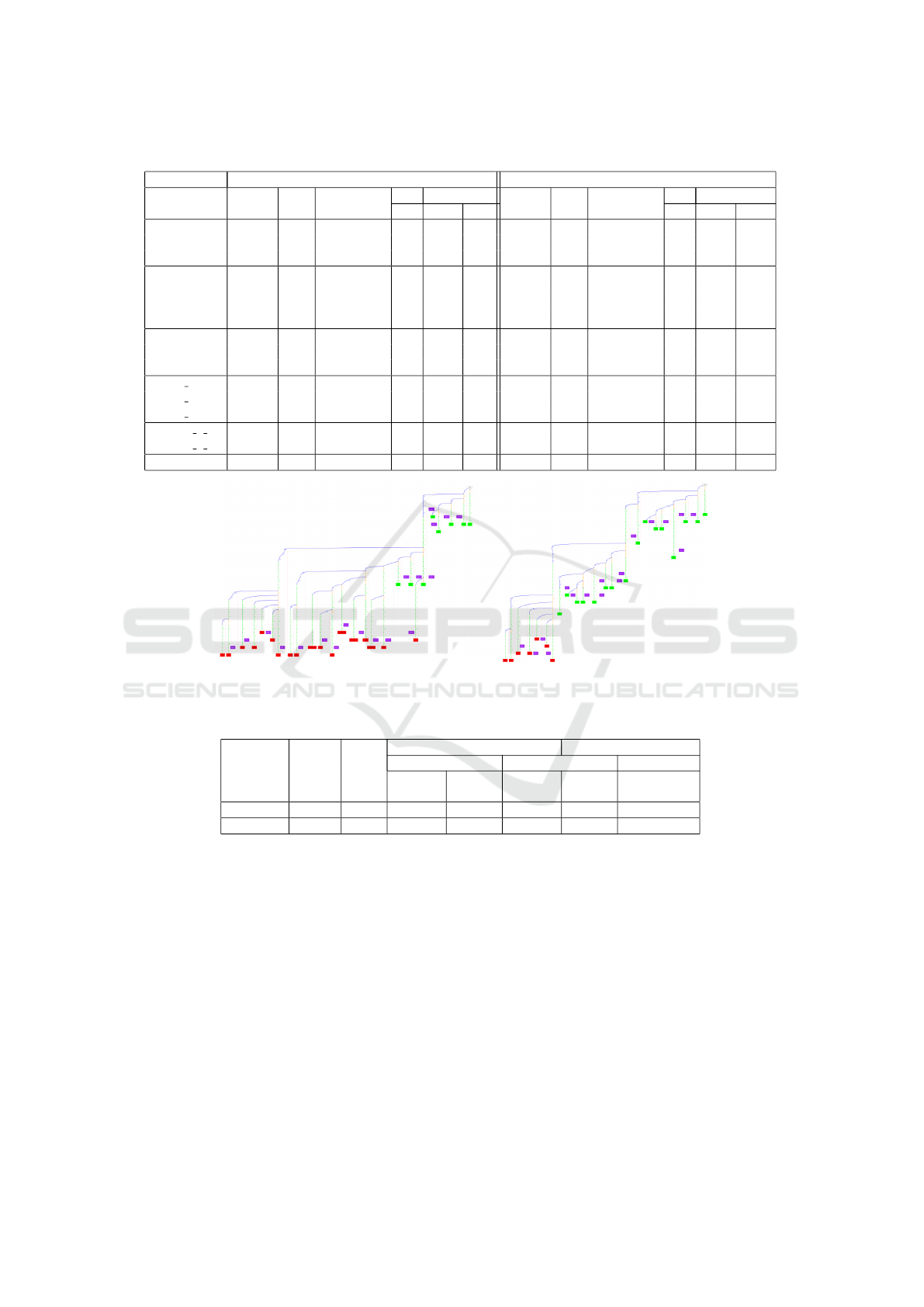
Table 1: Experimental results when the cache is used during the search with both regular and generalized isomorphisms.
CDCL (integrated cache, regular isomorphisms) CDCL (integrated cache, generalized isomorphisms)
Instance Conflicts Cache Subgraph Calls Time Conflicts Cache Subgraph Calls Time
size Isomorphisms Search GSS size Isomorphisms Search GSS
PHP
5
26 19 8 (2) 88 0.0 0.4 23 17 16 (11) 95 0.0 1.2
PHP
7
47 41 29 (8) 259 0.0 1.5 42 35 35 (21) 391 0.1 220.3
PHP
16
187 178 167 (32) 1020 0.7 166.1 - - - - - -
marg2x6 20 17 18 (17) 44 0.0 0.3 20 17 18 (17) 50 0.1 3.3
marg3x3add8 32 25 20 (20) 55 0.0 0.5 31 24 21 (21) 74 0.1 14.1
marg4x4 - - - - - - 41 39 39 (35) 186 0.1 130.5
marg6x6 86 84 84 (84) 276 0.2 15.2 - - - - - -
Urquhart-s3-b9 21 18 17 (17) 38 0.0 0.3 21 18 17 (17) 50 0.0 3.0
Urquhart-s3-b3 29 26 27 (25) 59 0.0 0.9 29 26 27 (26) 67 0.3 18.0
Urquhart-s5-b5 95 91 91 (90) 259 0.4 55.7 - - - - - -
x1 16 18 15 14 (14) 60 0.0 0.7 18 15 14 (14) 94 0.0 21.5
x2 32 - - - - - - 65 54 53 (40) 568 0.1 908.4
x1 96 2177 471 106 (76) 8513 1.8 423.4 - - - - - -
3col20 5 6 27 5 0 (0) 15 0.0 0.1 23 3 2 (2) 16 0.0 17.3
3col40 5 4 110 22 54 (3) 786 0.1 5.5 57 20 27 (4) 809 0.2 1474.8
homer06 102 95 92 (20) 462 0.5 47.7 - - - - - -
Figure 6: Search tree developed for the problem PHP
5
when the integrated cache is used with the generalized isomorphisms
(on the left) and with the generalized isomorphisms (on the right) in a CDCL solver.
Table 2: Comparison with (Blomme et al., 2023). Number of instances solved (number of single branch trees).
(Blomme et al., 2023) This work
Competition #UNSAT MiniSat DPLL (15min) CDCL (15min) CDCL (30min)
(1min) Post Integrated Post Integrated Integrated
processing regular processing regular generalized
SAT’02 382 276 42 (4) 106 (42) 78 (11) 113 (26) 51 (9)
SAT’03 198 78 17 (15) 87 (53) 39 (28) 72 (37) 38 (22)
the required mechanisms to take full advantage of the
recognized isomorphisms. In this section, we explain
how these proof formats could be extended to obtain
short proofs exploiting the recognized isomorphisms.
Basically, we have to instruct the proof checker
that the proof of unsatisfiability for the current for-
mula can be obtained by renaming literals in a previ-
ous subpart of the proof, and the checker must be able
to check this. Trivially, this could be done without
modifying the proof checker by storing in the cache
the proof of unsatisfiability P(E) next to each entry
E, and adding to the generated proof σ(P(E)), that
is the proof previously recorded with all literals cor-
rectly renamed. However, this basic approach will not
reduce the size of the generated proof, since P(E) is
essentially duplicated in the proof whenever E is rec-
ognized. Instead of copying, we use links to existing
proofs, and the proof checker has to verify that these
links are correct, in a reasonably efficient way.
Let us assume that the entry E of the cache was
obtained for an interpretation I
E
. Since E does not
contain in general all the clauses of F
|I
E
, let us denote
s
E
a selection function which indicates which clauses
of the current formula are kept. In essence, s
E
directly
encodes the sources of F but can be represented in a
simple way by an array of Booleans or a list of clause
identifiers. We have E = s
E
(F
|I
E
). For each entry E of
the cache, we thus need to record I
E
and the selection
function s
E
. Now, whenever an isomorphism is iden-
tified, that is, whenever ∃E, σ such that σ(E) ⊆ F
|I
,
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
798

we can add to the proof of unsatisfiability the tuple
I, I
E
, s
E
, σ, µ where µ maps the clauses of E to the cor-
responding clauses in F
I
. Strictly speaking, storing µ
is not necessary to check the proof, but reduces the
complexity of the verification.
E is associated to a conflict C discovered in F
|I
E
and obtained by unwinding the usual conflict analysis
performed by a CDCL solver. If the checker does not
erase any clause, its database contains all the learnt
and original clauses used by the CDLC solver to fal-
sify C by unit propagation from I
E
, and the checker
has already proved that each learnt clause was actu-
ally implied by the formula. Therefore, to verify that
E is unsatisfiable, the checker has to find one clause
C
′
of its database that is actually falsified by I
E
and
such that the sources S(C
′
, I
E
) are equal to E. This
can be done easily by keepingd if the checker keeps
track for every learnt clause of the clauses used in
the derivation of that clause, by following the defi-
nition of the sources. Now, the checker has to ver-
ify that σ(E) ⊆ F
|I
. Since I, I
E
, s
E
, σ are recorded
in the proof, it is easy to compute E = s
E
(F
|I
E
) and
check that σ(E) is a subset of F
I
. With µ, the checker
can also recover the set O of clauses of F
I
which are
mapped to clauses of E. At this point, the checker
knows that O
|I
is unsatisfiable and, as proved in Sec-
tion 4, that F |= ¬SELECT (O, I). Therefore, it can
add ¬SELECT (O, I) to its clause database. Remem-
ber that ¬SELECT (O, I) is used as a conflict. The
clause learnt from this conflict can be checked in the
usual way.
To sum up, in order to generate and check short
proofs of unsatisfiability based on our caching sys-
tem, we have to extend the proof format with a new
declaration that records I, I
E
, s
E
, σ, µ, add a new rule
in the checker that uses this declaration to infer a new
clause ¬SELECT (O, I). This can be done in a rea-
sonable way if the solver does not delete clauses from
its database and associates to each learnt clause the
clauses used to derive that learnt clause. Implement-
ing such a checker is the subject of future work.
8 CONCLUSION
Our goal in this work was to prune as much as pos-
sible the branches of an UNSAT CDCL search tree
to reduce its size for presenting it to the end user as
an explanation of unsatisfiability. To do so, we ex-
tended the work of (Blomme et al., 2023) to include
their caching mechanism directly in a CDCL solver
and generalized it to recognize entries with assigned
literals. The experimental results show that the in-
tegrated cache provides better results than the exist-
ing post-processing approach for CDCL. The gen-
eralized caching procedure improves the results on
crafted benchmarks but does not scale on real bench-
marks. We finally discussed the relationship between
our work and the computation of small certificates of
unsatisfiability. Unfortunately, the current proof for-
mats do not support yet the features needed to benefit
from our short trees to produce short certificates, but
can be extended to support these reduced proofs.
ACKNOWLEDGEMENTS
The first author is partly funded by region “Hauts-de-
France”. This work has been supported by the project
CPER Data from the region “Hauts-de-France”.
REFERENCES
Biere, A., Heule, M., van Maaren, H., and Walsh, T., editors
(2021). Handbook of Satisfiability - Second Edition.
Blomme, A., Le Berre, D., Parrain, A., and Roussel, O.
(2023). Compressing unsat search trees with caching.
In ICAART 2023, pages 358–365. INSTICC.
Cook, S. A. (1971). The complexity of theorem-proving
procedures. In 3rd Annual ACM, pages 151–158.
Davis, M., Logemann, G., and Loveland, D. W. (1962).
A machine program for theorem-proving. Commun.
ACM, 5(7):394–397.
Davis, M. and Putnam, H. (1960). A computing procedure
for quantification theory. J. ACM, 7(3):201–215.
E
´
en, N. and S
¨
orensson, N. (2003). An extensible sat-solver.
In SAT 2003, pages 502–518.
Gocht, S. and Nordstr
¨
om, J. (2021). Certifying parity rea-
soning efficiently using pseudo-boolean proofs. In
AAAI 2021, pages 3768–3777. AAAI Press.
Haken, A. (1985). The intractability of resolution. Theor.
Comput. Sci., 39:297–308.
Ignatiev, A., Previti, A., Liffiton, M. H., and Marques-Silva,
J. (2015). Smallest MUS extraction with minimal hit-
ting set dualization. In CP 2015, pages 173–182.
Marques-Silva, J., Lynce, I., and Malik, S. (2021). Conflict-
driven clause learning SAT solvers. In Handbook of
Satisfiability - Second Edition, pages 133–182.
McCreesh, C., Prosser, P., and Trimble, J. (2020). The glas-
gow subgraph solver: Using constraint programming
to tackle hard subgraph isomorphism problem vari-
ants. In ICGT 2020, pages 316–324.
Moskewicz, M. W., Madigan, C. F., Zhao, Y., Zhang, L.,
and Malik, S. (2001). Chaff: Engineering an efficient
SAT solver. In Proc. of DAC 2001, pages 530–535.
Silva, J. P. M. and Sakallah, K. A. (1999). GRASP: A search
algorithm for propositional satisfiability. IEEE Trans.
Computers, 48(5):506–521.
Wetzler, N., Heule, M., and Jr., W. A. H. (2014). Drat-
trim: Efficient checking and trimming using expres-
sive clausal proofs. In SAT 2014, pages 422–429.
Compressing UNSAT CDCL Trees with Caching
799