Investigation of Heuristics for PIBT Solving Continuous MAPF Problem

in Narrow Warehouse

Toshihiro Matsui

Nagoya Institute of Technology, Gokiso-cho Showa-ku Nagoya Aichi 466-8555, Japan

Keywords:

Multiagent Pathﬁnding Problem, Multiagent Pickup-and-Delivery Problem, Continuous, Lifelong, PIBT,

Heuristics.

Abstract:

We address the heuristics based on map structures in a solution method for continuous multiagent path ﬁnding

problems particularly in the case of relatively narrow warehouse maps. The multiagent pathﬁnding problem

has been studied as a fundamental problem in multiagent systems, and the lifelong/continuous multiagent

pickup-and-delivery problem is a major extension of it that represents the tasks performed by robot carriers

in automated warehouses. While basic methods of multiagent pathﬁnding are generally aimed at resolving

collisions among agents using precisely computed/reserved paths or locally performed resolving algorithms,

there might also be opportunities to employ information of maps and trafﬁc for the heuristics of solution

methods. As such an investigation, we focus on the case of multiagent pickup-and-delivery problems in narrow

warehouse environments and the solution method called Priority Inheritance with Backtracking (PIBT), which

is not based on the reservation of paths and is applicable to continuous problems within very narrow maps.

We experimentally investigate the effect of map settings and additional heuristics based on the structures of

maps.

1 INTRODUCTION

We address the heuristics based on map structures

in a solution method for continuous multiagent path

ﬁnding problems particularly in the case of relatively

narrow warehouse maps. The multiagent pathﬁnd-

ing problem has been studied as a fundamental prob-

lem in multiagent systems where the (ideally) shortest

paths, which also avoid collisions, are simultaneously

found in a time-space graph. There are various ap-

plications of this problem including robot navigation,

autonomous taxiing of airplanes and video games;

here, we focus on the case of automated warehouses

that deploy robot carriers. This class of problems is

called the lifelong/continuous multiagent pickup-and-

delivery problem (Ma et al., 2017), which is an exten-

sion of continuous multiagent pathﬁnding problems.

In a typical system, each agent is repeatedly allocated

to one of tasks generated on demand and moves from

its current location to a delivery location via a pickup

location.

The problem consists of task allocation and mul-

tiagent pathﬁnding problems that are continuously

https://orcid.org/0000-0001-8557-8167

solved. While the task allocation can be solved as a

combinatorial optimization problems for static prob-

lems (Liu et al., 2019), greedy allocation methods are

often employed for continuous problems with tasks

generated on demand (Ma et al., 2017).

There are several solution methods for multiagent

pathﬁnding problems. A greedy approach repeat-

edly ﬁnds and allocates each agent’s collision-free

path in a predetermined order among agents using

the A* algorithm (Hart and Raphael, 1968; Hart and

Raphael, 1972) on a time-space graph (Silver, 2005).

A major exact solution method, called Conﬂict Based

Search (Sharon et al., 2015), performs two layers of

search, where collisions of agents are managed by a

tree-search in the high-level layer while a pathﬁnd-

ing algorithm in the low-level layer is used to ﬁnd a

conﬂict-free path for each agent. However, this ap-

proach is computationally expensive, and several ex-

tensions of efﬁcient or approximation methods have

been proposed (Ma et al., 2019; Barer et al., 2014).

Several extended problems and solution methods have

also been proposed for more practical situations (Li

et al., 2021; Yamauchi et al., 2022; Miyashita et al.,

2023; Yakovlev and Andreychuk, 2017; Andreychuk

et al., 2022; Andreychuk et al., 2021).

Matsui, T.

Investigation of Heuristics for PIBT Solving Continuous MAPF Problem in Narrow Warehouse.

DOI: 10.5220/0012397900003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 1, pages 341-350

ISBN: 978-989-758-680-4; ISSN: 2184-433X

341

In another type of greedy method, each agent de-

termines its next move in each time step by locally

solving collisions of agents’ moves. Priority Inher-

itance with Backtracking (PIBT) (Okumura et al.,

2022; Okumura et al., 2019) is classiﬁed into this

type of algorithms based on push-and-rotate opera-

tions (De Wilde et al., 2014; Luna and Bekris, 2011),

and it employs priorities of agents and a limited back-

tracking method in the process of resolving collisions.

Although it requires the relatively restricted condition

such that any vertex in a graph representing a ﬂoor

plan must be contained in cycles, this is generally ac-

ceptable in the case of warehouses.

While fundamental methods generally resolve

collisions among agents using precisely computed/re-

served paths or locally performed resolving algo-

rithms, there might also be opportunities to employ

information of maps and trafﬁc for the heuristics of

solution methods. As such an investigation, we focus

on the case of multiagent pickup-and-delivery prob-

lems in narrow warehouse environments and the orig-

inal version of the solution method PIBT, which is

not based on the reservation of paths and is applica-

ble to continuous problems within very narrow maps.

We experimentally investigate the effect of map set-

tings and additional heuristics based on the structures

of maps.

In well controlled automated warehouses satisfy-

ing the solvable conditions of this kind of lightweight

MAPF algorithms, the low computational cost of the

solvers can be promising to develop real-time appli-

cations. As effective add-ons for such solvers, the

heuristic methods without exact searches/reservations

on time-space is also important.

The rest of the paper is organized as follows. In

the next section, we present the background of our

study, including multiagent pathﬁnding/pickup-and-

delivery problems, the solution method PIBT, and the

aim of this study. Then we present our proposed ap-

proaches in Section 3. We ﬁrst brieﬂy consider an

appropriate map settings in the case with sufﬁcient

space. Then, for the case of narrow maps, we em-

ploy additional heuristics based on maps structures

and inﬂuential agents. We experimentally investigate

these approaches in Section 4 and conclude the paper

in Section 5.

2 PRELIMINARY

2.1 Multiagent Pathﬁnding Problem

The multiagent pathﬁnding (MAPF) problem is a fun-

damental problem for ﬁnding multiple agents’ move-

White: passageway. Black: shelf (obstacle). Light blue:

pickup/delivery location.

Figure 1: Example of grid-world warehouse map.

ment paths avoiding collisions in a time-space graph.

A problem consists of graph G = (V, E) representing

a two-dimensional map such as a warehouse or maze,

a set of agents A, and a set of start-goal pairs of ver-

tices to be allocated to the agents. Each agent has

its origin and destination vertices and should move

along its (ideally) shortest path avoiding other agents.

There are two cases of colliding paths, called ver-

tex and edge collisions. In a vertex collision, two

agents stay at the same location at the same time,

while in an edge collision, two agents move on the

same edge at the same time from both ends of the

edge. In a typical setting, a grid-like map contain-

ing obstacles and discrete time steps are employed.

There are several classes of solution methods includ-

ing the CA* algorithm (Silver, 2005), Conﬂict Based

Search (Sharon et al., 2015), and variants of push-

and-rotate approach (Okumura et al., 2022).

The continuous MAPF problem is an extended

class of the MAPF problems where each agent up-

dates its next goal after the agent moves to its current

goal. A solution method for MAPF is repeatedly per-

formed for the new paths.

2.2 Lifelong Multiagent

Pickup-and-Delivery Problem

The lifelong multiagent pickup-and-delivery (MAPD)

problem (Ma et al., 2017) is a class of continuous

MAPF problems, where multiple pickup-and-delivery

tasks in a warehouse or construction site are repeat-

edly allocated to agents. Figure 1 shows an example

of warehouse map. The tasks can appear at arbitrary

timings in a time span, and they are represented by

a set of currently generated pickup-and-delivery tasks

T . Task τ

∈ T has its pickup and delivery locations

, g

), where s

, g

∈ V . After task τ

is allocated to

an agent, the agent moves from its current location

to a delivery location g

through a pickup location s

to complete the task. The problem can be decom-

posed into the task allocation and continuous MAPF

problems. While (continuous) MAPF solvers can be

applied to pathﬁnding, (partially) greedy approaches

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

342

1 UNDECIDED← A(t) // agents list

2 OCCUPIED←

0 // vertices list

3 update priorities p

(t) for all agents a

4 while UNDECIDED̸=

0 do

5 let a be the agent with highest priority p(a) in

UNDECIDED

6 PIBT(a,⊥)

7 end while

9 function PIBT(a

)

10 UNDECIDED←UNDECIDED\{a

}

11 C

← ({v|(v

(t), v) ∈ E}∪ {v

(t)})

12 \({v

(t)}∪OCCUPIED)

13 while C

̸=

0 do

14 v

∗

← arg max

v∈C

(v) // most preferred move

15 OCCUPIED←OCCUPIED∪{v

∗

}

16 if ∃a

∈UNDECIDED s.t. v

∗

= v

(t) then

17 if PIBT(a

) is valid then

18 v

(t + 1) ← v

∗

19 return valid

20 else

21 C

← C

\OCCUPIED

22 end if

23 else

24 v

(t + 1) ← v

∗

25 return valid

26 end if

27 end while

28 v

(t + 1) ← v

(t)

29 return invalid

30 end function

(t): location of agent a

at time step t

Figure 2: PIBT (Okumura et al., 2022) at time step t.

are commonly employed to allocate tasks generated

on demand.

A fundamental approach is based on the well-

formed MAPD problems that take into account end-

point vertices, which can be pickup, delivery, or park-

ing locations of agents (

ap et al., 2015; Ma et al.,

2017). In this approach, tasks can be greedily al-

located under several rules, and their paths are also

greedily reserved without deadlock situations. How-

ever, the paths basically cannot contain endpoints,

except for start/goal vertices, and this requires extra

aisle space in warehouses. Moreover, the greedily re-

served paths have relatively large redundancy in the

parallel execution of tasks.

We focus on a different type of solution method,

PIBT (Okumura et al., 2022), as a continuous MAPF

solver that can be applied to narrow maps with dense

populations of agents. Since this method is also a

greedy approach, there is a different restriction as

mentioned below, but it is relatively acceptable in the

case of warehouses.

2.3 PIBT

PIBT (Okumura et al., 2022) is a solution method for

the (continuous) MAPF problem that can be consid-

ered a variant of the push-and-rotate approach. The

method employs relatively simple operations that in-

troduce the priority of agents and limited backtrack-

ing into the push-and-rotate process, and each agent

determines its next move at each time step (Fig. 2).

For continuous problems, each agent a

has its

list of subgoals and moves to the ﬁrst subgoal, and

it also has a priority p(a

) based on the elapsed time

for the current subgoal and its name (for tie-break).

Each agent a with locally highest priority p(a) initi-

ates the process (line 6 in Fig. 2). An agent a

select

its most preferred move based on evaluation function

(line 14 in Fig. 2) and asks a neighboring agent on

’s shortest path to move if necessary (push) (lines

16 and 17 in Fig. 2). Here we simply deﬁne f

as the

distance from the current location of a

to its ﬁrst sub-

goal and implement f

as a distance map that is com-

puted for the ﬁrst subgoal. The pushed agent a

tries

to move to its neighboring vertex, and it also pushes

’s neighboring agent if necessary. If the all agents

obstructing agent a

can move, a chain of moves is

determined (line 18 in Fig. 2). Here, a pushed agent

in the chain may move into the current location of

the agent that initially pushes (rotation). If there is

no agent obstructing agent a

, its move is determined

(line 24 in Fig. 2).

If one of the (pushed) agents cannot move, back-

tracking is performed (line 29 in Fig. 2), and an agent

tries to push one of its other neighboring agents. This

search is limited, and an agent that cannot move stays

in its current location at the next time step (line 28 in

Fig. 2).

For all vertices v

and for all vertices v

neighbor-

ing v

, if the vertices v

and v

are contained in a cycle,

agents’ locations can be rotated through the cycle, and

PIBT can solve such a problem. Due to this condition,

the method cannot be applied to the maps with a dead

end. On the other hand, if the above condition is sat-

isﬁed, the method can work with narrow aisles and

dense populations of agents, even if all non-obstacle

vertices/cells are occupied by agents.

For MAPD problems, we employ a basic greedy

task allocation method where each idle agent selects a

task whose pickup location is nearest from its current

location.

2.4 Aim of Study

For MAPF problems, most of solution methods em-

ploy a pathﬁnding algorithm on time-space graphs

that computes individual agents’ paths, and the paths

are reserved even if a given situation can change.

Complete algorithms that resolve collisions among

agents require a relatively high computational cost,

while several greedy methods suffer from redundancy

Investigation of Heuristics for PIBT Solving Continuous MAPF Problem in Narrow Warehouse

343

in ﬂoor plans and sparse parallel execution of tasks.

These fundamental methods adjust individual agents’

paths without considering additional information of

map structures and trafﬁc.

On the other hand, the solution methods based on

push-and-rotate operations are ﬂexible for various sit-

uations, but there is global redundancy in the moves

of agents due to myopic planning. While previous

studies partially integrated pathﬁnding and reserva-

tion into PIBT to mitigate this drawback (Okumura

et al., 2019), there might be opportunities to investi-

gate several heuristics of agents’ moves and adjust-

ments of the maps themselves. We address this is-

sue in warehouse environments with narrow aisles. In

particular, we concentrate on the inﬂuence of map set-

tings and fundamental additional heuristics that might

be components to control relatively low-level solution

methods such as PIBT without precise reservation of

agent paths. Since it is not straightforward to grasp

such inﬂuences on a greedy solution method that is

affected by several biases, we experimentally investi-

gate a few properties as a ﬁrst case study.

3 ADJUSTING MAP SETTINGS

AND APPLYING HEURISTICS

BASED ON MAP STRUCTURES

3.1 Limitation on Moves

A simple way to improve the control of agents is a

limitation on moves in maps. Here, conventional grid-

like maps represented with undirected graphs are re-

placed by directed graphs, and some edges are re-

moved to indicate lanes. There is no edge conﬂict on

such a directed edge, and the settings with directed

edges have been evaluated as easier example prob-

lems in previous studies with the time-space A* algo-

rithms (Li et al., 2021). This modiﬁcation affects the

shortest paths to goals, and possible moves in push

operations in PIBT.

When there is relatively sufﬁcient space in a ﬂoor

plan, setting pairs of opposite-direction lanes is intu-

itively reasonable. Each lane inhibits agents to move

in inverted directions but allows them to turn into an-

other lane. While such maps are effective in gen-

eral applications, they are particularly suitable to so-

lution methods such as PIBT that locally solves colli-

sions on demand. On the other hand, for the solution

methods based on endpoints, two lanes are necessary

for each aisle in addition to endpoint zones, particu-

larly in warehouse settings, and this space redundancy

may not be acceptable. Note that PIBT allows agents

Non-obstacle cells with thick frames are intersections, and

other non-obstacle cells are aisles.

Figure 3: Map Structure.

to pass through pickup and delivery zones in ware-

houses, and the number of additionally required lanes

is relatively small. Therefore, we consider that a set-

ting using such opposite lanes is a promising solution

for improving the performance of PIBT for the cases

where relatively sufﬁcient space is available.

In the case of narrow aisle cells whose width is a

single unit, one-way lanes can be introduced. How-

ever, such settings might be too restrictive on the

moves of agents in several situations, and thus there

are an incentive to analyze the effect of such one-way

lanes.

When designing maps with directed graphs, care

must be taken not to lose cycles for any vertex, and

satisfying this requirement might sometimes be com-

plicated.

3.2 Employing Knowledge of Map

Structure

In the following, we extract the map structure and em-

ploy that information for heuristics in PIBT. The non-

obstacle cells (vertices) in the narrow grid-like maps

are categorized into aisles and intersections (Fig. 3).

An aisle is a set of neighboring non-obstacle cells that

has two neighboring non-obstacle cells, while an in-

tersection is a single non-obstacle cell that has three

or four neighboring non-obstacle cells. For simplic-

ity, we assume that maps consist of narrow aisles

whose width is one, and whose intersections are sin-

gle cells. Such structures of simple warehouses can be

captured in relatively simple preprocessing or given

as additional attributes of maps. In our experiment,

the aisles and intersections were extracted from man-

ually labeled areas (for analysis) in a preprocessing by

considering the number of neighboring non-obstacle

cells, although those can be easily extracted without

such labels.

The aisles and intersections are managed as areas.

Each area has its basic information including its label,

type, set of contained cells, and set of cells neighbor-

ing its ends. Each non-obstacle cell also has a label of

its corresponding area, and the label is used for cross

reference.

We employ a shared information store that has the

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

344

Circles: agents. Arrow: a part of an agent’s shortest path

to its goal. Dominant agent a

has highest priority p(a

)

within an aisle, and a neighboring intersection that is af-

fected by a

’s shortest path is identiﬁed.

Figure 4: Dominant agent in aisle.

information on map structures and agents related to

the parts of the structure. It is assumed that agents

access the shared information in a consistent order

and then update or refer to the information relevant

to them.

3.3 Managing Information of Dominant

Agent in Aisle

With the knowledge of map structure, we summarize

the information of agents in each aisle. Here, we fo-

cus on the agent that has the highest priority among

the agents in the same aisle and call it the dominant

agent in the aisle (Fig. 4). This is approximated infor-

mation, since the agent might not push other agents or

might be pushed by an agent outside of the aisle.

In addition to the name of the dominant agent, its

preferred move direction is computed and stored. Ac-

tually, the preferred direction is represented as a tem-

porary subgoal cell in relation to the current aisle.

When a dominant agent goes through the current

aisle, one of two neighboring intersections that has the

smaller distance value to the agent’s goal is selected.

On the other hand, when a dominant agent’s goal

is within the current aisle, the temporary subgoal cell

is selected as follows. When the dominant agent is in

its goal cell, the current cell is selected, and this in-

dicates that the agent will not push any other agents.

Otherwise, the direction from the dominant agent’s

current cell to its goal in the current aisle is computed,

and a neighboring intersection in that direction is se-

lected. Note that when an agent arrives at its goal cell,

its priority is reset. Therefore, such an agent is not the

dominant agent in most cases.

The information of the dominant agents is initial-

ized before the recursive process of PIBT (line 1 in

Fig. 6). It should also be updated in the process of

PIBT, since several agents’ next locations and pri-

orities are determined and reserved in this process.

When the next states of agents are determined, the

information on corresponding aisles are marked as

‘dirty’ (lines 20, 27 and 32 in Fig. 6) and recomputed

using the next states if necessary (line 15 in Fig. 6).

Agent a

should not be pushed into the path of ﬁrst pushing

agent a

Figure 5: Replacement of agent’s location.

3.4 Direction Selection 1: Replacement

of Agents’ Locations

We employ the information on map structure to adjust

the direction selection of agents in the recursive pro-

cess of PIBT. Since agents cannot pass each other in

aisles in the case of narrow maps, the substantial se-

lection of moving direction is performed by the agents

at intersections.

An important interaction among agents is to re-

place the locations of agents going in opposite direc-

tions around an intersection (Fig. 5). For this opera-

tion, we extend the recursive process of PIBT so that

the information of the root (ﬁrst pushing) agent a

the recursion is inherited in the process (lines 7, 10

and 18 in Fig. 6). When an agent a

at an intersec-

tion is pushed, the agent evaluates the preferred move

direction d

of the ﬁrst pushing agent by referring to

the information of a

. Here, we assume that a default

tie-breaking order of moving direction is common to

all agents. If direction d

is the direction where the

distance from pushed agent a

to its goal increases,

’s preference value f

′

of direction d

is modiﬁed to

avoid the move to the direction (line 15 in Fig. 6).

Since we simply use distance values to a goal as the

preference values f

of directions, the distance value

for d

is temporally increased to a sufﬁciently large

value as follows.

′

(v, a

) =



∞ v is in direction d

(v) otherwise

(1)

By this modiﬁcation, a pushed agent in an inter-

section will avoid a move where the agent is pushed

into the ﬁrst pushing agent’s moving path.

Although other agents in a push chain might also

affect an agent pushed at an intersection, we focus

only on the initiator agent of the push chain as the

most inﬂuential one.

3.5 Direction Selection 2: Tie-Breaking

for Shortest Paths to Avoid

Dominant Agents

Another situation to be considered by an agent at

an intersection is the dominant agents in neighbor-

Investigation of Heuristics for PIBT Solving Continuous MAPF Problem in Narrow Warehouse

345

1 UpdateAislesInformation() // *1

2 UNDECIDED← A(t) // agents list

3 OCCUPIED←

0 // vertices list

4 update priorities p

(t) for all agents a

5 while UNDECIDED̸=

0 do

6 let a be the agent with highest priority p(a) in

UNDECIDED

7 PIBT(a,a,⊥) // *2

8 end while

10 function PIBT(a

) // *2

11 UNDECIDED←UNDECIDED\{a

}

12 C

← ({v|(v

(t), v) ∈ E}∪ {v

(t)})

13 \({v

(t)}∪OCCUPIED)

14 while C

̸=

0 do

15 v

∗

← arg max

v∈C

′

(v, a

) // most preferred move // *1, *2

16 OCCUPIED←OCCUPIED∪{v

∗

}

17 if ∃a

∈UNDECIDED s.t. v

∗

= v

(t) then

18 if PIBT(a

) is valid then // *2

19 v

(t + 1) ← v

∗

20 MarkUpdateOfAislesInformation() // *1

21 return valid

22 else

23 C

← C

\OCCUPIED

24 end if

25 else

26 v

(t + 1) ← v

∗

27 MarkUpdateOfAislesInformation() // *1

28 return valid

29 end if

30 end while

31 v

(t + 1) ← v

(t)

32 MarkUpdateOfAislesInformation() // *1

33 return invalid

34 end function

(t): location of agent a

at time step t

*1: information of dominant agents in aisles

*2: propagation of root (ﬁrst pushing) agent

Figure 6: Extended PIBT at time step t.

ing aisles (Fig. 7). With the information of dominant

agents in aisles, each agent a

at an intersection eval-

uates their inﬂuences. When a neighboring aisle is

in the direction d

i,k

that decreases the distance to a

’s

goal, and the path of dominant agent a

(with a prior-

ity greater than a

) in the aisle contains the intersec-

tion of a

’s current location, dominant agent a

might

push back agent a

. In such a situation, the preference

value f

′

of direction d

i,k

is modiﬁed to weakly avoid

the move to that direction and to select another short-

est path in a different direction if one exists (line 15 in

Fig. 6). Here, the preference (distance) value for the

direction is slightly increased by adding a small value

less than unit distance so that priority value p(a

) of

dominant agent a

is taken into account as follows.

′

(v, ∗) =



(v) + w × p(a

) v is in direction d

i,k

(v) otherwise

(2)

Here, w is a sufﬁciently small coefﬁcient value.

This weighting to the preference value for the di-

rection can be integrated with the modiﬁcation of the

values to replace agents’ locations.

As an exception case, if the current goal of agent

Agent a

should not enter the aisle where dominant agent a

with higher priority is coming, and a direction on another

shortest path to goal g

should be selected.

Figure 7: Tie-breaking of shortest path.

at an intersection is within an aisle neighboring to

the intersection, agent a

enters to the goal aisle.

Note that this modiﬁcation only affects the tie-

breaking among shortest paths, and rerouting the

agent to a detour requires an additional operation that

introduces new intermediate subgoals and different

distance computations. One the other hand, such a

rerouting approach requires precise information on

reserved paths of agents and might be ineffective,

particularly in maps with narrow aisles where other

agents are affected by such rerouting.

3.6 Limitation on Preference to Move

by Map Settings

Our major interest is the control of solution methods

using maps and related information, and we investi-

gate the effect of map settings that might be com-

plementary with the heuristics for solution methods.

As mentioned in Section 3.1, the agents’ moves can

be partially restricted using directed graphs, while a

modiﬁcation must satisfy the condition of solvable

problems for PIBT. On the other hand, this limita-

tion can be separately applied to the maps used for

computing the shortest paths of agents, which only

requires the connectivity of directed graphs.

Since a fully automated optimization of such set-

tings needs various analyses, we experimentally com-

pare several heuristic settings that are manually set as

a ﬁrst investigation. Because PIBT has the capability

to locally solve a conﬂict among agents, excessively

restrictive settings might be totally ineffective. This

also depends on the number of agents in the environ-

ment.

A basic approach loosely causes rotation moves

of agents by a partial restriction of their moves in the

map referenced for the computation of their shortest

paths. In addition, such a restriction distributes short-

est paths of several agents that have to avoid restricted

moves in several vertices.

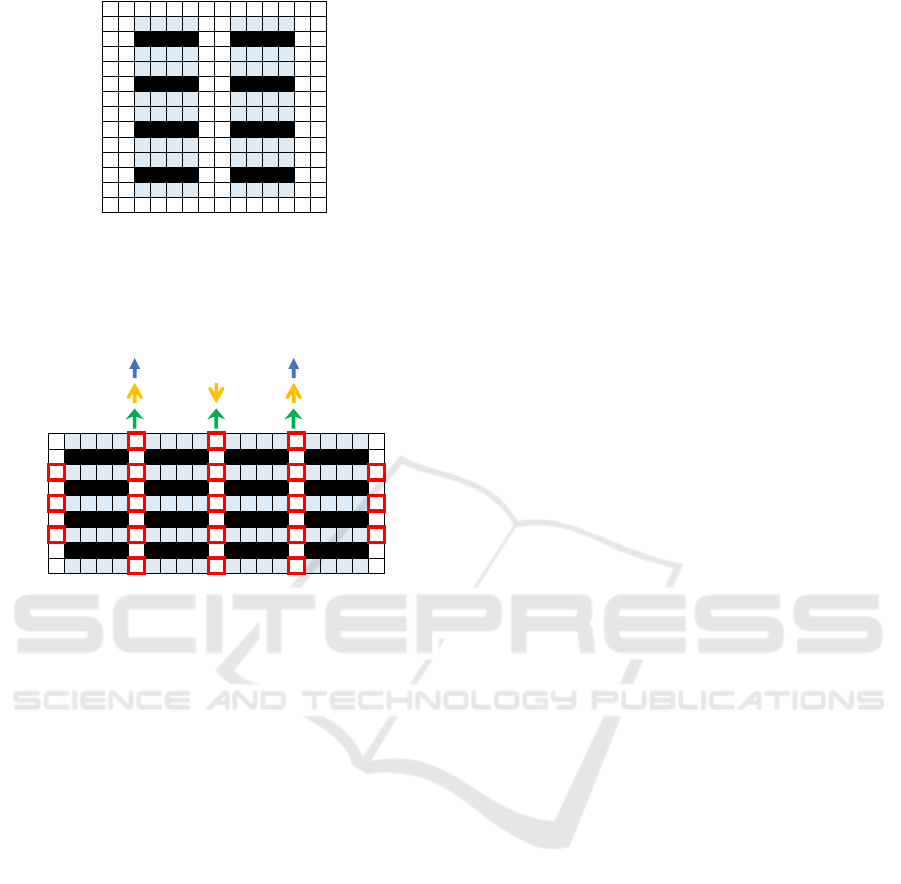
We select inﬂuential ‘streets’ in a map and set the

restriction on moves to them (Fig. 9). While there

are a number of possible selections, we choose sev-

eral combinations of vertical streets whose ends are

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

346

When opposite lanes are set, agents cannot move to back-

ward and must move on left-hand lanes, while they can

move to a neighboring opposite lane.

Figure 8: Relatively sparse map for opposite lanes.

Skip

Alternative

Uniform

Inverted move directions on several vertical streets are re-

stricted.

Figure 9: Map with narrow aisles.

the intersections with the top and bottom cells in a

map. Moreover, we investigate the cases where all

cells in the streets are restricted and the cases where

the restriction is only applied to intersections.

4 EVALUATION

Here, we report the experimental evaluation of our

proposed approaches.

4.1 Settings

We employed several maps that are modiﬁed ver-

sions of typical Kiva-like warehouse maps (Ma et al.,

2017), and they are narrowed by eliminating some

spaces. Figure 8 shows an example map for the case

with opposite lanes as mentioned in Section 3.1, and

Fig. 9 shows the case of narrower maps with aisles

whose width is a single unit. We varied the number

of agents up to the number of non-obstacle cells. For

MAPD problems, N pT tasks were randomly gener-

ated at every time step, up to 500 tasks in total.

We compared the following methods that were in-

crementally combined and applied to the case of nar-

row aisles maps.

• PIBT. Our baseline implementation of PIBT

based on the previous literature (Okumura et al.,

2022).

• DR. Modiﬁcation of direction selection to re-

place locations of agents going opposite direc-

tions shown in Section 3.4.

• DA. Modiﬁcation of direction selection to weakly

avoid an aisle in shortest paths where a dominant

agent is going in the opposite direction, as men-

tioned in Section 3.5.

For the limitation on moves in the maps referenced

in the computation of shortest paths as described in

Section 3.6, we compared several combinations of

one-way vertical streets in the map shown in Fig. 9,

as follows.

• Skip. Except for the ﬁrst and last columns of

the map whose ends are parts of aisles, every

other vertical street are selected, and the down-

ward edges from the corresponding vertices are

removed.

• Alternative. Except for the ﬁrst and last column

of the map, all vertical streets are selected, and the

downward or upward edges from the correspond-

ing vertices are removed. The directions of re-

moved edges are inverted for each selected street

alternatively.

• Uniform. Except for the ﬁrst and last column of

the map, all vertical streets are selected, and, the

downward edges from the corresponding vertices

are removed.

In addition, the restriction is applied to all cells in-

cluding aisles and intersections (All) or only intersec-

tions (Int).

We evaluated makespan (MS), which is the time

steps to complete all tasks, and service time (ST) to

complete each task. The results over ten executions

with random initial locations of agents were averaged

for each problem instance. The experiments were per-

formed on a computer with g++ (GCC) 8.5.0 -O3,

Linux 4.18, Intel (R) Core (TM) i9-9900 CPU @ 3.10

GHz and 64 GB memory.

4.2 Results

Tables 1-4 show the results, where the minimum value

in each setting of (#agent, N pT ) is marked in bold.

Table 1 shows the cases with/without opposite

lanes. We can conﬁrm that the setting of lanes re-

duced time steps for agent moves in most cases. In the

Investigation of Heuristics for PIBT Solving Continuous MAPF Problem in Narrow Warehouse

347

Table 1: Two opposite lanes (PIBT).

#agent 10 30 60 90 120 150

N pT prb. MS ST MS ST MS ST MS ST MS ST MS ST

1 no limit 654.3 76.7 529.2 24.2 530.4 24.8 534.2 28.8 545.3 39.2 576 61.4

opp. lanes 644.1 73.3 524.2 21.7 524.8 24.3 527 25.9 533.5 29.7 539.7 35.8

10 no limit 633.4 279.9 287.6 113.4 222.4 82.1 213.8 81.7 247.6 94.7 305.9 125.3

opp. lanes 615.9 270.2 247.8 94.9 183.2 64.7 176.1 60.8 184.6 63.9 200 72.1

Table 2: Narrow aisles (no restriction on moves in computation of shortest paths).

#agent 10 30 60 90 120 125

N pT alg. MS ST MS ST MS ST MS ST MS ST MS ST

1 PIBT 859.5 175.3 554.9 37.6 588.4 65.6 691.4 121.2 1040.8 297.4 1394.0 454.6

DR 801.4 144.9 543.2 34.4 575.6 61.1 635 107.2 1003.9 282.4 1412.2 457.5

DA 873.5 180.1 549.4 37.3 592.8 65.7 685.8 120.8 1018.1 290.3 1391.8 467.2

DR+DA 799.1 144.5 543 34.2 569.7 60.8 631 101.6 968.2 264.5 1366.9 436.7

10 PIBT 849.5 384.1 465.3 195.5 461.5 194.7 582.4 252.3 907.8 421.0 1281.2 576.1

DR 785.4 349.2 416.6 176.0 412.3 175.3 512.8 225.5 885.4 395.3 1256.7 553.5

DA 840.9 377.8 458.6 193.3 451.6 189.8 571.6 240.7 901.3 409.4 1274 572.5

DR+DA 779.1 345.6 418.7 175.7 410.8 175.0 500.4 221.9 870.2 397.4 1242.8 537.5

Table 3: Narrow aisles (restriction on moves in computation of shortest paths, PIBT).

#agent 10 30 60 90 120 125

N pT prb. MS ST MS ST MS ST MS ST MS ST MS ST

1 no limit 859.5 175.3 554.9 37.6 588.4 65.6 691.4 121.2 1040.8 297.4 1394 454.6

Skip-Int 864.8 175.0 553.7 37.1 589.3 65.4 688.7 124.5 1042.4 308.9 1396.3 463.6

Skip-All 934 208.7 579.3 49.0 606.5 72.1 710 128.4 1067.8 299.2 1375.7 435.0

Alt-Int 868.4 180.3 546.1 36.5 590.6 63.7 682.9 115.9 1028.1 295.9 1371 460.0

Alt-All 905.6 196.2 566.1 43.1 603.9 66.1 687.6 116.9 1042.3 284.9 1328.2 420.5

Uni-Int 922 204.3 552.3 38.4 576.3 60.0 660.3 109.9 1009.3 292.7 1425.9 480.6

Uni-All 1183.5 334.0 657.8 84.4 623.2 70.5 714.7 125.3 1046.1 286.0 1314.5 411.3

10 no limit 849.5 384.1 465.3 195.5 461.5 194.7 582.4 252.3 907.8 421.0 1281.2 576.1

Skip-Int 864.5 392.0 455.3 193.8 454.9 189.0 588.3 251.5 922.2 416.9 1288.8 582.1

Skip-All 934.8 428.7 527.9 228.4 502.1 212.0 618.3 263.9 942.9 415.2 1236.8 543.6

Alt-Int 859.2 387.6 444.1 189.0 431 180.8 571.9 245.0 916.8 416.6 1265.1 569.3

Alt-All 911.2 415.7 511.5 219.1 471.9 197.2 585.9 244.6 923.7 411.3 1266.8 549.4

Uni-Int 911.3 414.1 452.3 193.0 422.4 176.6 537 225.6 896.6 404.6 1291.4 581.3

Uni-All 1162 542.6 635.1 280.3 527.9 219.2 601.3 255.9 953.2 406.8 1230.8 539.3

Table 4: Narrow aisles (restriction on moves in computation of shortest paths, DR+DA).

#agent 10 30 60 90 120 125

N pT prb. MS ST MS ST MS ST MS ST MS ST MS ST

1 no limit 799.1 144.5 543 34.2 569.7 60.8 631 101.6 968.2 264.5 1366.9 436.7

Skip-Int 815.1 152.8 545.4 34.6 574.7 62.6 643.6 107.4 997 278.4 1361.9 438.6

Skip-All 819.2 154.9 541.3 35.9 576.3 63.6 643.9 110.7 1037.8 293.1 1457.5 464.6

Alt-Int 818.9 155.0 543.7 33.8 575.9 59.4 634 103.3 1003.2 276.8 1371.6 443.0

Alt-All 820 155.2 545 34.1 575.6 60.5 639.5 104.5 1046.1 288.4 1464.2 448.1

Uni-Int 870.6 176.8 543.5 34.3 573.9 56.8 622.8 96.3 990.3 270.1 1376.2 446.9

Uni-All 910.2 197.2 548.4 35.5 576.3 58.8 630.3 97.7 1097.5 297.7 1480 472.5

10 no limit 779.1 345.6 418.7 175.7 410.8 175.0 500.4 221.9 870.2 397.4 1242.8 537.5

Skip-Int 791.3 352.3 420.7 178.3 415.7 177.1 510.8 227.3 881.7 397.0 1232.8 539.3

Skip-All 797.9 357.7 427.2 178.8 424.9 181.4 514.2 230.8 917.2 401.5 1320.8 563.4

Alt-Int 797.7 357.1 412.2 173.7 394.5 168.7 506.1 226.8 873.5 394.0 1248.2 546.3

Alt-All 795.6 356.7 413 173.5 402.8 171.3 492.6 219.1 952.1 409.1 1352.5 563.2

Uni-Int 857.6 384.2 418.7 179.3 372.3 157.2 465.6 202.0 871.2 390.8 1234.9 540.4

Uni-All 890.7 402.3 433.3 185.4 383.7 158.8 477.6 208.2 955.1 408.9 1403 596.6

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

348

cases of relatively high concurrency of tasks (N pT =

10), and in the cases of dense populations of agents,

MS and ST were relatively reduced.

Table 2 shows the case of narrow aisles without

the restriction on moves in the computation of shortest

paths. The inﬂuence of heuristics for direction selec-

tion varied with the density of agents’ population. Ex-

cept very dense cases, DR was basically effective in

reducing MS and ST, while DA alone was often not so

effective. It revealed that the replacement of agents’

locations is a fundamental operation and more impor-

tant. On the other hand, the combination of them was

relatively effective in most cases. We found that these

local heuristics might disturb the process of original

solution method in several instances, while the results

were relatively better in average.

Table 3 shows the case of narrow aisles with a

restriction on moves in the computation of shortest

paths. There seems to be several complicated trade-

offs among different settings. While the comparison

between Skip and Alternative revealed that a sufﬁ-

cient restriction is necessary to affect agents’ moves,

the restriction is often excessive in the cases of sparse

populations of agents. In most cases, Int that only

limit moves for intersection vertices reduced the time

steps than All. It revealed some trade-off between the

limitation/control of agents’ moves and the planning

of agents on demand. The combination of Uniform

and Int was relatively better than others except the

cases of sparse populations of agents. Different re-

strictions on agents’ moves might enforce different

rotation paths, and it can be effective according to sit-

uations, as low-cost heuristics.

The case of combinations of heuristics for direc-

tion selection and the restriction on agents’ moves in

the computation of shortest paths is shown in Tbl. 4.

Similar to the case without any restriction on agents’

moves, the additional heuristics for PIBT were rel-

atively effective where the population of agents is

not too dense, and both approaches were complemen-

tary. On the other hand, it was revealed that the com-

bined heuristics were ineffective with the effect of

map settings in very dense cases. In the dense cases,

a global control/limitation method of agents’ moves

is more important and the heuristics for local interac-

tions of among can be inconsistent with such a control

method. There might be opportunities to employ ded-

icated heuristics in agents’ interaction for the dense

cases.

With our experimental implementation, the com-

putation time was 0.24 and 0.26 seconds for PIBT

and DR+DA, in the case of N pT = 1 and 125 agents

shown in Tbl. 2.

5 CONCLUSION

In developing methods that employ certain informa-

tion of maps and trafﬁc as the heuristics to con-

trol low-level solution methods for continuous multi-

agent pathﬁnding/pickup-and-delivery problems, we

focused on the case of such problems in narrow ware-

house environments and the solution method PIBT.

For this case study, we experimentally investigated

the effect of map settings and additional heuristics

based on the structures of maps. The experimental

results reveal the potential to employing such funda-

mental components to improve the behavior of so-

lution methods, while the optimum combination of

such settings remains a future work. One possible

approach is using statistics and learning for cases of

several situations in environments. Although we ad-

dressed the static restriction on agents’ moves as a

ﬁrst case study, methods to dynamically apply such

settings based on summarized information of agent

behaviors without precise reservation of agents’ paths

should also be included in future work. For real-

world applications, there are opportunities of several

extensions including those of PIBT itself in practi-

cal situations. In well controlled automated ware-

houses satisfying the solvable conditions of this kind

of lightweight MAPF algorithms, such an applica-

tion with effective add-ons including the proposed ap-

proaches can be promising.

ACKNOWLEDGEMENTS

This study was supported in part by The Public

Foundation of Chubu Science and Technology Center

(thirty-third grant for artiﬁcial intelligence research)

and JSPS KAKENHI Grant Number 22H03647.

REFERENCES

Andreychuk, A., Yakovlev, K., Boyarski, E., and Stern, R.

(2021). Improving Continuous-time Conﬂict Based

Search. In Proceedings of The Thirty-Fifth AAAI Con-

ference on Artiﬁcial Intelligence, volume 35, pages

11220–11227.

Andreychuk, A., Yakovlev, K., Surynek, P., Atzmon, D.,

and Stern, R. (2022). Multi-agent pathﬁnding with

continuous time. Artiﬁcial Intelligence, 305:103662.

Barer, M., Sharon, G., Stern, R., and Felner, A. (2014).

Suboptimal Variants of the Conﬂict-Based Search Al-

gorithm for the Multi-Agent Pathﬁnding Problem. In

Proceedings of the Annual Symposium on Combinato-

rial Search, pages 19–27.

Investigation of Heuristics for PIBT Solving Continuous MAPF Problem in Narrow Warehouse

349

De Wilde, B., Ter Mors, A. W., and Witteveen, C. (2014).

Push and rotate: A complete multi-agent pathﬁnding

algorithm. J. Artif. Int. Res., 51(1):443–492.

Hart, P., N. N. and Raphael, B. (1968). A formal basis

for the heuristic determination of minimum cost paths.

IEEE Trans. Syst. Science and Cybernetics, 4(2):100–

107.

Hart, P., N. N. and Raphael, B. (1972). Correction to ’a for-

mal basis for the heuristic determination of minimum-

cost paths’. SIGART Newsletter, (37):28–29.

Li, J., Tinka, A., Kiesel, S., Durham, J. W., Kumar, T. K. S.,

and Koenig, S. (2021). Lifelong Multi-Agent Path

Finding in Large-Scale Warehouses. In Proceedings

of the Thirty-Fifth AAAI Conference on Artiﬁcial In-

telligence, pages 11272–11281.

Liu, M., Ma, H., Li, J., and Koenig, S. (2019). Task and

Path Planning for Multi-Agent Pickup and Delivery.

In Proceedings of the Eighteenth International Con-

ference on Autonomous Agents and MultiAgent Sys-

tems, pages 1152–1160.

Luna, R. and Bekris, K. E. (2011). Push and swap: Fast

cooperative path-ﬁnding with completeness guaran-

tees. In Proceedings of the Twenty-Second Interna-

tional Joint Conference on Artiﬁcial Intelligence, vol-

ume 1, pages 294–300.

Ma, H., Harabor, D., Stuckey, P. J., Li, J., and Koenig, S.

(2019). Searching with consistent prioritization for

multi-agent path ﬁnding. In Proceedings of the Thirty-

Third AAAI Conference on Artiﬁcial Intelligence and

Thirty-First Innovative Applications of Artiﬁcial In-

telligence Conference and Ninth AAAI Symposium on

Educational Advances in Artiﬁcial Intelligence, pages

7643–7650.

Ma, H., Li, J., Kumar, T. S., and Koenig, S. (2017). Lifelong

Multi-Agent Path Finding for Online Pickup and De-

livery Tasks. In Proceedings of the Sixteenth Confer-

ence on Autonomous Agents and MultiAgent Systems,

pages 837–845.

Miyashita, Y., Yamauchi, T., and Sugawara, T. (2023). Dis-

tributed planning with asynchronous execution with

local navigation for multi-agent pickup and delivery

problem. In Proceedings of the Twenty-Second Inter-

national Conference on Autonomous Agents and Mul-

tiagent Systems, page 914–922.

Okumura, K., Machida, M., D

efago, X., and Tamura, Y.

(2022). Priority Inheritance with Backtracking for It-

erative Multi-Agent Path Finding. Artiﬁcial Intelli-

gence, 310.

Okumura, K., Tamura, Y., and D

efago, X. (2019). winPIBT:

Expanded Prioritized Algorithm for Iterative Multi-

agent Path Finding. CoRR, abs/1905.10149.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.

(2015). Conﬂict-Based Search for Optimal Multi-

Agent Pathﬁnding. Artiﬁcial Intelligence, 219:40–66.

Silver, D. (2005). Cooperative Pathﬁnding. pages 117–122.

ap, M., Vok

ınek, J., and Kleiner, A. (2015). Complete

Decentralized Method for On-Line Multi-Robot Tra-

jectory Planning in Well-Formed Infrastructures. In

Proceedings of the Twenty-Fifth International Confer-

ence on Automated Planning and Scheduling, pages

324–332.

Yakovlev, K. S. and Andreychuk, A. (2017). Any-angle

pathﬁnding for multiple agents based on SIPP al-

gorithm. In Proceedings of the Twenty-Seventh In-

ternational Conference on Automated Planning and

Scheduling, pages 586–593.

Yamauchi, T., Miyashita, Y., and Sugawara, T. (2022).

Standby-based deadlock avoidance method for multi-

agent pickup and delivery tasks. In Proceedings

of the Twenty-First International Conference on Au-

tonomous Agents and Multiagent Systems, pages

1427–1435.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

350