Real-Time 3D Information Visualization on Mobile Devices: Efﬁcient

Occlusion Detection for Geospatial Applications

Agata Migalska

Department of Control Systems and Mechatronics, Wrocław University of Science and Technology, Wrocław, Poland

Keywords:

Augmented Reality, Geospatial Data Visualization, Occlusion Detection.

Abstract:

The rapid advancement of geospatial applications on mobile devices has revolutionized outdoor activities

and professions by providing invaluable tools for navigating, exploring, and highlighting geographic features.

These applications often face notable challenges, including limited connectivity as well as battery and storage

constraints. The objective of this paper is to provide users with a seamless user experience and augmented

reality interactions in diverse outdoor scenarios within geospatial applications on mobile devices. Towards

this goal, we introduce visibility map of a point that contains distances from the point to the closest obstacles

at multiple angular viewpoints. We propose that every point of interest is associated with a such a visibility

map, pre-calculated on a digital world model, in order to render annotated data in real-time without relying

on time-consuming depth estimation. We speciﬁcally address the aspect of displaying 3D virtual information

that is registered at different elevations, justiﬁed by the importance of elevation information in domains such

as earth science, culture science or construction and by a lack of methods that would allow that. Through our

study, we demonstrate the real-time rendering capability and accuracy of our proposed method. We present

the ﬁndings, discuss potential limitations, and suggest future research directions.

1 INTRODUCTION

Geospatial applications on mobile devices have be-

come indispensable tools for outdoor activities and

professions, offering navigation assistance, explo-

ration capabilities, and the ability to highlight im-

portant geographic features. The integration of Aug-

mented Reality (AR) has further revolutionized the

user experience by enriching the perceived world with

additional information and expanding the user’s un-

derstanding of their surroundings (Bowman et al.,

2003; Billinghurst et al., 2015). Location-aware

AR applications enable the attachment of location-

speciﬁc virtual content to real-world scenes and allow

users to access and manage this information (H

ollerer

et al., 1999).

In many existing geospatial applications a point

of interest is described by geographical latitude and

longitude and assumed to be located at the ground

level. As an example, let us consider AR tourism

applications that suggests walking routes passing by

local attractions and provide additional content to the

user once they arrive at a certain location (Pica et al.,

https://orcid.org/0000-0002-0653-026X

2018; Gonz

alez-Delgado et al., 2020). An attraction

is considered to be at the altitude of Earth at given lat-

itude and longitude. Indeed, in many use cases, such

as navigation and routing, an exact object’s placement

above the ground is of little concern.

What remains unrepresented, however, are the fol-

lowing:

• Points in three-dimensional space that do not cor-

respond to ground-level entities, such as a bird’s

nest or a wall socket.

• Paths that vary in altitude, such as climbing routes

or the course of water and sewage systems within

a wall.

• Areas situated above the terrain, such as geolog-

ical layers within a towering rock wall or haz-

ardous portions of a building’s elevation.

Clearly, certain geospatial entities exist above the

ground level and necessitate that full and precise el-

evation information is captured, persisted and pre-

sented visually.

In addition to outdoor sports enthusiasts, such as

rock climbers, numerous professions can beneﬁt from

precise three-dimensional information rendering in

geospatial applications. Examples include highlight-

Migalska, A.

Real-Time 3D Information Visualization on Mobile Devices: Efﬁcient Occlusion Detection for Geospatial Applications.

DOI: 10.5220/0012398300003660

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 277-284

ISBN: 978-989-758-679-8; ISSN: 2184-4321

277

ing noteworthy parts of buildings and monuments

for further studies and for touristic purposes, mark-

ing boundaries discovered while working with digital

rock outcrop models (Tavani et al., 2019), identifying

loose rocks to ensure seamless functioning of a rock-

fall monitoring system (Cayla and Martin, 2018), or

annotating the course of water and electricity systems

within walls.

Geospatial applications operating in outdoor envi-

ronments often contend with challenges. Firstly, they

face limited internet connectivity, especially in rural

and mountain regions (Fedorov et al., 2016). Further-

more, they may be restricted on battery usage, given

the limited availability of power sources in outdoor

settings (Stylianidis et al., 2020). Finally, their opera-

tion may be opposed by limited storage capacity of a

mobile device (Shi et al., 2012).

It is therefore recommended that all calculations

and processing are performed ofﬂine on a mobile de-

vice, to ensure seamless operation regardless of the

network signal strength. Furthermore, these applica-

tions must be designed with low-power consumption

in mind to preserve battery life. Additionally, consid-

ering the constrained storage capacity of mobile de-

vices, it is crucial to minimize the volume of stored

data. Finally, for immaculate user experience the real-

time performance is necessary.

Our objective is thus to determine visibility of vir-

tual objects in a perceived real-world scene in order

to overlay these objects on top of a camera preview,

as showcased in Figure 1. The primary challenge to-

wards this goal is that the information about visibil-

ity and potential occlusions in the scene is not readily

available.

The authors of the comprehensive study of

research and development in the ﬁeld of AR

(Billinghurst et al., 2015) point towards depth estima-

tion techniques to accurately compose virtual and real

world images. However, existing depth-estimation

solutions lack real-time performance. For instance,

in the Mobile AI 2022 Monocular Depth Estimation

challenge (Ignatov et al., 2023), the fastest run time

achieved by the AHA HIT Team was 37ms (27 FPS).

In applications that involve additional tasks such as

calculating node visibility or scene rendering, depth

estimation becomes time-consuming and cannot of-

fer seamless user experience. Moreover, depth maps

generated by existing algorithms often have low res-

olutions (e.g., 640x480px), presenting an additional

challenge.

We propose to leverage information on angular

visibility of annotated points in order to efﬁciently

render a visible subset of them on the user’s mobile

device’s screen. Each point is thus accompanied by a

vector of distances from that point to the closest ob-

stacles at speciﬁc viewing angles. At runtime, this

visibility information is combined with the camera’s

location and attitude to render only the content that is

visible in the camera preview.

We make a two-fold contribution.

• We propose a novel method for visibility calcula-

tion in complex scenes that strikes a balance be-

tween accuracy and resource efﬁciency, allowing

for real-time performance and seamless user ex-

perience.

• We provide a data representation framework for

annotating three-dimensional points, polylines,

and polygons, facilitating the incorporation of rich

spatial information into applications while mini-

mizing storage requirements.

2 RELATED WORK

The problems our research addresses have been ob-

served and scrutinized by other authors as well. (Shi

et al., 2012) propose that the calculations for render-

ing are executed on a remote server in order to ensure

real-time interactive 3D mobile graphics. However,

this method relies on a stable connection to a remote

server and is not well suited for outdoor scenarios.

(Jain et al., 2015) recommend that geometric repre-

sentations of environment are utilized to reduce the

search space to device’s neighborhood. Our work fol-

lows this principle in that we propose that geospatial

data are split into regional chunks.

One prominent application of outdoor AR that

utilizes information about local world geometry is

mountain peak detection, where the goal is to overlay

mountain landscapes with peak information. (Karpis-

chek et al., 2009) propose to use so-called view-sheds

of mountain peaks; a view-shed is a union of geospa-

tial areas from which a given peak is visible. To deter-

mine which peaks are visible from a camera location,

view-sheds for all mountains are consulted. (Fedorov

et al., 2016) propose that the virtual panorama vis-

ible form the viewpoint of a user is estimated from

an online Digital Elevation Model (DEM) and from

its correspondence to the actual image framed by the

camera. Once the correspondence is found, meta-data

from DEM (e.g. peak name, altitude, distance) are

projected onto the view. DEM data supports only a

single z-value for each a x,y location which renders

the approach unsuitable for elevation-variable data.

(Westhead et al., 2013) recognize the potential

of AR techniques in transforming complex three-

dimensional information into a user-friendly format

GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications

278

Figure 1: Real-time 3D Information Visualization on Mobile Devices: two polylines rendered as a camera preview overlay

with their full visibility indicated with solid lines and partial visibility with a dashed line.

and introduce the British Geological Survey BGS

Map Viewer, which provides a 3D view but is limited

to presenting 2D information on a 3D surface.

A different approach to information display is pre-

sented in tourism AR applications. The work of

(Gonz

alez-Delgado et al., 2020) focuses on the de-

velopment of georoutes to enhance tourism in natu-

ral ﬁlming locations in Spain. Users scan QR codes

along their route to access relevant information, in-

cluding textual, graphical, and interactive content.

Once again, the elevation information is culled.

Elevation information is not discarded in (Stylian-

idis et al., 2020), the research that presents LARA,

a solution for visualizing 3D underground infrastruc-

ture models in real time. The models are retrieved

from a 3D GIS-Geodatabase residing on a mobile de-

vice. Their work, alike ours, is concerned with 3D

real-time rendering of 3D models. However, consid-

ering that the main goal for LARA is to provide an

”X-ray” viewing of the underground infrastructure,

occlusion detection is of no relevance.

3 PROBLEM STATEMENT

Assumptions Regarding the World. The follow-

ing assumptions are made regarding the world: (1) A

mesh model representing the world is created in ad-

vance. (2) A domain expert annotates features of in-

terest in the world model in the form of points, poly-

lines and polygons. (3) The world is considered to be

static and undergoes minimal changes over time.

Objective. For each annotated point, the objective

is to determine whether it is visible to a camera, given

the position and orientation of the camera and the ge-

ometry of the surrounding world, in order to be prop-

erly overlaid on the mobile device’s camera preview.

Requirements for the Mobile Application. The

mobile application has the following requirements

arising from concerns raised in relation to mobile

AR for outdoor use: (1) It operates without requir-

ing an internet connection during runtime. (2) The

data needed for the algorithm execution is of small

volume. (3) The algorithm implemented in the appli-

cation is resource-efﬁcient to minimize battery usage.

(4) The algorithm performs in real-time.

4 PROPOSED METHOD

Figure 2: System diagram.

The proposed solution consists of three modules:

(1) a geospatial data pre-processing module that is

responsible for the creation of visibility maps, (2)

a data serving module that serves spatially-cropped

ﬁles with annotations as well as their corresponding

visibility maps, and (3) a Mobile AR application that

performs visibility testing and overlays the camera’s

Real-Time 3D Information Visualization on Mobile Devices: Efﬁcient Occlusion Detection for Geospatial Applications

279

preview with rendered visible annotated points. The

proposed system is presented in Figure 2.

4.1 Geospatial Data Pre-Processing

Module

We propose to calculate visibility of each annotated

point from the world model, that is a 3D mesh model

that can be constructed from LIDAR scans, UAV pho-

tographs or hand-held camera photographs (Tavani

et al., 2019). A domain expert, for instance a geol-

ogist or an archaeologist, introduces virtual informa-

tion to the world model by annotating points, poly-

lines, and polygons in a 3D coordinate system. In or-

der to determine the visibility of an annotated point,

we introduce the concept of a point visibility map and

propose associating each annotated point with such

a map. Point visibility map is a vector of Euclidean

distances from a point to the closest world object in

each of selected angular directions. To construct a vis-

ibility map, we employ a spherical coordinate system

and assume a unit sphere. Each point on the sphere

can be represented by two parameters: a polar angle

θ (0 ⩽ θ ⩽ π) that measures the angle from the posi-

tive z-axis towards the xy-plane, and an azimuthal an-

gle φ (0 ⩽ φ ⩽ 2π) that represents the angle from the

positive x-axis towards the positive y-axis. We pro-

pose to employ equal-angle sphere sampling scheme

for its computational advantages but, in principle, any

deterministic sampling scheme can be utilized. In the

equal-angle sampling scheme, the ranges of both po-

lar and azimuthal angles are divided into N intervals

of equal width. We are then able to approximate the

sphere with N × N quadrilateral faces in 3D. An illus-

tration of a sphere approximation in spherical coordi-

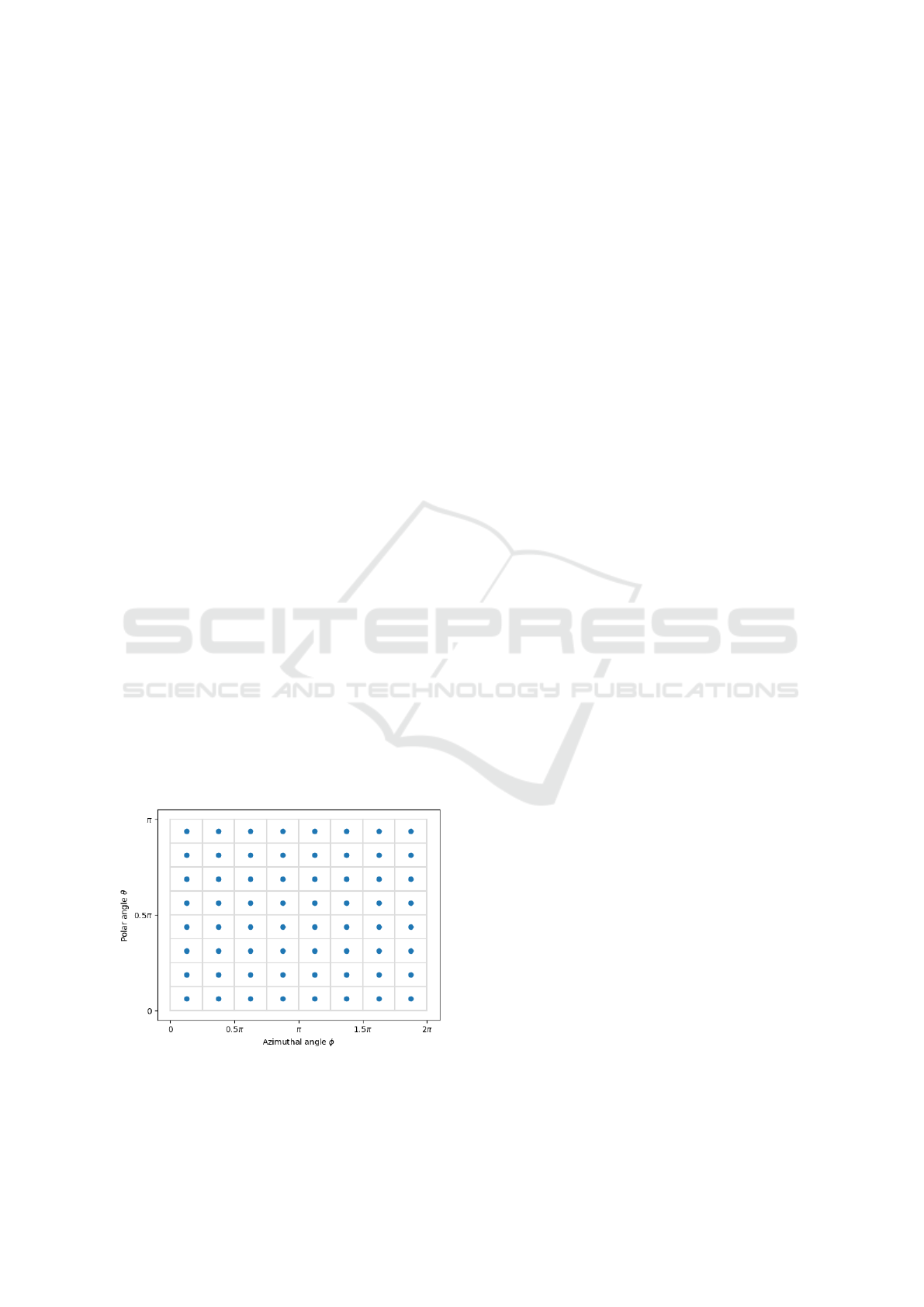
nates for N = 8 is presented in Figure 3.

Figure 3: Unit sphere approximation with 8 × 8 rectangular

cells of equally spaced azimuthal and polar angles. Blue

dots, in the middle of each cell, represent their centers.

A ray is emitted from the center of a sphere, i.e. an

annotated point, in the direction of the center of a cell

and continues until it encounters the nearest obstacle

in the world model. The distance traveled by the ray

is recorded in the visibility map under the index corre-

sponding to the ray’s azimuthal and polar angles. The

procedure is repeated for all considered directions and

yields a visibility map of a point in the world model.

4.2 Data Serving Module

The remote server module is responsible for serving

region-speciﬁc ﬁles containing annotated geometries

with their 3D world coordinates as well as visibility

maps for each point in annotated geometries.

In outdoor scenarios, the geometry of a scene can

be very complex; consider, for instance, rock out-

crops or a Romanesque stone bas relief on the portal

of a cathedral. Annotated geometries, such as points,

polylines, and polygons, are relatively small in size

compared to such complex geometry of a scene. Fol-

lowing the approach of existing map applications de-

signed for ofﬂine use (e.g. Mapy.cz (http://mapy.cz)

or MapsWithMe (http://maps.me)), it is assumed that

data for a particular region is downloaded and stored

on a mobile device in advance, allowing for ofﬂine

processing. The data transferred to a mobile device

includes only annotated geometries and calculated

visibility maps for each point.

4.3 Mobile AR Application

The following are the steps to determine the visibility

of a given point on a mobile device. It is assumed that

the camera is calibrated in an off-line process and that

the camera’s intrinsic matrix K is known.

1. Establish the camera’s location in the coordinate

system of the world model.

2. Prune the search space based on the camera’s lo-

cation and perform a frustum culling test (outside

of the proposed method).

3. Obtain the camera’s extrinsic matrix M, given by

M =



(3×3)

(3×1)

(1×3)

(1×1)



(4×4)

, (1)

where R is the camera rotation matrix and T is the

translation column vector.

4. For each point within the user’s frustum, perform

the visibility test described in Section 4.3.1.

5. If the point is visible, calculate the coordinates

(u,v) of the point in the Pixel Coordinate System

GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications

280

using the equation:









= KM













, (2)

where z

represents the z-coordinate of the camera

relative to the world origin, and draw the point.

6. For each pair of points in a polyline, draw the edge

if both points are visible. If only one of the points

is visible, indicate it with appropriate marking.

The procedure can be performed for all points si-

multaneously using matrix operations.

4.3.1 Point’s Visibility Test

We ﬁrst introduce a general approach applicable to

any sphere sampling scheme. We then reﬁne the ap-

proach to equal-angle sampling scheme.

Let P be a point for which we want to determine

visibility, and let Q be a camera’s position. Firstly,

compute the vector

⃗

R from point P to camera Q and

its norm d = ∥

⃗

R∥. Then, ﬁnd the index of the vector

that is closest to

⃗

R with respect to polar and azimuthal

angles. For an arbitrary sampling scheme, the clos-

est vector is the one that maximizes cosine similarity

between

⃗

R and itself,

(

⃗

R) =

⃗

D ·

⃗

∥

⃗

D∥∥

⃗

R∥

. (3)

Since ∥

⃗

D∥ = 1 for all vectors in the scheme, it is

enough to ﬁnd the vector that maximizes the dot prod-

uct between itself and

⃗

R. Once the closest vector is

found and its corresponding visibility retrieved from

the visibility map, the point is announced visible if

the interpolated value is no less than the distance d.

Otherwise, it is not visible to the camera. The steps

are outlined in Algorithm 1.

Data: Point P in 3D coordinates

Camera position Q in 3D coordinates

Visibility map V ∈ R

(N×N,1)

Visibility vectors D ∈ R

(N×N,3)

Result: true if Q visible from P, false

otherwise

⃗

R ← Q − P;

2 d ← ∥

⃗

R∥;

3 j ← arg max

i∈1,...,|

⃗

D[i] ·

⃗

4 return V [ j] ⩾ d;

Algorithm 1: Point Visibility Test.

Provided that equal-angle sphere sampling

scheme is selected, polar and azimuthal angles are

spaced by θ

∆

2π

and φ

∆

, respectively. That

allows for constant-time calculations of the vector

closest to

⃗

R. Step-by-step calculations of the pro-

posed Point’s Visibility Test for equal-angle sphere

sampling scheme are showcased in Algorithm 2.

Data: Point P in 3D coordinates

Camera position Q in 3D coordinates

Visibility map V ∈ R

(N×N,1)

∆

= π/N - spacing of Φ

∆

= 2π/N - spacing of Θ

Result: true if Q visible from P, false

otherwise

⃗

R ← Q − P;

2 d ← ∥

⃗

R∥;

3 φ

← atan2



⃗



;

4 θ

← arccos



⃗



;

5 i

← ⌊φ

/φ

∆

⌋;

6 j

← ⌊θ

/θ

∆

⌋;

7 return V [i

· N + j

] ⩾ d;

Algorithm 2: Point Visibility Test in equal-angle sphere

sampling scheme.

Regarding the time complexity of the method, it is

important to highlight that the algorithm is executed

only once per image, considering all eligible points

as a single M × 3 matrix. The code requires a to-

tal of three matrix multiplications (two to obtain the

points’ coordinates in the pixel coordinate system and

one to calculate the norm), along with one matrix ad-

dition, two invocations of inverse trigonometric func-

tions, and the complexity of the selected interpolation

method. Additionally, the algorithm beneﬁts from be-

ing executable in parallel. Due to its low time com-

plexity, the method ensures real-time performance.

5 RESULTS

5.1 Implementation

The Geospatial Data Pre-processing Module was im-

plemented in Python and is available in GitHub

. This

module takes in a 3D mesh model of the world, 3D

coordinates of annotated paths and the number of di-

rections N. For each annotated point, the module cal-

culates its N × N visibility map by calculating the z-

buffer from the point in the considered direction. In

our implementation we employed a ray-triangle in-

tersection algorithm (Snyder and Barr, 1987; Shirley

https://github.com/OutdoorAR-

POC/GeoDataPreProcessing

Real-Time 3D Information Visualization on Mobile Devices: Efﬁcient Occlusion Detection for Geospatial Applications

281

et al., 2021) that utilizes barycentric coordinates to

represent triangles in a world mesh model.

The Mobile AR Application was implemented in

Kotlin programming language, the default program-

ming language for applications dedicated for Android

devices. A Proof-of-Concept implementation can be

found in GitHub

. All input ﬁles, including visibil-

ity maps and geospatial annotations as well as images

and camera extrinsic information, were provided as

resources to the application.

5.2 Case Study

The case study was concerned with a rock outcrop,

representative of complexity observed in such sce-

narios, whose 3D model was obtained from pho-

tographs using the Structure from Motion (SfM) tech-

nique (Schonberger and Frahm, 2016; Carrivick et al.,

2016) in Meshroom software (Griwodz et al., 2021).

The resulting mesh was further cleaned and deci-

mated with Meshlab (Cignoni et al., 2008). To test the

visibility of different geometries around the rock out-

crop, four multi-point polylines and polygons were

designed, as illustrated in Figure 4.

Figure 4: 3D world model with annotated geometries. Left:

red and blue polygons. Right: yellow and green polylines.

In order to test the algorithm we utilized the same

set of images as for the 3D model creation enriched

with data output by the SfM process - camera intrin-

sic matrix and camera extrinsic matrices for each im-

age. The algorithm was tested on 77 views of the rock

formation, each captured from a different viewpoint.

Example results for N = 8 are presented in Figure 5,

showcasing correct outcomes of the method from var-

ious viewpoints.

5.2.1 Effect of Visibility Map Size

In our study, we experimented with different number

of equidistant angles (N), including 2, 4, 8, 16, and 32

angles. The resulting visibility maps had sizes |V | of

4, 16, 64, 256, and 1024, respectively. We present ac-

curacy and F1-score for varying sizes |V | in Table 1.

From the results, we ﬁnd that N = 8 provides accu-

rate visibility measurements with the accuracy score

https://github.com/OutdoorAR-POC/MobileApp

Figure 5: Example results for N = 8 from various view-

points.

of 0.9423 and F1-Score of 0.8793. Increasing N to 16

does not signiﬁcantly improve the accuracy (0.9649),

yet yield a signiﬁcant boost on the F1-Score that at-

tains 0.9272. Increasing N to 32 slightly improves the

scores but the increase in improvement is offset by a

fourfold increase in the required disk space.

When evaluated visually in images, the method

demonstrated some limitations when additional ob-

GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications

282

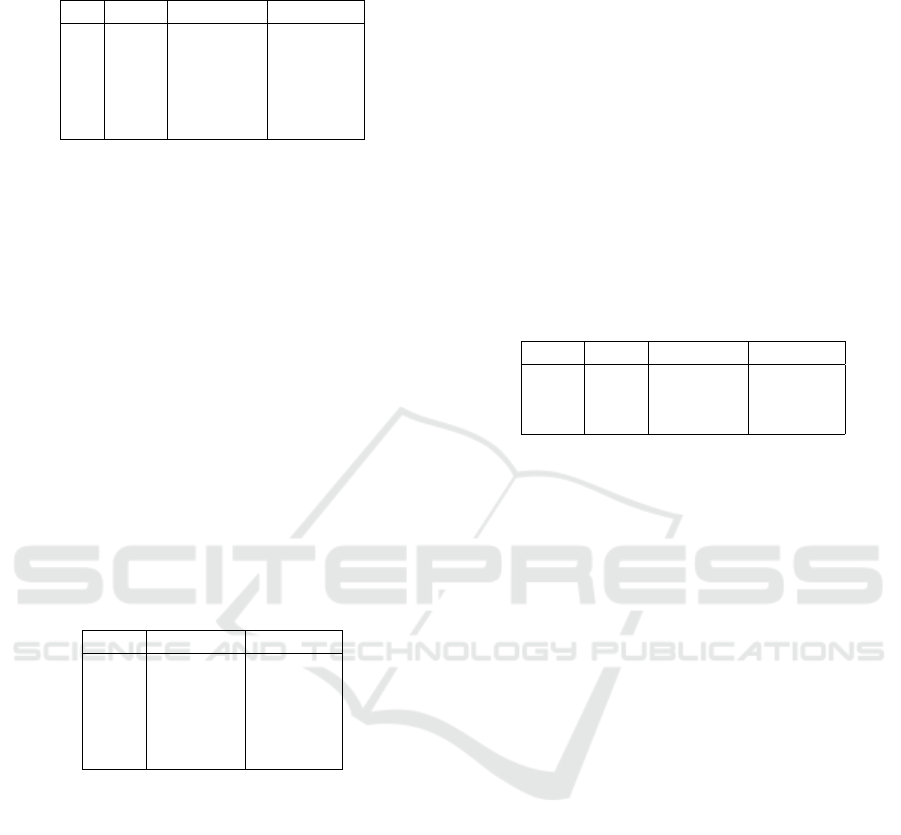
Table 1: Performance scores of the algorithm depending on

the number of viewpoints N.

N |V | Accuracy F1-Score

2 4 0.7609 0.4401

4 16 0.8793 0.7384

8 64 0.9423 0.8793

16 256 0.9649 0.9272

32 1024 0.9710 0.9402

jects, not included in the digital world model, were

present in images.

5.2.2 Effect of Sphere Sampling Scheme

Equal-angle sampling, although computationally at-

tractive, gives points that are not uniformly distributed

on a sphere. In the following experiment we uti-

lized the Fibonacci lattice (Gonz

alez, 2010), in which

points are almost evenly spaced on the sphere sur-

face, and we constructed visibility maps of the same

size as in the previous experiment. From the results,

presented in Table 2, it can be concluded that for

|V | ≥ 64 accuracy and F1 scores are comparable to

those obtained for the equal-angle sampling scheme.

For smaller sizes of |V |, the results are signiﬁcantly

better with the Fibonacci lattice, however, they are

still not sufﬁciently high.

Table 2: Performance scores of the algorithm for Fibonacci

lattice sphere sampling.

|V | Accuracy F1-Score

4 0.8335 0.6599

16 0.8980 0.7747

64 0.9423 0.8785

256 0.9618 0.9218

1024 0.9733 0.9446

5.2.3 “Small Mesh” Experiment

We conducted a space complexity comparison be-

tween a visibility map and a simpliﬁed mesh. Intu-

itively, complex scene geometries with a limited num-

ber of annotated geometries favor the use of a visibil-

ity map. On the other hand, a simple scene geometry

accompanied by a large number of annotated geome-

tries would likely beneﬁt from a simpliﬁed mesh. The

key question then is: how does the size of a visibility

map, i.e. a vector of |V | double precision numbers,

compare to that of a mesh ﬁle? The mesh ﬁle contains

a list of 3D vertices, with single precision coordinates,

and a list of faces, represented as triples of integer in-

dices of vertices. We assume 8B for double precision,

4B for single precision, and 4B for unsigned integer.

Let |W | and |F| be the numbers of vertices and faces

in the small mesh, respectively. The space require-

ment of the visibility map is then 8|V |, whereas that

of the mesh accounts for 12(|F| + |W |). That implies

that if |V | = 64 (N = 8), then the total number of faces

and vertices in a mesh, |F| + |W |, would have to be

approximately 43 for the space requirements to equal.

The original mesh was decimated to approxi-

mately 1024, 2048 and 4096 faces with Quadratic

Edge Collapse Decimation in Meshlab (Cignoni et al.,

2008). The obtained results are presented in Table 3.

It can be observed that, for the scene and annota-

tions considered in our case study, accuracy and F1

scores comparable to visibility maps of size |V | = 64

are achieved no sooner than when |F| +|W | = 2048+

4095.

Table 3: Performance scores of direct ray tracing on simpli-

ﬁed meshes.

|W | |F| Accuracy F1-Score

513 1023 0.8843 0.7335

1025 2047 0.9118 0.7979

2048 4095 0.9396 0.8674

6 DISCUSSION AND FUTURE

WORK

The proposed method offers several noteworthy ad-

vantages. It accurately renders annotated geometries

and it adheres to all four stated requirements, includ-

ing low time and space complexities. The method,

however, does have some limitations that need to be

considered. Firstly, it relies on a well-mapped world

where all objects are accurately scanned and included

in the digital model. If there exist discrepancies be-

tween the real world and a model then annotated

points may be incorrectly classiﬁed as visible or not

visible. Secondly, the method requires that the mesh

of the world is created in order to calculate visibil-

ity maps. While in multiple professional scenarios

such models are nevertheless created for analytic pur-

poses, this requirement could pose a computational

challenge.

One possible direction of future research is to

combine the proposed method with coarse depth

maps. This integration could help account for vegeta-

tion and objects that are not registered in the world’s

model. Additionally, alternative interpolation meth-

ods, such as bi-linear interpolation, could be explored

in search for more accurate results compared to the

nearest neighbor interpolation used in our study.

Real-Time 3D Information Visualization on Mobile Devices: Efﬁcient Occlusion Detection for Geospatial Applications

283

7 CONCLUSION

In this paper, we address the challenge of real-time

3D information visualization on mobile devices under

constraints of limited connectivity, battery capacity,

storage limitations, and real-time performance. We

propose associating each annotated point with a vis-

ibility map that captures visibility from that point in

multiple angular directions. By leveraging the cam-

era’s position and orientation and identifying the near-

est viewing angle within each point’s visibility map,

we efﬁciently determine the point’s visibility in the

scene. Obtained experimental results demonstrate

that the proposed method enables real-time rendering

of annotated data and provides an accurate alternative

to techniques relying on scene depth estimation.

REFERENCES

Billinghurst, M., Clark, A., and Lee, G. (2015). A survey

of augmented reality. Foundations and Trends® in

Human–Computer Interaction, 8(2-3):73–272.

Bowman, D. A., North, C., Chen, J., Polys, N. F., Pyla,

P. S., and Yilmaz, U. (2003). Information-rich virtual

environments: theory, tools, and research agenda. In

Proceedings of the ACM symposium on Virtual reality

software and technology, pages 81–90.

Carrivick, J. L., Smith, M. W., and Quincey, D. J. (2016).

Structure from Motion in the Geosciences. John Wiley

& Sons.

Cayla, N. and Martin, S. (2018). Chapter 16 - digital geovi-

sualisation technologies applied to geoheritage man-

agement. In Reynard, E. and Brilha, J., editors, Geo-

heritage, pages 289–303. Elsevier.

Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M.,

Ganovelli, F., and Ranzuglia, G. (2008). MeshLab:

an Open-Source Mesh Processing Tool. In Scarano,

V., Chiara, R. D., and Erra, U., editors, Eurographics

Italian Chapter Conference. The Eurographics Asso-

ciation.

Fedorov, R., Frajberg, D., and Fraternali, P. (2016). A

framework for outdoor mobile augmented reality

and its application to mountain peak detection. In

Augmented Reality, Virtual Reality, and Computer

Graphics: Third International Conference, AVR 2016,

Lecce, Italy, June 15-18, 2016. Proceedings, Part I 3,

pages 281–301. Springer.

Gonz

alez,

A. (2010). Measurement of areas on a sphere

using ﬁbonacci and latitude–longitude lattices. Math-

ematical Geosciences, 42:49–64.

Gonz

alez-Delgado, J.

A., Mart

ınez-Gra

na, A., Holgado,

M., Gonzalo, J. C., and Legoinha, P. (2020). Aug-

mented reality as a tool for promoting the tourist value

of the geological heritage around natural ﬁlming loca-

tions: A case study in “Sad Hill”(The Good, the Bad

and the Ugly Movie, Burgos, Spain). Geoheritage,

12:1–11.

Griwodz, C., Gasparini, S., Calvet, L., Gurdjos, P., Cas-

tan, F., Maujean, B., De Lillo, G., and Lanthony, Y.

(2021). Alicevision Meshroom: An open-source 3D

reconstruction pipeline. In Proc. 12th ACM Multimed.

Syst. Conf. - MMSys ’21. ACM Press.

ollerer, T., Feiner, S., Terauchi, T., Rashid, G., and Hall-

away, D. (1999). Exploring MARS: developing indoor

and outdoor user interfaces to a mobile augmented re-

ality system. Computers & Graphics, 23(6):779–785.

Ignatov, A., Malivenko, G., Timofte, R., Treszczotko, L.,

Chang, X., Ksiazek, P., Lopuszynski, M., Pioro, M.,

Rudnicki, R., Smyl, M., et al. (2023). Efﬁcient single-

image depth estimation on mobile devices, mobile

AI & AIM 2022 challenge: report. In Computer

Vision–ECCV 2022 Workshops: Tel Aviv, Israel, Octo-

ber 23–27, 2022, Proceedings, Part III, pages 71–91.

Springer.

Jain, P., Manweiler, J., and Roy Choudhury, R. (2015).

Overlay: Practical mobile augmented reality. In Pro-

ceedings of the 13th Annual International Conference

on Mobile Systems, Applications, and Services, pages

331–344.

Karpischek, S., Marforio, C., Godenzi, M., Heuel, S.,

and Michahelles, F. (2009). Swisspeaks–mobile aug-

mented reality to identify mountains. In Workshop

at the International Symposium on Mixed and Aug-

mented Reality 2009 (ISMAR 2009).

Pica, A., Reynard, E., Grangier, L., Kaiser, C., Ghiraldi,

L., Perotti, L., and Del Monte, M. (2018). Geoguides,

urban geotourism offer powered by mobile application

technology. Geoheritage, 10:311–326.

Schonberger, J. L. and Frahm, J.-M. (2016). Structure-

from-motion revisited. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 4104–4113.

Shi, S., Nahrstedt, K., and Campbell, R. (2012). A real-

time remote rendering system for interactive mobile

graphics. ACM Transactions on Multimedia Com-

puting, Communications, and Applications (TOMM),

8(3s):1–20.

Shirley, P., Ashikhmin, M., and Marschner, S. (2021). Fun-

damentals of computer graphics. AK Peters/CRC

Press, 5th ed. edition.

Snyder, J. M. and Barr, A. H. (1987). Ray tracing complex

models containing surface tessellations. ACM SIG-

GRAPH Computer Graphics, 21(4):119–128.

Stylianidis, E., Valari, E., Pagani, A., Carrillo, I.,

Kounoudes, A., Michail, K., and Smagas, K. (2020).

Augmented reality geovisualisation for underground

utilities. PFG, 88:173–185.

Tavani, S., Corradetti, A., Granado, P., Snidero, M., Seers,

T. D., and Mazzoli, S. (2019). Smartphone: An al-

ternative to ground control points for orienting vir-

tual outcrop models and assessing their quality. Geo-

sphere, 15(6):2043–2052.

Westhead, R., Smith, M., Shelley, W., Pedley, R., Ford, J.,

and Napier, B. (2013). Mobile spatial mapping and

augmented reality applications for environmental geo-

science. Journal of Internet Technology and Secured

Transactions, 2(1-4):185–190.

GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications

284