A Survey of Deep Learning: From Activations to Transformers
Johannes Schneider
1
and Michalis Vlachos
2
1
University of Liechtenstein, Vaduz, Liechtenstein
2
University of Lausanne, Lausanne, Switzerland
Keywords:
Survey, Review, Deep Learning, Architectures, Layers, Transformer, Graphs.
Abstract:
Deep learning has made tremendous progress in the last decade. A key success factor is the large amount
of architectures, layers, objectives, and optimization techniques. They include a myriad of variants related to
attention, normalization, skip connections, transformers and self-supervised learning schemes – to name a few.
We provide a comprehensive overview of the most important, recent works in these areas to those who already
have a basic understanding of deep learning. We hope that a holistic and unified treatment of influential,
recent works helps researchers to form new connections between diverse areas of deep learning. We identify
and discuss multiple patterns that summarize the key strategies for many of the successful innovations over
the last decade as well as works that can be seen as rising stars. We also include a discussion on recent
commercially built, closed-source models such as OpenAI’s GPT-4 and Google’s PaLM 2.
1 INTRODUCTION
Deep learning is widely regarded as the driving
force behind artificial intelligence. Its models have
achieved top leaderboard rankings in various fields,
including computer vision, speech, and natural lan-
guage processing. One of the major advantages of
deep learning is its layered, modular structure, which
allows for the construction of models from individ-
ual components in a flexible manner. Researchers
have created a large selection of layers, architectures,
and objectives. Keeping up with the ongoing devel-
opments in the various aspects of deep learning is a
difficult task. Although specific surveys are available,
there is currently no comprehensive overview of re-
cent progress covering multiple aspects of deep learn-
ing such as learning, layers and architecture. There
exist multiple reviews with a narrow focus such as
large language models ( e.g. (Min et al., 2021))
and convolutional neural networks (e.g. (Khan et al.,
2020)). Previous studies (Alom et al., 2019; Shrestha
and Mahmood, 2019; Dong et al., 2021; Alzubaidi
et al., 2021) with a wider focus have often over-
looked new developments such as transformers and
supervised-learning. However, taking a more com-
prehensive and more holistic look at various disci-
plines can be extremely advantageous: For example,
NLP and computer vision have often influenced each
other; CNNs were initially introduced in computer vi-
sion, but were later applied in NLP, while transform-
ers were introduced in NLP and later adapted in com-
puter vision. Therefore, removing barriers between
disciplines can be highly beneficial. This paper takes
this motivation by surveying the recent progress of
deep learning from a holistic standpoint, rather than
focusing on a particular niche area. We also believe
that this is a necessary step, since major innovations
have slowed down in terms, i.e., now most architec-
tures are based on the transformer architecture, which
dates back to 2017(Vaswani et al., 2017).
It is difficult, if not impossible, to provide an en-
compassing overview of the field due to the sheer
number of articles published yearly and the contin-
ual increase in relevant topics, such as transformers
and self-supervised learning that have become popu-
lar only recently. Our strategy is to choose influen-
tial works through (i) usage statistics and (ii) special-
ized surveys. We also offer an invigorating discussion
of shared design patterns across areas that have been
successful.
2 OVERVIEW
Figure 1 provides an overview of the areas included
in this survey. We have investigated deep learning de-
sign, including objectives and training. We have also
given special attention to works that have been some-
Schneider, J. and Vlachos, M.
A Survey of Deep Learning: From Activations to Transformers.
DOI: 10.5220/0012404300003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 2, pages 419-430
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
419

Figure 1: Categorization of deep learning and areas covered in the survey.
what established based on the usage statistics from the
popular platform ”Paperswithcode.com.” There has
been an increase in these types of platforms that en-
able the upload of papers (and models) and provide
information on citations, as well as leaderboards. Al-
though there are drawbacks when utilizing data from
these platforms, we believe that it offers a new per-
spective compared to traditional survey methods that
often select more arbitrarily. We have only included
a selection of the most influential works published
from 2016 onwards, as well as rising stars (from 2020
or newer) that have gained significant popularity in a
short time.
The extent to which each topic is covered depends
on the amount of recent research that has been con-
ducted and its foundational nature. We do not discuss
data or computational aspects such as data augmen-
tation, model compression, and distributed machine
learning. As a result of limited space, we had to be
selective when it came to model families and left out
relevant ones such as multi-modal models and autoen-
coders.
3 LOSS FUNCTIONS AND
OPTIMIZATION
We discuss common loss functions and optimizers.
3.1 Loss Functions
Loss functions (surveyed in (Wang et al., 2020)) of-
ten consist of multiple terms that are enhanced with
a regularization term. Loss functions are often task-
specific but some general ideas are applicable across
tasks. Commonly, multiple loss terms are aggregated
in a weighted manner. Many papers improve prior
work (simply) by using a different loss function.
The Triplet Loss (Dong and Shen, 2018) was intro-
duced for Siamese networks (Its origin dates back fur-
ther (Schultz and Joachims, 2003).) The high level
idea is to compare a given input to a positive and
a negative input and maximize association between
positively associated inputs, while minimizing those
of negative ones. It takes input pairs (x, y), each pro-
cessed by a separate but identical network. It maxi-
mizes the joint probability p(x, y) of all pairs (x, y):
L(V
p
,V
n
) = −
1
|V
p
|·|V
n
|
∑
x∈V
p
∑
y∈V
n
log p(x, y) (1)
= −
1
|V
p
|·|V
n
|
∑
x∈V
p
∑
y∈V
n
log(1 + e
x−y
)
(2)
Here, V
p
and V
n
are the positive and negative score
set respectively.
Focal Loss (Lin et al., 2017) focuses learning on hard
misclassified samples by altering the cross entropy
loss. It adds a factor (1 − p)
γ
, where p denotes the
probability of a sample stemming from the cross en-
tropy loss and γ is a tunable parameter.
L(p) = (1 −p)
γ
log(p) (3)
The Cycle Consistency Loss (Zhu et al., 2017) is tai-
lored towards unpaired image-to-image translation of
generative adversarial networks. For two image do-
mains X and Y , the loss supports the learning of map-
pings G : X →Y and F : Y → X so that one reverses
the other, i.e., F(G(x)) ≈ x and G(F(y)) ≈ y.
L(G,F) = E
x∼p
data
(x)
[||F(G(x)) −x||
1
] (4)
+ E
y∼p
data
(y)
[||G(F(y)) −y||
1
] (5)
The Supervised Contrastive Loss (Khosla et al.,
2020) pulls together clusters of points of the same
class in embedding space and pushes samples of dif-
ferent classes apart. It aims at leveraging label infor-
mation more effectively than cross-entropy loss.
L
sup
i
=
−1
2N
˜y
i
−1
· (6)
2N
∑
j=1
1
i̸= j
·1
˜y
i
= ˜y
j
·log
exp(z
i
·z
j
/τ)
∑
2N
k=1
1
i̸=k
·exp(z
i
·z
k
/τ)
(7)
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
420

where N
˜y
i
is the total number of images in the mini-
batch that have the same label ˜y
i
as the anchor i. The
total loss is the sum over the loss of all anchors i, i.e.,
L =
∑
i
L
sup
i
. The loss has important properties well
suited for supervised learning:
• generalization to an arbitrary number of positives
• contrastive power increases with more negatives.
3.2 Regularization
Regularization techniques in machine learning (sur-
veyed in (Moradi et al., 2020)) have proven very help-
ful for deep learning. Explicit regularization adds a
loss term R( f ) for a network f to the loss function
L(x) for data (x
i
,y
i
) with a trade-off parameter λ.
min
f
∑
i
L(x
i
,y
i
) + λR( f ) (8)
Implicit regularization is all other regularization, e.g.,
early stopping or using a robust loss function. Clas-
sical L2-regularization and dropout(Srivastava et al.,
2014), where activations of a random set of neurons
are set to 0, are among the most wildly used regular-
ization.
R
1
Regularization (Mescheder et al., 2018) is used
to penalize the discriminator in generative adversarial
networks based on the gradient with the goal of stabi-
lizing training:
R
1
(ψ) =
γ
2
E
p
D
(x)
[||∇D
ψ
(x)||
2
] (9)
Technically, the regularization term penalizes gradi-
ents orthogonal to the data manifold.
Entropy Regularization (Mnih et al., 2016) aims at
fostering diversity. Specifically, asynchronous meth-
ods for deep reinforcement learning (Williams and
Peng, 1991; Mnih et al., 2016). (Mnih et al., 2016)
ensures diversity of actions in reinforcment learn-
ing, i.e., it prevents overoptimizion towards a small
fraction of the environment. The entropy is simply
computed over the probability distribution of actions
given by the policy π(x) as:
H(x) =
∑
x
π(x) ·log(π(x)) (10)
Path Length Regularization (Karras et al., 2020a)
for generative adversarial networks aims at ensur-
ing that the fixed-size step length in the latent space
matches the fixed-magnitude change in the image.
The idea is to encourage that a fixed-size step in the
latent space W results in a non-zero, fixed-magnitude
change in the image. The goal is to ensure better con-
ditioning of GANs, simplifying architecture search
and generator inversion. Gradients with respect to
w ∈ W stemming from random directions in the im-
age space should be almost equal in length indepen-
dent of w or the image space direction. The local met-
ric scaling characteristics of the generator g : W →Y
are captured by the Jacobian matrix J
w
= δg(w)/δw.
The regularizer becomes:
E
w,y∼N (0,I)
(||J
T
w
y||
2
−a)
2
(11)
where y are random images with normally distributed
pixel values, and w ∼ f (z), where z is normally dis-
tributed. The constant a is the exponential moving
average of ||J
T
w
y||
2
. The paper further avoids the com-
putationally expensive, explicit computation of the Ja-
cobian.
DropBlock (Ghiasi et al., 2018) drops correlated ar-
eas of features maps rather than selecting features to
drop independently. This is especially suitable for
convolutional neural networks where features maps
exhibit spatial correlation and a (real-world) feature
often corresponds to a contiguous spatial area in fea-
ture maps.
3.3 Optimization
Optimization(surveyed in (Sun, 2020)) is the process
of estimating all network parameters so that the loss
function is minimized. The two most wildly known
technique is stochastic gradient descent(SGD) and
Adam. None strictly outperforms in all cases in terms
of generalization performance. SGD dates back at
least to the 50ies(Kiefer and Wolfowitz, 1952), while
Adam stems from 2014(Kingma and Ba, 2014).
Adafactor (Shazeer and Stern, 2018) reduces the
memory needs of the Adam optimization by maintain-
ing only row- and column-wise statistics of parameter
matrixes rather than per-element information.
Layerwise Adaptive Large Batch Optimization
(LAMB) (You et al., 2019) builds on Adam and accel-
erates training using large mini-batches. It performs
per-dimension and layerwise normalization.
Two Time-Scale Update Rule(TTUR). For genera-
tive adversarial networks trained with stochastic gra-
dient descent TTUR(Heusel et al., 2017) uses a sepa-
rate learning rate for the discriminator and generator.
For a fixed generator, the discriminator reaches a local
minimum. This still holds if the generator converges
slowly, e.g., using a small(er) learning rate. This helps
in convergence of the GAN and it can improve perfor-
mance since the generator captures the feedback of
the discriminator more profoundly before pushing it
into new regions.
Decoupled Weight Decay Regularization for
ADAM. AdamW(Loshchilov and Hutter, 2017) is
A Survey of Deep Learning: From Activations to Transformers
421

built on a simple observation and implemenation. The
orginal Adam optimization changes weights due to
(L2-)regularization after computation of gradients for
Adam. But intuitively moving averages of gradients
should not include regularization.
RAdam and AMSGrad. Both techniques tackle the
convergence problem of Adam. Rectified Adam(Liu
et al., 2019a) rectifies the variance of the adaptive
learning rate, which is large initially. Thus, similar to
the warm-up heuristic small initial learning rates can
help. AMSGrad (Reddi et al., 2019) uses the maxi-
mum of past squared gradients rather than the expo-
nential average.
Stochastic Weight Averaging. Simple averaging of
weights from different epochs during stochastic gra-
dient descent with constant or cycling learning rate
improves performance.(Izmailov et al., 2018)
Sharpness-Aware Minimization (Foret et al., 2020)
minimizes loss value and sharpness, which improves
generalization. It finds parameters with neighbor-
hoods of low loss value (rather than parameters that
only themselves have low loss value). The loss is:
min
w
max
||ε||
p
≤ρ
L(w + ε) (12)
4 SELF, SEMI-SUPERVISED AND
CONTRASTIVE LEARNING
Semi-supervised learning leverages a large amount
of unlabelled data based on a small amount of la-
beled data (see (Yang et al., 2022) for a survey).
Self-supervised learning benefits from self-generated
(pseudo)labels stemming from artificial tasks. Both
reduce the burden of collecting (human) labeled data.
Self-supervised (pre-)training combined with fine-
tuning on a (small) human-annotated dataset can lead
to state-of-the-art results. The paradigm has grown
extensively in recent years (surveyed in (Ericsson
et al., 2022)). It is commonly combined with con-
trastive learning. In contrastive learning, the goal is
to learn to distinguish between similar and dissimi-
lar data. Since data can be automatically distorted to
different extents, creating “pseudo-labeled” data for
self-supervised learning can be straightforward.
The simple framework for contrastive learning
(SimCLR)(Chen et al., 2020) maximizes agreement
between two inputs that result from augmenting the
same data sample differently. Augmentation can
be random cropping, color distortions, and Gaus-
sian blur. To obtain reprsentation vectors, a standard
ResNet(He et al., 2016) is used. Representations are
further processed using a simple MLP before the con-
trastive loss is applied.
Bootstrap Your Own Latent (BYOL) (Grill et al.,
2020) uses an online and a target network. Both have
the same architecture consisting of an encoder, a pro-
jector, and a predictor but they do not share weights.
The target network’s parameters are an exponential
moving average of the online network’s parameters.
The online network has to predict the target network’s
representation given an augmentation of the (same)
input.
Barlow Twins (Zbontar et al., 2021) rely on an ob-
jective function that aims to reduce cross-correlation
C between outputs for a set of image Y
A
and their dis-
torted versions Y
B
as close to the identity as possible,
i.e., the loss (including λ as a tuning parameter) is:
L =
∑
i
(1 −C
i,i
)
2
+ λ ·
∑
i
∑
j̸=i
C
2
i, j
(13)
Momentum Contrast (MoCo) (He et al., 2020)
builds a dynamic dictionary represented by an en-
coder using unsupervised contrastive learning. Train-
ing performs look-ups and enforces that an encoded
query should be similar to its matching encoded key
and dissimilar to others. The dictionary is a queue of
data samples. For every mini-batch, encoded samples
are added, and the oldest mini-batch are dequeud. The
key encoder is a momentum-based moving average of
the query encoder, which should help to maintain con-
sistency.
Noisy Student. The paper(Xie et al., 2020) describes
training an (EfficientNet) model on labeled data. This
model is used as a teacher to generate pseudo labels
for unlabeled images. A larger (EfficientNet) model
is trained on the union of all data. This process is
repeated, i.e., the student becomes the teacher of a
new student. During student training, noise such as
dropout and data augmentation are applied so that the
student’s learning is harder and it can improve on the
teacher.
FixMatch (Sohn et al., 2020) predicts the label of
a weakly-augmented image. If the confidence for a
label is above a threshold, then the model is trained
to produce the same label for the strongly-augmented
version of the image.
5 ARCHITECTURES AND
LAYERS
We elaborate on four important layers types, i.e.,
activation-, skip-, normalization-, and attention lay-
ers followed by numerous contemporary architectures
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
422

based on transformers as well as graph neural net-
works.
5.1 Activation
Activation functions are usually non-linear. They
have a profound impact on gradient flow and, thus,
on learning. Early activation functions commonly
used from the 1960s throuhout the early 2000s such
as sigmoid and tanh make training deep networks dif-
ficult due to the vanishing gradient when these func-
tions saturate. The introduction of the rectified linear
unit ReLU in 2010(Nair and Hinton, 2010) marked
a breakthrough result. While its original version is
still commonly used, transformer architectures have
popularized other activation functions and ReLU vari-
ants. Most of them still share qualitatively the behav-
ior of ReLU, i.e., for negative inputs, outputs are of
small magnitude and for positive inputs, they are un-
bounded (see (Apicella et al., 2021) for a survey).
Gaussian Error Linear Units (GELU)(Hendrycks
and Gimpel, 2016) weigh inputs by their precentile
(ReLUs only use the sign). Activation is the prod-
uct of the input and the standard Gaussian cumulative
distribution function Φ(x), i.e.,
GELU(x) = x ·Φ(x) (14)
The Mish activation(Misra, 2019) originates from
systematic experimentation inspired by Swish and
ReLU:
f (x) = x ·tanh(so f t
+
(x)) (15)
with so f t
+
(x) := ln(1 + e
x
) (16)
In comparison, the Swish activation(Ramachandran
et al., 2017) is:
f (x) = x ·sigmoid(βx) (17)
Here β is a learnable parameter.
5.2 Skip Connections
Skip connections originate from residual net-
works(He et al., 2016). In the simplest form, the
output y for an input x of a single layer L (or a set of a
few layers) with a skip connection is y(x) = L(x) + x.
The original paper used the term residual since the
layer L has to learn a residual L(x) = H(x) −x rather
than the desired mapping H itself. Since then, skip
connections have been used in many variations.
Inverted Residual Block (Sandler et al., 2018). By
inverting the channel width to a narrow-wide-narrow
layer sequence from the original wide-narrow-wide
order(He et al., 2016) in combination with depthwise
convolutions for the wide-layer, parameters are re-
duced, and residual blocks execute faster.
A Dense Block (Huang et al., 2017) receives in-
puts from all prior layers (with matching feature-map
sizes) and connects to all subsequent layers (with
matching feature-map sizes).
ResNeXt Block (Xie et al., 2017). This split-
transform-merge approach for residual blocks entails
evaluating multiple residual blocks in parallel and ag-
gregating them back into a single output.
5.3 Normalization
Since the introduction of batch-normalization(Ioffe
and Szegedy, 2015), normalization has been a very
successful concept in improving training speed, sta-
bility, and generalization of neural networks. How-
ever, their need is debated(Shao et al., 2020), e.g.,
for some applications careful initialization and adjust-
ments of learning rates might make them at least par-
tially redundant. The idea of normalization is to trans-
form a value x to a normalized value ˜x, by subtracting
the mean µ and scaling by the standard deviation σ,
i.e., ˜x =
x−µ
σ
. Normalization approaches differ in the
computation of µ and σ, e.g., µ and σ can be computed
across different channels.
Layer Normalization. Given summed inputs, nor-
malization statistics are computed(Ba et al., 2016) for
a layer L with |L| neurons as:
µ =
1
|L|
|L|−1
∑
i=0
a
i
σ =
v
u
u
t
1
|L|
|L|−1
∑
i=0
(a
i
−µ)
2
(18)
In contrast to batch-normalization, it poses no restric-
tions on batch size and also no dependencies between
batches. In particular, it can be used with batch size
1.
Instance Normalization (Ulyanov et al., 2016) com-
putes for a 4-dimensional input, such as an image with
height H, width W , channels C, and batch size T :
µ
t,c
=
1
HW T
∑
t<T,w<W,h<H
x
t,c,w,h
(19)
σ
t,c
=
s
1
HW T
∑
t<T,w<W,h<H
(x
t,c,w,h
−µ
t,c
)
2
(20)
It can be used, e.g., to normalize contrast for an im-
age. There exist multiple versions of it, e.g., a ver-
sion that scales based on weight norms(Karras et al.,
2020b).
LayerScale (Touvron et al., 2021) has been intro-
duced in the context of transformers as a per-channel
A Survey of Deep Learning: From Activations to Transformers
423

multiplication of outputs of a residual block with a
diagonal matrix:
x
l
′
= x
l
+ diag(λ
1
,...,λ
d
) ·SA(η(x)) (21)
x
l+1
= x
l
′
+ diag(λ
1
,...,λ
d
) ·FFN(η(x)) (22)
SA is the self-attention layer, FFN is the feed forward
network, and η the layer-normalisation (see Figure 2).
5.4 Attention
Attention mechanisms (surveyed in (Brauwers and
Frasincar, 2021; Guo et al., 2022b)) allow for learn-
ing relevance scores for inputs, similar to how cog-
nitive attention works. Some parts of the inputs can
be deemed highly important, while others are disre-
garded as irrelevant. The relevance of a particular in-
put can often be determined by contextual informa-
tion, such as the relevance of a word in a text docu-
ment often depends on nearby words.
Scaled Dot-Product Multi-Head Attention
(Vaswani et al., 2017). Using dot products combined
with down-scaling has proven very successful in
computing attention scores. Attention takes a query
Q, a key K and a value V as inputs and outputs an
attention score:
Att(Q,K,V) = softmax

QK
T
√
d
k

·V (23)
Using multiple, independent attention mecha-
nisms in parallel allows attending to various aspects
of the input. Formally, in multi-head attention, we
learn matrixes W:
MultiHead(Q,K,V) = [h
0
,...,h
n−1
]W
0
(24)
where head h
i
= Att(QW
Q
i
,KW
K
i
,VW
V
i
) (25)
Factorized (Self-)Attention (Child et al., 2019) re-
duces the computational and memory footprint of at-
tention. While (full) self-attention(Vaswani et al.,
2017) allows attending to every prior input element,
factorized self-attention allows only to attend to a sub-
set thereof. Formally, an output matrix is computed
given a matrix of input embeddings X and the con-
nectivity pattern S = {S
1
,...,S
n
}, where S
i
is the set
of indices of input vectors attended to by the ith out-
put vector.
FacAtt(X,S) = (A(x
i
,S
i
))
i∈[1,n]
(26)
a(x
i
,S
i
) = softmax(
(W
q
x
i
)K
T
S
i
√
d
) ·V
S
i
(27)
K
Si
= (W
k
x
j
)
j∈S
i
V
S
i
= (W
v
x
j
)
j∈S
i
(28)
For full self-attention S
F
i
:= {j|j ̸= i}(indexes to prior
inputs to i). In contrast, factorized self-attention has p
separate attention heads, where the mth head defines a
subset A
(m)
i
⊂ S
F
i
and lets S
i
= A
(m)
i
. For strided self-
attention:
A
(1)
i
= {t,t + 1, ...i} for t = max(0,i −l) (29)
A
(2)
i
= {j : (i − j) mod l = 0} (30)
This pattern is suitable, when structure aligns with the
stride-like images. For data without a periodic struc-
ture like text, fixed attention can be preferable:
A
(1)
i
= {j : ⌊j/l⌋ = ⌊i/l⌋} (31)
A
(2)
i
= {j : j mod l ∈ {t,t + 1, ...l}} (32)
where t = l −c and c is a hyperparameter. For ex-
ample, for stride 128 and c = 8, all future positions
greater than 128 can attend to positions 120-128, all
greater 256 to 248-256, etc.
A Residual Attention Network (RAN) (Wang et al.,
2017) module leverages the idea of skip connections.
It consists of a mask and a trunk branch. The trunk
branch performs feature processing. It can be any net-
work. The mask branch represents feature weights.
The output of an attention module is
H
i,c
(x) = (1 + M
i,c
(x)) ·F
i,c
(X) (33)
Here i is a spatial position and c is a channel. M(x)
should be approximatedly 0, H(x) approximates orig-
inal features F(x).
Large Kernel Attention (Guo et al., 2022a) decom-
poses a large scale convolution into three smaller
scale convolutions using common ideas, i.e., depth-
wise dilated convolution, a non-dilated depthwise
convolution, and a channel-wise 1x1 convolution. For
the output of these convolutions, an attention map is
learned.
Sliding Window Attention (Beltagy et al., 2020)
aims at improving the time and memory complexity
of attention. It reduces the number of considered in-
put pairs. More precisely, for a given window size w
each token attends to
w
2
tokens on each side.
5.5 Transformers
Transformers have quickly become the dominant ar-
chitecture in deep learning. Combined with self-
supervised training on large datasets, they have
reached state-of-the-art on many benchmarks in
NLP(see (Liu et al., 2023) for a survey) and computer
vision (surveyed in (Han et al., 2022; Khan et al.,
2022)). Since their introduction in 2017(Vaswani
et al., 2017) countless versions have emerged that
tackle issues of the original transformer such as com-
putational overhead and data efficiency.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
424

Transformers are said to have less inductive bias
and are in turn more flexible than other architec-
tures, such as convolutional neural networks and re-
current networks. Thus, they also require more train-
ing data to compensate for the lack of inductive bias.
Since large amounts of labeled data are difficult to ob-
tain, transformers are commonly trained using self-
supervised learning, i.e., pseudo-labels. The original
transformer(Vaswani et al., 2017), developed for nat-
ural language processing, employs an encoder and de-
coder like earlier recurrent neural networks. It stacks
multiple transformer blocks on top of each other, as
illustrated in Figure 2. Key elements are multi-head
attention, layer normalization, and skip connections.
Furthermore, positional encodings and embeddings
of inputs play an important role. The absolute po-
sitional encodings PE for position pos in (Vaswani
et al., 2017) uses sine and cosine functions varying in
frequency:
PE(pos,2i) = sin(pos/10000
2i/d
) (34)
PE(pos,2i + 1) = cos(pos/10000
(2i)/d
) (35)
where i is the dimension of the encoding and d is the
number of dimensions. The choice was motivated by
the fact that relative positions, which might be equally
relevant to absolute ones, are a linear function of ab-
solute position encodings.
Bidirectional Encoder Representations from
Transformers(BERT) (Devlin et al., 2018) yields
contextual word-embeddings using the encoder
of the transformer architecture. It relies on a
masked language model pre-training objective and
self-supervised learning. The model must predict
randomly chosen, masked input tokens given its
context. Thus, the model has bidirectional informa-
tion, i.e., it is fed tokens before and after the masked
words. In classical next-word prediction no tokens
after the word to predict are given. As a second
prediction task, the model must predict if a sentence
pair (A,B) consists of two consecutive sentences
A and B within some document (or two possibly
unrelated sentences). The pre-trained model based
on self-supervised training can be fine-tuned for
downstream tasks using labeled data.
The original BERT model has since then im-
proved in many ways, e.g., (Sanh et al., 2019) reduced
the computational burden of BERT, and (Liu et al.,
2019b) trained models longer, on longer sequences,
with bigger batches over more data, etc. This led to
more robust and generalizable representations.
GPT to GPT-3 on to ChatGPT and GPT-4. GPT
is based on the decoder of a transformer to predict
tokens sequentially. GPT(Radford et al., 2018) first
performs pre-training in an unsupervised way before
applying supervised fine-tuning. Pre-training takes
place on a large corpus of tokens U = (u
0
,u
1
,...,u
n−1
)
by maximizing the likelihood of the next token given
prior tokens:
L(U) =
∑
i
p(u
i
|u
i−k
,...,u
i−1
) (36)
where k is the size of the context window and the
conditional probability is modeled using a neural
network, i.e., using a multi-layer transformer de-
coder(Liu et al., 2018) by dropping the encoder in
(Vaswani et al., 2017). Rather than only predicting the
next token given an input, the model is also trained to
predict input tokens. Furthermore, the memory foot-
print of attention is lowered. GPT-2 (Radford et al.,
2019) builds on GPT with few modifications, e.g.,
layer normalization locations were changed (moved
to the input of each sub-block, and an extra normal-
ization was added after the final self-attention block),
initialization of residual weights was scaled, and the
vocabulary, context, and batch size were increased.
GPT-3’s(Brown et al., 2020) architecture is almost
identical to that of GPT-2, but the number of param-
eters is more than 100 times larger and it differs in
(amount of) training data. ChatGPT(OpenAI, 2022)
is a sibling to InstructGPT(Ouyang et al., 2022),
which is optimized towards following user intentions.
InstructGPT applies fine-tuning of GPT-3 in a two-
step process: (i) based on labeler demonstrations
through supervised learning and (ii) based on human
rankings of model outputs using reinforcement learn-
ing. ChatGPT follows the same procedure, i.e., (i)
for supervised learning, human AI trainers provided
conversations by playing both the human user and
the AI assistant. The resulting dialogue dataset was
enhanced with the InstructGPT dataset, which was
transformed into a dialogue format. (ii) Conversations
of AI trainers with ChatGPT were ranked, i.e., for a
randomly selected model-written message, AI train-
ers ranked several alternative completions. The rank-
ing dataset was used for reinforcement learning. The
process was repeated multiple times.
Technical details of the successor of ChatGPT, i.e.,
GPT-4 have not been disclosed(OpenAI, 2023). The
provided technical report indicates that it is similar to
ChatGPT. GPT-4 is multi-modal, i.e., it can also pro-
cess images, however, details are unknown. The re-
port only points towards major improvements in train-
ing efficiency. The accomplishment was to predict
the performance of large scale models using the per-
formance of small models (possibly trained on less
data). This is highly important as computational costs
and time can be a key factor for large deep learning
models.
Text-to-Text Transfer Transformer (T5) (Raffel
A Survey of Deep Learning: From Activations to Transformers
425

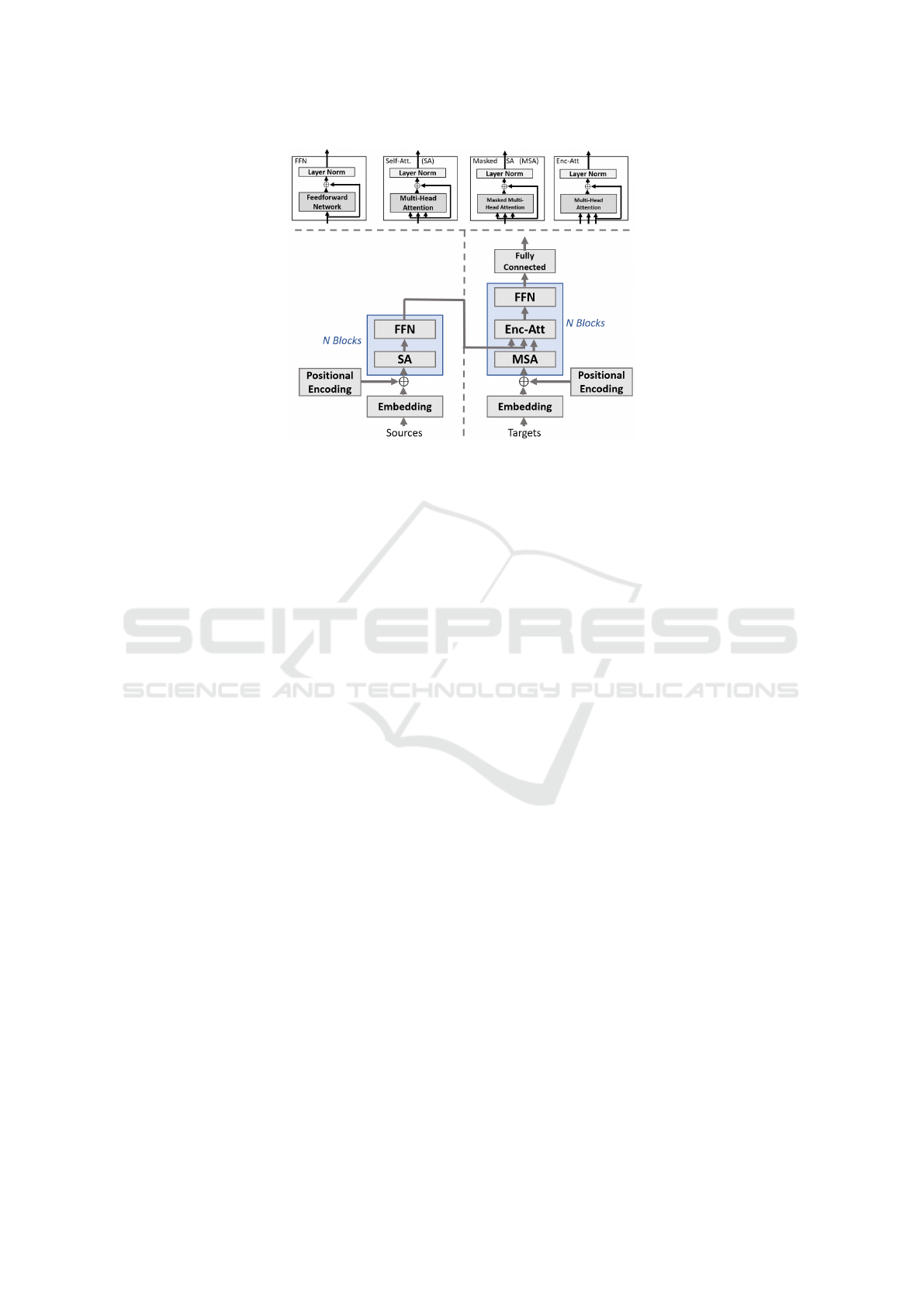
Figure 2: Transformer with the four basic blocks on top and the encoder and decoder at the bottom.
et al., 2020) views every text-based language mod-
els as generating an output text from a given input
text. It differs from BERT(Devlin et al., 2018) by us-
ing causal masking during training for predicting the
target. Causal masking prevents the network from ac-
cessing “future” tokens of the target. T5 also differs
in pre-training tasks.
BART (Lewis et al., 2020) is a denoising autoen-
coder for pretraining sequence-to-sequence models
that uses a standard transformer based machine trans-
lation architecture. It has been shown to be effective
for language generation, translation, and comprehen-
sion. Training is based on corrupting text with noising
functions ranging from token deletion, masking onto
sentence permutation and document rotation. Learn-
ing stems form reconstructing the original text from
its corrputed version. The flexibility in noising op-
tions is attributed due to BART’s generalization of
prior works such as BERT and GPT, i.e., the encoder
is bi-directional (like BERT), while the decoder is au-
toregressive (like GPT).
XLNet (Yang et al., 2019) combines advantages of
autoregressive modeling like GPT, predicting the next
token, and denoising auto-encoding BERT(Devlin
et al., 2018), reconstructing x given a noisy input ˆx
that originates through masking words of x. It does so
by using a permutation language model that samples
a permutation of Z = z
0
,z
1
,...,z
T −1
of the sequence
(0,1,2,...,T −1) leading to the objective:
max p(u
z
T
|u
z
0
,...,u
z
T −1
)
(37)
There is no actual permutation of inputs, which would
be unnatural (and not occurring during later fine-
tuning tasks). Rather, the permutation impacts the at-
tention mask to ensure that the factorization order by
Z is maintained.
The Vision Transformer (Dosovitskiy et al., 2020)
relies heavily on the original transformer. An image
is partitioned into small patches, which are flattened
and linearly embedded with position embeddings. A
standard transformer encoder then processes the cre-
ated vector of each patch.
The Swin Transformer (Liu et al., 2021) for com-
puter vision builds hierarchical feature maps rather
than just a single (resolution) feature map. It also only
computes self-attention within a local window reduc-
ing computation time.
PaLM (2). The original PaLM(Chowdhery et al.,
2022) is a large language model consisting of 540 bil-
lion parameters similar to other more prominent such
as GPT-3. Technical innovation discussed is mostly
on the scaling of model training, i.e., a single model
can be trained across tens of thousands of accelera-
tor chips efficiently. The original transformer archi-
tecture(Vaswani et al., 2017) is also adjusted slightly,
e.g., SwiGLU activations are used, i.e.,
Swish(xW ) ·xV (38)
, where Swish is given by Eq. 17, different positional
embeddings (better for long sequences), and multi-
query attention (faster computation), no biases (bet-
ter training stability), and shared input-output embed-
dings.
PaLM 2 (Google, 2023) is the better performing
successor of PaLM that differs in terms of dataset
mixtures, e.g., using more diverse languages as well
as domains (e.g., programing languages, mathemat-
ics). It also uses the classical transformer architecture.
However, it uses a smaller model than the first PaLM
version but more training compute. It also relies on
more diverse pre-training objectives (than simple next
word or masked word prediction).
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
426

5.6 Graph Neural Networks
Graph neural networks (surveyed in (Wu et al., 2020))
can be seen as a generalization of CNNs and trans-
formers. They operate on graph data, i.e., nodes con-
nected with edges. We discuss graph models, includ-
ing models to obtain node embeddings that can be
used for downstream tasks.
Graph Convolutional Networks (Kipf and Welling,
2016) use CNNs for semi-supervised learning. They
approximate spectral graph convolutions using poly-
nomials of order k, which a CNN can compute with k
linear layers.
Graph Attention Networks (Veli
ˇ
ckovi
´
c et al., 2017)
rely on masked self-attention layers allowing nodes
to attend flexibly over their neighborhoods’ features,
i.e., node j obtains importance scores for node i’s fea-
tures. Masking allows to only consider edges between
node pairs that are actually connected. In contrast
to GCN, different importances for nodes in the same
neighborhood can be assigned. Also, it does not rely
on costly matrix operations for eigendecompositions.
Graph Transformer (Dwivedi and Bresson, 2020)
extends the original transformer to graphs by using at-
tention over neighborhood connectivity for each node,
generalizing the position encoding, replacing layer-
with batch-normalization, and learning edge repre-
sentations (in addition to node representations).
TuckER (Bala
ˇ
zevi
´
c et al., 2019) performs factoriza-
tion for link prediction in knowledge graph. Knowl-
edge is represented as (subject, relation, object)
triplets, and the task is to predict whether two enti-
ties are related. The graph can be represented as a bi-
nary tensor with the subjects, relations, and objects as
dimensions. They use Tucker decompositions to de-
compose the binary tensor into a product of a core ma-
trix and embedding matrices for subjects, relations,
and objects.
Embedding by Relational Rotation (RotatE) (Sun
et al., 2019) performs missing link prediction
in knowledge graphs (like the priorly described
TuckER(Bala
ˇ
zevi
´
c et al., 2019)) to model more re-
lational properties such as composition and inversion.
They embed entities into a complex space and treat
the relation as an element-wise rotation that is opti-
mized to lead from one entity to the other.
Scalable Feature Learning for Networks
(Node2Vec) (Grover and Leskovec, 2016) learns
feature vectors that preserve a node’s neighborhood.
They use random walks to generate sample neighbor-
hoods, thereby, nodes are viewed based on their role
or communities they belong to.
6 DISCUSSION
Our survey focused on key design elements in build-
ing deep learning models. Taking a practical ap-
proach, we chose to ignore theoretical works, which
should be further explored in future studies. Our find-
ings suggest that despite many small and creative in-
novations since the original transformer architecture,
there have not been any significant ”breakthrough”
discoveries that have led to much better leaderboard
results. The last few years have been characterized
by the enlargement of existing networks such as GPT,
the increase of data volume (and quality), and a shift
towards self-supervised learning. This could indicate
a need for more daring approaches to research rather
than incremental improvements of existing works.
Combining different elements as outlined in this work
could be one way to achieve this.
In addition, we noted a few general patterns that
have been proven effective in many areas:
• “Multi-X”, i.e., using the same element multiple
times in parallel, such as using multiple residual
blocks (ResNeXt) or multi-head attention. This
idea is also closely related to “ensemble learning”.
• “Higher order layers”, i.e., classical CNNs and
MLPs only apply linear layers and simple ReLU,
but layers like Mish or attention layers perform
more complex operations.
• “Moving average”, i.e., averaging weights such as
for SGD and BYOL.
• “Decompose”, i.e., decomposing matrixes such as
for TuckER and large kernel attention.
• “Weighing functions”, i.e., using parameterized
weighing functions of inputs can be seen within
the attention mechanism but also for GELU units.
Therefore, rather than naively aggregating inputs,
inputs are weighed and aggregated. The weight
might stem from a function with learnt parame-
ters. Such functions can also be seen as “gates”
that only permit the flow of information within
some range of the input parameters.
Our survey was also deliberately geared towards more
recent works, but still well-established works; this
could be perceived as a strength or as a limitation.
The selection of papers and areas was driven by a
prominent platform providing leaderboards. While a
reader looking for “what works well and what is very
promising” benefits from this approach, it could po-
tentially leave out works with exciting ideas that re-
quire more research to reveal their full capabilities.
This could be seen as perpetuating the ”winner-takes-
all” paradigm that reinforces already successful ideas.
A Survey of Deep Learning: From Activations to Transformers
427

However, due to the sheer amount of papers, a se-
lection is necessary for conducting a holistic survey
of deep learning. We acknowledge that online plat-
forms providing leaderboards etc. are very beneficial
to the research community and that they should be fur-
ther advanced. Still, we found that manual verifica-
tion (e.g., by double checking relevance with Google
scholar citations and by reading surveys and papers)
was required as we identified works and methods that
were not listed correctly on the platform.
7 CONCLUSIONS
We have presented a brief but comprehensive
overview of the deep learning design landscape. We
have summarized key works from various significant
areas that have emerged in recent years. We believe
that our holistic overview in one paper can establish
connections that could inspire novel ideas. We have
also identified four patterns that characterize many
improvements. To further advance the development
of deep learning, we need to generate fundamentally
new and successful approaches, as the improvements
made in the past few years were numerous and often
very creative but mainly incremental.
REFERENCES
Alom, M. Z., Taha, T. M., Yakopcic, C., Westberg, S.,
Sidike, P., Nasrin, M. S., Hasan, M., Van Essen, B. C.,
Awwal, A. A., and Asari, V. K. (2019). A state-of-the-
art survey on deep learning theory and architectures.
electronics.
Alzubaidi, L., Zhang, J., Humaidi, A. J., Al-Dujaili, A.,
Duan, Y., Al-Shamma, O., Santamar
´
ıa, J., Fadhel,
M. A., Al-Amidie, M., and Farhan, L. (2021). Re-
view of deep learning: Concepts, CNN architectures,
challenges, applications, future directions. Journal of
big Data.
Apicella, A., Donnarumma, F., Isgr
`
o, F., and Prevete, R.
(2021). A survey on modern trainable activation func-
tions. Neural Networks.
Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer
normalization. arXiv:1607.06450.
Bala
ˇ
zevi
´
c, I., Allen, C., and Hospedales, T. M. (2019).
Tucker: Tensor factorization for knowledge graph
completion. arXiv:1901.09590.
Beltagy, I., Peters, M. E., and Cohan, A. (2020).
Longformer: The long-document transformer.
arXiv:2004.05150.
Brauwers, G. and Frasincar, F. (2021). A general survey on
attention mechanisms in deep learning. Transactions
on Knowledge and Data Engineering.
Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D.,
Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G.,
Askell, A., et al. (2020). Language models are few-
shot learners. Advances in neural information pro-
cessing systems.
Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. (2020).
A simple framework for contrastive learning of visual
representations. In Int. Conf. on machine learning.
Child, R., Gray, S., Radford, A., and Sutskever, I. (2019).
Generating long sequences with sparse transformers.
arXiv:1904.10509.
Chowdhery, A., Narang, S., Devlin, J., Bosma, M., Mishra,
G., Roberts, A., Barham, P., Chung, H. W., Sut-
ton, C., Gehrmann, S., et al. (2022). Palm: Scal-
ing language modeling with pathways. arXiv preprint
arXiv:2204.02311.
Devlin, J., Chang, M.-W., Lee, K., and Toutanova,
K. (2018). Bert: Pre-training of deep bidi-
rectional transformers for language understanding.
arXiv:1810.04805.
Dong, S., Wang, P., and Abbas, K. (2021). A survey on
deep learning and its applications. Computer Science
Review.
Dong, X. and Shen, J. (2018). Triplet loss in siamese net-
work for object tracking. In European Conf. on com-
puter vision (ECCV).
Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,
D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,
M., Heigold, G., Gelly, S., et al. (2020). An image is
worth 16x16 words: Transformers for image recogni-
tion at scale. arXiv:2010.11929.
Dwivedi, V. P. and Bresson, X. (2020). A generalization of
transformer networks to graphs. arXiv:2012.09699.
Ericsson, L., Gouk, H., Loy, C. C., and Hospedales, T. M.
(2022). Self-supervised representation learning: In-
troduction, advances, and challenges. Signal Process-
ing Magazine.
Foret, P., Kleiner, A., Mobahi, H., and Neyshabur, B.
(2020). Sharpness-aware minimization for efficiently
improving generalization. arXiv:2010.01412.
Ghiasi, G., Lin, T.-Y., and Le, Q. V. (2018). Dropblock:
A regularization method for convolutional networks.
Advances in neural information processing systems.
Google (2023). Palm 2 technical report. https://ai.google/
static/documents/palm2techreport.pdf .
Grill, J.-B., Strub, F., Altch
´
e, F., Tallec, C., Richemond, P.,
Buchatskaya, E., Doersch, C., Avila Pires, B., Guo,
Z., Gheshlaghi Azar, M., et al. (2020). Bootstrap your
own latent-a new approach to self-supervised learn-
ing. Adv. in neural information processing systems.
Grover, A. and Leskovec, J. (2016). node2vec: Scalable
feature learning for networks. In ACM SIGKDD Int.
Conf. on Knowledge discovery and data mining.
Guo, M.-H., Lu, C.-Z., Liu, Z.-N., Cheng, M.-M.,
and Hu, S.-M. (2022a). Visual attention network.
arXiv:2202.09741.
Guo, M.-H., Xu, T.-X., Liu, J.-J., Liu, Z.-N., Jiang, P.-T.,
Mu, T.-J., Zhang, S.-H., Martin, R. R., Cheng, M.-
M., and Hu, S.-M. (2022b). Attention mechanisms
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
428

in computer vision: A survey. Computational Visual
Media.
Han, K., Wang, Y., Chen, H., Chen, X., Guo, J., Liu, Z.,
Tang, Y., Xiao, A., Xu, C., Xu, Y., et al. (2022). A
survey on vision transformer. transactions on pattern
analysis and machine intelligence.
He, K., Fan, H., Wu, Y., Xie, S., and Girshick, R. (2020).
Momentum contrast for unsupervised visual represen-
tation learning. In Conf. on computer vision and pat-
tern recognition.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Conf. on com-
puter vision and pattern recognition.
Hendrycks, D. and Gimpel, K. (2016). Gaussian error linear
units (gelus). arXiv:1606.08415.
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., and
Hochreiter, S. (2017). Gans trained by a two time-
scale update rule converge to a local nash equilibrium.
Advances in neural information processing systems.
Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger,
K. Q. (2017). Densely connected convolutional net-
works. In Conf. on computer vision and pattern recog-
nition.
Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-
celerating deep network training by reducing internal
covariate shift. In Int. Conf. on machine learning.
Izmailov, P., Podoprikhin, D., Garipov, T., Vetrov, D.,
and Wilson, A. G. (2018). Averaging weights
leads to wider optima and better generalization.
arXiv:1803.05407.
Karras, T., Laine, S., Aittala, M., Hellsten, J., Lehtinen, J.,
and Aila, T. (2020a). Analyzing and improving the
image quality of stylegan. In Conf. on computer vision
and pattern recognition.
Karras, T., Laine, S., Aittala, M., Hellsten, J., Lehtinen, J.,
and Aila, T. (2020b). Analyzing and improving the
image quality of stylegan. In Conf. on computer vision
and pattern recognition.
Khan, A., Sohail, A., Zahoora, U., and Qureshi, A. S.
(2020). A survey of the recent architectures of deep
convolutional neural networks. Artificial intelligence
review.
Khan, S., Naseer, M., Hayat, M., Zamir, S. W., Khan, F. S.,
and Shah, M. (2022). Transformers in vision: A sur-
vey. ACM computing surveys (CSUR).
Khosla, P., Teterwak, P., Wang, C., Sarna, A., Tian, Y.,
Isola, P., Maschinot, A., Liu, C., and Krishnan, D.
(2020). Supervised contrastive learning. Advances
in neural information processing systems.
Kiefer, J. and Wolfowitz, J. (1952). Stochastic estimation
of the maximum of a regression function. The Annals
of Mathematical Statistics.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization. arXiv:1412.6980.
Kipf, T. N. and Welling, M. (2016). Semi-supervised
classification with graph convolutional networks.
arXiv:1609.02907.
Lewis, M., Liu, Y., Goyal, N., Ghazvininejad, M., Mo-
hamed, A., Levy, O., Stoyanov, V., and Zettlemoyer,
L. (2020). BART: Denoising Sequence-to-Sequence
Pre-training for Natural Language Generation, Trans-
lation, and Comprehension. In Proceedings of the
58th Annual Meeting of the Association for Compu-
tational Linguistics, pages 7871–7880.
Lin, T.-Y., Goyal, P., Girshick, R., He, K., and Doll
´
ar, P.
(2017). Focal loss for dense object detection. In Int.
Conf. on computer vision.
Liu, L., Jiang, H., He, P., Chen, W., Liu, X., Gao, J., and
Han, J. (2019a). On the variance of the adaptive learn-
ing rate and beyond. arXiv:1908.03265.
Liu, P., Yuan, W., Fu, J., Jiang, Z., Hayashi, H., and Neubig,
G. (2023). Pre-train, prompt, and predict: A system-
atic survey of prompting methods in natural language
processing. ACM Computing Surveys.
Liu, P. J., Saleh, M., Pot, E., Goodrich, B., Sepa-
ssi, R., Kaiser, L., and Shazeer, N. (2018). Gen-
erating wikipedia by summarizing long sequences.
arXiv:1801.10198.
Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D.,
Levy, O., Lewis, M., Zettlemoyer, L., and Stoyanov,
V. (2019b). Roberta: A robustly optimized bert pre-
training approach. arXiv:1907.11692.
Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin,
S., and Guo, B. (2021). Swin transformer: Hierarchi-
cal vision transformer using shifted windows. In Int.
Conf. on computer vision.
Loshchilov, I. and Hutter, F. (2017). Decoupled weight de-
cay regularization. arXiv:1711.05101.
Mescheder, L., Geiger, A., and Nowozin, S. (2018). Which
training methods for GANs do actually converge? In
Int. Conf. on machine learning.
Min, B., Ross, H., Sulem, E., Veyseh, A. P. B., Nguyen,
T. H., Sainz, O., Agirre, E., Heinz, I., and Roth, D.
(2021). Recent advances in natural language process-
ing via large pre-trained language models: A survey.
arXiv preprint arXiv:2111.01243.
Misra, D. (2019). Mish: A self regularized non-monotonic
activation function. arXiv:1908.08681.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,
Harley, T., Silver, D., and Kavukcuoglu, K. (2016).
Asynchronous methods for deep reinforcement learn-
ing. In Int. Conf. on machine learning.
Moradi, R., Berangi, R., and Minaei, B. (2020). A survey
of regularization strategies for deep models. Artificial
Intelligence Review.
Nair, V. and Hinton, G. E. (2010). Rectified linear units
improve restricted boltzmann machines. In Int. Conf.
on machine learning (ICML-).
OpenAI (2022). Chatgpt: Optimizing language models for
dialogue. https://openai.com/blog/ chatgpt/ .
OpenAI (2023). Gpt-4 technical report.
Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wain-
wright, C. L., Mishkin, P., Zhang, C., Agarwal, S.,
Slama, K., Ray, A., et al. (2022). Training language
models to follow instructions with human feedback.
arXiv:2203.02155.
Radford, A., Narasimhan, K., Salimans, T., Sutskever, I.,
et al. (2018). Improving language understanding by
generative pre-training.
A Survey of Deep Learning: From Activations to Transformers
429

Radford, A., Wu, J., Child, R., Luan, D., Amodei, D.,
Sutskever, I., et al. (2019). Language models are un-
supervised multitask learners. OpenAI blog.
Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S.,
Matena, M., Zhou, Y., Li, W., and Liu, P. J. (2020).
Exploring the limits of transfer learning with a uni-
fied text-to-text transformer. The Journal of Machine
Learning Research.
Ramachandran, P., Zoph, B., and Le, Q. V. (2017).
Searching for activation functions. arXiv preprint
arXiv:1710.05941.
Reddi, S. J., Kale, S., and Kumar, S. (2019). On the conver-
gence of adam and beyond. arXiv:1904.09237.
Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., and
Chen, L.-C. (2018). Mobilenetv2: Inverted residuals
and linear bottlenecks. In Conf. on computer vision
and pattern recognition.
Sanh, V., Debut, L., Chaumond, J., and Wolf, T. (2019).
DistilBERT, a distilled version of BERT: smaller,
faster, cheaper and lighter. arXiv:1910.01108.
Schultz, M. and Joachims, T. (2003). Learning a distance
metric from relative comparisons. Advances in neural
information processing systems, 16.
Shao, J., Hu, K., Wang, C., Xue, X., and Raj, B. (2020). Is
normalization indispensable for training deep neural
network? Advances in Neural Information Processing
Systems.
Shazeer, N. and Stern, M. (2018). Adafactor: Adaptive
learning rates with sublinear memory cost. In Int.
Conf. on Machine Learning.
Shrestha, A. and Mahmood, A. (2019). Review of deep
learning algorithms and architectures. IEEE access.
Sohn, K., Berthelot, D., Carlini, N., Zhang, Z., Zhang, H.,
Raffel, C. A., Cubuk, E. D., Kurakin, A., and Li, C.-
L. (2020). Fixmatch: Simplifying semi-supervised
learning with consistency and confidence. Advances
in neural information processing systems.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: a simple way
to prevent neural networks from overfitting. The jour-
nal of machine learning research.
Sun, R.-Y. (2020). Optimization for deep learning: An
overview. Operations Research Society of China.
Sun, Z., Deng, Z.-H., Nie, J.-Y., and Tang, J. (2019). Rotate:
Knowledge graph embedding by relational rotation in
complex space. arXiv:1902.10197.
Touvron, H., Cord, M., Sablayrolles, A., Synnaeve, G., and
J
´
egou, H. (2021). Going deeper with image transform-
ers. In Int. Conf. on Computer Vision.
Ulyanov, D., Vedaldi, A., and Lempitsky, V. (2016). In-
stance normalization: The missing ingredient for fast
stylization. arXiv:1607.08022.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,
L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.
(2017). Attention is all you need. Advances in neural
information processing systems.
Veli
ˇ
ckovi
´
c, P., Cucurull, G., Casanova, A., Romero, A., Lio,
P., and Bengio, Y. (2017). Graph attention networks.
arXiv:1710.10903.
Wang, F., Jiang, M., Qian, C., Yang, S., Li, C., Zhang, H.,
Wang, X., and Tang, X. (2017). Residual attention
network for image classification. In Conf. on com-
puter vision and pattern recognition.
Wang, Q., Ma, Y., Zhao, K., and Tian, Y. (2020). A compre-
hensive survey of loss functions in machine learning.
Annals of Data Science.
Williams, R. J. and Peng, J. (1991). Function optimiza-
tion using connectionist reinforcement learning algo-
rithms. Connection Science.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Philip,
S. Y. (2020). A comprehensive survey on graph neu-
ral networks. Transactions on neural networks and
learning systems.
Xie, Q., Luong, M.-T., Hovy, E., and Le, Q. V. (2020). Self-
training with noisy student improves imagenet clas-
sification. In Conf. on computer vision and pattern
recognition.
Xie, S., Girshick, R., Doll
´
ar, P., Tu, Z., and He, K. (2017).
Aggregated residual transformations for deep neural
networks. In Conf. on computer vision and pattern
recognition.
Yang, X., Song, Z., King, I., and Xu, Z. (2022). A survey
on deep semi-supervised learning. Transactions on
Knowledge and Data Engineering.
Yang, Z., Dai, Z., Yang, Y., Carbonell, J., Salakhutdinov,
R. R., and Le, Q. V. (2019). Xlnet: Generalized au-
toregressive pretraining for language understanding.
Advances in neural information processing systems.
You, Y., Li, J., Reddi, S., Hseu, J., Kumar, S., Bhojanapalli,
S., Song, X., Demmel, J., Keutzer, K., and Hsieh, C.-
J. (2019). Large batch optimization for deep learning:
Training bert in 76 minutes. arXiv:1904.00962.
Zbontar, J., Jing, L., Misra, I., LeCun, Y., and Deny, S.
(2021). Barlow twins: Self-supervised learning via re-
dundancy reduction. In Int. Conf. on Machine Learn-
ing.
Zhu, J.-Y., Park, T., Isola, P., and Efros, A. A. (2017).
Unpaired image-to-image translation using cycle-
consistent adversarial networks. In Int. Conf. on com-
puter vision.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
430