Curriculum for Crowd Counting: Is It Worthy?

Muhammad Asif Khan

1 a

, Hamid Menouar

1 b

and Ridha Hamila

2 c

Qatar Mobility Innovations Center, Qatar University, Doha, Qatar

Department of Electrical Engineering, Qatar University, Doha, Qatar

Keywords:

Crowd Counting, Curriculum Learning, CNN, Density Estimation.

Abstract:

Recent advances in deep learning techniques have achieved remarkable performance in several computer vi-

sion problems. A notably intuitive technique called Curriculum Learning (CL) has been introduced recently

for training deep learning models. Surprisingly, curriculum learning achieves signiﬁcantly improved results

in some tasks but marginal or no improvement in others. Hence, there is still a debate about its adoption as

a standard method to train supervised learning models. In this work, we investigate the impact of curriculum

learning in crowd counting using the density estimation method. We performed detailed investigations by con-

ducting 112 experiments using six different CL settings using eight different crowd models. Our experiments

show that curriculum learning improves the model learning performance and shortens the convergence time.

1 INTRODUCTION

Crowd counting is an interesting problem in com-

puter vision research (Khan et al., 2022; Fan et al.,

2022; Gouiaa et al., 2021). Though several methods

(Li et al., 2008; Topkaya et al., 2014; Chen et al.,

2012; Chan and Vasconcelos, 2009) have been pro-

posed earlier to estimate crowd in an image, the de-

facto state-of-the-art approach for crowd counting is

using density estimation. Density estimation employs

a deep learning model such as a convolution neural

network (CNN) to estimate the crowd density in an

image. The ground truths to train the model are den-

sity maps of crowd images. A density map is gener-

ated from the dot annotation map where each dot (rep-

resenting the head position of a person) is convolved

with a Gaussian function.

Over the years, several models have been pro-

posed to improve the accuracy performance over

benchmark datasets. Notably, CrowdCNN was the

ﬁrst CNN-based model proposed in (Zhang et al.,

2015). CrowdCNN is a single-column 6-layer CNN

network using density map prediction. Due to the sin-

gle column, CrowdCNN does not capture the scale

variations present in head sizes in crowd images.

CrowdNet (Boominathan et al., 2016) and MCNN

https://orcid.org/0000-0003-2925-8841

https://orcid.org/0000-0002-4854-909X

https://orcid.org/0000-0002-6920-7371

(Zhang et al., 2016) propose multi-column architec-

tures to cope with the scale variations. The CrowdNet

model uses a shallow and a deep network to predict

different crowd densities. The MCNN model used

three columns of CNN layers with different sizes of

convolution kernels in each layer to efﬁciently cap-

ture the scale variations. Though, these multi-column

networks achieve better accuracy, their performance

is poor on highly congested scenes mainly due to two

reasons. First, the model’s ability to capture scale

variations is limited by the number of columns. Sec-

ond, these shallow models become quickly saturated

due to the small number of neurons. To solve the scale

variation problem, improved model architectures such

as encoder-decoder e.g., TEDnet (Jiang et al., 2019),

SASNet (Song et al., 2021), and pyramid structure us-

ing multi-scale modules e.g., MSCNN (Zeng et al.,

2017), SANet (Cao et al., 2018) are proposed. For

crowd estimation in highly congested scenes, mod-

els using transfer learning from pre-trained models

such as VGG-16 (Simonyan and Zisserman, 2015),

ResNet (He et al., 2016), MobileNet (Sandler et al.,

2018), and Inception (Szegedy et al., 2015) achieved

best results. Few notable models using transfer learn-

ing include CSRNet (Li et al., 2018), C-CNN (Shi

et al., 2020), BL (Ma et al., 2019) (VGG), Mo-

bileCount (Gao et al., 2019) (MobileNet), MMCNN

(Peng et al., 2020), MFCC (Gu and Lian, 2022)

(ResNet), SGANet (Wang and Breckon, 2022) (In-

ception) etc.

Khan, M., Menouar, H. and Hamila, R.

Curriculum for Crowd Counting: Is It Worthy?.

DOI: 10.5220/0012414700003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

583-590

ISBN: 978-989-758-679-8; ISSN: 2184-4321

583

Recently, Curriculum Learning (CL) has gained

signiﬁcant attention as an alternative method to im-

prove performance in various deep-learning tasks.

Curriculum learning refers to the set of techniques to

train deep learning models by imitating human cur-

ricula. In a CL strategy, the training samples are or-

ganized in a speciﬁc order (typically by increasing or

decreasing difﬁculty) before feeding to the model. CL

was ﬁrst formalized in (Bengio et al., 2009) inspired

by the fact that humans learn better when the tasks

are presented in a meaningful order i.e., typically in

the order of increasing complexity (or difﬁculty). CL

potentially brings two beneﬁts: (i) faster convergence

and (ii) improved accuracy.

CL has been applied in several supervised learning

applications including object localization (Ionescu

et al., 2016; Shi and Ferrari, 2016; Tang et al., 2018),

object detection (Chen and Gupta, 2015; Li et al.,

2017; Sangineto et al., 2019) and machine translation

(Kocmi and Bojar, 2017; Platanios et al., 2019; Wang

et al., 2019). CL has also been successfully applied

in reinforcement learning (Narvekar et al., 2020). Al-

though CL applied in several problems achieved im-

proved training, faster convergence, and performance

gains; authors in (Wu et al., 2021) show CL could not

beneﬁt the accuracy performance of image classiﬁca-

tion on CIFAR10 dataset (Krizhevsky, 2009). Some

recent works also applied CL in crowd density esti-

mation (Khan et al., 2023b).

This paper aims to perform a rigorous evaluation

of CL in yet another important task in computer vi-

sion i.e., crowd counting. Crowd counting employs

density estimation using pixel-wise regression from

crowd images. Recently, very few works have ap-

plied CL in crowd density estimation reporting poten-

tial beneﬁts in some scenarios. As the results reported

in these works are only incremental, this paper aims

to extensively investigate the potential of CL in crowd

density estimation. The contribution of this paper is

as follows:

• We conducted ∼ 112 experiments using eight

mainstream crowd-counting models and six dif-

ferent CL settings over two benchmark crowd

datasets.

• The models’ performance is evaluated using two

widely used metrics for crowd counting and re-

sults are compared to understand when and to

which extent CL outperforms standard learning.

• Conclusions are drawn for prospective researchers

in the area of crowd counting.

2 BACKGROUND

Curriculum learning (CL) is deﬁned as ”training cri-

teria C over T training steps: C =< Q

,...Q

such that each criterion Q

is a reweighting of the tar-

get training distribution P(z)”:

(z) = W

(z)P(z) ∀z ∈ training set D (1)

In eq: 1, (i) the entropy of P(z) gradually increases

i.e., H(Q

) < H(Q

t+1

), (ii) the weight of any example

increases i.e., W

(z) ≤ W

t+1

(z), or (iii) Q

(z) = P(z)

(Wang et al., 2022b).

A formal description of the curriculum learning

method is presented in Algorithm 1.

Algorithm 1: Curriculum Learning.

Require: pacing function g, scoring function f , data X

Result: mini-batches [B

,...B

]

1: results = sort X using f

2: for i = 1, · · · M do

3: size ← g(i)

4: X

= X[1,...,size]

5: uniformly sample B

to results

6: append B

to result

7: end for

8: return results

There are two main parts of curriculum learning,

a scoring function, and a pacing function. The scor-

ing function is used to organize the training samples

in a speciﬁc meaningful order while the pacing func-

tion samples the amount of data exposed to the model

in each training step. Fig. 1 depicts the curriculum

learning process.

2.1 Scoring Function

A scoring function ( f ) is a function that sorts the

training data in the order of increasing or decreas-

ing difﬁculty (in curriculum versus anti-curriculum

learning, respectively). For a given scoring function

f : X → R, (x

) is more difﬁcult than (x

) if

f (x

) > f (x

). A scoring function can be deﬁned

in two ways; (i) self-taught, or (ii) transfer-scoring.

In self-taught scoring function, the network is trained

on uniformly-sampled (randomly ordered) batches to

compute the score (difﬁculty) for each training sam-

ple. In transfer-scoring function, a pre-trained model

is used to compute the score for each training sample.

2.2 Pacing Function

A pacing function g is a function that determines a

subset of training data fed to the model in a particular

iteration. For training data X of size N, g : [M] → [N]

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

584

Scoring

function

Full Dataset

(sorted)

Pacing

function

Minibatches

Full Dataset

(sorted)

Minibatches

Full Dataset

(unsorted)

iteration

Model

curriculum

anti-curriculum

Iterations

training data

Difficulty

Figure 1: Curriculum learning framework.

ﬁnds subsets X

,...X

⊂ X. From each X, mini-

batches {B

}

i=1

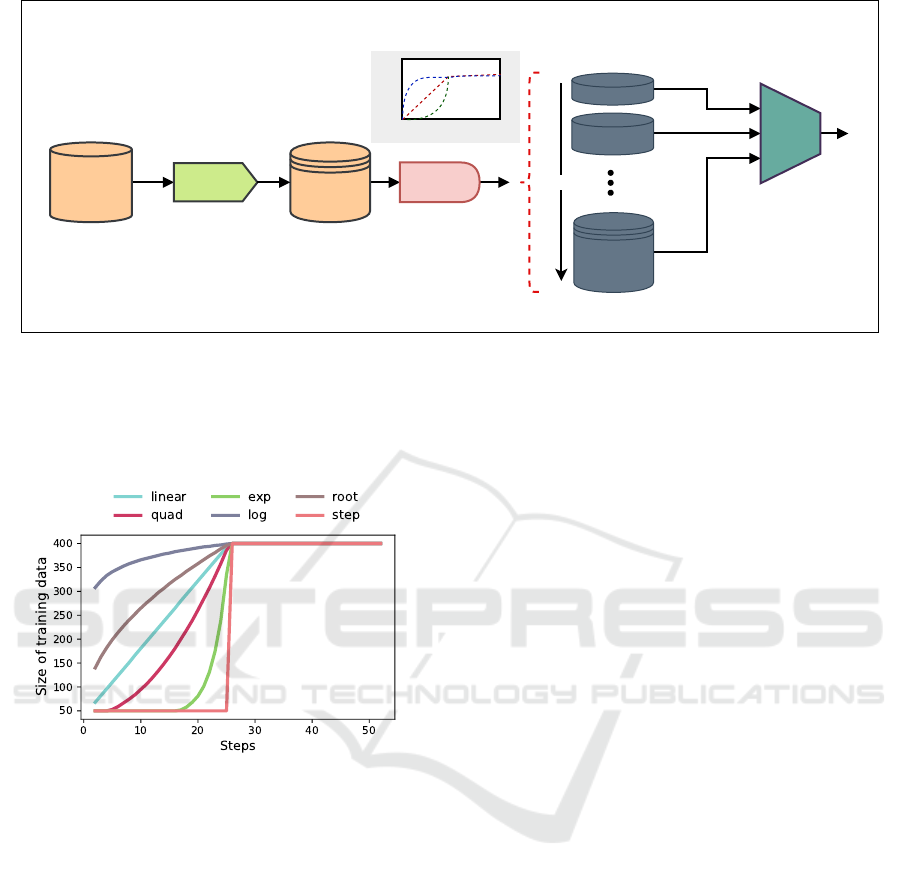
are uniformly sampled. Fig. 2 de-

picts six different pacing functions used in curriculum

learning.

Figure 2: Various pacing functions applied to ShanghaiTech

Part B dataset with a total number of samples (N) = 400 and

batch size = 8.

In the more native form of CL, the training ex-

amples are organized in order of increasing difﬁculty.

However, some works suggest anti-curriculum, in

which the training examples are organized in the or-

der of decreasing difﬁculty.

3 RELATED WORK

Recently, curriculum learning has been adopted in a

few crowd-counting works. In (Li et al., 2021), au-

thors propose TutorNet to improve density estimation

in crowd counting. A main network that generates

density maps for crowd images is supervised at the

training stage by a TutorNet network. The network

produces a weight map of the same shape as the den-

sity map. Each value in the weight map then rep-

resents the per-pixel learning rate of the model er-

ror. Thus, this weight map is used as a curriculum

to train the main network. TutorNet uses ResNet as

a frontend to extract features. The work also uses

scaling of the density map pixel values. TutorNet

is evaluated over ShanghaiTech (Zhang et al., 2016)

and Fudan-ShanghaiTech dataset (FDST) (Fang et al.,

2019). The results show major improvement using

density map scaling with further improvement using

TutorNet (pixel-level curriculum). The work did not

consider TutorNet alone, hence providing little intu-

ition on the efﬁcacy of CL. The authors in (Wang

et al., 2022a) followed a similar approach to imple-

ment CL in crowd-counting tasks. A weight is as-

signed to each pixel in a crowd image which indi-

cates the per-pixel difﬁculty. More speciﬁcally, a

region-aware density map (RAD) is ﬁrst generated

through an average pooling operation and then the

Gaussian function is applied to RAD to produce an at-

tention map. In the attention maps, the simple pixels

are assigned higher weights. A modiﬁed loss func-

tion is proposed to use the attention maps during the

model training. The learning performance is eval-

uated on ShanghaiTech (Zhang et al., 2016), UCF-

QNRF (Idrees et al., 2018), WorlExpo’10 (Zhang

et al., 2015), and GCC (Qi et al., 2020) datasets.

The computation of pixel-wise curricula can be a

more expensive task as compared to sample-wise cur-

ricula in many works on CL. A recent study (Khan

et al., 2023a) on curriculum learning integrated with

dataset pruning to improve the learning performance

and convergence time supports the efﬁcacy of sample-

wise curriculum learning.

A review of the aforementioned works provides

limited hints on the efﬁcacy of curriculum learning in

crowd-counting tasks. However, whether the perfor-

mance gains in these works are the results of the cur-

Curriculum for Crowd Counting: Is It Worthy?

585

riculum learning, the underlying crowd model, or of

both together? Whether curriculum learning can im-

prove the performance of any kind of crowd models

e.g., shallow, deep, multi-column, encoder-decoder,

and multi-scale, with and without transfer learning?

This work aims to further investigate to answer these

questions.

4 EXPERIMENTS AND

EVALUATION

We conducted more than 112 experiments using eight

(8) mainstream crowd models and two well-known

datasets to investigate the efﬁcacy of curriculum

learning in crowd counting.

4.1 Datasets

The two datasets chosen are ShanghaiTech Part A

and ShanghaiTech Part B datasets, both published in

(Zhang et al., 2016). The datasets contain cross-scene

crowd images with varying crowd densities and have

been extensively used for benchmarking in numerous

studies on crowd counting and density estimation.

4.2 Baseline Crowd Models

We choose eight (8) different crowd models to use in

our experiments. These include MCNN (Zhang et al.,

2016), CMTL (Sindagi and Patel, 2017), MSCNN

(Zeng et al., 2017), CSRNet (Li et al., 2018), SANet

(Cao et al., 2018), TEDnet (Jiang et al., 2019), Yang

et al. (Yang et al., 2020), and SASNet (Song et al.,

2021). The eight crowd models are chosen such that

they vary in terms of model size, complexity, and de-

sign.

4.3 Curriculum Settings

We consider six different types of pacing functions:

linear, quadratic, exponential, root, logarithmic, and

step. These pacing functions are calculated using Eq.

g =











Nb + aNb (linear)

Nb + N

1−b

− p = 1/2,1,2 (quad)

Nb +

N(1−b)

−1



exp



10t

− 1



(exp)

Nb + N (1 − b)



1 +

log



+ e

−10



(log)

Nb + N





(step)

(2)

For each dataset, we kept the value of b ﬁxed,

while choosing the value of a = [0.2,0.4, 0.6,0.8].

Thus, in each experiment, we take a fraction (b) of full

training data and incrementally add batches according

to the pacing function (with parameter a). The pacing

functions used are plotted in Fig. 2.

4.4 Evaluation Metrics

We used two commonly used metrics to test the per-

formance in the crowd-counting task i.e., mean ab-

solute error (MAE) and mean squared error (MSE).

MAE and MSE can be calculated using Eq. 3 and Eq.

4, respectively.

MAE =

∑

− g

) (3)

MSE =

∑

− g

) (4)

where N represents the total number of examples

in the dataset, g

is the actual count of people in the

crowd image, and e

is the estimated count (com-

puted as the sum of pixel values in the predicted den-

sity map for the same image). Other less frequently

used metrics are grid average mean error (GAME)

for more localized counting, structural similarity in-

dex (SSIM), and peak signal-to-noise ratio (PSNR)

for the quality of the predicted density maps.

4.5 Training Details

Each crowd model is trained ﬁrst on the Shang-

haiTech Part B dataset using standard training. The

same model is trained (from scratch) using curricu-

lum learning with a single pacing function. Since

there are six pacing functions used in this study, the

same model is trained six times with a different pac-

ing function. In each experiment, we carefully se-

lected the pacing function parameter α to deﬁne rea-

sonable subsets in each iteration by examining the rel-

ative performance over a few epochs (Fig. 3). Thus,

we conduct a total of seven (7) complete training for

a single model and an overall 56 experiments on the

ShanghaiTech Part B dataset. The same number of ex-

periments are then repeated for the ShanghaiTech Part

A dataset. All models are trained using the PyTorch

framework on two RTX-8000 GPUs. In all experi-

ments, we use Adam optimizer with an initial learning

rate of 1 × 10

−2

and a ReduceLROnPlateau learning

rate decay function based on MAE values.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

586

(a) Linear pacing function (b) Quadratic pacing function (c) Exponential pacing function

(d) Root pacing function (e) Log pacing function (f) Step pacing function

Figure 3: Pacing functions used in our experiments.

5 RESULTS AND ANALYSIS

The trained model in each experiment is evaluated

over the two metrics (i.e., MAE and MSE). We care-

fully chose the values of parameters a and b in the

pacing functions to achieve reasonable subsets of

training data in curriculum learning settings. In stan-

dard training, the batches are uniformly sampled from

the full training dataset. The best-achieved results in

each experiment are depicted in Table 1 and 2.

We note several interesting observations in the re-

sults. First, curriculum learning clearly brings signif-

icant improvements in some cases. For instance, on

the ShanghaiTech Part B dataset, the MAE for MCNN

was reduced from 26.4 to 19.2 using the linear pacing

function (best case) and 21.4 using the quadratic pac-

ing function (second best case). Similarly, the MAE

for CSRNet was reduced from 10.6 to 7.8 using the

linear pacing function. On the ShanghaiTech Part A

dataset, the MAE for MCNN was reduced from 110.2

to 102.4 (linear pacing function), and for CSRNet the

MAE was reduced from 68.2 to 58.4.

Second, curriculum learning brings marginal im-

provement in most cases. This is evident from the

MAE values of all models for several selections of

pacing functions. Third, curriculum learning could

not improve or underperforms the standard training

in some cases (indicated with red font color in both

tables). This observation highlights the importance

of the pacing function as an important hyperparam-

eter in curriculum learning. Fourth, the beneﬁt of

curriculum learning is evident for all models on both

datasets. However, the level of improvement varies

among the models which raise the logical question of

what makes curriculum learning outperform standard

training. The last observation is that the beneﬁts of

each pacing function have been consistent to a certain

level. For instance, the best results were produced

by linear function for MCNN (Zhang et al., 2016),

CSRNet (Li et al., 2018), and TEDnet (Jiang et al.,

2019) on both datasets. Similarly, SASNet (Song

et al., 2021) produces better results using the log pac-

ing function on both datasets. The Step function al-

most underperformed all other pacing functions ex-

cept for SANet (Cao et al., 2018) and TEDnet (Jiang

et al., 2019).

Besides the potentially signiﬁcant results dis-

cussed previously, Fig. 4 depicts the clear beneﬁt

of curriculum learning in terms of convergence time.

The y-axis shows the MSE loss of the model during

the training phase, whereas the top and bottom x-axes

show the number of samples seen by the model during

the curriculum learning and standard training settings.

The loss drops too quickly in curriculum learning as

compared to standard training highlighting the faster

convergence of curriculum learning.

Curriculum for Crowd Counting: Is It Worthy?

587

Table 1: A comparison of standard training versus curriculum learning (using six different pacing functions) over Shang-

haiTech Part B dataset using two metrics (MAE and MSE). The bold text shows the lowest error values.

Model

Standard Curriculum Learning

Random Linear Log Quadratic Exponential Step Root

MAE MSE MAE MSE MAE MSE MAE MSE MAE MSE MAE MSE MAE MSE

MCNN 26.4 41.3 19.2 32.2 23.8 38 21.4 33.8 23.1 37.4 23.4 37.4 22.8 37.1

CMTL 20.0 31.1 19.6 30.6 19.8 30.7 18.8 30.4 20.0 31.6 20.2 32.0 19.4 30.5

MSCNN 17.7 30.2 16.9 29.2 17.6 29.9 17.2 29.4 17.8 30.2 17.8 30.1 16.8 28.8

CSRNet 10.6 16.0 7.8 14.2 10.2 16 8.2 14.6 9.4 15.3 9.8 15.8 8.6 14.9

SANet 8.4 13.6 8.4 13.5 8.8 14.0 8.1 13.3 8.5 13.8 8.2 13.4 8.6 13.7

TEDnet 8.2 12.8 7.6 12.2 8.2 12.7 8.3 13 7.7 12.4 8.1 12.6 7.8 12.4

Yang et al. 12.3 21.2 11.8 20.4 11.4 20.0 10.6 18.3 12.2 21.4 12.6 21.6 12.0 20.8

SASNet 6.4 9.9 6.6 10 6.3 9.6 6.8 10.5 7.2 11.2 6.9 10.6 6.4 9.8

Table 2: A comparison of standard training versus curriculum learning (using six different pacing functions) over Shang-

haiTech Part A dataset using two metrics (MAE and MSE). The bold text shows the lowest error values.

Model

Standard Curriculum Learning

Random Linear Log Quadratic Exponential Step Root

MAE MSE MAE MSE MAE MSE MAE MSE MAE MSE MAE MSE MAE MSE

MCNN 110.2 173.2 102.3 150.8 109.6 172.4 108.8 170.6 106.7 169.0 112.4 177.6 102.4 151.2

CMTL 101.3 152.4 96.7 142.4 100.6 151.8 98.2 149.2 103.5 156.2 105.4 160.3 100.2 150.4

MSCNN 83.8 127.4 82.3 122.6 83.4 128.3 82.6 125.8 83.8 129.2 85.8 133.5 81.2 120.8

CSRNet 68.2 115.0 58.4 102.5 62.0 105.4 60.6 105.2 62.2 106.1 62.0 105.5 62.3 106.4

SANet 67.0 104.5 66.9 103.8 68.4 105.4 66.2 100.8 66.4 101.2 70.2 118.4 67.2 105.0

TEDnet 64.2 109.1 60.2 102.9 65.8 114.2 66.4 115.2 65.0 111.3 63.4 106.4 63.8 106.9

Yang et al. 104.6 145.2 102.3 139.0 104.4 143.7 98.4 134.2 104.8 145.8 105.6 147.2 99.1 134.8

SASNet 53.6 88.4 51.2 81.0 51.4 81.4 52.8 86.2 53.2 87.0 55.8 90.4 52.3 84.6

Figure 4: Illustration of model convergence using standard

training versus curriculum learning.

6 CONCLUSIONS

This article presents a detailed experimental analysis

of curriculum learning in crowd-counting. Although

curriculum learning has been effective in reinforce-

ment learning, its efﬁcacy in supervised learning is

not fully evident due to the lack of detailed inves-

tigations. We performed an extensive set of exper-

iments on eight mainstream crowd-counting models

to evaluate the performance of curriculum learning.

The results show signiﬁcant improvements in some

cases, marginal improvements in most cases with no

improvement in a few cases. Through the detailed

analysis of the results, we conclude that curriculum

learning can potentially improve the performance of

deep learning models by carefully choosing the pac-

ing function and its parameters. Moreover, given the

short training time budget, curriculum learning is a

good choice to cut the convergence time. For future

work, we suggest extending the investigation to other

computer vision tasks using large datasets and differ-

ent scoring functions appropriate to the task.

ACKNOWLEDGEMENT

This publication was made possible by the PDRA

award PDRA7-0606-21012 from the Qatar National

Research Fund (a member of The Qatar Foundation).

The statements made herein are solely the responsi-

bility of the authors.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

588

REFERENCES

Bengio, Y., Louradour, J., Collobert, R., and Weston, J.

(2009). Curriculum learning. In Proceedings of the

26th Annual International Conference on Machine

Learning, ICML ’09, page 41–48, New York, NY,

USA. Association for Computing Machinery.

Boominathan, L., Kruthiventi, S. S. S., and Babu, R. V.

(2016). Crowdnet: A deep convolutional network for

dense crowd counting. Proceedings of the 24th ACM

international conference on Multimedia.

Cao, X., Wang, Z., Zhao, Y., and Su, F. (2018). Scale aggre-

gation network for accurate and efﬁcient crowd count-

ing. In ECCV.

Chan, A. B. and Vasconcelos, N. (2009). Bayesian poisson

regression for crowd counting. In 2009 IEEE 12th

International Conference on Computer Vision, pages

545–551.

Chen, K., Loy, C. C., Gong, S., and Xiang, T. (2012). Fea-

ture mining for localised crowd counting. In BMVC.

Chen, X. and Gupta, A. K. (2015). Webly supervised learn-

ing of convolutional networks. 2015 IEEE Interna-

tional Conference on Computer Vision (ICCV), pages

1431–1439.

Fan, Z., Zhang, H., Zhang, Z., Lu, G., Zhang, Y., and Wang,

Y. (2022). A survey of crowd counting and density es-

timation based on convolutional neural network. Neu-

rocomputing, 472:224–251.

Fang, Y., Zhan, B., Cai, W., Gao, S., and Hu, B. (2019).

Locality-constrained spatial transformer network for

video crowd counting. In 2019 IEEE International

Conference on Multimedia and Expo (ICME), pages

814–819.

Gao, C., Wang, P., and Gao, Y. (2019). Mobilecount:

An efﬁcient encoder-decoder framework for real-time

crowd counting. In Pattern Recognition and Computer

Vision: Second Chinese Conference, PRCV 2019,

Xi’an, China, November 8–11, 2019, Proceedings,

Part II, page 582–595. Springer-Verlag.

Gouiaa, R., Akhlouﬁ, M. A., and Shahbazi, M. (2021). Ad-

vances in convolution neural networks based crowd

counting and density estimation. Big Data Cogn.

Comput., 5:50.

Gu, S. and Lian, Z. (2022). A uniﬁed multi-task learning

framework of real-time drone supervision for crowd

counting. ArXiv, abs/2202.03843.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. 2016 IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 770–778.

Idrees, H., Tayyab, M., Athrey, K., Zhang, D., Al-Maadeed,

S. A., Rajpoot, N. M., and Shah, M. (2018). Compo-

sition loss for counting, density map estimation and

localization in dense crowds. ArXiv, abs/1808.01050.

Ionescu, R. T., Alexe, B., Leordeanu, M., Popescu, M. C.,

Papadopoulos, D. P., and Ferrari, V. (2016). How hard

can it be? estimating the difﬁculty of visual search in

an image. 2016 IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 2157–2166.

Jiang, X., Xiao, Z., Zhang, B., Zhen, X., Cao, X., Doer-

mann, D. S., and Shao, L. (2019). Crowd counting

and density estimation by trellis encoder-decoder net-

works. 2019 IEEE/CVF Conference on Computer Vi-

sion and Pattern Recognition (CVPR), pages 6126–

6135.

Khan, M. A., Hamila, R., and Menouar, H. (2023a). Clip:

Train faster with less data. In 2023 IEEE International

Conference on Big Data and Smart Computing (Big-

Comp), pages 34–39. IEEE.

Khan, M. A., Menouar, H., and Hamila, R. (2022). Revisit-

ing Crowd Counting: State-of-the-art, Trends, and Fu-

ture Perspectives. arXiv preprint arXiv:2209.07271.

Khan, M. A., Menouar, H., and Hamila, R. (2023b). LCD-

net: a lightweight crowd density estimation model for

real-time video surveillance. Journal of Real-Time Im-

age Processing, 20:29.

Kocmi, T. and Bojar, O. (2017). Curriculum learning and

minibatch bucketing in neural machine translation. In

RANLP.

Krizhevsky, A. (2009). Learning multiple layers of features

from tiny images. Technical report.

Li, M., Zhang, Z., Huang, K., and Tan, T. (2008). Estimat-

ing the number of people in crowded scenes by mid

based foreground segmentation and head-shoulder de-

tection. In 2008 19th International Conference on Pat-

tern Recognition, pages 1–4.

Li, S., Zhu, X., Huang, Q., Xu, H., and Kuo, C.-C. J. (2017).

Multiple instance curriculum learning for weakly su-

pervised object detection. ArXiv, abs/1711.09191.

Li, W., Cao, Z., Wang, Q., Chen, S., and Feng, R. (2021).

Learning error-driven curriculum for crowd count-

ing. 2020 25th International Conference on Pattern

Recognition (ICPR), pages 843–849.

Li, Y., Zhang, X., and Chen, D. (2018). Csrnet: Dilated

convolutional neural networks for understanding the

highly congested scenes. 2018 IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

1091–1100.

Ma, Z., Wei, X., Hong, X., and Gong, Y. (2019). Bayesian

loss for crowd count estimation with point supervi-

sion. In 2019 IEEE/CVF International Conference

on Computer Vision (ICCV), pages 6141–6150, Los

Alamitos, CA, USA.

Narvekar, S., Peng, B., Leonetti, M., Sinapov, J., Taylor,

M. E., and Stone, P. (2020). Curriculum learning for

reinforcement learning domains: A framework and

survey. J. Mach. Learn. Res., 21:181:1–181:50.

Peng, T., Li, Q., and Zhu, P. F. (2020). Rgb-t crowd count-

ing from drone: A benchmark and mmccn network. In

ACCV.

Platanios, E. A., Stretcu, O., Neubig, G., P

oczos, B., and

Mitchell, T. M. (2019). Competence-based curricu-

lum learning for neural machine translation. ArXiv,

abs/1903.09848.

Qi, W., Gao, J., Wei, L., and Yuan, Y. (2020). Pixel-wise

crowd understanding via synthetic data. International

Journal of Computer Vision, 129:225–245.

Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., and

Chen, L.-C. (2018). Mobilenetv2: Inverted residu-

Curriculum for Crowd Counting: Is It Worthy?

589

als and linear bottlenecks. In 2018 IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

pages 4510–4520.

Sangineto, E., Nabi, M., Culibrk, D., and Sebe, N. (2019).

Self paced deep learning for weakly supervised object

detection. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 41:712–725.

Shi, M. and Ferrari, V. (2016). Weakly supervised

object localization using size estimates. ArXiv,

abs/1608.04314.

Shi, X., Li, X., Wu, C., Kong, S., Yang, J., and He, L.

(2020). A real-time deep network for crowd count-

ing. ICASSP 2020 - 2020 IEEE International Con-

ference on Acoustics, Speech and Signal Processing

(ICASSP), pages 2328–2332.

Simonyan, K. and Zisserman, A. (2015). Very deep convo-

lutional networks for large-scale image recognition. In

3rd International Conference on Learning Represen-

tations, ICLR 2015, San Diego, CA, USA, May 7-9,

2015, Conference Track Proceedings.

Sindagi, V. A. and Patel, V. M. (2017). Cnn-based cascaded

multi-task learning of high-level prior and density es-

timation for crowd counting. In 2017 14th IEEE In-

ternational Conference on Advanced Video and Signal

Based Surveillance (AVSS), pages 1–6, Los Alamitos,

CA, USA. IEEE Computer Society.

Song, Q., Wang, C., Wang, Y., Tai, Y., Wang, C., Li, J., Wu,

J., and Ma, J. (2021). To choose or to fuse? scale

selection for crowd counting. In AAAI.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S. E.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (2015). Going deeper with convolutions.

2015 IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR), pages 1–9.

Tang, Y., Wang, X., Harrison, A. P., Lu, L., Xiao, J., and

Summers, R. M. (2018). Attention-guided curriculum

learning for weakly supervised classiﬁcation and lo-

calization of thoracic diseases on chest radiographs.

ArXiv, abs/1807.07532.

Topkaya, I. S., Erdogan, H., and Porikli, F. (2014). Count-

ing people by clustering person detector outputs. In

2014 11th IEEE International Conference on Ad-

vanced Video and Signal Based Surveillance (AVSS),

pages 313–318.

Wang, Q. and Breckon, T. (2022). Crowd counting via seg-

mentation guided attention networks and curriculum

loss. IEEE Transactions on Intelligent Transportation

Systems.

Wang, Q., Lin, W., Gao, J., and Li, X. (2022a). Density-

aware curriculum learning for crowd counting. IEEE

Transactions on Cybernetics, 52:4675–4687.

Wang, W., Caswell, I., and Chelba, C. (2019). Dynamically

composing domain-data selection with clean-data se-

lection by “co-curricular learning” for neural machine

translation. In ACL.

Wang, X., Chen, Y., and Zhu, W. (2022b). A survey on

curriculum learning. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 44(9):4555–4576.

Wu, X., Dyer, E., and Neyshabur, B. (2021). When do cur-

ricula work? ArXiv, abs/2012.03107.

Yang, Y., Li, G., Wu, Z., Su, L., Huang, Q., and Sebe,

N. (2020). Weakly-supervised crowd counting learns

from sorting rather than locations. In Computer Vision

– ECCV 2020: 16th European Conference, Glasgow,

UK, August 23–28, 2020, Proceedings, Part VIII, page

1–17, Berlin, Heidelberg. Springer-Verlag.

Zeng, L., Xu, X., Cai, B., Qiu, S., and Zhang, T. (2017).

Multi-scale convolutional neural networks for crowd

counting. 2017 IEEE International Conference on Im-

age Processing (ICIP), pages 465–469.

Zhang, C., Li, H., Wang, X., and Yang, X. (2015). Cross-

scene crowd counting via deep convolutional neural

networks. 2015 IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 833–841.

Zhang, Y., Zhou, D., Chen, S., Gao, S., and Ma, Y. (2016).

Single-image crowd counting via multi-column con-

volutional neural network. In 2016 IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 589–597.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

590