Learning Projection Patterns for Direct-Global Separation

Takaoki Ueda, Ryo Kawahara

and Takahiro Okabe

Department of Artiﬁcial Intelligence, Kyushu Institute of Technology,

680-4 Kawazu, Iizuka, Fukuoka 820-8502, Japan

Keywords:

Direct-Global Separation, Projector-Camera System, Projection Patterns, End-to-End Optimization.

Abstract:

Separating the direct component such as diffuse reﬂection and specular reﬂection and the global component

such as inter-reﬂection and subsurface scattering is important for various computer vision and computer graph-

ics applications. Conventionally, high-frequency patterns designed by physics-based model or signal process-

ing theory are projected from a projector to a scene, but their assumptions do not necessarily hold for real

images due to the shallow depth of ﬁeld of a projector and the limited spatial resolution of a camera. Accord-

ingly, in this paper, we propose a data-driven approach for direct-global separation. Speciﬁcally, our proposed

method learns not only the separation module but also the imaging module, i.e. the projection patterns at the

same time in an end-to-end manner. We conduct a number of experiments using real images captured with a

projector-camera system, and conﬁrm the effectiveness of our method.

1 INTRODUCTION

When a scene is illuminated by a light source, the ra-

diance value observed at each point in the scene con-

sists of two components: a direct component and a

global component (Nayar et al., 2006). The direct

component such as (direct) diffuse reﬂection and (di-

rect) specular reﬂection is caused by the light rays

directly coming from the light source. On the other

hand, the global component is caused by the light rays

coming from the points in the scene other than the

light source due to inter-reﬂection, subsurface scatter-

ing, volumetric scattering, diffusion, and so on. Sepa-

rating those components is important for various com-

puter vision and computer graphics applications such

as shape recovery, image-based material editing, and

image quality improvement (Nayar et al., 2006; Gu

et al., 2011).

Nayar et al. (Nayar et al., 2006) show that the di-

rect and global components can be separated in the-

ory from at least two images captured by projecting

spatially high-frequency patterns to a scene of inter-

est from a projector. Speciﬁcally, they assume that

the global components are band-limited with a certain

frequency, and make use of a black-and-white check-

ered pattern and its negative-positive reversed pattern

with an appropriate interval. Unfortunately, however,

https://orcid.org/0000-0002-9819-3634

https://orcid.org/0000-0002-2183-7112

the direct-global separation from the two images often

causes artifacts around the boundaries in the black-

and-white patterns. This is because the patterns are

blurred due to the shallow depth of ﬁeld of a pro-

jector and the limited spatial resolution of a camera.

Therefore, the direct-global separation requires many

images, e.g. 25 images, captured by projecting the

shifted checkered patterns in practice (Nayar et al.,

2006).

To cope with the problem of the number of re-

quired images, Subpa-Asa et al. (Subpa-Asa et al.,

2018) and Duan et al. (Duan et al., 2020) propose

the direct-global separation from a single image. The

former uses a single checkered pattern, but separates

the direct and global components by using the linear

basis representation: the Fourier basis or PCA basis.

The latter makes use of non-binary patterns with 4 or

9 intensities instead of a binary checkered pattern, and

then separates the direct and global components via a

learning-based approach.

However, there is still room for improvement, es-

pecially in projection patterns and optimization. First,

the projection patterns are conventionally designed by

physics-based model or signal processing theory (Na-

yar et al., 2006; Gu et al., 2011; Torii et al., 2019;

Duan et al., 2020; Nisaka et al., 2021), but the as-

sumptions of those model and theory do not necessar-

ily hold for real images due to the shallow depth of

ﬁeld of a projector and the limited spatial resolution

of a camera. Second, the existing methods optimize

Ueda, T., Kawahara, R. and Okabe, T.

Learning Projection Patterns for Direct-Global Separation.

DOI: 10.5220/0012418900003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

599-606

ISBN: 978-989-758-679-8; ISSN: 2184-4321

599

only the separation module (Subpa-Asa et al., 2018)

or optimize the projection pattern and the separation

module on the basis of the different approaches (Duan

et al., 2020). Since the projection patterns and the

separation module depend on each other, the better

separation results could be expected by optimizing

them in an end-to-end manner.

Accordingly, in this paper, we propose a data-

driven method for direct-global separation. Speciﬁ-

cally, our proposed method learns not only the sepa-

ration module but also the imaging module, i.e. the

projection patterns at the same time in an end-to-end

manner. Especially, we focus on the fact that gen-

eral projection patterns can be represented by (1 × 1)

convolution kernels on the basis of the superposi-

tion principle, and then simultaneously optimize the

projection patterns and the separation module in the

framework of convolutional neural network (CNN).

We conduct a number of experiments using real im-

ages captured with a projector-camera system, and

conﬁrm the effectiveness of our method.

The main contributions of this paper are threefold.

First, we tackle a novel problem of data-driven direct-

global separation that learns not only the separation

module but also the imaging module. Second, we

show that the projection patterns and the separation

module can be optimized in an end-to-end manner

by using the framework of CNN. Third, we exper-

imentally conﬁrm the effectiveness of our proposed

method, in particular the data-driven projection pat-

terns and the end-to-end optimization.

2 RELATED WORK

2.1 Direct-Global Separation

Nayar et al. (Nayar et al., 2006) propose a method

for separating the direct and global components in a

scene by projecting high-frequency patterns such as

black-and-white checkered patterns from a projector

to the scene on the basis of the insight that global

components are low-frequency in general. We can

consider that their method consists of two modules;

one is the imaging module that captures the images

of a scene by projecting high-frequency patterns to it,

and the other is the separation module that separates

those components from the captured images. Then,

we summarize the existing techniques from the view-

points of the imaging and separation modules.

Regarding the imaging module, Nayar et al. (Na-

yar et al., 2006) themselves demonstrate that other

high-frequency patterns such as stripe patterns and

sinusoid-based patterns can be used instead of check-

ered patterns. In addition, a number of projection pat-

terns are proposed on the basis of signal processing

theory, in particular signal-to-noise ratio (SNR) anal-

ysis. Gu et al. (Gu et al., 2011) optimize a set of high-

frequency patterns in terms of SNR on the basis of il-

lumination multiplexing (Schechner et al., 2003), and

then extend the original direct-global separation for a

single light source to that for multiple light sources.

Torii et al. (Torii et al., 2019) make use of the tem-

poral dithering of a DLP projector (Narasimhan et al.,

2008), and achieves multispectral direct-global sepa-

ration of dynamic scenes. They optimize the two in-

tensities of the checkered patterns in terms of SNR.

Similarly, Nisaka et al. (Nisaka et al., 2021) achieve

the separation of specular, diffuse, and global com-

ponents via polarized pattern projections. Duan et

al. (Duan et al., 2020) designed non-binary patterns

with 4 or 9 intensities instead of a binary checkered

pattern for the direct-global separation from a single

image. Unfortunately, those projection patterns de-

signed by physics-based model or signal processing

theory are not necessarily suitable for real scenes, be-

cause the assumptions of those model and theory do

not necessarily hold for real images due to the shallow

depth of ﬁeld of a projector and the limited spatial res-

olution of a camera.

Regarding the separation module, some ap-

proaches are proposed. The original direct-global

separation by Nayar et al. (Nayar et al., 2006) is based

on the physics model. Subpa-Asa et al. (Subpa-Asa

et al., 2018) propose a statistics-based approach; they

achieve the direct-global separation from a single im-

age by using the linear representation with the Fourier

basis or PCA basis. Nie et al. (Nie et al., 2019) and

Duan et al. (Duan et al., 2020) propose a learning-

based approach to the direct-global separation from a

single image. The former is based on cycleGAN (Zhu

et al., 2017) with uniform white lighting, and the latter

is based on U-Net (Ronneberger et al., 2015) with the

non-binary patterns. The learning-based approach re-

ports impressive results, but there is still room for im-

provement; we can optimize both the imaging module

and the separation module in an end-to-end manner.

In contrast to the above existing techniques, our

proposed method learns not only the separation mod-

ule but also the imaging module, i.e. projection pat-

terns. In addition, our method simultaneously opti-

mizes the imaging module and the separation module

in an end-to-end manner.

2.2 Deep Optics/Sensing

Recently, a number of deep networks that optimize

not only application modules but also imaging mod-

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

600

Figure 1: Our proposed network with the imaging module and the separation module. The input to the imaging module is

a set of basis projection patterns and the images captured by projecting those basis patterns, and its output is the optimal

imaging condition, i.e. the optimal projection patterns and the images under the optimal imaging condition. The input to the

separation module is the output from the imaging module, and its output is the predicted separation result, i.e. the direct and

global components of the images. (a) In the training phase, the imaging module and the separation module are trained on the

basis of the loss function L in an end-to-end manner. (b) In the test phase, we actually capture the images under the trained

optimal illumination condition, and then separate the direct and global components by using the trained separation module.

ules in an end-to-end manner have been proposed.

This approach is called deep optics or deep sens-

ing. A seminal work by Chakrabarti (Chakrabarti,

2016) optimizes the color ﬁlter array as well as the

demosaicing algorithm in an end-to-end manner. Fol-

lowed by it, the idea of end-to-end optimization of the

imaging modules and the application modules is used

for hyperspectral reconstruction (Nie et al., 2018),

image-based relighting (Xu et al., 2018), compres-

sive video sensing (Yoshida et al., 2018), light ﬁeld

acquisition (Inagaki et al., 2018), passive single-view

depth estimation (Wu et al., 2019), single-shot high-

dynamic-range imaging (Metzler et al., 2020; Sun

et al., 2020), seeing through obstructions (Shi et al.,

2022), privacy-preserving depth estimation (Tasneem

et al., 2022), hyperspectral imaging (Li et al., 2023),

and time-of-ﬂight imaging (Li et al., 2022).

Our study also belongs to deep optics/sensing. In

contrast to most existing methods that optimize the

properties of a camera/sensor as well as the appli-

cation modules, our proposed method optimizes the

properties of a light source (projection patterns) as

well as the application module.

3 PROPOSED METHOD

3.1 Overview

Our proposed network consists of two modules: the

imaging module and the separation module. Figure 1

illustrates the outline of our network. The input to the

imaging module is a set of basis projection patterns

and the images captured by projecting those basis pat-

terns. The output from the imaging module is the op-

timal imaging condition, i.e. the optimal projection

patterns and the images under the optimal imaging

condition. The input to the separation module is the

output from the imaging module. The output from the

separation module is the predicted separation result,

i.e. the direct and global components of the images.

In the training phase, we train several networks,

in each of which the number of images N required

for separation is ﬁxed. We train our proposed net-

work in an end-to-end manner by using the ground

truth of the direct and global components as shown

in Figure 1 (a). Then, we obtain the optimal projec-

tion patterns and the separation module that separates

the direct and global components from the images ac-

quired under the optimal imaging condition.

In the test phase, we make use of the trained op-

timal imaging condition and the trained separation

module as shown in Figure 1 (b). Speciﬁcally, we ac-

tually capture the images of a scene/an object by pro-

jecting the optimal projection patterns and then sepa-

rates the direct and global components from the cap-

tured images by using the separation module. The

following subsections explain the details of our net-

work.

3.2 Imaging Module

In the same manner as the existing methods (Duan

et al., 2020), we represent the entire projection pat-

tern by repeating a fundamental projection pattern as

shown in Figure 2 (a). Since the discontinuous bound-

aries between the black-and-white checkered pattern

often cause artifacts in the separation results, we rep-

resent the fundamental projection pattern as the linear

combination of smooth basis functions, the DCT basis

Learning Projection Patterns for Direct-Global Separation

601

Figure 2: Projection patterns: (a) the entire black-and-white

checkered pattern (left) represented by repeating a funda-

mental pattern (right), and (b) a part of the DCT basis func-

tions for representing a fundamental pattern as their linear

combination.

Figure 3: The superposition principle; when we represent

the fundamental projection pattern (top left) as the linear

combination of the basis functions of the DCT, the image

captured by projecting the fundamental projection pattern

(bottom left) is also represented as the linear combination

of the images captured by projecting each of the basis func-

tions by using the same coefﬁcients w

functions in our implementation

. Since the direct-

global separation assumes that the global compo-

nents are band-limited with a certain frequency (Na-

yar et al., 2006), we use a part of the DCT basis func-

tions with low frequencies shown in Figure 2 (b)

We denote the number of the basis functions by M.

According to the superposition principle, an im-

age of an object taken under two light sources is a

linear combination (convex combination in a strict

sense) of the two images, each of which is captured

under one of the light sources. Therefore, we can

represent the image captured by projecting the fun-

damental projection pattern as the linear combina-

tion of the images captured by projecting each of

the low-frequency DCT basis functions. Here, the

fundamental projection pattern and the image cap-

tured by projecting the fundamental projection pattern

share the same coefﬁcients of the linear combination

(m = 1, 2, 3, ..., M) as shown in Figure 3.

In order to optimize the projection patterns, we fo-

cus on the fact that general projection patterns can be

represented by (1 × 1) convolution kernels on the ba-

sis of the superposition principle. Speciﬁcally, since

the fundamental projection patten is a linear combi-

We impose the continuity constraints on the bound-

aries of the fundamental projection patterns so that there

are no discontinuous boundaries.

Note that the entire projection patterns repeating the

fundamental projection patterns are high-frequency ones.

Figure 4: The (1× 1) convolution; the imaging module rep-

resents a fundamental projection pattern (right) as a linear

combination of the M basis functions (left). It is represented

by the sum of the products between the pixel values at each

pixel of the basis functions and the coefﬁcients of the linear

combination w

nation of the low-frequency DCT basis functions, it

is represented by the sum of the products between the

pixel values at each pixel of the DCT basis functions

and the coefﬁcients of the linear combination w

shown in Figure 4. It is the same for the image cap-

tured by projecting the fundamental projection pat-

tern. Thus, the weights of the (1× 1) convolution ker-

nel correspond to the coefﬁcients of the linear combi-

nation w

. Note that when we use N images (and pro-

jection patterns) for separation, we use N convolution

kernels and then optimize N × M weights in total.

Finally, we add two artiﬁcial noises to the im-

ages under the optimal imaging condition: one obeys

Gaussian distribution

and the other obeys uniform

distribution. The latter is for taking the quantization

of a pixel value into consideration. Therefore, the im-

age taken under darker projection pattern is more con-

taminated by the quantization errors of pixel values.

3.3 Separation Module

Note that our substantive proposals are the imaging

module and the end-to-end optimization of the imag-

ing module and the separation module. Then, we

could use an arbitrary end-to-end network for the sep-

aration module.

In our current implementation, we use the well-

known U-Net architecture (Ronneberger et al., 2015),

i.e. an encoder-decoder structure with skip connec-

tions. It is widely used not only for image-to-image

translation (Isola et al., 2017; Liu et al., 2018; Ho

et al., 2020; Rombach et al., 2022) but also for deep

optics/sensing (Nie et al., 2018; Xu et al., 2018;

Wu et al., 2019; Duan et al., 2020; Metzler et al.,

We use real images which inherently contain noises for

training, but random noises are almost canceled out by lin-

early combining the images. Therefore, we add artiﬁcial

noises to the linear combination of the real images in order

to simulate the noises in one-shot image taken under multi-

ple light sources.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

602

Figure 5: Our separation module; it has dual decoders for

recovering direct and global components, but shares a single

encoder.

Figure 6: Our projector-camera system with a half mirror

(left); the correspondence between the projector pixels and

the camera pixels is invariant to the depths of scenes (right).

2020; Sun et al., 2020; Shi et al., 2022). Since deep

optics/sensing often adds a kind of imaging mod-

ule ahead of a conventional application module, the

skip connections, which allows information to reach

deeper layers and can mitigate the problem of vanish-

ing gradients, are important.

Figure 5 illustrates our separation module. It has

dual decoders; one is for recovering direct compo-

nents and the other is for recovering the global com-

ponents. Those decoders share a single encoder.

We use the batch normalization (Ioffe and Szegedy,

2015), the convolution with the kernel size of 3 × 3,

the activation function of the ELU (Clevert et al.,

2016), the max pooling with the size of 2 × 2, and

the deconvolution with the kernel size of 3× 3. In or-

der to mitigate the vanishing gradients problem, we

use the Residual Blocks (He et al., 2016) in addition

to the skip connections.

3.4 Optimization

Thus, the projection patterns can be represented by

using convolution kernels as explained in Section 3.2.

Therefore, we simultaneously optimize them as well

as the separation module via a CNN-based network in

an end-to-end manner.

Our proposed network is trained by minimizing

the loss function L deﬁned as

L = L

+ L

. (1)

The ﬁrst and second terms come from the direct and

global components, and the third term comes from

the projection patterns. Speciﬁcally, the ﬁrst and sec-

ond terms are the mean squared errors between the

predicted components and the ground-truth compo-

nents. The third term penalizes the fundamental pat-

terns with the squared L

norm, if their intensities are

smaller or larger than the range of the projector out-

put.

4 EXPERIMENTS

4.1 Projector-Camera System

As shown in Figure 6, we used a projector-camera

system with a half mirror. The projector and the cam-

era were placed so that they have the same projection

centers and optical axes, and then the correspondence

between the projector pixels and the camera pixels is

invariant to the depths of scenes (Narasimhan et al.,

2008). The use of the half mirror is because our

proposed method using the learned projection patters

cannot automatically estimate the intensity of pro-

jected light at each pixel of the captured image, in

contrast to Nayar et al. (Nayar et al., 2006) using

a black-and-white checkered pattern and its reversed

pattern. We used an LED projector of P970 from

Crosstour and a color camera of Blackﬂy S USB3

from FLIR.

We calibrated the correspondence between the

projector pixels and the camera pixels via homogra-

phy in advance. We conﬁrmed that the radiometric

response function of the camera is linear, but that of

the projector is non-linear. The radiometric response

function of the projector was calibrated by using the

set of images captured with varying input pixel values

of the projector.

4.2 Setup

We captured the images of 26 scenes; the images of

22, 1, and 3 scenes were used for training, valida-

tion, and test respectively. We cropped 150 parches

with 80 × 80 pixels from each captured image. There-

fore, the actual number of scenes are considered to

be 3,300, 150, and 450 for training, validation, and

test respectively. Figure 7 shows some examples of

the scenes; they contain objects such as candles, ping

pong balls, cloths, and wrapping papers with subsur-

face scattering and inter-reﬂections. We obtained the

Learning Projection Patterns for Direct-Global Separation

603

Table 1: The quantitative comparison of the projection pattern in terms of the PSNR and SSIM.

scene 1 scene 2 scene 3

direct global direct global direct global

N = 1 Ours PSNR 34.50 35.52 34.62 35.88 31.20 33.67

SSIM 0.952 0.939 0.944 0.933 0.903 0.909

Duan PSNR 32.55 34.46 33.15 35.46 29.31 33.38

SSIM 0.931 0.934 0.923 0.934 0.862 0.915

N = 2 Ours PSNR 35.25 36.65 37.36 34.63 34.87 34.20

SSIM 0.964 0.945 0.962 0.919 0.953 0.915

Nayar PSNR 20.21 19.64 24.27 23.75 21.53 20.93

SSIM 0.621 0.697 0.664 0.780 0.637 0.706

N = 3 Ours PSNR 36.45 38.03 37.76 37.88 36.20 37.32

SSIM 0.965 0.952 0.960 0.929 0.952 0.926

Figure 7: Some examples of the scenes; they contain objects

with subsurface scattering and inter-reﬂections.

ground truths of the direct and global components of

those scenes from the 25 images captured by project-

ing the shifted checkered patterns (Nayar et al., 2006).

We consider the fundamental projection patterns

with 20 × 20 pixels. As described in Section 3.2,

since the direct-global separation assumes that the

global components are band-limited with a certain

frequency, we use a part of the DCT basis functions

with low frequencies. Speciﬁcally we used 16 (= M)

basis functions of the DCT out of the 400 (= 20 × 20)

basis functions. We experimentally conﬁrmed that

we can approximately represent the black-and-white

checkered patten by using the 16 basis functions.

We used the optimization algorithm of the

Adam (Kingma and Ba, 2016) for training. We set

the initial learning rate to 0.01, and then changed it to

0.001 and 0.0001. We set the attenuation coefﬁcients

as β

= 0.9 and β

= 0.999. The all of the weights

of our network are initialized by using the He normal

initialization (He et al., 2015). We used a desktop PC

with a graphics card of GeForce RTX 3090 for train-

ing. It took about four hours for training our proposed

network with about 200 epochs.

4.3 Results

To conﬁrm the effectiveness of the data-driven projec-

tion patterns and the end-to-end optimization of the

imaging module and the separation module, we com-

pared the following three methods:

• Our Proposed Method: the direct-global separa-

tion from N (N = 1, 2, 3) images. Both the imag-

ing module (projection patterns) and the separa-

tion module are trained in an end-to-end manner.

• Duan et al. (Duan et al., 2020): the state-of-the-

art method for the direct-global separation from a

single image. The single projection pattern with 4

intensities

is based on the signal processing the-

ory but the separation module is learning-based.

• Nayar et al. (Nayar et al., 2006): the baseline

method for the direct-global separation from two

images. Both the projection patterns and the sep-

aration module are based on the physics model.

In our current implementation, we trained the sepa-

ration module of Duan et al. (Duan et al., 2020) by

using our network for the ﬁxed projection pattern.

Figure 8 summarizes the qualitative comparison

with those methods: (a) the ground-truth images of

the direct and global components, (b) the results of

our proposed method using a single image, (c) the re-

sults of Duan et al. (Duan et al., 2020) using a single

image, (d) the results of our method using two images,

(e) the results of Nayar et al. (Nayar et al., 2006) us-

ing two images, and (f) the results of our method us-

ing three images from left to right, and the projection

patterns, the results of the scenes 1, 2, and 3 from top

to bottom. We can see that (b) our method and (c)

Duan et al. work better than (e) Nayar et al., even

though the formers use only a single image and the

latter uses two images. In particular, we can see the

artifacts around the boundaries in the black-and-white

patterns in the results of Nayar et al.

Table1 summarizes the quantitative comparison in

terms of the PSNR and SSIM; the higher, the better.

We can also see that our proposed method (N = 1)

and Duan et al. (N = 1) work better than Nayar et

al. (N = 2), even though the formers use only a sin-

It is reported that the projection pattern with 4 intensi-

ties outperforms that with 9 intensities.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

604

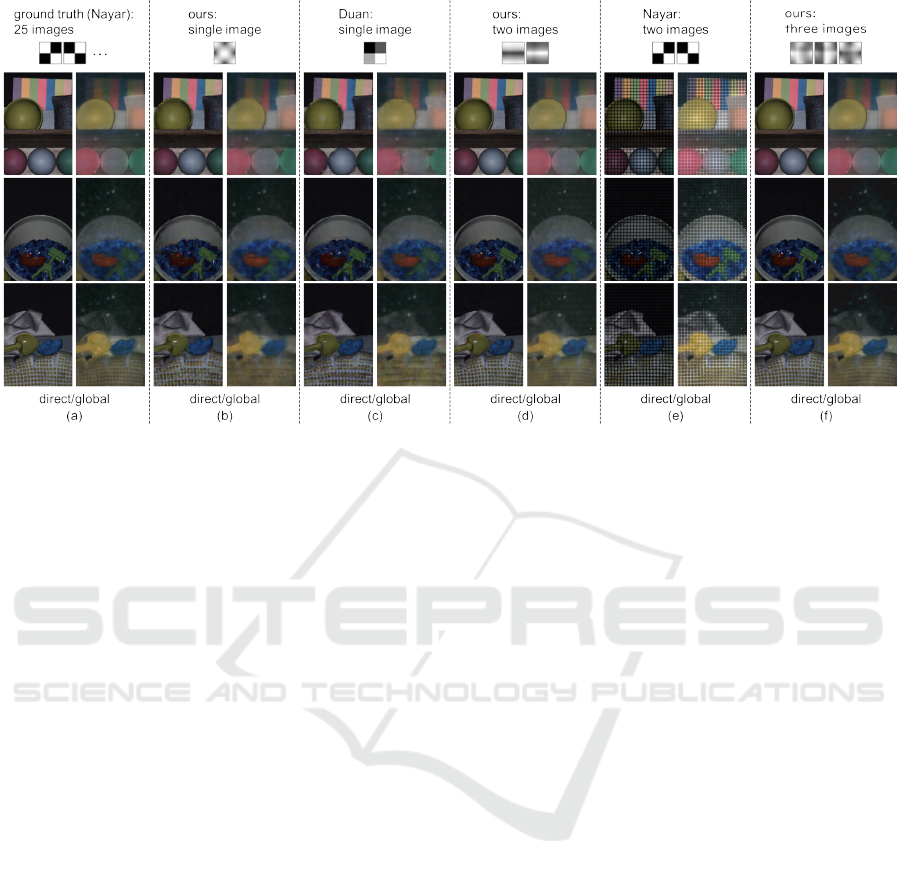
Figure 8: The qualitative comparison of the projection patterns: (a) the ground truth from 25 images, (b) the results of our

proposed method using a single image, (c) the results of Duan et al. (Duan et al., 2020) using a single image, (d) the results

of our method using two images, (e) the results of Nayar et al. (Nayar et al., 2006) using two images, and (f) the results of

our method using three images from left to right, and the projection patterns, the results of the scenes 1, 2, and 3 from top to

bottom. We applied the gamma correction to those images only for display purpose.

gle image and the latter uses two images. Further

more, we can see that our method performs better

than Duan et al.. This shows the effectiveness of our

method, in particular the data-driven projection pat-

tern and the end-to-end optimization of the imaging

module and the separation module. We can also see

that our method performs better as the number of im-

ages increases (N = 3).

5 CONCLUSION AND FUTURE

WORK

We proposed a data-driven approach for direct-

global separation with the optimal projection patterns.

Speciﬁcally, we show that the projection patterns can

be represented by (1 × 1) convolution kernels, and

then learn not only the separation module but also

the imaging module, i.e. the projection patterns at the

same time in an end-to-end manner via CNN frame-

work. We conducted a number of experiments using

real images captured with a projector-camera system,

and conﬁrmed the effectiveness of our method. The

extension of our approach from static scenes to dy-

namic scenes by taking motion blurs (Achar et al.,

2013) into consideration is one of the future directions

of our study.

ACKNOWLEDGEMENTS

This work was partly supported by JSPS KAKENHI

Grant Numbers JP23H04357 and JP20H00612.

REFERENCES

Achar, S., Nuske, S., and Narasimhan, S. (2013). Compen-

sating for motion during direct-global separation. In

Proc. IEEE ICCV2013, pages 1481–1488.

Chakrabarti, A. (2016). Learning sensor multiplexing de-

sign through back-propagation. In Proc. NIPS2016,

pages 3089–3097.

Clevert, D., Unterthiner, T., and Hochreiter, S. (2016). Fast

and accurate deep network learning by exponential

linear units (ELUs). In Proc. ICLR2016.

Duan, Z., Bieron, J., and Peers, P. (2020). Deep separation

of direct and global components from a single photo-

graph under structured lighting. Computer Graphics

Forum, 39(7):459–470.

Gu, J., Kobayashi, T., Gupta, M., and Nayar, S. (2011).

Multiplexed illumination for scene recovery in the

presence of global illumination. In Proc. IEEE

ICCV2011, pages 691–698.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Delving deep

into rectiﬁers: Surpassing human-level performance

on imagenet classiﬁcation. In Proc. IEEE ICCV2015,

pages 1026–1034.

Learning Projection Patterns for Direct-Global Separation

605

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proc. IEEE

CVPR2016, pages 770–778.

Ho, J., Jain, A., and Abbeel, P. (2020). Denoising diffusion

probabilistic models. Advances in Neural Information

Processing Systems, 33:6840–6851.

Inagaki, Y., Kobayashi, Y., Takahashi, K., Fujii, T., and

Nagahara, H. (2018). Learning to capture light

ﬁelds through a coded aperture camera. In Proc.

ECCV2018, pages 418–434.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: ac-

celerating deep network training by reducing internal

covariate shift. In Proc. ICML2015, pages 448–456.

Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. (2017). Image-

to-image translation with conditional adversarial net-

works. In Proc. IEEE CVPR2017, pages 5967–5976.

Kingma, D. and Ba, L. (2016). Adam: A method for

stochastic optimization. In Proc. ICLR2016.

Li, J., Yue, T., Zhao, S., and Hu, X. (2022). Fisher informa-

tion guidance for learned time-of-ﬂight imaging. In

Proc. IEEE/CVF CVPR2022, pages 16313–16322.

Li, K., Dai, D., and Van, G. L. (2023). Jointly learning

band selection and ﬁlter array design for hyperspec-

tral imaging. In Proc. IEEE WACV2023, pages 6384–

6394.

Liu, G., Reda, F., Shih, K., Wang, T.-C., Tao, A., and Catan-

zaro, B. (2018). Image inpainting for irregular holes

using partial convolutions. In Proc. ECCV2018, pages

85–100.

Metzler, C., Ikoma, H., Peng, Y., and Wetzstein, G. (2020).

Deep optics for single-shot high-dynamic-range imag-

ing. In Proc. IEEE/CVF CVPR2020, pages 1375–

1385.

Narasimhan, S., Koppal, S., and Yamazaki, S. (2008). Tem-

poral dithering of illumination for fast active vision.

In Proc. ECCV2008, pages 830–844.

Nayar, S., Krishnan, G., Grossberg, M., and Raskar, R.

(2006). Fast separation of direct and global compo-

nents of a scene using high frequency illumination. In

Proc. ACM SIGGRAPH 2006, pages 935–944.

Nie, S., Gu, L., Subpa-Asa, A., Kacher, I., Nishino, K., and

Sato, I. (2019). A data-driven approach for direct and

global component separation from a single image. In

Proc. ACCV2018 Part VI, pages 133–148.

Nie, S., Gu, L., Zheng, Y., Lam, A., Ono, N., and Sato,

I. (2018). Deeply learned ﬁlter response functions

for hyperspectral reconstruction. In Proc. IEEE/CVF

CVPR2018, pages 4767–4776.

Nisaka, Y., Matsuoka, R., Amano, T., and Okabe, T. (2021).

Fast separation of specular, diffuse, and global com-

ponents via polarized pattern projection. In Proc. IW-

FCV2021 (CCIS1405), pages 294–308.

Rombach, R., Blattmann, A., Lorenz, D., Esser, P., and

Ommer, B. (2022). High-resolution image synthe-

sis with latent diffusion models. In Proc. IEEE/CVF

CVPR2022, pages 10684–10695.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In Proc. MICCAI2015, pages 234–241.

Schechner, Y., Nayar, S., and Belhumeur, P. (2003). A

theory of multiplexed illumination. In Proc. IEEE

ICCV2003, pages 808–815.

Shi, Z., Bahat, Y., Baek, S.-H., Fu, Q., Amata, H., Li,

X., Chakravarthula, P., Heidrich, W., and Heide, F.

(2022). Seeing through obstructions with diffractive

cloaking. ACM TOG, 41(4):1–15.

Subpa-Asa, A., Fu, Y., Zheng, Y., Amano, T., and Sato, I.

(2018). Separating the direct and global components

of a single image. Journal of Information Processing,

26:755–767.

Sun, Q., Tseng, E., Fu, Q., Heidrich, W., and Heide, F.

(2020). Learning rank-1 diffractive optics for single-

shot high dynamic range imaging. In Proc. IEEE/CVF

CVPR2020, pages 1386–1396.

Tasneem, Z., Milione, G., Tsai, Y.-H., Yu, X., Veeraragha-

van, A., Chandraker, M., and Pittaluga, F. (2022).

Learning phase mask for privacy-preserving passive

depth estimation. In Proc. ECCV2022, pages 504–

521.

Torii, M., Okabe, T., and Amano, T. (2019). Multispectral

direct-global separation of dynamic scenes. In Proc.

IEEE WACV2019, pages 1923–1931.

Wu, Y., Boominathan, V., Chen, H., Sankaranarayanan, A.,

and Veeraraghavan, A. (2019). Phasecam3d-learning

phase masks for passive single view depth estimation.

In Proc. IEEE ICCP2019, pages 1–12.

Xu, Z., Sunkavalli, K., Hadap, S., and Ramamoorthi, R.

(2018). Deep image-based relighting from optimal

sparse samples. ACM TOG, 37(4):1–13.

Yoshida, M., Torii, A., Okutomi, M., Endo, K., Sugiyama,

Y., Taniguchi, R., and Nagahara, H. (2018). Joint

optimization for compressive video sensing and re-

construction under hardware constraints. In Proc.

ECCV2018, pages 634–649.

Zhu, J.-Y., Park, T., Isola, P., and Efros, A. (2017). Unpaired

image-to-image translation using cycle-consistent ad-

versarial networks. In Proc. IEEE ICCV2017, pages

2242–2251.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

606