RLAR: A Reinforcement Learning Abductive Reasoner

Mostafa ElHayani

Informatics, TUM, Munich, Germany

Keywords:

Logic, Knowledge Representation and Reasoning, Abduction, Deep Reasoning, Reinforcement Learning,

Machine Learning, Explainable Artiﬁcial Intelligence.

Abstract:

Machine learning (ML) algorithms are the foundation of the modern AI environment. They are renowned for

their capacity to solve complicated problems and generalize across a wide range of datasets. Nevertheless, a

noteworthy disadvantage manifests itself as a lack of explainability. Symbolic AI is at the other extreme of

the spectrum; in this case, every inference is a proof, allowing for transparency and traceability throughout

the decision-making process. This paper proposes the Reinforcement Learning Abductive Reasoner (RLAR).

A combination of modern and symbolic AI algorithms aimed to bridge the gap and utilize the best features

of both methods. A case study has been chosen to test the implementation of the proposed reasoner. A

knowledge-base (KB) vectorization step is implemented, and a Machine Learning model architecture is built

to learn explanation inference. Furthermore, a simple abductive reasoner is also implemented to compare both

approaches.

1 INTRODUCTION

Economics, linguistics, and artiﬁcial intelligence (AI)

research have become interested in reasoning about

knowledge. What does an agent need to know to act,

and how does it know whether it knows enough to per-

form such an action? When should an agent declare

that it doesn’t know the answer to a query? Based on

C.S. Pierce (Flach and Hadjiantonis, 2013), there are

three main types of reasoning: Reasoning from causes

to their effects, reasoning from experienced regulari-

ties to general rules, and reasoning from observed re-

sults to the basic reasons from which they follow. The

ﬁrst type is called deduction (Johnson-Laird, 1999),

while the second is called induction (Hayes et al.,

2010), and the third abduction (Walton, 2014). In this

paper, the focus is on abductive reasoning.

The abduction and logic programming combina-

tion is called Abductive logic programming (ALP)

(Kakas et al., 1998). ALP is explained as means by

which a goal claimed to be true can be extended to

facts that justify such a goal. Abduction has many

applications; For example, planning (Helft and Kono-

lige, 1990) where the goal is given as a speciﬁc state

and the facts to be derived are the detailed steps of

a plan to achieve such predicates; other examples in-

clude diagnosis (Pople, 1973; Console and Torasso,

https://orcid.org/0000-0002-3679-2076

1991) where the goal is the observed symptoms, and

the facts to be derived are the diagnosis. Another

area for abduction is language processing (Stickel,

1990), especially discourse analysis, where the dis-

course represents the observations, and the facts to be

derived are then the interpretation of that discourse.

In the early days of AI, researchers quickly ad-

dressed and solved intellectually difﬁcult problems

for humans but relatively simple for machines. The

main issue for AI has shown to be tackling activities

that are simple for humans to accomplish but chal-

lenging to formalize, i.e., problems that are solved in-

tuitively. The solution was found to be machines that

can not only act independently from human interac-

tion but also learn from experiences. This technique

eliminates the need for human operators to formally

specify all of the knowledge required by the machine.

The concept hierarchy enables the machine to acquire

complex concepts by building them up from simpler

ones.

Reinforcement learning (RL) (Sutton and Barto,

2018) is a branch of Machine Learning (ML) that

studies how intelligent agents should operate in a

given environment to maximize the concept of cumu-

lative reward. It encapsulates the notion of learning

by experience. RL is a well-established ﬁeld that is

frequently seen in ML. However, due to its concen-

tration on behavior learning, it has many linkages to

972

ElHayani, M.

RLAR: A Reinforcement Learning Abductive Reasoner.

DOI: 10.5220/0012425000003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 972-979

ISBN: 978-989-758-680-4; ISSN: 2184-433X

other subjects such as psychology, operation research,

mathematical optimization, etc. There are several

parallels between probabilistic and decision-theoretic

planning in AI. In this paper, the aim is to test the ca-

pabilities of an RL approach in performing abductive

reasoning.

2 LITERATURE REVIEW

Many of AI’s early breakthroughs occurred in rela-

tively antiseptic and formal surroundings and did not

necessitate machines’ extensive understanding of the

world. in 1997 IBM’s Deep Blue (Campbell et al.,

2002) chess-playing agent defeated the world cham-

pion. However, chess can be completely character-

ized by a very short list of completely formal rules,

which the programmer can readily specify before-

hand. Several AI projects have attempted to encode

global knowledge in formal languages. A machine

may automatically reason about claims in these for-

mal languages using logical inference rules. One of

the most famous projects to use a KB approach is

Cyc (Lenat and Guha, 1989). Cyc is a statement

database and inference engine written in the CycL

programming language. A team of human supervi-

sors inputs these statements. It’s a cumbersome pro-

cedure. People have a hard time developing formal

rules that are sophisticated enough to adequately ex-

plain the world. Furthermore, SCIFF (Alberti et al.,

2008) is a framework centered around abduction and

a reasoning paradigm that allows for formulating hy-

potheses (abducible) that explain given information.

The authors in (Christiansen and Dahl, 2004) showed

that rather than introducing a complex implementa-

tion apparatus, we could create a very direct and ef-

ﬁcient implementation in Prolog as a programming

language by merely adding a few lines of Constraint

Handling Rules (CHR) (Fr

uhwirth, 1998) code. In the

history of AI research, ML and logical reasoning have

almost been separately developed. However, there

has been research to address their integration. Prob-

abilistic Logic Programming (PLP) (De Raedt and

Kersting, 2008) attempts to extend First-Order Logic

(FOL) to accept probabilistic groundings to include

probabilistic inference. PLP also employs a “heavy-

reasoning light-learning” approach, which keeps log-

ical reasoning power while not completely utilizing

ML. However, Statistical Relational Learning (SRL)

(Koller et al., 2007) tries to build a probabilistic model

using domain information stated in FOL clauses. SRL

employs a “heavy-learning light-reasoning” approach

that keeps the strength of ML while not completely

utilizing logical reasoning. The authors of (Zhou,

2019) proposed abductive learning. A new framework

towards bridging machine learning and logical rea-

soning. The suggested approach’s learning technique

does not use supervised learning (Cunningham et al.,

2008), but is aided by a classiﬁer and a KB including

FOL sentences. The classiﬁer’s predictions are uti-

lized as pseudo-labels for the training cases, resulting

in pseudo-grounded facts. Knowledge-Base Artiﬁcial

Neural Networks (KBANNs) (Towell and Shavlik,

1994) work by ﬁrst converting logic instructions into

neural networks with one hidden layer and then train-

ing the networks using background knowledge and

training examples. They outperformed most purely

classical and hybrid learning systems at the time.

Not only that, but they were signiﬁcantly more data-

efﬁcient, requiring fewer training samples to reach the

same accuracy as their neural competition. In addi-

tion, the authors of (Payani and Fekri, 2019) proposed

dNL-ILP, a neural architecture capable of performing

inductive logic programming through deduction via

forward chaining. To accomplish this, they develop

a new conjunctive and disjunctive neuron type that

selects a subset of the input to perform their tasks.

They use fuzzy logic to make background knowledge

rules compatible with the neuron workings. In (Chen

et al., 2019), the authors presented Deep Reasoning

Networks (DRNets), an end-to-end system for tack-

ling complicated problems that integrate deep learn-

ing with reasoning, often in unsupervised or weakly

supervised situations. By tightly merging logic and

constraint reasoning with stochastic-gradient-based

neural network optimization, DRNets utilize issue

structure and prior knowledge. The effectiveness

of DRNets was demonstrated in de-mixing overlap-

ping hand-written Sudokus. Logical Tensor Networks

(LTNs) (Seraﬁni and Garcez, 2016) is an adaption

of Tensor Neural Networks (Socher et al., 2013) into

Real Logic, which the authors deﬁne as a redeﬁnition

of FOL. Understanding constants as real-valued vec-

tors rather than discrete things is a distinguishing fea-

ture of Real Logic. The major goal is to incorporate

proven logical formalisms with today’s abundant real-

valued data. This would incorporate logical thinking

as well as neural learning.

2.1 Hypothesis

It’s apparent that there is no shortage of attempts to

merge the ﬁelds of Neural Networks with Symbolic

Reasoning, but the literature also shows that there is

still room for improvement. In this paper, a solution

is proposed to address the issue of whether an RL al-

gorithm can be used instead of an abductive inference

algorithm, eliminating some of its limitations. Fur-

RLAR: A Reinforcement Learning Abductive Reasoner

973

thermore, the differences are discussed, and compar-

isons are shown for both implementations.

3 METHODOLOGY

3.1 Deﬁning Abductive Logic

Abduction is the process of inference to the

best explanation. Formally, an abductive logi-

cal program can be described as a quintuple <

K B, A, G, I C , P >, given a KB (K B), a set of ab-

ducible predicates (A), a set of observations (G ), a

set of Integrity Constraints (I C ) and an inference pro-

gram (P ). The program tries to ﬁnd the minimal set A

such that, A

⊆ A, K B ∪ A

|= G, and K B ∪ A

|= I C .

That is; the set of abduced predicates A

added to K B

logically implies the set of predicates G, while also

maintaining the set of predicates I C . The program

P contains the inference rules and I C s for a certain

environment.

3.2 Minimality

It is often the case that the abductive answer given by

the reasoner must be minimal. This means the number

of abduced predicates is minimal. A query on the hu-

midity of the garden given as ”grass is wet?” might

show three possible answers:

• A

= {rained last night}

• A

= {sprinkler was on}

• A

= {rained last night, sprinkler was on}

Suppose neither answer conﬂicts with any of the

given ICs. In that case, while the set A

passes as

a valid explanation for the observation it’s not a min-

imal set and is not preferred. However, the sets A

and A

are both possible minimal solutions.

3.3 Abductive Reasoning

Abductive reasoning is deﬁned as a search through

state space of possible abducibles. The generic search

procedure can be given by Algorithm 1.

Using the Breadth-First Search (BFS) strategy in

sorting the queue ensures search in the same level ﬁrst

before moving on to the next, which in turn ensures

minimality since the shallowest solutions are found

ﬁrst.

3.4 Updating the Knowledge-Base

Adding information to the KB is done using the ”tell”

function. This handles adding abducibles to the KB

Data: KB, A, G

Result: A

queue.push(KB);

while not queue.is empty() do

queue.sort();

state = queue.pop();

if isGoal(state,G) then

return state.abducibles;

else

for a in A do

KB’ = state.tell(a);

if KB’ not in visited then

visited.push(KB’);

queue.push(KB’);

else

continue;

end

return None;

Algorithm 1: Generic Search Procedure.

and using inference to generate new information. This

might lead to failures which means the reasoner has

to backtrack and search for alternative solutions. The

tell function is implemented with the help of CHR in

Prolog. The prolog program P is given to the reasoner

as input. An interface is implemented for the reasoner

to communicate with the environment.

3.5 Issues with Abductive Reasoning

Due to the minimality constraints posed on the rea-

soner, it could come up with un-informed solutions.

An un-informed solution is the minimal set A

which

maintains I C , however, the agent has no reason to

abduce it. For example, assume a doctor trying to di-

agnose a patient that shows a symptom S

, the doctor

has options {D

, D

} that includes S

as a symptom.

However, both diseases have several other symptoms

that the patient needs to be tested for before assuming

either of the diseases. Furthermore, it’s not the case

that we need to test for all possible symptoms to get a

solution, but to make the necessary number of tests for

an informed decision. Hence, although D

and D

are

both minimal abductive solutions only one of them

can be considered the best explanation. Furthermore,

the state space search strategy, in particular BFS, has

a time and space complexity of O(b

) where b is the

branching factor, and d is the depth of the shallow-

est solution. In this case, b is equal to the length of

A. Depending on the problem being addressed this

could be a huge number of states with many different

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

974

possibilities, all of which the reasoner has to search

through. For such reasons, a more optimal algorithm

is to be proposed. A reasoner that does not search

through possible states. Hence, the use of learning

strategies.

3.6 Reinforcement Learning

When the nature of learning is considered, the idea

that learning is done by interaction is the ﬁrst general

idea that comes to mind. Doctors need to learn to see

the patterns in certain symptoms to be able to abduce

the best possible disease that explains the symptoms.

They also need to use the experience to identify which

tests to run ﬁrst and use the outcomes to identify the

best possible actions to take. The approach of this pa-

per is based on this idea. RL problems involve learn-

ing how to map situations to actions to maximize a

certain objective function. An RL program contains 3

main elements

1. A policy

2. A reward Function

3. A model of the environment

3.6.1 Policy

The policy deﬁnes the learning agent’s way of behav-

ing at a given time. The behavior of the agent in this

paper is calculated by a Recurrent Neural Network

(RNN) (Medsker and Jain, 2001) that uses Long Short

Term Memory (LSTM) (Hochreiter and Schmidhu-

ber, 1997) layers. An RNN is a non-linear dynam-

ical system that models time series data holistically,

meaning that, it attempts to capture the temporal re-

lations from the beginning until the end of the time.

In an RNN paradigm, it is assumed that every point

in the time series is dependent on every previous time

instance. RNNs are used to detect temporal relations

between the features as well as the predictions in a

previous time step. The KB is modeled as a time-

series set of information, where every entry is its time

step. Furthermore, LSTMs show the ability to infer

variable lengths of input vectors; as such, the same

model architecture could be used for the same in-

stance of the environment with varying sizes of K B.

The architecture of the RNN built in this approach is

as follows: The model consists of two LSTM layers;

the ﬁrst has 16 cells, while the second consists of 8

cells, and a ﬁnal Dense layer is added with as many

neurons as the length of possible abducibles. A sig-

moid (Harrington, 1993) activation function was used

on the output layer with the idea that the agent could

infer multiple abducibles in the same step if they pass

a certain threshold. However, for the sake of sim-

plicity, only the abducible with the highest conﬁdence

level is added to the KB every time step. In addition,

to deal with the exploration vs exploitation dilemma

(Berger-Tal et al., 2014), an epsilon value of 0.5 and

a decay value 0.7 have been used, such that there is a

probability that an action taken by the reasoner while

training would be taken in random.

3.7 Reward Function

The reward deﬁnes the goal in an RL problem. The

goal is to ﬁnd the minimal predicates explaining the

given observation. This is done by rewarding the

agent for all abduction steps that add new informa-

tion to the KB while penalizing steps that add no new

information. The reward calculation algorithm em-

ploys a nuanced approach, deducting 50 points for

failure, adding 50 points for achieving the goal, pe-

nalizing with a deduction of 5 points for unchanged

states, and dynamically adjusting rewards based on

the occurrence count of recent additions, encouraging

exploration and penalizing repetitive behaviors in the

reinforcement learning process

3.8 Environment Model

The model is what mimics the behavior of the envi-

ronment. In this paper the model is given by the pro-

log ﬁle P , the set of predicates I

that contains all

predicates, the set of predicates I

that contains all

atoms, the set of predicates A that contains all ab-

ducibles, and the set of predicates G that contains all

observations.

3.9 Vectorization

To use a neural network to learn from the given data

points, a certain vectorization step needs to take place.

This is the process of turning an FOL predicate into

a feature vector. There have been other approaches

to doing this in the literature (Sakama et al., 2018).

However, the choice of a simpler approach has been

made, the steps in this procedure are as follows

1. Listify predicate

2. enumerate predicate symbols

3. enumerate atoms

4. enumerate variables

5. ﬂatten the list

6. list padding

Listifying a predicate turns a given FOL predicate into

a nested list such as the following

RLAR: A Reinforcement Learning Abductive Reasoner

975

• an atom a ⇒ [a]

• an n-ary predicate P(X

..X

) ⇒ [P,

[listify(X

),listify(X

),...listify(X

)]]

Afterward, an enumeration step is conducted such

that all elements in the list are encoded in numerical

values. In this paper, there are no function symbols,

as such, there is no nesting of predicate symbols. As

such, the ﬁrst element of the list is an identiﬁer of

the predicate, and every other element is an attribute.

A dictionary that maps predicate symbols and atoms

to numerical values is created. Furthermore, to map

variables to themselves, variables are encoded with

negative numbers starting from −1 to −N where N is

the total number of variables in the KB. Next, the list

is ﬂattened into a 1-D vector padded with the neutral

value zero for all vectors to be of equal sizes. For ex-

ample, vectorizing an FOL predicate f ather( john, X)

is done through the following steps; First, the predi-

cate is listiﬁed into [ f ather,[ john, X]], then an enu-

meration step of predicate symbols is conducted to

turn predicate symbols to numerical values. Sup-

pose the environment contains two predicates only

{ f ather(X,Y ), mother(X ,Y )} as such, the dictionary

would map father to 1 and mother to 2. Furthermore,

the atoms are also turned into numerical values; in

such case, John would be encoded in a number as

well, assuming 1, and the variable X takes on the

value of −1 as its only variable. As such, the list

turns to [1,[1,-1]]. Then, the list is ﬂattened into a 1-

D vector [1,1,-1], and since all predicates are binary

relations, there is no need for padding.

4 EXPERIMENTAL WORK

A logic gate circuit fault detection environment is

chosen as a case study to test the implementation of

the proposed approach. As trivial as it may seem, it’s

a good case study to showcase the capabilities of the

proposed approach. The environment explains a cir-

cuitry of logical gates, along with the inputs, and the

outputs of the circuit. The agent then needs to ex-

plain the reason behind the output. This is done by

explaining which gates are faulty and which are work-

ing properly.

4.1 Inference

Inference in the environment is given by an explana-

tion of how gates work. The program P contains a set

of rules for each logical gate that explains their behav-

ior. Furthermore, information on the actuality of the

state of the gate is given by certain predicates. The

predicates in the program are as follows

• and(Gate, In

,In

,Out).

• or(Gate, In

,In

,Out).

• not(Gate, In,Out).

• actually perfect(Gate).

• actually defect(Gate).

The predicates and, or, and not are predicates of the 3

main logical gates. ”Gate” is a variable symbol refer-

ring to an identiﬁcation of a given gate; Ins and Outs

are the inputs and outputs of each gate, respectively.

the predicates actually perfect and actually defect al-

lude to the actual state of the gate speciﬁed, and they

are predicates that the agent cannot see. A set of rules

are used to explain the behavior of each gate. For ex-

ample, given the predicate and(and

, 0,1,Out) and the

predicate actually perfect(and

), it can be infered that

Out = 0 whereas having actually defect(and

) instead

infers Out = 1.

4.2 Abducibles

The set of predicates the agent can abduce are as fol-

lows

• try gate(Gate,In

,In

)

• try gate(Gate,In)

• perfect(Gate)

• defect(Gate)

where the predicate try gate is the process of testing

a certain gate on given inputs and monitoring the re-

sults added to the KB. For example, assume the pres-

ence of a gate and1, its behavior can be tested by us-

ing try gate(and1,0,1), the result of such query is ei-

ther and(and1,0,1,1) or and(and1,0,1,0) depending on

whether the gate is actually defect or actually perfect

respectively. Knowing this, it’s easier now to have an

informed explanation of the state of the gate.

4.3 Integrity Constraints

The set I C is encapsulated inside the program P as

a set of rules that make sure the K B remains consis-

tent. For example, abducing that a gate is both perfect

and defective, or abducing that a gate that shows per-

fect results is defective, or vice versa all violate the

constraints and result in falsity or inconsistency in the

KB and are considered failed states.

5 RESULTS

The proposed approach has been tested on two differ-

ent scenarios. The scenarios represent two different

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

976

logic circuits, the agents can observe the connection

of the circuit, the inputs, as well as the outputs. As

discussed above, The environment is encapsulated to

the agent as an initial K B, a set of abducibles, and

a program that holds I C as well as inference rules.

For each of the two scenarios, the environment is ex-

plained and the output of each reasoner is shown in

the next two subsections. Furthermore, each subsec-

tion includes two experiments on the same scenario

by changing inputs/outputs or the actual state of gates.

This generates multiple different scenarios and exper-

iments for which the implementations could be tested

and the results logged and observed. However, for

the sake of space, only 4 of these experiments were

recorded in this paper. In Addition, for the following

experiment explanation, a gate is actually perfect un-

less stated otherwise; this is added inside the program

P ; however, it is not mentioned below.

5.1 Scenario 1

The ﬁrst scenario is a basic logic circuit with only ﬁve

gates and not many connections. It contains two AND

gates, two OR gates, and one NOT gate. There are

three input bits (A, B, and C) and one output bit (Out).

The schematic of the circuit can be seen in Figure 1.

Figure 1: Logic Circuit Scenario 1.

The initial K B is given by the following predi-

cates

1. and(and1,A,B,D)

2. or(or1,A,C,E)

3. and(and2,D,E,F)

4. not(not1,B,G)

5. or(or2,F,G,Out)

The two sub-experiments that have been conducted

in this scenario, are as follows; The ﬁrst is one where

gates and1, not1 are actually defect, and values for A,

B, C, and Out are all given to the reasoner as A = 1,

B = 0, C = 1, Out = 1. The other is where or1, not1,

and or2 are actually defect and values for A, B, C,

and Out are all given to the reasoner as A = 0, B = 1,

C = 1, Out = 0.

5.1.1 Search

The search algorithm ﬁnds all solutions starting from

the minimal one until a selected maximum number of

solutions. The ﬁrst solution was found in 0.9 seconds

in experiment 1 while taking 0.7 seconds in experi-

ment 2. However, as stated before, it’s an un-informed

solution, meaning it just might be correct. For exam-

ple, the solution in experiment 1, the solution is one

where all gates are perfect. In such case, the agent

has no information about the gates, so the possibil-

ity that all gates are perfect is possible since not(not1,

B, G) would have G evaluate to 1 and then or(or2,

F, G, Out) would evaluate Out to 1 as well. But it’s

known that this isn’t the case, and although one of the

possible solutions is one where the actual state of the

circuit holds, however, this is not an informed deci-

sion. Hence, to ﬁnd the correct solution, all solutions

have to be generated, and then the most informed de-

cision has to be searched for. the total number of so-

lutions generated for both experiments exceeded 100.

However, neither of the solutions after that added any-

thing new since the agent kept trying to add new ab-

ducibles which no longer adds new information to the

KB. The 100 solutions were found in 15 seconds for

experiment 1 while taking 14 seconds for experiment

2. After all solutions were found, searching for one

solution that was most informed but also minimal was

conducted in 5 seconds for both experiments.

5.1.2 RLAR

RLAR trains on different possibilities of the environ-

ment then can run on any instance of the same en-

vironment. For both environments, the agent was

trained once for a total of 200 episodes which took

500 seconds of training time. Afterward, solutions

were found in 0.18 seconds for experiment 1 and

0.28 seconds for experiment 2. The agent in this ap-

proach only generates 1 solution, which is supposedly

the most informed correct solution. The solution in

this case was correct for both experiments trying only

the needed gates to abduce which were defective and

which were not. For example, in experiment 1, the

agent tested the gate not1 ﬁnding out that it is a defect,

then for Out to be evaluated as 1, either or2 is a de-

fect or the output from and2 evaluates to 1. The agent

assumed that or1 was perfect. Hence, and1 needs to

be evaluated to 1 as well, but B is 0. Hence, the agent

abduced that and2 was perfect and tested and1, which

indeed turned out to be a defect. hence, the agent

could also make the assumption that or2 was perfect,

which turns out to be the actual solution.

RLAR: A Reinforcement Learning Abductive Reasoner

977

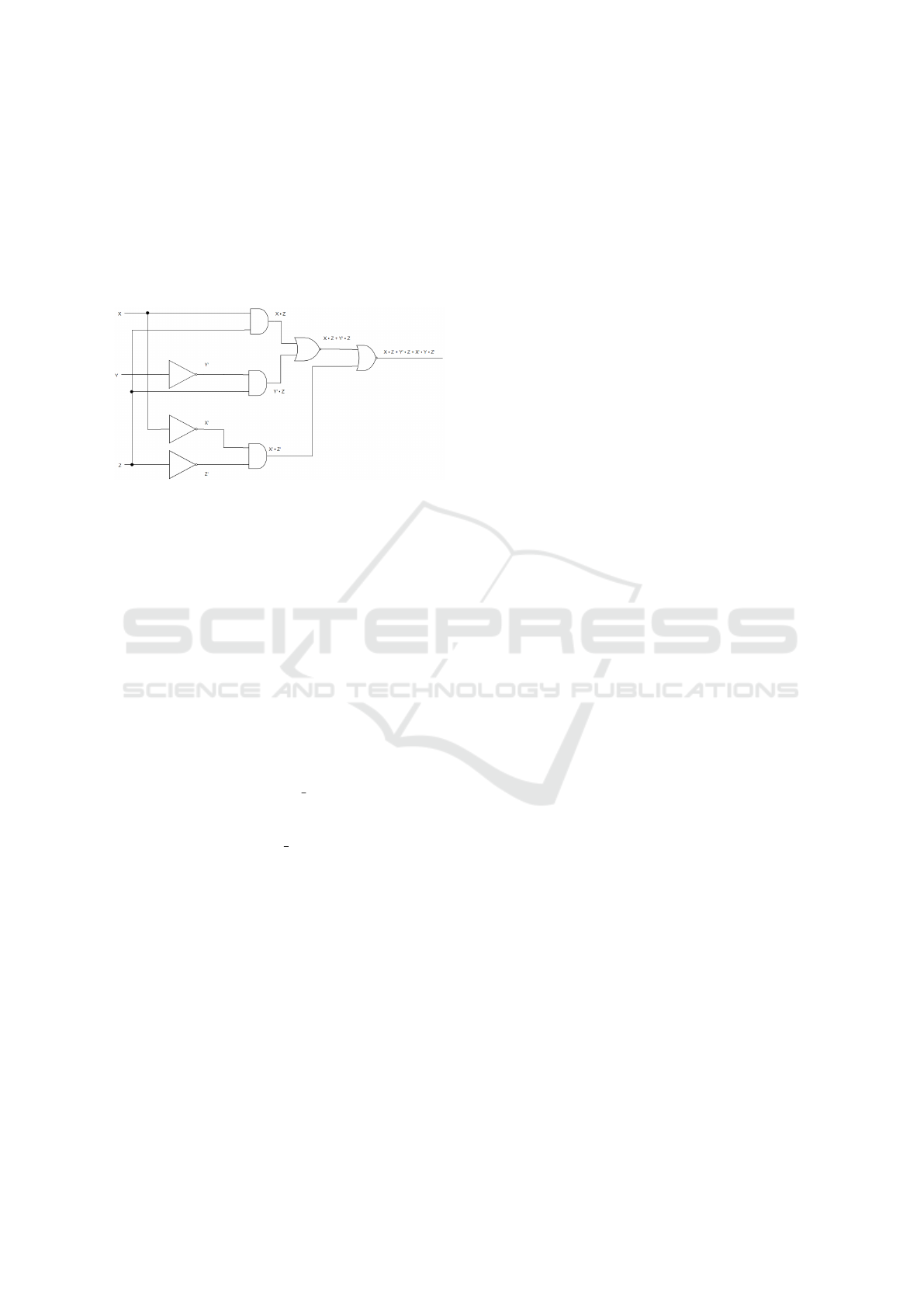
5.2 Scenario 2

The second scenario is a more complex circuit with

eight gates and more connections. It contains three

AND gates, two OR gates, and three NOT gates.

There are three input bits (X, Y, and Z) and one output

bit (Out). The schematic of the circuit can be seen in

Figure 2.

Figure 2: Logic Circuit Scenario 2.

The initial K B is given by the following predi-

cates

1. not(not1,X,A)

2. not(not2,Y,B)

3. not(not3,Z,C)

4. and(and1,X,Z,D)

5. and(and2,Z,B,E)

6. and(and3,A,C,F)

7. or(or1,D,E,G)

8. or(or2,F,G, Out)

Furthermore, the two sub-experiments conducted in

this scenario are as follows; The ﬁrst is one where

gates and2, and3 are actually defect, and values for

X, Y, Z, and Out are all given to the reasoner as X = 0,

Y = 0, Z = 1, Out = 0. The other is where not1, and1,

and3, and or2 are actually defect and values for X,

Y, Z, and Out are all given to the reasoner as X = 1,

Y = 0, Z = 0, Out = 0.

5.2.1 Search

The time to ﬁnd the ﬁrst solution was 1.7 seconds for

experiment 1 and 4.7 seconds for experiment 2. The

total number of solutions exceeded 100 for the ﬁrst

experiment; however, it did not exceed 45 for the sec-

ond. The total time to ﬁnd an informed solution was

40 seconds for experiment 1 and 45 for experiment 2.

5.2.2 RLAR

The total training time for this environment was 1500

seconds for the agent to train for 250 episodes. The

agent, however, was able to ﬁnd 1 solution for both

experiments in 1.4 seconds for the ﬁrst experiment

and 0.47 seconds for the second one. RLAR was also

able to ﬁnd the correct solution, abducing the correct

state of each gate in the least steps.

6 CONCLUSIONS

6.1 Discussion

It is apparent from the results, that RLAR has suc-

ceeded in performing the given task and proving

the hypothesis. However, the question remains of

whether the use of RL to aid in abductive reasoning

should be considered a computational necessity. Ab-

duction, while not always yielding accurate results, is

acceptable in certain contexts. In some situations, a

quicker search strategy might be more efﬁcient than

the suggested approach, especially if probability suf-

ﬁces. However, when precision is crucial and the opti-

mal solution must also be correct, exhaustive searches

become impractical, making the proposed approach

more favorable. The suggested method requires initial

learning on examples from a speciﬁc environment, of-

fering adaptability across instances of that environ-

ment. Additionally, implementing an online learning

strategy enables continuous improvement with each

new trial. One question that might still be vague

is whether the trade-off between the search time vs

training time is proﬁtable. It is clear from the results

that although the training time takes longer time than

the time needed to search, the proposed approach,

when used in inference, is even faster than the ﬁrst so-

lution the search ﬁnds. A solution could also be where

only tests are abducibles, and hence the agent only

needs to abduce what to test, then another algorithm

could reason from the test and generate possibili-

ties that would give faster results. However, RLAR

could already perform such a task without the need

for other algorithms. Although abductive reasoning

might show some limitations, such as un-informed so-

lutions or computationally expensive searches, an RL

approach to abductive reasoning has shown the ability

to not only succeed in inference to the best explana-

tion but also to back up its beliefs without the need to

search through all possibilities. RLAR has shown the

ability to learn, from experience, the needed informa-

tion from a given environment and the ability to come

up with a correct explanation for a given observation

in the least amount of time. However, the proposed

approach shows some limitations. For an RL algo-

rithm to be able to learn, an environment model must

be built in a way that encapsulates all needed informa-

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

978

tion, as well as, be able to generate multiple different

instances of itself. Furthermore, the agent would need

multiple training episodes to fully understand an envi-

ronment. For future research, an extension of the ap-

proach could be implemented to ease the creation of

new environments further. In addition, comparative

testing of this approach against other methods should

be conducted, as well as, testing it against non-trivial

use cases.

REFERENCES

Alberti, M., Chesani, F., Gavanelli, M., Lamma, E., Mello,

P., and Torroni, P. (2008). Veriﬁable agent interaction

in abductive logic programming: the sciff framework.

ACM Transactions on Computational Logic (TOCL),

9(4):1–43.

Berger-Tal, O., Nathan, J., Meron, E., and Saltz, D. (2014).

The exploration-exploitation dilemma: a multidisci-

plinary framework. PloS one, 9(4):e95693.

Campbell, M., Hoane Jr, A. J., and Hsu, F.-h. (2002). Deep

blue. Artiﬁcial intelligence, 134(1-2):57–83.

Chen, D., Bai, Y., Zhao, W., Ament, S., Gregoire, J. M.,

and Gomes, C. P. (2019). Deep reasoning net-

works: Thinking fast and slow. arXiv preprint

arXiv:1906.00855.

Christiansen, H. and Dahl, V. (2004). Assumptions and ab-

duction in prolog. In 3rd International Workshop on

Multiparadigm Constraint Programming Languages,

MultiCPL, volume 4, pages 87–101.

Console, L. and Torasso, P. (1991). A spectrum of logi-

cal deﬁnitions of model-based diagnosis 1. Computa-

tional intelligence, 7(3):133–141.

Cunningham, P., Cord, M., and Delany, S. J. (2008). Su-

pervised learning. In Machine learning techniques for

multimedia, pages 21–49. Springer.

De Raedt, L. and Kersting, K. (2008). Probabilistic in-

ductive logic programming. In Probabilistic Inductive

Logic Programming, pages 1–27. Springer.

Flach, P. A. and Hadjiantonis, A. (2013). Abduction and

Induction: Essays on their relation and integration,

volume 18. Springer Science & Business Media.

uhwirth, T. (1998). Theory and practice of constraint han-

dling rules. The Journal of Logic Programming, 37(1-

3):95–138.

Harrington, P. d. B. (1993). Sigmoid transfer functions in

backpropagation neural networks. Analytical Chem-

istry, 65(15):2167–2168.

Hayes, B. K., Heit, E., and Swendsen, H. (2010). Inductive

reasoning. Wiley interdisciplinary reviews: Cognitive

science, 1(2):278–292.

Helft, N. and Konolige, K. (1990). Plan recognition as ab-

duction and relevance. draft version. Artiﬁcial Intelli-

gence Center, SRI International, Menlo Park, Califor-

nia.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural computation, 9(8):1735–1780.

Johnson-Laird, P. N. (1999). Deductive reasoning. Annual

review of psychology, 50(1):109–135.

Kakas, A. C., Kowalski, R. A., and Toni, F. (1998). The

role of abduction in logic programming. Handbook of

logic in artiﬁcial intelligence and logic programming,

5:235–324.

Koller, D., Friedman, N., D

zeroski, S., Sutton, C., McCal-

lum, A., Pfeffer, A., Abbeel, P., Wong, M.-F., Meek,

C., Neville, J., et al. (2007). Introduction to statistical

relational learning. MIT press.

Lenat, D. B. and Guha, R. V. (1989). Building large

knowledge-based systems; representation and infer-

ence in the Cyc project. Addison-Wesley Longman

Publishing Co., Inc.

Medsker, L. R. and Jain, L. (2001). Recurrent neural net-

works. Design and Applications, 5:64–67.

Payani, A. and Fekri, F. (2019). Inductive logic program-

ming via differentiable deep neural logic networks.

arXiv preprint arXiv:1906.03523.

Pople, H. E. (1973). On the mechanization of abductive

logic. In IJCAI, volume 73, pages 147–152. Citeseer.

Sakama, C., Nguyen, H. D., Sato, T., and Inoue, K. (2018).

Partial evaluation of logic programs in vector spaces.

arXiv preprint arXiv:1811.11435.

Seraﬁni, L. and Garcez, A. d. (2016). Logic tensor net-

works: Deep learning and logical reasoning from data

and knowledge. arXiv preprint arXiv:1606.04422.

Socher, R., Chen, D., Manning, C. D., and Ng, A. (2013).

Reasoning with neural tensor networks for knowledge

base completion. In Advances in neural information

processing systems, pages 926–934.

Stickel, M. E. (1990). Rationale and methods for abductive

reasoning in natural-language interpretation. In Natu-

ral Language and Logic, pages 233–252. Springer.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-

ing: An introduction. MIT press.

Towell, G. G. and Shavlik, J. W. (1994). Knowledge-based

artiﬁcial neural networks. Artiﬁcial intelligence, 70(1-

2):119–165.

Walton, D. (2014). Abductive reasoning. University of Al-

abama Press.

Zhou, Z.-H. (2019). Abductive learning: towards bridg-

ing machine learning and logical reasoning. Science

China Information Sciences, 62(7):1–3.

RLAR: A Reinforcement Learning Abductive Reasoner

979