Towards Knowledge-Augmented Agents for Efﬁcient and Interpretable

Learning in Sequential Decision Problems

Reem Alansary and Nourhan Ehab

Department of Computer Science and Engineering, German University in Cairo, Cairo, Egypt

Keywords:

Neuro-Symbolic AI, Reinforcement Learning, Representation Learning.

Abstract:

The advantages of neurosymbolic systems as solvers of sequential decision problems have captured the at-

tention of reseachers in the ﬁeld of AI. The combination of perception and cognition allows for constructing

learning agents with memory. In this position paper, we argue that the decision-making abilities of such

knowledge-augmented solvers transcend those of black-box function approximators alone as the former can

generalize through inductive reasoning to behave optimally in unknown states and still remain fully or par-

tially interpretable. We present a novel approach leveraging a knowledge base structured as a layered directed

acyclic graph, facilitating reasoned generalization in the absence of complete information.

1 INTRODUCTION

With the onset of the third AI Summer (Kautz, 2020),

Neuro-Symbolic systems have captured the attention

of AI researchers, enthusiasts, and the scientiﬁc com-

munity to address problems where “solutions that

work” are no longer sufﬁcient. It is now of great im-

portance to have solutions that are efﬁcient and trans-

parent, at least to a certain degree. Our contention

is that a system integrating both neural and symbolic

components holds added value in achieving this ob-

jective. On the one hand, data-driven systems rarely

require expert interference or detailed and speciﬁc al-

gorithms to learn a solution of some task, but in most

cases they need to witness myriads of data. As a re-

sult, a system trained in this way is robust against

noise, but turns out to be costly in terms of compu-

tation time and resources. Furthermore, they tend

to produce solutions of an esoteric nature incapable

of being deciphered simply by scrutiny and analy-

sis. On the other hand, systems built using symbols

and rules have to have an internal store of knowl-

edge, known as a knowledge base (KB); this KB is

the deﬁning factor for the system’s behaviour as in-

dicated by the Knowledge Representation Hypothe-

sis (Brachman and Levesque, 2004). Nevertheless,

knowledge-based programs can not gracefully handle

erroneous input and the inference they employ is by

itself computationally expensive.

Our intent is not to undermine the success of either

neural or symbolic systems. Nonetheless, a single-

type program fails to emulate human cognitive capac-

ities, a quintessential feature of intelligent machines.

Humans learn new things all the time, but they do

not learn without background knowledge most of the

time. They can also utilize language to describe or

even explain their knowledge of the world. Thus,

they use both their perception and cognition abilities.

Therefore, we posit that a true emulation of the hu-

man mind demands a machine that amalgamates the

strengths of both data-driven and symbolic AI as each

type is comparable to a mode of thinking of the hu-

man mind (Evans and Stanovich, 2013).

This position paper speciﬁcally addresses prob-

lems inherently demanding a neuro-symbolic sys-

tem, particularly sequential decision problems (Barto

et al., 1989). We center our discussion on the sub-

set of such problems that are either too big or too

complex to have a complete KB. Solutions for these

problems must be learned through repeated observa-

tion and prediction. However, if a learning-only ap-

proach is adopted without utilizing cognition to rea-

son over the learned knowledge, generalization may

be a lethargic process, and if a neural network is used

for speeding up with increasing problem scale, inter-

pretability of the achieved solution would be compro-

mised. Hence, we argue that solvers of such problems

should begin by learning partial solutions that can be

represented symbolically in a layered directed acyclic

graph where similar nodes can be grouped together

and in a language that permits inductive reasoning to

enable fast and interpretable generalization.

1014

Alansary, R. and Ehab, N.

Towards Knowledge-Augmented Agents for Efﬁcient and Interpretable Learning in Sequential Decision Problems.

DOI: 10.5220/0012430900003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 1014-1019

ISBN: 978-989-758-680-4; ISSN: 2184-433X

2 SIMILARITY REVELATIONS

Before delving into the available approaches for tack-

ling the problem of efﬁcient and interpretable general-

ization in sequential decision problems, we introduce

a simple model of such problems: the Markov Deci-

sion Process (MDP). An MDP M is formally deﬁned

as the 4-tuple M = (S, T, A, R) where:

• S is the state space,

• T is the transition model,

• A is the action space, and

• R is the reward function.

The transition model T usually has a probabilistic

nature and the reward function is always deﬁned with

respect to some goal. In other words, for all states

s ∈ S, where the goal is achieved, the reward is maxi-

mum. Any MDP M exhibits the Markovian Property

that guarantees that the current state of the world is

affected only by the most recent previous state.

A solution for M then would be the optimal global

policy π

∗

found by an abstract embodiment of the

solver as a rational agent which learns by reinforce-

ment. This agent ﬁnds the optimal global policy by re-

peatedly observing state-action-reward sequences in

the MDP and making predictions as to which actions

would lead it to its goal.

Early efforts to build a reinforcement learning

(RL) agent capable of learning π

∗

, that were based on

temporal difference methods (Sutton, 1988), resulted

in the development of several analytically transpar-

ent algorithms (Yu et al., 2021). However, not much

later, it was found that emergent algorithms that were

model-free, such as Q-Learning or SARSA, did not

scale well (Kaelbling et al., 1996). This was due to

their operation without a model of the environment.

That is, these algorithms disregard the importance of

similarity of agent behaviour in state-action-reward

sequences and the similarity of state representations.

This early ﬁnding comports with our position that

capitalizing on such similarity would aid in the gen-

eralization process of any rational agent.

Subsequent research explored model-based algo-

rithms, such as Dyna and prioritized sweeping (Sutton

et al., 2012), that capitalize on similarity of agent be-

haviour or state representation. In the next section, we

delve into approaches aiming to learn representations

of the underlying problem to facilitate generalization.

3 MODEL REPRESENTATIONS

In order to mitigate the difﬁculties hindering fast

and interpretable generalization, researchers shifted

their attention from model-free to model-based algo-

rithms. However, not all proposed solutions revolved

around representing the environment model or parts

of it to discover regularities between states. Some ap-

proaches were motivated by abstracting the similar-

ity of agent behaviour across state-action-reward se-

quences.

One method of abstracting granular operations

transformed the underlying problem model from a

regular MDP into a Semi-MDP (SMDP) (Barto and

Mahadevan, 2003), where the agent may remain in

one state for more than a single time step. This char-

acteristic waiting time gives the agent the opportunity

to execute multiple primitive actions. Thus, the no-

tion of macros was introduced. Through the use of

macro operators, the agent behaviour is successfully

abstracted as the invocation of any macro is analogous

to compounding state-action-reward sequences. This

representation of the problem as an SMDP motivates

hierarchical RL, where a common architecture of a

solution is to segment the environment and assign an

agent to each segment, such that these agents report

back to a master agent that then would have “macro”

information of the optimal policy of each segment.

This approach can also be extended to function in

partially observable MDPs (POMDPs) by adding hi-

erarchical memory structures where agents, at each

level corresponding to an abstraction degree, repre-

sent their belief states. In a POMDP, every state can

be partially observable, thus an agent observes a be-

lief state that corresponds to a probability distribution

over the set of possible states that it can be in.

On a similar note, agent behaviour can be ab-

stracted by applying a bisimulation metric to the op-

timal policies in different states to measure their sim-

ilarity without depending on the knowledge of the

reward function (Agarwal et al., 2021). Although

we believe that incorporating reward information is

at the heart of goal-directed generalization (Landa-

juela et al., 2021), this approach has shown promising

results for control problems as it identiﬁes states as

close when their policies are similar. Hence, it can be

argued that since the policy is used to measure simi-

larity, then the reward function is taken into consider-

ation indirectly.

Another relevant endeavor to generalize and en-

able an RL agent to learn the optimal policy faster

adopted a data mining approach (Apeldoorn and

Kern-Isberner, 2017) to discover the best action in any

state quickly (Apeldoorn and Kern-Isberner, 2017).

The goal was to represent the optimal policy as a

structured KB of weighted rules, such that each ab-

stract rule may indicate the best action in a group of

states where the agent perceptions in each state are

Towards Knowledge-Augmented Agents for Efﬁcient and Interpretable Learning in Sequential Decision Problems

1015

similar. The agent starts exploiting the learned knowl-

edge according to the strategic depth measure that is

based on the size of the KB.

The previous approaches experimented with

learning symbolic knowledge to enable the learners

to act fast in large environments. There is another

research direction which assumes that background

knowledge is fully or in part available (Ledentsov,

2023, for instance). While we contend that this is

infeasible for every environment as knowledge may

not always be in abundance, the results support our

position that learning becomes faster and more inter-

pretable when a symbolic component is present.

Recent advances in this direction include works on

control problems, where deep RL is employed to learn

mathematical functions as approximations for each

action in the action space in a sequential manner (Lan-

dajuela et al., 2021); this approach reduces complex-

ity of the environment by building the function ap-

proximators step-by-step and giving a neural network

prior information of properties of certain functions to

inhibit the generation of trivial action represenations,

such as an invertible function and its inverse and ap-

plying one to the other or vice versa. This corresponds

to creating an ordering of actions (a

, a

, .., a

) for

some n ∈ N such that the function approximator for

i+1

is searched for only when the complexity of the

search space has been reduced by ﬁxing representa-

tions for action a

through a

for 1 ≤ i ≤ n.

Special attention has been accorded to the impor-

tance of model-aided learning in environments with

sparse rewards, where the nature of the reward func-

tion may render the modelling of the environment

as an MDP inadequate. The use of a partial model

representation in the form of a declarative planning

model provided to an RL agent from humans as ad-

vice was explored to simplify the underlying problem

(Guan et al., 2022). The planning model helped the

agent decompose the problem into sub-problems or

landmarks. Thus, hierarchical RL could be employed

to ﬁnd the optimal solution for each landmark and

the optimal policy is obtained by stitching together

these individual solutions. On a different note, such

environments could be regarded as completely non-

Markovian and as such a different learning approach

should be used. One example, which conforms with

our standpoint that generalizations should be learned,

learns a deterministic ﬁnite automaton (DFA) that

simpliﬁes the problem by providing a Markovian de-

composition of it (Christoffersen et al., 2023). Af-

ter this transformation, the DFA and observations are

used in conjunction to learn the optimal policy by tab-

ular Q-learning.

4 OUR PROPOSED APPROACH

Humans generalize efﬁciently only when they use

their memory to keep track of past experiences in a

language that allows for inductive reasoning and the

best decision-makers are those with the best general

experience. They are those with the best knowledge

bases. We believe that this idea should be maintained

as the heart of any solution that considers efﬁciency

and interpretability for any sequential decision prob-

lem. Otherwise, we would be running into the old

problem of having learning agents that are expected

to behave optimally in short time, but on every power-

on they must learn with a clean slate (Kaelbling et al.,

1996).

Learning with a clean slate is not enough for large

or complex environments. In order to behave opti-

mally and in a shorter time in such environments, an

agent must leverage its memory by reasoning with

past experience. We argue that such behaviour is

accomplished through a symbolic representation of

knowledge as the agent’s behaviour would be en-

trenched in this representation.

Means to this end, governed by the underlying

model of the sequential decision problem at hand,

vary depending on the nature of the domain; whether

it is discrete or continuous. Within this line of re-

search, endeavors can be categorized based on the

extent of available knowledge for utilization. Some

approaches assume either partial or complete access

to symbolic knowledge in a deﬁned format, employ-

ing it as a guiding framework for a learning agent.

Conversely, alternative methodologies avoid such as-

sumptions, opting to concurrently acquire the sym-

bolic representation while navigating the path to an

optimal policy.

We stand with the second view and propose a so-

lution with the initial absence of knowledge in fully

observable environments. Necessary knowledge can

then be acquired through symbolic function approx-

imators or by reasoning on some logical represen-

tation. We are currently working on systems that

use tabular Q-learning for learning logical knowledge,

stored in a layered graph-based KB, that can be gen-

eralized through inductive reasoning as it is our belief

that this approach is best suited for preserving inter-

pretability as well as for being efﬁcient.

4.1 KB Structure

Addressing the crux of efﬁcient learning and gener-

alization, we propose a graph-based Knowledge Base

(KB) structured into layers. Each layer corresponds

to the agent’s sensors, forming a hierarchy that aids

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1016

⊥ =⇒ >

. . .

(m−1)1

(m−1)2

. . .

(m−1)3

. . .

(m−1)4

(m−1)5

. . .

(m−1)6

. . .

1 j

2(k−1)

. . .

(m−1)(l−1)

m(n−1)

(m−1)l

Figure 1: An abstract example of the graph-based KB where each r

is a rule in level a and its index in that level is b.

in efﬁcient navigation and representation of learned

rules. The graph data structure is chosen over the clas-

sical ﬂat KB as it can separate the learned rules such

that similar ones remain closer together. Besides, the

directed links translate the relation between the rules

in two connected nodes.

The zeroth level of the KB is made up of one util-

ity node that holds the structure together but is not

representative of a rule speciﬁc to any decision prob-

lem; it will always hold the material conditional

⊥ =⇒ >,

which serves as a formalization of the fact that any

agent situated in an unknown environment without

prior knowledge will believe that it can execute any

action and that all actions are equally preferable with

respect to its goal, embodied by the reward function.

Although any valid sentence would have served the

same purpose, the above sentence was favored as it

conforms to the standard format of the rules and it

intuitively maps to the behaviour of a learning agent

starting out in any environment. Any node, other

than the utility node, holds a rule consisting of a dis-

cretized state from an environment, as the antecedent,

and the corresponding best action as the consequent

of a material conditional. Records of the total num-

ber of application and the number of successes of a

rule are kept alongside the rule in the corresponding

node. Furthermore, on the grounds that each rule is

obtained through an inductive process that generates

a belief that could be revised not absolute knowledge,

we associate with each rule a weight measuring its

credibility. For nodes in the bottom level, this weight

is based on the q-value of the rule, which comes di-

rectly from the learning algorithm and is a measure of

how relevant this rule is for the agent’s goal, and the

successes and tries of this rule. Each rule in any other

level is induced and its weight is computed from the

weights of the rules in the nodes that participated in

its induction.

The levels of the KB are ﬁnite and directly cor-

respond to the number of sensors of the agent; if the

agent has m sensors, then the graph has m + 1 lev-

els, where the i

level has i sensor values forming the

antecedent of every rule for 0 ≤ i ≤ m. Thus, the bot-

tom level contains the rules that directly map to states

and actions obtained from the learning algorithm. The

rules in every other level, where i 6= m, are created

by an inductive inference process using those in level

i + 1 or the level directly below. A graphic example

is shown in ﬁgure 1, where out of all the contents of

a single node only the rule is shown for simplicity.

These rules can be used to interpret the behaviour of

the agent and the outcome of the learning algorithm

as each rule maps either a full or partial state to the

perceived optimal action with respect to some goal;

rules in the bottom level correspond to full states, but

rules in any other level correspond to partial states as

they are induced. This mapping, enforced by the rule

format, helps in clarifying the agent’s belief about the

outcome of executing some action in some state and

why the agent’s beliefs may change with any change

of an observation.

4.2 KB Operations

The KB provides two functionalities; the ﬁrst is to

store knowledge and the second is to utilize it. In or-

der to accomplish both, the KB is furnished with 4

operations, brieﬂy described below.

Insert. This is a TELL-type operation invoked by an

agent to add knowledge to the KB. The knowledge

can be a new rule or experience for an already

existing rule. If a new rule is to be added, then

it added directly to the last level in a node with

Towards Knowledge-Augmented Agents for Efﬁcient and Interpretable Learning in Sequential Decision Problems

1017

application and successes numbers equal zero.

However, if experience is to be incorporated and

it is not contradictory, only the numbers of appli-

cation and successes are updated. In the case of

contradictory evidence, which may occur if a dif-

ferent best action for the same state is learned, the

old rule and its credibility are updated, and the

numbers of application and successes are reset.

Infer. This is an ASK-type operation to apply an in-

ference method for detecting implicit knowledge

in the KB. This operation adds the implicit knowl-

edge to the graph in the form of nodes as described

above in level i if they were inferred from rules in

nodes in level i + 1, where 0 ≤ i ≤ m and m is the

number of sensors of the agent. The addition of a

new node n

new

is accompanied by the addition of

directed edges from this node to each of the nodes

from which its rule was inferred. An edge is also

added from the node n

old

that was already con-

nected to these nodes, used in the inference pro-

cess, to n

new

, whereas the old edges are removed.

Thus, the implicit knowledge becomes explicit.

Search. This is an ASK-type operation for knowl-

edge present explicitly in the KB. The pattern to

be matched is the discretized state of the envi-

ronment, which is always a superset of the an-

tecedent of each rule. Searching the graph hap-

pens in a top-down manner, starting from the util-

ity node and moving down level by level. If sev-

eral matches are found in a single level, the tie

is broken by comparing the credibility measures

or the weights of each rule and only the subgraph

connected to the rule with the highest credibility

is further searched.

Prune. This is a utility operation to prevent clutter-

ing the KB with unnecessary knowledge. A rule

becomes redundant when there exists an inferred

rule that subsumes it. Therefore, the node that

contains the redundant rule should be removed.

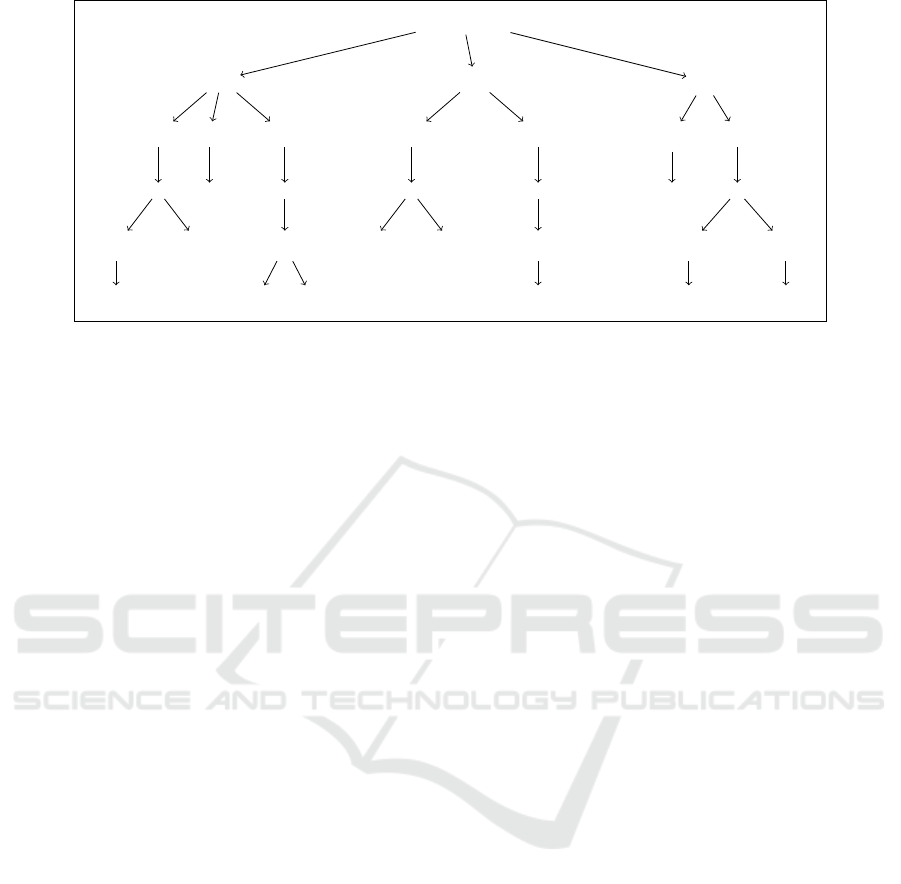
Figure 2 is an example that gives a concrete illus-

tration of the expected result of applying these oper-

ations on the learned policy by an agent in a 4x4 en-

vironment that is trying to reach the cell marked with

an “X” while avoiding obstacles, where again for sim-

plicity only the material implication in each node is

shown. The agent in this environment has two sen-

sors; one for the horizontal axis and the other for the

vertical axis. The arrows representing the consequent

of every rule give the direction the agent should fol-

low when in the state represented by the antecedent of

the same rule. Rules in the bottom level, which rep-

resent full states, are not pruned when they cannot be

subsumed by other rules in a higher level.

e f g h

a ↓ ↓

b ↓ ↓

c → → → ↓

d X

(a)

⊥ =⇒ >

e =⇒ ↓

c ∧ e =⇒ →

c =⇒ →

c ∧ h =⇒ ↓

g =⇒ ↓

c ∧ g =⇒ →

(b)

Figure 2: An example of a 2D environment (2a) and its cor-

responding KB (2b).

Usually the most expensive operations are the

ones concerned with utilizing knowledge and these

correspond to the ASK-type operations: infer and

search. By representing the knowledge in a layered

graph that is also directed and acyclic, we can greatly

improve the complexity of search, because intuitively

once the search goes from a level to the one below

it, many nodes would be disqualiﬁed without inspec-

tion of their contents. However, the structure does

not improve the complexity of the inference proce-

dure that much by itself; the graph will be built from

the bottom layer upwards using the experience of the

agent directly and at any given time when the infer-

ence procedure should be run, all nodes in a certain

level will be considered. Therefore, it is our inten-

tion to invoke the infer operation at regular intervals

separated by several learning episodes to prevent the

inference procedure from consuming resources when

the observed knowledge has not changed by much.

After the graph has been partially built, it can be con-

sulted by the agent to speed up the learning of the

optimal policy.

5 CONCLUSIONS

Solutions for sequential decision problems that scale

well and remain transparent to a degree must incor-

porate both components of a neurosymbolic system.

The data-driven component enables learning through

perception and the symbolic component endows the

system with cognitive power. We have argued that the

presence of knowledge in a KB allows the solver of a

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1018

sequential decision problem to reason in order to gen-

eralize faster and in a more interpretable manner.

In consequence, we proposed a solution for prob-

lems that are fully observable in the form of such a

system of two components. The reasoning compo-

nent will make use of a KB organized as a layered

directed acyclic graph and after a sufﬁcient period of

learning and generalization the learner will turn to the

KB to expedite the process of learning the optimal

policy. This is analogous to capitalizing on memory

of past experience, that forms the cognitive abilities of

the solver, in the face of the unknown, which is much

better than facing the unknown with high hopes.

We are currently investigating extensions of the

proposed neuro-symbolic framework to partially ob-

servable environments and the integration of addi-

tional cognitive elements in the KB. Furthermore, we

are exploring enhancing the efﬁciency of the inferen-

tial procedures in the proposed KB structure. Ad-

ditionally, we plan to conduct empirical validations

across diverse problem domains to provide insights

into the broader applicability and robustness of the

proposed approach, paving the way for advancements

in neuro-symbolic systems for artiﬁcial intelligence

applications.

REFERENCES

Agarwal, R., Machado, M. C., Castro, P. S., and Bellemare,

M. G. (2021). Contrastive behavioral similarity em-

beddings for generalization in reinforcement learning.

Apeldoorn, D. and Kern-Isberner, G. (2017). An agent-

based learning approach for ﬁnding and exploiting

heuristics in unknown environments. In International

Symposium on Commonsense Reasoning.

Apeldoorn, D. and Kern-Isberner, G. (2017). Towards an

understanding of what is learned: Extracting multi-

abstraction-level knowledge from learning agents. In

Rus, V. and Markov, Z., editors, Proceedings of the

Thirtieth International Florida Artiﬁcial Intelligence

Research Society Conference, FLAIRS 2017, Marco

Island, Florida, USA, May 22-24, 2017, pages 764–

767. AAAI Press.

Barto, A. G. and Mahadevan, S. (2003). Recent advances

in hierarchical reinforcement learning. Discrete Event

Dynamic Systems, 13:41–77.

Barto, A. G., Sutton, R. S., and Watkins, C. (1989). Sequen-

tial decision problems and neural networks. Advances

in neural information processing systems, 2.

Brachman, R. and Levesque, H. (2004). Knowledge Rep-

resentation and Reasoning. The Morgan Kaufmann

Series in Artiﬁcial Intelligence. Morgan Kaufmann,

Amsterdam.

Christoffersen, P. J. K., Li, A. C., Icarte, R. T., and McIl-

raith, S. A. (2023). Learning symbolic representations

for reinforcement learning of non-markovian behav-

ior.

Evans, J. S. B. T. and Stanovich, K. E. (2013). Dual-process

theories of higher cognition: Advancing the debate.

Perspectives on Psychological Science, 8(3):223–241.

PMID: 26172965.

Guan, L., Sreedharan, S., and Kambhampati, S. (2022).

Leveraging approximate symbolic models for rein-

forcement learning via skill diversity.

Kaelbling, L. P., Littman, M. L., and Moore, A. W.

(1996). Reinforcement learning: A survey. CoRR,

cs.AI/9605103.

Kautz, H. (2020). Rochester hci. https://roc-hci.com/

announcements/the-third-ai-summer/. Accessed on

January 6th, 2024.

Landajuela, M., Petersen, B. K., Kim, S., Santiago, C. P.,

Glatt, R., Mundhenk, N., Pettit, J. F., and Faissol, D.

(2021). Discovering symbolic policies with deep re-

inforcement learning. In Meila, M. and Zhang, T.,

editors, Proceedings of the 38th International Con-

ference on Machine Learning, volume 139 of Pro-

ceedings of Machine Learning Research, pages 5979–

5989. PMLR.

Ledentsov, A. (2023). Knowledge base reuse with frame

representation in artiﬁcial intelligence applications.

IAIC Transactions on Sustainable Digital Innovation

(ITSDI), 4(2):146–154.

Sutton, R. S. (1988). Learning to predict by the methods of

temporal differences. Mach. Learn., 3(1):9–44.

Sutton, R. S., Szepesv

ari, C., Geramifard, A., and Bowling,

M. P. (2012). Dyna-style planning with linear func-

tion approximation and prioritized sweeping. arXiv

preprint arXiv:1206.3285.

Yu, D., Yang, B., Liu, D., and Wang, H. (2021). A survey

on neural-symbolic systems. CoRR, abs/2111.08164.

Towards Knowledge-Augmented Agents for Efﬁcient and Interpretable Learning in Sequential Decision Problems

1019