Robust Long-Tailed Image Classiﬁcation via Adversarial Feature

Re-Calibration

Jinghao Zhang

1 a

, Zhenhua Feng

1 b

and Yaochu Jin

2 c

School of Computer Science and Electronic Engineering, University of Surrey, Guildford GU2 7XH, U.K.

School of Engineering, Westlake University, Hangzhou 310030, China

Keywords:

Deep Learning, Image Classiﬁcation, Adversarial Training, Long-Tailed Recognition.

Abstract:

Long-tailed data distribution is a common issue in many practical learning-based approaches, causing Deep

Neural Networks (DNNs) to under-ﬁt minority classes. Although this biased problem has been extensively

studied by the research community, the existing approaches mainly focus on the class-wise (inter-class) im-

balance problem. In contrast, this paper considers both inter-class and intra-class data imbalance problems for

network training. To this end, we present Adversarial Feature Re-calibration (AFR), a method that improves

the standard accuracy of a trained deep network by adding adversarial perturbations to the majority samples

of each class. To be speciﬁc, an adversarial attack model is ﬁne-tuned to perturb the majority samples by in-

jecting the features from their corresponding intra-class long-tailed minority samples. This procedure makes

the dataset more evenly distributed from both the inter- and intra-class perspectives, thus encouraging DNNs

to learn better representations. The experimental results obtained on CIFAR-100-LT demonstrate the effec-

tiveness and superiority of the proposed AFR method over the state-of-the-art long-tailed learning methods.

1 INTRODUCTION

Deep Neural Networks (DNNs) have achieved great

success in many practical computer vision tasks, e.g.,

image classiﬁcation (He et al., 2016; Tan and Le,

2019), object detection (Ren et al., 2015; Szegedy

et al., 2013), semantic segmentation (Girshick et al.,

2014; Long et al., 2015), etc. One key to the success

of the existing deep learning methods is the existence

of big and balanced training data. However, the train-

ing samples in many real-world datasets usually have

a long-tailed distribution across classes, where a small

number of classes have a huge number of samples but

the others only possess a few (Cui et al., 2019; Kang

et al., 2021; Liu et al., 2019; Menon et al., 2020).

Fig. 1 shows the sample distribution of the CIFAR-

100-LT dataset (with the imbalance factor of 0.01)

which is the long-tailed version of CIFAR-100. Such

imbalanced datasets can negatively impact the ﬁnal

performance of a trained DNN, which can easily over-

ﬁt to the majority classes with many training samples

so generalize poorly to minority classes (Cao et al.,

2019; Wang et al., 2020; Zhang et al., 2023).

https://orcid.org/0000-0001-5394-1814

https://orcid.org/0000-0002-4485-4249

https://orcid.org/0000-0003-1100-0631

Figure 1: The distribution of the number of class samples

of CIFAR-100-LT. The red and yellow histograms represent

the distributions of the feature embeddings of all the sam-

ples within the ‘apple’ and ‘chair’ classes, respectively.

In recent years, a variety of methods have

been proposed to deal with this long-tailed data

imbalance problem. These methods include re-

sampling (Chawla et al., 2002; Maciejewski and Ste-

fanowski, 2011; Oquab et al., 2014), class-sensitive

learning (Cui et al., 2019), logit adjustment (Menon

et al., 2020), transfer learning (Kang et al., 2021), data

augmentation (Kim et al., 2020; Liu et al., 2020), etc.

However, almost all the existing studies focus on the

inter-class long-tailed problem only. To the best of

our knowledge, no existing research tries to investi-

Zhang, J., Feng, Z. and Jin, Y.

Robust Long-Tailed Image Classiﬁcation via Adversarial Feature Re-Calibration.

DOI: 10.5220/0012432000003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 2: VISAPP, pages

213-220

ISBN: 978-989-758-679-8; ISSN: 2184-4321

213

Inter-class

Over

Sampling

With

Data Aug.

Majority Samples

…

Minority Samples

…

PGD

Fine

Tuning

Random

Attack (50%)

Original

Samples

New

Samples

Original Minority

Samples

…

Balanced

Data

Long-Tailed

Data

CutMix (25%)

…

Intra-class

Minority

Sample

Identification

Over-Sampled

Data

…

Figure 2: The proposed Adversarial Feature Re-calibration (AFR) pipeline for intra- and inter-class balancing. The term

‘PGD’ represents the Projected Gradient Descent (Madry et al., 2018a) for adversarial perturbation generation.

gate and address the intra-class long-tailed problem.

For a speciﬁc class in a training set, some samples

could be far away from the distribution of the major-

ity samples. In Fig. 1, the red and yellow histograms

illustrate the distances of the embeddings of the sam-

ples to their corresponding mean embeddings of the

‘apple’ and ‘chair’ classes, respectively. We can see

that the samples are not evenly distributed within a

class, which could further degrade the performance

of a trained DNN model.

Now the problem becomes ﬁnding the long-tailed

data in each class and balancing its distribution with-

out damaging the original learning process. To this

end, we propose a novel framework, namely Adver-

sarial Feature Re-calibration (AFR), that uses adver-

sarial examples to balance the training data of a class

with long-tailed distribution. It is well-known that the

prediction accuracy of a well-trained DNN is vulnera-

ble to adversarial perturbations (Madry et al., 2018b)

that are imperceptible to human eyes. To deal with

this challenge, many countermeasures have been de-

veloped to defend against adversarial perturbations.

Adversarial training (Kurakin et al., 2016) has be-

come the most widely applied method to improve the

adversarial robustness of a trained DNN model. It

uses augmented adversarial samples to improve the

robustness of a trained deep network against adver-

sarial attacks. Despite the problem caused by adver-

sarial perturbations, they also show useful features to

improve clean accuracy (Ilyas et al., 2019). A gener-

ated adversarial example preserves more features of

the attacked target label than its original label fea-

tures. This inspires us to use adversarial examples

in the proposed AFR method to balance long-tailed

intra-class data.

In the proposed AFR method, we ﬁrst use a pre-

trained model that solves the common inter-class

long-tailed problem. Speciﬁcally, we use Context-

rich Minority Oversampling (CMO) (Park et al.,

2022) as the pre-trained model. Then we use the pre-

trained model to project all the training samples into

their feature embeddings and propose an adaptive dis-

tance measure to distinguish the minority samples of

each class in the training set. Then, the minority sam-

ples are used to ﬁne-tune the Projected Gradient De-

scent (PGD) (Madry et al., 2018a) model that could

attack the pre-trained CMO network. The resulting

PGD model possesses a better understanding of mi-

nority samples and could be used to inject long-tailed

data features to the majority samples, resulting in an

intra-class balanced dataset. It should be noted that,

unlike most adversarial perturbations, the adversar-

ial examples generated in this method do not con-

tain toxic information to the clean accuracy of the

trained model. Last, we apply CutMix (Yun et al.,

2019) to the original long-tailed dataset and the aug-

mented dataset with both oversampled (with standard

data augmentation method for inter-class balancing)

and adversarial samples (for intra-class balancing) to

generate a balanced dataset set for ﬁne-tuning the pre-

trained CMO network. Fig. 2 illustrates the intra- and

inter-class long-tailed data balancing pipeline of the

proposed AFR method.

In summary, the main contributions of the pro-

posed AFR method include:

• We propose a novel framework that performs

intra-class balancing for the long-tailed image

classiﬁcation task. To the best of our knowledge,

this is the ﬁrst work that considers both intra- and

inter-class balancing in image classiﬁcation.

• We develop a class-wise minority sample identi-

ﬁcation method that adaptively splits the training

samples of each class into ‘majority’ and ‘minor-

ity’ samples for intra-class balancing.

• We propose to apply adversarial attacks to re-

calibrate the intra-class distribution by injecting

minority features into majority samples. This

helps to improve the performance of a trained

DNN on long-tailed data.

The rest of the paper is organized as follows. We

ﬁrst introduce the related work in Section 2. Then we

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

214

present the proposed AFR method in Section 3. Last,

we report the experimental results in Section 4, and

the conclusion is drawn in Section 5.

2 RELATED WORK

In this section, we introduce the most relevant studies

in long-tailed learning and adversarial training.

2.1 Long-Tailed Learning

Regular neural network training learns features from

randomly sampled datasets. However, researchers

have identiﬁed that traditional algorithms tend to fa-

vor the majority classes if the dataset is unbalanced,

resulting in poor performance of minority classes (Cui

et al., 2019; Kang et al., 2021; Liu et al., 2019;

Menon et al., 2020; Zhang et al., 2023). This has

motivated the development of specialized techniques

to handle class imbalance, such as data re-sampling,

cost-sensitive learning, and data augmentation. These

techniques aim to re-balance the class distribution and

give more emphasis to the tail classes during training.

Re-sampling (Liu et al., 2008) was proposed

to solve this problem by increasing (over-sample)

or decreasing (under-sample) the number of each

class’s samples in each batch during network train-

ing. Over-sampling (Chawla et al., 2002; Estabrooks

et al., 2004) techniques duplicate or generate syn-

thetic samples from the minority classes to increase

their representation in the dataset. This could re-

sult in overﬁtting to minority classes because the mi-

nority information in the dataset is lacking. Under-

sampling (Tomek, 1976) techniques reduce the num-

ber of samples from the majority classes to balance

the class distribution. But it would waste a lot of data

in the majority class.

Conventional DNNs use softmax cross-entropy

loss that ignores the imbalance distribution. A pos-

itive sample of one class could be regarded as a

negative sample of other classes. So that major-

ity classes have more supporting gradients than the

minority classes. Re-weighting techniques multiply

the training loss of different classes with different

weights (Huang et al., 2016; Wang et al., 2017). Some

multi-stage methods (Alshammari et al., 2022; Kang

et al., 2019) decouple the training of a classiﬁer on

long-tailed datasets. The idea is to ﬁrst obtain a de-

cent feature extractor and then adjust the feature ex-

tractor and ﬁne-tune the classiﬁer.

As another solution to the data imbalance prob-

lem, data augmentation has been widely used to in-

crease the quality and quantity of the tail data. Reg-

ular data augmentation methods include contrast and

brightness adjustment, image translation, image crop-

ping, image rotation, etc., as well as the recently

proposed data enhancement methods such as copy-

paste (Ghiasi et al., 2021), MixUp (Zhang et al.,

2018), mosica (Ge et al., 2021), etc. One way of

data augmentation in long-tailed learning is transfer-

based augmentation. This method tries to transfer

knowledge from the majority classes to the minor-

ity classes. Major-to-minor translation (M2m) (Kim

et al., 2020) presents an augmentation procedure by

adding adversarial perturbations to the majority class

samples. The perturbed samples containing minority

class features can build a more balanced training set.

In contrast to M2m, the proposed Adversarial Feature

Re-calibration (AFR) method considers the inter- and

intra-class imbalance problems simultaneously.

2.2 Adversarial Training

Adversarial perturbations have become a major threat

to DNNs since they can fool a trained network and in-

tentionally cause wrong prediction results. Fast Gra-

dient Sign Method (FGSM) (Goodfellow et al., 2015)

is the most widely-used one-step-gradient-based at-

tack method. It obtains the label of an input image

predicted by the target model and computes its loss

based on its corresponding ground-truth label. Then

FGSM calculates the gradients of the loss with respect

to the image. Last, it generates the adversarial exam-

ple based on the sign of the gradients. Unlike FGSM

which is completed in one optimization iteration, the

Projected Gradient Descent (PGD) method is a typ-

ical iterative-gradient-based attack that can generate

the highest degree of adversarial examples that maxi-

mizes the loss of a classiﬁcation model (Madry et al.,

2018a). After each step of perturbation, PGD projects

the adversarial noise back into the L

∞

norm ball of the

input image in this step.

Various types of approaches have been studied

to make DNNs more robust to adversarial attacks.

Adversarial training (Madry et al., 2018b; Kurakin

et al., 2016) is the most effective method for defend-

ing against adversarial attacks. The idea of adversar-

ial training is very simple and straightforward. It re-

places the training datasets with the adversarial sam-

ples generated by an adversarial attack algorithm. The

trained model can then learn the features of the in-

jected adversarial examples and improve its robust-

ness against adversarial attacks.

The objective function used by most of the

existing state-of-the-arts adversarial training algo-

rithms (Ding et al., 2019; Rony et al., 2019; Sinha

Robust Long-Tailed Image Classiﬁcation via Adversarial Feature Re-Calibration

215

et al., 2018; Zhang et al., 2019) is:

argmin

(x,y)∼D

[max

ε∈S

L (θ, x + ε, y)], (1)

where L (·, ·, ·) is the loss function, θ is the network

parameter, ε ∈ R

C×H×W

is the perturbation and S is

the allowed perturbation range, D is the underlying

data distribution, x ∈ R

C×H×W

is input image and y ∈

is its corresponding ground truth label.

The long-tailed image classiﬁcation problem can

be regarded as the lack of information in the tail

classes. Previous studies have found that adversar-

ial examples contain more features of the target label

rather than original labels (Ilyas et al., 2019). There-

fore our method generates samples that contain more

minority features by applying adversarial attacks to

majority samples of the same class for intra-class data

balancing.

3 THE PROPOSED METHOD

In this section, we present the proposed Adversar-

ial Feature Re-calibration (AFR) method, which aims

to solve the long-tailed image recognition task by

considering data imbalance of both inter- and intra-

class distributions. To be speciﬁc, we use adver-

sarial perturbations to re-calibrate the intra-class dis-

tribution. While adversarial examples could cause

misclassiﬁcation, they contain strong features of

their corresponding attack target labels (Ilyas et al.,

2019). Based on this observation, we propose a data-

balancing solution via adversarial attack.

Given a long-tailed training dataset, the proposed

AFR method has the following main steps:

1. We ﬁrst use a pre-trained model that is trained

with a general long-tailed learning method. In

this paper, we use Context-rich Minority Over-

sampling (CMO) (Park et al., 2022) as the pre-

trained model. This model deals with the inter-

class imbalance problem.

2. Second, we over-sample the long-tailed class

samples with data augmentation and project them

to their feature embeddings by the forward pass of

CMO. Then an adaptive intra-class discrimination

function is used to split the samples of each class

into majority and minority samples.

3. Third, we ﬁne-tune an attack model on the minor-

ity samples of all the classes. In this paper, we use

the Projected Gradient Descent (PGD) (Madry

et al., 2018a) model. The aim is to generate adver-

sarial samples from majority samples that contain

minority features. We add the generated adver-

Training

Samples

Pre-Trained

CMO

Feature

Embedding

…

Distance

Measure

: Majority

: Minority

…

Figure 3: Illustration of long-tailed sample identiﬁcation.

sarial samples to each class to balance intra-class

samples.

4. Last, we ﬁne-tune the CMO model on the intra-

and inter-class balanced training set to obtain the

ﬁnal network.

In the rest of this section, we ﬁrst present the met-

ric that identiﬁes the long-tailed samples in each class.

Then, we introduce how to generate samples contain-

ing features from minority classes. Last, we propose

an adaptive algorithm to adjust the threshold of ma-

jority and minority samples dynamically.

3.1 Identifying Long-Tailed Samples

The training samples of each class in a typical long-

tailed dataset are usually heavily imbalanced in size,

which could vary up to 100:1. This inter-class im-

balance problem has been widely studied in the exist-

ing literature. In this paper, we use CMO as a pre-

trained model to address this problem. However, for

each class, we argue that the training samples are not

evenly distributed. One way to ﬁx this intra-class data

imbalance issue is to generate new minority samples

for data augmentation. However, unlike inter-class

long-tailed problems that directly regard the number

of classes as the measurement of imbalance, we do

not have an obvious metric to decide which sample

is a minority (long-tailed sample) in each class. To

generate more minority samples from majority sam-

ples by adversarial attack, we need to ﬁrst separate

the samples of each class into majority and minority

samples.

A simple solution to the above problem is to cal-

culate the distance of the feature embedding of a sam-

ple to the mean feature embedding of a class. Fig. 3

shows the pipeline to separate the majority from the

minority. First, we get the feature embeddings of

all the training samples from the pre-trained CMO

model, which are the outputs of CMO before the

last fully connected layer. We use the embedding

of each sample instead of the raw image because its

embedding shows a more meaningful representation.

The embedding of similar images should be close to

each other, and visually different images should be far

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

216

away in the embedding space. Then a threshold λ is

set to decide the sample boundary of each class. We

label samples beyond λ as the long-tailed data (minor-

ity) and samples within λ as the majority. The label

of each sample L(x) is deﬁned as follows:

L(x) =



0 if cos(e

, e

) < λ

1 otherwise

, (2)

where e

is the embedding of the sample, e

is the

mean embedding of all the samples in the class of x,

cos(, ) is the Cosine similarity distance. The labels

0 and 1 represent the majority and minority classes,

respectively. The choice of λ is adaptive, which will

be introduced in Section 3.3.

3.2 Re-Balancing Data Distribution

In Fig. 2, we demonstrate the pipeline of the re-

balancing procedure. Given a long-tailed training

dataset, we ﬁrst use normal inter-class over-sampling

with data augmentation to perform inter-class bal-

ancing. Then we use the approach speciﬁed in Sec-

tion 3.1 to identify intra-class majority and minority

samples of each class. Next, we ﬁne-tune the PGD

model on the minority samples to attack the major-

ity samples to their corresponding minority ones in

each class. Note that, we cannot directly generate ad-

versarial examples of the same class using the pre-

trained CMO model because we cannot deliberately

generate the minority adversarial perturbation. The

key idea of ﬁne-tuning PGD is to consider the minor-

ity and majority samples in a class as two categories.

Therefore, we modify the standard adversarial attack

step of PGD and restrict the generated adversarial per-

turbation towards the minority of each class. Then

we use the ﬁne-tuned PGD model to attack 50% of

the majority samples randomly. This procedure cali-

brates the majority dataset toward the minority distri-

bution but still keeps the features of the original sam-

ples, which is different from the classic re-sampling

approaches (Chawla et al., 2002; Liu et al., 2008)

that could make the trained DNNs overﬁtting towards

head or tail classes.

Now we obtain a new dataset consisting of both

original samples and adversarial samples which has

an equal sample size across all the classes. We fur-

ther apply CutMix (Yun et al., 2019) to 25% of the

original long-tailed dataset with the new dataset to ob-

tain an intra- and inter-class balanced dataset. CutMix

combines two images by directly replacing part of the

image with a patch from the other image. The combi-

nation ratio between two images is sampled from the

beta distribution Beta(α, α). By default, we set α to

1. Last, we ﬁne-tune the pre-trained CMO model on

the balanced dataset as the ﬁnal network.

3.3 Adaptive Class-Wise Re-Balancing

In Section 3.1, we introduced a method that could

identify the minority samples of each class in the

dataset. However, just like the general class imbal-

ance problem, each class may have different classi-

ﬁcation accuracy during the training stage. In this

case, we need to set different thresholds λ for various

classes.

To this end, we introduce an adaptive class-wise

threshold decision strategy. The individual accuracy

of each class is recorded just before identifying the

minority or majority samples. We tried various com-

plicated strategies and found that simply using in-

dividual class accuracy a

achieves the best results.

While the training accuracy a

train

reaches a certain

level (between 60% to 70%), the threshold of each

class is set to λ or a

depending on the condition. λ

is a hyperparameter and we set it to 0.8 in advance. If

of the ith class is lower than a

train

, the threshold λ

is set to a

. Otherwise, we keep the threshold λ still.

This adaptive procedure allocates a more precise

majority-minority sample split of each class instead

of a ﬁxed threshold. Hence, ‘harder’ classes tend to

keep more original samples to learn the class minority

distribution, and ‘easier’ classes have more attacked

samples to enhance the classiﬁcation boundary.

4 EXPERIMENTAL RESULTS

4.1 Implementation Details

Dataset. We evaluate the proposed method on

CIFAR-100-LT, which is a subset of the CIFAR-

100 (Krizhevsky et al., 2009) dataset. CIFAR-100

consists of 60000 32x32 color images of 100 classes.

Each class has 500 training samples and 100 test sam-

ples. CIFAR-100-LT is created by reducing the train-

ing samples of CIFAR-100 with an imbalance fac-

tor that indicates the ratio between the class with the

smallest sample size and the class with the largest

sample size. In this paper, the imbalance factor is set

to 0.01.

Experimental Settings. We use ResNet32 (He et al.,

2016) as the backbone network. In our AFR method,

we ﬁrst train the CMO model for 200 epochs in the

ﬁrst stage with only inter-class balancing. Then we

ﬁne-tune it for 50 epochs in the second stage with the

proposed balancing strategy. The batch size is set to

128. The optimizer is SGD with a momentum of 0.9

and a weight decay of 2e-4. The learning rate starts at

0.1 and decays by a factor of 1e-2 at epoch 160 and

1e-4 at epoch 180. For training data augmentation,

Robust Long-Tailed Image Classiﬁcation via Adversarial Feature Re-Calibration

217

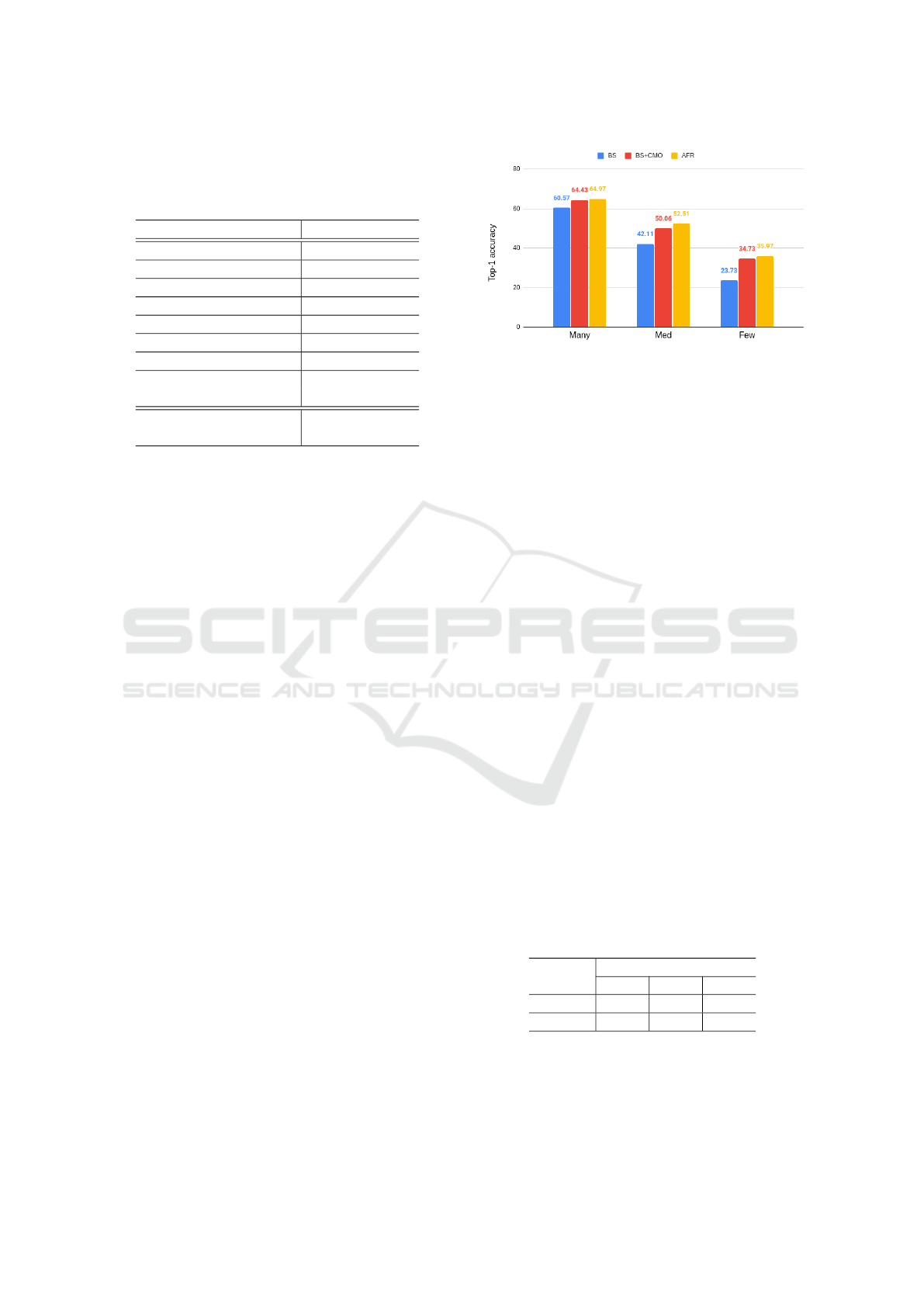
Table 1: A comparison between the proposed AFR method

with other state-of-the-art solutions, evaluated in the Top-1

accuracy on CIFAR-100-LT (Imbalance factor = 0.01). “*”

indicates the results reported in (Park et al., 2022).

Method Top-1 Accuracy

Cross Entropy (CE) 38.96

CE-DRW 41.43

LDAM-DRW* 41.70

Balanced Softmax (BS) 43.18

IB Loss* 45.00

Remix* 45.80

MiSLAS* 47.00

BS+CMO (200 epochs) 46.13

BS+CMO (400 epochs) 50.49

Our AFR (200 epochs) 47.32

Our AFR (400 epochs) 51.91

we use random crop, horizontal ﬂip, AutoAugment

& CutOut in the ﬁrst stage and only random crop &

horizontal ﬂip in the second stage.

We adopt Projected Gradient Descent

(PGD) (Madry et al., 2018a) as the adversarial

attack method to generate adversarial examples (on

the ﬂy) in the second stage for every 10 epochs. For

PGD, the perturbation size ε is set to 0.6, the number

of iterations is 3 and the attack step size is 1/255.

The methods are all evaluated in terms of the best

Top-1 Accuracy.

4.2 Performance Evaluation

We ﬁrst compare the proposed method with exist-

ing over-sampling, over-weighting, and other state-

of-the-art long-tailed solutions on the CIFAR-100-LT

dataset. Those methods include:

• Remix (Chou et al., 2020) uses Mixup to over-

sample minority classes.

• Deferred re-weighting (DRW) (Cao et al., 2019)

ﬁne-tunes the classiﬁer’s balance.

• Balanced Softmax (BS) (Ren et al., 2020) modi-

ﬁes the Softmax to make it unbiased.

• The Label-distribution-aware margin (LDAM)

loss (Cao et al., 2019) increases the minorities’

margins to the decision boundary.

• The Inﬂuence-balanced (IB) loss (Park et al.,

2021) re-weights samples base on their inﬂuences.

• MiSLAS (Zhong et al., 2021) enhances classiﬁer

learning and calibration during the training stage

via label-aware smoothing.

• The state-of-the-art Context-rich Minority Over-

sampling (CMO) (Park et al., 2022) method trans-

fers rich information from the majority to the

Figure 4: A comparison of the proposed AFR method with

the state-of-the-art ‘BS’ and ‘BS+CMO’ approaches on dif-

ferent subsets of CIFAR-100-LT (Imbalance factor = 0.01).

minority to overcome the inter-class long-tailed

problem using CutMix.

The imbalance factor of CIFAR-100-LT is set to

0.01 to validate our method under strong unbalanced

circumstances. Table 1 shows the image classiﬁca-

tion performance of the aforementioned methods, as

well as the proposed method. Our method does not

present an obvious improvement to MiSLAS under

the default setting of 200 epochs. But when we ex-

tend the training epochs to 400, the proposed AFR

method achieves 51.91% Top-1 Accuracy, which is

signiﬁcantly better than that of MisLAS and CMO.

We also report the Top-1 accuracy on three sub-

sets of CIFAR-100-LT: ‘Many’ (over 100 training im-

ages), ‘Med’ (20-100 training images), and ‘Few’

(under 20 training images) in Fig. 4. AFR achieves

the best accuracy for all the subsets, especially in

the Med and Few subsets. This is because there are

enough samples in the ‘Many’ subset so our method

could not provide more useful information. How-

ever, there are not sufﬁcient samples in the ‘Med’ and

‘Few’ subsets. Simply over-sampling/over-weighting

does not give more diverse or useful features. AFR

generates more minority features which was rare in

the original dataset, so the performance improvement

is more signiﬁcant.

Table 2: A comparison of applying different CutMix and

MixUp proportion on CIFAR-100-LT (Imbalance factor =

0.01) after 400 epochs.

Method

Propotion

0.25 0.5 1

CutMix 51.91 51.74 51.24

MixUp 51.65 51.21 51.14

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

218

4.3 Ablation Study

We apply an ablation study on the CIFAR-100-LT

dataset to investigate the effect on our proposed

method. In Table 2, we report the results obtained

by AFR with different data augmentation and propor-

tions to apply. MixUp (Zhang et al., 2018) and Cut-

Mix are the two choices of data augmentation used

in the second stage of AFR to fuse the original long-

tailed data and the new dataset with adversarial sam-

ples into a balanced dataset. MixUp generates mixed

images by linearly interpolating two images and their

corresponding labels of different classes. The mix-

ing ratio is also sampled from the beta distribution

Beta(1, 1). We gradually changed the percentage of

MixUp and CutMix to ﬁnd the optimal spot. The re-

sults illustrate that applying CutMix to 25% of the

long-tailed samples could get the best performance.

5 CONCLUSION

In this paper, we proposed the Adversarial Feature

Re-calibration (AFR) method to ﬁx the long-tailed

problem in image classiﬁcation. The existing stud-

ies focus on the imbalance number of samples among

different classes via over-sampling, over-weighting,

or other techniques, but do not consider the imbal-

ance within each class. To overcome this limitation,

we investigated the distribution and re-calibrated the

balance of each class in our AFR method. The experi-

mental results obtained on the CIFAR-100-LT dataset

indicate that AFR achieves signiﬁcantly better Top-1

accuracy than the existing state-of-the-art approaches.

The proposed method further veriﬁes that, in real-

world scenarios, the long-tailed problem exists not

only among different classes but also in each class.

This should be further considered in future research

on long-tailed data learning tasks.

REFERENCES

Alshammari, S., Wang, Y.-X., Ramanan, D., and Kong, S.

(2022). Long-tailed recognition via weight balancing.

In IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 6897–6907.

Cao, K., Wei, C., Gaidon, A., Arechiga, N., and Ma, T.

(2019). Learning imbalanced datasets with label-

distribution-aware margin loss. Advances in Neural

Information Processing Systems (NeurIPS), 32.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: synthetic minority over-

sampling technique. Journal of artiﬁcial intelligence

research, 16:321–357.

Chou, H.-P., Chang, S.-C., Pan, J.-Y., Wei, W., and Juan, D.-

C. (2020). Remix: rebalanced mixup. In European

Conference on Computer Vision (ECCV), pages 95–

110.

Cui, Y., Jia, M., Lin, T.-Y., Song, Y., and Belongie, S.

(2019). Class-balanced loss based on effective number

of samples. In IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 9268–9277.

Ding, G. W., Sharma, Y., Lui, K. Y. C., and Huang, R.

(2019). Mma training: Direct input space margin

maximization through adversarial training. In In-

ternational Conference on Learning Representations

(ICLR).

Estabrooks, A., Jo, T., and Japkowicz, N. (2004). A multi-

ple resampling method for learning from imbalanced

data sets. Computational intelligence, 20(1):18–36.

Ge, Z., Liu, S., Wang, F., Li, Z., and Sun, J. (2021).

Yolox: Exceeding yolo series in 2021. arXiv preprint

arXiv:2107.08430.

Ghiasi, G., Cui, Y., Srinivas, A., Qian, R., Lin, T.-Y., Cubuk,

E. D., Le, Q. V., and Zoph, B. (2021). Simple copy-

paste is a strong data augmentation method for in-

stance segmentation. In IEEE Conference on Com-

puter Vision and Pattern Recognition (CVPR), pages

2918–2928.

Girshick, R., Donahue, J., Darrell, T., and Malik, J. (2014).

Rich feature hierarchies for accurate object detection

and semantic segmentation. In IEEE Conference on

Computer Vision and Pattern Recognition (CVPR),

pages 580–587.

Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Ex-

plaining and harnessing adversarial examples. In

3rd International Conference on Learning Represen-

tations (ICLR).

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep

residual learning for image recognition. In IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 770–778.

Huang, C., Li, Y., Loy, C. C., and Tang, X. (2016). Learn-

ing deep representation for imbalanced classiﬁcation.

In IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 5375–5384.

Ilyas, A., Santurkar, S., Tsipras, D., Engstrom, L., Tran, B.,

and Madry, A. (2019). Adversarial examples are not

bugs, they are features. Advances in Neural Informa-

tion Processing Systems (NeurIPS), 32.

Kang, B., Li, Y., Xie, S., Yuan, Z., and Feng, J. (2021).

Exploring balanced feature spaces for representation

learning. In International Conference on Learning

Representations (ICLR).

Kang, B., Xie, S., Rohrbach, M., Yan, Z., Gordo, A., Feng,

J., and Kalantidis, Y. (2019). Decoupling representa-

tion and classiﬁer for long-tailed recognition. In In-

ternational Conference on Learning Representations

(ICLR).

Kim, J., Jeong, J., and Shin, J. (2020). M2m: Imbalanced

classiﬁcation via major-to-minor translation. In IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 13896–13905.

Robust Long-Tailed Image Classiﬁcation via Adversarial Feature Re-Calibration

219

Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple

layers of features from tiny images.

Kurakin, A., Goodfellow, I., and Bengio, S. (2016). Ad-

versarial machine learning at scale. arXiv preprint

arXiv:1611.01236.

Liu, J., Sun, Y., Han, C., Dou, Z., and Li, W. (2020). Deep

representation learning on long-tailed data: A learn-

able embedding augmentation perspective. In IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 2970–2979.

Liu, X.-Y., Wu, J., and Zhou, Z.-H. (2008). Exploratory

undersampling for class-imbalance learning. IEEE

Transactions on Systems, Man, and Cybernetics, Part

B (Cybernetics), 39(2):539–550.

Liu, Z., Miao, Z., Zhan, X., Wang, J., Gong, B., and Yu,

S. X. (2019). Large-scale long-tailed recognition in an

open world. In IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 2537–2546.

Long, J., Shelhamer, E., and Darrell, T. (2015). Fully con-

volutional networks for semantic segmentation. In

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 3431–3440.

Maciejewski, T. and Stefanowski, J. (2011). Local neigh-

bourhood extension of smote for mining imbalanced

data. In 2011 IEEE symposium on computational in-

telligence and data mining (CIDM), pages 104–111.

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and

Vladu, A. (2018a). Towards deep learning models re-

sistant to adversarial attacks. In International Confer-

ence on Learning Representations (ICLR).

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and

Vladu, A. (2018b). Towards deep learning models re-

sistant to adversarial attacks. In International Confer-

ence on Learning Representations (ICLR).

Menon, A. K., Jayasumana, S., Rawat, A. S., Jain, H., Veit,

A., and Kumar, S. (2020). Long-tail learning via logit

adjustment. arXiv preprint arXiv:2007.07314.

Oquab, M., Bottou, L., Laptev, I., and Sivic, J. (2014).

Learning and transferring mid-level image represen-

tations using convolutional neural networks. In IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 1717–1724.

Park, S., Hong, Y., Heo, B., Yun, S., and Choi, J. Y. (2022).

The majority can help the minority: Context-rich mi-

nority oversampling for long-tailed classiﬁcation. In

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 6887–6896.

Park, S., Lim, J., Jeon, Y., and Choi, J. Y. (2021). Inﬂuence-

balanced loss for imbalanced visual classiﬁcation.

In IEEE Conference on International Conference on

Computer Vision (ICCV), pages 735–744.

Ren, J., Yu, C., Ma, X., Zhao, H., Yi, S., et al. (2020). Bal-

anced meta-softmax for long-tailed visual recognition.

Advances in Neural Information Processing Systems

(NeurIPS), 33:4175–4186.

Ren, S., He, K., Girshick, R., and Sun, J. (2015). Faster

r-cnn: Towards real-time object detection with region

proposal networks. Advances in Neural Information

Processing Systems (NeurIPS), 28.

Rony, J., Hafemann, L. G., Oliveira, L. S., Ayed, I. B.,

Sabourin, R., and Granger, E. (2019). Decoupling

direction and norm for efﬁcient gradient-based l2 ad-

versarial attacks and defenses. In IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 4322–4330.

Sinha, A., Namkoong, H., and Duchi, J. (2018). Certifying

some distributional robustness with principled adver-

sarial training. In International Conference on Learn-

ing Representations (ICLR).

Szegedy, C., Toshev, A., and Erhan, D. (2013). Deep neu-

ral networks for object detection. Advances in Neural

Information Processing Systems (NeurIPS), 26.

Tan, M. and Le, Q. (2019). Efﬁcientnet: Rethinking model

scaling for convolutional neural networks. In Inter-

national Conference on Machine Learning (ICML),

pages 6105–6114.

Tomek, I. (1976). Two modiﬁcations of cnn. IEEE Trans-

actions on Systems, Man, and Cybernetics, SMC-

6(11):769–772.

Wang, X., Lian, L., Miao, Z., Liu, Z., and Yu, S. X.

(2020). Long-tailed recognition by routing di-

verse distribution-aware experts. arXiv preprint

arXiv:2010.01809.

Wang, Y.-X., Ramanan, D., and Hebert, M. (2017). Learn-

ing to model the tail. Advances in Neural Information

Processing Systems (NeurIPS), 30.

Yun, S., Han, D., Oh, S. J., Chun, S., Choe, J., and Yoo,

Y. (2019). Cutmix: Regularization strategy to train

strong classiﬁers with localizable features. In IEEE

Conference on International Conference on Computer

Vision (ICCV), pages 6023–6032.

Zhang, H., Cisse, M., Dauphin, Y. N., and Lopez-Paz, D.

(2018). mixup: Beyond empirical risk minimization.

In International Conference on Learning Representa-

tions (ICLR).

Zhang, H., Yu, Y., Jiao, J., Xing, E., El Ghaoui, L., and Jor-

dan, M. (2019). Theoretically principled trade-off be-

tween robustness and accuracy. In International Con-

ference on Machine Learning (ICML), pages 7472–

7482.

Zhang, Y., Kang, B., Hooi, B., Yan, S., and Feng, J. (2023).

Deep long-tailed learning: A survey. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence

(PAMI).

Zhong, Z., Cui, J., Liu, S., and Jia, J. (2021). Improving

calibration for long-tailed recognition. In IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 16489–16498.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

220