Alias-Free GAN for 3D-Aware Image Generation
Attila Szab
´
o
1
, Yevgeniy Puzikov
2
, Sahan Ayvaz
1
, Sonia Aurelio
2
,
Peter Gehler
2
, Reza Shirvany
2
and Malte Alf
1
1
Zalando SE, Switzerland
2
Zalando SE, Germany
Keywords:
GAN, NeRF, 3D-aware, Generative AI.
Abstract:
In this work we build a 3D-aware generative model that produces high quality results with fast inference times.
A 3D-aware model generates images and offers control over camera parameters to the user, so that an object
can be shown from different viewpoints. The model we build combines the best of two worlds in a very direct
way: alias-free Generative Adversarial Networks (GAN) and a Neural Radiance Field (NeRF) rendering,
followed by image super-resolution. We show that fast and high-quality image synthesis is possible with
careful modifications of the well designed architecture of StyleGAN3. Our design overcomes the problem
of viewpoint inconsistency and aliasing artefacts that a direct application of lower-resolution NeRF would
exhibit. We show experimental evaluation on two standard benchmark datasets, FFHQ and AFHQv2 and
achieve the best or competitive performance on both. Our method does not sacrifice speed, we can render
images at megapixel resolution at interactive frame rates.
1 INTRODUCTION
3D-aware image generative models aim to generate
2D images in a way that the viewpoint is control-
lable by the user, the camera parameters can be spec-
ified at inference time. Generative Adversarial Net-
works (GANs) (Goodfellow et al., 2014) can be used
to solve this task, where a generator is combined with
a renderer to produce an image. GAN training can
be unsupervised, only an image collection of unre-
lated samples and no ground truth labels are required.
However, there is no out-of-the-box solution, the task
is very challenging. The details of the GAN architec-
ture, the renderer and the 3D representation and the
interplay between these modules matter a lot. In this
work we propose a novel design for a 3D-aware GAN
that combines the best practices of modern 2D and
3D models. It is alias-free, produces high-resolution
results, is 3D-aware and has fast inference time.
The first 3D-aware GANs build on explicit 3D
representations, for example voxels (Gadelha et al.,
2017) and meshes (Szab
´
o et al., 2019). More re-
cent work (Chan et al., 2021), (Chan et al., 2022)
then used volumetric rendering and a Neural Radi-
ance Field (NeRF) (Mildenhall et al., 2022) renderer.
Compared to voxel- and mesh-based methods,
Figure 1: An example result of our model, three images
rendered under three different viewpoints that are manually
chosen. The images are of high-quality with no visible arte-
facts and high-resolution. Our 3D model is trained using
unlabelled 2D images without any knowledge of viewpoints
at training time. In contrast to previous work, it does not
employ any task-specific priors or regularization.
NeRF parameterisations offer more flexibility and
produce higher-quality images. Ideally, one would
just run a vanilla NeRF at a high resolution with
dense depth sampling. In principle, this could work
very well, but the computational cost and memory
requirements make this naive approach infeasible.
Thus, recent approaches were proposed to reduce
the requirements on computation and memory, e.g.
GIRAFFE (Niemeyer and Geiger, 2021b), where a
NeRF is used to render a feature map at a low res-
olution, followed by 2D super-resolution.
Rendering features at low resolution, however,
creates images artefacts. A slight change in the cam-
Szabó, A., Puzikov, Y., Ayvaz, S., Aurelio, S., Gehler, P., Shirvany, R. and Alf, M.
Alias-Free GAN for 3D-Aware Image Generation.
DOI: 10.5220/0012432700003660
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 2: VISAPP, pages
221-232
ISBN: 978-989-758-679-8; ISSN: 2184-4321
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
221

era viewpoint creates an wobbling effect in the im-
age. This wobbling effect is caused by aliasing ef-
fects that stem from the design of 2D convolution
networks. This aliasing effect motivated the work of
StyleGAN3 (Karras et al., 2021a), that was specifi-
cally designed be alias-free. In our work we take the
idea of (Karras et al., 2021a) and lift it to 3D. We show
that alias-free network can be lifted to 3D, thus we
can avoid the image artefacts. The empirical results
show that our model performs better or on par with
previous 3D-aware methods, that tried to address the
shortcomings with more complex components, such
as extra regularization terms.
Putting the ideas together, our model generates
images in three stages. First, we sample points on a
3D grid and apply alias-free convolutions on it, which
produces 3D feature grid. Second, the features are
processed with volumetric rendering, which techni-
cally is a weighted sum along the depth axis of the
3D grid. The result of the rendering is a low reso-
lution 2D grid (image) of a feature map. Finally, the
2D feature grid is supplied to the super-resolution net-
work, which is an alias-free 2D convolution network.
An example result can be seen in Figure 1, a sample
from our model using three different viewpoints.
The key contributions of this work are:
• We design and implement a novel alias-free 3D-
aware generative model that combines state of the
art NeRF and GAN components.
• Quantitative results show that our approach
achieves state-of-the-art (SOTA) and competitive
results on FFHQ and AFHQv2 on high resolu-
tions, while having interactive frame rates.
• Qualitatively we show viewpoint consistency
when we control variables such as appearance,
horizontal and vertical translation and rotation.
2 RELATED WORK AND MODEL
PRELIMINARIES
Different types of 3D-aware generative models ex-
ist, prominent examples are autoencoders (Shi et al.,
2021), diffusion models (Poole et al., 2022) (Kim and
Chun, 2022) (Wang et al., 2022) and GANs. The
GAN architecture (Szab
´
o et al., 2019) (Kwak et al.,
2022) (Chan et al., 2022) (Xue et al., 2022) (Sun et al.,
2022) remains a strong contender in this space and is
the model of choice for our construction. In this sec-
tion we quickly review the main ingredients for this
model and in Section 3 explain our 3D extension.
2.1 GAN
A GAN consists of a pair of neural networks, a gen-
erator G and a discriminator D that compete during
training. The generator network produces novel im-
ages and the discriminator network is trained to distin-
guish between real and generated images. The origi-
nal loss function from (Goodfellow et al., 2014) is a
min-max objective
min
G
max
D
E
x
real
[log(D(x
real
)] +
E
z
[log(1 −D(G(z))], (1)
where the training images are drawn from the real im-
age distribution x
real
∼ p
real
, the latent vectors are usu-
ally drawn from a Normal distribution z ∼N (0,I). In
theory, with perfect training, the generator learns the
create samples x
fake
= G(z) from the data distribu-
tion that are indistinguishable from real data points.
In practice, however, quite some engineering and net-
work design is required to train the models to achieve
good performance, e.g. trading off learning rates of
the generator and discriminator.
Several GAN variants have been propsed since
the inception and the Alias-Free GAN (Karras et al.,
2021a) is a modern variant that produces high-
quality images and includes equivariance properties
(especially, the StyleGAN3-R variant). Intuitively,
StyleGAN3-R emulates an implicit representation,
similar to a neural network applied to each pixel lo-
cation separately, which gives the RGB pixel color.
StyleGAN3-R operates on a band limited continu-
ous signals, but represents them as a discrete 2D
grid based on the Nyquist–Shannon sampling theo-
rem (Shannon, 1949). When a nonlinear function is
applied to a band limited signal, the result is not nec-
essarily band-limited. Thus, one can define an alias-
free non linear function by filtering the result of the
vanilla non-linear function f with a low-pass filter. In
the discrete domain the alias-free F function is
F(Z) = s
2
·X ⊙(φ
s
∗ f (φ
s
∗Z)), (2)
where Z is the sampling grid, s is the sampling rate,
φ
s
is the ideal low-pass filter with band limit s/2, X
is the Dirac comb, ⊙ denote element-wise multipli-
cation and ∗ is continuous convolution. StyleGAN-R
uses radially symmetrical jinc filters to achieve rota-
tional equivariance. Notice, that this operation can
only be performed by entering temporarily the con-
tinuous domain. However, in practice it is enough to
approximate it by first upsampling, then applying the
vanilla function f , and finally downsampling.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
222

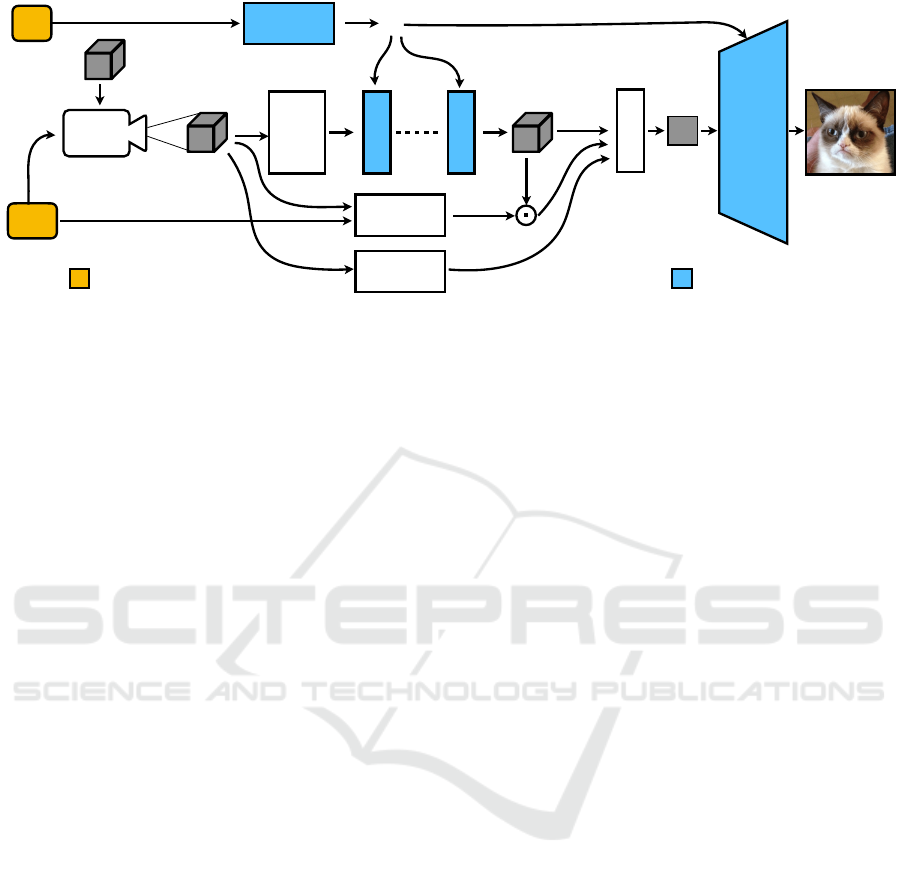
K, M
Fourier!
Features
p
w
AFConv
1
AFConv
r
f
r
Renderer
Mask
f
r+1
point!
casting
p
ndc
Superr-resolution!
Network
Distance
Mapping
z
w
x
fake
f
r
1
trainable networksgenerator inputs
Figure 2: Our generator takes the latent z and the intrinsic and extrinsic camera parameters K and M. 3D points are sampled
on a grid, then Fourier features are computed on them, which go through the alias-free 3D convolutional layers. Then the
features are rendered and passed to the super-resolution network to get the image as an output.
2.2 3D-Aware GAN
A 3D-aware GAN (Szab
´
o et al., 2019) can control
camera viewpoints by means of generator condition-
ing. More precisely, it takes the intrinsic and extrinsic
camera parameters K and M, respectively, as inputs.
The training objective now includes terms of camera
parameters and reads
min
G
max
D
E
x
real
[log(D(x
real
)] +
E
z,K,M
[log(1 −D(G(z,K, M))]. (3)
The camera parameters K,M are either sampled
from a fixed distribution (as in our work) or a
viewpoint distribution can be learned alongside the
netwroks (Niemeyer and Geiger, 2021a).
An image generator is now composed of a neural
network NN that produces a 3D representation (e.g. a
mesh), followed by a renderer R that takes the 3D rep-
resentation and camera parameters and produces the
image. As for all GAN models, optionally, a super-
resolution network can be used to upscale the image:
x
fake
= G(z,K,M)
= SuperRes(R(NN(z),K,M)). (4)
In order to train a generative model of 3D shapes from
natural 2D images, 3D GANs exploit the idea that
a realistic 3D object should yield a realistic render-
ing from any plausible viewpoint. By randomizing
the choice of the viewpoint, model training forces the
generator network to learn a 3D representation dis-
entangled from the viewpoint. The work of (Szab
´
o
et al., 2019) provides a theory for such systems, which
is a special case of a general theory of Ambient-
GAN (Bora et al., 2018).
This design then offers several possibilities re-
garding the choice of the 3D representation. One
can use meshes (Szab
´
o et al., 2019), voxels (Gadelha
et al., 2017) (Schwarz et al., 2022), multi-plane im-
ages (Kumar et al., 2023), radiance manifolds (Deng
et al., 2022b) (Xiang et al., 2022) (Deng et al., 2022a),
signed distance functions (Or-El et al., 2022) (Burkov
et al., 2022) (Liu and Liu, 2022); each of these rep-
resentations are paired with their corresponding dif-
ferentiable renderer. Arguably, the most popular rep-
resentation for modern 3D GANs is the Neural Radi-
ance Fields (Chan et al., 2021) (Gu et al., 2022) (Zhou
et al., 2021) (Kaneko, 2022) (Tang et al., 2022).
2.3 Volumetric Rendering
Volumetric rendering techniques (Max, 1995) (Meetz
et al., 1991) (Rushmeier and Torrance,
1987) (Williams and Max, 1992) (Kajiya, 1986)
are modelling the physical process of image for-
mation and are capable of representing the scene
unambiguously and accurately. A popular formula-
tion is the radiance field equation
C(r) =
Z
t
f
t
n
T (t)σ(r(t))c(r(t),d)dt, (5)
where T (t) = exp(−
Z
t
t
n
σ(r(s)ds). (6)
Here, T is the transmittance, σ is the density and c
is the color at the locations r(t) = o + td, o is the
camera center and d is the direction of a ray. The
integral bounds are the distances to the near and far
plane, t
n
and t
f
respectivelly. In practice, Eq. 5 is ap-
proximated by numerical integration, where, for each
pixel, points are sampled along the corresponding ray.
Recently Neural Radiance Fields (NeRF) (Mildenhall
et al., 2022) proposed to use a volumetric rendering,
where the volume is parameterised by a Multi-layer
Perceptron (MLP): it takes 3D coordinates as inputs,
Alias-Free GAN for 3D-Aware Image Generation
223

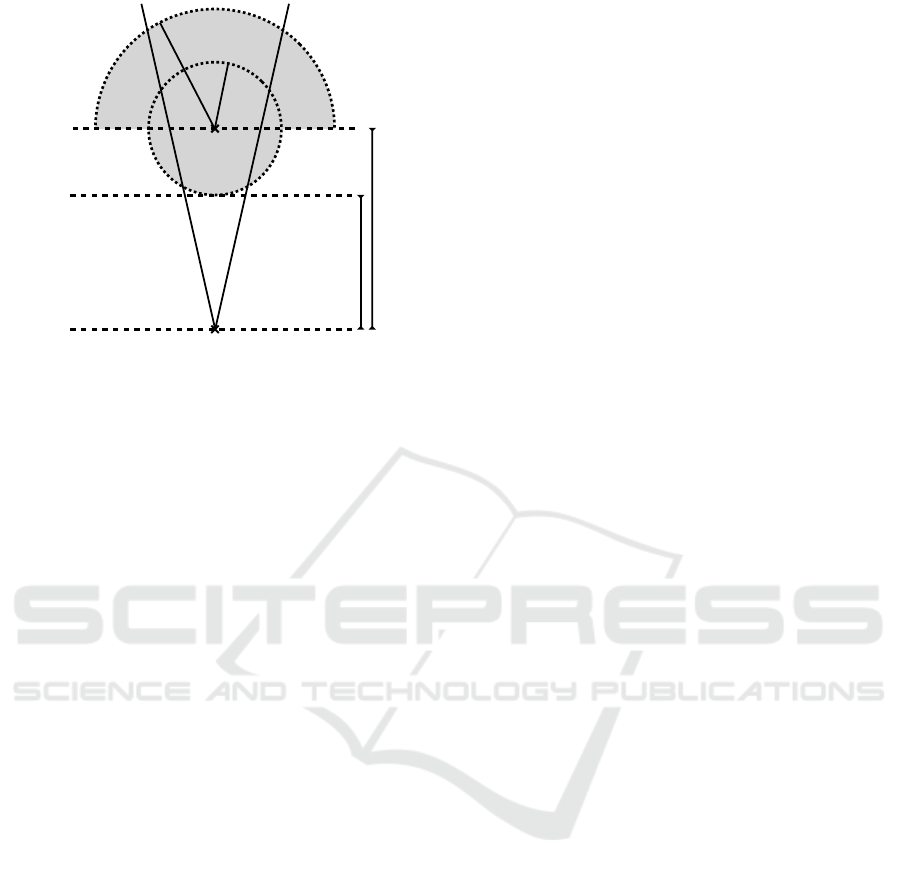
r
obj
r
bcg
n
d
frustum
Figure 3: The grey region shows the part of the scene that
are part of the object mask, i.e. potentially visible. We
render the part that is both masked and inside the frustum.
and outputs the corresponding density and color. In
our work instead of an MLP we use a 3D convolu-
tional network, which calculates the features for the
rendering on a 3D point grid of points.
For 3D-aware GANs, the NeRF is conditioned on
the latent variables z, so the neural network takes
both the 3D locations and z as inputs. The neural
network is not always an MLP. Their computational
cost is high, and with the current hardware it in not
feasible to use them in high-resolution image synthe-
sis as is. Thus, more efficient architectures were in-
troduced. VoxGRAF (Schwarz et al., 2022) uses a
sparse voxel grid to speed up computation by skip-
ping empty space. Tri-plane representations (Chan
et al., 2022) (Skorokhodov et al., 2022) (Xu et al.,
2023) run standard 2D convolutional networks, then
rearrange their outputs as three planes that are per-
pendicular to each other, then features are sampled
by projecting the 3D points onto them. This is much
faster than having to compute a full MLP forward pass
for each point.
GIRAFFE (Niemeyer and Geiger, 2021b) pro-
posed to render scenes using a low-resolution NeRF
model, followed by a super-resolution module. The
MLP in their case does not directly compute RGB
pixel values, but instead creates a high-dimensional
feature map.
In our work, we build upon StyleGAN3-R and
NeRF rendering. As they both produce and use im-
plicit representations, StyleGAN3-R can be naturally
modified to allow 3D viewpoint control. Similar to
GIRAFFE, we render a low-resolution feature map,
and then upsample it to produce high-resolution im-
ages.
3 APPROACH
In this section we present the construction of our
model, and show how we combine the alias free prop-
erties of (Karras et al., 2021a) with a 3D NeRF ren-
dering. For this we need to equip the generator with
an explicit rendering function that ensures geometry
and viewpoint consistency across different samples.
We will explain every steps in detail in this section,
the main flow are generation of the 3D representation,
alias free convolutions, rendering followed by a final
super-resolution step to map to the target resolution.
An overview of this method is shown in Figure 2.
The training procedure remains the same as be-
fore, we optimize the minimax objective w.r.t. the
generator G and discriminator D parameters as in
Eq. 3. The discriminator is taken as is from the vanilla
StyleGAN3 implementation. During training we need
to sample viewpoints and camera parameters and we
will explain the choices in the respective sections.
3.1 Viewpoint Sampling
Viewpoints are parameterised by polar coordinates.
The horizontal and vertical angles are sampled inde-
pendently within the ranges of ±80
◦
and ±20
◦
re-
spectively, while the radius is sampled within [5,25].
The camera center is placed according to the polar
coordinates and it points at the origin. The focal
length is set to be equal to the radius, thus the unit
ball around the origin always fits tightly to the ren-
dered square image. Once these parameters are given,
they determine the camera parameters K and M as de-
scribed below. Note we use dimensionless units for
the focal length and the 3D coordinates, as we do not
have any ground truth sizes in meters.
3.2 Camera Parameters
The cameras are parameterised with intrinsic K and
extrinsic M matrices:
K =


f 0 0
0 f 0
0 0 1


, M =

R t
0 1

, (7)
where f ∈ R
+
is the focal length, R ∈ R
3×3
is a rota-
tion matrix and t ∈ R
3
is a translation, thus M ∈R
4×4
is the (world-to-camera) matrix that describes a rigid
movement.
3.3 Normalised Device Coordinates
We use Normalised Device Coordinates (NDC) for
sampling points during the volumetric rendering.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
224

The points in this coordinate system are p
ndc
=
(x
ndc
,y
ndc
,z
ndc
) ∈ R
3
and they relate to the points in
the camera frame by a perspective transformation
p
h
ndc
∼ Pp
h
cam
, (8)
where the superscript denotes homogeneous coordi-
nates, p
h
cam
= (x
cam
,y
cam
,z
cam
,1). The perspective
transformation matrix is given by:
P =



f 0 0 0
0 f 0 0
0 0 a b
0 0 1 0



, (9)
where f ∈ R is again the focal length from P ∈ R
4×4
and a, b ∈ R. To remain consistent with K, only the
entries a and b are free parameters. We set them in
such a way that applying the transformation would
bring the near plane n > 0 of the camera to zero in
NDC, and at depth d > 0 the Jacobian of the transfor-
mation becomes proportional to the identity matrix,
a = f ·d/n, b = −f ·d. (10)
This way, P is designed to produce the least amount
of distortion in the rendered volume.
3.4 Scene
In our setting, we assume that the object is located
at the origin in the world coordinate frame inside a
sphere with radius r
obj
= 1.5 (which is slightly bigger
than
√
2, so the sides of the frustums we use for ren-
dering can fit inside it). We also set a background ra-
dius r
bcg
= 2.0, to allow the model to put some back-
ground behind the object. Figure 3 shows which part
of the scene is visible. The distance between the cam-
era and the object center is d. If a point is closer to
the camera than d and is inside the sphere with r
obj
,
it is considered for rendering. Points further than the
distance d are rendered, if they are inside the sphere
with r
bcg
. For calculating P in Eq. 9, we set the near
plane n = d −r
obj
.
3.5 Point Casting
We first generate points in NDC space in a regular
3D grid. The size of the grid is D ×H ×W , denot-
ing the grid sizes for depth, height and width, respec-
tively. We chose H = W = 52, which corresponds to
a 32 ×32 pixel grid plus a 10-point margin on each
side. We do not use margins for the depth axis, we
set D = 32. Excluding the margin, the ranges are
x
ndc
∈ [−1,+1], y
ndc
∈ [−1,+1] and z
ndc
∈ [0,+4].
Note that the neighboring points are 2× less dense
along the depth axis. We denote the point grid with
an overloaded notation p
ndc
, where a single point
p
ndc
[k, j,i] is indexed by k, j and i, which correspond
to the depth and v,u pixel coordinates, respectively.
To make the notation succinct, we omit indices if they
are not necessary, e.g. p
ndc
[k] is a 2D slice of the 3D
grid.
Next, we back-project the points to the world co-
ordinate frame by applying the inverse perspective
transformation by the matrix (PM)
−1
. We get a 3D
grid of points p
w
in the world coordinate frame:
p
h
w
∼ (PM)
−1
p
h
ndc
, (11)
where, as before, the superscript denotes homoge-
neous coordinates.
3.6 Fourier Features
Similarly to StyleGAN3-R, we first compute Fourier
features (Tancik et al., 2020), to supply the network
with input, except in our case we compute them for
3D points instead of 2D pixel locations. The Fourier
features are the input to the first layer, so we denote
them f
0
.
f
0
= [cos(ω
T
1
p
w
),sin(ω
T
1
p
w
),...,
cos(ω
T
L
p
w
),sin(ω
T
L
p
w
)], (12)
Fourier features are a concatenation of 2L sine and
cosine waves. The ω
l
∈ R
3
parameters are randomly
sampled from a uniform 3D ball and fixed at the be-
ginning of the training. We choose 2L = 128.
3.7 Alias-Free Convolutions
Next, we apply the StyleGAN3-R rotation-invariant
alias-free convolutional layer AFConv
1
for all of the
2D slices along the depth axis of the 3D grid. In order
to make the features alias-free, we apply a low pass
filter on them and downsample by 2× for every slice.
AFConv
1
is conditioned on w = Mapping(z),
where Mapping is an MLP, which enable condition-
ing on the latents z, thus,
f
1
[k] = AFConv
1
(down2x(f
0
[k]),w). (13)
AFConv
1
contains a convolution with a 1 ×1 ker-
nel and a leaky ReLU activation. The nonlinearity of
the leaky ReLU function is handled via Eq. 2, first
upsampling the features, then applying the nonlinear-
ity, then downsample with a low pass filter. The next
layers then depend on the one before them,
f
m
[k] = AFConv
m
((f
m−1
[k]),w) (14)
for a total of r layers. The last features f
r
are then
then input to the renderer. Please note that the down-
sampling is necessary only for the Fourier features
Alias-Free GAN for 3D-Aware Image Generation
225

Table 1: Quantitative evaluation results using Fr
´
echet Inception Distance (FID) ↓ for FFHQ and AFHQv2-Cats datasets. The
resolution of the generated images is given next to the dataset’s name. Scores for the compared approaches are taken from
the corresponding papers, † scores taken from (Xue et al., 2022). The best and second-best scores are coloured in red and
orange, respectively.
FFHQ-256 FFHQ-512 FFHQ-1024 AFHQv2-256 AFHQv2-512
GIRAFFE (Niemeyer and Geiger, 2021b) 32 - 70.08
†
33.39
†
-
Lift. SG (Shi et al., 2021) 29.81 - - - -
GRAM (Deng et al., 2022b) 17.9 - - 14.6 -
GRAM-HD (Xiang et al., 2022) 13.00 - 12.0 7.05 7.67
GIRAFFE-HD (Xue et al., 2022) 11.93 - 10.13 12.36 -
VoxGRAF (Schwarz et al., 2022) 9.6 - - 9.6 -
CIPS-3D (Zhou et al., 2021) 6.97 - 12.26 - -
GMNR (Kumar et al., 2023) 9.20 6.81 6.58 - 6.01
OmniAvatar (Xu et al., 2023) - 5.70 - - -
EG3D (Chan et al., 2022) 4.80 4.70 - 3.88 2.77
SURF-GAN (Kwak et al., 2022) 4.72 - - - -
IDE-3D (Sun et al., 2022) - 4.60 - - -
Ours 3.94 4.10 3.14 4.66 4.57
and not for the rest of the intermediate layers (m > 1).
The perspective transformation may cause aliasing
artefacts during the sampling process, which are han-
dled by a denser sampling and down-sampling the
Fourier features. The number of layers r = 3 before
rendering is set such that they correspond to the num-
ber of convolutional layers in StyleGAN3 with reso-
lution 16×16. We set the number of channels to 128.
3.8 Rendering
Now that the 3D features are computed, we use them
to render the 2D image. For each point on the 3D grid,
we calculate the corresponding distance and density.
The distance of a 3D point to the camera is
δ[k] =
∥
p
w
[k + 1] + p
w
[k −1]
∥
/2, (15)
where negative indices correspond to the points on the
margin.
The densities σ at a 3D point are chosen to be the
first channel of f
r
. Let Mask denote a masking func-
tion associated with the scene, it determines whether
a point should be used during rendering. The mask
will then remove points from the rendering process
by setting their densities to zero, further we clip any
negative values that may exist.
σ = max(0,Mask (p
w
,M) ⊙up2x(f
1
r
)), (16)
where the superscript denotes the index of the chan-
nel. Note that the mask computation requires the ex-
trinsic camera parameters and also up-sampling for
the features so that they match the sampling rate of
the 3D points.
Given the densities and the distances from the
camera we can perform volumetric rendering. We
sum along the depth axis and numerically integrate
the points k along the ray
f
r+1
=
D
∑
k=1
T [k](1 −exp(−δ[k]σ[k])up2x(f
r
[k]), (17)
where T are the transmittance values,
T [k] = exp

−
k−1
∑
m=1
δ[m]σ[m]

. (18)
The result f
r+1
is a 2D feature map.
Notice that full 3D equivariance with the perspec-
tive camera model and the volumetric rendering is
hard to define. Thus throughout the paper we only
use alias-free operations along the width and height
axes and not along the depth. This is an approxima-
tion, that we found to work well in practice.
3.9 Super-Resolution
The super-resolution part is then borrowed from the
StyleGAN3-R architecture. It is the convolutional
network comprising of the higher-resolution 2D con-
volutional layers. The output of the super-resolution
network is then the generated RGB image
x
generated
= SuperRes(f
r+1
). (19)
4 EXPERIMENTS
We evaluate our approach in the task of unconditional
multi-view image generation on two real-world image
datasets that allow a comparison with prior work. The
first dataset is FFHQ (Karras et al., 2021b), a set of
70,000 human face images at 1024
2
pixels resolution.
FFHQ exhibits considerable variation in terms of age,
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
226

Figure 4: Sample images generated by our model trained on FFHQ-1024
2
and AFHQv2-Cats-512
2
datasets.
ethnicity and image background. Because of its high
resolution we can test generation results on different
results, namely 256, 512, and 1024
2
. To test the gen-
eralization capability of the proposed approach, we
also conduct experiments on AFHQv2 (Choi et al.,
2020; Karras et al., 2021a), a collection of 15,000
images of animal faces at a resolution of 512
2
pix-
els. AFHQv2 includes three domains (cats, dogs,
wildlife), each consisting of ≈5,000 images. We
follow previous work and use the 5,065 cat image
subset of this dataset to evaluate our method and
compare it to the most recent SOTA image synthe-
sis methods: GMNR (Kumar et al., 2023), OmniA-
vatar (Xu et al., 2023), IDE-3D (Sun et al., 2022),
GIRAFFE-HD (Xue et al., 2022), GRAM-HD (Xi-
ang et al., 2022), SURF-GAN (Kwak et al., 2022),
VoxGRAF (Schwarz et al., 2022), EG3D (Chan et al.,
2022), Lift. SG (Shi et al., 2021), pi-GAN (Chan
et al., 2021), and GIRAFFE (Niemeyer and Geiger,
2021b). We adapt the same training setup as in pre-
vious work; we also augment both datasets with hori-
zontal flips. In contrast to other methods, e.g.EG3D),
we do not use any additional pose estimators, adaptive
data augmentation or transfer learning techniques.
4.1 Quantitative Results
In terms of metric-based evaluation, we assessed im-
age quality with the FID (Heusel et al., 2017), a com-
mon metric used to estimate the distance between
generated and real images. To compute the FID scores
for the proposed approach, we used 50,000 images
Alias-Free GAN for 3D-Aware Image Generation
227

(a) GIRAFFE (b) piGAN
(c) Lifting StyleGAN (d) GIRAFFE-HD
(e) EG3D (f) Ours
Figure 5: Qualitative comparison between our approach and recent SOTA methods on the FFHQ-256
2
dataset.
generated by a trained model and all real images
from the respective dataset. As can be seen from Ta-
ble 1, the proposed approach demonstrates compet-
itive FID performance on both datasets, surpassing
prior work on all FFHQ variants and being the sec-
ond best on AFHQ. The results on AFHQv2 are be-
hind those achieved by the best approach EG3D. We
attribute this to the difference in pose distribution be-
tween FFHQ and AFHQv2 where AFHQv2 is much
more complex and diverse. For EG3D a pose esti-
mator is used so that a pose distribution is known at
training time, for simplicity we choose the same dis-
tribution for both FFHQ and AFHQv2.
Following (Chan et al., 2022), we evaluate multi-
view facial identity consistency (ID) by calculating
the mean ArcFace (Deng et al., 2019) cosine similar-
ity score between pairs of views of the same synthe-
sized face rendered from random camera poses. As
can be seen from Table 2, our approach compares
favourably with the current SOTA contenders.
Table 2: Multi-view identity consistency (ID) for FFHQ.
We indicated the image resolution used for training and
evaluation.
resolution ID ↑
GIRAFFE 256
2
0.64
π-GAN 128
2
0.67
Lift. SG 256
2
0.58
EG3D 256
2
0.76
EG3D 512
2
0.77
SURF-GAN 128
2
0.66
IDE-3D 512
2
0.76
Ours 256
2
0.73
Ours 512
2
0.76
Ours 1024
2
0.78
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
228

Figure 6: Style-mixing with our approach on FFHQ-1024
with mixing regularization. We take the coarse layers (0-7)
from the images in the first column and the fine layers (8-15)
from the images in the first row. Coarse layers determine
the facial traits, hair length and hairstyle. Fine layers are
influence the skin tone and hair colouring.
4.2 Qualitative Results
In Figure 4 we show some sample images generated
by our approach on both datasets with the highest
available resolution, FFHQ-1024 and AFHQv2-512.
Manual examination of the images verifies the high
quality, viewpoint consistency and diversity of the
outputs.
To put the results into context, we follow previ-
ous work and compare the image samples generated
by the competing approaches side-by-side, shown in
Figure 5. Some of the methods have clearly visi-
ble artefacts. For example, the faces generated by
GIRAFFE exhibit a halo around the hair region, the
hair strands are also inconsistently positioned when
looked at from different viewpoints. π-GAN gener-
ates overly-smoothed faces, making them look un-
realistic. Lifting StyleGAN generates well-formed
faces, but struggles with capturing details (note the
blur around the hair regions). Our method, on the
other hand, synthesizes high-quality images which
are viewpoint-consistent, detailed and realistic: note
the correct positioning and lack of artefacts when
generating fine details, like hair strands or earrings.
Qualitatively, both ours, GIRAFFE-HD and EG3D
are photorealistic. Many images have the effect that
the eyes of the person look direclty into the camera
from all viewpoints. This is not an error in viewpoint
consistency, but a well known ambiguity. When the
Table 3: Rendering speed in images/second at three differ-
ent rendering resolutions. All compared approaches were
evaluated on a single GPU but the corresponding numbers
are taken from the original papers, so they serve as a refer-
ence, not a fair speed comparison.
resolution 256
2
512
2
1024
2
EG3D 36 35 -
GIRAFFE 181 161 -
GMNR 313 78.9 17.6
GRAM-HD - - 90
Lift. SG 51 - -
pi-GAN 5 1 -
SURF-GAN 72 - -
VoxGRAF 64 - -
Ours 30 26 23
geometry of the eye is inverted, it causes an illusion
that the eye looks at the camera all the time. As most
images look directly towards the camera in FHHQ, it
is natural for the network to learn the inverted geom-
etry, and all 3D-aware methods suffer from this.
4.3 Speed
In Table 3 we list the inference speed of our approach
and other methods we compared against. Since we
used standard components we achieve a high through-
put rate of the trained models of about 23 frames per
second for the highest tested resolution on a single
V100 GPU.
The numbers are given as a rough reference: the
approaches were benchmarked by the respective au-
thors on different hardware and with different re-
quirements. For example, while our method per-
forms end-to-end image synthesis, GRAM-HD (Xi-
ang et al., 2022) caches the manifold surfaces and HR
radiance maps as textured 3D meshes, and then runs
fast free-view synthesis with an efficient mesh raster-
izer from (Laine et al., 2020). Our method is capable
of real-time inference even at 1024
2
resolution, with-
out sacrificing image quality.
4.4 Style Mixing
The ability to modulate image style by feeding two or
more different latent code vectors to different layers
of the generator at inference time is known as style
mixing (Karras et al., 2021a; Karras et al., 2020; Kar-
ras et al., 2021b). Given the fact that our approach is
based on the StyleGAN3 architecture, it is reassuring
that the style mixing abilities are preserved. In Fig-
ure 6 we can observe that there is a clear separation of
the roles the coarse and fine layers of the model take
on: coarse layers are responsible for the overall head
Alias-Free GAN for 3D-Aware Image Generation
229

(a) object appearance
(b) horizontal translation
(c) vertical translation
(d) rotation
Figure 7: Conditioning and control: varying a) the latent z
that controls appearance, b) the camera matrix M for hori-
zontal translation, c) vertical translation and d) rotation.
pose, coarse face details and hairstyle, while fine lay-
ers perform appropriate skin tone and hair colouring.
4.5 3D Controllability
In Figure 7 we visually demonstrate that our method
is capable of generating 3D controllable images
which is a feature that emerges naturally from vol-
ume rendering of input Fourier features To explore
this capability, we decompose our camera into indi-
vidual components of (1) vertical translation, (2) hor-
izontal translation and (3) spherical rotation. For ver-
tical translation, Figure 7 (a) shows the object identi-
ties are preserved while the viewpoints are consistent.
Our qualitative results for horizontal translation and
spherical rotation show compelling evidence that our
method provides multi-view consistency, in terms of
subject identities and backgrounds.
5 DISCUSSION
In this paper we constructed a 3D-aware generative
model that is able to render images both of high qual-
ity and high resolution, while maintaining fast infer-
ence and gain viewpoint control for the user. We have
demonstrated these capabilities both qualitatively and
quantitatively, while we kept the design as simple as
possible.
We argue that a benefit of the proposed construc-
tion is the avoidance of extra regularization terms,
dual discriminators or specialized data-augmentation
strategies. The model retains the respective advan-
tages of its ingredients ”simply” by a careful com-
bination of NeRF and the alias-free StyleGAN3-R.
The training protocol follows the standard procedure
of StyleGAN3-R which is what we hoped for when
starting the investigation since specialized protocols
are hard to attain and prone to be sub-optimal.
There are several limitations that we plan to ad-
dress as future work. Currently our method does not
provide 3D depth or normals as output, as they can
only be extracted at a very low 16 ×16 pixel resolu-
tion. It would require specialized depth up-sampling
for any usable resolution.
Another interesting direction could be to
learn the viewpoint distribution similar to CAM-
PARI (Niemeyer and Geiger, 2021a). Training
a 3D-aware GAN requires a good match of the
viewpoint distribution used to sample and present in
the training data. Mismatch, either wider or narrower
viewpoints can lead to instability and incorrect
geometry. We expect that learning the viewpoint
distribution would lead to better performance e.g. on
the AFHQ dataset.
We understand the presented model and result as
a promising step to more complete 3D generation. In
particular we are interested in full 3D human genera-
tion and our model contains some necessary features
such as alias-free, high-quality, 3D-aware to move
into this more challenging domain.
ACKNOWLEDGEMENTS
We thank Nikolay Jetchev for the insights and sugges-
tions which helped us tremendously while developing
the approach. We also thank the anonymous review-
ers for their comments and suggestions.
REFERENCES
Bora, A., Price, E., and Dimakis, A. G. (2018). Ambi-
entgan: Generative models from lossy measurements.
In International Conference on Learning Representa-
tions.
Burkov, E., Rakhimov, R., Safin, A., Burnaev, E., and
Lempitsky, V. S. (2022). Multi-neus: 3d head por-
traits from single image with neural implicit functions.
IEEE Access, 11:95681–95691.
Chan, E. R., Lin, C. Z., Chan, M. A., Nagano, K., Pan, B.,
Mello, S. D., Gallo, O., Guibas, L. J., Tremblay, J.,
Khamis, S., Karras, T., and Wetzstein, G. (2022). Ef-
ficient geometry-aware 3d generative adversarial net-
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
230

works. In Conference on Computer Vision and Pattern
Recognition, pages 16102–16112.
Chan, E. R., Monteiro, M., Kellnhofer, P., Wu, J., and Wet-
zstein, G. (2021). Pi-gan: Periodic implicit generative
adversarial networks for 3d-aware image synthesis. In
Conference on Computer Vision and Pattern Recogni-
tion, pages 5799–5809.
Choi, Y., Uh, Y., Yoo, J., and Ha, J. (2020). Stargan v2: Di-
verse image synthesis for multiple domains. In Con-
ference on Computer Vision and Pattern Recognition,
pages 8185–8194.
Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2019). Ar-
cface: Additive angular margin loss for deep face
recognition. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition
(CVPR).
Deng, Y., Wang, B., and yeung Shum, H. (2022a). Learning
detailed radiance manifolds for high-fidelity and 3d-
consistent portrait synthesis from monocular image.
2023 IEEE/CVF Conference on Computer Vision and
Pattern Recognition (CVPR), pages 4423–4433.
Deng, Y., Yang, J., Xiang, J., and Tong, X. (2022b).
GRAM: generative radiance manifolds for 3d-aware
image generation. In Conference on Computer Vision
and Pattern Recognition, pages 10663–10673.
Gadelha, M., Maji, S., and Wang, R. (2017). 3d shape in-
duction from 2d views of multiple objects. In Interna-
tional Conference on 3D Vision, pages 402–411.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A. C., and Ben-
gio, Y. (2014). Generative adversarial nets. In Con-
ference on Neural Information Processing Systems,
pages 2672–2680.
Gu, J., Liu, L., Wang, P., and Theobalt, C. (2022). Stylenerf:
A style-based 3d aware generator for high-resolution
image synthesis. In International Conference on
Learning Representations.
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., and
Hochreiter, S. (2017). Gans trained by a two time-
scale update rule converge to a local nash equilibrium.
In Advances in Neural Information Processing Sys-
tems, pages 6626–6637.
Kajiya, J. T. (1986). The rendering equation. In Pro-
ceedings of the 13th annual conference on Computer
graphics and interactive techniques, pages 143–150.
Kaneko, T. (2022). Ar-nerf: Unsupervised learning of depth
and defocus effects from natural images with aper-
ture rendering neural radiance fields. In Conference
on Computer Vision and Pattern Recognition, pages
18387–18397.
Karras, T., Aittala, M., Laine, S., H
¨
ark
¨
onen, E., Hellsten, J.,
Lehtinen, J., and Aila, T. (2021a). Alias-free gener-
ative adversarial networks. In Conference on Neural
Information Processing Systems, pages 852–863.
Karras, T., Laine, S., and Aila, T. (2021b). A style-
based generator architecture for generative adversar-
ial networks. IEEE Trans. Pattern Anal. Mach. Intell.,
43(12):4217–4228.
Karras, T., Laine, S., Aittala, M., Hellsten, J., Lehtinen, J.,
and Aila, T. (2020). Analyzing and improving the im-
age quality of stylegan. In Conference on Computer
Vision and Pattern Recognition, pages 8107–8116.
Kim, G. and Chun, S. Y. (2022). Datid-3d: Diversity-
preserved domain adaptation using text-to-image dif-
fusion for 3d generative model. 2023 IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 14203–14213.
Kumar, A., Bhunia, A. K., Narayan, S., Cholakkal, H., An-
wer, R. M., Khan, S. S., Yang, M., and Khan, F. S.
(2023). Generative multiplane neural radiance for 3d-
aware image generation. ArXiv, abs/2304.01172.
Kwak, J., Li, Y., Yoon, D., Kim, D., Han, D. K., and Ko, H.
(2022). Injecting 3d perception of controllable nerf-
gan into stylegan for editable portrait image synthesis.
In European Conference on Computer Vision, volume
13677 of Lecture Notes in Computer Science, pages
236–253. Springer.
Laine, S., Hellsten, J., Karras, T., Seol, Y., Lehtinen, J.,
and Aila, T. (2020). Modular primitives for high-
performance differentiable rendering. ACM Trans.
Graph., 39(6):194:1–194:14.
Liu, F. and Liu, X. (2022). 2d gans meet unsupervised
single-view 3d reconstruction. In European Confer-
ence on Computer Vision, volume 13661, pages 497–
514. Springer.
Max, N. (1995). Optical models for direct volume render-
ing. IEEE Transactions on Visualization and Com-
puter Graphics, 1(2):99–108.
Meetz, K., Meinzer, H., Baur, H., Engelmann, U., and
Scheppelmann, D. (1991). The heidelberg ray tracing
model. IEEE Computer Graphics and Applications,
11(06):34–43.
Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T.,
Ramamoorthi, R., and Ng, R. (2022). Nerf: represent-
ing scenes as neural radiance fields for view synthesis.
Commun. ACM, 65(1):99–106.
Niemeyer, M. and Geiger, A. (2021a). CAMPARI: camera-
aware decomposed generative neural radiance fields.
In International Conference on 3D Vision, pages 951–
961.
Niemeyer, M. and Geiger, A. (2021b). GIRAFFE: repre-
senting scenes as compositional generative neural fea-
ture fields. In Conference on Computer Vision and
Pattern Recognition, pages 11453–11464.
Or-El, R., Luo, X., Shan, M., Shechtman, E., Park, J. J., and
Kemelmacher-Shlizerman, I. (2022). Stylesdf: High-
resolution 3d-consistent image and geometry genera-
tion. In Conference on Computer Vision and Pattern
Recognition, pages 13493–13503.
Poole, B., Jain, A., Barron, J. T., and Mildenhall, B. (2022).
Dreamfusion: Text-to-3d using 2d diffusion. ArXiv,
abs/2209.14988.
Rushmeier, H. E. and Torrance, K. E. (1987). The zonal
method for calculating light intensities in the presence
of a participating medium. ACM SIGGRAPH Com-
puter Graphics, 21(4):293–302.
Schwarz, K., Sauer, A., Niemeyer, M., Liao, Y., and Geiger,
A. (2022). Voxgraf: Fast 3d-aware image synthesis
with sparse voxel grids. In Conference on Neural In-
formation Processing Systems.
Alias-Free GAN for 3D-Aware Image Generation
231

Shannon, C. E. (1949). Communication in the presence of
noise. Proceedings of the IRE, 37(1):10–21.
Shi, Y., Aggarwal, D., and Jain, A. K. (2021). Lifting 2d
stylegan for 3d-aware face generation. In Conference
on Computer Vision and Pattern Recognition, pages
6258–6266.
Skorokhodov, I., Tulyakov, S., Wang, Y., and Wonka, P.
(2022). Epigraf: Rethinking training of 3d gans. In
Conference on Neural Information Processing Sys-
tems.
Sun, J., Wang, X., Shi, Y., Wang, L., Wang, J., and Liu,
Y. (2022). IDE-3D: interactive disentangled editing
for high-resolution 3d-aware portrait synthesis. ACM
Trans. Graph., 41(6):270:1–270:10.
Szab
´
o, A., Meishvili, G., and Favaro, P. (2019). Unsuper-
vised generative 3d shape learning from natural im-
ages. ArXiv, abs/1910.00287.
Tancik, M., Srinivasan, P. P., Mildenhall, B., Fridovich-
Keil, S., Raghavan, N., Singhal, U., Ramamoorthi,
R., Barron, J. T., and Ng, R. (2020). Fourier fea-
tures let networks learn high frequency functions in
low dimensional domains. In Conference on Neural
Information Processing Systems.
Tang, J., Zhang, B., Yang, B., Zhang, T., Chen, D., Ma, L.,
and Wen, F. (2022). 3dfaceshop: Explicitly control-
lable 3d-aware portrait generation. IEEE transactions
on visualization and computer graphics, PP.
Wang, T., Zhang, B., Zhang, T., Gu, S., Bao, J., Bal-
truvslet@tokeneonedotaitis, T., Shen, J., Chen, D.,
Wen, F., Chen, Q., and Guo, B. (2022). Rodin: A
generative model for sculpting 3d digital avatars us-
ing diffusion. 2023 IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
4563–4573.
Williams, P. L. and Max, N. (1992). A volume density op-
tical model. In Proceedings of the 1992 workshop on
Volume visualization, pages 61–68.
Xiang, J., Yang, J., Deng, Y., and Tong, X. (2022). Gram-
hd: 3d-consistent image generation at high reso-
lution with generative radiance manifolds. ArXiv,
abs/2206.07255.
Xu, H., Song, G., Jiang, Z., Zhang, J., Shi, Y., Liu, J.,
Ma, W.-C., Feng, J., and Luo, L. (2023). Omnia-
vatar: Geometry-guided controllable 3d head synthe-
sis. 2023 IEEE/CVF Conference on Computer Vi-
sion and Pattern Recognition (CVPR), pages 12814–
12824.
Xue, Y., Li, Y., Singh, K. K., and Lee, Y. J. (2022). GI-
RAFFE HD: A high-resolution 3d-aware generative
model. In Conference on Computer Vision and Pat-
tern Recognition, pages 18419–18428.
Zhou, P., Xie, L., Ni, B., and Tian, Q. (2021). Cips-3d:
A 3d-aware generator of gans based on conditionally-
independent pixel synthesis. ArXiv, abs/2110.09788.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
232