Advancements in Traffic Simulations with multiMATSim’s Distributed
Framework
Sara Moukir
1,3
, Miwako Tsuji
2
, Nahid Emad
1
, Mitsuhisa Sato
2
and Stephane Baudelocq
3
1
University of Paris Saclay, France
2
R-CCS RIKEN, Japan
3
Eiffage Energie Syst
`
emes, France
Keywords:
Road Traffic Simulation, Big Data Analysis, High Performance Computing, Complex and Heterogeneous
Dynamic System, Unite and Conquer, MATSim, Parallel Computing.
Abstract:
In an era characterized by massive volumes of data, the demand for advanced road traffic simulators has
reached an even greater scale. In response to this call, we propose an approach applied to MATSim, specif-
ically called multiMATSim. Beyond its tailor-made implementation in MATSim, this innovative approach is
designed with generic intent, aiming for adaptability to a variety of multi-agent traffic simulators. Its strength
lies in its blend of versatility and adaptability. Fortified by a multi-level parallelism and fault-tolerant frame-
work, multiMATSim demonstrates promising scalability across diverse computing architectures. The results of
our experiments on two parallel architectures based on x86 and ARM processors systematically underline the
superiority of multiMATSim over MATSim. This especially in load scaling scenarios. We highlight the gener-
ality of the multiMATSim concept and its applicability to other road traffic simulators. We will also see how
the proposed approach can contribute to the optimization of multi-agent road traffic simulators and, impact the
simulation time thanks to its intrinsic parallelism.
1 INTRODUCTION
Traffic simulation holds an instrumental position in
areas like urban planning, shaping infrastructure, and
crafting effective mobility strategies. With the pro-
gression of technology and advancements in model-
ing methodologies, simulators rooted in the multi-
agent paradigm have risen as the preferred method
for capturing the evolving nature of traffic systems.
These tools, characterized by their intricate detail, are
adept at replicating individual vehicular and road user
interactions within a digital realm. Yet, as scenarios
grow in intricacy and the quest for accuracy inten-
sifies, performance and scalability concerns become
glaringly apparent(Nguyen et al., 2021).
At the heart of such simulations, notably in MAT-
Sim(Horni et al., 2016), stands the convergence mech-
anism. Through a series of iterations, agents continu-
ally refine and enhance their choices, pinpointing op-
timal routes and timings in response to the prevailing
network state and decisions made by fellow agents.
The swiftness of this convergence is paramount, dic-
tating how long the simulation takes to reach a steady
state that mirrors real-world traffic patterns.
In response to these pressing concerns, we’ve ven-
tured into an innovative route aimed at hastening
the convergence timeline. Drawing inspiration from
the ”Unite and Conquer”(Emad and Petiton, 2016)
(UC) principle, our tactic deviates from the classic
”Divide and Conquer” perspective. Instead of dis-
secting a challenge, ”Unite and Conquer” revolves
around disseminating crucial data across co-methods.
Each can then address the overarching challenge au-
tonomously, refining the conditions for recommence-
ment and speeding up convergence. The approach
adopted is invariably influenced by the nature and
context of the problem at hand.
Leveraging this mindset, we birthed multiMAT-
Sim. In this exploration, we probe into multiMAT-
Sim’s ability to scale and evaluate its efficacy across a
spectrum of computational setups, encompassing the
esteemed Fugaku supercomputer(Sato et al., 2020).
Intriguingly, while MATSim faltered in its perfor-
mance on Fugaku, potentially owing to its CPU
structure, multiMATSim consistently showcased com-
mendable outcomes. These revelations not only un-
derscore the resilience and versatility of our universal
model but also illuminate ways in which traffic simu-
374
Moukir, S., Tsuji, M., Emad, N., Sato, M. and Baudelocq, S.
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework.
DOI: 10.5220/0012452600003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 1, pages 374-385
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

lation tools can be adeptly tailored to fit the nuances
of varied computing environments.
2 RELATED WORK
Road traffic simulation tools have become a focal
point in academic circles, especially when bolstered
by parallel and distributed computing methods to
expedite runtimes. Diverse approaches have been
charted to navigate this multifaceted domain.
Take, for instance, the strategy of network divi-
sion: here, the entire roadway system is broken down
into several sub-networks, with each segment over-
seen by an individual computational entity. At its
surface, this technique appears advantageous due to
its built-in parallel capabilities. Yet, it presents a
pronounced complication. As an agent transitions
from one segment to another, it mandates a dia-
logue between the corresponding computational en-
tities. Such inter-entity communications, essential for
system-wide consistency, can be resource-intensive
and time-consuming(Potuzak, 2020).
Esteemed simulation platforms like TRANSIMS,
AIMSUN, and Paramics(Nguyen et al., 2021) have
gravitated towards this method, though their founda-
tional structures were not natively agent-centric.
Venturing into the territory of inherently agent-
based simulation systems, distributing agents over nu-
merous computational entities has become a norma-
tive practice. However, this method wrestles with
a recurrent hurdle: the indispensable inter-entity up-
dates to maintain a holistic network integrity(Mastio
et al., 2018).
MATSim stands out with its trajectory of enhance-
ments. Beyond mere adoption of libraries tailored for
concurrent computation(Ma and Fukuda, 2015), the
system has seen transformative changes in its core
components. The Replanning component, as an ex-
ample, was fine-tuned to boost its rate of conver-
gence(Zhuge et al., 2021). Furthermore, the simula-
tor’s journey marked a shift from a ”chronologically
driven” model to one steered by events, as evident in
the transitions from QSIM to JDEQSIM, eventually
leading to HERMES(Horni et al., 2016).
In resonance with these developmental strides, our
research brings forth an inventive algorithmic rendi-
tion for MATSim’s Replanning component, tapping
into the virtues of concurrent processing. The pri-
mary goal is achieving brisker convergence, thereby
streamlining execution durations.
3 ROADWAYS TO
PARALLELISM: FROM MATSim
TO multiMATSim
MATSim is an open-source framework, written in
Java, dedicated to large-scale agent-based transport
simulations(Horni et al., 2016). Stemming from the
pioneering works in agent-based traffic modeling,
MATSim has been continuously improved over the
years.
In this simulation framework, each agent repre-
sents a virtual entity that can sense, think, and act
within the environment. These agents are designed
to mimic real-world individuals, ensuring they exhibit
human-like behaviors in a transport setting.
To kickstart the simulation, each agent is assigned
an initial plan crafted using various data sources.
These sources, such as census data, are gathered from
the communities of the geographical areas under sim-
ulation. This data-driven approach allows for a syn-
thetic population that closely mirrors real-world de-
mographics and behaviors.
As agents navigate the road network based on
their initial plans, each plan is evaluated and scored
using predefined criteria. This score encompasses el-
ements like travel duration, mode selection, and se-
quence of activities, reflecting the plan’s alignment
with the agent’s preferences, goals, and limitations.
The simulation process isn’t static. As it pro-
gresses, a designated subset of agents enters the Re-
planning phase(Horni et al., 2016). Here, agents,
starting from their original plan, create duplicates and
introduce modifications based on experiences from
previous iterations. This procedure fosters a dynamic
and evolving simulation environment, with agents in-
creasingly diversifying their strategies.
The entire simulation operates in cycles, with each
iteration representing a 24-hour period. Through
these repeated rounds, agents continually refine and
diversify their plans, striving for optimal solutions.
This iterative approach, combined with the adaptabil-
ity introduced by the Replanning phase, ensures the
system moves closer to desired outcomes as the simu-
lation advances. The user sets the number of iterations
through the variable max. Although MATSim doesn’t
have an inherent stopping criterion, there are some
proposed stopping criteria in the literature based on
convergence measures(Horni and Axhausen, 2012).
By default, max = 300 is often found in some MAT-
Sim scenarios. Figure 1 illustrates this mechanism.
Operational Modules. After gaining a fundamen-
tal understanding of MATSim’s operation, it’s crucial
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework
375

Figure 1: Iterative MATSim loop.
to delve into its core components. MATSim func-
tions around five foundational elements: Input, Scor-
ing, Execution, Replanning, and Output(Horni et al.,
2016). Let’s explore each of these in detail :
• Input. Essential inputs include the initial plan of
each agent and the network file detailing the road
and public transport networks specific to the sim-
ulated area.
• Execution Module (Mobsim). Simulates each
agent’s daily activities, capturing their movements
from one location to another.
• Scoring Module. Assesses daily plans, consider-
ing the agent’s Mobsim performance using a util-
ity function that incorporates movement and ac-
tivity facets.
• Replanning Module. Adapts plan components,
like departure times or transportation mode, in re-
sponse to the traffic conditions based on the plan
scores.
• Output. Outputs include plan scores, revised
plans for agents that experienced Replanning,
daily event logs, and statistics in text files and
graphical formats.
An overview of the sequence in which MATSim’s core
modules operate is presented in Algorithm 1. Having
elucidated the foundational elements of MATSim, it’s
imperative to focus our attention on the Replanning
module. This component serves as a linchpin in our
approach, shaping the dynamics and outcomes of the
simulations. We will now unpack the intricacies and
nuances of the Replanning process.
3.1 Replanning Module in MATSim
During the Replanning phase, a fraction R of agents
is given the opportunity to alter their existing plans,
leading to the generation and subsequent selection of
new plans. By default, MATSim subjects only 10%
of agents to this phase (i.e., R = 0.1M, with M the
total number of agents in a scenario). However, users
possess the flexibility to modify this proportion.
It’s crucial to note that an agent’s set of plans is
not infinite. Here, we opt to denote this value with the
variable nb plans. While we frequently encounter it
set as nb plans = 5 in many scenarios, it’s important
to note that it can be adjusted as needed. As time pro-
gresses, plans with the least scores get ”overwritten”
or replaced. Once agents select a new plan, they are
resimulated on the transportation network. The exe-
cuted plans are then scored, ushering in the genera-
tion and selection of fresher plans. The goal is to con-
duct enough iterations until reaching a point where
the plan scores of the agents no longer show improve-
ments, indicating a state of equilibrium.
MATSim offers a range of strategies for the Replan-
ning phase(Horni et al., 2016) :
• Plan Selector. Among several strategies avail-
able in MATSim, we focus on the ChangeExpBeta
method, which selects plans based on the proba-
bility derived from e
∆
score
, with ∆
score
denoting the
score difference between two plans.
• Route Innovation. A strategy that tweaks an ex-
isting random plan through re-routing trips. Route
decisions are influenced by the traffic conditions
observed in the preceding iteration. Multiple rout-
ing algorithms, like Dijkstra and A*, may be in-
voked.
• Time Innovation. Adapts a randomly chosen ex-
isting plan by shifting all activity end times, either
backwards or forwards.
• Mode Innovation. Modifies a random existing
plan by transitioning to a different transportation
mode.
3.1.1 Strategy Weights and Experiments
We’ll represent the relative weights of these strategies
as ρ
PlanSelector
, ρ
reroute
, ρ
time
, and ρ
transportmode
.
Every strategy module carries a weight, which
dictates the likelihood of that module’s action being
chosen. To maintain a balanced system, if the cu-
mulative weights of strategy modules don’t total one,
MATSim normalizes them.
Algorithm 1: MATSim algorithm.
Start. Choose max, nb plans and the strategies probabilities
weights such as
ρ
PlanSelector
+ ρ
rerout e
+ ρ
time
+ ρ
transportmode
= 1, R ...
Iterate. For l =1, ... , max
Run one iteration of MATSim for the M agents: Mobsim,
Scoring and Replanning only by the portion of R agents to which
the Replanning applies.
Having delineated the weight distribution of
strategies within the Replanning module, it is im-
perative to emphasize that this distribution serves as
the foundational framework for the implementation
of multiMATSim. A detailed exposition of this imple-
mentation will be presented in the subsequent section.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
376

3.2 Presentation of multiMATSim
Given the previously discussed nuances of MATSim,
one notable challenge remains its convergence rates
in complex transportation systems. Slow conver-
gence inevitably results in prolonged simulation times
and heightened computational requirements. In re-
sponse, we’ve formulated an approach drawing from
the Unite and Conquer methodology, designed specif-
ically to enhance MATSim’s convergence efficiency.
In MATSim, convergence is the point where each
agent’s plan scores stabilize, indicating that the sim-
ulation has achieved a balanced state regarding the
choices of travel plans. Essentially, agents have set-
tled on their optimal routes based on their interactions
within the transport system.
Our specific adaptation of the Unite and Conquer
approach entails running multiple MATSim instances
concurrently. Although MATSim already employs
some multi-threading, we’ve instituted a deeper level
of parallelism that remains largely untapped. These
simultaneous instances are consistent in their scenar-
ios and features but diverge in the weights given to
their Replanning strategies. Consequently, even when
starting with the same set of initial plans, the differing
weights lead to varied plans being produced during
each Replanning phase across instances.
By distributing the weights differently, we are able
to explore a wider range of potential solutions and
cover a broader set of possible plan variations.
In addition to this, our approach sets up, ev-
ery step iterations, a communication between the in-
stances so as to make an exchange of plans between
them. After a given iteration, instance i (with i ∈
{1, ..., N} and N the number of instances) will know
the scores of other instances for a given agent a
k
,
(with k ∈ {1, ..., M} and M the number of agents).
Consequently, instance i will know which instance
has the plan with the best score for agent a
k
. It can
decide to recover it or not, according to a very specific
criterion. This criterion is as follows: consider the
instance α and the instance β (α, β ∈ [1; N]).
For a given agent a
k
, instance α gets score S
k
α
and
instance β gets score S
k
β
, with S
k
α
< S
k
β
and S
k
β
> S
k
i
∀i ∈ [1;N].
The α instance could then simply retrieve the plan
associated with the S
k
β
score from β and run the next
iteration. However, if each instance retrieves for each
agent each time the plan of the instance that made the
best score, we would have instances that would all
execute the same plan for each of the agents.
The objective is to establish a criterion that en-
ables instances to determine whether it is beneficial to
adopt the plan of another instance, even if their own
plan has a lower score than that of the other instance
for a specific agent.
To develop this plan exchange criterion, we have
chosen to focus on the dispersion measure between
the scores obtained by different instances for the same
agent. By analyzing the dispersion measure, we can
indirectly assess the performance of plans and deter-
mine whether plan exchanges should be pursued. The
criterion ensures that plan exchanges are limited to in-
stances that have obtained the worst scores relative to
other instances for each agent.
By employing this criterion, we can leverage the
performance of plans as an indirect validation mech-
anism for plan exchanges. It allows for the possibility
of adopting more favorable plans while still maintain-
ing a limit on the exchanges, ensuring that they occur
primarily between instances with lower-performing
plans.
This criterion is the following: consider the vector
V
S
k
of size N, containing the scores of all the instances
for the agent a
k
.
If the absolute value of the subtraction of S
k
α
(α
being the instance concerned by this decision) by S
k
β
is greater than the standard deviation of V
S
k
, then the
plan exchange is favorable and α recovers the plan
associated with the score S
k
β
from the β instance.
The chosen criterion for plan evaluation is pre-
liminary and focuses on the scoring distance between
two plans, deeming one more suitable based on its
closeness to the best plan. Future research will refine
this criterion, with potential machine learning integra-
tion. Using an approach inspired by the Monte Carlo
method, MATSim’s subsequent iterations will priori-
tize higher-scoring plans. While this method aims for
improved plan quality, it’s an initial step, and upcom-
ing work will delve into advanced techniques for bet-
ter plan assessment and selection. Let’s summarize
the essential parameters listed in Algorithm 2:
• N: choose the number of MATSim instances that
will run in parallel
• max: MATSim stops after a predefined number of
iterations. It doesn’t stop by itself when conver-
gence is obtained.
• M is the number of agents in the current scenario
of MATSim
• R is subset of agents that undergo the Replanning
module
• step: Choose a number of iteration steps between
which communication will take place between the
different instances
• iter
processing: = max ÷ step, this is the number
of times the processing and communications are
performed.
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework
377

• Choose the weights for probabilities associated
with Replanning strategies. The assigned weights
are such that ρ
PlanSelector
+ ρ
reroute
+ ρ
time
+
ρ
transportmode
= 1. Each instance i has a different
distribution of weights.
• Set nb plans = 1. In this way, each instance will
focus on optimizing a single plan.
Consider an example with only two MATSim in-
stances (N = 2) and a single agent (M = 1), illustrated
on Figure 2. Two MATSim instances, i and j, oper-
ate on separate computing nodes (x and y). Although
these instances share the same scenario, geographi-
cal area, and simulated agent, they generate different
plans due to distinct Replanning strategies. Here is an
explanation of the elements in Figure 2:
• Run MATSim for step Iterations. Each instance
runs MATSim for a defined number of iterations
(step), including a 24-hour simulation, plan scor-
ing, and Replanning to generate optimized plans.
• STOP. After completing these iterations, MAT-
Sim instances i and j temporarily halt their execu-
tion.
• Send and Receive Plans.They exchange the plans
they executed and the associated scores for agent
a
k
. Thus, i sends its plan and its score S
k
i
to j,
while j does the same with its plan and score S
k
j
.
• Compute S
k
best
and std
k
. Now, i and j have each
other’s computational information. They deter-
mine which of the two plans achieved the best
score, denoted as S
k
best
(either S
k
best
= S
k
i
or S
k
best
=
S
k
j
).
• The decision is based on calculations involving
standard deviation operations (involving std
k
) for
agent a
k
in order to measure the relative distance
between the score obtained by the instance in
question and the best score. If the difference is
significant, the instance opts for the plan with the
best score. Otherwise, it retains its own plan.
• These steps repeat for a defined number of MAT-
Sim iterations (step), ensuring the optimization of
each agent’s plans.
Of course, in a realistic scenario, there are many more
agents, but this example helps to understand how it
works for a single agent, and it’s the same in a real
scenario with a larger number of agents. Similarly,
for the instances, we limited it to 2 in this example,
but in our experiments, we increased this number.
Figure 2: Illustration of the multiMATSim algorithm with
two ranks / instances and one agent.
Revisiting the Unite and Conquer approach, it’s
essential to delineate how it seamlessly integrates
with MATSim to birth the multiMATSim paradigm.
The Unite and Conquer method enhances conver-
gence by sharing intermediate solutions between co-
methods. In the context of MATSim, multiple in-
stances with varied inputs are deployed. While each
instance is adept at independently solving the prob-
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
378

lem, they achieve accelerated convergence by ex-
changing intermediate solutions. A more rapid aver-
age plan score convergence signifies agents efficiently
producing higher-quality travel plans as the simula-
tions unfold.
Finally, MultiMATSim utilizes distributed comput-
ing, allocating one MATSim instance to each comput-
ing node. Notably, it is also fault-tolerant, allowing
it to continue running with the remaining ’active’ in-
stances in the event of a software error.
4 METHODOLOGY
In this study, we embark on an exploration of mul-
tiMATSim using the Los Angeles 0.1% scenario as
our foundational ground. Our primary objective is
to assess scalability by increasing the number of in-
stances, and consequently, the number of computa-
tional nodes. To this end, we will conduct experi-
ments with both N = 4 and N = 8. While our cur-
rent experiments with 4 and 8 nodes may not provide
a complete assessment of scalability, they serve as an
initial exploration and offer valuable insights that set
the stage for a more comprehensive analysis as we
delve into the results. Additionally, we will introduce
a new scenario, still centered on Los Angeles but with
a higher agent count: Los Angeles 1%. This scenario
engages 191,649 agents, approximately a tenfold in-
crease compared to our initial scenario. Our aim is
to evaluate the scalability of our approach as data per
node grows, without introducing any unintended ar-
tifacts. This comprehensive investigation will pro-
vide valuable insights into the performance of multi-
MATSim in scenarios with varying computational de-
mands.
4.1 Technical Specifications
We had the privilege of gaining access to two dis-
tinct high-performance computing platforms: Ruche
and Fugaku. Ruche(of Paris-Saclay, 2020), a col-
laborative effort between the computing centers of
CentraleSup
´
elec and
´
Ecole Normale Sup
´
erieure, fea-
tures a high-performance computing cluster that be-
came operational in 2020. Ruche is equipped with
approximately 3500 processors and includes 8 nodes
optimized for GPU computing. Fugaku, on the other
hand, stands as a world-renowned supercomputer,
recognized for its exceptional computational power.
Developed by RIKEN in partnership with Fujitsu,
Fugaku is the second most powerful supercomputer
globally as of 2023(TOP500, 2023). It is built on the
Armv8-A architecture with SVE extensions, deliver-
ing unmatched performance across scientific simula-
tions, artificial intelligence, and various research do-
mains. With its A64FX processors and versatile ca-
pabilities, Fugaku has made significant contributions
to climate modeling, medical research, materials sci-
ence, and more[2]. Comprising over 150,000 nodes,
Fugaku continues to drive groundbreaking advance-
ments in global scientific research(Sato et al., 2020).
Please refer to Table I for node-level specifications
for each of the two supercomputers.
4.2 Experimental Protocol
As a reminder, each instance runs on its dedicated
computing node with multiMATSim method. More-
over, although multithreading is a built-in feature in
MATSim, we specifically configured it to utilize 20
threads, up from the default 8. Surprisingly, despite
having 40 or more available cores on each node, uti-
lizing only 20 threads resulted in the most remarkable
performance on both platforms. Several hypotheses
could account for this phenomenon: the reduction
of resource conflicts, improved utilization of cache
memory, or even decreased thread management over-
head. This configuration appears to have struck an op-
timal balance between task parallelism and hardware
capabilities. This blend of distributed instances and
multithreading highlights our multi-level parallelism
approach, leveraging both task and data parallelism
to enhance simulation performance. Concerning the
variables of multiMATSim, we have chosen the fol-
lowing values: step = 50, max = 300. Concretely,
this means there will be a total of 300 iterations, with
an exchange every 50 iterations.
5 RESULTS AND DISCUSSION
We provide a comprehensive account of the perfor-
mance outcomes obtained using multiMATSim across
two scenarios: 0.1% and 1% agent representation of
Los Angeles. Both scenarios underwent tests with 4
and 8 parallel instances. The following results and
measured performances were obtained on Ruche clus-
ter. The following observations are illustrated in Fig-
ure 3 (and Figure 5, 6) for 0.1% scenario and Figure
4 for 1% scenario. It displays the progression of the
average scores of plans executed by all agents in the
scenario. The black curve represents the progression
in MATSim 0.1% / 1% (baseline), while the colored
curves depict the various instances of multiMATSim.
Please note that in Figures 3, 4, 5 and 6 the charts dis-
play square peaks resulting from the stop-and-restart
procedures in MATSim. After 80% of the step iter-
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework
379

Table 1: Specifications for a Single Node in Each Supercomputer.
Specification Ruche Fugaku
CPU Reference Intel Xeon Gold 6230 Fujitsu A64FX
CPU Architecture x86 (Cascade Lake) Armv8.2-A SVE 512 bit
Total Cores per Node 40 (2 CPUs, 20 cores/CPU) 48 cores (compute) + 2/4 (OS)
Processor Base Frequence 2.10 GHz Normal: 2 GHz, Boost: 2.2 GHz
Cache L1: 32 KB per core (instruction) L1 : 64 KB per core (instruction)
+ 32 KB per core (data) + 64 KB per core (data)
L2: 1 MB per core L2 : 32 MB (8MB per 12-core group)
L3: Up to 27.5 MB (shared) L3: -
SIMD Extensions AVX-512 SVE (Scalable Vector Extension)
ations, these peaks represent the average of the his-
torical best scores during the last step iterations for
each agent. However, emphasis should be placed on
the overall evolution of the average scores, not these
artifacts.
5.1 Results: Scalability
5.1.1 Los Angeles 0.1
• Total Execution Time. The time taken for the
entirety of the 300 iterations was strikingly simi-
lar across configurations. The standard MATSim
culminated in 8h, multiMATSim with 4 instances
concluded in 8h40, and the setup with 8 instances
wrapped up in about 8h45. Notably, with the 8 in-
stances configuration, the convergence score was
swiftly surpassed shortly after the maiden data
exchange. For clarification, our goal is not to
achieve a shorter total execution time, but rather
a faster convergence time.
• Speedup. As we had previously presented, multi-
MATSim with 4 instances delivered a remarkable
acceleration in convergence. It achieved a conver-
gence score of 105 in just 1.5 hours (iteration 52,
right after the first exchange), contrasting starkly
with the standard MATSim which required 6 hours
for the same score (speedup of 4.0). The ultimate
anticipation was regarding the performance with
8 instances. Interestingly, the speedup with 8 in-
stances mirrored that of the 4 instances configura-
tion.
• Comparison Between 4 and 8 Instances. Re-
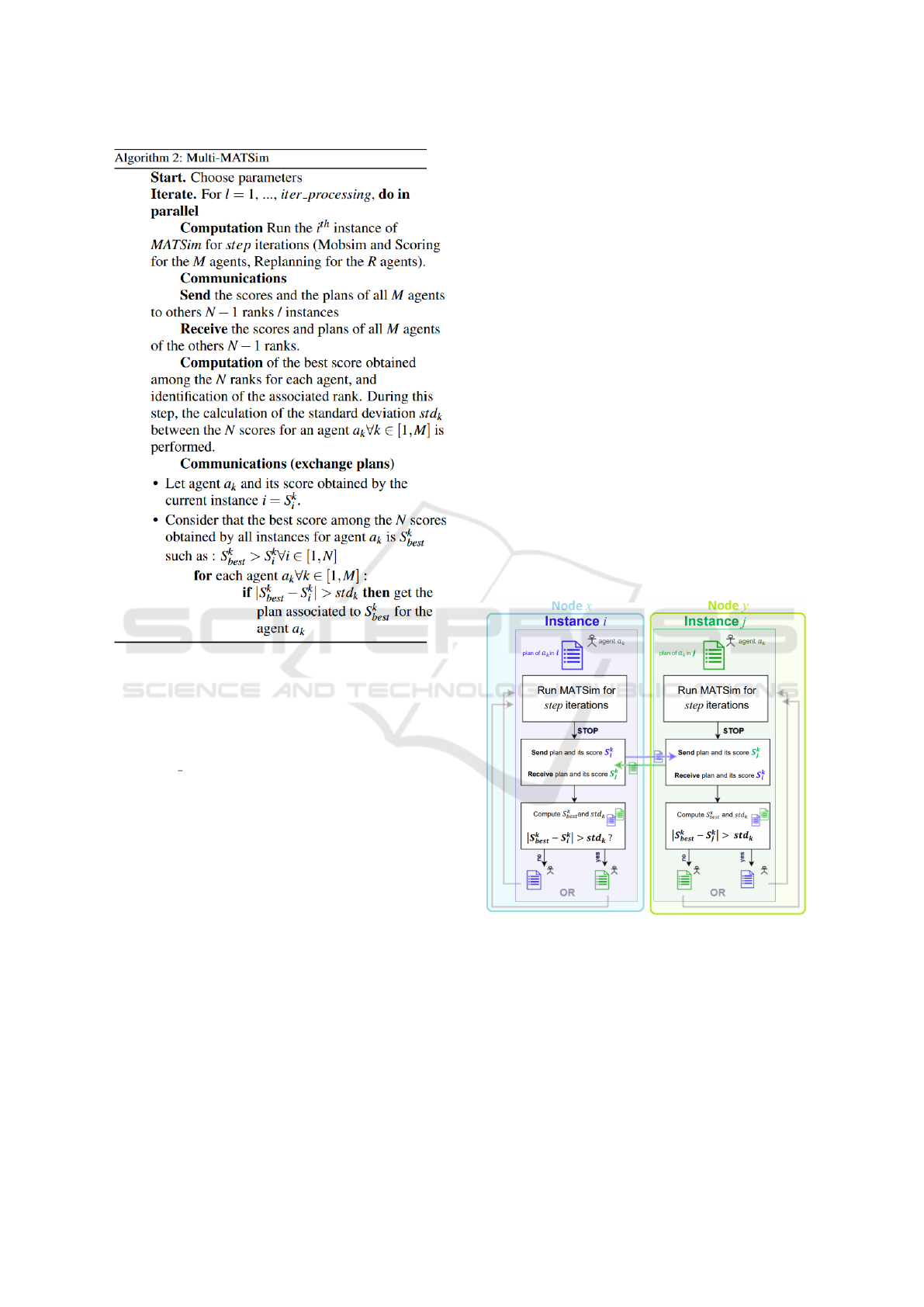
ferring to Figure 3, an immediate spike in the
performance of multiMATSim with 8 instances is
observable right after the first data exchange at
the 50th iteration. As touched upon earlier, our
past work showcased the sterling results with the
4 instances setup. The current analysis affirms
that while the 4 instances framework maintains
its exemplary performance, merely doubling the
instances to 8 does not definitively outpace the
former configuration. However, given the pro-
nounced leap post the initial exchange at the 50th
iteration with 8 instances, an earlier data exchange
could potentially have augmented the speedup,
making the 8 instances setup potentially more ad-
vantageous than its 4 instances counterpart.
5.1.2 Los Angeles 1
• Total Execution Time. The 1% scenario, being
inherently more data-intensive, demonstrated ex-
tended completion durations. The baseline MAT-
Sim necessitated a substantial 36 hours to com-
plete 300 iterations. On the other hand, multi-
MATSim, across its 4 and 8 instances configura-
tions, hovered around 50 hours. MATSim required
29 hours to achieve the convergence score. Re-
markably, multiMATSim with its 4 and 8 instances
setup reached this score in approximately 6 hours.
• Speedup. For the 1% scenario, a speedup of 4.8
was observed, slightly surpassing the 4.0 speedup
of the 0.1% scenario. This emphasizes the in-
creased efficiency of the multiMATSim as the data
density grows.
• Comparison Between 4 and 8 Instances. As il-
lustrated in Figure 4, the performance dynamics
between the 4 and 8 instances setups reveal simi-
lar patterns as with the 0.1% scenario. No defini-
tive speedup benefit was witnessed when transi-
tioning from 4 to 8 instances. However, an iden-
tical artefact was noticed, with the data exchange
occurring at the 50th iteration. Had this exchange
been initiated earlier, especially with the 8 in-
stances configuration, a faster convergence might
have been realized, primarily with instance 3 ex-
hibiting swifter convergence patterns, mirroring
the 0.1% scenario observations.
• System Stability. A captivating trend emerged in
the 1% scenario. Compared to the 0.1% scenario,
the score oscillations were discernibly reduced,
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
380

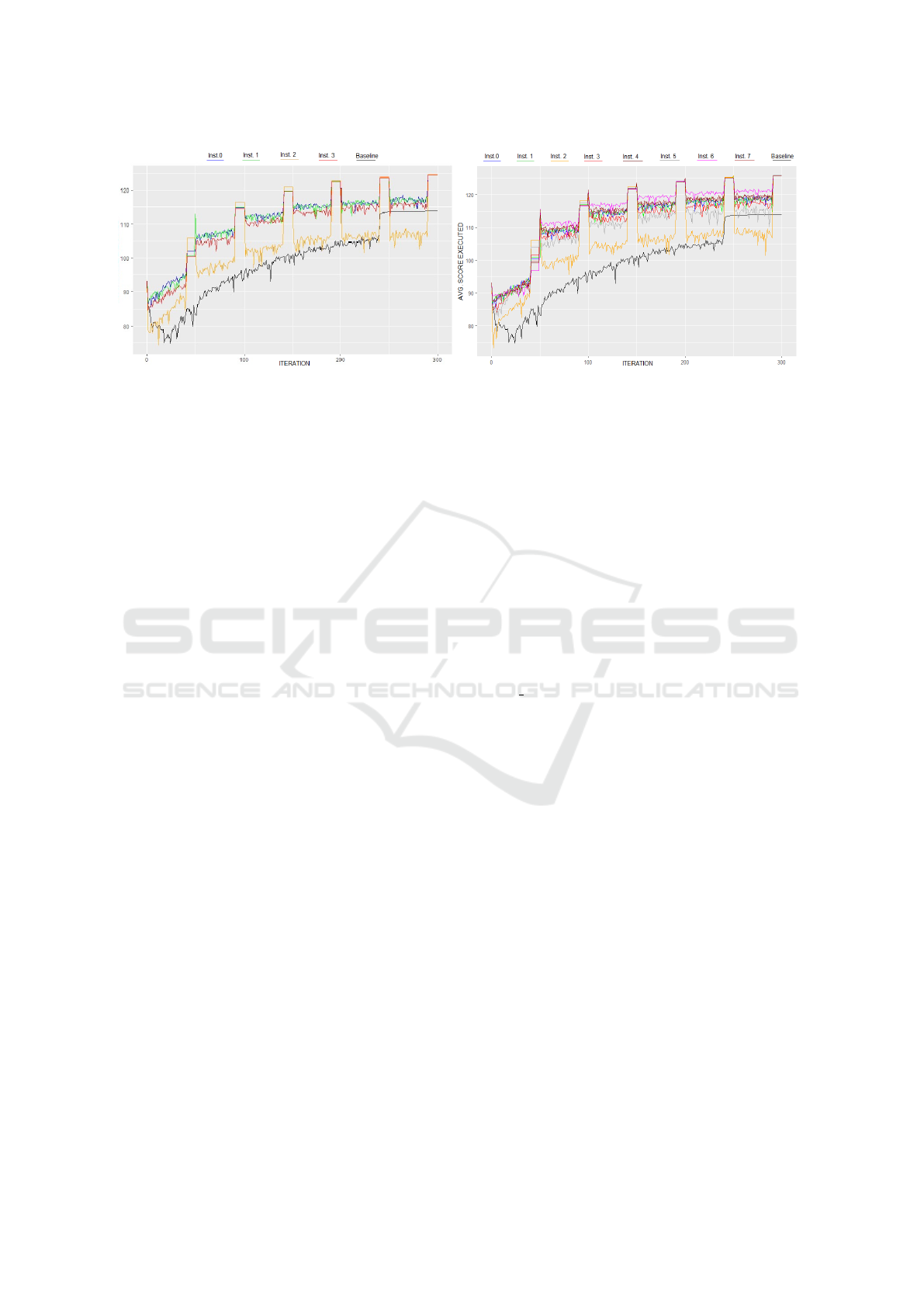
Figure 3: Average Scores of Executed Plans of multiMATSim 0.1% across Iterations: 4 and 8 Instances Side by Side (with
step = 50).
suggesting enhanced system stability when han-
dling an increased agent count.
5.2 Discussion: Scalability and
Performance Insights
Our results call for a closer examination of the per-
formance nuances of multiMATSim in comparison to
standard MATSim.
• Effect of Communication. One of the founda-
tional strengths of multiMATSim lies in the strate-
gic exchange of information between instances.
While the impact is clearly demonstrated with 4
instances, the inclusion of 8 instances, although
not necessarily yielding superior results in this
context, showcases undeniable potential, partic-
ularly with the marked score increase following
the initial exchange. Had this first exchange oc-
curred earlier, we might have witnessed even bet-
ter scalability with 8 instances. Such an improve-
ment could be attributed to a broader and quicker
exploration of potentialities with 8 instances. Op-
timizing the granularity, frequency, and timing of
these exchanges can be a potential avenue for fur-
ther refining performance. This may involve so-
phisticated strategies like adaptive exchange in-
tervals based on observed system performance or
even agent-specific data exchanges.
• Trade-off Between Duration and Convergence.
Although the total execution time may increase
more or less, we witness a markedly quicker con-
vergence. Furthermore, the surge in data pro-
cessed within a single node (via the 1% scenario)
attests to the effective scalability of the approach.
The heightened resource allocation, paired with
data amounts proportional to these resources (dur-
ing the transition from 4 to 8 nodes with 4 to
8 instances), shows no performance degradation.
This hints at a potential for even better scalabil-
ity with suitable tuning, especially when consid-
ering a step < 50. This assumption prompted us
to delve deeper into experiments by adjusting the
step value to assess its impact. The findings can
be found in Section C.
• Influence of Strategy Parametrization on
Execution. The influence of Replanning strategy
parametrization on execution duration is signifi-
cant. Specifically, Instance 2 had an execution
time up to 1.5 times longer than its peers. This, in
a system with synchronous communications, af-
fects the entire execution of multiMATSim. With
nb plans = 1, planselector is neutral. Then, low-
ering its weight amplifies other strategies, slow-
ing execution. However, Instance 2 still outper-
forms the sequential version in terms of conver-
gence. Possible reconfiguration could enhance its
performance.
• Stark Difference in Total Execution Times. The
variance in total execution times between MAT-
Sim 0.1% and multiMATSim 0.1%, and MAT-
Sim 1% and multiMATSim 1% scenarios demands
attention. The disparity can be attributed to
the weightage of Replanning strategies, increased
number of agents, and the time-consuming pro-
cessing of XML files in the 1% scenario. A re-
duction in the frequency of data exchanges might
be more beneficial in data-intensive setups.
5.3 Results and Influence of Step Value
Variation
Upon observing encouraging results with multiMAT-
Sim at step = 50, both for N = 4 and N = 8, we no-
ticed that the improvements with N = 8 were only
modest compared to those with N = 4, despite dou-
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework
381

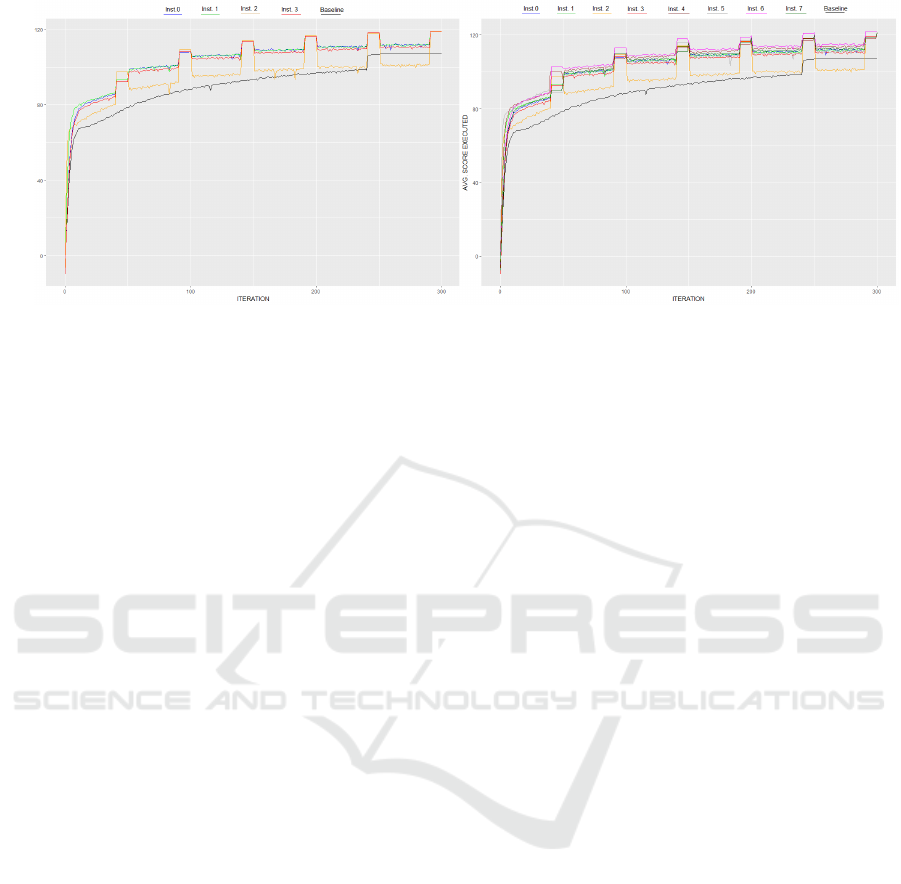
Figure 4: Average Scores of Executed Plans of multiMATSim 1% across Iterations: 4 and 8 Instances Side by Side (with
step = 50).
bling the resources. This observation prompted us to
explore a lower step value, aiming to assess the im-
pact of earlier exchanges when using a larger number
of instances. We thus opted to conduct experiments
using step = 25 and N = 8, enabling exchanges every
25 iterations among the 8 MATSim instances. Figure
5 displays the average score of the executed plans in
multiMATSim for the Los Angeles 0.1% scenario, us-
ing N = 8 and step = 25. Figure 6 shows similar data,
but for N = 4. While the graphical results for the Los
Angeles 1% scenario are not shown here, we noticed
the same patterns. The observations are as follows:
Configuration: step = 25; Instances: N = 8
(Figure 5):
• Some exchanges, notably from Instance 6, not
only match but even surpass the convergence
score of 105 right after the initial exchange.
• Some instances require more iterations after the
first exchange to match or exceed this score.
• The convergence score of 105 is achieved within
roughly 45 minutes.
In light of the promising results observed with the cur-
rent setup, we felt compelled to further assess the im-
pact of step = 25 while retaining N = 4.
Configuration: step = 25; Instances: N = 4
(Figure 6):
• There’s no immediate benefit observed after the
first exchange.
• However, performance improvements become ev-
ident following the second exchange.
Observation Summary. The results underscore
the effectiveness of the multiMATSim approach in
hastening convergence compared to the baseline. The
frequency of data exchanges plays a crucial role in
performance, yet, even when increasing the number
of instances, the added execution time remains min-
imal. This sets the stage for a deeper analysis in the
subsequent sections.
5.3.1 Analysis and Discussion
We observed and analyzed the following three phe-
nomena:
• Synergistic Effect of Instance Count and
Exchange Frequency. The initial exchange at
25 iterations manifests benefits for N = 8 (as seen
in Figure 5) but not for N = 4 (as per Figure 6).
With an augmented number of instances, there’s
presumably a heightened diversity in generated
plans. This could signify that during the pre-
liminary stage, there’s an enhanced probability of
possessing significantly divergent plans between
instances, rendering early exchanges beneficial.
With N = 4, the diversity might not be adequately
expansive for the early exchange to be effective.
• Exploratory Space Influence. An expanded ex-
ploratory space is available with N = 8, and the
exchange at 25 iterations could enable the supe-
rior dissemination of propitious strategies across
this space (as depicted in Figure 5). For N = 4 (as
seen in Figure 6), the same initial exchange might
not infuse ample novelty.
• Inference. The apparent lack of benefits with
a preliminary 25 iteration exchange for N = 4,
as opposed to N = 8, implies that the utility of
exchanges hinges not merely on plan maturity,
but also on the diversity of plans accessible for
exchange. This underlines the paramountcy of
contemplating both the instance count and ex-
change frequency when optimizing convergence
speed and quality.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
382

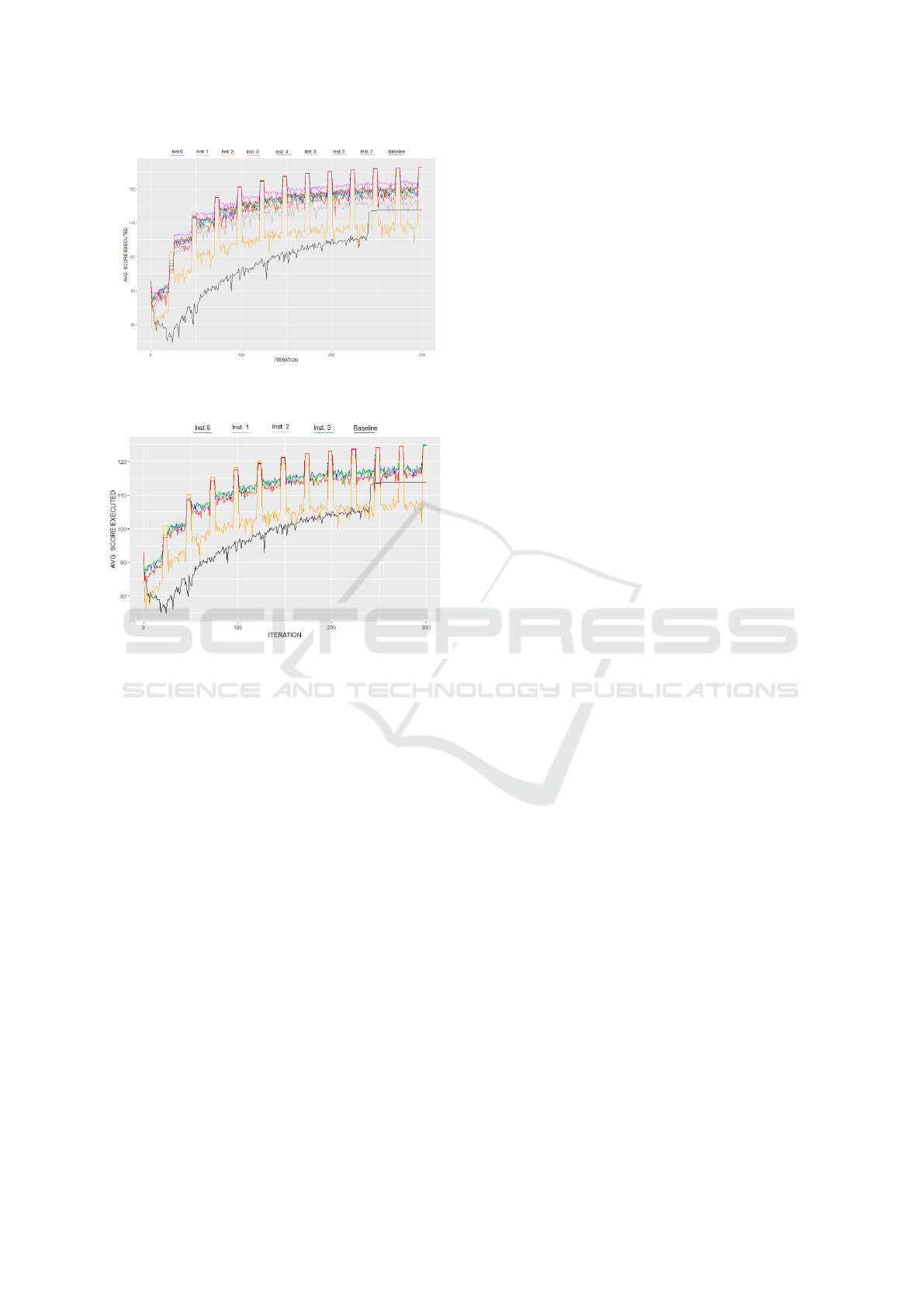
Figure 5: Average Scores of Executed Plans of multiMAT-
Sim 0.1% across Iterations: 8 Instances with step = 25.
Figure 6: Average Scores of Executed Plans of multiMAT-
Sim 0.1% across Iterations: 4 Instances with step = 25.
5.4 Performance Comparison Between
A64FX and Intel Xeon Gold 6230
for MATSim
In the following sections, all analyses used step = 50.
While the results were based on Ruche’s nodes, MAT-
Sim’s performance on Fugaku was markedly slower.
Therefore, for the 0.1% scenario, we shifted to com-
paring the durations of a limited number of iterations.
As MATSim underpins multiMATSim, this clearly had
implications for it.
1. Execution Duration.
• A64FX. For a typical MATSim LA 0.1% itera-
tion, the execution time is 10 minutes.
• Intel Xeon Gold 6230. Under similar condi-
tions, the Intel Xeon Gold 6230 CPU com-
pleted an iteration in just 2/3 minutes.
2. Processing Efficiencies.
• A64FX. Despite being designed for HPC work-
loads, efficiency for predominantly sequential
programs like MATSim is lower, with notable
observations of pipeline stalls, particularly for
loops with a complex body.
• Intel Xeon Gold 6230. Demonstrating better
adaptability for sequential or slightly parallel
applications, this architecture exhibited a supe-
rior ability to process MATSim efficiently.
5.4.1 Results on Fugaku
Although the execution time of MATSim was longer
on Fugaku, we still wanted to verify our approach.
We launched multiMATSim LA 0.1% × 4 with a re-
duced number of iterations (60), exchanging at the
50th iteration. The behavior was consistent with that
on Ruche, with a convergence that seemed faster com-
pared to MATSim LA 0.1%. It took about 8 hours on
Fugaku to reach the score of 105 with multiMATSim
LA 0.1%, while it took about 30 hours with baseline
MATSim LA 0.1%.
5.4.2 Architectural Differences
The profiler revealed differing behaviors of the JVM,
with JVM settings varying between the CPUs. The
number of calls to the garbage collector remained the
same between the two CPUs, but the GC intervention
times were much longer on the A64FX.This might
simply be due to the architectural differences between
the two CPUs and may not be related to the differ-
ence in performance. Other differences were noted,
such as thread management or memory management,
which can be explained in the same manner.
5.5 Discussion on Performance
Differences
The observed performance variations between the
A64FX and Intel Xeon Gold 6230 architectures when
executing MATSim are intriguing. These differences
can be elucidated by examining the interplay of ar-
chitectural attributes and MATSim’s inherent software
characteristics.
5.5.1 Sequential Nature of MATSim
MATSim’s design leans heavily towards sequential
execution, with only intermittent multithreading on
specific modules. Such a design paradigm is intrin-
sically reliant on stable and robust CPU performance.
• The A64FX’s compact core structure and di-
minished resources for out-of-order optimization
are not optimally suited for applications that are
chiefly sequential.
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework
383

• MATSim’s inability to exploit SIMD instructions
means that SVE functionalities within the A64FX
are not leveraged.
• The longer pipeline structure of A64FX, prone to
stalls for loops with intricate bodies, may act as
a bottleneck for MATSim, which is replete with
complex looped structures.
5.5.2 Java and MATSim
It is possible that the JVM operates different op-
timizations for the two distinct CPU architectures.
Some studies(Poenaru et al., 2021)(Jackson et al.,
2020) have revealed that the performance of A64FX
could be greatly enhanced through the use of libraries
specifically compiled by Fujitsu. However, the only
available version of OpenJDK compiled by Fujitsu is
OpenJDK 11, which is relatively old. For instance,
during an iteration of MATSim on Los Angeles 0.1%
with Fugaku, the execution time reduces from approx-
imately 15 minutes using OpenJDK 11 (compiled by
Fujitsu) to 10 minutes using OpenJDK 17 (compiled
by GCC). The improvement can be partly attributed
to the fact that OpenJDK version 17 incorporates spe-
cific optimizations for ARM processors. It is plausi-
ble that a version of OpenJDK 17 or later, compiled
by Fujitsu, could yield even better results.
5.5.3 Intel Xeon Gold 6230’s Affinity
Considering the Intel Xeon Gold 6230 architecture:
• Its potential for a more generous die-size provides
enhanced resources for out-of-order executions,
which can be a boon for predominantly sequen-
tial tasks such as MATSim.
• This architecture’s universalistic approach might
encompass optimizations that harmoniously cater
to both sequential and sporadically parallel tasks.
5.5.4 Concluding Thoughts
While the A64FX boasts commendable prowess, par-
ticularly in memory-focused benchmarks and power
efficiency, its design principle appears to be skewed
towards applications that are intensively parallel. In
contrast, the Intel Xeon Gold 6230, possibly equipped
with larger core sizes and generalized optimizations,
seems more in tune with MATSim’s operational pat-
terns.
The insights gathered suggest that harness-
ing MATSim’s potential on architectures similar to
A64FX would entail a significant overhaul to maxi-
mize its parallel processing proficiencies. Conversely,
future computational architectures might need to
strike a balanced chord, catering seamlessly to both
parallel and sequential workflows for holistic effi-
ciency.
6 CONCLUSION
In our investigation of the multiMATSim method, the
outcomes regarding scalability have been heartening.
Although limiting our tests to 4 and 8 nodes doesn’t
capture the full essence of scalability, the data of-
fers informative and optimistic views on how mul-
tiMATSim responds with an increasing number of
nodes. These initial outcomes lay the groundwork for
deeper dives into how our method scales as we en-
hance computational resources. Additionally, as the
per-node load grows, we noticed a reliable enhance-
ment in performance. Augmenting the computational
nodes while simultaneously upping the MATSim in-
stances for multiMATSim maintains steady perfor-
mance. Given the pronounced improvements in aver-
age plan scores, it’s plausible that initiating exchanges
earlier might yield a pronounced acceleration. Such
outcomes leave us optimistic about achieving better
results with heightened load, alluding to the potential
of augmented horizontal and vertical scalability. For
our forthcoming experiments, the LA 10% scenario
emerges as a favorable choice, pressing our system’s
limits with additional instances, nodes, and optimized
parameters. On a distinct note, while running our
framework on two varied CPU architectures - x86 and
ARM, we detected subtle behavioral variations. Al-
though the ISA (Instruction Set Architecture) may not
be the sole determinant, the differences in core sizes
between these CPUs probably have a role. In this con-
text, our intention is to delve into Amazon’s Gravi-
ton 3, an ARM-centric CPU boasting larger cores.
It’s pertinent to mention that the A64FX, which is
tailored for intensive parallel tasks using innovations
like SVE or HBM memory, might not reach its full
potential with a primarily sequential tool like MAT-
Sim. Given the fact that MATSim is optimized more
for the x86 architecture and the opportunities pre-
sented by a JVM library recently launched by Fujitsu,
there’s an open avenue for additional inquiry. Still, in
terms of convergence velocity on Fugaku, multiMAT-
Sim manages to surpass MATSim. Our grand vision
is to gauge the universality of this Unite and Conquer
strategy on alternative multi-agent traffic simulators,
such as SUMO(Alvarez Lopez et al., 2018) or PO-
LARIS(Auld et al., 2016), underscoring its extensive
relevance.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
384

REFERENCES
Alvarez Lopez, P., Behrisch, M., Bieker-Walz, L., Erdmann,
J., Fl
¨
otter
¨
od, Y.-P., Hilbrich, R., L
¨
ucken, L., Rum-
mel, J., Wagner, P., and Wießner, E. (2018). Micro-
scopic traffic simulation using sumo. In IEEE Intelli-
gent Transportation Systems Conference (ITSC).
Auld, J., Hope, M., Ley, H., Sokolov, V., Xu, B., and
Zhang, K. (2016). Polaris: Agent-based modeling
framework development and implementation for inte-
grated travel demand and network and operations sim-
ulations. Transportation Research Part C: Emerging
Technologies.
Emad, N. and Petiton, S. (2016). Unite and conquer ap-
proach for high scale numerical computing. Inter-
national Journal of Computational Science and En-
gineering, 14:5–14. hal-01609342.
Horni, A. and Axhausen, K. (2012). Matsim agent het-
erogeneity and a one-week scenario. Technical Re-
port 836, Institute for Transport Planning and Systems
(IVT), ETH Zurich, Zurich.
Horni, A., Nagel, K., and Axhausen, K. W. (2016). Intro-
ducing MATSim, chapter Introducing MATSim, pages
3–8. Ubiquity Press, London. License: CC-BY 4.0.
Jackson, A., Weiland, M., Brown, N., Turner, A., and Par-
sons, M. (2020). Investigating applications on the
a64fx. In 2020 IEEE International Conference on
Cluster Computing (CLUSTER), pages 549–558, Los
Alamitos, CA, USA. IEEE Computer Society.
Ma, Z. and Fukuda, M. (2015). A multi-agent spatial sim-
ulation library for parallelizing transport simulations.
In 2015 Winter Simulation Conference (WSC), pages
115–126.
Mastio, M., Zargayouna, M., Sc
´
emama, G., and Rana, O.
(2018). Distributed agent-based traffic simulations.
IEEE Intelligent Transportation Systems Magazine,
10.
Nguyen, J., Powers, S. T., Urquhart, N., Farrenkopf, T.,
and Guckert, M. (2021). An overview of agent-based
traffic simulators. Transportation Research Interdis-
ciplinary Perspectives, 12:100486.
of Paris-Saclay, U. (2020). M
´
esocentre de l’universit
´
e paris-
saclay. Accessed on: August 17, 2023.
Poenaru, A., Deakin, T., McIntosh-Smith, S., Hammond,
S., and Younge, A. (2021). An evaluation of the fujitsu
a64fx for hpc applications. In Cray User Group 2021.
Cray User Group 2021 ; Conference date: 03-05-2021
Through 05-05-2021.
Potuzak, T. (2020). Reduction of inter-process commu-
nication in distributed simulation of road traffic. In
2020 IEEE/ACM 24th International Symposium on
Distributed Simulation and Real Time Applications
(DS-RT), pages 1–10.
Sato, M. et al. (2020). Co-design for a64fx manycore pro-
cessor and ”fugaku”. In SC20: International Confer-
ence for High Performance Computing, Networking,
Storage and Analysis, pages 1–15, Atlanta, GA, USA.
TOP500 (2023). The list: June 2023. Accessed on: August
17, 2023.
Zhuge, C., Bithell, M., Shao, C., Li, X., and Gao, J. (2021).
An improvement in matsim computing time for large-
scale travel behaviour microsimulation. Transporta-
tion, 48.
Advancements in Traffic Simulations with multiMATSim’s Distributed Framework
385