Enhancing Constraint Optimization Problems with Greedy Search and
Clustering: A Focus on the Traveling Salesman Problem
Sven L
¨
offler, Ilja Becker and Petra Hofstedt
Brandenburg University of Technology Cottbus, Senftenberg, Konrad-Wachsmann-Allee 5, 03046 Cottbus, Germany
Keywords:
Constraint Satisfaction, Planning and Scheduling, Hybrid Intelligent Systems, Traveling Salesman Problem,
Greedy Search, Clustering.
Abstract:
Constraint optimization problems offer a means to obtain at a global solution for a given problem. At the same
time the promise of finding a global solution, often this comes at the cost of significant time and computational
resources. Greedy search and cluster identification methods represent two alternative approaches, which can
lead fast to local optima. In this paper, we explore the advantages of incorporating greedy search and clustering
techniques into constraint optimization methods without forsaking the pursuit of a global solution. The global
search process is designed to consider clusters and initially behave akin to a greedy search. This dual strategy
aims to achieve two key objectives: firstly, it accelerates the attainment of an initial solution, and secondly,
it ensures that this solution possesses a high level of optimality. This guarantee is generally elusive for con-
straint optimization problems, where solvers may struggle to find a solution, or find one of adequate quality
in acaptable time. Our approach is an improvement of the general Bunch-and-Bound approach in constraint
programming. Finally, we validate our findings using the Traveling Salesman Problem as a case study.
1 INTRODUCTION
Constraint programming serves a dual purpose: solv-
ing satisfiability problems and tackling optimization
problems. In the realm of optimization, constraint
problems provide a global solution approach capable
of discovering a globally optimal solution given am-
ple time. Regrettably, the required time can quickly
escalate to unacceptable levels due to the exponential
growth in complexity with the problem size, necessi-
tating compromise with locally optimal solutions.
Alternative strategies for substantial optimization
problems include using greedy methods, systemati-
cally selecting locally optimal actions at each step,
aiming for an overall good solution in a condensed
timeframe. Strategically forming clusters can be an-
other way to reduce the problem size and accelerate
the solution process of problem instances. While this
method concentrates on promising search space areas,
it may unintentionally miss other regions that contain
potentially better solutions.
In this paper, we aim at amalgamating greedy
search and cluster utilization into constraint prob-
lems. Our goal is to accelerate the process of attain-
ing an initial, high-quality solution, finally reducing
the overall runtime of the search while preserving the
global and comprehensive nature of the approach.
The remaining paper is structured as follows:
Chapter 2 provides the essential foundations of the
Traveling Salesman Problem, Constraint Program-
ming, Greedy Algorithms, and Clustering methods.
Chapter 3 introduces three typical constraint-based
models of the Traveling Salesman Problem, which
are then examined in Chapter 4 using Greedy and
Clustering-based approaches. Chapter 5 discusses the
quality of results achieved by these different models
when employing greedy search and clustering meth-
ods in comparison to the original formulations. Fi-
nally, Chapter 6 offers a brief summary and outlines
prospects for future work.
2 PRELIMINARIES
Below, we briefly introduce the Traveling Salesman
Problem and explain the fundamentals of constraint
programming, greedy search, and clustering methods.
2.1 The Traveling Salesman Problem
The Traveling Salesman Problem (TSP) is a classi-
cal and widely studied problem in the field of op-
1170
Löffler, S., Becker, I. and Hofstedt, P.
Enhancing Constraint Optimization Problems with Greedy Search and Clustering: A Focus on the Traveling Salesman Problem.
DOI: 10.5220/0012453000003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 3, pages 1170-1178
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

timization and computer science (Cheikhrouhou and
Khoufi, 2021; Pintea, 2015). It is a combinatorial op-
timization problem that can be described as follows:
Given a list of n cities and the distances between
each pair of cities by a cost matrix M with M
i, j
are
the costs to go from city i to j, the goal is to find
the shortest possible route that visits each city exactly
once and returns to the original starting city. The chal-
lenge is to determine the optimal order in which the
cities should be visited to minimize the total cost, i.e.
the total distance travelled.
The TSP can manifest in both symmetric form
(costs of an edge from node i to j and from j to i are
equal) and asymmetric form (costs of an edge from
node i to j and from j to i can differ). In the subse-
quent sections of this paper, we exclusively address
symmetric TSPs; however, the approaches outlined
can be extended to asymmetric TSPs.
The problem is known to be NP-hard, which
means that as the number of cities increases, the num-
ber of possible routes grows exponentially, making it
computationally challenging to find an optimal solu-
tion for large instances of the TSP. For small TSP in-
stances (typically ≤ 20 cities), exact algorithms like
the Branch-and-Bound algorithm or dynamic pro-
gramming can be employed to find an optimal solu-
tion. These algorithms explore all possible routes and
identify a shortest one (Roberti and Ruthmair, 2021).
In the case of medium-sized TSP instances,
heuristic methods such as the Nearest Neighbor
heuristic, the Insertion heuristic, or the 2-opt heuris-
tic are often utilized. These methods quickly pro-
vide good solutions without exhaustively examining
all potential routes (Bernardino and Paias, 2021).
In this paper, we are not comparing existent meth-
ods to solve the TSP, but rather, we are striving to
enhance an exact approach (a constraint optimiza-
tion problem, COP) to initially operate like a heuris-
tic method (Greedy Search), and subsequently, ex-
plore the entire search space. While traditional greedy
search is not complete (no guarantee to find a global
optimum), we use this method within a branch-and-
bound approach to find a first good solution as a
bound for further search. Due to the nature of how
COPs are handled and solved, the overall proceedure
remains complete, and, given an unlimited amount of
time, a global optimal solution can be achieved.
2.2 Constraint Programming
Constraint programming (CP) stands as a methodol-
ogy for the declarative modeling and resolution of
complex problems, particularly those falling within
the NP-complete and NP-hard categories. Problem
domains addressed by CP encompass rostering, graph
coloring, optimization, and satisfiability (SAT) chal-
lenges (Marriott and Stuckey, 1998). In this section,
we present the fundamental concepts of constraint
programming that are the basic of our approach.
The general process of constraint programming
unfolds in two distinct phases:
1. The declarative formulation and representation of
a problem as a constraint model. This encap-
sulates the articulation of constraints, variables,
and their interrelationships, effectively defining
the problem’s or solution’s logical structure.
2. The resolution of the constraint model via a ded-
icated constraint solver. The solver operates in-
dependently, akin to a self-contained black box,
tackling the intricacies of the problem.
In essence, the CP user’s role primarily entails the
crafting of the application-specific problem model us-
ing constraints, along with the setup and initiation of
the solver. The solver, acting autonomously, employs
advanced techniques to explore potential solutions
and reach an optimal or satisfactory solution. This
separation of responsibilities simplifies the problem-
solving process and empowers domain experts to con-
centrate on the abstract representation of their real-
world challenges.
A constraint satisfaction problem (CSP) is for-
mally defined as a 3-tuple P = (X, D,C), comprising
the following components: X = {x
1
, x
2
, . . . , x
n
} rep-
resents a set of variables. D = {D
1
, D
2
, . . . , D
n
} is a
collection of finite domains, where D
i
denotes the do-
main of variable x
i
. C = {c
1
, c
2
, . . . , c
m
} constitutes a
set of constraints, with each constraint c
j
defined over
a subset of variables from X (Apt, 2003).
A constraint, denoted by a tuple (X
′
, R), consists
of a relation R and an ordered set of variables X
′
,
which is a subset of X, over which the relation R is
defined (Dechter, 2003). For instance, examples of
constraints include ({x, y}, x < y), ({x, y, z}, x+y = z),
or ({A, B}, A → B). Given that the variables involved
in a constraint are explicitly identifiable within their
corresponding relation, we solely specify the relation
in the subsequent sections of this paper.
A solution of a CSP involves the instantiation of
all variables x
i
with values d
i
from their respective
domains D
i
, such that all constraints are satisfied.
Additionally, a constraint optimization problem
(COP) extends the scope of a CSP. In a COP, an opti-
mization variable x
opt
is explicitly identified, and the
objective is to minimize or maximize this variable to
reach an optimal solution.
Below, some globally significant constraints for
the work are introduced. According to (van Hoeve
Enhancing Constraint Optimization Problems with Greedy Search and Clustering: A Focus on the Traveling Salesman Problem
1171

and Katriel, 2006), Global Constraints describe com-
plex conditions that would otherwise be represented
by a multitude of simpler constraints. The two main
advantages of global constraints over the combination
of multiple primitive constraints are, on the one hand,
better-tailored propagation algorithms, allowing for
faster propagation and more accurate exclusion of do-
main values in most cases, and, on the other hand, the
ability to model complex scenarios with few, concise,
and understandable constraints.
The allDifferent constraint is one of the most ex-
tensively researched constraints (L
´
opez-Ortiz et al.,
2003; Van Hoeve, 2001). It ensures that for a set of
variables {x
1
, ..., x
n
}, each variable is assigned a pair-
wise distinct set of domain values {d
1
, ..., d
n
}.
allDifferent({x
1
, ..., x
n
}) := {(d
1
, ..., d
n
) |
d
i
̸= d
j
∀i, j ∈ {1, ..., n}, i < j}
(1)
The count constraint is a modification of the alld-
ifferent constraint. For an ordered set of variables
{x
1
, ..., x
n
} = X and an additional variable occ with
an associated domain D
occ
= {occ
min
, ..., occ
max
}, it is
required that the number of occurrences of the value
v ∈ N in an assignment of the variable set X corre-
sponds to the value of the variable occ:
count(X, occ, v) ⇔ (
∑
x∈X
(
0 x ̸= v
1 x = v
) = occ (2)
The element constraint demands that for a value
variable v, an index variable i, and a list of values
m
1
, ..., m
n
, the variable v must take on the value m
i
(Demassey and Beldiceanu, 2022).
elememt(v, {m
1
, ..., m
n
}, i) ⇔ v = m
i
(3)
The circuit constraint requires, for an ordered
set of variables {x
1
, x
2
, ..., x
n
}, that the value d
i
of a
variable x
i
indicates the next value in the sequence.
Across the n variables, a path, free of cycles, must be
created from variable x
1
back to variable x
1
. The val-
ues d
i
of the variables {x
1
, x
2
, ..., x
n
} must thus all be
distinct from each other (Demassey and Beldiceanu,
2022).
circuit({x
1
..., x
n
}) ⇔ {(d
1
, ..., d
n
) with d
1
, d
d
1
,
d
d
(d
1
)
, ... is a cycle-free path from d
1
to 1}
(4)
An example solution of a circuit constraint is the
following number sequence 4312, indicating that one
travels from city 1 (always the start) to city 4 (value d
1
of the 1st no.), then from there to city 2 (value d
(d
1
)
=
d
4
of the 4th no.), followed by city 3 (value d
(d
(d
1
)
)
=
d
2
of the 2nd no.), and finally back to city 1 (value
d
(d
(d
(d
1
)
)
)
= d
3
of the 3rd no.).
2.3 Greedy Search
Greedy Search (an instance of Best-First Search) is a
highly straightforward heuristic approach. It is conse-
quently efficient and easy to implement. In each step,
it simply selects the best-rated successor (Aggarwal,
2021; Russell and Norvig, 2010). This search evokes
a greedy focus on the immediate next step, consis-
tently prioritizing the investigation of cost-favorable
areas of the search space. However, it is important to
note that the best-rated successor does not necessarily
lead to the overall best solution. Greedy Search can-
not tolerate the selection of a single lower-rated node,
even if that choice would eventually lead to a signifi-
cantly superior solution path.
As Greedy Search prioritizes the current moment
over holistic considerations, it can favor local op-
tima over global optima. However, for many com-
plex search problems, a local optimum is sufficient.
Greedy Search explores only one solution path in the
search tree, requiring little memory and time.
2.4 Clustering Algorithms
Clustering, a key aspect of data mining, is a mean
of grouping data into multiple collections or clusters
based on similarities in the features and characteris-
tics of data points (Abualigah, 2019; Jain, 2010). In
recent years, numerous techniques for data clustering
have been proposed and implemented to address data
clustering challenges (Abualigah et al., 2018; Zhou
et al., 2019). Clustering analysis techniques can be
broadly classified as being hierarchical (Ran et al.,
2023) or partitional (Sch
¨
utz et al., 2023).
Hierarchical clustering algorithms break up the
data in to a hierarchy of clusters. They repeat a cycle
of either merging smaller clusters in to larger ones or
dividing larger clusters to smaller ones. Either way,
it produces a hierarchy of clusters called a dendo-
gram. Partitional clustering algorithms produce mul-
tiple partitions which are then assessed using a crite-
rion. They are also known as non-hierarchical since
every instance is assigned to exactly one of k clusters
that are mutually exclusive. As a typical partitional
clustering algorithm only yields a single set of clus-
ters, the user is required to input the desired number
of clusters, typically referred to as k.
While the methods falling under these two groups
have shown remarkable effectiveness and efficiency,
they usually necessitate prior knowledge or informa-
tion of the precise number of clusters in each dataset
to be clustered and analysed (Chang et al., 2010).
When working with real-world datasets, it is typical to
lack prior information about the number of naturally
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1172

occurring groups in the data objects (Liu et al., 2011).
Hence, automatic data clustering algorithms are intro-
duced to address this limitation (Garc
´
ıa and G
´
omez-
Flores, 2023). These are clustering techniques used
to determine the number of clusters in a dataset with-
out prior knowledge of its features and attributes, as
well as to assign elements to these clusters based on
inherent patterns within the data.
3 TYPICAL TSP CONSTRAINT
MODELS
In the literature, the Miller-Tucker-Zemlin modeling
(Miller et al., 1960) is frequently employed for Trav-
eling Salesman Problems. This modeling approach
relies on the use of Boolean variables and linear
constraints. In the following, we will refer to this
modeling approach as the Boolean-based COP. Other
plausible modeling approaches could utilize the well-
known allDifferent constraint or the global circuit
constraint as their foundation. Below, we will briefly
introduce these three modeling approaches.
3.1 A Boolean-Based COP
Figure 1 illustrates our Boolean-based COP. This
model mirrors the Miller-Tucker-Zemlin model, with
one main difference: it employs count constraints in
place of certain linear constraints. Our preference
for count constraints is founded on our empirical re-
search, showing their superior propagation speed.
The main idea of this approach is it to decide for
every possible edge i to j whether it must be part of
the solution path, or not. Therfore, every node must
have exactly one incoming and one outgoing edge.
Furthermore it must be checked that no cycles with
less then all vriables exists.
In this model, each Boolean variable x
B
i, j
∈ X
B
(line 1) denotes whether a path from i to j is included
in the solution (x
B
i, j
= 1) or not (x
B
i, j
= 0). The vari-
ables within X
P
(line 2) serve as auxiliary variables
with the constraints C
S
(line 7) to prevent cycles. The
constraints C
S
are linear representations of the logical
constraint x
B
i, j
⇒ x
P
i
< x
P
j
. This means, that there can
not be a path l to i and j to l, because l can not be
lower then i and bigger then j at the same time.
The variable x
t
(line 2) represents the total cost.
Constraint C
T
(line 9) guarantees that the costs
precisely correspond to the summation of elements
within the cost matrix attributed to the solution path.
The remaining constraints C
C
ensure that there is al-
ways exactly one path leading to each city (line 6) and
also away from it (line 5).
Critical in this model are the Boolean variables in
X
B
. When these are entirely instantiated, the entire
model is instantiated. Conversely however, the in-
stantiation of position variables X
P
does not imply an
instantiation of the Boolean variables. This implies
that in this direction, inevitably, more assignments
must be made through the search, potentially requir-
ing more time-consuming backtracking in the search
process. To prevent this, the search strategy was de-
vised in such a way that initially, only the Boolean
variables are assigned.
Expectation: A first solution may not be found
without backtracking, as the constraints in line 7 may
contrast with the previous assignments of the vari-
ables X
B
.
3.2 An AllDifferent-Based COP
Figure 2 illustrates our allDifferent-based COP. This
model incorporates, as a central element, an allDiffer-
ent constraint (line 6) covering all position variables
(line 1). Each position variable is thereby assigned a
city (from 1 to n). Every variable assignment x
P
i
= c
indicates that city c is visited at the i-th position. City
1 is defined as the starting city (line 5). The constraint
in line 7 specifies that the cost to travel from city x
P
i
to city x
P
i+1
must be equal to M
x
P
i
,x
P
i+1
. The constraint
in line 8 additionally considers the cost to return from
the last city back to the first city. Finally, the total
costs are added (line 10) and minimized (line 11).
Expectation: A first solution can be found with-
out backtracking when the X
P
variables are sequen-
tially assigned different values, all variables X
C
and
x
t
become unique. The allDifferent constraint is con-
sistent, and the x
C
variables are uniquely determined
without contradictions through the X
P
variables and
element constraints.
3.3 A Circuit-Based COP
A central component of the circuit-based COP is the
circuit constraint (line 5), ensuring that the variable
X
P
i
at index i always indicates the index of the next
city to be visited. This means that the values of the
variables x
P
1
, x
P
2
, ..., x
P
n
do not reflect the order of the
cities to be visited in this sequence. Instead, starting
from city 1, the next city to be visited must have an
index i equal to the value of x
P
1
. Subsequently, the
city with an index j equal to the value of x
P
i
is visited,
and so on. An example of the circuit constraint was
provided in Section 2.
The element constraints in line 6 ensure that the
costs are calculated, which are needed to go from city
i to the city whose index is equal to the value of x
P
i
.
Enhancing Constraint Optimization Problems with Greedy Search and Clustering: A Focus on the Traveling Salesman Problem
1173

P = (X, D,C, f ) with:
1 X = X
B
= {x
B
i, j
| ∀i ∈ {1, ..., n}, j ∈ {1, ..., n}} ∪ (n × n Boolean variables)
2 X
P
= {x
P
i
| ∀i ∈ {2, ..., n}} ∪ {x
t
} (n − 1 position variables and 1 total cost variable)
3 D = {D
B
= {D
B
1,1
, D
B
1,2
, ..., D
B
n,n
} with D
B
i, j
= {0, 1}} ∪
4 {D
P
= {D
P
2
, D
P
3
, ..., D
P
n
} with D
P
i
= {2, 3, ..., n}} ∪ {D
t
= N}
5 C = {C
C
= {count({x
B
1, j
, x
B
2, j
, ..., x
B
n, j
}, 1, 1), (Come-from constraints)
6 count({x
B
i,1
, x
B
i,2
, ..., x
B
i,n
}, 1, 1) | ∀i ∈ {1, ..., n}} ∪ (Go-to constraints)
7 C
S
= {x
P
i
− x
P
j
+ (n − 1) ∗ x
B
i, j
≤ n − 2 | ∀i, j ∈ {2, 3, ..., n} with i ̸= j} ∪
8 (x
P
i
must have a smaller value then x
P
j
if x
B
i, j
= 1)
9 C
T
= {Σ
∀i, j∈{1,...,n}
x
B
i, j
∗ M
i, j
= x
t
}}
10 minimize(x
t
)
Figure 1: The Boolean-based COP.
P = (X, D,C, f ) with:
1 X = X
P
= {x
P
i
| ∀i ∈ {1, ..., n}} ∪ (n city position variables)
2 X
C
= {x
C
i
| ∀i ∈ {1, ..., n}} ∪ {x
t
} (n cost variables and 1 total cost variable)
3 D = {D
P
= {D
P
1
, D
P
2
, ..., D
P
n
} with D
P
i
= {1, 2, ..., n}} ∪
4 {D
C
= {D
C
1
, D
C
2
, ..., D
C
n
} with D
C
i
= {1, 2, ..., maximum(M)}} ∪ {D
c
= N}
5 C = {C
S
= {x
P
1
= 1} ∪ (Home town constraint)
6 {allDifferent(X
P
)} ∪ (Visit each city ones)
7 C
E
= {element(x
C
i
, f latten(M), x
P
i
∗ n + x
P
i+1
) | ∀i ∈ {1, 2, ..., n − 1}} ∪
8 {element(x
C
n
, f latten(M), x
P
n
∗ n + x
P
1
)} ∪
9 (If there is a path from city i to j, then apply the costs M
i, j
)
10 C
T
= {Σ
∀i∈{1,...,n}
x
C
i
= x
t
}}
11 minimize(x
t
)
Figure 2: The allDifferent-based COP.
Finally, the total costs are summarized (line 8) and
minimized (line 9) as in the allDifferent-approach.
Expectation: Due to the circuit constraint, similar
to the allDifferent COP, it should be possible to find
a first solution without backtracking by only instanti-
ating the position variables X
P
. The circuit constraint
enforces local consistency over these variables, and
the cost variables X
C
and x
t
can be uniquely derived
from the assignments of the position variables X
P
.
4 GREEDY AND CLUSTERING
APPROACHES FOR COPs
In this section, we will discuss how the above COP
models (from Sect. 3) and search strategies can be
modified for greedy solution search while considering
known clusters. This still involves a standard branch
and bound algorithm, which is designed to speed up
the elimination of suboptimal areas during the solu-
tion search by using a greedy search and clustering.
The expectation is that changing the backtracking-
based search of constraint programming to a greedy
form will result in a first solution found having in av-
erage a better optimal value.
A good initial solution in a COP has the advantage
that, during the backtracking-based search, areas that
can only yield worse solutions can be omitted earlier.
The better the solution already found, the larger the
area that can be excluded. Therefore, it is advisable
to find a good solution as quickly as possible.
Clustering aims at two things. Firstly, it is in-
tended to find a good initial solution. Furthermore,
the clusters are created for the purpose of bundling the
most promising solutions within a cluster. If the clus-
tering algorithm is effective, it is expected that fol-
lowing these clusters will lead to, on average, good
solutions. The other anticipated effect is that clusters
may be beneficial for cutting off subareas with poorer
solutions in the backtracking-based search. The clus-
ters structure the solution space and groups together
solution areas. The hope is that the optimality value
for a cluster can be predicted as accurately as possi-
ble, and thus, it can be excluded from the search if a
better solution has already been found.
For this work, we used a simple clustering method
(see Equation 5). All nodes of a cluster Cl
i
always
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1174

P = (X, D,C, f ) with:
1 X = X
P
= {x
P
i
| ∀i ∈ {1, ..., n}} ∪ (n city position variables)
2 X
C
= {x
C
i
| ∀i ∈ {1, ..., n}} ∪ {x
t
} (n cost variables and 1 total cost variable)
3 D = {D
P
= {D
P
1
, D
P
2
, ..., D
P
n
} with D
P
i
= {1, 2, ..., n}} ∪
4 {D
C
= {D
C
1
, D
C
2
, ..., D
C
n
} with D
C
i
= {1, 2, ..., maximum(M)}} ∪ {D
c
= N}
5 C = {C
C
= {circuit(X
P
)} ∪ (Visit each city ones)
6 C
E
= {element(x
C
i
, M
i,∗
, x
P
i
) | ∀i ∈ {1, 2, ..., n}} ∪
7 (If there is a path from city i to x
P
i
, then apply the costs M
i,x
P
i
)
8 C
T
= {Σ
∀i∈{1,...,n}
x
C
i
= x
t
}}
9 minimize(x
t
)
Figure 3: The circuit-based COP.
have a minimum distance d to all nodes outside the
cluster. If a cluster contains more than one node, then
for each node in the cluster, there is at least one other
node in the cluster with a distance less than d.
Cluster = {Cl
1
, ...,Cl
m
| ∀Cl
i
: c ∈ Cl
i
⇔
∃c
j
∈ Cl
i
: dist(c, c
j
) ≤ d,
∀c
j
∈ {1, 2, ..., n} \Cl
i
: dist(c, c
j
) > d}
(5)
The clustering was applied in such a way that,
through newly added cluster variables x
Cl
j
for each
cluster Cl
j
, it is controlled whether this cluster is ap-
plied (x
Cl
j
= 1) or not (x
Cl
j
= 0). During the search,
the cluster variables are initially assigned to 1 before
all other variables are assigned. Thus, solutions are
always first found that include the cluster and then
those that do not include the cluster. The search re-
mains global, i.e. complete in this way.
Subsequently, for each of the three COP-models
from Section 3, the integration of greedy search, clus-
tering, and greedy search with clusters is explained.
4.1 The Boolean-Based COP
We consider the boolean-based COP from Figure 1.
Here, for a combination with greedy search, only the
search strategy of the solver must be adjusted. Since
each Boolean variable X
B
i, j
can be directly associated
with its cost value M
i, j
, a cost function for the greedy
method can be implemented. In this approach, the
Boolean variable x
P
i, j
with a value of 1 is initially ini-
tialized, corresponding to the route from city i to j
with the lowest cost. Thus, in each step, the route
connecting two cities A and B with the lowest cost is
greedily added to the solution path, where up to that
point, no successor has been determined for city A
and no predecessor for city B. This approach does
not generate the solution continuously from the start-
ing city over all other cities back to the starting city
but initially plans individual cost-effective segments,
which are then assembled into a complete solution
1
.
Technically, the variables X
B
are sorted in ascending
order based on their corresponding cost value in M,
and starting with the cheapest uninstantiated variable,
each one is instantiated with a value of 1.
After obtaining an initial solution, the
backtracking-based search continues using the
same search strategy. However, due to the high
quality of the initial solution (value for x
t
), few new
subtrees are explored. This is because only subtrees
with a better value of x
t
need to be considered.
The cluster-based approach attempts to cluster dif-
ferent solutions with the hope that, for each cluster,
the optimization value x
t
can be more accurately esti-
mated. This, in turn, enables the exclusion of an ear-
lier and a greater number of areas in the search, which
can only achieve a worse optimality value x
t
. For
the cluster-based approach, additional Boolean vari-
ables X
Cl
= {x
Cl
1
, x
Cl
2
, ..., x
Cl
k
} are introduced, where
k is equal to the number of clusters, and each vari-
able x
Cl
j
indicates whether the cluster j is adhered to
(x
Cl
j
= 1) or not (x
Cl
j
= 0). For each cluster Cl
j
, an
additional cluster constraint C
Cl
, as shown in Equa-
tion 6, is added to the model. This constraint requires
that the cluster variable x
Cl
j
is set to 1 iff the Boolean
variables X
P
describing connections within the clus-
ter (∀x
i
1
,i
2
∈ X
B
, i
1
, i
2
∈ Cl
j
), exactly k −1 of them are
set to 1. This constraint sets the cluster variable x
Cl
j
to
1 iff are k − 1 paths to cities within the cluster. Due
to the other constraints of the model, this implies that
there must be a path through all cities of cluster Cl
j
,
without visiting a city outside the cluster in between,
if x
Cl
j
is equal to 1, and otherwise not.
C
Cl
= {count({x
B
i
1
,i
1
, ..., x
B
i
k
,i
k
}, 1, |Cl
j
| − 1)
⇔ x
Cl
j
= 1 | ∀i ∈ Cl
j
}
(6)
1
The procedure is inspired by the Kruskal algorithm
for determining the shortest spanning trees within a graph
(Kruskal, 1956).
Enhancing Constraint Optimization Problems with Greedy Search and Clustering: A Focus on the Traveling Salesman Problem
1175

In the search process, the cluster variables x
Cl
j
with
a value of 1 must be instantiated before the other vari-
ables are assigned. This means that the search initially
looks for solutions that satisfy the respective clusters.
If both approaches (greedy search and clustering) are
considered simultaneously, the cluster variables x
Cl
j
must be instantiated first, followed by the Boolean
variables X
B
as described in the greedy approach.
4.2 The AllDifferent-Based COP
In the case of the allDifferent-based COP, the greedy
approach cannot be executed in the same manner as in
the Boolean-based COP. This is due to the fact that in
this model, the paths are directly tied to the order of
the city variables X
P
, which is not the case in the other
two models. This means that even if we know that the
most cost-effective connection of two cities should be
part of the solution, there are still n alternative posi-
tions for this segment in the overall route. Thus, a dif-
ferent greedy approach has been implemented here.
Gradually, starting from the last instantiated position
variable X
P
i
in the model (Figure 2), i.e., starting from
i = 1, the value of the next position variable is set such
that the costs between the cities x
P
i
and x
P
i+1
are mini-
mized. During the search, for each city, the next city
is chosen initially, which has not been selected yet and
has the lowest costs to the previous city.
For the Cluster approach, a Boolean cluster vari-
able x
cl
j
was created for each cluster Cl
j
, indicating
whether the cluster was adhered to or not. For this
purpose, a dedicated cluster constraint was developed,
which checks whether in the variables X
P
, k consecu-
tive assignments with values from the respective clus-
ter Cl
j
occur. There was also the option to use the
regular constraint for this task (a corresponding reg-
ular automaton is easy to model), however, the prop-
agation speed of the self-developed constraint is sig-
nificantly higher. In the search process, the cluster
variables x
Cl
j
with a value of 1 must be instantiated
first before the other variables are assigned.
If both approaches (greedy search and clustering)
are to be considered simultaneously, the cluster vari-
ables x
Cl
j
must be instantiated first, followed by the
position variables X
P
as described in the greedy ap-
proach.
4.3 The Circuit-Based COP
In implementing the greedy approach for the circuit-
based COP, the procedure is analogous to the boolean-
based COP. Initially, the cost variable x
C
j
∈ X
C
with
the smallest value in the domain is set to its smallest
value. Subsequently, the algorithm proceeds with the
cost variable that has not been instantiated yet and has
the lowest cost value.
A new constraint has been developed for the clus-
ter approach, which only takes input from the posi-
tion variables X
P
′
⊂ X
P
that are part of the cluster Cl
j
and newly created cluster variables x
Cl
j
. Within a clus-
ter Cl
j
, |Cl
j
| − 1 cities must have a successor within
the cluster to satisfie the cluster constraint (the clus-
ter variable x
Cl
j
receives the value 1). A city within
the cluster Cl
j
has a successor outside the cluster to
be able to exit the cluster after all cities of the clus-
ter are visited. Based on the other constraints of the
model, it is necessary that the cities within the cluster
are sequentially visited once any of them is visited.
In the search process, the cluster variables x
Cl
j
with a
value of 1 must be instantiated first before the other
variables are assigned. If both approaches (greedy
search and clustering) are to be considered simulta-
neously, the cluster variables x
Cl
j
must be instantiated
first, followed by the cost variables X
C
as described in
the greedy approach.
5 EXPERIMENTS AND RESULTS
All experiments were carried out on a LG Gram
laptop featuring an 11th Gen Intel(R) Core(TM) i7-
1165G7 quad-core processor running at a clock speed
of 2.80 GHz and 16 GB DDR3 RAM, operating at
2803 MHz. The operating system used was Microsoft
Windows 10 Enterprise.
The Java programming language with JDK ver-
sion 17.0.7 and constraint solver ChocoSolver ver-
sion 4.10.7 (Prud’homme et al., 2017) were utilised.
The DomOverWDeg search strategy, as detailed in
(Boussemart et al., 2004), is the default approach im-
plemented in the ChocoSolver. This search strategy
was chosen based on its effectiveness and is widely
recognised within the academic field.
All 12 approaches previously introduced
{Boolean, AllDifferent, Circuit} × {default,
greedy, cluster, greedy and cluster} were executed
with random generated identical cost matrices, each
with 10 runs for 10, 30, 50, 100, 500, and 1000 cities.
In Table 1, the results of the various test runs are
presented. For each approach, it is indicated how
many times the best solution (not of the problem but
of the 4 identical models, #Best) was found in the 60
experiments. Note that the developed approaches still
seek a global solution; however, due to the imposed
time limit (5 minutes), global solutions may not
always be found or confirmed. The table shows fur-
thermore, the number of times no solution could be
found (#NoSol), in how many cases the solution was
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1176

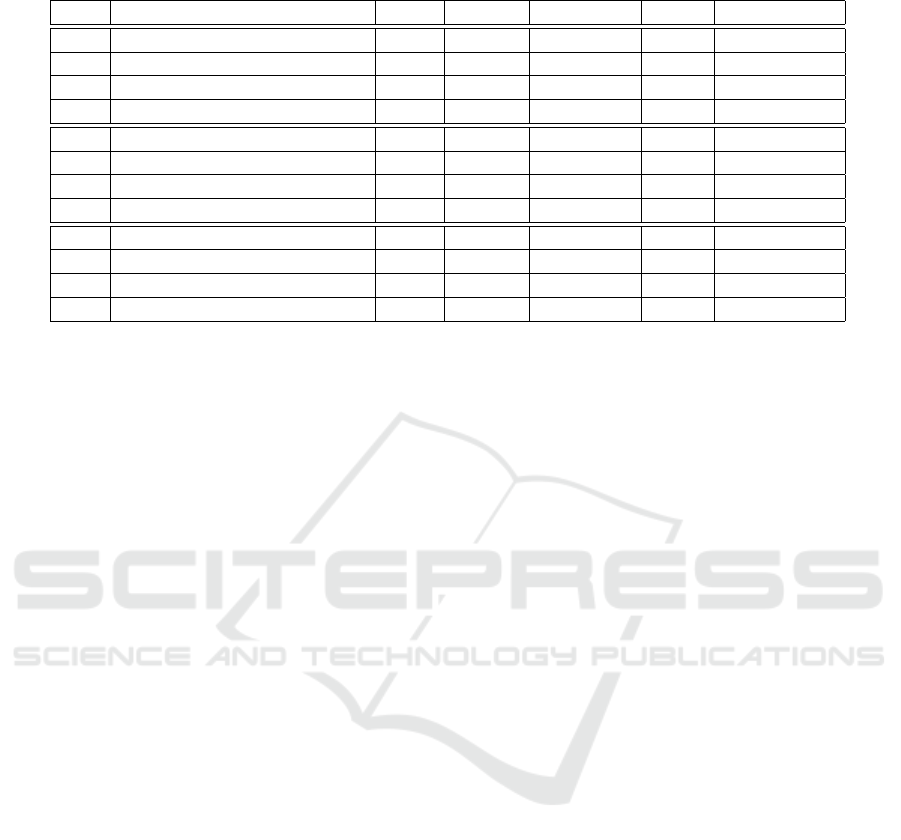
Table 1: Results of 60 TSP runs (10 times each for 10, 30, 50, 100, 500, and 1000 cities, g = greedy COP, c = cluster COP).
Line Apporach #Best #NoSol #Complete ∅x
t
Improvement
1 Boolean-based COP 10 0 10 58444 -
2 Boolean-based COP (g) 56 0 10 4137 96.66
3 Boolean-based COP (c) 10 0 18 57462 1.78
4 Boolean-based COP (g, c) 37 9 18 5597 1.84
5 AllDifferent-based COP 10 20 10 8227 -
6 AllDifferent-based COP (g) 50 0 10 4059 18.79
7 AllDifferent-based COP (c) 10 15 18 7933 1.65
8 AllDifferent-based COP (g, c) 43 1 18 4271 8.72
9 Circuit-based COP 15 0 12 5361 -
10 Circuit-based COP (g) 56 0 13 3977 6.85
11 Circuit-based COP (c) 15 4 20 5933 0.65
12 Circuit-based COP (g, c) 34 2 19 5933 1.43
complete (#Complete), the average solution value
(∅x
t
), and the improvement factor (Improvement)
were compared to the respective original approach.
The improvement factor describes how much less
time was needed to find an equally good or better
solution. In all runs, a time limit of 5 minutes was
taken into account. If the original approach did not
find a solution within this time limit, only 5 minutes
were considered for the improvement factor. This
results in the actual improvement being even higher.
Consider Table 1 it can be observed that the orig-
inal COPs significantly differ in their average best-
found solution (∅x
t
). The Boolean-based COP is
much worse with an average optimization value of
58444 (line 1) compared to the other two. The
AllDifferent-based COP has an average value of 8227
(line 5), and the circuit-based one has an average
value of 5361 (line 9). It should be noted that the
AllDifferent COP most frequently does not find a so-
lution (#NoSol = 20, line 5). These cases are not con-
sidered in the average calculation, so the real average
value would be significantly worse.
It can be seen that the greedy approaches consis-
tently perform the best (lines 2, 6, and 10). They
always find the relatively best solutions (compared
to the other 3 approaches of the same COP, #Best),
they always find a solution (#NoSol = 0), they al-
ways achieve the best average value for the optimiza-
tion variable (∅x
t
), and they have the largest improve-
ment factor (Improvement). Only in the number of
completely solved problems (best solution of the TSP
was found and confirmed, #Complete) they perform
worse than the cluster-based approaches (lines 3, 7,
and 11). The cluster-based COPs could be completely
searched most frequently, thus finding an optimal so-
lution for the corresponding TSP. This is because, af-
ter finding a good solution, the clusters help by the
exclusion of areas of the search space that only lead
to a worse solution. Therefore, the entire search space
can be explored more quickly for the best solution.
Hence, we had the hope that a combined approach
of greedy and cluster would combine the advantages
of both methods and perform even better. Unfortu-
nately, this idea could not be confirmed. The likely
cause for this is that the two methods sometimes hin-
der each other and lead to more backtracks than they
individually require.
6 CONCLUSION AND FUTURE
WORK
We have demonstrated how greedy search and cluster-
ing can be used in COPs and what impact they have
on the solution speed of COPs. For this, we used the
well-known Traveling Salesman Problem (TSP) as a
test application. Three different COP models of the
TSP were considered, and for each of the three mod-
els, an unchanged version, a greedy, a cluster-based,
and a greedy cluster-based variant were implemented.
For the cluster-based variant, a simple custom clus-
tering algorithm was used, which can be replaced in
the future with better clustering algorithms. It was
observed that the greedy approach always led to ac-
celeration, and the cluster-based approach resulted in
more frequent complete searches. The described pro-
cedures enhance the well-known branch and bound
approach in a way that the initial solution can typi-
cally be found more quickly and additionally exhibits
better quality. The approach remains global and, thus
with sufficient computational time, achieves a global
solution.
An attempt was made to combine the two ap-
proaches to leverage their advantages. However, the
current combination tends to exhibit the behavior of
Enhancing Constraint Optimization Problems with Greedy Search and Clustering: A Focus on the Traveling Salesman Problem
1177

the cluster-based approaches, which can solve simple
problems completely (global optimum) but requires
more time for larger problems to find an equivalent
solution to the greedy approach.
Future work includes improving the interaction
between the greedy approach and cluster methods so
that their respective advantages can be combined. The
effectiveness of cluster-based approaches, of course,
also depends on the number and size of clusters in
individual problems. Initial investigations into when
cluster approaches are particularly promising have
been made, but further research is needed in the fu-
ture. Additional goals include integrating further op-
timizations for the TSP and transferring elements of
local search into the COPs. Furthermore, the greedy
and local approaches should naturally be extended to
address other problems such as Warehouse Location
Problems, Transshipment Problems, or Vehicle Rout-
ing Problems.
REFERENCES
Abualigah, L. M. (2019). Feature Selection and Enhanced
Krill Herd Algorithm for Text Document Clustering,
volume 816 of Studies in Computational Intelligence.
Springer.
Abualigah, L. M., Khader, A. T., and Hanandeh, E. S.
(2018). A new feature selection method to improve the
document clustering using particle swarm optimiza-
tion algorithm. J. Comput. Sci., 25:456–466.
Aggarwal, C. C. (2021). Artificial Intelligence - A Textbook.
Springer.
Apt, K. (2003). Constraint satisfaction problems: exam-
ples. Cambridge University Press. Principles of Con-
straint Programming: chapter 2.
Bernardino, R. and Paias, A. (2021). Heuristic approaches
for the family traveling salesman problem. Int. Trans.
Oper. Res., 28(1):262–295.
Boussemart, F., Hemery, F., Lecoutre, C., and Sais, L.
(2004). Boosting systematic search by weighting con-
straints. In Proceedings of the 16th Eureopean Con-
ference on Artificial Intelligence, ECAI’2004, includ-
ing Prestigious Applicants of Intelligent Systems, PAIS
2004, Valencia, Spain, August 22-27, 2004, pages
146–150.
Chang, D., Zhang, X., Zheng, C., and Zhang, D. (2010). A
robust dynamic niching genetic algorithm with niche
migration for automatic clustering problem. Pattern
Recognit., 43(4):1346–1360.
Cheikhrouhou, O. and Khoufi, I. (2021). A comprehensive
survey on the multiple traveling salesman problem:
Applications, approaches and taxonomy. Comput. Sci.
Rev., 40:100369.
Dechter, R. (2003). Constraint networks. pages 25–49.
Elsevier Morgan Kaufmann. Constraint processing:
chapter 2.
Demassey, S. and Beldiceanu, N. (2022). Global Constraint
Catalog. http://sofdem.github.io/gccat/. last visited
2022-07-14.
Garc
´
ıa, A. J. and G
´
omez-Flores, W. (2023). CVIK: A
matlab-based cluster validity index toolbox for auto-
matic data clustering. SoftwareX, 22:101359.
Jain, A. K. (2010). Data clustering: 50 years beyond k-
means. Pattern Recognit. Lett., 31(8):651–666.
Kruskal, J. B. (1956). On the Shortest Spanning Subtree
of a Graph and the Traveling Salesman Problem. In
Proceedings of the American Mathematical Society, 7.
Liu, Y., Wu, X., and Shen, Y. (2011). Automatic cluster-
ing using genetic algorithms. Appl. Math. Comput.,
218(4):1267–1279.
L
´
opez-Ortiz, A., Quimper, C., Tromp, J., and van Beek,
P. (2003). A fast and simple algorithm for bounds
consistency of the alldifferent constraint. In IJCAI-
03, Proceedings of the Eighteenth International Joint
Conference on Artificial Intelligence, Acapulco, Mex-
ico, August 9-15, 2003, pages 245–250.
Marriott, K. and Stuckey, P. J. (1998). Programming with
Constraints - An Introduction. MIT Press, Cambridge.
Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960). In-
teger programming formulation of traveling salesman
problems. J. ACM, 7(4):326–329.
Pintea, C. (2015). A unifying survey of agent-based ap-
proaches for equality-generalized traveling salesman
problem. Informatica, 26(3):509–522.
Prud’homme, C., Fages, J.-G., and Lorca, X. (2017). Choco
documentation.
Ran, X., Xi, Y., Lu, Y., Wang, X., and Lu, Z. (2023).
Comprehensive survey on hierarchical clustering al-
gorithms and the recent developments. Artif. Intell.
Rev., 56(8):8219–8264.
Roberti, R. and Ruthmair, M. (2021). Exact methods for the
traveling salesman problem with drone. Transp. Sci.,
55(2):315–335.
Russell, S. and Norvig, P. (2010). Artificial Intelligence: A
Modern Approach. Prentice Hall, 3 edition.
Sch
¨
utz, L., Bade, K., and N
¨
urnberger, A. (2023). Com-
prehensive differentiation of partitional clusterings.
In Filipe, J., Smialek, M., Brodsky, A., and Ham-
moudi, S., editors, Proceedings of the 25th Interna-
tional Conference on Enterprise Information Systems,
ICEIS 2023, Volume 2, Prague, Czech Republic, April
24-26, 2023, pages 243–255. SCITEPRESS.
Van Hoeve, W.-J. (2001). The alldifferent constraint: A sur-
vey. In Sixth Annual Workshop of the ERCIM Working
Group on Constraints. Prague.
van Hoeve, W.-J. and Katriel, I. (2006). Global Constraints.
Elsevier, Amsterdam, First edition. Chapter 6.
Zhou, Y., Wu, H., Luo, Q., and Abdel-Baset, M. (2019).
Automatic data clustering using nature-inspired sym-
biotic organism search algorithm. Knowl. Based Syst.,
163:546–557.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1178